Stability and Delay Analysis of an Adaptive Channel-Aware Random Access Wireless Network

Abstract

In this work, we consider an asymmetric two-user random access wireless network with interacting nodes, time-varying links and multipacket reception capabilities. The users are equipped with infinite capacity buffers where they store arriving packets that will be transmitted to a destination node. Moreover, each user employs a general transmission control protocol under which, it adapts its transmission probability based both on the state of the other user, and on the channel state information according to a Gilbert-Elliot model. We study a two-dimensional discrete time Markov chain, investigate its stability condition, and show that its steady state performance is expressed in terms of a solution of a Riemann-Hilbert boundary value problem. Moreover, for the symmetrical system, we provide closed form expressions for the average delay at each user node. Numerical results are obtained and show insights in the system performance.

1 Introduction

Random access has re-gained attention recently because of the need for massive uncoordinated access in large networks which will be common in the fifth generation of mobile networks (5G) era [1, 4, 28] (not an exhaustive list). Thus, the study of random access in large networks is of major importance [4]. However, there are still many unanswered fundamental questions regarding the performance of random access even in small networks [14, 18].

When the traffic in a network is bursty, a meaningful performance measure is the stable throughput region i.e. the stability region, which gives the set of arrival rates such that there exist transmission probabilities under which the system is stable [24, 32, 34]. Characterizing the stability region in random access networks is a well known difficult problem because of the interaction of the queues. The stability region is a throughput metric with bounded delay guarantees, but in most of the works appeared in the past, stability and delay were studied in isolation. The stability region of a two-user random access network with traditional collision channel has been studied in [32, 34, 35]. A more detailed treatment of stable throughput for various cases can be found in [22]. In [21], the stability region of a cognitive radio system of two source-destination pairs in the presence of imperfect sensing was studied. For a three-user random access network with collision channel model the stability region was obtained in [34], while for the case of more than three users the exact stability region is not known yet except for some derived bounds given in [24].

Although stable throughput region in random access systems has been studied for several cases, the delay performance is so far overlooked in the research. 5G was proposed aiming to enhance the networking capabilities of mobile users [1, 28]. Differentiated from 4G, benefits offered by 5G will be much more than the increased maximum throughput [1]. Thus, the rapid growth on supporting real-time applications requires delay-based guarantees. However, the characterization of delay even in small networks with random access is rather difficult, even for the traditional collision model [26]. Although the traditional collision channel model is suitable for wire-line communications, it is not an appropriate model for probabilistic reception in wireless multiple access scenarios. Moreover, most of the related works are based on the strong assumption of the absolute symmetry of the network; e.g., [15, 27, 33]. More importantly they did not take into account the impact of time-varying links, e.g., [27, 33], as well as the ability of a node to adapt its transmission probability based on the knowledge of the status of neighbor nodes, which in turn, leads to self-aware networks. Note that this feature is very common in cognitive radios [5, 6, 21, 25].

Contribution. In this work, we study an asymmetric two-user random access wireless network where the user’s transmission probability is adapted based both on the status of the other user, and on the channel state. We model the state of the wireless channels as a Gilbert-Elliot model that changes between a “good” and a “bad” state. Our motivation stems from the fact that the channel conditions may vary, and thus, the success probability of a packet transmission is affected. Moreover, we take account advances in multiuser detection, which allow the receiver to employ multipacket reception (MPR) capabilities, and to correctly receive at most one user packet, even if many users transmit (i.e., the “capture” effect).

We analyze a system of two queues, we investigate the stable throughput, and the queueing delay. Finally, we evaluate numerically the derived analytical results. Our system is modeled as a two-dimensional discrete time Markov chain, and we show that its steady-state performance is expressed in terms of the solution of a Riemann-Hilbert problem [19]. For related works on queueing systems using the theory of boundary value problems see e.g. [2, 3, 8,9,10,11,12,13, 16, 17, 26, 31, 36]. To the best of our knowledge there is no other work in the related literature in which exact expressions for the stability conditions of a random access system where a user adapts its transmission probability based on its “knowledge” about both the status of the other, and of the channel state. In such a case, we take into account the wireless interference as well as the complex interdependence among users’ nodes due to the shared medium. Clearly, such a protocol leads to substantial performance gains, since each user exploits the idle slots of the other. More importantly, besides its applicability, our work is also theoretically oriented, since we provide, for the first time, an exact detailed analysis of an asymmetric adapted random access wireless system with MPR capabilities, and obtain the generating function of the stationary joint queue length distribution with the aid of the theory of boundary value problems.

The rest of the paper is organized as follows. In Sect. 2 we describe the model in detail, and derive the fundamental functional equation. In Sect. 3 we obtain some important results for the following analysis, and investigate the stability conditions. Section 4 is devoted to the formulation and solution of two boundary value problems, the solution of which provides the generating function of the joint queue length distribution of user nodes. In Sect. 5 we obtain explicit expressions for the average delay at each user for the symmetrical system. Finally, in Sect. 6 we obtain useful numerical examples that show insights in the system performance.

2 Model Description and the Functional Equation

We consider an asymmetric random access system consisting of $N=2$ users communicating with a common receiver. Each user has an infinite capacity buffer, in which stores arriving and backlogged packets. Packets have equal length and the time is divided into slots corresponding to the transmission time of a packet. At the beginning of each slot, there is an opportunity for the user node k, $k=1,2,$ to transmit a packet to the receiver.

The channel of a particular link is independent between users, and varies between slots according to a Gilbert-Elliott model, where it can be in one of two states at any given time slot: the good state, denoted by “G” and the bad state, denoted by “B”. The channel state is assumed to be fixed during a slot duration and varies in an independent and identically distributed (i.i.d.) manner between slots¹. The long term proportion of time in which user k’s channel is in state i is denoted by $s_{i}^{(k)}$, $i\in \{B,G\}$, $k\in \{1,2\}$; and can be obtained either through channel measurements or through a physical model of the channels.

Users have perfect channel knowledge and adjust their transmission probabilities (transmission control) according to the channel state. Due to the interference among the stations we consider the following opportunistic policy: If both stations are non empty, station k, $k=1,2,$ transmits a packet according to a Bernoulli stream with probability $q_{ik}$ independently, $\bar{q}_{ik}$ is the probability that station k does not make a transmission in a slot, given that his channel is in state $i\in \{B,G\}$. If station 1 (resp. 2) is the only non-empty, it changes its transmission probability to $q_{ik}^{*}$ independently², $\bar{q}_{ik}^{*}=1-q_{ik}^{*}$ is the probability that station k does not make a transmission in the given slot. Note that in our case, a node is aware of the state of the other node. This is a common assumption in the literature related to cognitive wireless networks [5, 6, 22, 25].

The success of a transmission depends on the underlying channel model. The MPR channel model used in this paper is a generalized form of the packet erasure model. In particular we focus on a subclass of MPR model, the “capture” channels [7, 23, 37]. In such a case, at most one packet can be successfully received at the destination if more than one nodes transmit. A common assumption in wireless networks is that a packet can be decoded correctly by the receiver if the received SINR (Signal-to-Interference-plus-Noise-Ratio) exceeds a certain threshold. The set of transmitting nodes in a given timeslot is denoted by T. Let $f_{ik/T}$ the probability that a packet transmitted from node k with channel state i is successfully decoded at the destination, i.e., $f_{ik/T}=Pr(\gamma _{ik/T}>\theta )$, where $\gamma _{ik/T}$ denotes the SINR of the signal transmitted from node i with channel state k at the receiver given the channel states of the transmitters and the threshold for the successful decoding $\theta$, which depends on the modulation scheme, target bit error rate and the number of bits in the packet. Without loss of generality we assume that when the channel state is “bad” and transmission fails with probability 1,³ i.e., $f_{B,k/T}=0$, $k=1,2$. Furthermore, let $\tilde{f}_{i,k/\{i,k\}}$ be the success probability of node k when it is the only non empty ($\tilde{f}_{B,k/\{B,k\}}=0$, $k=1,2$). We consider the following success probabilities for nodes 1 and 2

$$\begin{aligned} \begin{array}{c} \tilde{f}_{G,1/\{G,1\}}>f_{G,1/\{G,1\}}>f_{G,1/\{G,1;B,2\}}>f_{G,1/\{G,1;G,2\}},\\ \tilde{f}_{G,2/\{G,2\}}>f_{G,2/\{G,2\}}>f_{G,2/\{B,1;G,2\}}>f_{G,2/\{G,1;G,2\}}. \end{array} \end{aligned}$$

Note that the success probability when a packet is transmitted in the presence of interference cannot exceed the success probability when it is transmitted alone. Let also denote by $f_{0/\{G,1;G,2\}}=1-f_{G,1/\{G,1;G,2\}}-f_{G,2/\{G,1;G,2\}}$, $f_{0/\{G,k\}}=1-f_{G,k/\{G,k\}}$, $\tilde{f}_{0/\{G,k\}}=1-\tilde{f}_{G,k/\{G,k\}}$, the probabilities that no packets will be successfully transmitted.

In case of unsuccessful transmissions the packets have to be re-transmitted in a later slot. We assume that the receiver gives an instantaneous (error-free) feedback of all the packets that were successful in a slot at the end of the slot to all the nodes. The nodes remove the successfully transmitted packets from their buffers while unsuccessful packets are retained.

Let $\{A_{k,n}\}_{n\in \mathbf {N}}$ be a sequence of i.i.d. random variables where $A_{k,n}$ represents the number of packets which arrive at buffer k in the interval $(n,n+1]$, with $E(A_{k,n})=\widehat{\lambda }_{k}<\infty$. Denote by $D(x,y)=\lim _{n\rightarrow \infty }E(x^{A_{1,n}}y^{A_{2,n}})$, $|x|\le 1$, $|y|\le 1$, the generating function of the stationary joint distribution of the number of arriving packets in any slot. In this work we assume that the arrival processes at both user nodes are independent and geometrically distributed, i.e.,

$$\begin{aligned} \begin{array}{c} D(x,y)=[(1+\widehat{\lambda }_{1}(1-x))(1+\widehat{\lambda }_{2}(1-y))]^{-1}. \end{array} \end{aligned}$$

Denote by $N_{k,n}$ the number of packets at user node k at the beginning of the n-th slot. Then, $Y_{n}=(N_{1,n},N_{2,n})$ is a discrete time Markov chain with state space $E=\{(i,j):i,j=0,1,2,\ldots \}$. The users’ queues evolve as

$$\begin{aligned} \begin{array}{c} N_{k,n+1}=[N_{k,n}-D_{k,n}]^{+}+A_{k,n},\,k=1,2, \end{array} \end{aligned}$$

(1)

where $D_{k,n}$ is the number of departures from user k queue at time slot n. Let H(x, y) be the generating function of the joint stationary queue process, viz.

$$\begin{aligned} \begin{array}{c} H(x,y)=\lim _{n\rightarrow \infty }E(x^{N_{1,n}}y^{N_{2,n}}),\,|x|\le 1,\,|y|\le 1. \end{array} \end{aligned}$$

Then, by exploiting (1) (see Appendix A), we obtain after lengthy calculations,

$$\begin{aligned} \begin{array}{c} R(x,y)H(x,y)=A(x,y)H(x,0)+B(x,y)H(0,y)+C(x,y)H(0,0), \end{array} \end{aligned}$$

(2)

where,

$$\begin{aligned} \begin{array}{rl} R(x,y)=&{}D^{-1}(x,y)+s_{G}^{(1)}q_{G1}\widehat{q}_{12}(1-\frac{1}{x})+s_{G}^{(2)}q_{G2}\widehat{q}_{21}(1-\frac{1}{y}),\\ A(x,y)=&{}s_{G}^{(2)}q_{G2}\widehat{q}_{21}(1-\frac{1}{y})+d_{1,2}(1-\frac{1}{x}),\\ B(x,y)=&{}s_{G}^{(1)}q_{G1}\widehat{q}_{12}(1-\frac{1}{x})+d_{2,1}(1-\frac{1}{y}),\\ C(x,y)=&{}d_{2,1}(\frac{1}{y}-1)+d_{1,2}(\frac{1}{x}-1), \end{array} \end{aligned}$$

and,

$$\begin{aligned} \begin{array}{rl} \widehat{q}_{km}=&{}(s_{G}^{(m)}\bar{q}_{Gm}+s_{B}^{(m)}\bar{q}_{Bm})f_{G,k/G,k}+s_{B}^{(m)}q_{Bm}f_{G,k/\{G,k;B,m\}}\\ &{}+s_{G}^{(m)}q_{Gm}f_{G,k/\{G,k;G,m\}},\,k,m\in \{1,2\},\,k\ne m,\\ d_{k,m}=&{}s_{G}^{(k)}q_{Gk}\widehat{q}_{km}-s_{G}^{(k)}q_{Gk}^{*}\tilde{f}_{G,k/G,k},\,k,m\in \{1,2\},\,k\ne m. \end{array} \end{aligned}$$

Some interesting relations can be obtained directly from the functional Eq. (2). Taking $y = 1$, dividing by $x-1$ and taking $x\rightarrow 1$ in (2), and vice versa, yield the following “conservation of flow” relations:

$$\begin{aligned} \begin{array}{rl} \widehat{\lambda }_{1}=&{}s_{G}^{(1)}q_{G1}\widehat{q}_{12}(1-H(0,1))-d_{1,2}(H(1,0)-H(0,0)),\\ \widehat{\lambda }_{2}=&{}s_{G}^{(2)}q_{G2}\widehat{q}_{21}(1-H(1,0))-d_{2,1}(H(0,1)-H(0,0)). \end{array} \end{aligned}$$

(3)

Using (3), we distinguish the analysis in two cases, which differ both from the modeling and the technical point of view:

• 1. For $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}=1$, Eq. (3) yields

  $$\begin{aligned} \begin{array}{c} H(0,0)=1-\left( \frac{\widehat{\lambda }_{1}}{s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/G,2}}\right) =1-\rho . \end{array} \end{aligned}$$

• 2. For $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ne 1$, Eq. (3) yields

  $$\begin{aligned} \begin{array}{rl} H(1,0)=&{}\frac{d_{2,1}\widehat{\lambda }_{1}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}(s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G2/\{G2\}}-\widehat{\lambda }_{2})+d_{2,1}s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}H(0,0)}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}-d_{1,2}d_{2,1}},\\ H(0,1)=&{}\frac{d_{1,2}\widehat{\lambda }_{2}+s_{G}^{(2)}q_{G2}\widehat{q}_{21}(s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G1/\{G1\}}-\widehat{\lambda }_{1})+d_{1,2}s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}H(0,0)}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}-d_{1,2}d_{2,1}}. \end{array} \end{aligned}$$

  (4)

3 Preparatory Analysis

We now focus on the derivation of some preparatory results in view of the resolution of the functional Eq. (2). We first investigate the stability criteria, and then, we focus on the analysis of the kernel equation $R(x,y)=0$.

3.1 Stability Region

Based on the concept of stochastic dominant systems [32, 34], we derive the stability region, i.e., the set of vectors $(\widehat{\lambda }_{1},\widehat{\lambda }_{2})$, for which our system is stable.

Lemma 1

The stability region $\mathcal {R}$ for a fixed transmission probability vector $\mathbf {q}:=[q_{G1},q_{G2},q_{G1}^{*},q_{G2}^{*}]$ is given by

• 1. In case $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ne 1$, $\mathcal {R}=\mathcal {R}_{1}\cup \mathcal {R}_{2}$ where,

  $$\begin{aligned} \begin{array}{c} \mathcal {R}_{1}=\{(\widehat{\lambda }_{1},\widehat{\lambda }_{2}):\widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}+d_{1,2}\frac{\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}},\,\widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}\widehat{q}_{21}\},\\ \mathcal {R}_{2}=\{(\widehat{\lambda }_{1},\widehat{\lambda }_{2}):\widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}+d_{2,1}\frac{\widehat{\lambda }_{1}}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}},\,\widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}\widehat{q}_{12}\}. \end{array} \end{aligned}$$

• 2. In case $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}=1$, $\mathcal {R}=\{(\widehat{\lambda }_{1},\widehat{\lambda }_{2}):\,\rho <1\}$.

Proof:

In order to determine the stability region, we apply the stochastic dominance technique developed in [32, 34], which consists of considering hypothetical auxiliary systems that closely parallel the operation of the original system but dominate it in a well defined manner. Under this approach, we consider the $R_{1}$, and $R_{2}$ dominant systems. In the $R_{k}$ dominant system, whenever the queue of user node k, $k=1,2$ empties, it continues to transmit “dummy” packets.

The dominant system has the following properties [32]: (i) the queue lengths in the dominant system are no shorter than the queues in the original system. Thus, if the queues in the dominant system are stable, then, the queues in the original system are stable as well, (ii) the two systems coincide at saturation, that is, if the queue of user 1 never empties (that is, if it is saturated or unstable), then the dominant system, and the original system are indistinguishable; and thus, the instability of the dominant system implies the instability of the original system. Clearly, (i) and (ii) imply that the stability condition of the dominant system is a necessary and sufficient for the stability of the original system and hence, the stable throughput regions of both systems coincide for fixed transmission probabilities.

Thus, in $R_{1}$, user node 1 never empties, and its service rate depends on whether user node 2 is empty or not. On the other hand, user node 2 “sees” a constant service rate. Therefore, in the $R_{1}$ dominant system, $\widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}\widehat{q}_{21}$. Moreover, the stability condition for the user node 1 is given by,

$$\begin{aligned} \begin{array}{c} \widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}\left( 1-\frac{\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}\right) +s_{G}^{(1)}q_{G1}\widehat{q}_{12}\frac{\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}. \end{array} \end{aligned}$$

Thus, the sufficient condition for the ergodicity of the $R_{1}$ dominant system is,

$$\begin{aligned} \begin{array}{c} \widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}+\frac{d_{1,2}\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}},\,\,and\,\,\widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}\widehat{q}_{21}. \end{array} \end{aligned}$$

(5)

Similarly, the sufficient ergodicity condition of the $R_{2}$ system is given by,

$$\begin{aligned} \begin{array}{c} \widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}\widehat{q}_{12},\,\,and\,\, \widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}+\frac{d_{2,1}\widehat{\lambda }_{1}}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}. \end{array} \end{aligned}$$

(6)

Combining the sufficient conditions for both the dominant systems (i.e., (5), (6)) yields the sufficiency part of the lemma. The necessary part of the lemma follows by an “indistinguishability” argument similar to the one used in [32].    $\square$

Remark:

$\mathcal {R}$ is a convex polyhedron when $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ge 1$. When equality holds, the region is a triangle and coincides with the case of time-sharing. Convexity is an important property since it corresponds to the case when parallel concurrent transmissions are preferable to time-sharing.

3.2 Analysis of the Kernel

We now provide some detailed properties of the kernel R(x, y), which are important for the formulation and solution of the boundary value problems. Clearly,

$$\begin{aligned} R(x,y)=a(x)y^{2}+b(x)y+c(x)=\widehat{a}(y)x^{2}+\widehat{b}(y)x+\widehat{c}(y), \end{aligned}$$

where, $a(x)=\widehat{\lambda }_{2}x(\widehat{\lambda }_{1}(x-1)-1)$, $c(x)=-s_{G}^{(2)}q_{G2}\widehat{q}_{21}x$, $b(x)=x(\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}+s_{G}^{(2)}q_{G2}\widehat{q}_{21})-s_{G}^{(1)}q_{G1}\widehat{q}_{12}-\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2})x^{2}$, $\widehat{a}(y)=\widehat{\lambda }_{1}y(\widehat{\lambda }_{2}(y-1)-1)$, $\widehat{c}(y)=-s_{G}^{(1)}q_{G1}\widehat{q}_{12}y$, $\widehat{b}(y)=y(\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}+s_{G}^{(2)}q_{G2}\widehat{q}_{21})-s_{G}^{(2)}q_{G2}\widehat{q}_{21}-\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1})y^{2}$. The roots of $R(x,y)=0$ are $X_{\pm }(y)=\frac{-\widehat{b}(y)\pm \sqrt{D_{y}(y)}}{2\widehat{a}(y)}$, $Y_{\pm }(x)=\frac{-b(x)\pm \sqrt{D_{x}(x)}}{2a(x)}$, where $D_{y}(y)=\widehat{b}(y)^{2}-4\widehat{a}(y)\widehat{c}(y)$, $D_{x}(x)=b(x)^{2}-4a(x)c(x)$.

Lemma 2

For $|y|=1$, $y\ne 1$, the kernel equation $R(x,y)=0$ has exactly one root $x=X_{0}(y)$ such that $|X_{0}(y)|<1$. For $\widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}\widehat{q}_{12}$, $X_{0}(1)=1$. Similarly, we can prove that $R(x,y)=0$ has exactly one root $y=Y_{0}(x)$, such that $|Y_{0}(x)|\le 1$, for $|x|=1$.

Proof:

It is easily seen that $R(x,y)=\frac{xy-\varPsi (x,y)}{xyD(x,y)}$, where $\varPsi (x,y)=D(x,y)[xy-y(x-1)s_{G}^{(1)}q_{G1}\widehat{q}_{12}-x(y-1)s_{G}^{(2)}q_{G2}\widehat{q}_{21}]$, where for $|x|\le 1$, $|y|\le 1$, $\varPsi (x,y)$ is a generating function of a proper probability distribution. Now, for $|y|=1$, $y\ne 1$ and $|x|=1$ it is clear that $|\varPsi (x,y)|<1=|xy|$. Thus, from Rouché’s theorem, $xy-\varPsi (x,y)$ has exactly one zero inside the unit circle. Therefore, $R(x,y)=0$ has exactly one root $x=X_{0}(y)$, such that $|x|<1$. For $y=1$, $R(x,1)=0$ implies $(x-1)[\widehat{\lambda }_{1}-\frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{x}]=0$. Therefore, for $y=1$, and since $\widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}\widehat{q}_{12}$, the only root of $R(x,1)=0$ for $|x|\le 1$, is $x=1$.   $\square$

Lemma 3

The algebraic function Y(x), defined by $R(x,Y(x)) = 0$, has four real branch points $0< x_{1}<x_{2}\le 1<x_{3}<x_{4}<\frac{1+\widehat{\lambda }_{1}}{\widehat{\lambda }_{1}}$. Moreover, $D_{x}(x)<0$, $x\in (x_{1},x_{2})\cup (x_{3},x_{4})$ and $D_{x}(x)>0$, $x\in (-\infty ,x_{1})\cup (x_{2},x_{3})\cup (x_{4},\infty )$. Similarly, X(y), defined by $R(X(y),y) = 0$, has four real branch points $0\le y_{1}<y_{2}\le 1<y_{3}<y_{4}<\frac{1+\widehat{\lambda }_{2}}{\widehat{\lambda }_{2}}$, and $D_{x}(y)<0$, $y\in (y_{1},y_{2})\cup (y_{3},y_{4})<$ and $D_{x}(y)>0$, $y\in (-\infty ,y_{1})\cup (y_{2},y_{3})\cup (y_{4},\infty )$.

Proof:

The proof is based on simple algebraic arguments; see also [13].   $\square$

Consider now the cut planes: , , where $C_{x}$, $C_{y}$ the complex planes of x, y, respectively. In (resp. ), let $Y_{0}(x)$ (resp. $X_{0}(y)$) be the zero of $R(x,Y(x))=0$ (resp. $R(X(y),y)=0$) with the smallest modulus.

Lemma 4

• 1. For $y\in [y_{1},y_{2}]$, the algebraic function X(y) lies on a closed contour $\mathcal {M}$, which is symmetric with respect to the real line and defined by

  $$\begin{aligned} \begin{array}{l} |x|^{2}=m(Re(x)),\,m(\delta )=\frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}\zeta (\delta ))},\,|x|^{2}\le \frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}y_{2})}, \end{array} \end{aligned}$$

  where, $k(\delta ):=\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}+s_{G}^{(2)}q_{G2}\widehat{q}_{21}-2\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2})\delta$ and, $\zeta (\delta )=\frac{k(\delta )-\sqrt{k^{2}(\delta )-4s_{G}^{(2)}q_{G2}\widehat{q}_{21}\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}(1-2\delta ))}}{2\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}(1-2\delta ))}$.

  Set $\beta _{0}:=\sqrt{\frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}y_{2})}}$, $\beta _{1}:=-\sqrt{\frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}y_{1})}}$ the extreme right and left point of $\mathcal {M}$, respectively.

• 2. For $x\in [x_{1},x_{2}]$, the algebraic function Y(x) lies on a closed contour $\mathcal {L}$, which is symmetric with respect to the real line and defined by

  $$\begin{aligned} \begin{array}{l} |y|^{2}=v(Re(y)),\,v(\delta )=\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}{\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}-\widehat{\lambda }_{1}\theta (\delta ))},\,|y|^{2}\le \frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}{\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}-\widehat{\lambda }_{1}x_{2})}, \end{array} \end{aligned}$$

  where $l(\delta ):=\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}+s_{G}^{(2)}q_{G2}\widehat{q}_{21}-2\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1})\delta$, and $\theta (\delta )=\frac{l(\delta )-\sqrt{l^{2}(\delta )-4s_{G}^{(1)}q_{G1}\widehat{q}_{12}\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}(1-2\delta ))}}{2\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}(1-2\delta ))}$.

  Set $\eta _{0}:=\sqrt{\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}{\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}-\widehat{\lambda }_{1}x_{2})}}$, $\eta _{1}:=-\sqrt{\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}{\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1}-\widehat{\lambda }_{1}x_{1})}}$ the extreme right and left point of $\mathcal {L}$, respectively.

Proof:

We only focus on the first part. For $y\in [y_{1},y_{2}]$, $D_{y}(y)<0$, so $X_{\pm }(y)$ are complex conjugates. Thus, $|X(y)|^{2}=\frac{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{\widehat{\lambda }_{1}(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}y)}=g(y)$. It also follows that

$$\begin{aligned} \begin{array}{l} Re(X(y))=\frac{y(\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}+s_{G}^{(2)}q_{G2}\widehat{q}_{21})-s_{G}^{(2)}q_{G2}\widehat{q}_{21}-\widehat{\lambda }_{2}(1+\widehat{\lambda }_{1})y^{2}}{2\widehat{\lambda }_{1}y(1+\widehat{\lambda }_{2}-\widehat{\lambda }_{2}y)}. \end{array} \end{aligned}$$

(7)

Clearly, g(y) is an increasing function for $y\in [0,1]$ and thus, $|X(y)|^{2}\le g(y_{2})=\beta _{0}$. Using simple algebraic considerations we can prove that, $X_{0}(y_{1})=\beta _{1}$ is the extreme left point of $\mathcal {M}$. Finally, $\zeta (\delta )$ is derived by solving (7) for y with $\delta = Re(X(y))$, and taking the solution such that $y\in [0,1]$.   $\square$

4 The Boundary Value Problems

In the following, we distinguish the analysis in two cases, which differ from both the modeling and the technical point of view.

4.1 A Dirichlet Boundary Value Problem

Assume that $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}=1$. Then, $A(x,y)=\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}{d_{2,1}}B(x,y)$. Therefore, for $y\in \mathcal {D}_{y}=\{y\in C_{y}:|y|\le 1,|X_{0}(y)|\le 1\}$,

$$\begin{aligned} \begin{array}{l} s_{G}^{(2)}q_{G2}\widehat{q}_{21}H(X_{0}(y),0)+d_{2,1}H(0,y)+\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}C(X_{0}(y),y)}{A(X_{0}(y),y)}(1-\rho )=0. \end{array} \end{aligned}$$

(8)

For $y\in \mathcal {D}_{y}-[y_{1},y_{2}]$ both $H(X_{0}(y),0)$, H(0, y) are analytic and the right-hand side in (8) can be analytically continued up to the slit $[y_1, y_2]$, or equivalently, for $x\in \mathcal {M}$

$$\begin{aligned} \begin{array}{c} s_{G}^{(2)}q_{G2}\widehat{q}_{21}H(x,0)+d_{2,1}H(0,Y_{0}(x))+\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}C(x,Y_{0}(x))}{A(x,Y_{0}(x))}(1-\rho )=0. \end{array} \end{aligned}$$

(9)

Then, by multiplying both sides of (9) by the imaginary complex number i, and noticing that $H(0,Y_{0}(x))$ is real for $x\in \mathcal {M}$, since $Y_{0}(x)\in [y_{1},y_{2}]$, we have

$$\begin{aligned} \begin{array}{c} Re\left( iH(x,0)\right) =Re\left( -i\frac{C(x,Y_{0}(x))}{A(x,Y_{0}(x))}\right) (1-\rho ),\,x\in \mathcal {M}. \end{array} \end{aligned}$$

(10)

To proceed, we have to check for possible poles of H(x, 0) in $S_{x}:=G_{\mathcal {M}}\cap \bar{D}_{x}^{c}$, where $G_{\mathcal {U}}$ be the interior domain bounded by $\mathcal {U}$, and $D_{x}=\{x:|x|<1\}$, $\bar{D}_{x}=\{x:|x|\le 1\}$, $\bar{D}_{x}^{c}=\{x:|x|>1\}$. These poles, if exist, they coincide with the zeros of $A(x,Y_{0}(x))$ in $S_{x}$ (see Appendix B). In order to solve (10) we must firstly conformally transform the problem from $\mathcal {M}$ to the unit circle $\mathcal {C}$. Let the conformal mapping $z=\gamma (x):G_{\mathcal {M}}\rightarrow G_{\mathcal {C}}$, and its inverse given by $x=\gamma _{0}(z):G_{\mathcal {C}}\rightarrow G_{\mathcal {M}}$. Then, we have the following problem: Find a function $\tilde{T}(z)=H^{(0)}(\gamma _{0}(z))$ regular for $z\in G_\mathcal {C}$, and continuous for $z\in \mathcal {C}\cup G_\mathcal {C}$ such that, $Re(i\tilde{G}(z))=w(\gamma _{0}(z))$, $z\in \mathcal {C}$.

In the following, we need a representation of $\mathcal {M}$ in polar coordinates, i.e., $\mathcal {M}=\{x:x=\rho (\phi )\exp (i\phi ),\phi \in [0,2\pi ]\}$. In the following we summarize the basic steps; see [8]. Since $0\in G_{\mathcal {M}}$, for each $x\in \mathcal {M}$, a relation between its absolute value and its real part is given by $|x|^{2}=m(Re(x))$ (see Lemma 4). Given the angle $\phi$ of some point on $\mathcal {M}$, the real part of this point, say $\delta (\phi )$, is the solution of $\delta -\cos (\phi )\sqrt{m(\delta )}$, $\phi \in [0,2\pi ].$ Since $\mathcal {M}$ is a smooth, egg-shaped contour, the solution is unique. Clearly, $\rho (\phi )=\frac{\delta (\phi )}{\cos (\phi )}$, and the parametrization of $\mathcal {M}$ in polar coordinates is fully specified. Then, the mapping from $z\in G_{\mathcal {C}}$ to $x\in G_{\mathcal {M}}$, where $z = e^{i\phi }$ and $x= \rho (\psi (\phi ))e^{i\psi (\phi )}$, satisfying $\gamma _{0}(0)=0$ and $\gamma _{0}(z)=\overline{\gamma _{0}(\bar{z})}$ is uniquely determined by (see [8]),

$$\begin{aligned} \begin{array}{rl} \gamma _{0}(z)&{}=z\exp [\frac{1}{2\pi }\int _{0}^{2\pi }\log \{\rho (\psi (\omega ))\}\frac{e^{i\omega }+z}{e^{i\omega }-z}d\omega ],\,|z|<1,\\ \psi (\phi )&{}=\phi -\int _{0}^{2\pi }\log \{\rho (\psi (\omega ))\}\cot (\frac{\omega -\phi }{2})d\omega ,\,0\le \phi \le 2\pi , \end{array} \end{aligned}$$

(11)

i.e., the angular deformation $\psi (.)$ is uniquely determined as the solution of Theodorsen integral equation with $\psi (\phi )=2\pi -\psi (2\pi -\phi )$. If H(x, 0) has no poles in $S_{x}$, the solution of the problem defined in (10) is,

$$\begin{aligned} \begin{array}{c} H(x,0)=-\frac{1-\rho }{2\pi }\int _{|t|=1}f(t)\frac{t+\gamma (x)}{t-\gamma (x)}\frac{dt}{t}+S,\,x\in \mathcal {M}, \end{array} \end{aligned}$$

(12)

where $f(t)=Re\left( -i\frac{C(\gamma _{0}(t),Y_{0}(\gamma _{0}(t)))}{A(\gamma _{0}(t),Y_{0}(\gamma _{0}(t)))}\right)$. S is a constant to be defined by setting $x=0\in G_{\mathcal {M}}$ in (12), and using the fact that $H(0,0)=1-\rho$, $\gamma (0)=0$ (In case H(x, 0) has a pole, i.e. $x=\bar{x}$, we have still a Dirichlet problem for the function $(x- \bar{x})H(x,0)$; see Appendix B). Following the discussion above, $S=(1-\rho )(1+\frac{1}{2\pi }\int _{|t|=1}f(t)\frac{dt}{t})$. Setting $t=e^{i\phi }$, $\gamma _{0}(e^{i\phi })=\rho (\psi (\phi ))e^{i\psi (\phi )}$, we arrive after some algebra in,

$$\begin{aligned} \begin{array}{c} f(e^{i\phi })=\frac{d_{1,2}s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,1/\{G,1\}}\sin (\psi (\phi ))(1-Y_{0}(\gamma _{0}(e^{i\phi }))^{-1})}{\rho (\psi (\phi ))\{[s_{G}^{(2)}q_{G2}\widehat{q}_{21}(1-Y_{0}^{-1}(\gamma _{0}(e^{i\phi })))+d_{1,2}(1-\frac{\cos (\psi (\phi ))}{\rho (\psi (\phi ))})]^{2}+(d_{1,2}\frac{\sin (\psi (\phi ))}{\rho (\psi (\phi ))})^{2}\}}, \end{array} \end{aligned}$$

which is an odd function of $\phi$. Thus, $S=1-\rho$. Substituting back in (12):

$$\begin{aligned} \begin{array}{c} H(x,0)=(1-\rho )\lbrace 1+\frac{2\gamma (x)i}{\pi }\int _{0}^{\pi }\frac{f(e^{i\phi })\sin (\phi )d\phi }{1-2\gamma (x)\cos (\phi )-\gamma (x)^{2}}\rbrace ,\,x\in G_{\mathcal {M}}. \end{array} \end{aligned}$$

(13)

Similarly, we can determine H(0, y) by solving another Dirichlet boundary value problem on the contour $\mathcal {L}$. Then, using (2) we uniquely obtain H(x, y).

4.2 A Homogeneous Riemann-Hilbert Boundary Value Problem

In case $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ne 1$, consider the following transformation:

$$\begin{aligned} \begin{array}{rl} G(x):=&{}H(x,0)+\frac{s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}d_{2,1}H(0,0)}{d_{1,2}d_{2,1}-s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}},\\ L(y):=&{}H(0,y)+\frac{s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}d_{1,2}H(0,0)}{d_{1,2}d_{2,1}-s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}}. \end{array} \end{aligned}$$

Then, for $y\in D_{y}$,

$$\begin{aligned} \begin{array}{c} A(X_{0}(y),y)G(X_{0}(y))=-B(X_{0}(y),y)L(y). \end{array} \end{aligned}$$

(14)

For $y\in D_{y}-[y_{1},y_{2}]$ both $G(X_{0}(y))$, L(y) are analytic and the right-hand side in (14) can be analytically continued up to the slit $[y_1, y_2]$, or equivalently,

$$\begin{aligned} \begin{array}{c} A(x,Y_{0}(x))G(x)=-B(x,Y_{0}(x))L(Y_{0}(x)),\,x\in \mathcal {M}. \end{array} \end{aligned}$$

(15)

Clearly, G(x) is holomorphic in $D_{x}$, and continuous in $\bar{D}_{x}$. However, G(x) might have poles in $S_{x}=G_{\mathcal {M}}\cap \bar{D}_{x}^{c}$. These poles (if exist) coincide with the zeros of $A(x,Y_{0}(x))$ in $S_{x}$; see Appendix B. For $y\in [y_{1},y_{2}]$, let $X_{0}(y)=x\in \mathcal {M}$, and realize that $Y_{0}(X_{0}(y))=y$ (note that $B(x,Y_{0}(x))\ne 0$, $x\in \mathcal {M}$). Taking into account the poles of G(x), and noticing that $L(Y_{0}(x))$ is real for $x\in \mathcal {M}$,

$$\begin{aligned} \begin{array}{c} Re[iU(x)\tilde{G}(x)]=0,\,x\in \mathcal {M},\\ U(x)=\frac{A(x,Y_{0}(x))}{(x-\bar{x})^{r}B(x,Y_{0}(x))},\,\tilde{G}(x)=(x-\bar{x})^{r}G(x), \end{array} \end{aligned}$$

(16)

where $r=0,1$, whether $\bar{x}$ is zero or not of $A(x,Y_{0}(x))$ in $S_{x}$ (see Appendix B). Thus, $\tilde{G}(x)$ is regular for $x\in G_{\mathcal {M}}$, continuous for $x\in \mathcal {M}\cup G_{\mathcal {M}}$, and U(x) is a non-vanishing function on $\mathcal {M}$. As usual, we must firstly conformally transform the problem (16) from $\mathcal {M}$ to the unit circle $\mathcal {C}$. Let the conformal mapping $z=\gamma (x):G_{\mathcal {M}}\rightarrow G_{\mathcal {C}}$, and its inverse given by $x=\gamma _{0}(z):G_{\mathcal {C}}\rightarrow G_{\mathcal {M}}$.

Then, the Riemann-Hilbert problem formulated in (16) is reduced to the following: Find a function $F(z):=\tilde{H}(\gamma _{0}(z))$, regular in $G_{\mathcal {C}}$, continuous in $G_{\mathcal {C}}\cup \mathcal {C}$ such that, $Re[iU(\gamma _{0}(z))F(z)]=0,\,z\in \mathcal {C}$.

To proceed with the solution of the boundary value problem we have to determine its index $\chi =\frac{-1}{\pi }[arg\{U(x)\}]_{x\in \mathcal {M}}$, where $[arg\{U(x)\}]_{x\in \mathcal {M}}$, denotes the variation of the argument of the function U(x) as x moves along $\mathcal {M}$ in the positive direction, provided that $U(x)\ne 0$, $x\in \mathcal {M}$. Following [16] we have,

Lemma 5

• 1. If $\widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}\widehat{q}_{21}$, then $\chi =0$ is equivalent to

  $$\begin{aligned} \begin{array}{l} \frac{d A(x,Y_{0}(x))}{dx}|_{x=1}<0\Leftrightarrow \widehat{\lambda }_{1}<s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}+d_{1,2}\frac{\widehat{\lambda }_{2}}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}},\\ \frac{d B(X_{0}(y),y)}{dy}|_{y=1}<0\Leftrightarrow \widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}+d_{2,1}\frac{\widehat{\lambda }_{1}}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}. \end{array} \end{aligned}$$

• 2. If $\widehat{\lambda }_{2}\ge s_{G}^{(2)}q_{G2}\widehat{q}_{21}$, $\chi =0$ is equivalent to $\frac{d B(X_{0}(y),y)}{dy}|_{y=1}<0\Leftrightarrow \widehat{\lambda }_{2}<s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}+d_{2,1}\frac{\widehat{\lambda }_{1}}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}}$.

Thus, under stability conditions (see Lemma 1), the problem defined in (16) has a unique solution for $x\in G_{\mathcal {M}}$ given by,

$$\begin{aligned} \begin{array}{l} H(x,0)=K(x-\bar{x})^{r}e^{[\frac{1}{2i\pi }\int _{|t|=1}\frac{\log \{J(t)\}dt}{t-\gamma (x)}]}-\frac{s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}d_{2,1}H(0,0)}{d_{1,2}d_{2,1}-s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}}, \end{array} \end{aligned}$$

(17)

where K is a constant, $J(t)=\frac{\overline{U_{1}(t)}}{U_{1}(t)}$, $U_{1}(t)=U(\gamma _{0}(t))$. Setting $x=0$ in (17) we derive a relation among K, H(0, 0). Now set $x=1\in G_{\mathcal {M}}$ in (17), and use the first in (4) to obtain K, H(0, 0). Substituting back in (17) we finally obtain,

$$\begin{aligned} \begin{array}{rl} H(x,0)=&{}\frac{\widehat{\lambda }_{1}d_{2,1}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}(s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G2/\{G2\}}-\widehat{\lambda }_{2})}{(s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}-d_{1,2}d_{2,1})(\bar{x}-1)^{r}}\left( (\bar{x}-x)^{r}\right. \\ &{}\left. \times \exp [\frac{\gamma (x)-\gamma (1)}{2\pi i}\int _{|t|=1}\frac{\log \{J(t)\}}{(t-\gamma (x))(t-\gamma (1))}dt]\right. \\ &{}\left. +\frac{q_{G1}^{*}\tilde{f}_{G1/\{G1\}}d_{2,1}\bar{x}^{r}}{q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G2/\{G2\}}}\exp [\frac{-\gamma (1)}{2\pi i}\int _{|t|=1}\frac{\log \{J(t)\}}{t(t-\gamma (1))}dt]\right) ,\,x\in G_{\mathcal {M}}. \end{array} \end{aligned}$$

(18)

Similarly, we can determine H(0, y) by solving another Riemann-Hilbert boundary value problem on the closed contour $\mathcal {L}$. Then, using the fundamental functional Eq. (2) we uniquely obtain H(x, y).

Performance Metrics: In the following we derive formulas for the expected number of packets, and the average delay at each user node in steady state, say $M_{i}$ and $D_{i}$, $i=1,2,$ respectively. Denote by $H_{1}(x,y)$, $H_{2}(x,y)$ the derivatives of H(x, y) with respect to x and y, respectively. Then, $M_{i}=H_{i}(1,1)$, and using Little’s law $D_{i}=H_{i}(1,1)/\widehat{\lambda }_{i}$, $i=1,2$. Using (2), (3) after simple calculations we have

$$\begin{aligned} \begin{array}{lccr} M_{1}=\frac{\widehat{\lambda }_{1}+d_{1,2}H_{1}(1,0)}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}},&\,&\,&M_{2}=\frac{\widehat{\lambda }_{2}+d_{2,1}H_{2}(0,1)}{s_{G}^{(2)}q_{G2}\widehat{q}_{21}}. \end{array} \end{aligned}$$

(19)

We only focus on $M_{1}$, $D_{1}$ (similarly we can obtain $M_{2}$, $D_{2}$). Note that $H_{1}(1,0)$ can be obtained using (18) or (13) depending on the value of $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}$. For $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ne 1$, and using (18) we obtain,

$$\begin{aligned} \begin{array}{rl} H_{1}(1,0)=&{}\frac{\widehat{\lambda }_{1}d_{2,1}+s_{G}^{(1)}q_{G1}\widehat{q}_{12}(s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G1/\{G1\}}-\widehat{\lambda }_{2})}{s_{G}^{(1)}q_{G1}\widehat{q}_{12}s_{G}^{(2)}q_{G2}\widehat{q}_{21}-d_{1,2}d_{2,1}}\{\frac{\gamma ^{\prime }(1)}{2\pi i}\int _{|t|=1}\frac{\log \{J(t)\}}{(t-\gamma (1))^{2}}dt\\ &{}+\frac{r}{1-\bar{x}}1_{\{r=1\}}\}. \end{array} \end{aligned}$$

(20)

Substituting in (19) we obtain $M_{1}$, and dividing with $\widehat{\lambda }_{1}$, the average delay $D_{1}$. Note that the calculation of (11) requires the evaluation of integrals (11), and $\gamma (1)$, $\gamma ^{\prime }(1)$. For an efficient numerical procedure see [8], Section 4.1.

5 Explicit Expressions for the Symmetrical Model

In this section we consider the symmetrical model and obtain exact expressions for the average delay without computing the generating function of the stationary joint relay queue length distribution. As a symmetrical, we mean the model where $q_{Gk}^{*}=q_{G}^{*}$, $q_{ik}=q_i$, $i\in \{B,G\}$, $\lambda _{k}=\lambda$, $f_{i,k/\{i,k\}}=f_{i/\{i\}}$, $f_{G,k/\{G,k;G,m\}}=f_{G/\{G;G\}}$, $f_{G,k/\{G,k;B,m\}}=f_{G/\{G;B\}}$, $\tilde{f}_{G,k/\{G,k\}}=\tilde{f}_{G}$, $s_{i}^{(k)}=s_{i}$, $i\in \{G,B\}$, $k=1,2$. Then, $\widehat{q}_{12}=\widehat{q}_{21}=\widehat{q}$ and $d_{1,2}=d_{2,1}=d$.

Due to the symmetry of the model, $H_{1}(1,1)=H_{2}(1,1)$, $H_{1}(1,0)=H_{2}(0,1)$. Note that $M_{j}=H_{j}(1,1)$, $j=1,2$. Thus, using (2) we obtain,

$$\begin{aligned} \begin{array}{c} M_{1}=\frac{\widehat{\lambda }+dH_{1}(1,0)}{s_{G}q_{G}\widehat{q}-\widehat{\lambda }}, \end{array} \end{aligned}$$

(21)

where $s_{G}q_{G}\widehat{q}>\widehat{\lambda }$, due to the stability condition. Set $x=y$ in (2), differentiate it with respect to x at $x=1$, and use the first in (3) to obtain,

$$\begin{aligned} \begin{array}{c} M_{1}+M_{2}=2M_{1}=\frac{2\widehat{\lambda }-\widehat{\lambda }^{2}+2H_{1}(1,0)(s_{G}q_{G}\widehat{q}+d)}{s_{G}q_{G}\widehat{q}-\widehat{\lambda }}. \end{array} \end{aligned}$$

(22)

Using (21), (22), and applying Little’s law we finally derive,

$$\begin{aligned} \begin{array}{lr} M_{1}=M_{2}=\frac{\widehat{\lambda }[2s_{G}q_{G}\widehat{q}+\widehat{\lambda }d]}{2s_{G}q_{G}^{*}\tilde{f}_{G}(s_{G}q_{G}\widehat{q}-\widehat{\lambda })},&D_{1}=D_{2}=\frac{2s_{G}q_{G}\widehat{q}+\widehat{\lambda }d}{2s_{G}q_{G}^{*}\tilde{f}_{G}(s_{G}q_{G}\widehat{q}-\widehat{\lambda })}. \end{array} \end{aligned}$$

(23)

Fig. 1.

Effect of transmission control on the average delay for $q_{G}=0.7$ (left), and for $\widehat{\lambda }=0.1$ (right).

6 Numerical Results

Example 1:

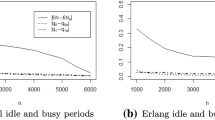
The symmetrical model. In this example, we focus on the symmetrical model and investigate the effect of transmission control on the average delay. We assume that $\tilde{f}_{G}=0.9$, $f_{G/\{G\}}=0.8$, $f_{G/\{G,B\}}=0.7$, $f_{G/\{G,G\}}=0.6$, $q_{B}=0.5$. In Figs. 1 and 2 we also assume that $q_{G}^{*}=0.9$. Recall that $q_{G}^{*}$ is the transmission probability of a station when the other is empty.

In Fig. 1 (left) we observe that the average delay increases for increasing values of $\widehat{\lambda }$ by letting $q_{G}=0.7$. More importantly, we can identify the advantage of transmission control regarding delay. Note that when the channel remains in the good state for longer period (i.e., $s_{G}=0.9$), the users adapt their transmission probability $q_{G}$ to 0.7, and thus, significant performance gains are achieved. Similar observations can be deduced from Fig. 1 (right), where we can see that the average delay decreases, as we increase $q_{G}$. That decrease becomes more apparent when the channel remains for longer period in the good state.

Figure 2 (left) shows the average delay as a function of $(\widehat{\lambda },q_{G})$. We can see how sensitive is the average delay when $\widehat{\lambda }$ increases, and especially, when the portion of time where the channel is in good state decreases. Similarly, when $s_{G}$ decreases (see Fig. 2 (right)), the average delay increases rapidly, especially when $q_{G}$ takes small values (this maybe happened when users falsely detect that the channel is in the bad state). Finally in Fig. 3 (left) we observe that when the channel is in good state for longer period (e.g., $s_{G}=1$), the average delay decreases, even when $q_{G}^{*}$ takes small values, a fact that justifies the importance of transmission control, from the delay point of view.

Fig. 2.

Effect of transmission control on the average delay.

Fig. 3.

Effect of transmission control ($s_{G}$, $q_{G}^{*}$) on the average delay for $q_{G}=0.7$ (left), and effect of channel state on the stability region (right). (Color figure online)

Example 2:

Stability region for the general model. In this example we focus on the general model, and specifically on the case $\frac{q_{G1}\widehat{q}_{12}}{q_{G1}^{*}\tilde{f}_{G,1/G,1}}+\frac{q_{G2}\widehat{q}_{21}}{q_{G2}^{*}\tilde{f}_{G,2/G,2}}\ne 1$. Our aim is to investigate the effect of channel state on the stability region. We assume that $s_{G}^{(1)}=0.9$, $q_{G1}=0.6$, $q_{G2}=0.7$, $q_{B1}=0.3$, $q_{B2}=0.4$, $q_{G1}^{*}=0.9=q_{G2}^{*}$, and $\tilde{f}_{G,k/\{G,k\}}=0.9$, $f_{G,k/\{G,k\}}=0.8$, $f_{G,1/\{G,1;B,2\}}=f_{G,2/\{G,2;B,1\}}=0.7$, $f_{G,k/\{G,1;G,2\}}=0.6$, $k=1,2$.

In Fig. 3 (right) we observe the impact of channel state of user 2 on the stability region. In particular, when we decrease $s_{G}^{(2)}$ from 0.8 to 0.4, the stability region (i.e., the set of arrival vectors $(\widehat{\lambda }_{1},\widehat{\lambda }_{2})$ for which both queues are stable) apparently decreases. Note, that the adequate arrival rate referring to queue 2 is greatly reduced due the change of $s_{G}^{(2)}$. This is expected, since when $s_{G}^{(2)}=0.4$, the channel remains in the bad state for longer period and user 2 becomes reluctant to transmit. Thus, in order to ensure stability the $\widehat{\lambda }_{2}$ must be reduced.

7 Summary

In this work, we considered the problem of characterizing stability and delay behavior of an asymmetric adaptive two-user random access wireless network with MPR capabilities. Each user node use its knowledge about both the channel state (characterized according to the Gilbert-Elliot model), and the status of the other node, and accordingly adjusts its transmission probability. Stability conditions were investigated based on the concept of stochastic dominant systems. The generating function of the stationary joint queue length distribution was derived in terms of the solution of a Riemann-Hilbert boundary value problem. For the symmetrical system we also derived explicit expressions for the average queueing delay at each user node without solving a boundary value problem. Extensive numerical results shown insights into the system performance.

Appendices

A Appendix

Regarding the derivation of (2), the queue evolution in (1) implies,

$$\begin{aligned} \begin{array}{l} E(x^{N_{1,n+1}}y^{N_{2,n+1}})=D(x,y)\left( P(N_{1,n}=N_{2,n}=0)\right. \\ \left. +E(x^{N_{1,n}}1_{\{N_{1,n}>0,N_{2,n}=0\}})[1+s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G,1/\{G,1\}}(\frac{1}{x}-1)]\right. \\ \left. +E(y^{N_{2,n}}1_{\{N_{1,n}=0,N_{2,n}>0\}})[1+s_{G}^{(2)}q_{G2}^{*}\tilde{f}_{G,2/\{G,2\}}(\frac{1}{y}-1)\right. \\ \left. +E(x^{N_{1,n}}y^{N_{2,n}}1_{\{N_{1,n}>0,N_{2,n}>0\}})[s_{G}^{(1)}q_{G1}(s_{G}^{(2)}\bar{q}_{G2}+s_{B}^{(2)}\bar{q}_{B2})\right. \\ \left. \times (1+f_{G,1/\{G,1\}}(\frac{1}{x}-1)) +s_{G}^{(2)}q_{G2}(s_{G}^{(1)}\bar{q}_{G1}+s_{B}^{(1)}\bar{q}_{B1})(1+f_{G,2/\{G,2\}}(\frac{1}{y}-1))]\right. \\ \left. +s_{G}^{(1)}q_{G1}s_{G}^{(2)}q_{G2}(1+f_{G,1/\{G,1;G,2\}}(\frac{1}{x}-1)+f_{G,2/\{G,1;G,2\}}(\frac{1}{y}-1))\right. \\ \left. +s_{G}^{(1)}q_{G1}s_{B}^{(2)}q_{B2}(1+f_{G,1/\{G,1;B,2\}}(\frac{1}{x}-1))+s_{B}^{(1)}q_{B1}s_{G}^{(2)}q_{G2}\right. \\ \left. \times (1+f_{G,2/\{B,1;G,2\}}(\frac{1}{y}-1))+(s_{G}^{(1)}\bar{q}_{G1}+s_{B}^{(1)}\bar{q}_{B1})(s_{G}^{(2)}\bar{q}_{G2}+s_{B}^{(2)}\bar{q}_{B2})\right. \\ \left. +s_{B}^{(1)}q_{B1}s_{B}^{(2)}q_{B2}+s_{B}^{(2)}q_{B2}(s_{G}^{(1)}\bar{q}_{G1}+s_{B}^{(1)}q_{B1})+s_{B}^{(1)}\bar{q}_{B1}(s_{G}^{(2)}\bar{q}_{G2}+s_{B}^{(2)}\bar{q}_{B2})\right) , \end{array} \end{aligned}$$

where $1_{\{A\}}$ denotes the indicator function of the event A. Note that

$$\begin{aligned} \begin{array}{c} H(x,0)-H(0,0)=\lim _{n\rightarrow \infty }E(x^{N_{1,n}}1_{\{N_{1,n}>0,N_{2,n}=0\}}),\\ H(0,y)-H(0,0)=\lim _{n\rightarrow \infty }E(y^{N_{2,n}}1_{\{N_{1,n}=0,N_{2,n}>0\}}),\\ H(x,y)-H(x,0)-H(0,y)+H(0,0)=\lim _{n\rightarrow \infty }E(x^{N_{1,n}}y^{N_{2,n}}1_{\{N_{1,n}>0,N_{2,n}>0\}}). \end{array} \end{aligned}$$

B Appendix

In the following, we proceed with the study of the location of the intersection points of $R(x,y)=0$, $A(x,y)=0$ (resp. B(x, y)). These points (if exist) are potential singularities for the functions H(x, 0), H(0, y), and thus, their investigation is crucial regarding the analytic continuation of H(x, 0), H(0, y) outside the unit disk. We only focus on the intersection points of $R(x,y)=0$, $A(x,y)=0$.

For and $R(x,y) = 0$, $y = Y_{\pm }(x)$, the resultant in y of the two polynomials R(x, y) and A(x, y) is $Res_{y}(R,A;x)=x(x-1)s_{G}^{(2)}q_{G2}\widehat{q}_{21}Z(x)$, where

$$\begin{aligned} \begin{array}{rl} Z(x)=&{}-\widehat{\lambda }_{1}(s_{G}^{(2)}q_{G2}\widehat{q}_{21}+(1+\widehat{\lambda }_{1})d_{1,2})x^{2}+x[(\widehat{\lambda }+\widehat{\lambda }_{1}\widehat{\lambda }_{2})d_{1,2}\\ {} &{}+(s_{G}^{(2)}q_{G2}\widehat{q}_{21}+d_{1,2})s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G1/\{G1\}}]-s_{G}^{(1)}q_{G1}^{*}\tilde{f}_{G1/\{G1\}}d_{1,2}. \end{array} \end{aligned}$$

Note also that $Z(0)>0$ since $d_{1,2}<0$, and $Z(1)>0$, due to the stability conditions (see Lemma 1). If $q_{G1}^{*}\le min\{1,\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}+(1+\widehat{\lambda }_{2})s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{(1+\widehat{\lambda }_{2})s_{G}^{(1)}\tilde{f}_{G1/\{G1\}}}\}$, then $\lim _{x\rightarrow \infty }Z(x)=-\infty$, and $Z(x)=0$ has two roots of opposite sign, say $x_{*}<0<1<x^{*}$. If $\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}+(1+\widehat{\lambda }_{2})s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{(1+\widehat{\lambda }_{2})s_{G}^{(1)}\tilde{f}_{G1/\{G1\}}}<\alpha _{1}^{*}\le 1$, then $\lim _{x\rightarrow \infty }Z(x)=+\infty$, and $Z(x)=0$ has two positive roots, say $1<\tilde{x}_{*}<x_{3}<x_{4}<\tilde{x}^{*}$ (due to the stability conditions). In the former case we have to check if $x^{*}\in S_{x}$, while in the latter case if $\tilde{x}_{*}\in S_{x}$. These zeros, if they lie in $S_{x}$ such that $|Y_{0}(x)|\le 1$, are poles of A(x, y). Denote from hereon $\bar{x}=x^{*}$, if $\alpha _{1}^{*}\le min\{1,\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}+(1+\widehat{\lambda }_{2})s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{(1+\widehat{\lambda }_{2})s_{G}^{(1)}\tilde{f}_{G1/\{G1\}}}\}$, and $\bar{x}=\tilde{x}_{*}$, if $\frac{s_{G}^{(2)}q_{G2}\widehat{q}_{21}+(1+\widehat{\lambda }_{2})s_{G}^{(1)}q_{G1}\widehat{q}_{12}}{(1+\widehat{\lambda }_{2})s_{G}^{(1)}\tilde{f}_{G1/\{G1\}}}<\alpha _{1}^{*}\le 1$.