Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The last decades of research on the theory of signalized traffic intersections put a lot of emphasis on estimation methods of delays and queue lengths at individual intersections regulated by actuated control and on the strategies that can be designed upon the results of such estimation and on the analysis of traffic characteristics. The performance of signalized intersections is indeed usually measured by the mean queue length and the mean delay (sojourn time in system) of vehicles.

Different approaches to the estimation problem can be found in the literature. The approach based on microscopic simulation models, essentially car-following models (see, e.g., [2, 16, 20]), presents some important disadvantages since, in spite of the fact that they mimic quite well the behaviour of traffic in real world, they need to be fed with a lot of parameters, not easily known or measured in practice, and require a considerable computational effort. Popular models like the HCM model [18] and Webster’s model [25] are known to have also some drawbacks.

As an alternative, this paper explores the use of queueing theory in order to obtain the performance measures just mentioned above. The main difficulties involved in such an approach come from the need of a good characterization of the circulating vehicles and drivers, and from the fact that the cyclic deactivation of the server (the red signal) has to be incorporated in the behaviour of the queueing system. In the work published in [15] we have addressed pre-timed control intersections. However actuated or semi-actuated traffic signals are generally more efficient, since they better accommodate fluctuation of vehicle arrivals as they are able to adapt the green time given to a traffic stream according to demand, by incorporating the possibility of extending the green signal (see e.g. [23]).

The paper by Lin et al. [13] explores simple probabilistic arguments to obtain the mean duration of the green signal in semi-actuated controlled intersections, but their approach is restricted to small volumes of traffic in the secondary street, smaller than 500 vehicles per hour. Even in the case of Poisson vehicle arrivals, models like M/D/1 and \(M/D^X/1\) do not correctly describe the deactivation of the server, taking place when the signal changes from green to red. In fact, queueing systems with server vacations (see [3] for a survey) are a more convenient way of modelling the stochastic behaviour of the traffic system (see also previous work in [7, 8, 24] for the case of pre-timed control).

Signalized traffic intersections have similarities with polling systems (see e.g. [21] or [22] for an overview on polling systems), where a single server is handling two queues and switches between them according to some control rule. In the case of semi-actuated signalized intersections, queues are attended by the server during given periods of time, which may have random duration – at least for one of the queues. However, as far as we know, the diversity of polling systems found in the literature do not encompass the specificity of the semi-actuated signalized traffic addressed in the paper. Several authors (see e.g. [5, 6, 11] or [1]) stress the fact that systems characterized by time limited service disciplines, as it is the case for semi-actuated signal intersections, should not be expected to have closed formulas for the expected customer waiting time. The papers just cited focus on cases of exponential or phase-type service times, which do not apply to signalized traffic. However, time limited server systems are often used when in presence of heavy loaded queues that tend to monopolize the server, leaving lightly loaded queues with a negligible part of the service time.

In this paper, we consider a semi-actuated isolated signalized intersection, meaning that the mechanism that triggers red times relies on the evolution of the traffic demand, leading to green times of random duration. Specifically, the green time is extended, from a fixed minimum duration, in case there are vehicles waiting at the intersection at the end of a minimum green time period. Additional individual extensions of the green time by T seconds are performed if the time interval between arriving vehicles remains smaller than T seconds, up to the green time reaching a maximum pre-fixed total duration. For implementing the green time extension mechanism, a sensor located a couple of meters before the stop line is responsible for the detection of vehicle at the intersection.

We model the semi-actuated signalized intersection as an M/D/1 queueing model with server vacations, in which clients (vehicles) are served in a first-in first-out (FIFO) regime. The server starts a vacation of fixed duration as soon as a red time initiates. As described in the previous paragraph, server working periods, corresponding to green times, have random duration. We explore in the paper the specific nature of the resulting M/D/1 server vacation queue, and in particular its Markov regenerative structure, to characterize the distributions of queue length, vehicle delay, and duration of the green signal in the long-run regime. Our approach is different from that of [12], which relies on the derivation of a functional equation for the system behavior and its solution by means of a numerical technique based on Laguerre-function approximations. We compare the results obtained for the derived long-run measures with those obtained by applying a microscopic simulation model (see [19]). Our main contribution lies in providing expressions for the means of waiting time of drivers, length of queue at the intersection, and total duration of the green signal, which are of interest for traffic engineers.

The paper is organized as follows. The assumptions made and the Markov chain model that is used in the paper for investigating semi-actuated signalized traffic intersections are introduced in Sect. 2. The main results on long-run performance measures for semi-actuated signalized traffic intersections are included in Sect. 3, and a case study that is used to validate the results obtained from the proposed model is presented in Sect. 4. The paper ends with some brief conclusions drawn in Sect. 5.

2 The Signalized Intersection Traffic Model

A signalized intersection regulated by semi-actuated control is assumed to be a traffic server system for which each vehicle arriving at the intersection during a green (light) period has to wait if there are vehicles in front of it, or if arriving during a red (light) period. In a detailed way, we consider a model for a signalized intersection having the following specifications, with time in seconds:

  • Vehicles arrive at the intersection according to an homogeneous Poisson process with rate \(\lambda \), and are served one by one in order of arrival.

  • The intersection possesses infinite vehicle waiting capacity, and the light alternates between green and red periods.

  • The service time of a vehicle is constant and equal to T, and services are initiated during green periods at instants that are integer multiples of T.

  • Red periods have constant duration of value RT, and green periods have random durations, taking values on the set

    $$\{MT, (M+1)T,\ldots ,GT\}$$

    such that: starting from an initial interval of duration MT for a green period, successive extensions of length T of the green period occur if there are vehicles to be served at the intersection at the end of the interval, with extensions being allowed only up to the point when the length of the green period reaches the corresponding maximum duration of GT.

Note that T is an arbitrary positive constant that denotes the time that a vehicle spends to move through the intersection, i.e., its service time, R and M are positive integers, and \(G-M\) is a nonnegative integer number denoting the maximum number of extensions of T seconds that are allowed to be performed in green periods. Our assumptions imply that signal cycles have maximum duration \((G+R)T\), and are divided in a server working period of minimum length MT and maximum length GT, corresponding to a green period, followed by a server vacation period of fixed length RT, corresponding to a red period.

We should stress that the approach that will be followed in the paper could be adapted with small effort to accommodate: vehicles arriving at the intersection according to a non-homogeneous compound-Poisson process; the intersection having finite vehicle waiting capacity, and group service of vehicles – with a maximum size group being allowed, as considered in [8]. The time discretization, with time step T, which is implicit in the Markov chain that we will use to analyze the system, represents a reasonable approximation of the real world traffic; and the use of a constant service time to represent the time spent by a vehicle driving across the intersection is also a fair approximation of the real world behaviour of drivers.

For \(t\ge 0\), let \(\left( L(t), \xi (t)\right) \) denote the state of the system at instant t, with L(t) representing the number of vehicles in the system (in brief, the queue length) at instant t and \(\xi (t)\) the state of the signal (in brief, the phase) at the same instant, with the set of phases being \(\{1,2,\ldots ,G+1\}\), such that: phases \(1,2,\ldots ,M\) correspond to the initial M time intervals of duration T of a green period, phases \(M+1,M+2,\ldots ,G\) correspond to the successive time intervals of duration T associated with extensions of a green period, and phase \(G+1\) corresponds to the red periods of duration RT. In addition, let \(\tau _n\) denote the instant (of time) of occurrence of the n-th change of state in the phase process \(\left( \xi (t)\right) \), with \(\tau _0=0\).

A careful analysis of the traffic process \(\{(L(t),\xi (t))\}\) leads to the conclusion that it is a Markov regenerative process with state space \(\mathbb N \times \left\{ 1,2,\ldots ,G+1\right\} \); see, e.g., [9] for details on Markov regenerative processes. Moreover, by observing the process \(\{(L(t),\xi (t))\}\) at times \(\tau _n\), we obtain the embedded Markov chain \(\{X_n\}\), with \(X_n=(L(\tau _n), \xi (\tau _n))\), \(n\in \mathbb N\), denoting the state of the system immediately after the n-th phase change, being an M/G/1 type Markov chain, a type of chain that was investigated in detail in [14].

The Markov chain \(\{X_n\}\) has state space \(\mathbb N \times \left\{ 1,2,\ldots ,G+1\right\} \) and transition probability matrix

$$\begin{aligned} Q = \left[ \begin{array}{cccc} B_0' &{} A_1 &{} A_2 &{} \cdots \\ A_0' &{} A_1 &{} A_2 &{} \cdots \\ 0 &{} A_0 &{} A_1 &{} \cdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots \\ \end{array} \right] , \end{aligned}$$
(1)

where the \(A_k\), \(A_0'\), and \(B_0\) are \((G+1)\times (G+1)\) nonnegative matrices. The entries of the matrices \(A_k\) are given by

$$\begin{aligned} \displaystyle \left( A_k\right) _{ij}= & {} \left\{ \begin{array}{ll} e^{-\lambda T}\displaystyle \frac{\left( \lambda T\right) ^k}{k!}, &{} i=1,2,\ldots , G,\, j=i+1\\ \, e^{-\lambda R T}\displaystyle \frac{\left( \lambda R T\right) ^{k-1}}{(k-1)!},\, &{} i=G+1, j=1,\, k\ge 1\\ \, 0,&{}\text {otherwise,} \end{array}\right. \end{aligned}$$

The two matrices \(A_0'\) and \(B_0'\) have similar forms but must be treated separately; in detail,

$$\begin{aligned} \displaystyle \left( B_0'\right) _{ij}= & {} \left\{ \begin{array}{ll} e^{-\lambda T}, &{} i=1,2,\ldots , M-1,\, j=i+1\\ \, e^{-\lambda T}, &{} i=M,M+1,\ldots , G,\, j=G+1\\ \, e^{-\lambda RT}, &{} i=G+1,\, j=1\\ \, 0,&{}\text {otherwise}, \end{array}\right. \end{aligned}$$

and \((A_0')_{i,i+1} = (B_0')_{i,i+1}\) for \(i=1,2,\ldots ,M-1\), \((A_0')_{i,G+1} = (B_0')_{i,G+1}\) for \(i=M,M+1,\ldots ,G+1\), and all remaining entries of \(A_0'\) are 0.

Note that, for \(k\ge 1\): \((A_k)_{i\,i+1}\), \(1\le i \le G\), denotes the probability that k vehicles arrive in a time interval, of duration T, elapsing from a transition to phase i to the next subsequent phase transition, to phase \(i+1\); conversely, \((A_{k})_{G+1\, 1}\) denotes the probability that \(k-1\) vehicles arrive in a time interval elapsing from a transition to phase \(G+1\), starting a red signal, to the subsequent phase transition, to phase 1 and starting a green signal. The particular shape of Q is intuitive; in particular, the need for the introduction of the blocks \(A_0'\) and \(B_0'\) in the first column of Q arises from the fact that the decision on whether an extension of the green signal will occur is exclusively determined by having vehicles waiting in line or not at the moment at which a decision on such extension needs to be made.

From the structure of the matrix Q in (1), it follows that the Markov chain \(\{X_n\}\) is of M/G/1 type, and the invariant probability vector associated with the stochastic matrix Q can be computed using a procedure similar to the one described in [15] in case the stationarity condition \(\lambda (G+R)<G\) is satisfied, as assumed in the rest of the paper.

To end the section, we let \(\mathbf{u}=[u^{(0)}\, u^{(1)}\, u^{(2)} \ldots ]\) denote the invariant probability vector associated with the stochastic matrix Q, an infinite row vector such that \(u^{(k)}=[u_{k1}\, u_{k2} \ldots u_{k\,G+1}]\), \(k\ge 0\), is an \((G+1)\)-dimension row vector and \(\mathbf{u} Q=\mathbf{u}\), \(\mathbf{u}\mathbf {1}=1\), with \(\mathbf {1}\) denoting a column vector of ones. Solving this equation for \(\mathbf{u}\) involves using a recursive matrix formula that is nicely described in [17]. The element \(u_{ki}\) denotes the stationary probability that, at the beginning of a period in a phase, there are k vehicles in the system and the system is in phase i. As such, the stationary probability of the number of vehicles in the system at the beginning of a phase being equal to k is given by

$$ u_{k\bullet }=\sum _{i=1}^{G+1} u_{ki}, \quad k\ge 0. $$

Then, if we let \(\mathbf {r}=[r_1\,r_2\,\dots \,r_{G+1}]\) denote the stationary probability vector of the embedded phase process \(\{\xi (\tau _n)\}\), we have \(r_i=\sum _{j=0}^\infty u_{ji}\) since we may also view \(u_{ki}\) as the long-run fraction of phase transitions that lead to phase i with k vehicles staying in the system immediately after the phase transition, and \(r_i\) as the long-run fraction of phase transitions that lead to phase i.

3 Long-Run Properties of the Traffic Process

In this section we characterize the long-run properties of the Markov regenerative traffic process \(\{(L(t),\xi (t))\}\). We first derive the long-run distribution of the number of vehicles in the system, in Theorem 1, and obtain an expression for the long-run mean number of vehicles in the system, in Theorem 2. After that, we give an expression for the long-run mean sojourn time of vehicles in the system. Finally, we present the long-run distribution of the number of extensions of the green period, along with its mean.

We first note that the long-run fraction of phase i intervals that are initiated with k vehicles in the system, denoted by \(\pi _{ki}\), satisfies

$$\begin{aligned} \pi _{ki}= \frac{u_{ki}}{\sum _{j=0}^\infty u_{ji}}=\frac{u_{ki}}{r_i}. \end{aligned}$$
(2)

Of particular relevance are the long-run (and stationary) distributions of the number of vehicles in the system at the beginning of green light periods, \(\{\pi _{k1}\}_{k\ge 0}\), and at the beginning of red light periods \(\{\pi _{k,G+1}\}_{k\ge 0}\). For later use, we let \(\mathbb E [L_i]\) denote the long-run mean number of vehicles in the system immediately after a transition to phase i, i.e.,

$$\begin{aligned} \mathbb E [L_i] = \sum _{k=0}^\infty k\, \pi _{ki}. \end{aligned}$$
(3)

We now address the long-run properties of the phase process \(\{\xi (t)\}\). This is a semi-Markov process with embedded Markov chain at phase transition epochs \(\{\xi _n\}\), such that the amount of time the process remains in phase i in each visit to the phase is the constant

$$\begin{aligned} T_i=\left\{ \begin{array}{ll} T, &{} i\ne G+1\\ RT, &{} i=G+1 \,.\\ \end{array}\right. \end{aligned}$$

Resorting to the theory of semi-Markov processes (see, e.g., [4], Theorem 4.6) we conclude that the long-run fraction of time the traffic process spends in phase i,

$$ p_{\bullet i}= \lim _{t\rightarrow \infty } \left[ \frac{1}{t} \int _0^{t}\mathbf {1}_{\left\{ \xi (s)=i\right\} } \,d s\right] , $$

can be written as \( p_{\bullet i}= r_i T_i/\sum _{j=1}^{G+1} r_j T_j, \) which reduces to

$$\begin{aligned} p_{\bullet i}=\left\{ \begin{array}{ll} \frac{r_i}{\sum _{j=1}^{G} r_j+ R\, r_{G+1}}, &{} i\ne G+1\\ \frac{R\, r_{G+1}}{\sum _{j=1}^{G} r_j+ R\, r_{G+1}}, &{} i=G+1. \end{array}\right. \end{aligned}$$
(4)

We next address the computation of the long-run distribution of the number of vehicles in the system, L. For that, we let \(p_{ki}\) denote the long-run fraction of time there are k vehicles in the system with the system being in phase i, i.e.,

$$ p_{ki} = \lim _{t\rightarrow \infty } \left[ \frac{1}{t} \int _0^{t}\mathbf {1}_{\left\{ L(s)=k,\xi (s)=i\right\} }\,d s\right] , $$

implying that \(p_{\bullet i}=\sum _{k=0}^{\infty } p_{ki}\), for \(i=1,2,\dots ,G+1\). The following theorem expresses how the \(\{p_{ki}\}\) may be computed from the \(\{u_{ki}\}\).

Theorem 1

For \(k\in \mathbb N\) and \(i\in \left\{ 1,2,\ldots ,G+1\right\} \),

$$\begin{aligned} \displaystyle { p_{ki}=\frac{\sum _{j=0}^k u_{ji} \,\mu _{k-j}(i)}{(\sum _{j=1}^{G} r_j+ R \,r_{G+1})T},} \end{aligned}$$
(5)

where \(\mu _l(i)\), \(l\in \mathbb N\), is given by

$$\begin{aligned} \mu _l(i)= & {} \left\{ \begin{array}{ll} \frac{1}{\lambda }\left[ 1-e^{-\lambda T}\sum \nolimits _{m=0}^{l}\frac{(\lambda T)^m}{m!}\right] \,, &{} i\ne G+1\\ \frac{1}{\lambda }\left[ 1-e^{-\lambda RT}\sum \nolimits _{m=0}^{l}\frac{(\lambda RT)^m}{m!}\right] \,, &{} i=G+1 \end{array}\right. . \end{aligned}$$
(6)

Proof

From the theory of Markov regenerative processes (see, e.g., [4], Theorem 4.7), the definition of \(p_{ki}\) and the structure of the traffic process \(\{L(t), \xi (t)\}\), it follows that

$$ p_{ki}=\frac{\sum _{j=0}^k u_{ji} \,\theta _{ji}(k)}{\sum _{l=1}^{G+1} r_l T_l}, $$

with \(\theta _{ji}(k)\) denoting the expected amount of time there are k vehicles in the system during an interval of time in phase i initiated with j vehicles in the system. From (2) and since \(\sum _{l=1}^{G+1} r_l T_l=(\sum _{j=1}^{G} r_j+ R r_{G+1})T\), in order to prove the theorem it remains to show that the quantities \(\theta _{ji}(k)\) are equal to the quantities \(\mu _{k-j}(i)\) defined in (6). This follows, for \(i\in \left\{ 1,2,\ldots ,G+1\right\} \) and \(0\le j\le k\), from the following set of equalities:

$$\begin{aligned} \theta _{ji}(k)= & {} \mathbb {E}\left[ \int _0^{T_j}\mathbf {1}_{\left\{ L(t)=k|L(0)=j,\xi (0)=i\right\} } \,d t\right] \\= & {} \int _0^{T_j}P\left( L(t)=k|L(0)=j,\xi (0)=i\right) \,d t\\= & {} \left\{ \begin{array}{ll} \displaystyle \int _0^{T}e^{-\lambda t}\frac{(\lambda t)^{k-j}}{(k-j)!}dt\,, &{} i\ne G+1\\ \displaystyle \int _0^{RT}e^{-\lambda t}\frac{(\lambda t)^{k-j}}{(k-j)!}dt\,, &{} i=G+1 \end{array}\right. \\= & {} \left\{ \begin{array}{ll} \frac{1}{\lambda }\left[ 1-e^{-\lambda T}\sum _{m=0}^{k-j}\frac{(\lambda T)^m}{m!}\right] , &{} i\ne G+1\\ \frac{1}{\lambda }\left[ 1-e^{-\lambda RT}\sum _{m=0}^{k-j}\frac{(\lambda RT)^m}{m!}\right] , &{} i=G+1 \end{array}\right. , \end{aligned}$$

where the last equality may be obtained using induction on \(k-j\) (see [10]).    \(\square \)

Let \(p_{k\bullet }\) denote the long-run fraction of time there are k vehicles in the system,

$$\begin{aligned} p_{k\bullet }= \lim _{t\rightarrow \infty } \left[ \frac{1}{t} \int _0^{t}\mathbf {1}_{\left\{ L(s)=k\right\} } ds\right] . \end{aligned}$$

Then, as \(p_{k\bullet }= \sum _{i=1}^{G+1} p_{ki}\), we conclude from Theorem 1 that for \(k\in \mathbb N\),

$$\begin{aligned} p_{k\bullet }= \frac{\sum _{i=1}^{G+1} \sum _{j=0}^k u_{ji} \,\mu _{k-j}(i)}{\left( \sum _{j=1, j\ne G+1}^{G} r_j+ R\, r_{G+1}\right) T}, \end{aligned}$$
(7)

with \(\mu _{k-j}(i)\) given in (6).

The following theorem provides a formula for the long-run mean number of vehicles in the system.

Theorem 2

The long-run mean number of vehicles in the system is given by

$$\begin{aligned} \mathbb E [L]&= \displaystyle \frac{\displaystyle \sum _{i=1}^{G+1} r_i \mathbb E [L_i] T_i}{\left( \displaystyle \sum _{j=1}^{G} r_j+ R r_{G+1}\right) T} + \frac{\lambda T}{2} \frac{\displaystyle \sum _{j=1}^{G} r_j+ R^2 r_{G+1}}{\displaystyle \sum _{j=1}^{G} r_j+ R r_{G+1}}. \end{aligned}$$
(8)

Proof

From the structure of the traffic process \(\{L(t), \xi (t)\}\) and the fact that

$$\begin{aligned} \mathbb E [L] = \lim _{t\rightarrow \infty } \left[ \frac{1}{t} \int _0^{t} \sum _{k=0}^{\infty } k\,\mathbf {1}_{\left\{ L(s)=k\right\} } \,d s\right] , \end{aligned}$$

it follows from the theory of Markov regenerative processes (see, e.g., [4], Theorem 4.7) that

$$\begin{aligned} \mathbb E [L] = \frac{\sum _{i=1}^{G+1} \sum _{k=0}^{\infty } u_{ki} \,\delta _{ki}}{\sum _{l=1}^{G+1} r_l T_l} \end{aligned}$$
(9)

with

$$ \delta _{ki} = \mathbb {E}\left[ \int _0^{T_i} \sum _{l=0}^\infty (k+l) \mathbf {1}_{\left\{ L(t)=(k+l)|L(0)=k,\xi (0)=i\right\} } \,d t\right] . $$

This equality can also be written as

$$\begin{aligned} \delta _{ki}&= \int _0^{T_i} \sum _{l=0}^{\infty } (k+l) P(L(t)=(k+l)|L(0)=k,\xi (0)=i)\,d t\\&= \int _0^{T_i} \sum _{l=0}^{\infty } (k+l) e^{-\lambda t}\frac{(\lambda t)^{l}}{l!}\,d t\\&= kT_i+\frac{\lambda T_i^2}{2}\,. \end{aligned}$$

From (9), taking into account (2) and the fact that \(\sum _{l=1}^{G+1} r_l T_l^2=(\sum _{j=1}^{G} r_j+ R^2 r_{G+1})T^2\), we have

$$ \mathbb E [L] =\frac{\sum _{i=1}^{G+1} r_i\sum _{k=0}^{\infty } k \pi _{ki} T_i}{(\sum _{j=1}^{G} r_j+ R r_{G+1})T}+\frac{\lambda }{2} \frac{\left( \sum _{j=1}^{G} r_j+ R^2 r_{G+1}\right) T^2}{(\sum _{j=1}^{G} r_j+ R r_{G+1})T}. $$

The expression (8) for \(\mathbb E [L]\) now follows since \(\sum _{k=0}^{\infty } k \pi _{ki}= \mathbb E [L_i]\).    \(\square \)

When assessing traffic systems, delay of vehicles is a major concern. The long-run distribution of the sojourn time of a vehicle in the system is complex, but can be derived following a procedure similar to the one used in Sect. 4 of [15], with the necessary adaptations. One immediate contribution can be put in terms of the computation of the long-run mean sojourn time of a vehicle in the system, \(\mathbb E [W]\). According to our model, it can be derived from Little’s formula (cf. for instance [9]) applied to expression (8), giving:

$$\begin{aligned} \mathbb E [W]=\frac{\mathbb E [L]}{\lambda }= \displaystyle \frac{\displaystyle \sum _{i=1}^{G+1} r_i \mathbb E [L_i] T_i}{\lambda T\left( \displaystyle \sum _{j=1}^{G} r_j+ R r_{G+1}\right) } + \frac{T}{2} \frac{\displaystyle \sum _{j=1}^{G} r_j+ R^2 r_{G+1}}{\displaystyle \sum _{j=1}^{G} r_j+ R r_{G+1}}. \end{aligned}$$
(10)

The setting considered in this paper allows extensions of the green signal, which occur when there are cars waiting to be served at the end of the minimum duration of a green period. An important measure is the long-run mean number of extensions (or equivalently the time of extension) of a green period, which is clearly not constant as it is the case in a non-actuated signalized intersection.

Let us consider a random variable \(N_G\) whose distribution is the long-run distribution of the number of extensions of the green period. By establishing that \(P(N_G > k-1) = \frac{r_{M+k}}{r_M}\), for \(k=1, 2,\ldots , G-M\), one can conclude that the long run fraction of green periods with k extensions is

$$\begin{aligned} P(N_G=k) = {\left\{ \begin{array}{ll} \displaystyle \frac{r_{M+k}-r_{M+k+1}}{r_M}, &{} k=0,1,\ldots ,G-M-1 \\ \displaystyle \frac{r_{G}}{r_M}, &{} k=G-M \end{array}\right. } \end{aligned}$$
(11)

and the long-run mean number of extensions of the green period is

$$\begin{aligned} \mathbb E [N_G] = \displaystyle \sum _{k=1}^{G-M}\frac{r_{M+k}}{r_M}. \end{aligned}$$
(12)

4 Case Study

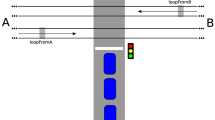
In order to illustrate the applicability of the formulation that we propose, we consider an intersection with 3 traffic streams having a primary phase and a secondary phase as illustrated in Fig. 1. The primary phase, associated to the two main traffic streams, is not actuated. A sensor is placed two meters before the stop line on the secondary street and the control of the secondary phase, associated to this street, is actuated by means of the information provided by the sensor (inter-arrival times). The time plan is the following: \(M=4\), \(G=15\), \(R=15\). We consider \(T=2 \, \mathrm{s}\). With this time plan, the maximum duration of extended green is \(T(G-M)=22\,\mathrm{s}\). The vehicle arrival rate on the main street is assumed to be 800 veh/hour for each stream. The performance measures that we present correspond only to the actuated stream. Note that, in this situation, the vehicle arrival rates on the main street do not influence the measures on the secondary street.

Fig. 1.
figure 1

Scheme of the intersection, indicating the two phases. (Color figure online)

Full size image
Fig. 2.
figure 2

Comparison between estimates provided by the Markov chain based model and by the microsimulation model: long-run mean delay of drivers (top); and long-run mean queue length (bottom).

Full size image

Regarding the microsimulator, the following set up was used (see [19] for details):

  • vehicle’s characteristics: desired speed - Gaussian \((13.9\, \mathrm{m/s}, 0.2\,\mathrm{m/s})\); maximum acceleration - Gaussian \((1.7\,\mathrm{m/s^2}, 0.3\,\mathrm{m/s^2})\); length of a vehicle - Gaussian \((4.0\,\mathrm{m}, 0.3\,\mathrm{m})\);

  • number of replications: between 100 and 1000, depending on arrival rate, controlling for the standard deviation of the Monte-Carlo error to be smaller than 1;

  • warm up time: \(600\,\mathrm{s}\);

  • run time: 2 h/replica.

Vehicle’s characteristics have been set on the basis of information collected concerning the real operations of traffic in urban areas (see [19]). In the simulator, vehicles move according to a car-following model, that is, essentially drivers adapt the speed of their vehicles to that of the vehicle in front of them, so that their heading is kept above a minimum value which corresponds to the drivers perception of safety (see, e.g. [16] for a review of car-following models). This level of detail in the description of the behaviour of vehicles, which is typical of micro-simulation models, is not possible in the Markov model that we propose.

Fig. 3.
figure 3

Estimates of the long-run mean queue length provided by the Markov chain based model: long-run mean queue length; long-run mean queue length at the start of the green signal; long-run mean queue length at the start of the red signal (overflow queue).

Full size image

Figure 2 shows estimates of the long-run mean waiting time of drivers and the long-run mean duration of the green signal obtained by the model presented in the previous sections together with the results obtained by using the simulation model described in [19], considering different vehicle arrival rates on the secondary street. We use the word “Markov” in the figures to refer to the proposed model.

The long-run mean queue length in depicted in Fig. 3, along with the long-run mean queue length at two different time points that are of interest in the signal cycle, namely at the start of the green signal and at the start of the red signal.

We can see the exponential increase of the mean waiting time when the vehicle arrival rate increases, as expected. The results suggest that, from moderate values of the vehicle arrival rate to considerable higher values (but away from the saturation level) the estimates of the mean delay of drivers given by the Markov based model through expressions (8)–(10) are quite close to the simulation results. Unfortunately the approximation is not so good when we consider very large vehicle arrival rates (i.e. close to the saturation level). This fact may be explained by the diversity of reactions that are typical of drivers’ behaviour and of interactions between vehicles which is mimicked in the simulation model quite closely (cf. [19]) but is hardly taken into account in a Markov or renewal type process modelling. For instance, drivers may decelerate promptly when approaching a slowing vehicle or queue. Interactions between vehicles have a major impact when system parameters are close to the boundary of the stationarity region of the traffic system. We can also observe the exponential increase of the queues when the vehicle arrival rate increases, as expected, and an increasing mean duration of the green period due to the occurrence of several extensions of the green period becoming common.

5 Conclusions and Future Work

A detailed probabilistic description of the delay of vehicles in semi-actuated signalized traffic intersections, as well as of the length of queues and the duration of the green signal can be obtained by considering an M/D/1 queue with server vacations and using, for its investigation, a Markov-regenerative process that keeps track of the number of vehicles at the intersection along the phase of the signal cycle over time.

When compared to simulation results, the expressions that we give in the paper provide realistic estimates of the relevant performance measures investigated. However, for large traffic flows (congestion scenarios) the queue length and delay measures obtained from the proposed model tend to be larger than the estimates returned by the numerical simulator.

Future work will address the extension of the analysis for the case of semi-actuated control in which extensions are also allowed for the red signal.