New Multi-criteria Decision-Making Based on Fuzzy Similarity, Distance and Ranking

Abstract

We propose a new method for group decision making by using trapezoidal fuzzy numbers to describe decisions. A team of decision makers (or experts) must choose the most appropriate alternative using fuzzy logic. Each expert will give his opinion about every alternative in accordance with the criteria of choice by a fuzzy number. The decisions taken are aggregated respecting the similarity and dissimilarity (distance) between each pair of opinions, in addition to the hierarchical weights (importance) of each decision-maker (DM). The result is a fuzzy number representing the general appreciation of each alternative. In order to able to choose one, an appropriate ranking method is proposed. In this article we treat four issues, namely, similarity and distance between opinions represented by fuzzy numbers, aggregation of opinions while preserving similarity and in accordance with the hierarchical weight, and finally ranking fuzzy numbers.

Abridged version.

1 Introduction

In a decision-making situation, conflicting and agreeing opinions emerge. The main problem is how to find a reasonable method to aggregate individual opinions into a group consensus opinion. In the fuzzy logic framework, several methods aim to reach the consensus by fuzzy preference relation. Otherwise, two methods have been studied by computing the cohesion between each pair of DMs. Firstly, Hsu and Chen [1] proposed the similarity aggregation method (SAM). One of its weaknesses is that it requires the intersection of the estimations to a certain level in order to calculate the similarity between each pair of opinions. Secondly, the approach of Lu et al. [2] computes the consistency on the basis of similarity and distance. Our work concerns some variations and improvements of these approaches. First, each DM will evaluate each alternative under the criteria of evaluation, and the importance of each criterion by a trapezoidal fuzzy number or a linguistic variable. Then the individual fuzzy opinions will be aggregated according to the proposed method in order to obtain the fuzzy collective opinions for each alternative. After that, a ranking method is proposed to classify the alternatives. Many systematic comparisons with earlier works are given to show the effectiveness of our method.

This abridged version is organized as follows. Section 2 introduces some notations. Section 3 defines our notions of distance, similarity, aggregation, ranking and their properties. In Sect. 4, we give comparisons with earlier works. Section 5 summarizes the steps of our Multi-criteria Decision Making (MCDM) method with a numerical example. Section 6 concludes the paper.

2 Preliminaries

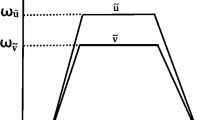
A fuzzy number $\tilde{A}$ [3] is a fuzzy set defined by its membership function $\mu_{{\tilde{A}}}$: ${\mathbb{R}} \to [0,1]$. We restrict ourselves to trapezoidal fuzzy numbers (cf. Fig. 1) given by 4-tuples (a, b, c, d) where a $\leqslant$ b $\leqslant$ c $\leqslant$ d and represented by:

Fig. 1.

Trapezoidal fuzzy number

Considering two trapezoidal fuzzy numbers $\tilde{A}$ (a ₁, b ₁, c ₁, d ₁) and $\tilde{B}$ (a ₂, b ₂, c ₂, d ₂), the inverse Eq. (1), the fuzzy addition Eq. (2), multiplication Eq. (3), and division Eq. (4) are defined as follows:

$$ 1/\tilde{B} = (1/d_{2} ,1/c_{2} ,1/b_{2} ,1/a_{2} ). $$

(1)

$$ \tilde{A} \oplus \tilde{B} = (a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} ,d_{1} + d_{2} ). $$

(2)

$$ \tilde{A} \otimes \tilde{B} = (a_{1} *a_{2} ,b_{1} *b_{2} ,c_{1} *c_{2} ,d_{1} *d_{2} ). $$

(3)

$$ \tilde{A}\, {\emptyset }\,\tilde{B} = (a_{1} /d_{2} ,b_{1} /c_{2} ,c_{1} /b_{2} ,d_{1} /a_{2} ). $$

(4)

Note that these operations preserve the trapezoidal shape. Furthermore we suppose our fuzzy numbers have positive supports and are normalized.

Each DM will make his opinion either by constructing his own trapezoidal fuzzy number or by linguistic variables that will be converted into a trapezoidal fuzzy number as shown in the next figures. Figure 2 is to qualify the importance of each criterion. Figure 3 is to qualify alternatives in accordance to the criteria.

Fig. 2.

Linguistic variables for each criterion

Fig. 3.

Linguistic variables for ratings

3 Similarities, Aggregation and Ranking

Lu et al. [2] noted that similarity should not only contain the commonalities as calculated by Eq. (5), but also dissimilarity which can be represented by a distance D ₁. So they proposed the coherence Eq. (6) which is extremely depending on the parameter of calculation.

$$ S_{w} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right) = \frac{{\int_{x} {\left( {\hbox{min} \left\{ {\mu_{{\tilde{R}_{i} }} (x),\mu_{{\tilde{R}_{j} }} (x)} \right\}} \right)}^{2} dx}}{{\int_{x} {\left( {\hbox{max} \left\{ {\mu_{{\tilde{R}_{i} }} (x),\mu_{{\tilde{R}_{i} }} (x)} \right\}} \right)}^{2} dx}}. $$

(5)

$$ r\left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right) = \beta *S_{w} \left( {A,B} \right) + \left( {1 - \beta } \right)*(1 - D_{1} \left( {A,B} \right)) $$

(6)

where 0 $\leqslant$ β  $\leqslant$ 1.

For $\tilde{R}_{1} = \left( {a_{1} ,b_{1} ,c_{1} ,d_{1} } \right), \tilde{R}_{2} = (a_{2} ,b_{2} ,c_{2} ,d_{2} )$ two trapezoidal fuzzy numbers, set

$$ \begin{array}{*{20}c} {A = \frac{1}{2}\int_{{a_{1} }}^{{d_{1} }} {\mu_{1} - \hbox{min} \left( {\mu_{1} ,\mu_{2} } \right)} + \frac{1}{2}\int_{{a_{2} }}^{{d_{2} }} {\mu_{2} } - \hbox{min} \left( {\mu_{1} ,\mu_{2} } \right),} \\ {B = \int_{{min(c_{1} ,c_{2} )}}^{{max(b_{1} ,b_{2} )}} {1 - max(\mu_{1} ,\mu_{2} )^{2} .} } \\ \end{array} $$

We introduce the following distance

$$ D_{1} = \left\{ {\begin{array}{*{20}c} {A,} & {if\,\hbox{max} \left( {b_{1} ,b_{2} } \right) \,{<} \, min(c_{1} ,c_{2} )} \\ {A + B,} & {else.} \\ \end{array} } \right. $$

(7)

In order to normalize D ₁, we must divide it by a parameter M = 10 which is the maximum of the notation scale. In the sequel we will continue to denote by D ₁ the normalized distance.

For p a positive real number, we define the new parameterized similarity defined by:

$$ r_{p} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right) = \frac{1}{p + 1}*\left\{ {p + S_{w} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)} \right\}*\left\{ {1 - D_{1} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)} \right\}. $$

(8)

The similarities (8) are quasi-equivalent regarding the parameter p which is not the case of the similarities (6) regarding the parameter β. Quasi-equivalent fuzzy similarities where defined in [4]. The individual global cohesion of the i^th DM 1 $\leqslant$ i $\leqslant$ n is calculated by the equation:

$$ GC_{i} (t,s) = \sum\limits_{j = 1}^{n} {\left\{ {r_{p} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)} \right\}^{t} \{ e_{j} \}^{s} } $$

(9)

where t, s are positive real numbers, $e_{1} , \ldots ,e_{n}$ are hierarchical weights with 0 $\leqslant$ e _i $\leqslant$ 1 and $\sum\nolimits_{i = 1}^{n} {e_{i} = 1.}$

The consistency of the i^th decision maker, is calculated by the equation:

$$ C_{i} = \frac{{GC_{i} }}{{\mathop \sum \nolimits_{j = 1}^{n} GC_{i} }}. $$

(10)

The collective decision for an alternative according to one criterion is given by:

$$ \tilde{R} = \mathop \sum \limits_{i = 1}^{n} C_{i} \otimes \tilde{R}_{i} . $$

(11)

In the context of MCDM we have n decision makers, m criteria and K alternatives. We will denote by $\tilde{w}_{{c_{1} }} , \ldots ,\tilde{w}_{{c_{m} }}$ the fuzzy trapezoidal weights of the m criteria.

For the needs of ranking we introduce the score of each alternative as

$$ \tilde{N}_{i} = \left( {\mathop \sum \limits_{i = 1}^{m} \tilde{R}\left( i \right) \otimes \tilde{w}_{{c_{i} }} } \right)\, {\emptyset}\,\mathop \sum \limits_{i = 1}^{m} \tilde{w}_{{c_{i} }} $$

(12)

where 1 $\leqslant$ i $\leqslant$ m and $\tilde{R}(i)$ is calculated by (12). For each trapezoidal number $\tilde{A}(a,b,c,d)$ we define the following rank:

$$ F(\tilde{A}) = M - \frac{1}{3}*\int_{{c_{i} }}^{M} {\left( {1 - \mu_{i}^{2} } \right)} - \frac{2}{3}*\int_{0}^{bi} {M - \left( {1 - \mu_{i} } \right)} . $$

(13)

where M = 10. We have:

$$ F(\tilde{A}) = \frac{1}{3}*a_{i} + \frac{1}{3}*b_{i} + \frac{2}{9}*c_{i} + \frac{1}{9}*d_{i} . $$

(14)

We denote by $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$ if and only if $F(\tilde{A}_{1} ) \ge F(\tilde{A}_{2} )$, and $\tilde{A}_{1} \sim \tilde{A}_{2}$ if and only if $F(\tilde{A}_{1} ) = F(\tilde{A}_{2} )$. Here, the symbol $\underline{\succ }$ means better than and the symbol ~ means the same ranking.

Let $\tilde{A}_{1} ,\tilde{A}_{2} \;{\text{and}}\; \tilde{A}_{3}$ three fuzzy numbers it is easy to verify the following six reasonable ordering properties introduced in [5, 6].

Property 1:

if $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$ and $\tilde{A}_{2} \,\underline{\succ }\, \tilde{A}_{1}$ then $\tilde{A}_{1} \sim \tilde{A}_{2}$.

Property 2:

if $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$ and $\tilde{A}_{2} \,\underline{\succ }\, \tilde{A}_{3}$ then $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{3}$.

Property 3:

if $\tilde{A}_{1} \, \cap \,\tilde{A}_{2} \, = \,\emptyset \;{\text{and}}\;\tilde{A}_{1}$ is at the right of $\tilde{A}_{2}$ then $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$.

Property 4:

the order of $\tilde{A}_{1} \;{\text{and}}\;\tilde{A}_{2}$ is not affected by the other fuzzy numbers under comparison.

Property 5:

if $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$ then $\tilde{A}_{1} \oplus \tilde{A}_{3} \,\underline{\succ }\, \tilde{A}_{2} \oplus \tilde{A}_{3} .$

Property 6:

if $\tilde{A}_{1} \,\underline{\succ }\, \tilde{A}_{2}$ then $\tilde{A}_{1} \otimes \tilde{A}_{3} \,\underline{\succ }\, \tilde{A}_{2} \otimes \tilde{A}_{3} .$

It is easy to prove that the aggregation method proposed fulfils the properties presented in [2]. If all values are crisp, or if there is no intersection between each couple of the fuzzy opinions of DMs in order that the similarity term S _w will have no influence on the coherence, we will choose p → +∞ leading to:

$$ r_{\infty } \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right) = 1 - D_{1} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right). $$

(15)

4 Comparisons with Earlier Works

In this section, we will compare at first the proposed coherence based on similarities, with existing similarity methods. Figure 4 shows the compared sets, and Table 1 the numerical values of the similarities under comparison, in addition to the proposed method with different values of its parameter p.

Fig. 4.

Compared fuzzy sets (similarity)

Table 1. Compared fuzzy similarities

Lee’s method [7] fails to calculate the similarity of the 2^nd configuration because of the denominator required by the method, as it does not distinguish between the 5^th, 6^th and 7^th configurations even though they are clearly different.

Chen’s method [8] produces the same result for the 5^th, 6^th and 12^th configurations and configurations from 7 to 11, even though they are all different from each other.

Chen’s method [9] does not distinguish the 9^th and 10^th configurations even if they are different. It presents a brutal jump as soon as there is intersection between the compared fuzzy numbers, the last remark is valid for the method proposed in [11] as well as Young’s method [10], that can be illustrated by the 7^th and 8^th configurations.

Observing the configurations 5 and 6, one realizes that they are very similar, resulting in values of similarity nearby for all methods otherwise identical, the method proposed by Allahivandro et al. [11] offers very distinct values, while the 5^th configuration is more similar to the 6^th as the 3^rd or the 7^th configuration, unlike the values proposed by the method.

Several methods were proposed to rank fuzzy numbers [12,13,14,15,16,17,18,19,20,21,22]. In this section, we use six sets to compare the method proposed to rank fuzzy numbers (Fig. 5). The Table 2a and b show the results for the six sets.

• Set 1: it is obvious that $\tilde{B}$ should be greater than $\tilde{A},$ however the method proposed by Cross and Setness in [17] fails to distinguish the compared fuzzy numbers. The method proposed by Ramli and Mohamad in [19] is extremely depending on the parameter of calculation, and occur in an incorrect ranking if the parameter is not well-chosen.

• Set 2: from Set 2 we can see that the figure shows two different fuzzy numbers. However the methods proposed in [12, 13, 15, 17, 21, 22] and [19] for β = 0.5 fail to distinguish them. The method proposed in [19] for β = 0 get incorrect ranking.

• Set 3: from Set 3 we can see that the figure shows two different fuzzy numbers however the methods proposed in [12,13,14,15, 17, 20,21,22] and [19] β = 0.5 fail to distinguish them. The method proposed in [19] for β = 1 results in incorrect ranking.

• Set 4: the methods proposed in [12,13,14,15, 17, 19] cannot calculate the ranking value for the second fuzzy number under comparison.

• Set 5: except the method proposed in [17, 19] all other methods result in correct ranking.

• Set 6: recent methods proposed in [21, 22] propose the ranking $\tilde{A} \,{<}\, \tilde{B} \,{<}\, \tilde{C}$ which is the same order proposed in [12, 13, 18] and in our method. The other methods [14,15,16,17, 19, 20] result in a wrong ranking.

Fig. 5.

Compared fuzzy sets (ranking)

Table 2. Compared ranking methods.

5 Steps of the Proposed MCDM Method

The successive steps of our MCDM are:

• Step 1: Each DM assesses the importance of each criterion either by linguistic variable as shown in Fig. 2 that will be translated into trapezoidal fuzzy number, or by building its own trapezoidal fuzzy number.

• Step 2: each DM evaluates each alternative depending on the assessment criteria. This evaluation also is either by linguistic variable as shown in Fig. 3 that will be translated into trapezoidal fuzzy number, or by building its own trapezoidal fuzzy number.

• Step 3: calculate the similarity $S_{w} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)$ between each couple of DMs by Eq. (5) for each alternative under the chosen criteria.

• Step 4: calculate the distance $D_{1} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)$ between each couple of DMs by Eq. (7) for each alternative under the chosen criteria.

• Step 5: choose the parameter p and calculate the coherence $r_{p} \left( {\tilde{R}_{i} ,\tilde{R}_{j} } \right)$ between each couple of DMs by Eq. (8) for each alternative under the chosen criteria.

• Step 6: choose the parameters t and s and calculate the individual global coherence GC _i for each expert by Eq. (9) for each alternative under the chosen criteria.

• Step 7: calculate the consistency of each decision C _i for each expert by Eq. (10) for each alternative under the chosen criteria.

• Step 8: aggregate the fuzzy decision in accordance to Eq. (11) to obtain the collective appreciation for each alternative under the chosen criteria.

• Step 9: calculate the final score for each alternative $\tilde{N}_{i}$ by Eq. (12).

• Step 10: deffuzify the final value according to Eq. (14) to obtain the ranking.

We illustrate the proposed method by using the example given by Chen [23]. A company desires to select the suitable supplier from 5 alternatives (A ₁, A ₂, A ₃, A ₄, A ₅). Three decision makers with the following hierarchical weight (e ₁ = 0.42; e ₂ = 0.25; e ₃ = 0.33) are responsible for making the choice, using five criteria (C ₁, C ₂, C ₃, C ₄, C ₅) adopting the notations of Figs. 2 and 3 (cf. the Tables 3a and b and 4 below).

Table 3. Ratings of the five suppliers by DM

Table 4. Importance weights of criteria from DM

6 Conclusion

In this article, we presented an approach to decision-making by introducing new distance, consistency, aggregation and ranking methods. The general idea is that the opinion of each DM would have larger weight in aggregation if it is more consistent with other opinions taking into account the hierarchical weights. The ranking is based on the idea of the TOPSIS method: the alternative with the score closest to the ideal goal and farthest possible from the worst solution would be the best one. We have implemented our MCDM method which compares favorably with earlier works.