Keywords

1 Introduction

The empirical mode decomposition (EMD) method and the Hilbert–Huang transform were introduced in [8] to analyze nonstationary and nonlinear signals. The EMD method is a decomposition process to reduce any given data into a collection of intrinsic mode functions (IMFs) to which the Hilbert spectral analysis can be applied.

An IMF represents a simple oscillatory mode as a counterpart to the simple harmonic function but with variable amplitude and frequency along the time axis. In [8], IMF is defined as a function for which the cubic spline envelope through the maxima coincides with the negative of the cubic spline envelope through the minima.

The EMD has proven to be very effective in great variety of applications. The convergence of the method, its properties, and alternative characterizations of IMF inspired intense research in the area. Among the major results are the B-spline EMD, introduced in [3], and the synchrosqueezed wavelet transform, introduced in [4].

The EMD is a procedure to decompose a signal into intrinsic mode functions with presumably well-defined instantaneous frequencies. The analytic signal for a real f is \(F=f+iHf\) where \(Hf(t)=\mathrm{p.v.}\int _{-\infty }^\infty \frac{f(x)}{t-x}\; dx\) is the Hilbert transform of f. In the case of a periodic f, the Hilbert transform is replaced by the conjugate operator \(Hf(t)=\frac{1}{2\pi }\int _{-\pi }^\pi f(x)\tan \frac{t-x}{2}\; dx\). The frequency of f is denoted by \(\theta (t)\) and is defined through the relation \(\tan \theta (t)=\frac{Hf(t)}{f(t)}\) and its derivative is the instantaneous frequency, that is,

$$ \theta '(t)=\frac{Hf'(t)f(t)-Hf(t)f'(t)}{f^2(t)+Hf^2(t)}. $$

In order to have a meaningful definition from a physical point of view, \(\theta '\) has to be positive.

In this paper, we study relations between the Fourier coefficients of a periodic function and the properties expected from IMF. In [10], we discussed that the function \(\psi (t)=e^{\varepsilon \cos t}\sin (\varepsilon \sin t)\) has upper and lower envelopes differing only by sign for any \(\varepsilon >0\), but the instantaneous frequency is negative for \(\varepsilon =2.97\). The Fourier spectrum of \(\psi \) has a peak at 3 and is spread over all frequencies. Our interest in this paper is to provide sufficient conditions on the Fourier coefficients such that the resulting function is an IMF with positive frequency. The functions that we consider have dominant frequency and we are interested in how the Fourier coefficients can spread from that frequency while preserving the properties expected from IMF. In the next section, we provide sufficient conditions for positiveness of the instantaneous frequency, number of zeros and extrema, and the proximity of upper and lower envelopes. In Sect. 3 in a series of numerical examples, we discuss the necessity of the conditions. Functions for which the number of zeros and the number of extrema differ by at most 1 are called weak IMF. A special class of variable frequencies \(\theta \) that generate an orthogonal basis of weak IMF in \(L_2\) is considered in Sect. 4.

2 Intrinsic Trigonometric Mode Polynomials

In this section, we consider functions with dominant frequency. Without loss of generality, we assume that n is the dominant frequency and the corresponding harmonic is \(\cos nt\). The function \(\cos nt\) is an ideal IMF with a derivative \(-n\sin nt\) and interlacing extrema

$$\begin{aligned} x_j=\frac{2j}{n}\pi , \;\;\; y_j=\frac{2j+1}{n}\pi , \;\;\; j=0,1,\ldots , n-1 \end{aligned}$$
(1)

where \(x_j\) are the zeros of \(\sin \frac{nt}{2}\) and \(y_j\) are the zeros of \(\cos \frac{nt}{2}\). The main problem we study is how to add harmonics and preserve the positive instantaneous frequency and the IMF properties. Since \(\cos nt\) is our starting function, we define upper and lower envelopes as the interpolating trigonometric polynomials to f at the two sets of points x and y, defined in (1).

Definition 1

For positive integers n and \(l(l<n)\), a trigonometric polynomial with real coefficients \(c_j\) and real \(\beta _j, j=1,\ldots \),

$$\begin{aligned} f(t)=\cos nt +\sum _{j=n-l, j\ne n}^{n+l}c_j\cos (jt+\beta _j), \end{aligned}$$
(2)

is an intrinsic trigonometric mode polynomial (ITMP) if it has positive instantaneous frequency and the interpolating trigonometric polynomials at each of the two collections \(x_j, j=0,\ldots ,n-1\) and \(y_j, j=0,\ldots ,n-1\) differ only by sign.

The coefficients \(c_j\) are the spectrum of f. The example from the introduction is the reason why we consider the spectrum of candidate IMF bounded from above by twice the dominant frequency. The points x and y are not extrema of the function, but if

$$\begin{aligned} A(n,l)=\sum _{j=n-l,\; j\ne n}^{n+l}|c_j| \end{aligned}$$
(3)

is small, then f has maxima close either to the points x or to y, depending on oddity of n, and minima close to the other set, more details are considered in Lemma 2. In the next three lemmas, we provide upper bounds for A(n, l) in order that the corresponding polynomial (2) to be an ITMP. Our first result is a sufficient condition for a positive instantaneous frequency.

Lemma 1

A polynomial f of the form (2) has a positive instantaneous frequency if

$$ A(n,l)<\frac{n}{n+\frac{l}{2}+\sqrt{\left( n+\frac{l}{2}\right) ^2+n(n+l)}}, \; l=1,\ldots , n-1. $$

Proof

For the periodic function f, the analytic signal is \(F(t)=f(t)+i Hf(t)=r(t)e^{i\theta (t)}\) where \(Hf(t)= \sin nt +\sum _{j=n-l,\; j\ne n}^{n+l}c_j\sin (jt+\beta _j)\) is the conjugate function of f. The amplitude of f is defined as \(r(t)=\sqrt{f^2(t)+Hf^2(t)}\) and the instantaneous frequency is defined as \(\theta '(t)=\frac{Hf'(t)f(t)-Hf(t)f'(t)}{f^2(t)+Hf^2(t)}\). Let \(c_n=1\) and \(\beta _n=0\), then in terms of the coefficients \(c_j\), we have that

$$\begin{aligned} r^2(t)\theta '(t)= & {} \left( \sum _{j=n-l}^{n+l}jc_j\cos (jt+\beta _j)\right) \left( \sum _{j=n-l}^{n+l}c_j\cos (jt+\beta _j)\right) \\+ & {} \left( \sum _{j=n-l}^{n+l}jc_j\sin (jt+\beta _j\right) \left( \sum _{j=n-l}^{n+l}c_j\sin (jt+\beta _j))\right) \\= & {} \sum _{j=n-l}^{n+l}jc_jf_j(t) \end{aligned}$$

where \(f_j(t)=\sum _{k=n-l}^{n+l}c_k\cos ((k-j)t+\beta _k-\beta _j)\). Since n and l are fixed, to simplify the notations, we set \(A=A(n,l)\). By using the estimates \(f_n>1-A\) and \(|f_j|\le A+1\) for \(j\ne n\), we have that

$$\begin{aligned} r^2(t)\theta '(t)= & {} nf_n(t)+\sum _{j=n-l,\; j\ne n}^{n+l} jc_jf_j(t) \ge n(1-A)-\sum _{j=n-l, j\ne n}^{n+l} j|c_j|(1+A)\\\ge & {} n(1-A)-(1+A)\sum _{j=n-l, j\ne n}^{n+l} j|c_j|\ge n(1-A)-(n+l)(1+A)A\\= & {} -(n+l)A^2-(2n+l)A+n. \end{aligned}$$

From the choice of \(A<\frac{n}{n+\frac{l}{2}+\sqrt{\left( n+\frac{l}{2}\right) ^2+n(n+l)}}\), it follows that the quadratic polynomial above is positive for \(0<l<n\). To finish the proof, we need to show that \(r^2>0\). Similarly to the above, we have for \(r^2=f^2+Hf^2\) that

$$ f^2+Hf^2=\sum _{j=n-l}^{n+l}c_jf_j=f_n+\sum _{j=n-l,\; j\ne n}^{n+l}c_jf_j\ge 1-A-A(1+A)=2-(A+1)^2 $$

and is positive for \(A<\sqrt{2}-1\). Since the estimate for A(n, l) is decreasing as a function of l and for \(l=0\) equals \(\sqrt{2}-1\), we complete the proof of the lemma. \(\square \)

In [10], we defined a weak IMF as a function whose number of zeros and number of extrema differ at most by one. The next lemma provides a sufficient condition in terms of A(n, l), defined in (3), for a polynomial of type (2) to be a weak IMF.

Lemma 2

A polynomial f of type (1) is a weak IMF if

$$ A(n,l)<\frac{n^2}{(n+l)\sqrt{n^2+(n+l)^2}}, \; l=1,\ldots , n-1. $$

Proof

Since we consider n and l fixed throughout the proof, we set \(A=A(n,l)\). We prove that under the assumption for A the polynomial f has exactly 2n zeros and 2n extrema on \([0,2\pi )\). The function \(P(t)=f(t)-\cos nt\) is a trigonometric polynomial of degree at most \(n+l\) and as such from Bernstein’s inequality for trigonometric polynomials it follows that \(|P^{(k)}|\le (n+l)^k\Vert P\Vert _\infty \le (n+l)^kA\). The polynomial f has a zero between any two consecutive \(\xi _j=\frac{j}{n}\pi \) for \(j=0,\ldots ,2n-1\). Indeed, \(f(\xi _j)=\cos n\xi _j+P(\xi _j)=(-1)^j+P(\xi _j)\) and, since \(A<1\), we have that \(f(\xi _j)\) has sign \((-1)^j\). If we assume that there are two zeros, say \(z_1<z_2\), between \(\xi _j\) and \(\xi _{j+1}\), then from Rolle’s theorem it follows that \(f'(e)=0\) for some point \(e\in (z_1,z_2)\). Furthermore, from \(0=f(z_1)=\cos nz_1+P(z_1)\) we have that \(|\cos ( nz_1)|=|P(z_1)|\le A\). The same estimate holds at \(z_2\), and since \(\cos nt\) is strictly monotone on \((\xi _j,\xi _{j+1})\), it follows that \(|\cos nt|<A\) on \((z_1,z_2)\) and hence \(|\sin nt|>\sqrt{1-A^2}\) on \((z_1,z_2)\). On the other hand, for the derivative \(f'(t)=-n\sin nt+P'(t)\) on the interval \((z_1,z_2)\) we have that \(|f'|\ge n\sqrt{1-A^2}-(n+l)A>0\) for \(A<\frac{n}{\sqrt{n^2+(n+l)^2}}\). We arrived at contradiction with the assumption that there are two zeros between \(\xi _j\) and \(\xi _{j+1}\).

From \(f'(t)=n(-\sin nt+\frac{P'(t)}{n})\) and \(\frac{|P'|}{n}<\frac{n+l}{n}A<1\), we have that \(f'\) has a zero between any two consecutive \(z_j=\frac{2j+1}{2n}\pi , j=0,\ldots ,2n-1\). If we assume that there are at least two, say \(e_1\) and \(e_2\), on one of those intervals, then from Rolle’s theorem it follows that there is an inflection point on that interval. Similarly to the case for the count of the zeros of f, we estimate \(|\cos nt|> \sqrt{1-\frac{(n+l)^2}{n^2}A^2}\) and \(|f''(t)|>n^2\sqrt{1-\frac{(n+l)^2}{n^2}A^2}-P''(t)>n^2\sqrt{1-\frac{(n+l)^2}{n^2}A^2}-(n+l)^2A>0\) for the choice of A. Again, we arrived at contradiction and hence f has exactly 2n zeros and 2n extrema on \([0,2\pi )\). The proof of the lemma is complete. \(\square \)

For polynomials of type (2) with symmetric spectrum, i.e., \(c_{n+k}=c_{n-k}\), and \( \beta _{n+k}=-\beta _{n-k}, k=1,\ldots ,n-1\) the condition on A(n, l) from Lemma 1 can be relaxed.

Corollary 1

Let \(R_{n-1}(t)=1+\sum _{j=1}^{n-1}c_j\cos (jt+\beta _j)\); then, the function \(f(t)=R_{n-1}(t)\cos nt\) has symmetric spectrum with respect to the dominant frequency n, \(\theta '=n\) if \(\sum _{j=1}^{n-1}|c_j|<1 \), and is a weak IMF if \(\sum _{j=1}^{n-1}|c_j|<\frac{1}{2\sqrt{5}} \).

Proof

It is a straightforward computation to check that f has symmetric spectrum. For \(\sum _{j=1}^{n-1}|c_j|<1 \) the polynomial \(R_{n-1}\) is positive and from [9], Theorem 3.1, it follows that \(R_{n-1}(t)\cos nt\) has instantaneous frequency n. In the case \(\sum _{j=1}^{n-1}|c_j|<\frac{1}{2\sqrt{5}} \), from Lemma 2, with \(l=n-1\), it follows that f is a weak IMF. \(\square \)

Our last lemma in the section holds for any trigonometric polynomial of degree less than 2n and is similar in nature to the results in [13].

Lemma 3

For \( T_n(t)=\frac{a_0}{2}+\sum _{j=1}^{2n-1} (a_j\cos jt+b_j\sin jt) \), the trigonometric interpolant at \(x_j, j=0,\ldots ,n-1 \), defined by (1), is

$$\begin{aligned} U_{n}(t)= & {} \frac{A_0}{2}+\sum _{j=0}^{\frac{n}{2}-1}( A_j\cos jt +B_j \sin jt)+\frac{A_{\frac{n}{2}}}{2}\cos \frac{n}{2}t,\\ A_j= & {} a_j+a_{n-j}+a_{n+j}+a_{2n-j}, j=0,\ldots ,\frac{n}{2}\\ B_j= & {} b_j-b_{n-j}+b_{n+j}-b_{2n-j}, j=1,\ldots ,\frac{n}{2}-1, \end{aligned}$$

and the trigonometric interpolant at \(y_j, j=0,\ldots ,n-1\), defined by (1), is

$$\begin{aligned} L_{n}(t)= & {} \frac{C_0}{2}+\sum _{j=0}^{\frac{n}{2}-1}( C_j\cos jt +D_j \sin jt)+\frac{C_{\frac{n}{2}}}{2}\cos \frac{n}{2}t,\\ C_j= & {} a_j-a_{n-j}-a_{n+j}+a_{2n-j}, j=0,\ldots ,\frac{n}{2}\\ D_j= & {} b_j+b_{n-j}-b_{n+j}-b_{2n-j}, j=1,\ldots ,\frac{n}{2}-1. \end{aligned}$$

Proof

The proof follows from [13]. Briefly, the result for \(U_n\) is a direct corollary from [2]. The interpolant \(L_n\) can be considered as the interpolant, say \(S_n\), at the points x to \(T_n(t+\frac{\pi }{n})\). From \(L_n(t)=S_n(t-\frac{\pi }{n})\), the proof follows from simple trigonometry. \(\square \)

Summing up we obtain a sufficient condition on A(n, l), defined in (3), for a function of type (2) to be an ITMP.

Theorem 1

For any \(0\le l<\frac{n}{2}\) and \(0\le A(n,l)<\frac{1}{3}\), the trigonometric polynomial f of the form (2) is an ITMP.

Proof

Since the estimates for A(n, l) in Lemmas 1 and 2 are decreasing functions of l, we need to compute them only for \(l=\frac{n}{2}\). From Lemma 1, we have that \(A(n,l)<A(n,\frac{n}{2})<\frac{1}{3}\) for any \(l<\frac{n}{2}\) and hence f has positive instantaneous frequency. The estimate \(A(n,l)<\frac{1}{3}\) is stronger than \(A(n,\frac{n}{2})<\frac{4}{3\sqrt{13}}\) that is required in Lemma 2 with \(l=\frac{n}{2}\) and hence f is a weak IMF for any \(l<\frac{n}{2}\).

From Lemma 3 with \(a_j=b_j=0\) for \(j\ge \frac{n}{2}\), we get that

$$ U_n(t)=1+\sum _{j=0}^{\frac{n}{2}-1}\left( (a_{n-j}+a_{n+j})\cos jt -(b_{n-j}-b_{n+j})\sin (jt)\right) $$

where \(a_j=c_j\cos \beta _j, b_j=c_j\sin \beta _j\) and \(L_n=-U_n\). The proof is complete. \(\square \)

The condition on the Fourier coefficients of f provided in Theorem 1 is only sufficient, and in the next section, we will consider a series of numerical examples to discuss its necessity. We also illustrate the application of EMD with trigonometric envelopes.

The above result suggests a modification of the pure greedy algorithm, for details see [11], in the trigonometric basis, when one picks the largest in absolute value Fourier coefficients and adds the adjacent terms compared to \(\frac{1}{6^k}\) of the largest coefficient.

3 Numerical Examples

The extreme polynomials in all of the lemmas from Sect. 2 are of the form

$$\begin{aligned} f(t)=b\cos mt+(1+a\cos kt)\cos nt. \end{aligned}$$
(4)

Next, we study their analytic properties and the performance of EMD on them. In [4], the polynomials of type (4) with \(a=\frac{1}{5}\) and \(b=0\) were considered as examples for different interpretations of the IMF depending on the Fourier coefficients. In the examples of the section, we discuss the relation of their Fourier coefficients of polynomials of type (4) and EMD and the resulting IMF.

The instantaneous frequency for real parameters a and b of the model signals (4) is computed explicitly in the next proposition.

Proposition 1

The instantaneous frequency of f is \(\theta '(t)=n\) if \(b=0\) and \(k <n\). If \(b=0\) and \( k \ge n\), then

$$ \theta '(t)=\frac{2n+2a^2k\cos ^2 nt+(2n+k)a\cos kt+ak\cos (2n-k)t}{2+2a^2\cos ^2 nt+2a\cos kt+2a\cos (2n-k)t}, $$

and if \(a=0\), then

$$\begin{aligned} \theta '(t)=\frac{n+b( m+n)\cos (n-m)t+b^2 m}{1+2b\cos (n-m)t+b^2}. \end{aligned}$$
(5)

Proof

The proof follows from Theorem 1. The statement for \(b=0\) and \(k<n\) also follows from the Bedrosian theorem, for details see [1, 9].

Our first example is an ideal IMF with a spectrum spreading outside \([0,2n-1]\). This example shows that the spectral band conditions of Lemmas 1 and 2 are not necessary since the function still has positive instantaneous frequency (conclusion of Lemma 1) and is also a weak IMF (conclusion of Lemma 2). Further in each lemma, the corresponding bound conditions on the absolute sums A(n, l), defined in (3), of the example are also violated and therefore not necessary conditions.

Example 1

Bounded spectrum and aliasing

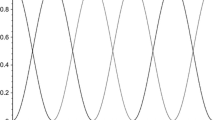
For \(b=0\), \(n=12\), and \(k=24,\)

$$ f(t)=1.4\left( \cos 12t+\frac{2}{7}\cos 36t\right) =(1+0.8\cos 24t)\cos 12t $$

and the derivative \(f'(t)=-12\sin 12t(3a\cos 24t+2a+1)\) has extrema at the zeros of \(\sin 12t\) where f has alternating values \(\pm (1+a)\) and hence for \(|a|<1\) the function f is an IMF. The function \(\theta '\) does not have real zeros, but the real part of the complex zeros, \(z=\frac{1}{2n}\left( \pi -\arccos \frac{1+a+a^2}{a(a+2)}\right) \), could be arbitrary close to 0 as \(a\rightarrow 1\). Figure 1 shows the graph of f and its widely varying instantaneous frequency. The effect is due to aliasing, for more details see [2].

Fig. 1
figure 1

\(f(t)=(1+0.8\cos 24t)\cos 12t\) and its \(\theta '\)

Full size image

In the next example, the support of the spectrum satisfies the condition of Theorem 1, but the coefficients have larger magnitude.

Example 2

Magnitude of the coefficients

For \(a=0\), \(n=15\), \(m=28<2n-1=29\), and \(b=-\frac{1}{3}\), the function \(f(t)=\cos 15t -\frac{1}{3}\cos (28t-\frac{\pi }{7})\) does not fit the form in (4) due to the shift \(\frac{\pi }{7}\), so the Proposition 1 cannot be used. However, a direct computation shows that the function still has positive instantaneous frequency. Direct computations also show that on the interval [2.92, 2.96] the function has a positive local minimum and hence it is not a weak IMF. The numerical results are illustrated in Fig. 2. Clearly, \(A(15,13)=\frac{1}{3}\) in that particular case while the estimates provided by Lemmas 1, 2 are 0.2930 and 0.2530. A(15, 13) exceeds both upper bounds which agrees with the observation that f is not a weak IMF.

Fig. 2
figure 2

\(f(t)=\cos 15t-\frac{1}{3}\cos (28t-\frac{\pi }{7})\) and its \(\theta '\)

Full size image

The final two examples demonstrate the effectiveness of the trigonometric envelopes replacing the usual cubic spline envelopes. The next example is an ITMP with symmetric spectrum in \([\frac{n}{2}+1,\frac{3n}{2}-1]\) to which the results from Theorem 1 can be applied.

Example 3

Controlled spectrum and coefficients

For \(b=0, a=0.8, n=12\), and \(k=4\), the function \(f=(1+0.8\cos 4t)\cos 12t=0.4 \cos 8t+\cos 12t +0.4\cos 16 t\) has spectrum as in Theorem 1 and \(A(12,4)=0.8\). In that case, the spline envelopes are very close to the trigonometric envelopes, see Fig. 3, and f is an IMF in the classical sense with \(\theta '=12\).

Fig. 3
figure 3

\(f=(1+0.8\cos 4t)\cos 12t\) and its envelopes

Full size image

In the next example, we apply the EMD with trigonometric envelopes to a signal of type (4).

Example 4

New frequency introduction and aliasing

For \(b=-0.1, a=-0.2, n=12, k=9\), and \(m=3\), the polynomial is \(f(t)=-0.1\cos 3t+(1-.2\cos 9t)\cos 12t=\cos 12t+0.1\cos 21t\). From (5), we have that \(\theta '=\frac{12.21+3.3\cos 9t}{1.01+0.1\cos 9t}>0\). On the other hand, f can be considered as a superposition of two signals with frequencies 12 and 21. The EMD applied with cubic spline envelopes through the extrema produces mean very close to \(-0.1\cos 3t\). The envelopes are close to \(U=1-0.1\cos 3t, L=-1-0.1\cos 3t\) and the resulting IMF is \(\psi =(1-0.2\cos 9t)\cos 12t\) which has instantaneous frequency 12. The mean is an IMF with instantaneous frequency 3. Since \(21-12>12-6\), we can conclude that the introduction of a component with instantaneous frequency 3 is due to aliasing (Fig. 4).

Fig. 4
figure 4

\(f=\cos 12t+0.1\cos 21t\) and its means

Full size image

4 Nonlinear Phase

The result in Lemma 2 can be readily extended to polynomials spanned by \(1, \cos j\theta (t),\sin j\theta (t), j=1,2,\ldots \) for any variable \(2\pi \)-periodic phase function \(\theta \) with a positive continuous first derivative. The above system is orthogonal in \(L_2[0,2\pi ]\) with the weighted inner product \(<f,g>=\int _{0}^{2\pi } \theta '(t)f(t)g(t)\; dt\). Since the weight is variable, Lemma 3 cannot be used directly. In this section, we consider orthonormal basis in the Hilbert space \(L_2[0,2\pi ]\) with an inner product \(<f,g>=\int _0^{2\pi } f(t)g(t)\; dt\), namely the functions

$$ \sqrt{\frac{\theta '(t)}{\pi }},\sqrt{\frac{\theta '(t)}{\pi }}\cos j\theta (t),\sqrt{\frac{\theta '(t)}{\pi }}\sin j\theta (t),\; j=1,2,\ldots $$

for a sufficiently smooth increasing function \(\theta \) s.t. \(\theta (0)=0, \theta (2\pi )=2\pi \). The corresponding Fourier series for a function f is

$$\begin{aligned} f(t)=\sqrt{\frac{\theta '(t)}{\pi }}\left( \frac{c_0}{2}+\sum _{j=1}^\infty (c_j\cos j\theta (t) +d_j\sin j\theta (t) ) \right) \end{aligned}$$
(6)

where

$$ c_j=\int _0^{2\pi }\sqrt{\frac{\theta '(t)}{\pi }}f(t)\cos j\theta (t)\; dt, d_j=\int _0^{2\pi }\sqrt{\frac{\theta '(t)}{\pi }}f(t)\sin j\theta (t)\; dt. $$

In [12], we considered a method to construct phase functions of the type \(\theta (t)=t+T_M(t)\) with \(\min _{t\in [0,2\pi ]} \theta '(t)=\delta >0\), for a trigonometric polynomial \(T_M\) of degree M. Those functions can be further modified to satisfy particular conditions.

Proposition 2

Let \(k\ge 2\) be an integer and \(p>0\) then for any trigonometric polynomial \(T_M\) of degree M such that \(\theta (t)=t+T_M(t)\) satisfies \(\min _{t\in [0,2\pi ]} \theta '(t)=\delta >0\), the functions \(\theta _\alpha (t)=\frac{1}{2\alpha }\int _{-\alpha }^{\alpha } \theta (t+x)\; dx\) are such that

$$ \lim _{\alpha \rightarrow \pi }\frac{\theta ^{(k)}_\alpha (t)}{(\theta '_\alpha (t))^p}\rightarrow 0. $$

Proof

Let \(\theta (t)=t+\sum _{j=1}^M c_j \cos (jt+\beta _j)\), for some real \(\beta _j\). Then for \(k>1\), we have that \(\theta ^{(k)}(t)=\sum _{j=1}^M \varepsilon _k j^kc_j \cos (jt+\tau _{j,k}), \varepsilon _k=\pm 1, \tau _{j,k}\) real. It follows that \(\theta _\alpha ^{(k)}(t)=\sum _{j=1}^M \frac{\sin (j\alpha )}{j\alpha }\varepsilon _kj^kc_j \cos (jt+\tau _{j,k})\). Hence, \( \lim _{\alpha \rightarrow \pi } \theta _\alpha ^{(k)}(t)=0\). On the other hand, since \(\theta '\ge \delta \), we have that \(\theta _\alpha '(t)=\frac{1}{2\alpha }\int _{-\alpha }^\alpha \theta '(t+x)\;dx\ge \delta \) for any \(\alpha \). From continuity argument, we complete the proof. \(\square \)

In [12], the proximity of the analytic signal, \(H\cos n\theta (t)\), for \(\cos n\theta (t)\), and the quadrature one, \(\sin n\theta (t)\), was estimated in terms of the ratios as in the above proposition.

Next, we consider a sufficient condition for the basis functions to be weak IMF.

Lemma 4

For a smooth increasing \(\theta \), \(\theta (0)=0\), \(\theta (2\pi )=2\pi \), with a \(2\pi \) periodic derivative \(\theta '\) and an integer n such that \(\frac{\theta '''}{(\theta ')^3}<2n^2\), the function \(v(t)=\sqrt{\theta '(t)}\cos N\theta (t)\) is a weak IMF for any \(N\ge n\).

Proof

It is enough to prove the statement only for \(N=n\). In that case, the function v has 2n zeros. Its derivative is

$$ v'(t)=\frac{\theta ''(t)}{2\sqrt{\theta '(t)}}\cos n\theta (t)-n(\theta '(t))^\frac{3}{2}\sin n\theta (t)=R(t)\sin n\phi (t) $$

where \(R(t)=-\sqrt{n^2(\theta '(t))^3+\frac{(\theta ''(t))^2}{4\theta '(t)}}\), \(\phi (t)=\theta (t)-\frac{\alpha (t)}{n}\), and \(\tan \alpha (t)=\frac{\theta ''(t)}{2n(\theta '(t))^2}\). The derivative \(\phi '(t)=\theta '(t)\frac{4n^2(\theta '(t))^4+5(\theta ''(t))^2-2\theta '''(t)\theta '(t)}{4n^2(\theta '(t))^4+(\theta ''(t))^2}\) is positive if \(\frac{\theta '''}{(\theta ')^3}<2n^2\). Since \(\alpha \) is an inverse tangent of a bounded function, we have that \(-\frac{\pi }{2}<\alpha (t) <\frac{\pi }{2}\). It follows that \(n(\phi (2\pi )-\phi (0))<(2n+1)\pi \) and hence \(v'\) has no more than 2n zeros. The proof of the lemma is complete. \(\square \)

The statement of the lemma is trivial for \(\theta (t)=t+at(t-2\pi ), |a|<\frac{1}{2\pi }\) or any concave instantaneous frequency \(\theta '\), i.e., \(\theta '''<0\). For any other function, it is asymptotically true as \(n\rightarrow \infty \). In the case of splines or trigonometric polynomials from the Bernstein inequality for positive functions, for details see [5],

$$ \theta '''\le \Vert \theta '''\Vert _\infty \le M\Vert \theta ''\Vert _\infty \le M\sqrt{Mr}\Vert \theta '\Vert _\infty $$

for some \(r\le M\). The last inequality is due to the fact that \(\theta '>0\).

We conclude the section with a comment on the Fourier series approximation with the system considered above in the space \(L_2[0,2\pi ]\) with inner product \(<f,g>= \int _0^{2\pi } f(t)g(t)\; dt\). For a fixed \(\theta \), the corresponding series expansion (6) has the same coefficients as the expansion of the function \(g(x)=\frac{f(\theta ^{-1}(x))}{\sqrt{\theta '(\theta ^{-1}(x))}}\) where \(\theta ^{-1}\) is the inverse of \(\theta \), in the classical Fourier series, and hence, for a periodic function \(f\in C^1\) we have that

$$ \left\| f-\sqrt{\frac{\theta '}{\pi }}\sum _{j=0}^{n-1}(c_j\cos j\theta +d_j\sin j\theta ) \right\| _\infty \le \frac{C}{\sqrt{n}}\left\| \frac{1}{(\theta ')^\frac{3}{2}}\left( f'-\frac{\theta ''}{2\theta '}f\right) \right\| _2 $$

where C is an absolute constant. This follows directly from the corresponding classical approximation estimate for absolutely converging Fourier series where the right-hand side involves the \(L_2\) norm of the derivative of g.

5 Conclusion

In this paper, we considered two types of functions that exhibit properties expected from IMF. The class of ITMP, which is an extension from the simple harmonics, also illustrates the relation between the positive instantaneous frequency and the interlacing of zeros and extrema. The second class considered in Sect. 4 has the advantage both of a variable instantaneous phase and a convergent approximation method.

A further direction for investigations is to vary the phase function \(\theta \) with the variation of n. This can be achieved by considering a greedy-type approximation, for details see [11], and matching pursuit-type algorithms, for details see [6, 7], with the dictionary \(D=\Bigl \{ \sqrt{\frac{\theta '(t)}{\pi }}\cos n\theta (t)\Big | \theta '>0\Bigr \}\) and selecting a candidate weak IMF by maximizing

$$\begin{aligned}&\left| \int _0^{2\pi }\sqrt{\theta '(t)}\cos n\theta (t)f(t)\; dt\right| =\\&\frac{1}{n}\left| \int _0^{2\pi }\frac{1}{\sqrt{\theta '(t)}}\left( f'(t)-\frac{\theta ''(t)}{2\theta '(t)}f(t)\right) \sin n\theta (t)\; dt\right| . \end{aligned}$$

The dictionary D for a particular choice of the smoothness on \(\theta \) is related to the dictionary considered in [6, 7] while the optimization process is different and requires further study.