Optimal Stock Sizing in a Cutting Stock Problem with Stochastic Demands

Abstract

One dimensional cutting stock problems arise in many manufacturing domains such as pulp and paper, textile and wood. In this paper, a new real life variant of the problem occuring in the rubber mold industry is introduced. It integrates both operational and strategical planning optimization: on one side, items need to be cut out of stocks of different lengths while minimizing trim loss, excess of production and the number of required cutting operations. Demands are however stochastic therefore the strategic choice of which mold(s) to build (i.e. which stock lengths will be available) is key for the minimization of the operational costs. A deterministic pattern-based formulation and a two-stage stochastic problem are presented. The models developed are solved with a mixed integer programming solver supported by a constraint programming procedure to generate cutting patterns. The approach shows promising experimental results on a set of realistic industrial instances.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Classical one-dimensional Cutting Stock Problems (CSP) consist of minimizing the trim loss in the manufacturing process of cutting small items out of a set of larger size stocks. Each item (also referred to as small object) $i = 1, \dots , I$ has an associated demand $d_i,$ and a length $l_i$; the stock (also referred to as large object or roll) has a length L out of which one or more items can be cut out. The objective is to utilize the minimum amount of stocks, i.e. minimize the trim loss (problem type 1/V/I/R, according to Dyckhoff’s classification [1]). Many different variations of the classical CSP have been proposed since the first formulation was introduced by Kantorovich in 1939 [2], including stock of different lengths, setup costs, open stock minimization, number of pattern minimization, to name just a few (see [3] for a survey).

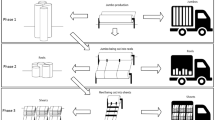
In this paper, we present a new variation of the problem arising in the production of a set of specific items in the rubber mold industry. In this manufacturing process, a mold is used to create one stock typology of a given length. From the mold, several stocks can be produced and they are then cut by an operator (with the help of a cutting machine) in multiple pieces to meet the individual item demands. Possibly, the left-over of the initial stock may be discarded (trim loss) in case its trim length does not correspond to the length of any required items; alternatively, if the remaining length matches one of the item lengths and the demand for that particular item is already met, it is stored in inventory (with an associated cost) as excess of production for future use. Due to process constraints, inventory items cannot be further reworked, i.e. they cannot be re-cut to meet future demands of smaller items. The operational planning optimization consists of minimizing the trim loss, the over-production (i.e., inventory costs) and the number of cuts to be performed by the operator.

The peculiarity of the problem at hand comes from the fact that the mold(s) also needs to be built; that is, the stock length(s) has to be decided up-front in order to meet the future demands. In the unrealistic case of infinite budget and capacity, the trivial optimal solution would be to produce one mold for each item length. In reality, however, the number of molds that can be manufactured is limited. This leads to an integrated strategical and operational real-life planning problem that, to the best of the author’s knowledge, has not been explored before in the literature.

The contributions of the paper are: the introduction and formalization of a new real-life cutting stock problem and its solution via an integrated strategical and operational CSP model with either deterministic or stochastic demands. The problems have been solved with a Mixed Integer Programming (MIP) solver supported by a Constraint Programming (CP) procedure to generate different cutting patterns.

The remainder of the paper is organized as follows: Sect. 2 summarizes the relevant literature; Sect. 3 formalizes the strategical and operational planning problem; experimental results are shown in Sect. 4; Sect. 5 draws some conclusions and describes future work.

2 Background

One-dimensional cutting stock problems have been extensively studied in the literature; several approaches have been proposed such as approximation algorithms, heuristics and meta-heuristics, population-based methods, constraint programming, dynamic programming and mathematical programming (please refer to the recent survey in [4] for an ample review and comparison). Among many, the most employed mathematical formulations are either item-based (originally introduced in [2]) or pattern-based (see [5]). In the former, a binary variable is used to indicate whether item i is cut out of stock j. In the latter, a cutting pattern defines a priori how many items and which item types are cut out of a single stock; then an integer variable i represents the number of stocks that are cut according to a given pattern i. As the number of cutting patterns grows exponentially with the average number of items that can fit into a stock, the problem is typically solved with column generation approaches. Pattern-based branch-and-price and branch-and-cut-and-price algorithms are considered the state-of-the-art complete methods (see [4, 6]).

Very few research papers investigate uncertainty of demands arising in cutting stock problems. Kallrath et al. [8] studied a real-life problem arising in the paper industry where they minimize the trim loss and the number of patterns used, while not allowing over production. They solved the problem using a column generation approach that falls back to column enumeration in certain cases (i.e. precomputing all the columns explicitly). The column enumeration is claimed to be easily applicable to MILP problems, easier to implement and maintain and at times more efficient when the pricing problem becomes difficult or when the number of columns is relatively small (see also [9]). In the same paper, they also introduced a two-stage stochastic version of the problem with uncertain demands: the first stage variables represent the patterns employed, and in the second stage the related production is defined. They employ column enumeration in a sample average approximation framework; unfortunately, no experimental results are shown for the stochastic problem. Beraldi et al. studied in [10] a similar problem for which they proposed an ad-hoc approach designed to exploit the specific problem structure. Alem et al. in [7] also considered stochastic CSP, where in the first stage the patterns and production plans are decided and the second stage decision determines over and under production.

The main differences between the problems already studied in the literature and this contribution are: firstly, the main cost drivers are the trim loss and the allowed over production; as a secondary objective the number of cuts to be performed (as opposed to the numbers of patterns utilized); secondly, the molds to be built are the key initial investment and they determine the available stock lengths (as opposed to predefined stock lengths).

In order to clarify the difference in solutions between minimizing the total number of cuts or alternatively the number of patterns, let’s consider an example in which the stock length is equal to 16 and two items, of lengths 7 and 8 respectively, need to be produced with a demand of 2 each. All the solutions that are optimal in term of trim loss require 2 stocks. The solution that minimizes the number of patterns employs only one pattern (8, 7); it will be used twice to meet the demand and the production will require a total of 4 cutting operations. Oppositely, the minimization of the number of cuts will make use of one pattern (8, 8) and one pattern (7, 7); the first pattern requires only one cut to produce two items, whereas the second two cuts.

3 Problem Formulation

In this section the problem is formalized: at first the deterministic operational planning problem is shown followed by the integrated strategical and operational planning problem. All the approaches use a pattern-based modelling¹.

3.1 Operational Planning with Deterministic Demands

In this section, the lengths of the molds is assumed to be already defined and the problem is to find the optimal production plan fulfilling some deterministic demands. We will use the following notation:

Parameters and Variables
I	The total number of different items to be produced; the items are indexed by $i=1,\dots ,I$
$l_i$	The length of the item i
$d_i$	The demand for item i
$c_i$	The cost for over producing item i
M	The total number of molds; molds are indexed by $m=1,\dots ,M$
$L_m$	The length of the stock produced with mold m
$P_m$	The total number of patterns related to the stock m; the patterns are indexed by $j=1,\dots ,P_m$
$p_{mji}$	The number of items i produced with pattern j of mold m
$w_{mj}$	The amount of trim loss caused by pattern j of mold m
$o_{mj}$	The number of cutting operations needed for pattern j of mold m
W	The trim loss cost per unit of length
$\alpha$	The weight on the secondary objective function, i.e. number of cutting costs ($\alpha \ll 1$)
$x_{mj}$	The integer non-negative variable indicating the number of times pattern j of mold m is used in the final solution

Note that the cost of over production is linked to the length $l_i$ (the longer the higher will be the cost) and to the demand of item i, i.e. the higher is its demand, the lower will be the inventory cost; in general: $W\cdot l_i \ge c_i \ge 0.$ The real industrial problem analyzed in this paper exhibits integer item and stock lengths. The following mathematical model formalizes the problem for the optimal production planning:

$$\begin{aligned}&\min \sum _{m = 1}^M \sum _{j=1}^{P_m} \big ( W\cdot w_{mj}\cdot x_{mj} + \alpha \cdot o_{mj} \cdot x_{mj}\big ) + \sum _{i=1}^{I} c_i \cdot \big (\sum _{m = 1}^M \sum _{j=1}^{P_m}p_{mji} \cdot x_{mj} - d_i\big ) \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{m = 1}^M \sum _{j=1}^{P_m}p_{mji} \cdot x_{mj} \ge d_i, \quad \quad i = 1,\dots ,I \end{aligned}$$

(2)

$$\begin{aligned}&x_{mj} \in \mathbb {Z} \end{aligned}$$

(3)

The objective function in Eq. (1) is composed by three main elements: the waste produced ($w_{mj}\cdot x_{mj}$), the number of cuts required ($o_{mj} \cdot x_{mj}$) and lastly, the over production. Equation (2) constrains the production of item i to meet its demand $d_i.$

Pattern Enumeration. An early analysis of the industrial instances showed that for relevant mold sizes, the number of feasible cutting patterns is relatively contained (about up to 50). For this reason and for the simplicity of the approach, we decided to enumerate exhaustively all the patterns (see [8, 9]). The pattern enumeration is a pure constraint satisfaction problem that has been solved with Constraint Programming.² Once all the patterns have been generated, they are fed as input to the mathematical model defined in Sect. 3.1. The parameters $p_{mji}$, $w_{mj}$ and $o_{mj}$ of the previous section become variables for this sub-problem, respectively:

• $Z_i \in \{0,\dots , \lfloor L_m/l_i \rfloor \}$ represents the number of units produced for item i

• $Q \in \{0,\dots \,L_m\}$ represents the amount of trim loss for the pattern

• $O \in \{0,\dots \,L_m - 1\}$ indicates the number of cut operations required

The model follows:

$$\begin{aligned}&L_m = Q + \sum _{i=1}^I l_i\cdot Z_i \end{aligned}$$

(4)

$$\begin{aligned}&Q \ne q\cdot l_i, \quad \quad q = 1, \dots , \lfloor L_m/l_i \rfloor , \quad i=1,\dots ,I \end{aligned}$$

(5)

$$\begin{aligned}&O = \sum _{i=1}^I Z_i - 1 + (Q > 0) \end{aligned}$$

(6)

Equation (4) constrains the waste and the sum of the item lengths to be equal to the mold size. The set of Eq. (5) avoids that the waste is equal to (or a multiple of) the size of one of the items in demand. This restricts the number of feasible patterns and it is valid as long as $c_i \le W\cdot l_i;$ that is, the inventory cost of an item of length $l_i$ is at most as expensive as throwing away the same quantity.³ Finally, Eq. (6) defines the number of cuts to be equal to the number of items in the pattern minus 1; an additional cut is required if there is also a final trim (reified constraint).

3.2 Strategical and Operational Planning Under Stochastic Demands

In this industrial context the main practical challenge is that an initial investment is required for the construction of the molds that will be used to meet future stochastic demands. The problem is a two-stage stochastic problem in which the first stage decision variables are the mold to be built, and the second-stage is the actual production plan once the demands are known.

We follow a sample average approximation approach in which a set of scenarios $s \in \varOmega$ with corresponding probabilities $\sum _{s\in \varOmega }p_s=1$ is Monte Carlo sampled. The vector of demands $d_i^s$ now depends on the specific scenario realization. We further introduce the binary variables $y_{m}$ indicating whether mold m is produced or not. Due to manufacturing and operational constraints the molds considered have to be limited to a maximum length $\mathbb {L}$ ($L_m \le \mathbb {L}$). The model follows:

$$\begin{aligned} \min \sum _{s\in \varOmega } p_s\Big (\sum _{m = 1}^M \sum _{j=1}^{P_m} \big ( W\cdot w_{mj}\cdot x_{mjs} + \alpha \cdot o_{mj} \cdot x_{mjs}\big ) + \sum _{i=1}^{I} c_i \cdot \big (\sum _{m = 1}^M \sum _{j=1}^{P_m}p_{mji} \cdot x_{mjs} - d_{is}\big )\Big ) \end{aligned}$$

$$\begin{aligned}&\sum _{m=1}^M y_m \le \mathbb {M} \end{aligned}$$

(7)

$$\begin{aligned}&x_{mjs} \le B\cdot y_m, \quad \quad s\in \varOmega , m=1,\dots ,M, j=1,\dots ,P_m\end{aligned}$$

(8)

$$\begin{aligned}&\sum _{j=1}^{P_m} x_{mjs} \ge y_m, \quad \quad s\in \varOmega , m=1,\dots ,M\end{aligned}$$

(9)

$$\begin{aligned}&\sum _{m = 1}^M \sum _{j=1}^{P_m}p_{mji} \cdot x_{mjs} \ge d_{is}, \quad \quad s\in \varOmega , i = 1,\dots ,I\end{aligned}$$

(10)

$$\begin{aligned}&y_m \in \{0,1\}, \quad x_{mjs} \in \mathbb {Z} \end{aligned}$$

(11)

where $\mathbb {M}$ is the maximum number of molds that can be built (Eq. (7)). Equations (8) and (9) indicate that if a mold is not built then none of its pattern can be employed, and vice versa, if only one pattern is used then the associated mold must be built (B is a large number). Finally, Eq. (10) constrains the production to meet the demand for each possible scenario.

For pure cutting stock problems minimizing the number of stocks used, a still open conjecture, the Modified Integer Round-Up Property (MIRUP), states that the integral optimal solution is close to the linear relaxation: $z_{opt} - \lceil L_{LP} \rceil \le 1$ (see [4] and [11]). In order to render the second stage sub-problem computationally tractable, the integrality constraints on $x_{mjs}$ have been lifted ($y_m$ are kept binary).

4 Experimental Results

The MIP and CP model have been developed using Google OR-Tools. The MIP solver employed is the open source CBC. All the experiments have been conducted on a MacBook Pro with an Intel Dual-core i5-5257U and 8 GB of RAM.

Pattern Enumeration. Creating all the possible patterns for all the molds ranging from length 1 to 16 (lengths relevant in the studied industrial context) takes 30 ms for a total combined number of patterns of about 200. For reference, the enumeration of the patterns for molds of lengths 15, 25 and 35 takes respectively 2, 28 and 300 ms, to enumerate resp. 40, 328 and 1995 patterns.

Operational Planning with Deterministic Demands. We generated 2250 synthetic instances with $\mathbb {L}=20,$ and random demands (the ratio between the maximum demand and the minimum demand - $\frac{\max _i d_i}{\min _i d_i}$ - ranged from 3 to 20); in this deterministic version the molds are predefined (M ranged from 1 to 3).

For brevity, we will not report the detailed results but just some observations. Firstly, all the generated instances but one were solved to optimality within one second (with all the integrality constraints); evidently, the item and stock lengths at play in this domain are not challenging for the MIP solver.

Secondly, we compared the optimal objective value of the integer solution with the one from the linear relaxation: the difference between the two is at most 0.03%. This is reassuring for the two-stage stochastic approach in which the integrality constraints on the second-stage decision variables have been lifted.

Thirdly, we used the deterministic model to analyze the variability of the number of cutting operations on a real industrial instance after the trim loss and over production had been fixed to their respective optimal values. Despite being a secondary objective, the best and worst solutions showed as much as almost 10% of difference in the number of cutting operations; in the analyzed industrial context, this translates to about 50 h of reduced time in cutting operations for producing the same quantity of items (about 150 thousands).

Strategical and Operational Planning Under Stochastic Demands. We generated the stochastic instances starting from a real industrial demand vector. We perturbated it using a gaussian distribution in order to create 20 different demand vectors. Each of them represents the mean demand vector, on which another set of gaussian distributions are centered for the scenario generation; their standard deviations is proportional to the demands: $\sigma _i= \frac{d_i}{k}.$ We tested different standard deviation with $k \in \{1,3,5\}$, scenario set cardinalities, $|\varOmega | \in \{10,20,50\},$ and number of molds to be constructed, $\mathbb {M} \in \{3,4\};$ $\mathbb {L}$ and $\max _i \{d_i\}$ are both set to 16, as per the industrial setting. The total number of tests amount to 360 instances.

In order to evaluate the quality of the stochastic approach, we computed the Expected Value of Perfect Information (EVPI) and the Value of the Stochastic Solution (VSS). The EVPI represents how much one could gain with a wait-and-see strategy, i.e. the expected decrease of the objective value in case of a priori knowledge of the stochastic variable realizations; a high EVPI connotes that the stochastic approach is not capable of capturing well the uncertainty on the demands. The VSS indicates the expected increase of the objective value when using a deterministic optimization fed with the expected values of the stochastic variables (see [12] for a general procedure to compute it); a high VSS means that capturing uncertainty with the stochastic approach is actually bringing a benefit; oppositely, a low VSS shows that a deterministic optimization using expected values leads to a solution that is similar to the one computed by the stochastic approach.

The results are presented in Table 1: each row reports aggregated values for 20 instances; the first three columns represent the instance parameters (described at the beginning of the paragraph); four pairs of columns follow reporting averages and standard deviations of respectively the solution time, the objective value, the EVPI and the VSS.

Table 1. Aggregated results for 360 instances.

As expected, by decreasing the level of stochasticity (lower standard deviation of the scenario generation, $k=5$), the VSS drops significantly as well as the EVPI. Oppositely, as the scenario set cardinality grows, the VSS gets bigger in proportion than the EVPI. Finally, increasing $\mathbb {M}$ allows to significantly decrease the value of the objective function, though the VSS, in proportion, increases. From a computational standpoint, for reference, should the integrality constraints be kept, an instance takes more than one minute to solve (with $|\varOmega | = 10$). The parameters that impact the most the solution time are $|\varOmega |$ and $\mathbb {L}$. Increasing $|\varOmega |$ to 100, 200 and 500 leads to a solution time of respectively about 65, 189 and 831 s. Similarly, increasing $\mathbb {L}$ (the real life problem presents $\mathbb {L} = 16$) to 20, 25 and 30 (with $|\varOmega | = 10$) results to a solution time of respectively about 17, 162 and 852 s.

5 Conclusion

In this paper, we introduced a new two-stage stochastic problem arising in the production of some rubber elements in the rubber mold industry. The uniqueness comes from deciding the stock lengths before knowing the actual production demand. We believe this problem setup can be relevant for other domains as well where stock purchase orders need to be placed despite uncertainty on the demands. We formalized the problem and developed a solution that was able to solve real-life instances to optimality within an acceptable time. Future work includes the exploration of other optimization techniques to improve scalability, the integration of other real-life constraints and explore a multi-stage stochastic setup for planning the production and inventory for multiple time slots.