Fuzzy Multi-attribute Grey Relational Analysis Using DEA and AHP

Abstract

This research applies the method of grey relational analysis (GRA) for multiple attribute decision making (MADM) problems in which the attribute weights are completely unknown and attribute values take the form of fuzzy numbers. In order to obtain the attribute weights, this research proposes an integrated data envelopment analysis (DEA) and analytic hierarchy process (AHP) approach. According to this, we define two sets of weights in a domain of grey relational loss, i.e., a reduction in grey relational grade, between each alternative and the ideal alternative. The first set represents the weights of attributes with the minimal grey relational loss in DEA. The second set represents the priority weights of attributes, bounded by AHP, with the maximal grey relational loss. Using a parametric goal programming model, we explore the various sets of weights in a defined domain of grey relational loss. This may result in various ranking positions for each alternative in comparison to the other alternatives. An illustrated example of a nuclear waste dump site selection is used to highlight the usefulness of the proposed approach.

1 Introduction

Multiple attribute decision making (MADM) aims to find the ranking position of alternatives in the presence of multiple incommensurate attributes. Many MADM problems take place in an environment in which the information about attribute weights are incompletely known and attribute values take the form of intervals and fuzzy numbers [16, 24, 29].

Grey relational analysis (GRA) is part of grey system theory [3], which is suitable for solving a variety of MADM problems with both crisp and fuzzy data. The application of GRA with fuzzy data has recently attracted the attention of many scholars [5, 8, 25].

GRA solves MADM problems by aggregating incommensurate attributes for each alternative into a single composite value while the weight of each attribute is subject to the decision maker’s judgment. When such information is unavailable equal weights seem to be a norm. However, this is often the source of controversies for the final ranking results. Therefore, how to properly select the attribute weights is a main source of difficulty in the application of this technique. Fortunately, the development of modern operational research has provided us two excellent tools called data envelopment analysis (DEA) and analytic hierarchy process (AHP), which can be used to derive attribute weights in GRA.

DEA is an objective data-oriented approach to assess the relative performance of a group of decision making units (DMUs) with multiple inputs and outputs [2]. Traditional DEA models require crisp input and output data. However, in recent years, fuzzy set theory has been proposed as a way to quantify imprecise and vague data in DEA models [7, 14, 26]. In the field of GRA, DEA models without explicit inputs are applied, i.e., the models in which only pure outputs or index data are taken into account [11, 27, 28]. In these models, each DMU or alternative can freely choose its own favorable system of weights to maximize its performance. However, this freedom of choosing weights is equivalent to keeping the preferences of a decision maker out of the decision process.

Alternatively, AHP is a subjective data-oriented procedure which can reflect the relative importance of a set of attributes and alternatives based on the formal expression of the decision maker’s preferences. AHP usually involves three basic functions: structuring complexities, measuring on a ratio-scale and synthesizing [23]. Some researchers incorporate fuzzy set theory in the conventional AHP to express the uncertain comparison judgments as fuzzy numbers [9, 12, 17].

However, AHP has been a target of criticism because of the subjective nature of the ranking process [4]. The application of AHP with GRA can be seen in [1, 10, 30].

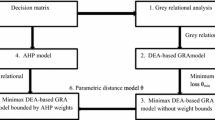
In order to overcome the problematic issue of confronting the contradiction between the objective weights in DEA and subjective weights in AHP, this research proposes an integrated DEA and AHP approach in deriving the attribute weights in a fuzzy GRA methodology. This can be implemented by incorporating weight bounds using AHP in DEA-based GRA models. It is worth pointing out that the models proposed in this article are not brand-new models in the DEA-AHP literature. Conceptually, they are parallel to the application of DEA and AHP in GRA using crisp data as discussed in [20]. Nevertheless, it is the first time that these models are applied to a fuzzy GRA methodology. Further research on the integration of DEA and AHP approach in deriving the attribute weights with fuzzy data can be seen in [19].

2 Methodology

2.1 Fuzzy Multiple Attribute Grey Relational Analysis

Let $A = \{ A_1 ,A_2 ,\cdots , A_m \}$ be a discrete set of alternatives and $C = \{ C_1 ,$ $C_2 ,\cdots , C_n \}$ be a set of attributes. Let $\tilde{y}_{ij} = (y_{1ij} ,y_{2ij} ,y_{3ij} ,y_{4ij} )$ be a trapezoidal fuzzy number representing the value of attribute $C_j (j = 1,2,\cdots , n)$ for alternative $A_i (i = 1,2,\cdots , m)$. Using $\alpha$-cut technique, a trapezoidal fuzzy number can be transformed into an interval number as follows:

$$\begin{aligned} y_{ij} = [y_{ij}^{-} ,y_{ij}^ + ] = [\alpha y_{2ij} + (1 - \alpha )y_{1ij} ,\alpha y_{3ij} + (1 - \alpha )y_{4ij} )], \end{aligned}$$

(1)

where $y_{ij} = [y_{ij}^ - ,y_{ij}^ + ],y_{ij}^ - \le y_{ij}^ +$, is an interval number representing the value of attribute $C_j (j = 1,2,\cdots , n)$ for alternative $A_i (i = 1,2,\cdots , m)$. Then alternative $A_i$ is characterized by a vector $Y_i = \left( {[y_{i1}^ - ,y_{i1}^ + ],[y_{i2}^ - ,y_{i2}^ + ],\cdots , [y_{in}^ - ,y_{in}^ + ]} \right)$ of attribute values. The term $Y_i$ can be translated into the comparability sequence $R_i = ( [r_{i1}^ - ,r_{i1}^ + ]$, $[r_{i2}^ - ,r_{i2}^ + ],\cdots , [r_{in}^ - ,r_{in}^ + ] )$ by using the following equations [31]:

$$\begin{aligned}&[r_{ij}^ - ,r_{ij}^ + ] = \left[ {\frac{{y_{ij}^ - }}{{y_{j(\max )}^ + }},\frac{{y_{ij}^ + }}{{y_{j(\max )}^ + }}} \right] ~~\forall j,~~ y_{j(\max )}^ + = \max \{ y_{1j}^ + ,y_{2j}^ + ,\cdots , y_{mj}^ + \} \end{aligned}$$

(2)

for desirable attributes,

$$\begin{aligned}&[r_{ij}^ - ,r_{ij}^ + ] = \left[ {\frac{{y_{i(\min )}^ - }}{{y_{ij}^ - }},\frac{{y_{i(\min )}^ - }}{{y_{ij}^ + }}} \right] ~~\forall j,~~ y_{j(\min )}^ - = \min \{ y_{1j}^ - ,y_{2j}^ - ,\cdots , y_{mj}^ - \} \end{aligned}$$

(3)

for undesirable attributes.

Now, let $A_0$ be a virtual ideal alternative which is characterized by a reference sequence $U_0 = \left( {[u_{01}^ - ,u_{01}^ + ],[u_{02}^ - ,u_{02}^ + ],\cdots ,[u_{0n}^ - ,u_{0n}^ + ]} \right)$ of the maximum attribute values as follows:

$$\begin{aligned}&u_{0j}^ - = \max \{ r_{1j}^ - ,r_{2j}^ - ,\cdots , r_{mj}^ - \}~~ \forall j, \end{aligned}$$

(4)

$$\begin{aligned}&u_{0j}^ + = \max \{ r_{1j}^ + ,r_{2j}^ + ,\cdots , r_{mj}^ + \}~~ \forall j. \end{aligned}$$

(5)

To measure the degree of similarity between $r_{ij} = [r_{ij}^ - ,r_{ij}^ + ]$ and $u_{0j} = [u_{0j}^ - ,u_{0j}^ + ]$ for each attribute, the grey relational coefficient, $\xi _{ij}$, can be calculated as follows:

$$\begin{aligned} \xi _{ij} = \frac{{\min _i \min _j \left| {[u_{0j}^ - ,u_{0j}^ + ] - [r_{ij}^ - ,r_{ij}^ + ]} \right| + \rho \max _i \max _j \left| {[u_{0j}^ - ,u_{0j}^ + ] - [r_{ij}^ - ,r_{ij}^ + ]} \right| }}{{\left| {[u_{0j}^ - ,u_{0j}^ + ] - [r_{ij}^ - ,r_{ij}^ + ]} \right| + \rho \max _i \max _j \left| {[u_{0j}^ - ,u_{0j}^ + ] - [r_{ij}^ - ,r_{ij}^ + ]} \right| }}, \end{aligned}$$

(6)

while the distance between $u_{0j} = [u_{0j}^ - ,u_{0j}^ + ]$ and $r_{ij} = [r_{ij}^ - ,r_{ij}^ + ]$ is measured by $\left| {u_{0j} - r_{ij} } \right|$ $= \max \left( {\left| {u_{0j}^ - - r_{ij}^ - } \right| ,\left| {u_{0j}^ + - r_{ij}^ + } \right| } \right)$. $\rho \in [0,1]$ is the distinguishing coefficient, generally $\rho =0.5$. It should be noted that the final results of GRA for MADM problems are very robust to changes in the values of $\rho$. Therefore, selecting the different values of $\rho$ would only slightly change the rank order of attributes [13]. To find an aggregated measure of similarity between alternative $A_i$, characterized by the comparability sequence $R_i$, and the ideal alternative $A_0$, characterized by the reference sequence $U_0$, over all the attributes, the grey relational grade, $\varGamma _i$, can be computed as follows:

$$\begin{aligned} \varGamma _i = \sum \limits _{j = 1}^n {w_j \xi _{ij} }, \end{aligned}$$

(7)

where $w_j$ is the weight of attribute $C_j$ and $\sum _{j = 1}^n {w_j } = 1$. In practice, expert judgments are often used to obtain the weights of attributes. When such information is unavailable equal weights seem to be a norm. Nonetheless, the use of equal weights does not place an alternative in the best ranking position in comparison to the other alternatives. In the next section, we show how DEA can be used to obtain the optimal weights of attributes for each alternative in GRA.

2.2 DEA-Based GRA Models

Since all the grey relational coefficients are benefit (output) data, a DEA-based GRA model can be formulated similar to a classical DEA model without explicit inputs [15]:

$$\begin{aligned}&\varGamma _k = \max \sum \limits _{j = 1}^n {w_j \xi _{kj} }, \end{aligned}$$

(8)

$$\begin{aligned}&\sum \limits _{j = 1}^n {w_j \xi _{ij} } \le 1~~\forall i, \end{aligned}$$

(9)

$$\begin{aligned}&w_j > 0 ~~\forall j, \end{aligned}$$

(10)

where $\varGamma _k$ is the grey relational grade for alternative under assessment $A_k$ (known as a decision making unit in the DEA terminology). k is the index for the alternative under assessment where k ranges over $1, 2,\cdots , m$. $w_j$ is the weight of attribute $C_j$. The first set of constraints (9) assures that if the computed weights are applied to a group of m alternatives, $(i=1, 2,\cdots , m)$, they do not attain a grade of larger than 1. The process of solving the model is repeated to obtain the optimal grey relational grade and the optimal weights required to attain such a grade for each alternative. The objective function (8) in this model maximizes the ratio of the grey relational grade of alternative $A_k$ to the maximum grey relational grade across all alternatives for the same set of weights $\left( {{{\max \varGamma _k }/{\mathop {\max }_{i = 1,\cdots , m} \varGamma _i } }} \right)$. Hence, an optimal set of weights in the DEA based-GRA model represents $A_k$ in the best light in comparison to all the other alternatives. It should be noted that the grey relational coefficients are normalized data. Consequently, the weights attached to them are also normalized. In addition, adding the constraint $\sum _{j = 1}^n {w_j } = 1$ to the DEA-based GRA model is not recommended here. In fact, the sum-to-one constraint is a non-homogeneous constraint (i.e., its right-hand side is a non-zero free constant) which can lead to underestimation of the grey relational grades of alternatives or infeasibility in the DEA-based GRA model (see [22])

2.3 Minimax DEA-Based GRA Model Using AHP

We develop our formulation based on a simplified version of the generalized distance model (see for example [6]). Let $\varGamma _k^*(k=1,2,\cdots , m)$ be the best attainable grey relational grade for the alternative under assessment, calculated from the DEA-based GRA model. We want the grey relational grade, $\varGamma _k(w)$, calculated from the vector of weights $w=(w_1,\cdots , w_n)$ to be closest to $\varGamma _k^*$. Our definition of “closest” is that the largest distance is at its minimum. Hence we choose the form of the minimax model: $\min _w \max _k \{ \varGamma _k^* - \varGamma _k (w)\}$ to minimize a single deviation which is equivalent to the following linear model:

$$\begin{aligned} \min ~&\theta \end{aligned}$$

(11)

$$\begin{aligned} \text {s. t.}~&\varGamma _k^* - \sum \limits _{j = 1}^n {w_j \xi _{kj} } \le \theta , \end{aligned}$$

(12)

$$\begin{aligned}&\sum \limits _{j = 1}^n {w_j \xi _{ij} } \le \varGamma _i^* ~~\forall i, \end{aligned}$$

(13)

$$\begin{aligned}&\theta \le 1, \end{aligned}$$

(14)

$$\begin{aligned}&\theta ,w_j \ge 0~~\forall j. \end{aligned}$$

(15)

The combination of (11)–(15) forms a minimax DEA based-GRA model that identifies the minimum grey relational loss $\theta _{\min }$ needed to arrive at an optimal set of weights. The first constraint ensures that each alternative loses no more than $\theta$ of its best attainable relational grade, $\varGamma _k^*$. The second set of constraints satisfies that the relational grades of all alternatives are less than or equal to their upper bound of $\varGamma _k^*$. It should be noted that for each alternative, the minimum grey relational loss $\theta =0$. Therefore, the optimal set of weights obtained from the minimax DEA based-GRA model is exactly similar to that obtained from the DEA-based GRA model.

On the other hand, the priority weights of attributes are defined out of the internal mechanism of DEA by AHP. In order to more clearly demonstrate how AHP is integrated into the newly proposed minimax DEA-based GRA model, this research presents an analytical process in which attributes’ weights are bounded by the AHP method. The AHP procedure for imposing weight bounds may be broken down into the following steps:

Step 1. :

A decision maker makes a pairwise comparison matrix of different attributes, denoted by B with the entries of $b_{hq} (h = q = 1,2,\cdots , n)$. The comparative importance of attributes is provided by the decision maker using a rating scale. Saaty [23] recommends using a 1–9 scale.

Step 2. :

The AHP method obtains the priority weights of attributes by computing the eigenvector of matrix B (Eq. (16)), $e = (e_1 ,e_2 ,\cdots , e_j )^T$, which is related to the largest eigenvalue, $\lambda _{\max }$.

$$\begin{aligned} Be = \lambda _{\max } e. \end{aligned}$$

(16)

To determine whether or not the inconsistency in a comparison matrix is reasonable the random consistency ratio, C.R. can be computed by the following equation:

$$\begin{aligned} C.R. = \frac{{\lambda _{\max } - N}}{{(N - 1)R.I.}}, \end{aligned}$$

(17)

where R.I. is the average random consistency index and N is the size of a comparison matrix.

In order to estimate the maximum relational loss $\theta _{\max }$ necessary to achieve the priority weights of attributes for each alternative, the following set of constraints is added to the minimax DEA-based GRA model:

$$\begin{aligned} w_j = \alpha e_j ~~\forall j. \end{aligned}$$

(18)

The set of constraints (18) changes the priority weights of attributes to weights for the new system by means of a scaling factor $\alpha$. The scaling factor $\alpha$ is added to avoid the possibility of contradicting constraints leading to infeasibility or underestimating the grey relational grade of alternatives (see [22]).

2.4 A Parametric Goal Programming Model

In this stage we develop a parametric goal programming model that can be solved repeatedly to generate the various sets of weights for the discrete values of the parameter $\theta$, such that $0 \le \theta \le \theta _{\max }$. Let $w(\theta )$ be a vector of attribute weights for a given value of parameter $\theta$. Let $w^*(\theta _{\max })$ be the vector of priority weights of attributes obtained from the minimax DEA-based GRA model after adding the set of constraints (18). Our objective is to minimize the total deviations between $w(\theta )$ and $w^*(\theta _{\max })$ with a city block distance measure. Choosing such a distance measure, each deviation is being equally weighted subject to the following constraints:

$$\begin{aligned} \min ~&Z_k (\theta ) = \sum \limits _{j = 1}^n {(d_j^ + } + d_j^ - ) \end{aligned}$$

(19)

$$\begin{aligned} \text {s. t.}~&w_j - d_j^ + + d_j^ - = \alpha e_j ~~ \forall j, \end{aligned}$$

(20)

$$\begin{aligned}&d_j^ + ,d_j^ - \ge 0. \end{aligned}$$

(21)

and constraints (12)–(15), where $d_j^+$ and $d_j^-$ are the positive and negative deviations from the priority weight of attribute $C_j(j=1,2,\cdots , n)$ for alternative $A_k(k=1,2,\cdots , m)$. The set of Eq. (20) indicates the goal equations whose right-hand sides are the priority weights of attributes adjusted by a scaling variable.

Because the range of deviations computed by the objective function is different for each alternative, it is necessary to normalize it by using relative deviations rather than absolute ones. Hence, the normalized deviations can be computed by:

$$\begin{aligned} \varDelta _k (\theta ) = \frac{{Z_k^* (0) - Z_k^* (\theta )}}{{Z_k^* (0)}}, \end{aligned}$$

(22)

where $Z_k^*(\theta )$ is the optimal value of the objective function for $0 \le \theta \le \theta _{\max }$. We define $\varDelta _k(\theta )$ as a measure of closeness which represents the relative closeness of each alternative to the weights obtained from the minimax DEA-based GRA model in the range [0, 1] after adding the set of constraint (18) to it. Increasing the parameter $(\theta )$, we improve the deviations between the two systems of weights obtained from the minimax DEA-based GRA model before and after adding the set of constraints (18). This may lead to different ranking positions for each alternative in comparison to the other alternatives. It should be noted that in a special case where the parameter $\theta =\theta _{\max }=0$, we assume $\varDelta _k(\theta )= 1$.

3 Numerical Example: Nuclear Waste Dump Site Selection

In this section we present the application of the proposed approach for nuclear waste dump site selection. The multiple attribute data, adopted from Wu and Olson [27], are presented in Table 1. There are twelve alternative sites and 4 performance attributes. Cost, Lives lost, and Risk are undesirable attributes and Civic improvement is a desirable attribute. Cost is in billions of dollars. Lives lost reflects expected lives lost from all exposures. Risk shows the risk of catastrophe (earthquake, flood, etc.) and Civic improvement is the improvement of the local community due to the construction and operation of each site. Cost and Lives lost are crisp values as outlined in Table 1, but Risk and Civic improvement have fuzzy data for each nuclear dump site.

We use the processed data as reported in [27]. First the trapezoidal fuzzy data are used to express linguistic data in Table 1. Using the $\alpha$-cut technique, the raw data are expressed in fuzzy intervals as shown in Table 2. These data are turned into the comparability sequence by using the Eqs. (2) and (3). Each attribute is now on a common 0–1 scale where 0 represents the worst imaginable attainment on an attribute, and 1.00 the best possible attainment.

Table 1. Data for nuclear waste dump site selection

Table 2. Fuzzy interval nuclear waste dump site data

Table 3 shows the results of a pairwise comparison matrix in the AHP model as constructed by the author in Expert Choice software. The priority weight for each attribute would be the average of the elements in the corresponding row of the normalized matrix of pairwise comparison, shown in the last column of Table 3. One can argue that the priority weights of attributes must be judged by nuclear safety experts. However, since the aim of this section is just to show the application of the proposed approach on numerical data, we see no problem to use our judgment alone.

Using Eq. (6), all grey relational coefficients are computed to provide the required (output) data for the DEA-based GRA model as shown in Table 4. Note that grey relational coefficients depend on the distinguishing coefficient $\rho$, which here is 0.80.

Table 3. Pairwise comparison matrix of 4 attributes

Table 4. Results of grey relational coefficient for nuclear waste dump site selection

Solving the minimax DEA-based GRA model for the site under assessment, we obtain an optimal set of weights with minimum grey relational loss $(\theta _{\min })$. It should be noted that the value of the grey relational grade of all waste dump sites calculated from the minimax DEA-based GRA model is identical to that calculated from the DEA-based GRA model. Therefore, the minimum grey relational loss for the site under assessment is $\theta _{\min }=0$ (Table 5). This implies that the measure of relative closeness to the AHP weights for the site under assessment is $\varDelta _k(\theta _{\min })=0$. On the other hand, solving the minimax DEA-based GRA model for the site under assessment after adding the set of constraints (18), we adjust the priority weights of attributes (outputs) obtained from AHP in such a way that they become compatible with the weights’ structure in the minimax DEA-based GRA model. This results in the maximum grey relational loss, $\theta _{\max }$, for the site under assessment (Table 5). In addition, this implies that the measure of relative closeness to the AHP weights for the site under assessment is $\varDelta _k(\theta _{\max })=1$.

Table 6 presents the optimal weights of attributes as well as its scaling factor for all nuclear waste dump sites. It should be noted that the priority weights of AHP (Table 3) used for incorporating weight bounds on the attribute weights are obtained as $e_j = \frac{{w_j }}{\alpha }$.

Table 5. Minimum and maximum grey relational losses for each nuclear waste dump site

Table 6. Optimal weights of minimax DEA-based GRA model for all nuclear waste dump sites bounded by AHP

Table 7. The ranking position of each site based on the minimum distance to priority weights of attributes

Going one step further to the solution process of the parametric goal programming model, we proceed to the estimation of total deviations from the AHP weights for each site while the parameter $\theta$ is $0\le \theta \le \theta _{\max }$. Table 7 represents the ranking position of each site based on the minimum deviation from the priority weights of attributes for $\theta =0$. It should be noted that in a special case where the parameter $\theta =\theta _{\max }=0$, we assume $\varDelta _k(\theta )=0$. Table 7 shows that Wells is the best alternative in terms of the grey relational grade and its relative closeness to the priority weights of attributes.

Nevertheless, increasing the value of $\theta$ from 0 to $\theta _{\max }$ has two main effects on the performance of the other sites: improving the degree of deviations and reducing the value of the grey relational grade. This, of course, is a phenomenon, one expects to observe frequently. The graph of $\varDelta (\theta )$ versus $\theta$, as shown in Fig. 1, is used to describe the relation between the relative closeness to the priority weights of attributes, versus the grey relational loss for each site. This may result in different ranking positions for each site in comparison to the other sites. In order to clearly discover the effect of grey relational loss on the ranking position of each nuclear dump site, as shown in Table 8 in Appendix, we performed a Kruskal-Wallis test. The Kruskal-Wallis test compares the medians of rankings to determine whether there is a significant difference between them. The result of the test reveals that its p-value is quite smaller than 0.01. Therefore, we conclude that increasing grey relational loss in the whole range [0.0, 0.33] changes the ranking position of each site significantly. Note that at $\theta =0$ sites can be ranked based on $Z_k^*(0)$ from the closest to the furthest from the priority weights of attributes. For instance, at $\theta =0$, Nome, Newark and Rock Sprgs with grey relational grades of one, are ranked in $12^{th}$, $4^{th}$ and $2^{nd}$ places, respectively (Tables 5 and 7). However, with a small grey relational loss at $\theta =0.01$, Nome, Newark and Rock Sprgs take $9^{th}$, $10^{th}$ and $5^{th}$ places in the rankings, respectively. Using this example, as a guideline, it is relatively easy to rank the sites in terms of distance to the priority weights of attributes. At $\theta =0.02$, Newark moves up into $9^{th}$ place while Nome and Rock Sprgs drop in $10^{th}$ and $6^{th}$ places, respectively. It is clear that both measures, $Z_k^*(0)$ and $\varDelta _k(\theta )$, are necessary to explain the ranking position of each nuclear dump site.

Fig. 1.

The relative closeness to the priority weights of attributes $[\varDelta (\theta )]$, versus grey relational loss $(\theta )$ for each site

4 Conclusion

We develop an integrated approach based on DEA and AHP methodologies for deriving the attribute weights in GRA with fuzzy data. We define two sets of attribute weights in a minimax DEA-based GRA framework. The first set represents the weights of attributes with minimum grey relational loss. The second set represents the corresponding priority weights of attributes, using AHP, with maximum grey relational loss. We assess the performance of each alternative (or DMU) in comparison to the other alternatives based on the relative closeness of the first set of weights to the second set of weights. Improving the measure of relative closeness in a defined range of grey relational loss, we explore the various ranking positions for the alternative under assessment in comparison to the other alternatives. To demonstrate the effectiveness of the proposed approach, an illustrative example of a nuclear waste dump site using twelve alternative sites and 4 attributes is carried out. Further studies can apply the simultaneous application of DEA and AHP to the field of GRA by considering the hierarchical structures of attributes in the ranking positions of alternatives [18, 21].

Appendix

Table 8. The measure of relative closeness to the priority weights of attributes [$\varDelta _k(\theta )$] verses grey relational loss[$\theta$] for each nuclear waste dump site