Semi-calibrated Near-Light Photometric Stereo

Abstract

We tackle the nonlinear problem of photometric stereo under close-range pointwise sources, when the intensities of the sources are unknown (so-called semi-calibrated setup). A variational approach aiming at robust joint recovery of depth, albedo and intensities is proposed. The resulting nonconvex model is numerically resolved by a provably convergent alternating minimization scheme, where the construction of each subproblem utilizes an iteratively reweighted least-squares approach. In particular, manifold optimization technique is used in solving the corresponding subproblems over the rank-1 matrix manifold. Experiments on real-world datasets demonstrate that the new approach provides not only theoretical guarantees on convergence, but also more accurate geometry.

This work was supported by the ERC Consolidator Grant “3D Reloaded”.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Photometric stereo [1] (PS) is a classic inverse problem arising from computer vision. It consists in estimating the shape and the reflectance of a surface, given $m \ge 2$ images $I^i:\, {\mathbb {R}}^2 \rightarrow {\mathbb {R}}$, $i \in [1,m]$, of this surface obtained from the same angle, but under varying lighting ${\mathbf {s}}^i$, $i \in [1,m]$. Figure 1 shows two PS images, and the 3D-reconstruction result obtained by the proposed approach.

Traditional PS methods assume that the lighting is induced by infinitely distant point light sources. Under this assumption, vector ${\mathbf {s}}^i \in {\mathbb {R}}^3$ represents a uniform light beam whose direction is that of the i-th source, and whose norm is related to its intensity $\phi ^i >0$. It is usually assumed that the sources intensities are known. From the user perspective, relaxing both these assumptions has two advantages: assuming close-range sources allows using low-cost lighting devices such as LEDs, and assuming unknown sources intensities (semi-calibrated PS) simplifies the calibration procedure.

Fully uncalibrated (i.e., unknown intensities and locations of the sources) close-range photometric stereo has been studied in a few papers [2,3,4]. Nevertheless, calibration of the sources locations can easily be achieved using specular spheres [5], and assuming known sources locations considerably simplifies the numerical resolution. On the other hand, calibration of the sources intensities is not so easy, since they are relative to the radiometric parameters of the camera [6]. Hence, semi-calibrated close-range photometric stereo represents an interesting intermediate case: it retains the advantage of using known locations, but it is robust to uncontrolled radiometric variations, which allows for instance using the camera in “auto-exposure” mode.

Fig. 1.

Left: 2 out of $m=8$ images of a plaster statuette. Each image is acquired while turning on one different nearby LED with calibrated position and orientation, but uncalibrated intensity. Right: result of our semi-calibrated PS approach, which automatically estimates the shape, the reflectance (mapped on the 3D-reconstruction on the rightest figure) and the intensities.

However, existing methods for semi-calibrated PS [6, 7] are restricted to distant sources. In addition, the semi-calibrated PS approach from [6] lacks robustness, as it is based on non-robust least-squares. The recent method in [7] solves this issue by resorting to a non-convex variational formulation: in the present paper we use the same numerical framework, but extend it to the case of nearby sources. Apart from fully uncalibrated ones [2,3,4], methods for PS with non-distant sources do not refine the intensities, and sometimes lack robustness. For instance, the near-light PS approach from [3] is based on least-squares, and it alternatively estimates the normals and integrates them into a depth map, which may be a source of drift. These issues are solved in [4] by using $l^p$-norm optimization, $p<1$, to ensure robustness, and by treating the normals and the depth as two different entities. Still, the normals and the depth should correspond to the same geometry, hence approaches estimating directly the global geometry may be better suited. This is achieved in [8] by mesh deformation, yet again in a least-squares framework. PDE methods have also been suggested in [9]. The resulting Fast Marching-based numerical scheme is the only provably convergent strategy for near-light PS, yet it is restricted to the $m=2$ images case, thus it has been recently replaced by variational methods in [10]. Still, this ratio-based procedure has several drawbacks: it results in a combinatorial number of equations to solve (limiting the approach to few and small images), it does not provide the albedo, and it biases the solution in shadowed areas.

Hence, there is still a need for a near-light PS method which is robust, provably convergent, and able to estimate the intensities. Our aim is to fill this gap. The proposed approach relies on a new variational formulation of PS under close-range sources, which is detailed in Sect. 2. Section 3 proposes an alternating minimization strategy to tackle the nonconvex variational model numerically. The construction of each subproblem utilizes the iteratively reweighted least-squares method. Convergence analysis on the generic version of the proposed algorithm is conducted in Sect. 4. Section 5 demonstrates an empirical evaluation of the new method, and Sect. 6 summarizes our achievements.

2 Variational Model for Semi-calibrated Near-Light PS

Photometric Model. Assuming $m \ge 3$ images of a Lambertian surface, the graylevel in a pixel ${\mathbf {p}} \in {\mathbb {R}}^2$ conjugate to a surface point ${\mathbf {x}} \in {\mathbb {R}}^3$ is given by:

$$\begin{aligned} I^i({\mathbf {p}}) = {\tilde{\rho }}({\mathbf {x}}) \phi ^i \left\{ {\mathbf {s}}^i({\mathbf {x}}) \cdot {\mathbf {n}}({\mathbf {x}})\right\} _+,~i \in [1,m], \end{aligned}$$

(1)

where:

• ${\tilde{\rho }}({\mathbf {x}}) > 0$ is the albedo in ${\mathbf {x}}$ (unknown);

• $\phi ^i >0$ represents the intensity of the i-th light source (unknown);

• ${\mathbf {s}}^i({\mathbf {x}}) \in {\mathbb {R}}^3$ is a vector representing the i-th incident lighting (see Eq. (3));

• ${\mathbf {n}}({\mathbf {x}}) \in {\mathbb {S}}^2 \subset {\mathbb {R}}^3$ is the outgoing normal vector to the surface in ${\mathbf {x}}$ (unknown);

• $\{\cdot \}_+$ encodes self-shadows (cf. Fig. 2-b), and it is defined as follows:

  $$\begin{aligned} \{t\}_+ = \max \left\{ t,0\right\} . \end{aligned}$$

  (2)

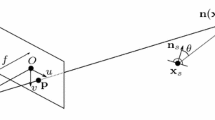
We consider the imperfect Lambertian light source model, representing the i-th source by the parameters $\{{\mathbf {n}}^i_s, {\mathbf {x}}^i_s, \mu ^i, \phi ^i\}$, where ${\mathbf {n}}^i_s \in {\mathbb {S}}^2$ is the (unit-length) principal direction of the source, ${\mathbf {x}}_s^i \in {\mathbb {R}}^3$ is its location, $\mu ^i > 0$ is its anisotropy parameter and $\phi ^i > 0$ is its unknown intensity. Apart from $\phi ^i$, all the sources parameters are assumed to be known: anisotropy is provided by the manufacturer, the locations of the sources can be estimated by using reflective spheres [4, 5], and their orientations can be deduced from images of a plane [5]. Vector ${\mathbf {s}}^i({\mathbf {x}})$ in Eq. (1) is then written as follows:

$$\begin{aligned} {\mathbf {s}}^i({\mathbf {x}}) = \left( {\mathbf {n}}_s^i \cdot \left[ \frac{{\mathbf {x}} - {\mathbf {x}}_s^i}{\left\| {\mathbf {x}} - {\mathbf {x}}_s^i \right\| } \right] \right) ^{\mu ^i} \frac{1}{\left\| {\mathbf {x}} - {\mathbf {x}}_s^i \right\| ^2} \frac{\left[ {\mathbf {x}}_s^i - {\mathbf {x}} \right] }{\left\| {\mathbf {x}} - {\mathbf {x}}_s^i \right\| },~\forall i \in [1,m], \end{aligned}$$

(3)

where the first factor represents attenuation due to anisotropy, the second factor stands for attenuation due to distance (inverse-of-square falloff), and the third one gives the unit-length lighting direction. This is illustrated in Fig. 2-a.

Fig. 2.

(a) Near-light PS setup. Surface point ${\mathbf {x}}$ is conjugate to pixel ${\mathbf {p}}$ according to the pinhole camera model (4), where ${\tilde{z}}({\mathbf {p}})$ is the unknown depth. According to Eq. (3), the lighting in ${\mathbf {x}}$ induced by the first source is strongly attenuated by anisotropy, while that induced by the second source is strongly attenuated by the distance to the source. (b) Pixel ${\mathbf {p}}$ appears shadowed in both images $I^1$ and $I^2$, because ${\mathbf {x}}$ is self-shadowed w.r.t. the first light source (${\mathbf {s}}^1({\mathbf {x}}) \cdot {\mathbf {n}}({\mathbf {x}}) <0$), and the second light source is occluded by the surface (cast-shadow). The first case is handled by our model (Eq. (2)), and the second one is treated as an outlier within a robust estimation framework (Eq. (12)).

Geometric Setup. Under perspective projection, the conjugation relationship between ${\mathbf {x}}$ and ${\mathbf {p}} = \left[ x,y\right] ^\top$ reads as:

$$\begin{aligned} {\mathbf {x}}(x,y) = {\tilde{z}}(x,y) {\mathbf {K}}^{-1} \begin{bmatrix}x,&y,&1\end{bmatrix}^\top , \end{aligned}$$

(4)

with ${\tilde{z}}:\varOmega \subset {\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ the depth map over the reconstruction domain $\varOmega$, and ${\mathbf {K}}$ the (calibrated) intrinsics matrix [11]:

$$\begin{aligned} {\mathbf {K}} = \begin{bmatrix} f_x&s&x_0 \\ 0&f_y&y_0 \\ 0&0&1 \end{bmatrix}. \end{aligned}$$

(5)

The normal vector ${\mathbf {n}}({\mathbf {x}})$ in Eq. (1) is the unit-length vector proportional to $\partial _x {\mathbf {x}}(x,y) \times \partial _y {\mathbf {x}}(x,y)$. Using (4) and introducing the logarithmized depth $z = \log {\tilde{z}}$, we obtain after some algebra:

$$\begin{aligned} {\mathbf {n}}({\mathbf {x}}) = \frac{1}{d({\mathbf {p}};z({\mathbf {p}}))} {\mathbf {J}}({\mathbf {p}})^\top \begin{bmatrix} \nabla z({\mathbf {p}}) \\ -1 \end{bmatrix}, \end{aligned}$$

(6)

where we denote:

$$\begin{aligned} z({\mathbf {p}}) = \log {\tilde{z}}({\mathbf {p}}),~&{\mathbf {J}}({\mathbf {p}}) = \begin{bmatrix} f_x&-s&-(x - x_0) \\ 0&f_y&-(y - y_0) \\ 0&0&1 \end{bmatrix},&d({\mathbf {p}};z({\mathbf {p}}))&= \left\| {\mathbf {J}}({\mathbf {p}})^\top \begin{bmatrix} \nabla z({\mathbf {p}}) \\ -1 \end{bmatrix} \right\| . \end{aligned}$$

(7)

Discrete Variational Model. Instead of estimating the albedo ${\tilde{\rho }}({\mathbf {p}})$ in each pixel ${\mathbf {p}}$, we follow [7] and rather estimate the following “pseudo”-albedo:

$$\begin{aligned} \rho ({\mathbf {p}}) := \frac{{\tilde{\rho }}({\mathbf {p}})}{d({\mathbf {p}},z({\mathbf {p}}))}, \end{aligned}$$

(8)

which eliminates the nonlinearity due to the denominator. Once the scaled albedo and the depth map are estimated, the “real” albedo is easily deduced.

Combining Eqs. (1), (6), (7) and (8), photometric model (1) is turned into the following system of nonlinear PDEs in $(\rho :\,\varOmega \rightarrow {\mathbb {R}},z:\,\varOmega \rightarrow {\mathbb {R}},\{\phi ^i \in {\mathbb {R}}\}_i)$:

$$\begin{aligned} I^i({\mathbf {p}}) = \phi ^i \rho ({\mathbf {p}}) \, \left\{ \left[ {\mathbf {J}}({\mathbf {p}}) {\mathbf {s}}^i({\mathbf {p}};z({\mathbf {p}}))\right] ^\top \begin{bmatrix} \nabla z({\mathbf {p}}) \\ -1 \end{bmatrix} \right\} _+,~\forall i \in [1,m],~\forall {\mathbf {p}}\in \varOmega , \end{aligned}$$

(9)

where ${\mathbf {s}}^i({\mathbf {p}};z({\mathbf {p}}))$ stands for ${\mathbf {s}}^i({\mathbf {x}})$ as defined in Eq. (3), knowing that ${\mathbf {x}}$ depends on z and ${\mathbf {p}}$ according to Eq. (4), and where we denote from now on $\rho ({\mathbf {p}})$ instead of $\rho ({\mathbf {x}})$, knowing that there exists a bijection between ${\mathbf {x}}$ and ${\mathbf {p}}$ (Eq. (4)).

Instead of continuous images $I^i:\,\varOmega \rightarrow {\mathbb {R}}$, we are given a finite list of graylevels over a discrete subset $\varOmega$ of a 2D grid. Let us denote $j = 1 \dots n$ the corresponding pixel indices, $I^i_j$ the graylevel at pixel j in image $I^i$, ${\mathbf {z}}\in {\mathbb {R}}^n$ and ${\varvec{\rho }}\in {\mathbb {R}}^n$ the stacked depth and albedo values, ${\mathbf {s}}^i_j(z_j) \in {\mathbb {R}}^3$ the lighting vector ${\mathbf {s}}^i$ at pixel j, which smoothly depends on $z_j$, and ${\mathbf {J}}_j \in {\mathbb {R}}^{3 \times 3}$ the matrix ${\mathbf {J}}$ defined in Eq. (7) at pixel j. Then, the discrete counterpart of Eq. (9) is written as:

$$\begin{aligned} I^i_j = \phi ^i \rho _j \left\{ ({\mathbf {s}}^i_j(z_j))^\top {\mathbf {J}}_j^\top \begin{bmatrix} \left( \nabla {\mathbf {z}}\right) _j \\ -1 \end{bmatrix} \right\} _+,~\forall i \in [1,m],~\forall j \in [1,n], \end{aligned}$$

(10)

where $\left( \nabla {\mathbf {z}}\right) _j \in {\mathbb {R}}^2$ represents a finite differences approximation of the gradient of z at pixel j (in our implementation, we used first-order forward finite differences with Neumann boundary conditions).

Our goal is to jointly estimate the albedo values ${\varvec{\rho }}\in {\mathbb {R}}^n$, the depth values ${\mathbf {z}}\in {\mathbb {R}}^n$ and the intensities $\phi \in {\mathbb {R}}^m$ from the set of nonlinear Eq. (10). Let ${\mathcal {M}}$ be the set of all rank-1 n-by-m matrices (known to be a smooth manifold [12]), ${T_{{\mathcal {M}}}({\varvec{\theta }})}$ the tangent space of ${\mathcal {M}}$ at ${\varvec{\theta }}$, and ${\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }})}}\left( \cdot \right)$ the (linear) projection onto ${T_{{\mathcal {M}}}({\varvec{\theta }})}$. By introducing the rank-1 matrix ${\varvec{\theta }}\in {\mathcal {M}}$ such that $\theta ^i_j\equiv \phi ^i\rho _j$, we consider the following discrete optimization problem:

$$\begin{aligned} \min _{\begin{array}{c} {\mathbf {z}}, {\varvec{\theta }}:\,{\varvec{\theta }}\in {\mathcal {M}} \end{array}} F({\varvec{\theta }},{\mathbf {z}}) = \sum _{j=1}^n \sum _{i=1}^m\varPhi \left( r^i_j({\varvec{\theta }},{\mathbf {z}})\right) . \end{aligned}$$

(11)

Here, $\varPhi$ is a robust estimator (possibly non-convex), e.g. Cauchy’s estimator:

$$\begin{aligned} \varPhi (x) = \lambda ^2 \log ( 1+ x^2 / \lambda ^2) \end{aligned}$$

(12)

for some user-defined parameter $\lambda >0$ (in our implementation $\lambda = 0.1$).

We also define

$$\begin{aligned} r^i_j({\varvec{\theta }},{\mathbf {z}}) = \theta ^i_j\left\{ \varPsi ^i_j({\mathbf {z}})\right\} _{+,\delta }-I^i_j,&\varPsi ^i_j({\mathbf {z}}) = ({\mathbf {s}}^i_j(z_j))^\top {\mathbf {J}}_j^\top \begin{bmatrix} \nabla {\mathbf {z}})_j \\ -1 \end{bmatrix}, \end{aligned}$$

where it is convenient to avoid non-differentiability by smoothing $\left\{ \cdot \right\} _{+}$ with

$$\begin{aligned} \left\{ t\right\} _{+,\delta }&= {\left\{ \begin{array}{ll} t-\delta /2 &{} \text {if~} t\ge \delta ,\\ t^2/(2\delta ) &{} \text {if~} 0\le t<\delta ,\\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

for some $\delta >0$. If $\delta =0$, we regain $\left\{ \cdot \right\} _{+,\delta }=\left\{ \cdot \right\} _{+}$.

3 Optimization

Now we present a generic scheme which minimizes the nonconvex model (11) alternatively over variables ${\varvec{\theta }}$ and ${\mathbf {z}}$. In each subproblem, we solve a local quadratic model of (11) with positive definite approximation of the Hessian. A backtracking line search is then performed to guarantee a sufficient descent in the objective. In particular, we note that in the ${\varvec{\theta }}$-subproblem the rank-1 constraint is handled implicitly, and the resulting subproblem represents a weighted least-squares problem over the rank-1 matrix manifold. In the sequel, $\left\langle \cdot ,\cdot \right\rangle$ denotes scalar product for either vectors or vectorized matrices.

The iterates generated by the above algorithm are guaranteed to converge (subsequentially) to a critical point of the problem (11); see detailed analysis in Sect. 4.

Yet, the practical efficiency of the overall algorithm hinges on the choices of the scaling matrices $H_\theta ^{(k,k)}$ and $H_z^{(k+1,k)}$ and the subroutines for solving (13) and (15). In this work, our choices for $H_\theta ^{(k,k)}$ and $H_z^{(k+1,k)}$ (see formulas (18) and (21) below) will be structured Hessian approximations motivated from the iteratively reweighted least-squares (IRLS) method [13, 14]. The solution of the resulting subproblem can be interpreted as a regularized Newton step; see [15,16,17].

For the ease of presentation, we introduce the following notations:

$$\begin{aligned}&(r^{({\tilde{k}},k)})^i_j = r^i_j({\varvec{\theta }}^{({\tilde{k}})},{\mathbf {z}}^{(k)}),&(w^{({\tilde{k}},k)})^i_j = \varPhi '((r^{({\tilde{k}},k)})^i_j)/(r^{({\tilde{k}},k)})^i_j, \\&(\varPsi ^{(k)})^i_j = \varPsi ^i_j({\mathbf {z}}^{(k)}),&(\chi ^{(k)})^i_j = \left\{ \varPsi ^i_j({\mathbf {z}}^{(k)})\right\} _{+,\delta }', \end{aligned}$$

where ${\tilde{k}}$ is either k or $k+1$. Note that

$$\begin{aligned} \left( \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\right) ^i_j&= (w^{(k,k)})^i_j (r^{(k,k)})^i_j\left\{ (\varPsi ^{(k)})^i_j\right\} _{+,\delta }. \end{aligned}$$

(17)

By choosing $H_\theta ^{k,k}$ such that

$$\begin{aligned} \left\langle {\varvec{\theta }},H_\theta ^{(k,k)}{\varvec{\theta }}\right\rangle&= \sum _{j=1}^n \sum _{i=1}^m (w^{(k,k)})^i_j \left( \left\{ (\varPsi ^{(k)})^i_j\right\} _{+,\delta }\theta ^i_j\right) ^2, \end{aligned}$$

(18)

for all ${\varvec{\theta }}\in {\mathbb {R}}^{n\times m}$, the ${\varvec{\theta }}$-subproblem (13) with $\tau _\theta =1$ is equivalent to the following weighted least-squares problem:

$$\begin{aligned} \min _{{\varvec{\theta }}\in {\mathcal {M}}} \sum _{j=1}^n \sum _{i=1}^m(w^{(k,k)})^i_j \left| \left\{ (\varPsi ^{(k)})^i_j\right\} _{+,\delta } \theta ^i_j -I^i_j\right| ^2. \end{aligned}$$

(19)

Analogously for the ${\mathbf {z}}$-subproblem, we note that

$$\begin{aligned} \frac{\partial F}{\partial {\mathbf {z}}}({\varvec{\theta }}^{(k+1)},{\mathbf {z}}^{(k)})&= \sum _{j=1}^n\sum _{i=1}^m(w^{(k+1,k)})^i_j (r^{(k+1,k)})^i_j ({\varvec{\theta }}^{(k+1)})^i_j (\chi ^{(k)})^i_j (\varPsi ^i_j)'({\mathbf {z}}^{(k)}), \end{aligned}$$

(20)

and choose $H_z^{(k+1,k)}$ such that

$$\begin{aligned} \left\langle {\mathbf {z}},H_z^{(k+1,k)}{\mathbf {z}}\right\rangle&= \sum _{j=1}^n \sum _{i=1}^m (w^{(k+1,k)})^i_j \left( ({\varvec{\theta }}^{(k+1)})^i_j(\chi ^{(k)})^i_j {\mathbf {z}}^\top (\varPsi ^i_j)'({\mathbf {z}}^{(k)}) \right) ^2, \end{aligned}$$

(21)

for all ${\mathbf {z}}\in {\mathbb {R}}^n$. As a result, the ${\mathbf {z}}$-subproblem (15) with $\tau _z=1$ becomes

$$\begin{aligned} \min _{{\mathbf {z}}}&\sum _{j=1}^n \sum _{i=1}^m(w^{(k+1,k)})^i_j \Big |(r^{(k+1,k)})^i_j +({\varvec{\theta }}^{(k+1)})^i_j(\chi ^{(k)})^i_j ({\mathbf {z}}-{\mathbf {z}}^{(k)})^\top (\varPsi ^i_j)'({\mathbf {z}}^{(k)})\Big |^2. \end{aligned}$$

(22)

We remark that $H_\theta ^{(k,k)}$ and $H_z^{(k+1,k)}$ above are only sure to be positive semidefinite. To enforce their (uniform) positive definiteness along iterations (as being assumed in the convergence theory), one may always add cI (with arbitrarily small $c>0$) to $H_\theta ^{(k,k)}$ and $H_z^{(k+1,k)}$. This, however, seems unnecessary according to our numerical experiments.

In addition, it is empirically observed that $\tau _z^{(k)}=1$ and $\tau _z^{(k)}=1$ are always accepted by the backtracking line search, i.e. Steps 4 and 6 of Algorithm 1, for certain small $\varepsilon$ even if $\delta$ is set zero. Thus, in practice, Algorithm 1 reduces to the following alternating reweighted least-squares (ARLS) scheme.

Concerning the subproblem solvers in Steps 3 and 4 of Algorithm 2, (22) can be solved by conjugate gradient iterations. Meanwhile, (19) represents the least-squares problem over the rank-1 matrix manifold, for which a local minimizer is pursued by a simple Riemannian gradient descent scheme in Algorithm 3. We refer to [18] for possibly more efficient numerical schemes for the same purpose.

4 Convergence Analysis

This section is devoted the convergence analysis of the Algorithm 1. We shall assume that the iterates $\{({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\}$ are contained in a bounded subset over which both $\frac{\partial F}{\partial {\varvec{\theta }}}$ and $\frac{\partial F}{\partial {\mathbf {z}}}$ are Lipschitz continuous. We also assume that $\{{\varvec{\theta }}^{(k)}\}$ are uniformly bounded away from 0, thus avoiding the pathological case of having 0 as a limit point. In addition, there exist constants $c,C>0$ such that $cI\preceq H_\theta ^{(k,k)}\preceq CI$ and $cI\preceq H_z^{(k+1,k)}\preceq CI$ for all k. Without loss of generality, let $\frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})$ and $\frac{\partial F}{\partial {\mathbf {z}}}({\varvec{\theta }}^{(k+1)},{\mathbf {z}}^{(k)})$ be nonzero throughout the iterations.

Lemma 1

The admissible step sizes $\tau _\theta ^{(k)}$ and $\tau _z^{(k)}$ in Algorithm 1 can be found in finitely many trials.

Proof

We only prove the case for $\tau _\theta ^{(k)}$, since the other case is analogous (if not easier). Define

$$\begin{aligned} \kappa (\tau _\theta )=F({\widehat{{\varvec{\theta }}}}_{(k)}(\tau _\theta ),{\mathbf {z}}^{(k)}) - F({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})+\varepsilon \Vert {\widehat{{\varvec{\theta }}}}_{(k)}(\tau _\theta )-{\varvec{\theta }}^{(k)}\Vert ^2. \end{aligned}$$

Note that ${\widehat{{\varvec{\theta }}}}_{(k)}(0)={\varvec{\theta }}^{(k)}$, $\kappa (0)=0$, and $\kappa '(0)= \left\langle \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)}),{\widehat{{\varvec{\theta }}}}_{(k)}'(0)\right\rangle$. It suffices to show $\kappa '(0)<0$.

Since ${\widehat{{\varvec{\theta }}}}_{(k)}(\tau _\theta )$ is a local minimizer of (13), it must hold that

$$\begin{aligned} \tau _\theta \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})+H_\theta ^{(k,k)}({\widehat{{\varvec{\theta }}}}_{(k)}(\tau _\theta )-{\varvec{\theta }}^{(k)})+\eta (\tau _\theta )=0, \end{aligned}$$

(23)

where $\eta (\tau _\theta )$ belongs to the normal space of ${\mathcal {M}}$ at ${\widehat{{\varvec{\theta }}}}_{(k)}(\tau _\theta )$ for all $\tau _\theta \ge 0$ and $\eta (0)=0$. By differentiating (23) at $\tau _\theta =0$, and since $\eta '(0)=0$, we obtain

$$\begin{aligned} \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})+H_\theta ^{(k,k)}{\widehat{{\varvec{\theta }}}}_{(k)}'(0)=0. \end{aligned}$$

(24)

It follows that $\kappa '(0)=-\left\langle \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)}),(H_\theta ^{(k,k)})^{-1}\frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\right\rangle <0$.    $\square$

Theorem 1

The iterates $\{({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\}$ generated by Algorithm 1 satisfy

$$\begin{aligned}\liminf _{k\rightarrow \infty }{\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(k)})}}\left( \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\right) =0, \quad \liminf _{k\rightarrow \infty }\frac{\partial F}{\partial {\mathbf {z}}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})=0.\end{aligned}$$

Proof

Again, we only prove $\liminf _{k\rightarrow \infty }{\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(k)})}}\left( \frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\right) =0$. Since $F({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})\le F({\varvec{\theta }}^{(k+1)},{\mathbf {z}}^{(k)})\le F({\varvec{\theta }}^{(k+1)},{\mathbf {z}}^{(k+1)})$ for all k and $F(\cdot ,\cdot )$ is bounded from below, we have $\lim _{k\rightarrow \infty }\Vert {\varvec{\theta }}^{(k+1)}-{\varvec{\theta }}^{(k)}\Vert =0$. For brevity, we denote $g_\theta ^{(k)}=\frac{\partial F}{\partial {\varvec{\theta }}}({\varvec{\theta }}^{(k)},{\mathbf {z}}^{(k)})$ in the remainder of the proof.

We first consider the case where $\liminf _{k\rightarrow \infty }\tau _\theta ^{(k)}>0$. In particular, the identity in (23) yields

$$\begin{aligned} {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(k+1)})}}\left( \tau _\theta ^{(k)}g_\theta ^{(k)}+H_\theta ^{(k,k)}({\varvec{\theta }}^{(k+1)}-{\varvec{\theta }}^{(k)})\right) = 0, \end{aligned}$$

and ultimately $\lim _{k\rightarrow \infty }{\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(k)})}}\left( g_\theta ^{(k)}\right) =0$.

Now consider the case $\tau _\theta ^{(k)}\rightarrow 0$ along a subsequence indexed by ${\tilde{k}}$. Assume, for the sake of contradiction, that $\left\| {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(k)})}}\left( g_\theta ^{(k)}\right) \right\|$ is uniformly bounded away from 0. Due to the nature of the backtracking line search, we have

$$\begin{aligned} F(\widehat{\varvec{\theta }}_{(\tilde{k})}(2\tau _\theta ^{(\tilde{k})}),{\mathbf {z}}^{(\tilde{k})})- F({\varvec{\theta }}^{(\tilde{k})},{\mathbf {z}}^{(\tilde{k})})+\varepsilon \Vert \widehat{\varvec{\theta }}_{(\tilde{k})}(2\tau _\theta ^{(\tilde{k})})-{\varvec{\theta }}^{(\tilde{k})}\Vert ^2>0, \end{aligned}$$

which further implies $2\tau _\theta ^{({\tilde{k}})}\left\langle g_\theta ^{({\tilde{k}})},{\widehat{{\varvec{\theta }}}}_{({\tilde{k}})}'(0)\right\rangle +o(2\tau _\theta ^{({\tilde{k}})})>0.$ Thus, we must have $\liminf _{{\tilde{k}}\rightarrow \infty }\left\langle g_\theta ^{(\tilde{k})},\widehat{{\varvec{\theta }}}_{(\tilde{k})}'(0)\right\rangle \ge 0$. Recalling (24), we obtain the contradiction:

$$\begin{aligned} 0&\le \liminf _{\tilde{k}\rightarrow \infty }\frac{\left\langle g_\theta ^{(\tilde{k})},\widehat{\varvec{\theta }}_{(\tilde{k})}'(0)\right\rangle }{\left\| {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(\tilde{k})})}}\left( g_\theta ^{(\tilde{k})}\right) \right\| ^2} = \liminf _{\tilde{k}\rightarrow \infty }-\frac{\left\langle g_\theta ^{(\tilde{k})},(H_\theta ^{(\tilde{k},\tilde{k})})^{-1}g_\theta ^{(\tilde{k})}\right\rangle }{\left\| {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(\tilde{k})})}}\left( g_\theta ^{(\tilde{k})}\right) \right\| ^2} \\&\le \limsup _{\tilde{k}\rightarrow \infty }-\frac{\left\langle g_\theta ^{(\tilde{k})},(H_\theta ^{(\tilde{k},\tilde{k})})^{-1}g_\theta ^{(\tilde{k})}\right\rangle }{\left\| {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(\tilde{k})})}}\left( g_\theta ^{(\tilde{k})}\right) \right\| ^2} \le \limsup _{\tilde{k}\rightarrow \infty }-\frac{\left\| g_\theta ^{(\tilde{k})}\right\| ^2}{C\left\| {\mathcal {P}}_{{T_{{\mathcal {M}}}({\varvec{\theta }}^{(\tilde{k})})}}\left( g_\theta ^{(\tilde{k})}\right) \right\| ^2} \le -\frac{1}{C}. \end{aligned}$$

This completes the whole proof.    $\square$

Fig. 3.

Comparison of several 3D-reconstructions obtained by PS. Top: 3D-reconstruction. Bottom: absolute error between the PS reconstruction and laser-scan ground truth (blue is zero, red is $>1$ cm. State-of-the-art calibrated near-light PS [10] corrects the bias due to the distant-light assumption [1], yet it remains unsatisfactory in shadowed areas (e.g., the ears), and it requires knowledge of the lighting intensities. Our approach is more robust, and it can be used without calibration of the intensities. (Color figure online)

5 Empirical Evaluation

We first consider the plaster statuette from Fig. 1, and compare existing calibrated near- and distant-light PS methods with the proposed near-light one. For competing methods, we used the calibrated intensities. For the proposed semi-calibrated one, intensities were initially set to the arbitrary (and wrong) values $\phi \equiv 1$. The result of distant-light PS was used as initial guess for the shape and the albedo, and then the proposed alternating scheme was run until the relative residual of the energy falls below $10^{-3}$. Standard PS was used as initialization to accelerate the reconstruction, but we observed that this initalization had no impact on the final result. To evaluate our semi-calibrated method, this initial guess was obtained while assuming wrongly that $\phi \equiv 1$. The proposed method is thus entirely independent from the initial estimates of the intensities.

As shown in Fig. 3, the distant light assumption induces a bias, which is corrected by state-of-the-art calibrated near-light PS [10]. Yet, this result remains unsatisfactory in shadowed areas, because it treats self-shadows as outliers instead of modeling them. Our near-light approach provides more accurate results, because it explicitly accounts for self-shadows (cf. Eq. (1)) and it utilizes a more robust estimator (Cauchy’s, instead of the $L^1$ norm one used in [10]). Interestingly, the semi-calibrated approach is more accurate than the calibrated one: this proves that calibration of intensities always induces a slight bias, which can be avoided by resorting to a semi-calibrated approach.

Figure 4 confirms on another dataset that the proposed method is more robust to shadows than state-of-the-art, because self-shadows are explicitly taken into account in the model and a robust M-estimator is used. Overall, the state-of-the-art is thus advanced both in terms of accuracy, simplicity of the calibration procedure, and convergence analysis.

Fig. 4.

Top: 3 out of $m=8$ images of a box, and 3D-model (3D-reconstruction and estimated albedo) recovered by our semi-calibrated approach. Bottom: 3D-reconstructions using (from left to right) standard distant-light PS [1], the calibrated near-light method from [10], the proposed one with calibrated intensities, and the proposed one with uncalibrated intensities. The top face of the box is severely distorded with the distant-light assumption. This is corrected by the near-light method from [10], yet robustness to shadows is not granted, which biases the 3D-reconstruction of both the other faces. Our approach is robust to shadows (self-shadows are handled in the model), and it removes the need for calibration of the intensities.

6 Conclusion

We have proposed a new variational approach for solving the near-light PS problem in a robust manner, considering unknown lighting intensities (semi-calibrated setup). Our numerical strategy relies on an alternating minimization scheme which builds upon manifold optimization. It is shown to overcome the state-of-the-art in terms of accuracy, while being the first approach to remove the need for intensity calibration and to be provably convergent.

As future work, the proposed approach could be extended to the fully uncalibrated case, by including inside the alternating scheme another step aiming at refining the positions and orientations of the sources.