Dynamics of Self-replicating DNA-Tile Patterns

Abstract

DNA tiles serve as molecular components for the self-assembly of programmable 2-dimensional patterns at the nanoscale. To produce identical copies of a pre-assembled DNA tile pattern, we use a theoretical framework of non enzymatic cross-coupled self-replication system based on tile self-assembly model. This paper presents a kinetic modelling of the pattern self-replication and analyses the influence of physicochemical parameters of tile self-assembly process over the reliability and replication gain. We demonstrate that the tile assembly errors, introduced in tile patterns during their assembly, set a limit over the size of a tile pattern that can be replicated exponentially and reliably.

R. Prasath—A part of this was carried out when the author was in Indian Institute of Information Technology (IIIT) Sricity, India.

1 Introduction

Self-replication is a fundamental mechanism in biology, that nature applies to create elegant molecular systems inexpensively using processes of growth and selection. Application of this inspiration to engineer artificial molecular systems has been a constant pursuit of nanosciences. Gunter von Kiedorowski [10] first introduced a minimal system of molecular self-replication, which typically involves a three-step process. First, a template molecule assembles with few substrate molecules resulting in an intermediate complex formation. Second, the substrate molecules within the complex join together irreversibly by covalent binding, and thereby forming a replica of the template. Third, the complex molecule dissociates into two templates: the former template and the newly created replica. Each of these templates can reiterate the three-step process adding to the template population. The population have been observed to grow sub-exponentially (parabolic) [16].

Template directed non-enzymatic self-replication has been used for the synthesis of nucleic acid sequences using only linear organization of short sequences of nucleic acids (primers). However, recent advances in structural DNA self-assembly have opened up perspectives for the non-enzymatic self-replication of two-dimensional (2-D) and three-dimensional (3-D) patterns of DNA [1, 9, 14, 18, 23]. A 2-D DNA pattern replication based on crystal growth followed by random splitting has been experimentally demonstrated for the amplification of combinatorial information [15].

DNA tile self-assembly [20] is an emerging paradigm for nanostructure construction and molecular scale computation. DNA tiles [19], the building blocks of tile self-assembly, can be designed to interact with strength and specificity for the assembly of logically and/or algorithmically directed periodic and aperiodic 2-D intricate patterns. For a theoretical modelling of tile assembly, Erik Winfree first introduced an abstract Tile Assembly Model (aTAM) [20]. In the aTAM framework, the assembly starts from a single seed tile and the pattern grows in 2-D as more tiles adjoin one-by-one following a simple assembly rule — the total binding strength of an incumbent tile should be greater than or equal to a threshold value known as temperature parameter of assembly. However, DNA tile assembly is essentially a physico-chemical process, where local reaction temperature and tile concentration are the governing factors. Therefore, for a realistic modelling of tile assembly process, Winfree introduced kinetic Tile Assembly Model (kTAM) [21]. The kTAM considers each tile assembly step as a reversible process governed by the tile concentration, local reaction temperature and binding strengths of tiles. The model enables analysis of the assembly errors and growth rate for a given tile assembly system.

Fig. 1.

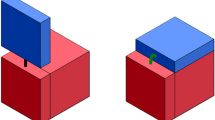
A simplistic view of the tile pattern self-replication system: the self-replication starts with a pre-assembled target tile pattern (a 4$\,\times \,$5 tile pattern is shown in gray); a mold (shown in black) assembles around the South-West border of the pattern; a cyclically generated inhibitor signal dissociates the mold and pattern, which initiate a cross-coupled cycle of pattern self-replication.

A very high level abstract version of tile pattern self-replication system [6], shown in Fig. 1, is designed using additional tiles, which self-assemble to form a mold structure around the L-shaped South-West border of the target pattern. The assembled mold consists of switching enabled tiles that are dynamically triggered by an externally supplied inhibitor signal of DNA to dissociate the pattern and mold templates. The dissociated mold and pattern structures further catalyse the assembly of new templates of patterns and mold structures, respectively. The inhibitor signal is cyclically released by a chemical oscillator tuned to the time intervals involved in the mold formation and pattern formation. Thus, the entire process forms the basis of a cross-coupled self-replication system of 2-D patterns of tiles.

In this paper, we derive a kinetic model for the population growth of pattern self-replicator using chemical kinetic rates of tile assembly and disassembly in the kTAM. Kinetic rates of tiles are governed by physicochemical parameters (local assembly temperature, total binding strength and concentration of tiles), which causes erroneous assembly of tiles. We analyse the impact of these parameters in population growth dynamics of the pattern self-replicator and reliability of the replicated patterns. Population growth, fidelity and size of replicating patterns are important metrics that we investigate quantitatively using mathematical modelling.

The remainder of the article is structured as follows: background of DNA tile self-assembly, tile assembly models and tile pattern self-replication system are described in Sect. 2. Section 3 presents kinetic model of the tile pattern self-replicator. In Sect. 4, we present simulation results based on kinetic model, and discuss design choices in terms of assembly error and pattern size. Section 5, concludes the article.

2 Background

In this section we discuss briefly the background of the main concepts used in this article. This includes: a brief introduction to the self-assembly mechanism of DNA tile patterns, the abstract and kinetic modelling of tile assembly, and previously introduced tile pattern self-replication system [6].

2.1 Self-assembly of Programmable DNA Tile Patterns

A connection between algorithmic self-assembly and computation was studied by Wang in his theoretical tiling model [17]. The Wang Tiling theory demonstrates the implementation of a Turing machine by a finite set of square tiles with four colored edges.

Erik Winfree [20] applied the theoretical concepts of Wang tilling for the realization of programmable self-assembly patterns using DNA molecular structures (DNA tiles [19]) as analogue to the Wang’s abstract tiles. DNA tiles serve as building blocks of self-assembly for the construction of 2-D physical patterns. DNA tiles consist of four ($\approx 50$ nucleotide) ss-DNA molecules, synthesized for a given DNA tile design. Figure 2 illustrates the construction of a Double Crossover (DX) molecular DNA tile with four DNA strands. As shown in Fig. 2(a), each ss-DNA consists of a sequence of nucleotides (A, T, G, C). The tiles self-assemble through the bonding of these ss-DNAs at room temperature. The bonding process occurs when two complimentary strands meet and their base pairs: A-T and G-C, bind. Any left-over bases from each of the bonded strands form a sticky end(s) — as shown in Fig. 2(b). As the term implies, this end is available to “stick” or bond to another strand. DX molecular DNA tiles are square shaped structures where sticky-ends are represented by their respective square edges — as illustrated in Fig. 2(c).

Fig. 2.

DX DNA tile structure (a) Four ss-DNA (b) Assembled DNA tile (c) Abstract representation

2.2 Tile Self-assembly Models

The physical implementation of tile self-assembly in a wet-lab is often time-consuming, expensive and challenging with respect to reproducibility of results. Simulation of realistic models of DNA self-assembly provides a cheaper, faster (and more reliable) media in which to explore and refine new avenues of research, prior to experimentation. There are two simulation models of tile self-assembly, developed by Winfree [13, 20]: (1) The abstract Tile Assembly Model (aTAM), and (2) The kinetic Tile Assembly Model (kTAM).

Abstract Tile Assembly Model (aTAM): The aTAM [20] is based on Wang’s tiling theory [17], which requires creation of a finite set of square shape tiles that are abstract representations of DX DNA-tile shown in Fig. 3(a). In aTAM, a tile t is represented by a quadruple ($\sigma _{S}(t), \sigma _{W}(t), \sigma _{N}(t), \sigma _{E}(t)$), where $\sigma \in \varSigma$ is glue type associated with the four sides (North(N), South(S), West(W), East(E)) of a rotationally asymmetric unit square. The glue type, $\varSigma$, is a finite set, which is used to derive a glue strength function ($s : \varSigma \times \varSigma \rightarrow N$) for a legitimate tile association between two glues of tiles. The glue strength function is symmetric, i.e., s($\sigma _{1}, \sigma _{2}$) = s($\sigma _{2}, \sigma _{1}$) $\forall \sigma _{1}, \sigma _{2} \in \varSigma$.

A tile pattern assembly system (TPAS) $\mathcal {T} = (T, S, s, \tau )$ consists of a finite set T of tile types, an assembly S termed as seed assembly, a glue strength function s and a temperature parameter $\tau \in Z^{+}$. A tile assembly system has a temperature ‘$\tau$’ if any larger structure of tiles cannot be dissociated into smaller assemblies without breaking bonds of total strength at least ‘$\tau$’. Alternatively, a tile can join the assembly as long as the sum of the strengths of the bonds that it makes with tiles already in the assembly is at least $\tau$.

Figure 3 illustrates the self-assembly process of the Sierpinski pattern [12, 21] at temperature 2 ($\tau = 2$). The tile set comprises a seed tile, two boundary tiles and four rule tiles - see Fig. 3(a). Tile edges are marked by non-negative integers illustrating their respective glue strengths. The South and West glues of the tiles are designed as inputs and the North and East glues are outputs.

Tile pattern assembly in the aTAM starts from a given seed structure that nucleates the pattern formation which grows into a finite or infinite pattern as more tiles join - see Fig. 3(b). Tiles join by forming bonds with strength at least of $\tau$. For example, in a $\tau =2$ assembly, each tile that binds with the growing pattern of tiles needs an attachment of total binding strength $\ge 2$. For a given TPAS, a pattern assembly P is said to be terminal, if no tile can be added further that satisfies the $\tau -stability$ criteria.

The aTAM has given insights to important theoretical aspects of the tile assembly systems [3, 13]: (1) what can or can’t be self-assembled?, and (2) if something can be assembled, how efficient it could be?

Fig. 3.

Sierpinski pattern self-assembly. (a) Sierpinski tile set (XOR tile set). (b) Steps of self-assembly of Sierpinski pattern of size 9$\,\times \,$9. (c) Kinetics of tile assembly in kTAM.

The Kinetic Tile Assembly Model (kTAM): Tile binding in the tile self-assembly is a reversible physico-chemical process that has been modelled using the kTAM [20]. The rate of tile attachment at a binding site of an aggregate is directly proportional to the tile concentration. The concentration of each type of tile (except the seed tile) can be given by $e^{-G_{mc}}$, where $G_{mc}$ is the decrease in entropy when a tile binds at a vacant site. Therefore, the forward reaction rate ($r_{f}$) can be given by $r_{f} = k_{f} e^{-G_{mc}}$ where $k_{f}$ is the reaction rate constant. Similarly, the tile detachment process is controlled by the energy required to break any single tile-aggregate bond and denoted by $G_{se}$. The value of $G_{se}$ depends on the sticky end length (s) and the temperature (T), where $G_{se}\approx (4000/T-11)s$. The tile reverse reaction rate involving b tile bonds is given by $r_{r,b} = k_{f} e^{-bG_{se}}$.

A larger value of $G_{mc}$ thus implies a lower tile concentration and consequently a slower forward reaction rate (or vice versa). Similarly, a larger value of $G_{se}$ results in a slower detachment rate. The optimum growth rate with low error rates happens near thermodynamic equilibrium ($G_{mc} \approx 2G_{se}$) [21], and may be given by $r^{*}\approx {r_{f}-r_{r,2}}$ and $\varepsilon \approx e^{-G_{se}}$, respectively. Therefore, a relation between optimum growth rate and minimum error rate may be given by $r^{*}\approx \beta \varepsilon ^{2}$ where, $\beta = 0.75 \times 10^{6}$ /M/sec. Thus, any effort to reduce the error rate ($\varepsilon$) by tuning physical parameters ($G_{mc}$ and $G_{se}$) would result in a quadratic reduction of the growth rate. However, error reduction without significant fall off in assembly growth rate has been achieved by adding redundant tiles [8, 21] and by protecting tile’s inputs and outputs [5, 11].

2.3 The Tile Pattern Self-replication System

Figure 4 shows the design of Tile Pattern Self-replication System (TPSS), earlier introduced in [6]. The L-shaped seed of the target pattern (P) is highlighted with a blue colour. The unique corner tile of the pattern is shown in red. Starting with the pattern structure (left cycle), pattern-mold (P-M) complex forms as CST attaches with the unique corner tile of the pattern, and further tiles from the v-MTS and h-MTS sets assemble to form the vertical and horizontal arms of the mold, respectively. The P-M complex is dissociated into the seed and the mold (M) through external switching. The dissociated mold (M) serves as a new seed to assemble a new P-M complex (right cycle) that subsequently dissociates in the seed and the mold. Thus, the process initiates cross-coupled cycles catalyzing the formation of one another.

Fig. 4.

Tile pattern self-replication system. (Color figure online)

Let a pre-assembled target pattern, P, be self-replicated. L-shaped South-West border of the pattern P serves as seed, which enables entire rectangular pattern of tiles to be uniquely identified by the glues placed on its interior border. Considering that each tile in the pattern requires at least two bonds for a stable attachment (a case of $\tau = 2$ algorithmic tile self-assembly), the formation of pattern from the L-shaped seed would be a terminal assembly process [2]. A terminal assembly system forms a unique final structure from a set of supplied components.

The replication process starts with a pre-assembled rectangular pattern (P), Corner Super Tile (CST), and a set of Mold forming Tile Set (MTS). The MTS consists of two subsets: (1) Vertical Mold forming Tile Set (v-MTS) assembles to form a vertical double layer of the mold; (2) Horizontal Mold forming Tile Set(h-MTS) assembles the horizontal arm of the mold.

We require that the target pattern contains a unique, red-coloured tile on its lower-left corner position, which is not used on any other position inside the pattern. Observe that the CST consists of eight tiles, and therefore it is stable at temperature-2. The CST is designed to bind (using two strength-1 glues) on the special red-coloured tile. Mold formation is initiated with the binding of the CST, and further proceeds as more tiles cooperatively join one by one until the entire South-West boundary of the pattern structure is covered by a double layer of tiles, creating a pattern-mold complex (P-M). Tiles forming the inner layer of the mold are designed as SWET type (now shown in the above schematics) with switch-enabled glue on the side that binds with the seed (pattern). The assembled pattern-mold complex undergoes a controlled dissociation, splitting into the Pattern P and the mold M structures. Observe that the dissociated mold structure has two layers of tiles, thus ensuring its stability under temperature-2 assembly framework.

In the next replication cycle, the dissociated pattern structure (P) repeats the left hand side pathway, and thereby, creates two (P-M) complexes, whereas the dissociated mold structure (M) drives the right hand side pathway using tiles from the PTS. Indeed, assuming we have at our disposal a tile set capable of assembling the pattern, we use the mold to reassemble the complete pattern P. Thus, by supplying the system with sufficiently many copies of the tiles within the MTS and PTS tile sets, and by continuing the process for i complete cycles, the replicator could theoretically produce $2^{i-1}$ copies of both the mold and the pattern structures. In a potential experimental implementation, one has to provide enough time for both the mold formation process (from a template pattern) and the pattern formation process (using the mold as a seed). Then, one adjusts the cycle of inhibitor signal supply, which triggers the pattern-mold dissociation such as to be at least as long as the maximum of the two expected time values.

3 Kinetic Model of the TPSS

In this section, we derive a simplified kinetic model of pattern self-replication system using the kTAM. The kinetic model consists of two cross-coupled pathways as shown in Fig. 5 — the left hand side pathway I corresponds to the cycle that is seeded with a target Pattern (P), whereas for the right hand side cycle II, Mold (M) acts as a seed. Intermediate product of both assembly pathways is Pattern-Mold (P-M) complex, which dissociates into copies of seed and mold.

Using the kTAM and its analytic model of kinetic trapping [20], macroscopic kinetic rates ¹ ($k_1$ and $k_2$) of assembly steps leading to P-M complex from seed and mold are: $k_1 = \frac{r^{*}}{\sqrt{n^{2} +4}}$ and $k_2 = \frac{r^{*}}{n\sqrt{2}}$, respectively, where n denotes the size of $n\times n$ pattern and $r^{*}$ is an optimal kinetic rate of tile assembly, as discussed in Sect. 2.2. Kinetic rate of dissociation of P-M complexes is a DNA strand displacement reaction. A typical kinetic rate of a toehold-mediated DNA strand displacement process involving a toehold of 3 nucleotides (nt), and a 7 nt long branch migration [22] is $k_d \approx 10^{5} \ M^{-1} s^{-1}$.

Fig. 5.

Kinetic model of pattern self-replication system of rectangular patterns

Let number of copies of P, M and P-M structures at a time i are, s[i], m[i], and sm[i], respectively. Therefore, under chemical equilibrium conditions, number of copies of P, M, and P-M complexes in discrete time are given in Eqs. (1) and (2).

$$\begin{aligned} s[i+1] = m[I] = k_d sm[i] \end{aligned}$$

(1)

$$\begin{aligned} sm[i] = k_1 s[i] + k_2 m[i-1] - k_d sm[i] \end{aligned}$$

(2)

Using Eqs. (1) and (2), the concentration of pattern-mold complexes after i replication cycles is

$$\begin{aligned} sm[i] = \frac{k_1s[i] + k_2 m[i-1]}{1+k_d} \end{aligned}$$

(3)

From Eqs. (3) and (1), $s[i+1]$ and m[i] can be given as

$$\begin{aligned} s[i+1] = m[i] = \frac{k_d k_1}{1+k_d} s[i] + \frac{k_d k_2}{1+k_d} m[i-1] \end{aligned}$$

(4)

The coefficient terms, s[i] and $m[i-1]$ in Eq. (4), can be replaced with $k_a$ and $k_b$, respectively. The equivalent equation is given as below

$$\begin{aligned} s[i+1] = k_a s[i] + k_b m[i-1] \end{aligned}$$

(5)

Replacing $m[i-1]$ by $s[i-1]$ in Eq. (5) gives the following difference equations in discrete time.

$$\begin{aligned} s[i+1] = k_a s[i] + k_b s[i-1] \end{aligned}$$

(6)

Applying z-transformation² in Eq. (6), it turns into following quadratic equation in the z-domain

$$\begin{aligned} z^2 - k_a z - k_b =0 \end{aligned}$$

(7)

Let $\lambda _1$ and $\lambda _2$ are the two roots of the quadratic equation (7): $\lambda _1 = \frac{k_a+ \sqrt{k_a^2 +4k_b}}{2}$ and $\lambda _2 = \frac{k_a - \sqrt{k_a^2 +4k_b}}{2}$. Hence, a general solution of Eq. (5) can be represented as

$$\begin{aligned} s[i] = c_1\lambda _1^i + c_2\lambda _2^i \end{aligned}$$

(8)

The $c_1$ and $c_2$ are arbitrary constants. For a replicator system supplied with c copies of seeds in the start, $s[0]= c$ and $m[0]= 0$, as mold is not yet assembled. Putting $i = 0$ in Eq. (5), it gives $s[1] = k_ac$. Applying these boundary conditions for $i=0$ and $i = 1$ in (7), it gives

$$\begin{aligned} c = c_1 + c_2 \end{aligned}$$

(9)

$$\begin{aligned} k_a c = c_1 \lambda _1 + c_2 \lambda _2 \end{aligned}$$

(10)

Solving Eqs. (9) and (10) for $c_1$ and $c_2$, and putting these values in Eq. (8), the general solution of the difference equation (6) is

$$\begin{aligned} s[i]= \frac{(k_a -\lambda _2)c}{(\lambda _1-\lambda _2)} \lambda _1^i - \frac{(k_a -\lambda _1)c}{(\lambda _1-\lambda _2)}\lambda _2^i \end{aligned}$$

(11)

The expression of s[i] in Eq. (11) represents the population growth with respect to replication cycles (i). Clearly, the population s[i] at a given replication cycle is proportional to the initially supplied seed concentration, and is a polynomial in $\lambda _1$ and $\lambda _2$. Dynamics of the population growth is governed by parameters: $k_a$, $k_b$, $\lambda _1$, and $\lambda _2$. These parameters depend on physicochemical conditions (local assembly temperature (T), tile concentration ($G_{mc}$) and total binding strength of tile (b and $G_{se}$)) of the tile self-assembly medium.

4 Results and Discussion

The kTAM based analysis of tile assembly has demonstrated the effect of physical parameters over the growth rate and the error rate of tile assembly. It was established that a target error rate can be achieved only at a certain growth rate. Therefore, owing to the constraints of experimental feasibility, a proper choice for an optimum error rate and its corresponding growth rate has to be made. Herein, we analyse quantitatively the effect of these constraints over population growth dynamics and reliability of pattern replicator.

In Fig. 6, $\lambda _1$ is plotted against error rate and target pattern size using the replication gain derived in Eq. (11).

Fig. 6.

$\lambda _1$ estimated from mathematical simulations

For an exponential gain of self-replication, value of $\lambda _1$ should be $\approx 2$. From the plot, it is evident that for an error rate ($\epsilon \approx 5\times 10^{-3}$), $\lambda _1 \approx 2$. In Fig. 7, $\lambda _2$ is plotted against error rate and target pattern size using mathematical model. From the plot, it is evident that $|\lambda _2| < 1$ for an error rate $\epsilon \approx 5\times 10^{-3}$.

For a given set of kinetic parameter values of $k_1$, $k_2$ and $k_d$, $|\lambda _1|$ is $>1$, and $|\lambda _2|$ is $<1$. Therefore, an approximate population of self-replicating patterns after many replication cycles i.e., ${i\rightarrow \infty }$, can be given as

$$\begin{aligned} s[i]\approx \frac{(k_a -\lambda _2)c}{(\lambda _1-\lambda _2)} \lambda _1^i \end{aligned}$$

(12)

Fig. 7.

$\lambda _2$ estimated from mathematical simulations

For an approximate replication gain, derived in Eq. (12), we plotted the pattern replication gain for replication cycles. Figure 8 shows exponential replication gains for two sets of parameters: initially introduced pre-assembled target patterns (c), size of target pattern (n), and assembly error rate ($\epsilon$).

Fig. 8.

Exponential replication growth of pattern self-replication: c = 2 n = 18, and $\epsilon$ = $5\times 10^{-3}$) (LHS); c = 1, n = 60, and $\epsilon$ = $10^{-2}$ (RHS).

5 Conclusion

In this study, we constructed a kinetic model of a tile pattern self-replication system. Our model captures the dynamics of self-replicating tile patterns using equivalent kinetic rates for the two cross-coupled cycles of the self-replicator. The physico-chemical parameters of tile self-assembly influence the overall replication dynamics of the tile pattern self-replication process. It is observed that both size of target pattern and parameters should be carefully chosen so as to produce an exponential self-replication gain.

The observations of this paper could be useful for an experimental implementation of the pattern self-replication. To increase the robustness of self-replicating patterns in error accumulating tile self-assembly medium, error-correction tiles [7] can be used. A reliable self-replicator with error levels not exceeding a minimum threshold may further open up new directions for investigation of fundamental principles behind reproduction and selection-driven evolution.