Keywords

1 Introduction

Nowadays, consideration of vibration in the design of structures is a significant issue. We can see much difference in the structure design methods used today compared to those used in the past. These days, in structure design, vibration control has become more important than deflection control. The American Institute of Steel Construction (AISC) and the Canadian Standards Association (CSA) have presented some formulations for the determination of the natural frequency in building structures. Other researchers have also presented methods to calculate the natural frequency in beams and plates, but these methods tend to be complex, making their use in vibration control of structures difficult and time consuming, with increased probability of errors. In this study we propose a method, using dynamic analysis, finite element analysis and artificial neural networks for the calculation of the natural frequency in cantilever beams.

There have been many studies on determining the natural frequency in beams and on vibration control in structures. Hamdan and Jubran [1], calculated the natural frequency of a cantilever beam with an intermediate concentrated load, where the effects of concentrated mass on natural frequency, and the effects of natural frequency on the beam vibration were shown.

Bokaian [2], presented the effects of a constant axial tensile force on the natural frequencies and mode shapes of a uniform single-span beam, having different combinations of end conditions. Liu and Haung [3], used the Laplace transform method to study the free vibration of a beam with one concentrated mass at the tip of the beam and another at an intermediate point. Liu and Yeh [4], used the Rayleigh-Ritz method to study the free vibration of restrained non-uniform and cantilever beams with intermediate loads. Goel [5], studied the free vibration of a cantilever beam carrying a concentrated mass at an arbitrary intermediate location. Kounadis [6], studied the free and forced vibrations of a restrained cantilever beam with attached masses. Kojima et al. [7], derived the equations of motion and presented solutions satisfying all boundary conditions at the beam ends. They then used this to investigate the forced response of a cantilever beam having a tip mass and a magnetic vibration absorber at the middle of the beam. Al-Ansari [8], studied two methods for calculating the natural frequency in a stepped cantilever beam; one by using finite element modeling, and the other, using the Rayleigh method. To improve the accuracy in using the Rayleigh method, a new method for calculating the equivalent moment of inertia of the stepped beam was used. He used four different types of beam cross-sections, which were circular, square, rectangular with step in the width only and rectangular with step in the height only. The results using the Rayleigh method was then compared with those from the FEM analysis. Mutra [9], presented an application of artificial neural networks (ANN) in predicting the natural frequency of laminated composite plates. The natural frequencies were calculated by FEM. For training and testing of the ANN model, a number of finite element analyses were carried out and the back propagation algorithm was used to create the network. Hornik et al. [10], showed that the number of hidden layers and neurons will affect the optimum results in each try of a network. He showed that increasing the number of hidden layers can improve the generalization capacity.

2 Dynamic Analysis

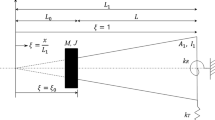
To determine the natural frequency in cantilever beams, we first used dynamic analysis to find the governing equations. We define Eq. (1) as the governing differential equation for the cantilever beam shown in Fig. 1.

$$ \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {EI\left( x \right)\frac{{\partial^{2} v\left( {x,t} \right)}}{{\partial x^{2} }}} \right] - \frac{\partial }{\partial x}\left[ {N\left( x \right)\frac{{\partial v\left( {x,t} \right)}}{\partial t}} \right] + m\left( x \right)\frac{{\partial^{2} v\left( {x,t} \right)}}{{\partial t^{2} }} = f\left( {x,t} \right) $$
(1)
Fig. 1.
figure 1

Cantilever beam with non-uniform loading

Full size image

In Eq. (1), \( E \) is the elastic modulus, \( I \) is the moment of inertia and \( m \) is the mass per unit length of the beam. If we ignore the effects of the lateral forces and assume that the moment of inertia is constant along the beam, Eq. (1) can be written as Eq. (2).

$$ \left[ {EI\frac{{\partial^{4} v\left( {x,t} \right)}}{{\partial x^{4} }}} \right] + \left[ {m\left( x \right)\frac{{\partial^{2} v(x,t)}}{{\partial t^{2} }}} \right] = f(x,t) $$
(2)
$$Equvalently, \frac{EI}{\rho A}\frac{{\partial^{4} v(x,t)}}{{\partial x^{4} }} + \frac{{\partial^{2} v(x,t)}}{{\partial t^{2} }}=f(x,t) $$
(3)

Here, \( \rho \) is density and \( A \) is the cross section area of the beam. To solve Eq. (3) in the free vibration mode, we used the method of separation of variables of the differential equations, assuming homogeneous mass and constant flexural rigidity throughout the beam. Hence, Eq. (3) can be written as Eq. (4), with \( v\left( {x,t} \right) = B\left( x \right)T\left( t \right) \).

$$ \frac{{c^{2} }}{B(x)}\frac{{d^{4} B(x)}}{{dx^{4} }} = - \frac{1}{T(t)}\frac{{d^{2} T(t)}}{{dt^{2} }} ,\, c = \sqrt {\frac{EI}{\rho A}} $$
(4)

Where \( B\left( x \right) \) is the displacement function and \( T\left( t \right) \) is the time function. Then, the solution for displacement is

$$ B(x) = C1cos (x\lambda )\,+\, C2sin (x\lambda ) + {\text{C3}}cosh (x\lambda )+ C4sinh (x\lambda ) $$
(5)

where

$$ \lambda = \left( {\frac{\rho A}{EI}\omega^{2} } \right)^{{\frac{1}{4}}} $$
(6)

and \( C_{1} ,C_{2} ,C_{3} \) and \( C_{4} \) are constants that can be found from the boundary conditions. For a cantilever beam, at the fixed end, the displacement and slope are zero, but at the free end, the moment and shear are zero. Therefore,

$$ x = 0;\,B\left( 0 \right) = 0\,\, \frac{dB\left( x \right)}{dx} = 0 $$
(7)
$$ x = L;\, \frac{{d^{2} X}}{{dx^{2} }} = 0,\,\, \frac{{d^{3} X}}{{dx^{3} }} = 0 $$
(8)

These boundary conditions give \( C_{2} = - C_{4} \) and \( C_{1} = - C_{3} \).

$$ \cos \left( {\beta L} \right)\cosh \left( {\beta L} \right) = - 1 $$
(9)

Solving Eq. (5) for \( C_{2} \) and \( C_{1} \), gives

Then, the roots of Eq. (9) are

$$ \beta_{n} L = \frac{{\left( {2n - 1} \right)\pi }}{2} $$
(10)

Now Eq. (4) can be solved for the time function, giving

$$ T(t) = k_{1} \sin \left[ {\left( {\beta_{n}^{2} \sqrt {\frac{EI}{\rho A}} } \right)t} \right] + k_{2} \cos \left[ {\left( {\beta_{n}^{2} \sqrt {\frac{EI}{\rho A}} t} \right)} \right] $$
(11)

The frequency in rad/s same can be written a

$$ \omega = \left( {\frac{{\beta_{n} }}{L}} \right)^{2} \sqrt {\frac{EI}{\rho A}} $$
(12)

Converting Eq. (12) into Hz gives:

$$ f_{n} = \frac{{\omega_{n} }}{2\pi } = \frac{{\beta_{n}^{2} }}{{\left( {2\pi L} \right)^{2} }}\sqrt {\frac{EI}{\rho A}} = \frac{{\beta_{n}^{2} }}{{\left( {2\pi } \right)^{2} }}\sqrt {\frac{EI}{{\rho A L^{4} }}} $$
(13)

Now, using \( n = 1 \) gives the natural frequency as

$$ f = \beta \sqrt {\frac{I}{{PL^{4} }}} $$
(14)

In Eq. (14), \( f \) is the natural frequency, \( I \) is the moment of inertia, \( P \) is dead load per length of beam, \( L \) is the length of the beam, and \( \beta \) is a constant that, in this article, will be determined through the use of neural networks. In this study, the beam material is steel, whose elasticity modulus, E is taken to be \( 2 \times 10^{6} \,{\text{kg/cm}}^{2} \).

3 Prediction of Natural Frequency Using Artificial Neural Networks

Figure 2, shows the network architecture of the ANN used in this study. The input layer consists of 3 items; moment of inertia \( \left( I \right) \), length of beam \( \left( L \right) \) and dead load along the beam \( \left( P \right) \), while the output layer is the natural frequency of the beam \( \left( f \right) \). For the hidden layers, one and two layer architectures were used.

Fig. 2.
figure 2

Network architecture

Full size image

The transfer functions used were Tangent-sigmoid (Tansis) and Purelin for the hidden layer, and Purelin, Log-sigmoid (Logsis) and Tangent-sigmoid for the output layer.

Carpenter and Barthelemy [11] presented Eq. (15) as a guide for finding the minimum number of neurons in each hidden layer.

$$ h_{n} = i_{n} + 1 $$
(15)

Here, \( h_{n} \) is the number of nodes in the hidden layers and \( i_{n} \) is the number of nodes in the input layer. Hence, in this study the minimum number of nodes in the hidden layer was four.

The next important step in creating a neural network is to determine the number of training data. Increasing the number of training data increases the total training time required, but a larger number of training data improves training performance.

Calculating the needed number of training data depends on the hidden layer nodes, input nodes and output layer nodes. The number of training data used in this work is given by Eq. (16).

$$ Tn = h_{n} \left( {i_{n} + 1} \right) + o_{n} (h_{n} + 1) $$
(16)

Where \( T_{n} \) is the minimum number of training data, \( h_{n} \) is the number of hidden layer nodes, \( i_{n} \) is the number of input layer nodes and \( o_{n} \) is the number of output layer nodes. In this study we used 15 nodes for the hidden layer, 3 nodes for input layer (length of beam, moment inertia and dead load) and 1 output layer node (natural frequency of beam), giving

$$ Tn = 15\left( {3 + 1} \right) + 1\left( {15 + 1} \right) = 76 $$
(17)

To improve results of the network, all data were normalized in the range of [0, 1],

$$ X_{n} = X_{i} /X_{max} $$
(18)

Where \( X_{n} \) is the normalized data, \( X_{i} \) is the original data, and \( X_{max} \) is the maximum value of all data.

Evaluation of the network performance was based on the Mean Squared Error (MSE) as shown in Eq. (19), where \( R_{s} \) is the estimated value and \( R_{a} \) is the actual value. The best performance would be given by the lowest MSE value. Table 1 shows the details of the neural network used.

Table 1. Details of the neural networks used in this study
Full size table
$$ MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (R_{s} - R_{a} )^{2} $$
(19)

In this study we generated 45 different networks, where the details of the networks are shown in Tables 2, 3 and 4. Table 2 shows the MSE and the coefficient of determination (\( R^{2} \)) results for the network with one hidden layer and Purelin and Tansis as the output transfer functions. Here, the numbers of nodes used in the hidden layer were 5, 10, 15 and 20, the training functions used were Trainbr (Bayesian Regularization) and Trainlm (Levenberg Marquart), the learning functions were Learngd (Gradient descent) and Learngdm (Gradient descent with momentum). Table 3 gives the MSE and \( R^{2} \) results for networks with one hidden layer and Tansis as the output transfer function, where fixed training and learning functions (Trainbr and Learngdm) were used. The hidden layer transfer function and number of neurons were varied to find the combination that gives the best network performance. Table 4 shows the results for networks with two hidden layers where the output transfer function was Purelin, and the fixed training and learning functions were Trainbr and Learngdm. Here, the hidden layers had 5, 10 or 15 neurons, and the hidden layer transfer functions were combinations of Tansis, Purelin and Lonsig.

Table 2. MSE and R2 results - one hidden layer and Purelin as output transfer function
Full size table
Table 3. MSE and R 2 results - one hidden layer and tansis as output transfer function
Full size table
Table 4. MSE and R 2 results - two hidden layers and purelin as output transfer function
Full size table

The performance of the neural networks depends on many factors such as the training and testing parameters, and the range of data values. From all the created networks, we selected two that gave the best performances. The selection was based on the MSE and \( R^{2} \) results from the whole range of networks. Table 5 shows the parameter values for the two selected networks, denoted Net 1 and Net 2.

Table 5. MSE, R 2 and other parameters of Net 1 and Net 2 - the best performance between all 45 networks
Full size table

Figure 3 shows the \( R^{2} \) results for Net 2. The horizontal axis is the target frequency obtained from FEM analysis and the vertical axis is the predicted frequency obtained from ANN. The regression analysis graph gives a straight line, which means low error and good performance. A comparison of the predicted frequency from generated neural networks to the frequencies obtained from theory and FEM analysis is shown in Fig. 4. A close correlation is clearly evident.

Fig. 3.
figure 3

Regression analysis for Net 2

Full size image
Fig. 4.
figure 4

Comparison of natural frequency from 5 test data between 3 methods

Full size image

4 Conclusion

There are many different methods for the calculation of the natural frequency of cantilever beams. However, these methods tend to be complex. Here, a simple method to predict the natural frequency using artificial neural networks has been presented. Both generated networks used in this study were found to be trustworthy and can be used as references for natural frequency calculation in steel cantilever beams of any length and any cross section, and subjected to any lateral load. While this work has concentrated on steel cantilever beams, it is envisaged that in future, the method can be extended to beams made from other materials as well.