Abstract
GNU  is a free software for editing scientific documents with mathematical formulas, which can also be used as an interface for many computer algebra systems. We present the design of a new experimental mathematical editing mode which preserves the syntactic correctness of formulas during the editing process (i.e. all formulas can be parsed using a suitable, sufficiently rich grammar). The main constraint is to remain as closely as possible to the existing presentation-oriented formula editor, which has the advantage of being very user friendly.
is a free software for editing scientific documents with mathematical formulas, which can also be used as an interface for many computer algebra systems. We present the design of a new experimental mathematical editing mode which preserves the syntactic correctness of formulas during the editing process (i.e. all formulas can be parsed using a suitable, sufficiently rich grammar). The main constraint is to remain as closely as possible to the existing presentation-oriented formula editor, which has the advantage of being very user friendly.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
A.M.S. Subject Classification
1 Introduction
Most mathematical formulas in current scientific papers only carry very poor semantics. For instance, consider the two formulas \(f (x + y)\) and \(a (b + c)\). People typically enter these formulas using the LaTeX pseudo-code $f(x+y)$ and $a(b+c)$. Doing so, we do not transmit the important information that we probably meant to apply f to \(x + y\) in the first formula and to multiply a with \(b + c\) in the second one. The problem to automatically recover such information is very hard in general. For this reason, it would be desirable to have mathematical authoring tools in which it is easy to write formulas which systematically carry this type of information.
One important application where semantics matters is computer algebra. Popular computer algebra systems such as Mathematica and Maple contain formula editors in which it is only possible to input formulas which can at least be understood from a syntactical point of view by the system. However, these systems were not really designed for writing scientific papers: they only offer a suboptimal typesetting quality, no advanced document preparation features, and no support for more informal authoring styles which are typical for scientific papers.
The GNU  editor was designed to be a fully fledged wysiwyg alternative for
editor was designed to be a fully fledged wysiwyg alternative for  , as well as an interface for many computer algebra systems. The software is free and can be downloaded from http://www.texmacs.org. Although formulas only carried barely more semantics than LaTeX in old versions of
, as well as an interface for many computer algebra systems. The software is free and can be downloaded from http://www.texmacs.org. Although formulas only carried barely more semantics than LaTeX in old versions of  , we have recently started to integrate more and more semantic editing features. Let us briefly discuss some of the main ideas behind these developments; we refer to [11] for more details and historical references to related work.
, we have recently started to integrate more and more semantic editing features. Let us briefly discuss some of the main ideas behind these developments; we refer to [11] for more details and historical references to related work.
First of all, we are only interested in what we like to call “syntactical semantics”. In the formula \(2 + 3\), this means that we wish to capture the fact that \(+\) is an infix operator with arguments 2 and 3, but that we are uninterested in the fact that \(+\) stands for addition on integers. Such syntactical semantics can be modeled adequately using a formal grammar. Several other mathematical formula editors are grammar-based [1,2,3, 6, 8, 9], and they make use of various kinds of formal grammars. In  , we have opted for so-called packrat grammars [4, 5], which are particularly easy to implement and customize.
, we have opted for so-called packrat grammars [4, 5], which are particularly easy to implement and customize.
A second question concerns the precise grammar that we should use to parse formulas in scientific documents. Instead of using different grammars for various areas with different notations, we were surprised to empirically find out that a well-designed “universal” mathematical grammar is actually sufficient for most purposes; new notations can still be introduced using a suitable macro-mechanism.
The last main point concerns the interaction between the editor and the grammar. So far, we implemented a packrat parser for checking the correctness of a formula. While editing a formula, its correctness is indicated using colored boxes. It is also possible to detect and visualize the scopes of operators through the grammar. In addition to the parser, we implemented a series of tools which are able to detect and correct the most common syntactical mistakes and enhance existing documents with more semantics.
In the present paper, we wish to go one step further and enforce syntactic correctness throughout the editing process. Ideally speaking, the following requirements should be met:
-
As far as user input is concerned, there should be no essential difference between editing formulas with or without the new mechanism for preserving syntactic correctness. For instance, we do not wish to force users to provide additional “annotations” for indicating semantics. It should also be possible to perform any editing action which makes sense from the purely visual point of view.
-
The implementation should be as independent as possible from the actual grammar being used. In other words, we strive for a generic approach, not one for which specific editing routines are implemented for each individual grammar symbol.
The main technique that we will use for sticking as close as possible to the old, presentation-oriented editing behavior is to automatically insert “transient” markup for enforcing correctness during the editing process. For instance, when typing  ,
,  will display
will display

The transient box is used to indicate a missing symbol or subexpression and will be removed as soon as the user enters the missing part.
The use of transient boxes for missing symbols or subexpressions is common in other editors [7]. The question which interests us here is how to automatically insert such markup when needed in a way that is essentially independent from specific grammars. In this paper, we work out the following approach which was suggested in [11]: before and after each editing operation, subject the formula to suitable “correction” procedures that are only allowed to add or remove transient markup. Correcting all errors in a general formula is a very difficult problem, but the power of our approach comes from the fact that the editing process is incremental: while typing, the user only introduces small errors—mostly incomplete formulas—which are highly localized; we may thus hope to deal with all possible problems using a small number of “kinds of corrections”.
Obviously, the simplest kinds of corrections are adding or removing a transient box at the current cursor position. This is indeed sufficient when typing simple formulas such as \(x + y + z\), but additional mechanisms are needed in other situations. For instance, in the formula  (with the cursor between the “\(+\)” and the “\(\beta \)”), entering another \(+\) results in
(with the cursor between the “\(+\)” and the “\(\beta \)”), entering another \(+\) results in  (instead of
(instead of  or \(a + + b\)). Hitting backspace in the same formula
or \(a + + b\)). Hitting backspace in the same formula  yields
yields  ; in this case, the transient “\(+\)” should be parsed as an infix addition, and not as an ordinary symbol (as was the case for a transient box).
; in this case, the transient “\(+\)” should be parsed as an infix addition, and not as an ordinary symbol (as was the case for a transient box).
The appropriate corrections are not always so simple. For instance, consider the quantified expression \(\forall x, \exists y, P (x, y)\). Just after we entered the existential quantifier “\(\exists \)”, the formula will read  , i.e. it was necessary to add three transient symbols in order to make the expression syntactically correct. The fact that our approach should apply to general scientific documents with mathematical formulas raises several further problems. For instance, in the formula
, i.e. it was necessary to add three transient symbols in order to make the expression syntactically correct. The fact that our approach should apply to general scientific documents with mathematical formulas raises several further problems. For instance, in the formula
the trailing punctuation “,” is incorrect from a mathematical point of view, but needed inside the surrounding English sentence. Similarly, more work remains to be done on the most convenient way to include English text inside formulas while maintaining syntactic correctness.
Yet another difficulty stems from the implementation: one needs to make sure that the necessary corrections take place after any kind of editing operation. However, for efficiency reasons, it is important to only run the correction procedures on small parts of the document. Inside an existing editor such as  , these requirements turn out to be quite strong, so some trade-offs may be necessary.
, these requirements turn out to be quite strong, so some trade-offs may be necessary.
In what follows, we report on our first implementation of these ideas inside  . We describe and motivate the current design, discuss remaining problems, and outline directions for future improvements. Of course, more user feedback will be necessary in order to make the new mechanisms suitable for widespread use.
. We describe and motivate the current design, discuss remaining problems, and outline directions for future improvements. Of course, more user feedback will be necessary in order to make the new mechanisms suitable for widespread use.
2 Survey of Formula Editing with 
In this section, we briefly recall the main design philosophy behind the  formula editor. We start with the description of the original, purely presentation-oriented mathematical editing mode. We pursue with the more recent grammar-based editing features, which are presented in more detail in [11].
formula editor. We start with the description of the original, purely presentation-oriented mathematical editing mode. We pursue with the more recent grammar-based editing features, which are presented in more detail in [11].
2.1 Presentation-Oriented Editing
The original goal behind  was to provide a user friendly editor for mathematical papers with a similar typesetting quality as
was to provide a user friendly editor for mathematical papers with a similar typesetting quality as  . The challenge was to design a real-time WYSIWYG editor for complex, structured documents. Some early inspiration came from the idea [1] that graphically oriented math editors achieve the highest level of user friendliness. For instance, when pressing the right arrow key, the cursor should move to the right if possible (instead of moving forward in some abstract document tree, as was the case in some other existing editors). Early versions of
. The challenge was to design a real-time WYSIWYG editor for complex, structured documents. Some early inspiration came from the idea [1] that graphically oriented math editors achieve the highest level of user friendliness. For instance, when pressing the right arrow key, the cursor should move to the right if possible (instead of moving forward in some abstract document tree, as was the case in some other existing editors). Early versions of  used algorithms for the cursor movement which achieved this in a systematic way [10], while still making sure that all possible cursor positions in the corresponding document tree could be reached.
used algorithms for the cursor movement which achieved this in a systematic way [10], while still making sure that all possible cursor positions in the corresponding document tree could be reached.
Another aspect of user friendliness concerned the efficiency of mathematical input methods. We designed highly efficient (and easy to memorize) keyboard shortcuts for entering common mathematical symbols, such as  for \(\rightarrow \),
for \(\rightarrow \),  for \(\leqslant \),
for \(\leqslant \),  for \(\not \in \),
for \(\not \in \),  for \(\mathbbm {R}\), etc.
for \(\mathbbm {R}\), etc.  also implements many “structured editing operations”, so as to fully exploit the structure of documents. For instance, adding a row or column to a matrix can be done by pressing a single key or keyboard combination. Similarly, it is easy to change a matrix into a determinant or vice versa.
also implements many “structured editing operations”, so as to fully exploit the structure of documents. For instance, adding a row or column to a matrix can be done by pressing a single key or keyboard combination. Similarly, it is easy to change a matrix into a determinant or vice versa.
2.2 Grammar-Based Editing
The next challenge for  is to ensure that we can only enter syntactically correct formulas, while keeping a presentation-oriented interface, which proved to be most user friendly. The first steps of this program were made in [11]. Now syntactic correctness is usually modeled as “parsability against a suitable grammar”. Before anything else, one should decide on the grammar. In particular, does a single “universal grammar” suffice, or do we need many different grammars, depending on the preferred notations of authors?
is to ensure that we can only enter syntactically correct formulas, while keeping a presentation-oriented interface, which proved to be most user friendly. The first steps of this program were made in [11]. Now syntactic correctness is usually modeled as “parsability against a suitable grammar”. Before anything else, one should decide on the grammar. In particular, does a single “universal grammar” suffice, or do we need many different grammars, depending on the preferred notations of authors?
For reasons that are explained in detail in [11], we opted for the development of a universal packrat grammar [4, 5] for parsing all our mathematical formulas. In order to conserve a sufficient degree of flexibility for the introduction of new notations, we rely on a combination of two techniques: on the one hand,  comes with a powerful macro-language for introducing new markup elements. On the other hand, we introduced a special construct which allows a symbol or expression to be behave (i.e. be parsed) as an arbitrary other symbol or expression. This allows you for instance to annotate the symbol \(\vee \) to behave as \(+\), which implies that \(a = b \mathbin {\vee } c\) will be parsed as \(a = (b \vee c)\) instead of \((a = b) \vee c\).
comes with a powerful macro-language for introducing new markup elements. On the other hand, we introduced a special construct which allows a symbol or expression to be behave (i.e. be parsed) as an arbitrary other symbol or expression. This allows you for instance to annotate the symbol \(\vee \) to behave as \(+\), which implies that \(a = b \mathbin {\vee } c\) will be parsed as \(a = (b \vee c)\) instead of \((a = b) \vee c\).
One of the major difficulties of semantic editing is a clean treatment of homoglyphs, i.e. symbols with the same graphical shape, but a different syntactical meaning. The most annoying homoglyph is the multiplication/function-application ambiguity mentioned in the introduction. Another good example concerns the wedge product \(\mathrm {d}x \wedge \mathrm {d}y\) and logical conjunction \(a = b \wedge x = y\), which admit different binding forces. Fortunately, there are not that many mathematical homoglyphs; for this reason, we advocate the introduction of separate symbols for them into the Unicode standard.
3 Preservation of Correctness
In this section, we describe several strategies that can be used to preserve the syntactic correctness of formulas under editing operations.  currently implements the “multiple correction schemes” strategy from Sects. 3.2 and 3.3. The reader may try this implementation by downloading version \(\geqslant \)1.99.3 or SVN revision \(\geqslant \)9718. The new editing mode is still experimental and can be enabled inside math mode by clicking on the
currently implements the “multiple correction schemes” strategy from Sects. 3.2 and 3.3. The reader may try this implementation by downloading version \(\geqslant \)1.99.3 or SVN revision \(\geqslant \)9718. The new editing mode is still experimental and can be enabled inside math mode by clicking on the

icon and checking Semantic correctness.
3.1 The Ideal Strategy for Preserving Correctness
Ideally speaking, maintaining the syntactic correctness of mathematical formulas throughout the editing process can be done by
-
1.
Writing a “formula correction” procedure which takes any (correct or incorrect) formula on input and which inserts or removes transient markup in order to make it correct.
-
2.
Run the correction procedure on all modified formulas in the document(s) after every editing operation.
This ideal strategy is simple and robust; it trivially guarantees the correctness of all formulas throughout the editing process. However, it does not take into account the specific nature of certain editing operations. In particular, it does not exploit the locality of many editing actions.
Example 1
Consider the strict application of the ideal strategy to the creation of a subscript in the formula  . Since
. Since  is a valid symbol, the main editing action would create an empty subscript for it. We next launch the correction procedure, which replaces the empty subscript by a transient box, yielding
is a valid symbol, the main editing action would create an empty subscript for it. We next launch the correction procedure, which replaces the empty subscript by a transient box, yielding  . However, the
. However, the  being transient, the user would rather expect to endow the “\(+\)” operator with a subscript: this is indeed what happens in the old presentation-oriented editing mode when ignoring all transient markup. In other words, we rather expect to obtain
being transient, the user would rather expect to endow the “\(+\)” operator with a subscript: this is indeed what happens in the old presentation-oriented editing mode when ignoring all transient markup. In other words, we rather expect to obtain  .
.
The above example shows that an indiscriminate global correction procedure does not provide enough control. In fact, there are usually many ways to correct a formula by adding or removing transient markup. In order to determine the “best” solution, one typically needs to take into account the precise editing operation and the current cursor position.
Another constraint is that we would like the editor to behave as closely as possible as the old presentation-oriented editing mode when ignoring all transient markup. The above example shows that a global correction procedure does not necessarily respect this constraint. One theoretic solution to this problem is to remove all transient markup before performing the editing action and then put it back in when running the correction procedure. However, this approach may lead to non local changes in the document for every editing action, which is obviously not desirable.
Remark 1
For the above reasons, we have not implemented the correction strategy from this section yet. The idea nevertheless remains interesting for future research. Indeed, on the one hand side it raises the interesting theoretical question of correcting a string so as to make it parsable by a given (packrat) grammar. From the practical point of view, the ideal strategy has the important advantage of trivially guaranteeing syntactic correctness all along. In cases where this is hard to achieve using other means, it thereby remains a good fallback strategy.
3.2 Multiple Correction Schemes
Instead of implementing one global correction procedure, our current  implementation relies on multiple “correction schemes”. Each correction scheme is allowed to add or remove transient markup both before and after the actual editing operation. In other words, it really encapsulates the editing action into a semantically enhanced editing action. Furthermore, the correction scheme is allowed to fail (i.e. to produce an incorrect formula at the end). For this reason, we try multiple correction schemes in a row (the set of “eligible” schemes depends on the specific editing action), and stop as soon as we managed to obtain a correct formula.
implementation relies on multiple “correction schemes”. Each correction scheme is allowed to add or remove transient markup both before and after the actual editing operation. In other words, it really encapsulates the editing action into a semantically enhanced editing action. Furthermore, the correction scheme is allowed to fail (i.e. to produce an incorrect formula at the end). For this reason, we try multiple correction schemes in a row (the set of “eligible” schemes depends on the specific editing action), and stop as soon as we managed to obtain a correct formula.
In summary, we proceed as follows:
-
1.
Depending on the editing action, determine a list of eligible correction schemes.
-
2.
Try each eligible correction scheme in the list until we managed to obtain a correct formula.
-
3.
If none of the correction schemes succeeded, then cancel the editing action.
For the actual implementation, it is clearly crucial to be able to undo editing actions whenever necessary, and in a way that is orthogonal to the usual undo/redo operations in  .
.
Example 2
When inserting a mathematical symbol, the first correction scheme we try is the following: first remove all transient markup around the cursor, then insert the symbol, and finally insert a transient box at the cursor position (if needed). For instance, typing  in an empty mathematical formula successively yields
in an empty mathematical formula successively yields  ,
,  ,
,  , and
, and  .
.
Example 3
The basic correction scheme from the previous example sometimes fails. For instance, assume that we are in the situation  , and that we add a second “\(\wedge \)”. When applying the basic correction scheme, we need to correct
, and that we add a second “\(\wedge \)”. When applying the basic correction scheme, we need to correct  through the insertion of a single transient box. However, the formula
through the insertion of a single transient box. However, the formula  is still incorrect. For this particular case, we therefore use the following correction scheme: first add a transient box (
is still incorrect. For this particular case, we therefore use the following correction scheme: first add a transient box ( ), then perform the editing action (
), then perform the editing action ( ), and finally correct (nothing needs to be done at this step).
), and finally correct (nothing needs to be done at this step).
In Step 3, we simply canceled the editing action if all correction schemes failed. Several other fallback strategies can be considered. If we do not aim to maintain correctness at all costs, then we may apply the editing action without any corrections, and temporarily tolerate incorrect formulas. We might also implement an unconditionally successful fallback strategy as in Remark 1; by always adding such a strategy at the end of our list of eligible correction schemes, we will never reach Step 3. Yet another idea is to introduce a correction scheme which annotates subexpressions with exotic notations in such a way that they become correct.
3.3 Quick Survey of Some of the Implemented Correction Schemes
Our approach of using multiple correction schemes allows for fine-grained control, but also requires an increased amount of manual labor. Indeed, we both have to cover the complete set of editing actions, and for each editing action, we have to implement at least one correction scheme that will succeed in all possible situations.
Fortunately, the most common editing operations fall into four main categories: insertions and deletions that operate either on selections or not. Some other operations such as “search and replace” have not yet been adapted (see also the next section). Ultimately, the idea would be to provide manual support for the most common operations and to implement a suitable fallback strategy for the other ones.
Correction schemes for insertions Let us briefly list how we perform the most prominent correction schemes for insertions, in the absence of active selections. For each of the schemes, we show the successive states of the formula for a simple example.
-
The basic scheme from Example 2.
-
“Starting a prime or right script after a transient box” (e.g. inserting a new subscript in the formula
 from Example 1): first jump over the box with the cursor (
from Example 1): first jump over the box with the cursor ( ), then perform the action (
), then perform the action ( ), and finally add a transient box if necessary (
), and finally add a transient box if necessary ( ).
). -
“Inserting a pure infix operator after a transient box” (e.g. inserting the infix operator “\(\circ \)” in
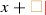 ): perform the editing action (
): perform the editing action ( ) and add a transient box if necessary (
) and add a transient box if necessary ( ).
). -
The scheme from Example 3 for inserting two infix operators in a row.
-
“Starting an extensible arrow with a script” (e.g. in the situation
 ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), perform the operation (
), perform the operation ( ), add a transient box after the arrow (
), add a transient box after the arrow ( ), as well as a transient box at the cursor position (
), as well as a transient box at the cursor position ( ).
). -
“Insert content after an ordinary symbol” (e.g., entering
 ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert a transient “explicit space” (
), insert a transient “explicit space” ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
). -
“Insert content before an ordinary symbol” (e.g. entering \(\psi \) before
 ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert a transient “explicit space” after the cursor (
), insert a transient “explicit space” after the cursor ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
). -
“Insert content in the middle of an operator” (e.g. starting a fraction in
 ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert transient “explicit spaces” before and after the cursor (
), insert transient “explicit spaces” before and after the cursor ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
).
The last three schemes also show that it is sometimes necessary to insert transient markup with different semantics as an ordinary symbol in order to make the formula correct.
Correction schemes for deletions For completion, we continue our list of examples with the most prominent correction schemes for deletions.
-
“The basic deletion scheme if there is transient markup around the cursor” (e.g. hitting backspace in
 or in
or in  ): remove the transient markup around the cursor (
): remove the transient markup around the cursor ( resp.
resp.  ), perform the editing action (
), perform the editing action ( resp.
resp. 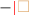 ), again remove all transient markup around the cursor if we deleted any composite tag (
), again remove all transient markup around the cursor if we deleted any composite tag ( resp.
resp.  ), add transient box if needed (
), add transient box if needed ( resp.
resp.  ).
). -
“The basic deletion scheme” (e.g. hitting backspace in
 ): remove transient markup around the cursor (
): remove transient markup around the cursor ( ), perform the deletion (
), perform the deletion ( ), again remove all transient markup around the cursor if we deleted any composite tag (
), again remove all transient markup around the cursor if we deleted any composite tag ( ), add transient box if needed (
), add transient box if needed ( ).
). -
“Removal of actual infix operators” (e.g. hitting backspace in
 , but not in
, but not in  ): remove transient markup around the cursor (
): remove transient markup around the cursor ( ), perform the deletion
), perform the deletion  , add a transient version of the deleted infix operator after the cursor (
, add a transient version of the deleted infix operator after the cursor ( ), add transient boxes around the cursor if needed (
), add transient boxes around the cursor if needed ( ).
). -
“Need to jump over cursor before deletion” (e.g. hitting backspace in
 ): jump over the cursor (
): jump over the cursor ( ), perform the “deletion” (
), perform the “deletion” ( ), add transient boxes around the cursor if needed (
), add transient boxes around the cursor if needed ( ).
).
These examples show that the correction schemes have to be implemented with quite a lot of care. This is due to the fact that it is convenient to design the schemes to apply with the right level of generality (e.g. not only to the deletion of symbols for the basic schemes, but also to the deletion of more complex structures, such as subscripts, fractions, etc.).
4 Problematic Cases and Challenges
Several problems arose during the implementation of the new semantic mathematical editing mode which preserves syntactic correctness. Some of them were more or less expected and have been solved; others require more work and further experimentation. So far, all problematic cases that we encountered fall into two categories
-
1.
The incorrect treatment of special syntactic forms (and informal content in particular).
-
2.
Complex editing operations (such as search and replace) that require special attention.
In this section, we will survey the most interesting issues that came up and highlight some of the remaining challenges.
4.1 Informal Content Inside Formulas
One difficulty with mathematical formulas in scientific papers with respect to formulas in, say, computer algebra systems, is that they may contain punctuation, decorations, typesetting directives, or explicative text. For instance, consider the following formula:
This formula concentrates three difficulties:
-
We used a trailing punctuation period “.” to finish the formula.
-
Since the formula does not fit on a single line, we used an “equation array” to manually break it into two rows. The cells of the underlying table should not be regarded as separate formulas (in which case the empty lower left cell would be incorrect), but rather be concatenated from left to right and from top to bottom.
-
The formula involves English text “and” and “almost everywhere”. The word “and” has the same semantics as the “\(\wedge \)” operator, whereas “almost everywhere” should be interpreted as a “postfix quantification”.
The best approach to these problems is to introduce suitable annotation markup which describes the semantics of informal content of this kind. For instance, we might introduce a tag “punctuation” for annotating the trailing period, and which would be ignored by the parser. Alternatively, one might use a special symbol “punctuation period in math mode”. In a similar spirit, AMS-LaTeX provides special environments (split, align, gather, etc.) for typesetting large formulas while preserving some of the intended semantics.  also contains a general purpose tag “syntax”, which may be used to parse an expression according to the rules of another specified expression. This allows us for instance to parse the word “and” in the same way as the infix operator “\(\wedge \)”. However, we have no “postfix quantification” rule in our grammar yet. More generally, the design of a complete DTD for informal annotations is an interesting challenge.
also contains a general purpose tag “syntax”, which may be used to parse an expression according to the rules of another specified expression. This allows us for instance to parse the word “and” in the same way as the infix operator “\(\wedge \)”. However, we have no “postfix quantification” rule in our grammar yet. More generally, the design of a complete DTD for informal annotations is an interesting challenge.
Assuming suitable markup, the design of user-friendly ways to perform the necessary annotations is another matter. Trailing periods are so common that we actually would like to enter them simply by pressing  . There are two approaches to this problem. Our current solution is to adapt the grammar for displayed formulas so as to accept trailing punctuation (which also means that we do not need any special annotation semantics). A better solution would be to “requalify” symbols whenever needed. For instance, in the formula
. There are two approaches to this problem. Our current solution is to adapt the grammar for displayed formulas so as to accept trailing punctuation (which also means that we do not need any special annotation semantics). A better solution would be to “requalify” symbols whenever needed. For instance, in the formula
the trailing comma would be interpreted by default as a “punctuation symbol”. However, as soon as we add a new character z to the line, we remove the annotation markup and requalify the comma to become a separator.
Of course, for arbitrarily complex informal text (such as the “almost everywhere” example), it will be hard to completely avoid user feedback on how to insert the necessary annotations. Nevertheless, some of the most common words (“and”, “or”, “iff”, etc.) might be annotated automatically.
4.2 Special Syntactic Constructs
One obvious drawback of our strategy to manually design the necessary correction schemes is completeness: every additional mathematical notation potentially requires one or more new correction schemes. Fortunately, most mathematical notations are quite simple, so this disadvantage is not as bad as it might seem. General purpose scientific papers nevertheless involve far more special syntactic constructs than, say, computer algebra input. Let us illustrate some typical issues that occur on the hand of a few somewhat unorthodox constructs.
-
The “universal grammar” from [11] contains special rules for decorated operators (as in \(a +_E' b \hat{*} c\)) and big operators (as in \(\sum _{k = 1}^{\infty } 1 / k^2 = \pi ^2 / 6\)). The usual correction schemes are mostly sufficient for editing this kind of formulas. One example of a remaining problem is entering \(a \hat{+} b\). In the old, presentation-oriented editing mode, we would type
 (insert a, start an empty hat, enter \(+\), move out of the hat, insert b). However, in the new semantic mode, this successively yields
(insert a, start an empty hat, enter \(+\), move out of the hat, insert b). However, in the new semantic mode, this successively yields  ,
,  ,
,  ,
,  ; a new correction scheme should be designed to treat this case more smoothly. Notice that an alternative way to enter \(a \hat{+} b\) is to first type \(a + b\), then select “\(+\)”, and finally insert a hat.
; a new correction scheme should be designed to treat this case more smoothly. Notice that an alternative way to enter \(a \hat{+} b\) is to first type \(a + b\), then select “\(+\)”, and finally insert a hat. -
The “universal grammar” from [11] also contains a few rules that are uncommon in programming languages, but crucial for general purpose mathematical texts. For instance, the formula \(a \prec \!\!\!\prec b \leqslant c = d \ne e\) is interpreted as \(a \prec \!\!\!\prec b \wedge b \leqslant c \wedge c = d \wedge d \ne e\), and the formula \(x_1, \ldots , x_n \in E\) as \(x_1 \in E \wedge \cdots \wedge x_n \in E\). Less common is \(n = 1, \ldots , 10\); what is the correct semantics? Fortunately, these special rules do not require any special correction schemes.
-
Different authors use wildly varying notations for quantified expressions:
$$ \begin{array}{c} \forall x, \exists y, P (x, y)\\ \forall x \exists y : P (x, y)\\ (\forall x) (\exists y) P (x, y)\\ \vdots \end{array} $$We already noticed in the introduction that it is “nice” to correct \(\forall x, \exists \) into
 . However, \((\forall x)\) might be corrected just as well as
. However, \((\forall x)\) might be corrected just as well as  or as
or as  , depending on the author’s preferred style. Our present solution to this kind of ambiguities is to further relax our grammar, by considering \((\forall x)\) to be a correct expression.
, depending on the author’s preferred style. Our present solution to this kind of ambiguities is to further relax our grammar, by considering \((\forall x)\) to be a correct expression. -
One of the advantages of the new correctness-preserving editing mode is that missing expressions are clearly indicated to the user. When entering a \(2 \times 2\) matrix
 in a computer algebra system, this is indeed quite pleasant. But in the example $$ \left( \begin{array}{ccc} \lambda _1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} \lambda _n \end{array}\right) $$
in a computer algebra system, this is indeed quite pleasant. But in the example $$ \left( \begin{array}{ccc} \lambda _1 &{} &{} \\ &{} \ddots &{} \\ &{} &{} \lambda _n \end{array}\right) $$of a diagonal matrix, this also forces users to manually fill out six of the cells with “invisible zeros”. Our present solution is therefore to only require tables cells to be explicitly entered inside computer algebra sessions.
-
The “universal grammar” from [11] also contains a few rules for “personal use”. In particular, inside subscripts, we allow for notations such as \(L_{\times \varphi , + \psi }\) and \(f_{n ;}\). Here \(\times \varphi \) has the semantics of “post-multiplication” with \(\varphi \). Given a power series \(f = f_0 + f_1 z + f_2 z^2 + \cdots \), the notation \(f_{n ; }\) stands for \(f_n z^n + f_{n + 1} z^{n + 1} + \cdots \). Now we are facing a dilemma: on the one hand, we are fond of these notations, which do not harm anyone. On the other hand, some users might want to be constrained to input something behind the “;” in
 . One solution would be to depart from the idea from [11] to promote using a “universal grammar”. Instead, we might provide special style packages for specific notations. Another approach is to introduce suitable prefix and postfix homoglyphs of \(\times \) and \(;\), together with simple keyboard shortcuts for entering them.
. One solution would be to depart from the idea from [11] to promote using a “universal grammar”. Instead, we might provide special style packages for specific notations. Another approach is to introduce suitable prefix and postfix homoglyphs of \(\times \) and \(;\), together with simple keyboard shortcuts for entering them.
4.3 Special Editing Operations and Markup
Let us finally investigate to which extent existing editing operations have to be adapted to the new, more semantic editing mode. We will start with a few issues that are already dealt with and then turn our attention to the remaining challenges.
-
 provides a special “\-style” input method for people who already know LaTeX. For instance, one may enter \(\alpha \) by typing
provides a special “\-style” input method for people who already know LaTeX. For instance, one may enter \(\alpha \) by typing  , or start a fraction by typing
, or start a fraction by typing  . The fact that a wide variety of editing actions can be triggered in this way required us to implement special correction schemes for this input method.
. The fact that a wide variety of editing actions can be triggered in this way required us to implement special correction schemes for this input method. -
The main
 input method for mathematical symbols is particularly powerful and intuitive. For instance, one may enter \(\rightarrow \) and \(\leqslant \) by typing
input method for mathematical symbols is particularly powerful and intuitive. For instance, one may enter \(\rightarrow \) and \(\leqslant \) by typing  resp.
resp.  . However, this facility requires a lot of control over the undo-mechanism: when typing a shortcut
. However, this facility requires a lot of control over the undo-mechanism: when typing a shortcut  ,
,  “forgets” the incomplete keystroke
“forgets” the incomplete keystroke  and treats the shortcut
and treats the shortcut  as an atomic operation. In other words, typing
as an atomic operation. In other words, typing  and pressing “undo” will remove the entire arrow and not leave any −. Now remember from Sect. 3.2 that trying several correction schemes in succession also makes use of the undo-mechanism inside
and pressing “undo” will remove the entire arrow and not leave any −. Now remember from Sect. 3.2 that trying several correction schemes in succession also makes use of the undo-mechanism inside  . Trying corrections while entering shortcuts such as
. Trying corrections while entering shortcuts such as  necessitates the mechanism to work in a nested way. We had to further tweak our implementation so as to make that possible.
necessitates the mechanism to work in a nested way. We had to further tweak our implementation so as to make that possible. -
Certain editing operations such as “save the current selection as an image” have side-effects that cannot be undone. Additional care is needed when implementing correction schemes for such operations. Fortunately, such operations usually do not need to be corrected.
-
One interesting editing action which is not necessarily local is “search and replace”. Global editing actions of this kind are harder to support since the corresponding correction schemes need to track all modifications made throughout the document, and less indication is provided by the local context which corrections to choose in case of ambiguities. The “search and replace” operation also raises the question whether adapting the operation to a semantic context actually involves more than corrections via the addition or removal of transient markup: if we replace y by \(a + b\) in \(x \cdot y\), do we expect to obtain \(x \cdot a + b\) or \(x \cdot (a + b)\)?
-
For some editing operations, it is not always clear what their semantic counterparts should be. One good example concerns the facility to compute and inspect the structured differences between two versions of a document. When applied to the formulas \(a + bc - d\) and \(a + bcy\), the differences are indicated using red and green colors:
 . How should we parse this formula? Both \(a + bc - d\) and \(a + bcy\) do make sense, but not \(a + bc - dy\). It is not clear to us yet how the editor should behave in this situation.
. How should we parse this formula? Both \(a + bc - d\) and \(a + bcy\) do make sense, but not \(a + bc - dy\). It is not clear to us yet how the editor should behave in this situation.
References
Arsac, O., Dalmas, S., Gaëtano, M.: The design of a customizable component to display and edit formulas. In: ACM Proceedings of the 1999 International Symposium on Symbolic and Algebraic Computation, July 28–31, pp. 283–290 (1999)
Bertot, Y.: The CtCoq system: design and architecture. Formal Aspects Comput. 11(3), 225–243 (1999)
Borras, P., Clement, D., Despeyroux, T., Incerpi, J., Kahn, G., Lang, B., Pascual, V.: Centaur: the system. SIGSOFT Softw. Eng. Notes 13(5), 14–24 (1988)
Ford, B.: Packrat parsing: a practical linear-time algorithm with backtracking. Master’s thesis, Massachusetts Institute of Technology, Sept (2002)
Ford, B.: Packrat parsing: simple, powerful, lazy, linear time. In: Proceedings of the Seventh ACM SIGPLAN International Conference on Functional Programming, ICFP ’02, pp. 36–47. ACM Press, New York (2002)
Kajler, N.: Environnement graphique distribué pour le calcul formel. PhD thesis, Université de Nice-Sophia Antipolis (1993)
Padovani, L., Solmi, R.: An investigation on the dynamics of direct-manipulation editors for mathematics. In: Asperti, A., Bancerek, G., Trybulec, A. (eds.) Mathematical Knowledge Management, vol. 3119, Lecture Notes in Computer Science, pp. 302–316. Springer, Berlin (2004)
Soiffer, N.M.: The Design of a User Interface for Computer Algebra Systems. Ph.D. thesis, University of California at Berkeley (1991)
Théry, L., Bertot, Y., Kahn, G.: Real theorem provers deserve real user-interfaces. SIGSOFT Softw. Eng. Notes 17(5), 120–129 (1992)
van der Hoeven, J.: GNU TeXmacs: a free, structured, wysiwyg and technical text editor. In: Filipo, D. (eds.) Le document au XXI-ième siècle, vol. 39–40, pp. 39–50. Metz, 14–17 mai 2001. Actes du congrès GUTenberg (2001)
van der Hoeven, J.: Towards semantic mathematical editing. J. Symb. Comput. 71, 1–46 (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
van der Hoeven, J., Lecerf, G., Raux, D. (2017). Preserving Syntactic Correctness While Editing Mathematical Formulas. In: Kotsireas, I., Martínez-Moro, E. (eds) Applications of Computer Algebra. ACA 2015. Springer Proceedings in Mathematics & Statistics, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-56932-1_29
Download citation
DOI: https://doi.org/10.1007/978-3-319-56932-1_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56930-7
Online ISBN: 978-3-319-56932-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)







 from Example
from Example  ), then perform the action (
), then perform the action ( ), and finally add a transient box if necessary (
), and finally add a transient box if necessary ( ).
).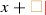 ): perform the editing action (
): perform the editing action ( ) and add a transient box if necessary (
) and add a transient box if necessary ( ).
). ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), perform the operation (
), perform the operation ( ), add a transient box after the arrow (
), add a transient box after the arrow ( ), as well as a transient box at the cursor position (
), as well as a transient box at the cursor position ( ).
). ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert a transient “explicit space” (
), insert a transient “explicit space” ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
). ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert a transient “explicit space” after the cursor (
), insert a transient “explicit space” after the cursor ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
). ): remove all transient markup around the cursor (
): remove all transient markup around the cursor ( ), insert transient “explicit spaces” before and after the cursor (
), insert transient “explicit spaces” before and after the cursor ( ), perform the editing action (
), perform the editing action ( ), insert further transient boxes if needed (
), insert further transient boxes if needed ( ).
). or in
or in  ): remove the transient markup around the cursor (
): remove the transient markup around the cursor ( resp.
resp.  ), perform the editing action (
), perform the editing action ( resp.
resp. 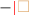 ), again remove all transient markup around the cursor if we deleted any composite tag (
), again remove all transient markup around the cursor if we deleted any composite tag ( resp.
resp.  ), add transient box if needed (
), add transient box if needed ( resp.
resp.  ).
). ): remove transient markup around the cursor (
): remove transient markup around the cursor ( ), perform the deletion (
), perform the deletion ( ), again remove all transient markup around the cursor if we deleted any composite tag (
), again remove all transient markup around the cursor if we deleted any composite tag ( ), add transient box if needed (
), add transient box if needed ( ).
). , but not in
, but not in  ): remove transient markup around the cursor (
): remove transient markup around the cursor ( ), perform the deletion
), perform the deletion  , add a transient version of the deleted infix operator after the cursor (
, add a transient version of the deleted infix operator after the cursor ( ), add transient boxes around the cursor if needed (
), add transient boxes around the cursor if needed ( ).
). ): jump over the cursor (
): jump over the cursor ( ), perform the “deletion” (
), perform the “deletion” ( ), add transient boxes around the cursor if needed (
), add transient boxes around the cursor if needed ( ).
). (insert a, start an empty hat, enter
(insert a, start an empty hat, enter  ,
,  ,
,  ,
,  ; a new correction scheme should be designed to treat this case more smoothly. Notice that an alternative way to enter
; a new correction scheme should be designed to treat this case more smoothly. Notice that an alternative way to enter  . However,
. However,  or as
or as  , depending on the author’s preferred style. Our present solution to this kind of ambiguities is to further relax our grammar, by considering
, depending on the author’s preferred style. Our present solution to this kind of ambiguities is to further relax our grammar, by considering  in a computer algebra system, this is indeed quite pleasant. But in the example
in a computer algebra system, this is indeed quite pleasant. But in the example  . One solution would be to depart from the idea from [
. One solution would be to depart from the idea from [ provides a special “\-style” input method for people who already know LaTeX. For instance, one may enter
provides a special “\-style” input method for people who already know LaTeX. For instance, one may enter  , or start a fraction by typing
, or start a fraction by typing  . The fact that a wide variety of editing actions can be triggered in this way required us to implement special correction schemes for this input method.
. The fact that a wide variety of editing actions can be triggered in this way required us to implement special correction schemes for this input method. input method for mathematical symbols is particularly powerful and intuitive. For instance, one may enter
input method for mathematical symbols is particularly powerful and intuitive. For instance, one may enter  resp.
resp.  . However, this facility requires a lot of control over the undo-mechanism: when typing a shortcut
. However, this facility requires a lot of control over the undo-mechanism: when typing a shortcut  ,
,  “forgets” the incomplete keystroke
“forgets” the incomplete keystroke  and treats the shortcut
and treats the shortcut  as an atomic operation. In other words, typing
as an atomic operation. In other words, typing  and pressing “undo” will remove the entire arrow and not leave any −. Now remember from Sect.
and pressing “undo” will remove the entire arrow and not leave any −. Now remember from Sect.  . Trying corrections while entering shortcuts such as
. Trying corrections while entering shortcuts such as  necessitates the mechanism to work in a nested way. We had to further tweak our implementation so as to make that possible.
necessitates the mechanism to work in a nested way. We had to further tweak our implementation so as to make that possible. . How should we parse this formula? Both
. How should we parse this formula? Both