Microslip Induced Damping in the Contact of Nominally Flat Surfaces with Geometric Defects

Abstract

It is well known that the friction between interfaces at bolted joints plays a major role in the characterization of damping. Friction can be either induced by macroslip or microslip. The aim of this chapter is to model and quantify the dissipated energy by microslip in the joints in order to compute the damping ratio. It is assumed that the coefficient of friction between the nominally flat surfaces is constant and that friction is the only source of energy dissipation. An experimental study is reported to measure static normal load and dynamic tangential load without any coupling between these two main directions. A rheological contact model, Extended Greenwood Model (EGM), based on microcontacts and statistical distributions is developed and studied. Experimental results and simulations are compared in order to assess and discuss the model.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this chapter, a rheological contact model (the EGM) is developed in order to quantify the energy dissipated by microslip in a jointed interface. The proposed rheological contact model is based upon a statistical description of contact between asperities. The key assumption for this model is that the coefficient of friction between the nominally flat surfaces is constant and that friction is the only source of energy dissipation. Measurements of static normal load and dynamic tangential load without any coupling between these two directions are used to inform and guide the model development.

1 Historical Perspectives on Dissipation Due to Microsliding

For many industrial applications in which the products are designed for dynamic solicitation (shock and vibration excitation), the vibration amplitudes of mechanical systems are not well predicted during the design phase. The source of inaccuracy in prediction of the vibration amplitudes is due to the lack of understanding of how to predict the amount of energy dissipated by an interface. Current approaches require that models be calibrated from measurements of existing systems, which precludes the prediction of the response of a system before it is fabricated for the first time. Thus, the ultimate goal of joints modeling is to predict the dynamic properties (mode shapes, natural frequencies, and damping in particular) of a jointed system accurately.

1.1 Sources of Energy Dissipation

The sources of damping in assembled structures are classified into two categories: material damping (which is often low) and damping in joints (which is more difficult to quantify due to its dependence on vibration level). Material damping, while difficult to model in inelastic solids, is typically low and easily modeled in engineering metals, which are the primary material of concern in this work. Damping due to joints, however, is significantly more difficult to model due to the complex interactions that occur at the interface surfaces (including wear, plasticity, etc.). Consequently, the measurement and prediction of damping in joints is an active research area (Le Loch 2003; Caignot et al. 2005).

In assembled structures, the damping is due to both macroslip (Berthillier et al. 1998; Poudou and Pierre 2003) (i.e., the bulk movement of the entire interface) and microslip (Goodman and Klumpp 1956; Beards and Williams 1977) (i.e., the relative motion of sub-elements of the interface). In order to study the damping due to both microslip and macroslip, a number of different experimental setups have been developed (see, for instance, Chap. 5). One experimental setup, in particular, is a clamped beam with a longitudinal interface (see Goodman and Klumpp 1956 and Fig. 19.1).

Fig. 19.1

A press-fit joint subjected to a clamping pressure p and a vertical shear load F. (a) A bolted structure—A free-free beam with a lap joint subjected to an axial load F. (b) A press-fit joint subjected to a clamping pressure p and a vertical shear load F. (c) A lap-shear joint subjected to a clamping pressure p and an axial load F

1.2 Perspectives on Dissipation Due to Microslip

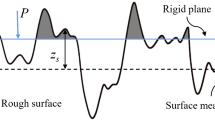
Contact between two bodies, either in motion or stationary, is a phenomenon that all interacting parts of a mechanism are subjected to. Regardless of the condition of the surface finish (whether cut, or polished to a mirror-like smoothness), contact at the nano- and microscale is rough. Often, a relative movement between the elements in contact occurs producing microslip at the interface of contact. Such slip should be well studied to evaluate frictional forces induced on the surface. Thus, the relative motion at the interface of a contact is a source of friction that is dependent upon the area of contact engaged in microslip, which plays an important role in energy dissipation.

As the adhesion area and microslip zone are not well known a priori, it should be obtained from experiments. This kind of problem is referred to in the literature as incipient sliding or quasi-static contact. The problem with partial slip was addressed for the first time by Cattaneo (1938). Cattaneo considers the case of quasi-static contact of two spheres with the same elastic properties, loaded normally and tangentially. In the absence of microslip, Cattaneo shows that the tangential force is expected to generate an infinite tangential traction along the contact, which is physically inadmissible. So under the action of a tangential force, even very small, microslip is inevitable at the contact edges. Cattaneo assumes that the tangential force is equal to the normal force multiplied by the coefficient of friction, and the elliptical contact area is divided into two parts:

• Elliptical central area in which there is no relative movement between surfaces and where the tangential traction (tension) q(x) satisfies the equation q(x) < μp(x)

• An annular-elliptical zone of microslip where q(x) = μp(x)

This decomposition leads to a tangential traction q, shown in Fig. 19.2.

Fig. 19.2

Partial slip distribution of tangential traction by Cattaneo (1938)

Building on the results of Cattaneo (1938), Mindlin investigated the compliance of two perfectly smooth elastic spheres, loaded normally and tangentially (Mindlin 1949). Mindlin determined the distribution of tangential tractions (Fig. 19.3) assuming that both bodies have the same geometry and elastic properties. The results from both (Cattaneo 1938; Mindlin 1949) serve as a basis for modeling the contact of asperities.

Fig. 19.3

Distribution of normal traction p and tangential traction q on the surface (Mindlin 1949)

1.3 Contact of Asperities

For contact between rough surfaces, Greenwood and Williamson (1966) proposed a rough model, using several assumptions including:

• The asperities are spherical, with the same mean curvature ρ at the top.

• Asperities are sufficiently far apart to behave independently.

• The heights of asperities follow a probability distribution φ(y _i ).

• Individual behavior of each asperity can be described by the Hertz theory (Hertz 1882; Johnson 1985).

This statistical representation for contact along an interface has been extensively developed over the last 50 years (for instance, see the review presented in Chap. 18). In what follows, this branch of contact modeling is further extended to study the energy dissipation within a jointed interface.

Therefore, the aim of this chapter is to quantify the dissipated energy by microsliding using both experimental and model based approaches. In Sect. 19.2, the experimental procedure is presented and experimental results are discussed. In Sect. 19.3, a mathematical model is developed considering the hypotheses of Greenwood and Williamson (1966) for the contact between two nominally flat surfaces. The energy dissipated and the damping ratio are determined in Sect. 19.4. Numerical results are presented, discussed, and compared with those obtained experimentally.

2 Tribometer and Measurements

2.1 Tribometer Set

In order to perform accurate measurements, a tribometer with a hydraulic actuator is used. This kind of tribometer is described in Dion et al. (2009). The test fixture allows uncoupling normal and tangential loads over a wide frequency bandwidth to ensure good quality of measurements and test conditions (Fig. 19.4). This tribometer allows obtaining at 200 Hz and 1–100 μm displacement range, inducing a 1.2–120 mm/s velocity range.

Fig. 19.4

Global description of the tribometer

The studied surface (approximately 2 cm²) is a small planar contact (Fig. 19.4). The normal static load F _n varies between 100 and 5000 N while the tangential load F _t is dynamic and varies between −5000 N and +5000 N. The studied samples shown in Fig. 19.5 are in allied aluminum Al 2017 machined by milling. For this sample, the roughness R _a is lower than 0.4 µm and the flatness error is lower than 0.02 mm (see Fig. 19.6). The effective contact area (measured after the test) is estimated to 10% of the apparent contact area with 2000 N normal load. For all the tests, the hydraulic jack movements are displacement controlled with the feedback signal of the internal displacement transducer (LVDT) (Fig. 19.4). Here, it is assumed that there is no coupling between normal and tangential loads. When the dynamic tangential load is applied, the static normal load keeps its nominal value with a 2% maximum deviation that stems from the dynamic tangential load. The displacement excitation is controlled and assumed to be sinusoidal. The harmonic ratio (between the fundamental and the 3rd harmonic) is around 5% in the worst case.

Fig. 19.5

The sample in allied aluminum Al 2017 machined by milling

Fig. 19.6

Roughness of the surface. (a) Position along surface, mm. (b) Probability of asperity heights, %

2.2 Experimental Result

The evolution of the normalized load T∕N versus the tangential displacement is depicted in Fig. 19.7. This type of representation is often used to show a contact’s dissipative behavior. The area inside the curve is the dissipated energy during microslip per cycle. The nature of the behavior (linear or not, dissipative or not) is clearly shown through the shape of the curve. The quasi-horizontal parts of the curve are indicative of macroslip and the oblique parts represent the tangential stiffness.

Fig. 19.7

Slipping behavior under normalized load T∕N versus tangential displacement

3 Microcontact Model

Consider a contact between a plane and a nominally flat surface covered with a large number of asperities. It is assumed that all asperity summits are spherical with the same radius ρ and that their heights vary randomly φ(y _i ). Figure 19.8 shows schematically the considered type of contact.

Fig. 19.8

Contact between a rough surface and a rigid plane

3.1 Normal Distribution of the Load on the Asperities

The contact model between an individual spherical asperity and a rigid plane is shown in Fig. 19.9. It is assumed that the elastic proprieties of the contacting bodies are identical to an equivalent elastic material on a rigid plane (Greenwood and Williamson 1966). The frictional load is parallel to the x-axis.

Fig. 19.9

The contact model for a single asperity

The behavior of an individual asperity can be derived from the Hertzian equations. For the contact between a sphere of radius ρ and a rigid plane, the contact radius a _i , area A _i , and load N _i can be expressed in terms of the compliance δ _ni by Greenwood and Williamson (1966), Johnson (1985)

$$\displaystyle\begin{array}{rcl} a_{i} = \sqrt{\rho \delta _{ni}}& &{}\end{array}$$

(19.1)

$$\displaystyle\begin{array}{rcl} A_{i} =\pi \rho \delta _{ni}& &{}\end{array}$$

(19.2)

$$\displaystyle\begin{array}{rcl} N_{i} = \frac{4} {3}\sqrt{\rho }E^{{\ast}}\delta _{ ni}^{3/2}.& &{}\end{array}$$

(19.3)

Here, E ^∗ is a composite modulus of elasticity given by

$$\displaystyle{ \frac{1} {E^{{\ast}}} = \frac{1 -\nu _{1}^{2}} {E_{1}} + \frac{1 -\nu _{2}^{2}} {E_{2}}, }$$

(19.4)

where ν and E are Poisson’s ratio and Young’s modulus, with the subscripts referring to the two bodies in contact. For a distance δ _n between the rigid plane and the mean plane of the rough surface (Fig. 19.8), there will be contact at any asperity whose height is greater than δ _n . Thus, the probability of contact at any given asperity of height y _i is

$$\displaystyle{ \mathrm{Prob}(y_{i}>\delta _{n}) =\int _{ \delta _{n}}^{\infty }\varphi (y_{ i})\mathrm{d}y_{i}. }$$

(19.5)

The total number of asperities is N _a = ρ _a S _a , where ρ _a is the density of asperities distributed over the apparent area of contact S _a . The number of asperities in contact is given by Greenwood and Williamson (1966)

$$\displaystyle{ n_{a} = N_{a}\int _{\delta _{n}}^{\infty }\varphi (y_{ i})\mathrm{d}y_{i}. }$$

(19.6)

The total contact area is expressed by

$$\displaystyle{ S =\pi N_{a}\rho \int _{\delta _{n}}^{\infty }(y_{ i} -\delta _{n})\varphi (y_{i})\mathrm{d}y_{i}. }$$

(19.7)

For the compliance δ _ni = y _i −δ _n (the distance over which points outside the deforming zone move together during the deformation), the total load supported by asperities is expressed as (Greenwood and Williamson 1966)

$$\displaystyle{ N = \frac{4} {3}N_{a}E^{{\ast}}\sqrt{\rho }\int _{\delta _{ n}}^{\infty }(y_{ i} -\delta _{n})^{3/2}\varphi (y_{ i})\mathrm{d}y_{i}. }$$

(19.8)

3.2 Distribution of Tangential Load on the Asperities

Consider an asperity in contact with the plane submitted first to a constant normal force N _i then to a tangential displacement δ _ti . Two slip conditions can be distinguished as partial slip and total slip in what follows.

3.2.1 The Partial Slip Condition

The contact area is split into a stick zone and slip zone (Fig. 19.10). The maximum tangential force T _imax does not exceed in absolute value the product of the normal force by the coefficient of friction T _imax < μN _i .

Fig. 19.10

Contact area

The stick region is the circle of radius c whose value can be found from the magnitude of the tangential force

$$\displaystyle{ \frac{c} {a_{i}} = \left (1 - \frac{T_{i}} {\mu N_{i}}\right )^{1/3}. }$$

(19.9)

The force displacement relationship for an individual asperity is given by Gallégo (2007)

$$\displaystyle{ T_{i} =\mu N_{i}\left (1 -\left (1 - \frac{16a_{i}\delta _{ti}} {3\mu N_{i}G^{{\ast}}}\right )^{3/2}\right ), }$$

(19.10)

where G ^∗ is a composite shear modulus

$$\displaystyle{ \frac{1} {G^{{\ast}}} = \frac{2 -\nu _{1}} {G_{1}} + \frac{2 -\nu _{2}} {G_{2}}. }$$

(19.11)

The tangential force has maximum T _i = μN _i for total slip. Correspondingly, from Eq. (19.10), the maximum tangential deflection before the inception of sliding is

$$\displaystyle{ \delta _{Li} = \frac{3} {16} \frac{G^{{\ast}}\mu N_{i}} {a_{i}}. }$$

(19.12)

3.2.2 The Total Slip Condition

In this state, there is no area that is permanently adhered. During the cycle, the maximum tangential force reaches the absolute product of the normal force by the coefficient of friction T _imax = μN _i . From Johnson (1985), the solutions of a circular contact initially charged by constant normal force P and subjected to a tangential load Q _x (Q _x < μP ₀) oscillating between the values ± Q ^∗ are given (see Fig. 19.11).

Fig. 19.11

Load–displacement cycle (Johnson 1985)

During unloading (between A and C), the distribution of tangential load on the asperities is (Gallégo 2007)

$$\displaystyle{ T_{id} = 2\mu N_{i}\left (\left (\frac{1} {2}\left ( \frac{16a_{i}\delta _{ti}} {3\mu N_{i}G^{{\ast}}} + \left (1 - \frac{T_{i\max }} {\mu N_{i}}\right )^{2/3} + 1\right )^{3/2}\right ) - 1\right ) - T_{ i\max }. }$$

(19.13)

The situation at Q _x = −Q ^∗ is identical with that at Q _x = Q ^∗, except for the reversal of sign. Hence, between (C and A) the distribution of tangential load on the asperities then becomes (Gallégo 2007)

$$\displaystyle{ \begin{array}{rcl} T_{ic}& =& - T_{id}(-\delta ) \\ & =& - 2\mu N_{i}\left (\left (-\frac{1} {2}\left ( \frac{16a_{1}\delta _{ti}} {3\mu N_{i}G^{{\ast}}} -\left (1 - \frac{T_{i\max }} {\mu N_{i}}\right )^{2/3} - 1\right )^{3/2}\right ) - 1\right ) - T_{i\max }.\end{array} }$$

(19.14)

In Greenwood and Williamson (1966), a model based on a statistical distribution of asperities in contact in the state of partial sliding is proposed. In order to generalize the Greenwood model for damping in an assembly, stick, partial slip, and total sliding have to be modeled with independent initial conditions and a standalone set of equations for each asperity Eqs. (19.15)–(19.17).

If δ _timax > δ _Li (total slip), the maximum tangential force reaches the absolute product of the normal force by the coefficient of friction T _imax = μN _i and the asperity moves by an amount δ ₀ = δ _timax −δ _Li . Thus, Eqs. (19.10), (19.13), and (19.14) are recast as

$$\displaystyle\begin{array}{rcl} T_{i} = \left \{\begin{array}{ll} \mu N_{i}\left (1 -\left (1 - \frac{16a_{i}\delta _{ti}} {3\mu N_{i}G_{eq}}\right )^{3/2}\right ),&\qquad \delta _{ti} <\delta _{Li} \\ \mu N_{i}, &\qquad \delta _{ti} \geq \delta _{Li} \end{array} \right.& &{}\end{array}$$

(19.15)

$$\displaystyle\begin{array}{rcl} T_{id} = \left \{\begin{array}{lcr} \multicolumn{2}{l}{2\mu N_{i}\left (\left (\frac{1} {2}\left (\frac{16a_{i}\left (\delta _{ti}-\delta _{0}\right )} {3\mu N_{i}G_{eq}} + \left (1 - \frac{T_{i\max }} {\mu N_{i}}\right )^{2/3} + 1\right )^{3/2}\right ) - 1\right ) + T_{i\max },\qquad \qquad }& \\ &\multicolumn{2}{r} {\delta _{ti}>\delta _{0} -\delta _{Li}} \\ -\mu N_{i},&\multicolumn{2}{r} {\delta _{ti} \leq \delta _{0} -\delta _{Li}} \end{array} \right.& &{}\end{array}$$

(19.16)

$$\displaystyle\begin{array}{rcl} T_{ic} = \left \{\begin{array}{lcr} \multicolumn{2}{l}{ - 2\mu N_{i}\left (\left (-\frac{1} {2}\left (\frac{16a_{i}\left (\delta _{ti}+\delta _{0}\right )} {3\mu N_{i}G_{eq}} -\left (1 - \frac{T_{i\max }} {\mu N_{i}}\right )^{2/3} - 1\right )^{3/2}\right ) - 1\right ) - T_{i\max },\qquad }& \\ &\multicolumn{2}{r} {\delta _{ti} <\delta _{Li} -\delta _{0}} \\ -\mu N_{i},&\multicolumn{2}{r} {\delta _{ti} \geq \delta _{Li} -\delta _{0}} \end{array} \right.& &{}\end{array}$$

(19.17)

Notice that this EGM allows partial slip and total sliding for two asperities in the same interface.

4 Model Properties

It is assumed that the coefficient of sliding friction μ between the surfaces is constant and that dry friction is modeled by Coulomb’s law. In accordance with experimental results, numerical simulations will be performed with the following material data: μ = 0. 55 and E ₁ = E ₂ = 69 GPa.

4.1 Changing Phases for a Single Asperity

In this section, an asperity in contact with the rigid plane is compressed by a constant normal force N _i parallel to the y-axis (Fig. 19.9), to which a tangential displacement δ _ti oscillating is subsequently applied.

4.1.1 Oscillating Tangential Displacement with a Constant Amplitude

First, an oscillating tangential displacement with a constant amplitude ±δ _timax is considered. The contact radius and the contact area due to N _i are held constant and as given by Hertz. Figure 19.12 shows the evolution of the tangential displacement versus time.

Fig. 19.12

The loading path for the constant amplitude case

The first application of δ _ti in a positive direction $\dot{\delta }_{ti}> 0$ causes microslip in the annulus c ≤ r ≤ a _i . The tangential force is given by Eq. (19.10), and shown by the curve OA in Fig. 19.13. Keeping the normal force constant, the tangential force is increased from zero and the stick region decreases in size according to Eq. (19.9).

Fig. 19.13

Tangential force evolution according to the tangential displacement (partial slip)

At point A in Fig. 19.12, the tangential displacement begins to decrease $\dot{\delta }_{ti} <0$, which is equivalent to the application of a negative increment in δ _ti . During unloading, the tangential force is given by Eq. (19.13), and shown by the curve ABC in Fig. 19.13. The slip region is then defined by Gallégo (2007)

$$\displaystyle{ \left ( \frac{c} {a_{i}}\right )^{3} = \frac{1} {2}\left (1 + \left (\frac{c_{{\ast}}} {a_{i}}\right )^{3}\right ), }$$

(19.18)

where c _∗ is the value of c in A.

At point C, when the tangential displacement is completely reversed, substituting δ _ti = −δ _timax in Eq. (19.14) gives T _ic = T _imax. Thus, original slip is covered by the reversed slip and the state achieved is a complete reversal of that at δ _ti = δ _timax. Further loading leads to a series of states similar to unloading from δ _ti = δ _timax, but of opposite sign, as depicted by the curve CDA in Fig. 19.13.

In fact, it is shown in what follows that the effect of a tangential displacement with a magnitude lower than the limit deflection δ _Li does not give rise to a total slip motion but, nevertheless, induces a partial slip referred to as slip or microslip. Conversely, when δ _timax > δLi, the tangential force increases from zero to a limiting value T _imax = μN _i , the asperity moves by an amount δ ₀ = δ _timax −δ _Li , and the stick region dwindles to a single point at the origin resulting in the bodies being on the verge of sliding. Taking into account Eqs. (19.15)– (19.17), the hysteretic force–deflection relation for a contact is shown in Fig. 19.14.

Fig. 19.14

Tangential force evolution according to the tangential displacement (total slip)

Keeping N _i constant and increasing the amplitude of the tangential displacement per iteration (Fig. 19.15a), the hysteretic force–deflection relations for a contact are shown in Fig. 19.15b.

Fig. 19.15

The (a) loading path, and (b) hysteretic force–deflection from partial slip to total slip

4.1.2 Oscillating Tangential Displacement with Variable Amplitude

The second case considered is the case where the tangential displacement oscillates with variable amplitude acting along the x-direction, as shown in Fig. 19.16.

Fig. 19.16

The loading path for the variable amplitude case

In this case, the force–deflection relationship between the relative tangential displacement δ _ti of the contact surface and the corresponding tangential load in the case of constant normal load are given by

• During the loading between O and A ($\dot{\delta }_{ti}> 0$)

  $$\displaystyle{ T_{i} =\mu N_{i}\left (1 -\left (1 - \frac{16a_{i}\delta _{ti}} {3\mu N_{i}G^{{\ast}}}\right )^{3/2}\right ). }$$

  (19.19)

• During the unloading between A and B ($\dot{\delta }_{ti} <0$)

  $$\displaystyle{ T_{id} = 2\mu N_{i}\left (\left (\frac{1} {2}\left ( \frac{16a_{i}\delta _{ti}} {3\mu N_{i}G^{{\ast}}} + \left (1 - \frac{T_{i\max }} {\mu N_{i}}\right )^{2/3} + 1\right )^{3/2}\right ) - 1\right ) + T_{ i\max }. }$$

  (19.20)

• During the reloading between B and C ($\dot{\delta }_{ti}> 0$)

  $$\displaystyle\begin{array}{rcl} & & T_{ic} = -2\mu N_{i}\left (\left (-\frac{1} {2}\left (\frac{16a_{i}\left (\delta _{ti} -\delta _{0}\right )} {3\mu N_{i}G^{{\ast}}} -\left (1 -\frac{\max \left \vert T_{id}\right \vert } {\mu N_{i}} \right )^{2/3} - 1\right )^{3/2}\right ) - 1\right ) \\ & & \qquad \ \ -\max \left \vert T_{id}\right \vert, {}\end{array}$$

  (19.21)

  where

  $$\displaystyle{ \delta _{0} =\delta _{ti}(\mathrm{B}) -\left (-\delta _{Li} +\delta _{Li}\left (1 -\frac{\max \left \vert T_{id}\right \vert } {\mu N_{i}} \right )^{2/3}\right ), }$$

  (19.22)

  and δ _ti (B) is the value of δ _ti in B.

• During the unloading between C and D ($\dot{\delta }_{ti} <0$)

  $$\displaystyle\begin{array}{rcl} & & T_{id} = 2\mu N_{i}\left (\left (\frac{1} {2}\left (\frac{16a_{i}\left (\delta _{ti} +\delta _{0}\right )} {3\mu N_{i}G^{{\ast}}} + \left (1 -\frac{T_{ic\max }} {\mu N_{i}} \right )^{2/3} + 1\right )^{3/2}\right ) - 1\right ) \\ & & \ \ \qquad + T_{ic\max }, {}\end{array}$$

  (19.23)

  with

  $$\displaystyle{ \delta _{0} = \left (\delta _{Li} -\delta _{Li}\left (1 -\frac{\max (T_{ic})} {\mu N_{i}} \right )^{2/3}\right ) -\delta _{ ti}(\mathrm{C}), }$$

  (19.24)

  and δ _ti (C) is the value of δ _ti in C.

If the limit tangential deflection δ _Lt (total slip) is reached, the force–deflection relationships during unloading T _id and reloading T _ic for an individual asperity are given by Eqs. (19.16) and (19.17). According to Eqs. (19.19)– (19.21), (19.23), (19.16), and (19.17), the corresponding hysteretic force–deflection relations for a contact are shown in Fig. 19.17.

Fig. 19.17

Hysteretic force–deflection from partial slip to total slip

4.2 Case of N Asperities

In this section, a Gaussian (or normal) distribution of asperity heights φ(y _i ) is used. Several experimental results (Greenwood and Williamson 1966) show that for many surfaces the height distribution is Gaussian to a very good approximation. The probability density function of a Gaussian distribution (see Fig. 19.18) is given by

$$\displaystyle{ \varphi (y_{i}) = \frac{1} {\sigma \sqrt{2\pi }}e^{-(y_{i}-m)^{2}/2\sigma ^{2} }, }$$

(19.25)

where parameter m (location of the peak) is the mean and σ ² is the variance (the measure of the width of the distribution). The cumulative distribution function (Fig. 19.18b) is

$$\displaystyle{ \varphi (y_{i}) = \frac{1} {2}\mathrm{erf}\left ( \frac{1} {\sqrt{2}} \frac{y_{i} - m} {\sigma } \right ). }$$

(19.26)

Fig. 19.18

(a) Normal distribution of asperity heights, and (b) cumulative distribution function

The total normal load N applied to the contact between a plane and a nominally flat surface (Fig. 19.8) can be expressed as the sum of each elementary normal load on each asperity N _i

$$\displaystyle{ N =\sum N_{i}. }$$

(19.27)

Keeping N constant, the loading cycle for the tangential displacement δ _t oscillates between δ _tmax and −δ _tmax. The total tangential force T that can be supported by N _a asperities is

$$\displaystyle{ T =\sum T_{i}. }$$

(19.28)

The evolution of total tangential force T versus tangential displacement δ _t is shown in Fig. 19.19. The shape of this curve is very similar to that obtained experimentally (see Fig. 19.7).

Fig. 19.19

Slipping behavior under tangential force T versus tangential displacement δ _t

4.3 Relations Between the Iwan, Coulomb, and Extended Greenwood Models

In this section, N is kept constant and the total number of asperities N _a in contact with the flat surface is varied. The hysteretic force–deflection relations for a contact are depicted in Fig. 19.20. It is interesting to mention that the variation of the total number of asperities influences significantly the load–deflection curve, although with an increase of the parameter N _a the stiffness characteristics of the model increase. When the number of asperities in contact increases, the EGM tends to the Coulomb friction model. Notice that this result is different from that obtained by the Iwan model (Segalman 2005; Argatov and Butcher 2011). The Iwan model is based on several cells composed of a stiffness and Coulomb friction model. When the number of cells increases, the Iwan model is close to the EGM composed with a single asperity (Fig. 19.21).

Fig. 19.20

Evolution of Extended Greenwood Model (EGM) against the number of asperities

Fig. 19.21

Likeness between the Coulomb model, Iwan model, and EGM

4.4 Extended Greenwood Model Identification

In Fig. 19.22, the theoretical model is compared with experimental results. It is observed that the shape of the curve obtained by the theoretical model is very similar to that obtained experimentally.

Fig. 19.22

The theoretical model and measured result for the material aluminum allied Al 2017

4.5 Damping Ratio

This section aims to define the dissipated energy in order to compute the damping ratio. The area enclosed by the curves T _id [Eq. (19.16)] and T _ic [Eq. (19.17)] gives the energy dissipation E _d during microslip per cycle by integration over displacement limits:

$$\displaystyle{ E_{d} =\int _{ -\delta _{t\max }}^{\delta _{t\max } }T_{ic} - T_{id}\mathrm{d}\delta _{t}. }$$

(19.29)

The curve in Fig. 19.23 shows the evolution of dissipated energy E _d as a function of the tangential displacement δ _t . The energy dissipated by the friction increases as the magnitude of the tangential displacement increases. It can thus be concluded that the dissipated energy depends strongly on the amplitude of the displacement. This dependence induces nonlinear effects, which are shown clearly in Fig. 19.23 by the fact that the curve is parabolic.

Fig. 19.23

Dissipated energy as a function of tangential displacement

The damping ratio ξ can be defined by the ratio between the dissipated energy E _d and the supplied energy E _s

$$\displaystyle{ \xi = \frac{4} {\pi } \frac{E_{d}} {E_{s}}, }$$

(19.30)

where E _s = 4δ _tmax T _max. Figure 19.24 shows the evolution of ξ as a function of the tangential displacement δ _t .

Fig. 19.24

Damping ratio as a function of tangential displacement

It is noticed that the damping ratio increases as the tangential displacement increases. Figure 19.24 also shows the nonlinear character of this evolution.

5 Summary of the Extended Greenwood Model

In this chapter, an extension of the Greenwood model is proposed (the Extended Greenwood Model, EGM) that is based on a statistical distribution of asperities in contact between two assembled parts. These micro-contacts produce a damping effect in both total sliding and partial sliding. This new model is studied and identified with experimental results. The numerical results show that for a cyclic tangential displacement, the dissipated energy increases with the tangential displacement. The shape of the hysteretic force–deflection for a contact is very similar to that obtained experimentally.