Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Following the pioneering work of Biot [1], folded buckle patterns in structural geology have traditionally been assumed to be periodic. A beam in viscous medium, for example, would be expected to display the dominant wavelength, suggested by linear analysis as that growing most rapidly over time. In contrast, some elastic buckling problems display spatially localised solutions, driven by material and geometric nonlinearities [2,3,4]. In this, much progress has developed around stability of a compressed beam supported by a nonlinear elastic foundation, with carefully selected properties to mimic either softening and/or stiffening characteristics in the supporting medium. Synergy between these two separate developments then naturally led to study of viscoelastic systems with the same nonlinearities [5].

Here, a beam supported by a nonlinear viscoelastic (Kelvin-Voigt) material under slow end-compression is described by the nonlinear Swift-Hohenberg PDE, together with a constraint condition. The foundation has an elastic part that first softens and then re-stiffens. This reflects many purely elastic formulations [6,7,8,9], where the equilibrium states are known to comprise two alternative forms of localised snaking path, one spatially symmetric and the other anti-symmetric, that emerge from the flat state at a critical bifurcation point. These paths are generally disconnected, but are linked by ladders of non-symmetric equilibria, bringing with them regions of bi-stability. For the dynamical PDE, interest then naturally falls on the transitions between these two attractors as the system evolves.

To explore the qualitative aspects further, a modified one degree-of-freedom Galerkin description is introduced, built on the evolving modeshapes of the statical equilibrium states. Total potential energy is then plotted against the single degree of freedom and the end-shortening to provide an evolutionary energy landscape. Movement on the surface, governed by a viscous gradient-flow process in one dimension and a constant flow rate in the other, describes the dynamics. Changing patterns of minima and maxima in the (constrained) energy then bring about possibilities for dynamical bifurcation and related reversals in the direction of flow.

Fig. 1
figure 1

Strut supported by nonlinear springs and linear dashpots in parallel. Axial load P would normally be accompanied by bending moments and shear forces at points of application (not shown)

Full size image

2 The Model

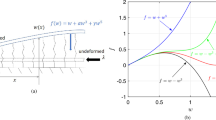
We consider the model for dynamic localized folding seen in Fig. 1, comprising an infinitely long inextensible elastic beam, supported by a nonlinear viscoelastic foundation and subjected to end-shortening at a constant rate R. Deformation is characterised by vertical displacement of the centreline u(x, t), where x is arc-length measured along the beam, and \(t>0\) is time. The shortening at time t is given by

$$\begin{aligned} \varDelta =\frac{1}{2}\int _{-\infty }^{\infty } u'\, ^ 2 \,\mathrm {d}x= Rt, \end{aligned}$$
(1)

to first order, where primes denote differentiation with respect to x. For moderately-large deflections the bending energy is \(\frac{1}{2}B\int u''^2\,\mathrm {d}x\), where B is the beam bending stiffness. The Winkler foundation, comprising a nonlinear spring and linear dashpot in parallel, provides a strictly local and vertical total resistive force,

$$\begin{aligned} f(u) = f_e(u) + f_v(u) = k_1u - k_2u^3 + k_3u^5 + \eta \dot{u}, \end{aligned}$$
(2)

where \(\dot{(\;\;)}\) denotes differentiation with respect to time t. The negative cubic and positive quintic coefficients mean that, as displacements into the foundation grow, the resisting stiffness initially drops and then increases [7].

We introduce the Lagrangian

$$\begin{aligned} \mathscr {L}(x,t,u) = \frac{1}{2}B u''^2 + \frac{1}{2}k_1u^2 - \frac{1}{4}k_2u^4 + \frac{1}{6}k_3u^6 + \frac{1}{2}\eta \dot{u} u - \frac{1}{2}Pu'^2. \end{aligned}$$
(3)

Elastic strain energy at time t is given by the functional

$$\begin{aligned} E(t,u) = \int _{-\infty }^{\infty }\frac{1}{2}B u''^2 + \frac{1}{2}k_1u^2 - \frac{1}{4}k_2u^4 + \frac{1}{6}k_3u^6\,\mathrm {d}x, \end{aligned}$$
(4)

whereas

$$\begin{aligned} D(t,u) = \frac{1}{2}\eta \int _0^t\int _{-\infty }^{\infty } \dot{u} u\,\mathrm {d}x\;\mathrm{d}s, \quad \text{ and } \quad W(t,u) = \frac{1}{2}\int _0^t\int _{-\infty }^{\infty } P(s) u'^2\,\mathrm {d}x\;\mathrm{d}s, \end{aligned}$$
(5)

are the energy dissipated in the dashpot and the work done by the load up to time t, respectively. Evolution of the system is described by the Euler-Lagrange equation,

$$\begin{aligned} \frac{\partial \mathscr {L}}{\partial u} - \frac{\partial }{\partial t}\left( \frac{\partial \mathscr {L}}{\partial \dot{u}}\right) + \frac{\partial ^2}{\partial x^2}\left( \frac{\partial \mathscr {L}}{\partial u''}\right) - \frac{\partial }{\partial x}\left( \frac{\partial \mathscr {L}}{\partial u'}\right) = 0, \end{aligned}$$
(6)

subject to appropriate initial, essential and natural boundary conditions. This can be physically interpreted as a vertical force balance on \(\,\mathrm {d}x\), at time t. Appropriate differentiation of (3) yields the constrained nonlinear fourth-order PDE,

$$\begin{aligned} Bu'''' + Pu'' + k_1u - k_2u^3 + k_3u^5 + \eta \dot{u} = 0, \quad \text{ subject } \text{ to } \quad \frac{1}{2}\int _{-\infty }^{\infty } u'^2\,\mathrm {d}x= Rt. \end{aligned}$$
(7)

We can reduce this to the non-dimensional form,

$$\begin{aligned} \dot{u} = -\left( u'''' + p u'' + u - u^3 + \alpha u^5\right) \quad \text{ and } \quad \frac{1}{2}\int _{-\infty }^{\infty } u'^{\; 2}\,\mathrm {d}x= \rho t, \end{aligned}$$
(8)

by the following transformation: \(x \mapsto \left( {B}/{k_1}\right) ^{1/4} x\); \(t \mapsto {(\eta }/{k_1)}\,t\); \(u \mapsto \sqrt{{k_1}/{k_2}} u\): where \(p(t) = {P(t)}/{\sqrt{Bk_1}}\); \(\alpha = {k_1k_3}/{k_2^2}\); and \(\rho = {R\eta k_2}/{k_1^2}\sqrt{{B}/{k_1}}\). We note that the final system is in fact a two parametric group in \((\alpha ,\rho )\), as the load p(t) is a free variable directly imposed by the shortening constraint.

3 Static Equilibrium—Snakes and Ladders

Before seeking solutions to PDE (8), it is useful to review the associated stationary states, using the fourth-order reversible ordinary differential equation (ODE) in x:

$$\begin{aligned} u'''' + p u'' + u - u^3 + \alpha u^5 = 0. \end{aligned}$$
(9)

with the same ‘cubic-quintic’ foundation force characteristic: \(f_e(u) = u - u^3 + \alpha u^5\). This is known to exhibit a Hamiltonian-Hopf bifurcation from the unbuckled state into a periodic buckling mode at \(p=2\) [3, 4]. We compute such solutions in AUTO [10] over \(x \in [-L, L]\), starting arc-length continuation close to the bifurcation point and seeding it with the eigenmode in two configurations, one symmetric about \(x=0\) (cosine) and the other anti-symmetric (sine). For convenience, pinned (\(u = u^{\prime \prime } = 0\)) rather than homoclinic [11] boundary conditions are chosen, the difference being numerically inconsequential for a long beam [12]. End-shortening \(\varDelta \) is chosen as the continuation parameter, with the load p in Eq. (9) being regarded as free.

Fig. 2
figure 2

Snakes and ladders equilibrium paths for \(\alpha = 0.3\). Stable and unstable states are shown as black and grey respectively

Full size image

Figure 2 shows a typical load–end-shortening bifurcation diagram and corresponding solution shapes. This shows the classic snakes-and-ladders scenario of a pair of snaking equilibrium solutions, one symmetric in x about its mid-point and the other anti-symmetric, each fluctuating in load as \(\varDelta \) increases. The equilibrium shapes themselves are all homoclinic, with a central region that grows with \(\varDelta \); these are the initial stages of a heteroclinic connection to a periodic state at the Maxwell load [7]. Along the snakes the folded profiles are each a function of both x and \(\varDelta \), so they change shape but also grow in amplitude as \(\varDelta \) increases. The snaking paths are connected at bifurcation points by ladders [8, 9], comprising states of transition between symmetry and anti-symmetry; for a recent account of such behaviour see [13]. Unlike the response under controlled load where limit points have a part to play, stability here is only lost or gained at the bifurcation points.

4 Evolution of Transient Folding Patterns

4.1 Finite Element (FE) Procedure for Constrained Gradient Flow

Equation (8) can be solved as a constrained gradient flow problem over a large-but-finite domain \(X := [-L,L]\), discretized into N nodes \(x_i = ih - L\) where \(h = 2L/N\) and \(i = 0,1,\ldots ,N\). The weak form is found by multiplying by a suitable test function v, integrated over the domain X and then by parts, to give

$$\begin{aligned} \int _X \dot{u} v \,\mathrm {d}x = - \int _X u'' v'' \;\mathrm {d}x + p\int _X u^{\prime } v^{\prime } \,\mathrm {d}x - \int _X f_e(u) v \,\mathrm {d}x \quad \text{ such } \text{ that }\quad \frac{1}{2}\int _X u'^2\;\mathrm {d}x = \rho t. \end{aligned}$$
(10)

By approximating u and v as piecewise cubic functions spanned by the cubic FE shape functions \(\phi _i(x)\), this constrained time-dependent variational equation converts to a system of differential algebraic equations (DAEs) of index-1 given by

$$\begin{aligned} \begin{bmatrix} \underline{U}^T C&0 \\ A&0 \end{bmatrix} \begin{bmatrix} \dot{\underline{U}} \\ \dot{p} \end{bmatrix} = \begin{bmatrix} R \\ -(B - pC)\underline{U} - \underline{D} \end{bmatrix}. \end{aligned}$$
(11)

Here the matrices are defined as follows

$$\begin{aligned} A_{ij} = \int _X \phi _i \phi _j \;\mathrm {d}x , \,\; B_{ij} = \int _X \phi ^{\prime \prime }_i \phi ^{\prime \prime }_j\;\mathrm {d}x,\,\; C_{ij} = \int _X \phi ^{\prime }_i \phi ^{\prime }_j\;\mathrm {d}x, \text{ and } D_i = \int _X f_e(\underline{U})\phi _i\;\mathrm {d}x. \end{aligned}$$
(12)

where the nonlinear functional defined by \(D_i\) is computed using a high order Gaussian quadrature rule. To produce an index 1 DAE, we differentiate the constraint equation in time and impose the constraint as \(\int _X u'u'_T\;\mathrm {d}x = \rho \). Full details of the FE procedure can be found for a similar problem in [14, Sect. 6.1].

Up to now the formulation is general, without consideration of boundary conditions. We impose homoclinic boundary conditions at each end of the finite domain by setting end nodal values (\(u_1,u_1',u_N,u_N'\)), such that the linearisation of (6) i.e.

$$\begin{aligned} u(x) = A_1e^{\xi _1x} + A_2e^{-\xi _1x} + A_3e^{\xi _2x} + A_4e^{-\xi _2x} \end{aligned}$$
(13)

is satisfied in the homoclinic tails [11]. Here \(\xi _1\) and \(\xi _2\) are the characteristics of the linear equation \(\xi ^4 + p\xi ^2 + 1 = 0\). As \(x \rightarrow - \infty \), solutions must remain bounded and therefore \(A_2 = A_4 = 0\). This leads to the outset condition,

$$\begin{aligned} u_1 = A_1e^{-\xi _1 L} + A_3e^{-\xi _2 L}\quad \text{ and } \quad u_1' = A_1\xi _1e^{-\xi _1 L} + A_3\xi _2e^{-\xi _2 L}. \end{aligned}$$
(14)

Solving for \(A_1\) and \(A_3\) enables solutions for \(u_1\) and \(u_1'\) to be computed. The process is repeated at \(x = x_N = L\), where the inset condition (\(A_1 = A_3 = 0\)) is imposed.

4.2 Numerical Experiments

The dynamic behaviour of (11) under different rates of applied end-shortening \(\rho \) is next investigated. An error convergence study indicates that a uniform FE mesh with \(N = 70\) over length \(L=30\) is suitably accurate and efficient. The quintic coefficient of (8) was taken as \(\alpha = 0.3\), allowing comparisons with the stationary solutions of Fig. 2 as computed in Sect. 3. Figure 3 shows a series of numerical solutions for increasing rates of loading from top to bottom: \(\rho = 10^{-4}\), \(10^{-3}\) and \(10^{-2}\) respectively. To avoid the system becoming locked in the trivial equilibrium state, all runs are seeded by an incremental displacement into a symmetric localised shape.

Fig. 3
figure 3

Load p against end-shortening \(\varDelta \) at rates \(\rho =10^{-4}\) (top), \(10^{-3}\) (middle), \(10^{-2}\) (bottom), compared against stationary solutions of Fig. 2. Inset plots show solutions profiles at positions indicated

Full size image

First we make some general observations:

  • For rates of end-shortening \(\rho < 10^{-4}\) say, the system is quasi-static. Jumps between near-equilibrium states occur immediately or soon after stability is lost.

  • Increasing \(\rho \) mean that solutions tend to drift from the static state, and can also delay the unstable jumps so they occur with increasing as well as decreasing load.

  • Behaviour at high rates is dominated by the dynamics. Significantly, a high rate can lead to a jump being by-passed, so the system can remain in a symmetric or anti-symmetric state even when its stationary counterpart has become unstable.

Figure 3 suggests a change in rate causes a dynamical jump to drift, but it is also possible for it to change suddenly at a dynamical bifurcation. Figure 4 shows solution paths for two rates, \(10^{-7}\) apart, found via a root searching algorithm, bounding the critical rate \(\rho ^* \simeq 1.6135\,\times \,10^{-4}\). This is explored phenomenologically later in Fig. 6.

Fig. 4
figure 4

Numerical evidence of a dynamical bifurcation at a critical rate \(\rho ^*\simeq 1.6135\,\times \,10^{-4}\), at which solution branching occurs at \(\varDelta ^* \simeq 2.274\). Plots shows \(\varDelta \) against p of the dynamic paths blue (solid) and the primary stationary states (thin-dashed) for \(\rho = 1.613\,\times \,10^{-4}\) (left); \(\rho = 1.614\,\times \,10^{-4}\) (right)

Full size image

5 Evolutionary Galerkin Procedure and Energy Landscape

To help interpret the dynamics it is useful to model the system with just a single degree of freedom. We thus decompose the description into linear combinations of the symmetric and anti-symmetric stationary modes at the given \(\varDelta = \rho t\), as follows,

$$\begin{aligned} \tilde{u}(x,t) = q_s(t) \psi _s(x,t) + q_a(t) \psi _a(x,t). \end{aligned}$$
(15)

where \(\psi _i\) are the mode shapes of Fig. 2, with amplitudes \(q_i\). End-shortening is now,

$$\begin{aligned} \varDelta = \rho t = \frac{1}{2}\int _X \tilde{u}'^2 \,\mathrm {d}x= \frac{1}{2}q_s^2\int _X \psi _s'^2 \,\mathrm {d}x+ \frac{1}{2}q_a^2\int _X \psi _a'^2 \,\mathrm {d}x \end{aligned}$$
(16)

at time t, where X is the (long) domain over which the modeshapes are computed. Since \(\frac{1}{2}\int \psi _s'^2\mathrm{d}x\) and \(\frac{1}{2}\int \psi _a'^2\mathrm{d}x\) compute to the same value independently, \(q_s\) and \(q_a\) lie on the unit circle. Thus \(q_a = \sqrt{1-q_s^2}\) and the system has a single degree of freedom. Energy levels can then be computed directly from (4).

Substituting (15) into (8) gives

$$\begin{aligned} \dot{q_s}\psi _s + q_s\dot{\psi _s} + \dot{q_a}\psi _a + q_a\dot{\psi _a} = -\big (q_s\psi _s^{\prime \prime \prime \prime } + q_a\psi _a^{\prime \prime \prime \prime } + p(q_s\psi _s^{\prime \prime } + q_a\psi _a^{\prime \prime }) + f_e(q_a \psi _a + q_s \psi _s)\big ). \end{aligned}$$
(17)

Evolution equations for the \(q_i\) are found by multiplying by the corresponding \(\psi _i\) and integrating over the domain X. These, along with the constraint equation, lead to the following governing equations, written in matrix form,

$$\begin{aligned} \begin{bmatrix} A&0 \\ 2t\underline{Q}^T&0 \end{bmatrix} \begin{bmatrix} \dot{\underline{Q}} \\ \dot{p} \end{bmatrix} = - \begin{bmatrix} (B - pC)\underline{Q} + \underline{D} + \frac{1}{2}\dot{A}\underline{Q}\\ \underline{Q}^T \underline{Q} - 1 \end{bmatrix} \end{aligned}$$
(18)

where \(\underline{Q} = [q_s;\ q_a]\). A, B, C and D are defined by (12) but with the \(\phi _i\) replaced by \(\psi _i\). Load p is fixed by the constraint condition (16) which, after differentiating with respect to time yields the bottom row in (18). We note, in contrast to the FE formulation, the appearance of momentum-like terms due to variations of the shape functions with time.

The constrained gradient flow equation (8) is thus reduced to three DAEs of index-1, which again can be solved using MATLAB’s inbuilt function ode23s. To avoid the system sitting unrealistically on an energy maximum, zero values of \(q_s\) or \(q_a\) are replaced by the small non-zero quantity \(+10^{-12}\), the positive sign ensuring that solutions are all found in the first quadrant of the unit circle. Typical dynamical outcomes are seen in Fig. 6 later.

Fig. 5
figure 5

Left energy landscape. Right three sections at different \(\varDelta \) values, that embrace a region of bistability and illustrate transfer of stability from symmetry to anti-symmetry

Full size image
Fig. 6
figure 6

Dynamical paths from a start close to the symmetric shape at different rates. The ridge line of equilibria associated with the second ladder of Fig. 2 is shown in black

Full size image

Figure 5 shows contours of the change in energy from the symmetric state, as computed from (4), at different but constant values of \(\varDelta \). This is plotted against the polar angle \(\theta \) on the unit circle (\(q_s = \cos \theta \), \(q_a = \sin \theta \)), with the darker regions representing higher energies. Sections at constant \(\varDelta \) are shown on the right. For small \(\varDelta \), as seen in the bottom and middle slices, the symmetric form is preferred while the anti-symmetric form changes from a global maximum to a local minimum. As \(\varDelta \) is increased, the symmetric form first relinquishes its status as the global minimum (somewhere around \(\varDelta = 2.18\)), and then evolves into a local maximum as seen at the top. When symmetric and anti-symmetric minima coexist the system is bistable, and we note the appearance then of a third equilibrium state in the form of a local maximum; this reflects the first ladder of Fig. 2.

As seen in Figs. 3 and 4, typical dynamical responses of the PDE can be subject to dynamical bifurcations. The reduced view of Fig. 5 is useful in describing how this comes about. Figure 6 shows a set of runs at differing rates on the landscape of Fig. 5, all starting from the same position close to the symmetric state. After venturing into the mixed region the runs either return to the symmetric state, or veer off to the anti-symmetric one. The critical rate \(\rho ^*\simeq 8.2077455491\,\times \,10^{-4}\) defines the transition, and the difference between the two closest diverging paths is \(\varDelta \rho = 10^{-15}\). Separation occurs close to, but not coincident with, the ridge line, the difference being due to the (small) velocity component provided by the rate \(\rho \). Starts from closer to the symmetric state bifurcate at a lower critical rate and closer to the ridge line.

6 Concluding Remarks

We have presented two models for the nonlinear visco-elastic system of Fig. 1, a multi degree-of-freedom FE formulation, and a single degree-of-freedom evolutionary Galerkin procedure based on static modal shapes obtained from the path-following routine AUTO [10]. According to the associated dynamical responses, the two models show good qualitative agreement at low rates of end-shortening. The pure symmetric and anti-symmetric snaking equilibrium paths and associated modeshapes are the same, but the ladder equilibrium states of Fig. 2, being based on these pure forms, fail to match precisely. The first ladder extends over the range \(2.157< \varDelta < 2.198\) for the FE model, for example, whereas for the Galerkin it covers \(1.90< \varDelta < 2.35\). Better accuracy could be obtained with the addition of further shapes derived from the ladders, but this would be at the expense of simplicity.

The single degree-of-freedom Galerkin model is shown to be a useful phenomenological tool. The reduction allows the dynamics to be seen as movement on a 2D surface, with velocity governed by a constant rate of end-shortening on one dimension and visco-elastic flow in the other. The benefit is neatly demonstrated by Fig. 6, which shows visually how a dynamical bifurcation associated with the energy maxima of the ladder equilibrium states comes about, and thus provides the key ingredient for many chaotic situations. It is interesting to see that in this instance there is an intimate link to the spatial chaos of the snakes-and-ladders scenario. We are of course aware that the solution of a nonlinear PDE is not exactly expressible as a linear combination of two stationary states, but the numerical evidence suggests that the stationary states are such strong attractors (in terms of the energy surface) that the process does offer a fair and highly illustrative new interpretation.