1 Introduction

1.1 Extended Abstract

This chapter consists of an overview of recent results concerning the convergence and regularization of the quintessential sampling series, the cardinal sine series. Conditions, that go beyond those associated with the standard theory, are formulated that ensure reconstruction by this series. The conditions are one of two types: (i) on the coefficients or samples or (ii) on the functions or signals being reconstructed.

Regularization or summability methods based on the Bernstein-Boas formula for entire functions of exponential type that are bounded on the real axis are discussed. A result that ensures that the methods are regular, in the sense that they reproduce all the functions that are representable as cardinal sine series, is formulated. Also, it is shown that not all entire functions that are frequency band limited can be reproduced by these methods.

It turns out that Schoenberg’s spline summability method for cardinal sine series is a summability method of the type mentioned above. This is also the case for other sampling series that are based on shift invariant subspace generators.

1.2 Background

Suppose the sequence {c n } = {c n : n = 0, ±1, ±2, …} represents the point evaluations or samples c n = f(n∕ρ) of a continuous function or signal f(t). Here ρ is a positive constant that is often referred to as the sampling rate.

A sampling series is an expression of the form

$$\displaystyle{ \sum _{n=-\infty }^{\infty }c_{ n}\varPhi (\rho t - n)\,, }$$
(1)

where Φ(t) is a continuous function, −∞ < t < ∞, with the property that for n = 0, ±1, ±2, …

$$\displaystyle{\varPhi (n) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\mbox{ if $n = 0$}\\ 0\quad &\mbox{ otherwise.} \end{array} \right.}$$

The objective is for (1) to reconstruct or approximate the function f(t) in terms of the sequence of samples {c n }.

The classical cardinal sine series where

$$\displaystyle{\varPhi (t) = \frac{\sin \pi t} {\pi t}}$$

is an important example. In this case, if f(t) is frequency band limited to the interval [−πρ, πρ] and is in \(L^{2}(\mathbb{R})\) or, in engineering terminology, has finite power, then the celebrated sampling theorem associated with the names of Whittaker, Kotelnikov, and Shannon (WKS) asserts that (1) represents f(t) in the sense that it actually converges to f(t), −∞ < t < ∞. There is a vast literature on the subject, including [12–17, 19, 29, 30, 32, 67–69, 71–74]. It is known that certain other classes of functions that are frequency band limited to the interval [−πρ, πρ] also enjoy representation (1). When f(t) satisfies certain continuity and decay conditions but fails to be frequency band limited the series (1) is known to approximate or converge to f(t) as the sampling rate ρ tends to infinity.

In this chapter we will be interested in the series (1) only in the case when the sampling rate ρ is fixed. A dilation argument shows that any result or fact that is true for one fixed sampling rate is also true for all fixed sampling rates. Hence, without loss of generality, we may and do restrict our attention to the case ρ = 1.

As suggested by the WKS Theorem, the Fourier transform and frequency band limited functions play a significant role in what follows. The Fourier transform of a tempered distribution u is denoted by \(\widehat{u}\) and, in the normalization used here, is defined by

$$\displaystyle{\widehat{u}(\xi ) =\int _{ -\infty }^{\infty }e^{-i\xi t}u(t)dt}$$

when u is an integrable function. For σ > 0, E σ denotes the class of those entire functions of exponential type no greater than σ that have no greater than polynomial growth along the real axis, in other words, if u(z) is in E σ , then there are constants C and m such that

$$\displaystyle{\vert u(z) \leq C(1 + \vert z\vert ^{m})e^{\sigma \vert \mathop{\mathrm{Im}}\nolimits z\vert }}$$

for all z in the complex plane \(\mathbb{C}\). According to the distributional variant of a theorem of Paley and Wiener, E σ consists of the Fourier transforms of distributions supported in the interval [−σ, σ]. Thus E σ is a class of functions that are frequency band limited to the interval [−σ, σ]. In most applications only the restrictions of such functions to the real axis is of interest. But it is natural and often convenient to regard them as functions of a complex variable z = x + iy and, when restricted to the real axis, functions of the real variable x.

1.3 Contents

With these conventions the classical cardinal sine series with coefficients {c n } is

$$\displaystyle{ \sum _{n=-\infty }^{\infty }c_{ n}\frac{\sin \pi (z - n)} {\pi (z - n)}\,. }$$
(2)

In Section 2, as mentioned in the abstract, we will provide various conditions under which this series converges and represents an entire function f(z) with f(n) = c n .

In Section 3 we consider sampling series of the form

$$\displaystyle{ \sum _{n=-\infty }^{\infty }c_{ n}\frac{\sin \pi (z - n)} {\pi (z - n)}\phi _{\alpha }(z - n)\,, }$$
(3)

where \(\{\phi _{\alpha }(z):\alpha \in \mathcal{I}\}\) is a family of functions parameterized by the index set \(\mathcal{I}\). For this type of sampling series both the complex and, with certain applications in mind, the restriction to the real case will be considered.

Piecewise polynomial cardinal splines are defined only in the real variable scenario and can be viewed as sampling series

$$\displaystyle{\sum _{n=-\infty }^{\infty }c_{ n}L(x - n)}$$

where the functions L(x) are the so-called fundamental splines. In Section 4 we consider the even order cases and show that they can be regarded as specific examples of sampling series of the form (3). Piecewise polynomial splines of a fixed order are a specific instance of a so-called shift invariant subspace with one generator. In Subsection 4.3 we give several examples of such generators and indicate that, in certain instances, the corresponding sampling series can exhibit limiting behavior analogous to that of piecewise polynomial splines.

The Appendix contains miscellaneous material, mainly further comments and documentation.

2 Cardinal Sine Series

The symmetric partial sums of the cardinal sine series (2)

$$\displaystyle{ f_{N}(z) =\sum _{ n=-N}^{N}c_{ n}\frac{\sin \pi (z - n)} {\pi (z - n)} }$$
(4)

N = 1, 2, … , are entire functions in E π . Expressing f N (z) as

$$\displaystyle{f_{N}(z) = \frac{\sin \pi z} {\pi } \sum _{n=-N}^{N}\frac{(-1)^{n}c_{ n}} {z - n} }$$

leads to the following conclusion. The details can be found in [3].

Theorem 1.

Suppose {f N (z)} N = 1 ∞ is the sequence of symmetric partial sums (4) of the cardinal sine series (2) with coefficients {c n }.

  1. 1.

    The sequence {f N (z)} N = 1 ∞ converges for every z in the complex plane \(\mathbb{C}\) if and only if both

    $$\displaystyle{\sum _{n=1}^{\infty }(-1)^{n}\,\frac{c_{n} + c_{-n}} {n^{2}} \quad \mathit{\text{and}}\quad \sum _{n=1}^{\infty }(-1)^{n}\,\frac{c_{n} - c_{-n}} {n} }$$

    converge.

  2. 2.

    If the sequence {f N (z)} N = 1 ∞ converges for every z in the complex plane, then the sequence converges uniformly on compact subsets of \(\mathbb{C}\).

  3. 3.

    If the sequence {f N (z)} N = 1 ∞ does not converge uniformly on compact subsets of \(\mathbb{C}\) , then {f N (z)} N = 1 ∞ converges for at most one non-integer value of z and diverges for all other non-integer z. In particular, if {f N (z)} N = 1 ∞ converges for two points z = z 1 and z = z 2 that are not integers, then {f N (z)} N = 1 ∞ converges uniformly on compact subsets of C.

In what follows, we say that f(z) is a convergent cardinal series if the sequence of partial sums (4) converges to f(z) uniformly on compact subsets of \(\mathbb{C}\). If that is the case, then f(z) is an entire function and f(n) = c n , n = 0, ±1, ±2… .

The even and odd parts of an entire function f(z) are denoted by f e (z) and f o (z) and defined as

$$\displaystyle{f_{e}(z) = \tfrac{1} {2}\{f(z) + f(-z)\}\quad \text{and}\quad f_{o}(z) = \tfrac{1} {2}\{f(z) - f(-z)\}.}$$

The following theorem, whose details can also be found in [3], shows that a convergent cardinal series cannot grow too rapidly as | z | → ∞.

Theorem 2.

If f(z) is a convergent cardinal series with even and odd parts f e (z) and f o (z), then

$$\displaystyle{\vert f_{e}(z)\vert e^{-\pi \vert \mathop{\mathrm{Im}}\nolimits z\vert } = o(\vert z\vert ^{2})\quad \mathit{\text{and}}\quad \vert f_{ o}(z)\vert e^{-\pi \vert \mathop{\mathrm{Im}}\nolimits z\vert } = o(\vert z\vert )\quad \mathit{\mbox{ as $\vert z\vert \rightarrow \infty $.}}}$$

In particular, a convergent cardinal series is in E π .

Theorem 2 provides bounds on the rate of growth of a convergent cardinal sine series along the real axis. On the other hand, examples show that not all functions in E π that enjoy these growth bounds are convergent cardinal sine series.

In view of Theorem 1, the sequence of coefficients {c n } of a convergent cardinal sine series f(z) need not decay as n → ±∞. Several results that indicate how the growth of the coefficients are reflected in the growth of f(z) as | z | → ∞ are recorded in [44].

Note that in general lim n → ±∞ c n = 0 does not imply that the sequence of coefficients {c n } gives rise to a convergent cardinal sine series. On the other hand, if for some p in the range 1 ≤ p < ∞

$$\displaystyle{\sum _{n=-\infty }^{\infty }\vert c_{ n}\vert ^{p} <\infty }$$

then an application of Hölder’s inequality shows that the sequence of coefficients {c n } gives rise to a convergent cardinal sine series. If 1 < p < ∞ the Plancherel-Polya Theorem [39, p. 152, Theorem 3], a far reaching extension of the WKS sampling theorem, asserts that the corresponding entire function f(z) is in \(L^{p}(\mathbb{R})\) when restricted to the real axis and that every function in E π that is in \(L^{p}(\mathbb{R})\) when restricted to the real axis is a convergent cardinal sine series.

Concerning functions that are merely bounded on the real axis, it is known that if f(z) is in E σ for some σ < π and bounded on the real axis then f(z) is a convergent cardinal sine series. For more details see [14].

If an entire function f(z) is in E π but is not a member of one of the classes covered by the above results, in spite of the characterization provided by Theorem 1, determining whether it is a convergent cardinal sine series is, in many instances, not a completely routine matter. One reason for this is, that in view of functions like sinπz and zsinπz, the sequence of samples c n = f(n), n = 0, ±1, ±2, … , may not uniquely determine f(z). Another reason is that the description of f(z), e.g. the subclass of E π it belongs to, may not evidently provide enough information concerning the sequence of samples {f(n)}.

In what follows we give several results that provide alternate conditions that guarantee that a function f(z) in E π be a convergent cardinal sine series.

Theorem 3.

Suppose f(z) is in E π and f e (z) and f o (z) are its even and odd parts, respectively. If f e (x) = o( | x | ) and f o (x) = o(1) as | x | → ∞, then f is a convergent cardinal series.

Theorem 3 implies that, among those even and odd functions in E π that fail to be convergent cardinal sine series, the examples zsin(πz) and sin(πz) exhibit the slowest possible rates of growth along the real axis. The proof and more details can be found in [4]

It is important to note that the assumptions on f e (z) and f o (z) involve their behavior on the real axis. Examples show that knowledge of the behavior of the samples alone is generally not sufficient to obtain the conclusion. For instance,

$$\displaystyle{f(z) = \frac{\sin \pi z} {\pi } \sum _{n=2}^{\infty }\frac{1} {\log n}\, \frac{2z^{2}} {n(z^{2} - n^{2})}}$$

is an odd function in E π that is not a convergent sine series but for integers n, f(n) = o(1) as n → ∞. Plots of this function can be found in the Appendix.

The following is a corollary of Theorem 3 and the fact that the sequence of coefficients \(c_{n} =\mathop{ \mathrm{sgn}}\nolimits (n)\), n = 0, ±1, ±2, … , gives rise to a convergent cardinal sine series.

Theorem 4.

If f(z) is in E π and there are complex numbers a and b such that

$$\displaystyle{\lim _{x\rightarrow \infty }f(x) = a\quad \mathit{\text{and}}\quad \lim _{x\rightarrow -\infty }f(x) = b}$$

then f(z) is a convergent cardinal series.

The next theorem is a corollary of Theorem 4 and the fact that zf(z) is a convergent cardinal sine series whenever f(z) is an odd convergent cardinal sine series.

Theorem 5.

If f(z) is an even function in E π and there is a complex number a such that

$$\displaystyle{\lim _{x\rightarrow \pm \infty }\frac{f(x)} {\vert x\vert } = a}$$

then f(z) is a convergent cardinal series.

The following theorem may be regarded as a kind of converse to Theorem 2. It involves the appropriate conditions on the growth of the samples with an additional condition that involves the decay of some, possibly high order, derivative of f(z).

We use the standard notation f (k)(z), where k is a non-negative integer, to denote the derivative of order k of the function f(z). In other words f (0)(z) = f(z), f (1)(z) = f′(z), etc. The proof of the following theorem and its corollaries can also be found in [4].

Theorem 6.

The entire function f(z) is a cardinal sine series if one of the following two conditions holds:

  1. (i)

    f(z) is an odd function in E π such that f(n) = o(n) as n → ∞ over the integers and for some non-negative integer k, lim x → ∞ f (k)(x) = 0.

  2. (ii)

    f(z) is an even function in E π such that f(n) = o(n 2) as n → ∞ over the integers and for some non-negative integer k, \(\lim _{x\rightarrow \infty }\frac{f^{(k)}(x)} {x} = 0\).

The next two theorems are basically corollaries of Theorem 6

Theorem 7.

Suppose f(z) is in E π and satisfies both

$$\displaystyle{\lim _{x\rightarrow \infty }f_{o}\prime(x) = 0\quad \mathit{\text{and}}\quad \lim _{x\rightarrow \infty }\frac{f_{e}\prime(x)} {x} = 0\,.}$$

Then f(z) is a convergent cardinal series.

If f(z) is an even function in E π and lim x → ∞ f″(x) = 0, then f is a convergent cardinal series.

Theorem 8.

Suppose f(z) is in E π and, for some non-negative integer k, f (k)(z) is in \(L^{p}(\mathbb{R})\) on the real axis for some value p, 1 ≤ p < ∞. Then f(z) is a cardinal sine series if and only if both

$$\displaystyle{f(n) + f(-n) = o(n^{2})\quad \mathit{\text{and}}\quad f(n) - f(-n) = o(n)\quad \mathit{\mbox{ as $n \rightarrow \infty $.}}}$$

If f(z) is in E π and, for some integer k ≥ 1, f (k)(z) is in \(L^{p}(\mathbb{R})\) on the real axis for some p, 1 ≤ p < ∞, then

$$\displaystyle{f^{(k)}(x) = o(1)\quad \text{and}\quad f(x) = O(\vert x\vert ^{k-1/p})\quad \mbox{ as $x \rightarrow \pm \infty $.}}$$

Hence, as a corollary of Theorem 8, in the case k = 1 all such functions f(z) are convergent cardinal sine series. In the case k = 2 all such functions f(z) that are even are convergent cardinal sine series.

Earlier it was mentioned that functions f(z) in E σ , σ < π, that are bounded on the real axis are convergent cardinal sine series. As a significant extension of that result and as a kind of converse to Theorem 2 the following was verified in [6].

Theorem 9.

Suppose f(z) is in E σ for some σ, 0 ≤ σ < π, and also satisfies both

$$\displaystyle{f_{e}(n) = o(n^{2})\quad \mathit{\mbox{ and}}\quad f_{ o}(n) = o(n)\quad \mathit{\mbox{ as $n \rightarrow \infty $.}}}$$

Then f(z) is a convergent cardinal sine series.

3 Regularized Cardinal Sine Series

3.1 Bernstein-Boas Type Regularization

The Bernstein class B σ is the class of those entire functions in E σ that are bounded on the real axis. If f(z) is in B σ for some σ < π and ε satisfies 0 < ε < π −σ, then the Bernstein-Boas formula asserts that

$$\displaystyle{ f(z) =\sum _{ n=-\infty }^{\infty }f(n)\frac{\sin \pi (z - n)} {\pi (z - n)} \frac{\sin \epsilon (z - n)} {\epsilon (z - n)} }$$
(5)

where the series converges absolutely, [10, 10.2.9, p. 181] or [39, Theorem 3, p. 160].

Replacing \(\frac{\sin \epsilon z} {\epsilon z}\) in expression (5) with other functions that may decay more rapidly gives rise to a wide family of regularizations for the cardinal sine series. We refer to such regularizations as being of Bernstein-Boas type. For example, if

$$\displaystyle{ \phi (z) = \left \{\frac{\sin (z/k)} {z/k} \right \}^{k} }$$
(6)

for some positive integer k and f(z) is an entire function in E σ , σ < π, that grows no more rapidly on the real axis than a polynomial of degree k − 1 then

$$\displaystyle{ f(z) =\sum _{ n=-\infty }^{\infty }f(n)\frac{\sin \pi (z - n)} {\pi (z - n)}\phi (\epsilon (z - n)) }$$
(7)

whenever 0 < ε < π −σ.

In fact, if ϕ(z) is an entire function in E 1 that decays faster than any polynomial and ϕ(0) = 1, then (7) is valid for all f(z) in E σ when σ < π and 0 < ε < π −σ. Such functions ϕ(z) cannot be elementary functions but use can be made of the fact that their Fourier transforms are infinitely differentiable to express them as inverse Fourier transforms. A specific example of such a function is given by

$$\displaystyle{ \phi (z) = \frac{\gamma } {2\pi }\int _{-1}^{1}\exp \left (iz\xi + \frac{1} {\xi ^{2} - 1}\right )d\xi }$$
(8)

where γ is a constant chosen so that ϕ(0) = 1,

$$\displaystyle{\frac{2\pi } {\gamma } =\int _{ -1}^{1}\exp \left ( \frac{1} {\xi ^{2} - 1}\right )d\xi \;.}$$

By taking the limit as ε tends to 0 on the right-hand side of (7) the restriction σ < π −ε can be removed. For example, if ϕ(z) is the function defined by (8) and ε > 0, then

$$\displaystyle{ f(z) =\lim _{\epsilon \rightarrow 0}\sum _{n=-\infty }^{\infty }f(n)\frac{\sin \pi (z - n)} {\pi (z - n)}\phi (\epsilon (z - n)) }$$
(9)

is valid for all entire functions in E σ when σ < π.

Indeed, (9) is valid for even wider classes of entire functions in E π . For instance, suppose f(z) is in E π and its Fourier transform is integrable. Such a function need not be in E σ for any σ < π. Nevertheless (9) is valid for such a function f(z).

However, the subclass of functions in E π for which (9) is valid has not been characterized. In fact, it is not evident that (9) is valid for entire function f(z) that are convergent cardinal sine series. On the other hand, it is known that (9) is not valid for all functions f(z) in E π ; in other words, (9) can only be valid for a proper subclass of functions in E π .

In Subsection 3.2 we formulate conditions on the function ϕ in E 1 that are sufficient to guarantee that (9) is valid whenever f(z) is a cardinal sine series. We also show that (9) cannot be valid for all entire function f(z) in E π whenever ϕ satisfies these conditions.

Formula (9) can be viewed as a summability method for the cardinal sine series. We will refer to it as a Bernstein-Boas type summability method. As is customary, we will call the method regular if (9) is valid whenever f(z) is a convergent cardinal sine series.

In all the instances above the function ϕ was a member of E 1. This membership is not a necessary restriction. For examples, the Gaussian was used in several important applications and elsewhere, [52, 53, 60]. The function ϕ need not be an entire function. On the real axis good approximations of f(x) can be obtained in terms of nearby samples by using functions ϕ that have compact support.

In Subsection 3.3 we consider extensions of (9) where ϕ(εz), ε > 0, is replaced by a more general family of functions of a real variable \(\{\phi _{\alpha }(x):\alpha \in \mathcal{I}\}\) indexed by α in the index set \(\mathcal{I}\) and formulate conditions that are sufficient to guarantee that the analog of (9) is valid on the real axis whenever f(z) is a cardinal sine series. We continue to refer to the resulting summability methods as being of Bernstein-Boas type.

3.2 Regularity and Limitations of Bernstein-Boas Summability

In what follows we assume that ϕ(z) is an entire function in E 1 that satisfies

$$\displaystyle{ \phi (0) = 1, }$$
(10)
$$\displaystyle{ \phi (-z) =\phi (z), }$$
(11)

and

$$\displaystyle{ \int _{-\infty }^{\infty }\vert x\phi (x)\vert dx <\infty. }$$
(12)

Examples of such functions include those defined by (6) when k = 3, 4, … , or, more generally,

$$\displaystyle{ \phi (z) = \frac{1} {2\pi }\int _{-1}^{1}e^{iz\xi }\widehat{\phi }(\xi )d\xi }$$
(13)

where \(\widehat{\phi }(\xi )\) is any sufficiently smooth even function on \(\mathbb{R}\) with support in the interval [−1, 1] that satisfies \(\widehat{\phi }(-\xi ) =\widehat{\phi } (\xi )\) and \(\int _{-1}^{1}\widehat{\phi }(\xi )d\xi = 2\pi\).

Since we are interested in the case when ε → 0, for simplicity we also always assume that 0 < ε ≤ 1.

Theorem 10.

Suppose f(z) is a convergent cardinal sine series. Then the series

$$\displaystyle{ f_{\epsilon }(z) =\sum _{ n=-\infty }^{\infty }f(n)\frac{\sin \pi (z - n)} {\pi (z - n)}\phi (\epsilon (z - n)) }$$
(14)

converges absolutely and uniformly on compact subsets of \(\mathbb{C}\) to an entire function f ε (z) in E π+ε and

$$\displaystyle{ \lim _{\epsilon \rightarrow 0}f_{\epsilon }(z) = f(z)\quad \mathit{\mbox{ uniformly on compact subsets of $\mathbb{C}$.}} }$$
(15)

The assumptions on the function ϕ(z) in E 1 have not been optimized. For example, the assumption (12) may not be the least restrictive possible. However, some such condition is required since the boundedness of | xϕ(x) | on the real axis is not sufficient to obtain Theorem 10. An example illustrating this fact and a proof of the theorem can be found in [8].

Also, (11) may not be necessary. However, all the important examples enjoy this property and its use is convenient in the proof of Theorem 10.

Representations (15) are valid not only for convergent cardinal sine series but also for a much wider class of functions in E π . For example, if the function \(\widehat{\phi }(\xi )\) in (13) is infinitely continuously differentiable, then (14) is also valid for any function f(z) in E π when σ < π; such functions can grow as fast as any polynomial on the real axis and need not be convergent cardinal sine series.

However, (14) cannot be valid for all functions f(z) in E π . To see this consider

$$\displaystyle{ f(z) = \frac{z^{2}\sin \pi z} {\pi } \sum _{n=1}^{\infty } \frac{2} {n(z^{2} - n^{2})}\;. }$$
(16)

The function f(z) is well defined for all z on the complex plane \(\mathbb{C}\) by (16) and enjoys the following properties:

$$\displaystyle{ \mbox{ $f(z)$ is an odd function, namely $f(-z) = -f(z)$ for all $z$,} }$$
(17)
$$\displaystyle{ f(n) = (-1)^{n}\quad \mbox{ when $n = 1,2,\ldots \;$.} }$$
(18)

and

$$\displaystyle{ \mbox{ $f(z)$ is in $E_{\pi }$.} }$$
(19)

That f(z) is an entire function that satisfies (17) and (18) is evident from its definition (16). Property (19) follows by estimating the size of | f(z) | for large | z |.

Theorem 11.

Suppose f(z) is the entire function defined by (16), ϕ(z) satisfies the hypothesis of Theorem 10 , and f ε (z) is the corresponding series (14). Then f ε (z) is an entire function in E π+ε and when z is not an integer f ε (z) fails to converge as ε tends to 0. More specifically,

$$\displaystyle{ \lim _{\epsilon \rightarrow 0}\vert f_{\epsilon }(z)\vert = \infty \quad \mathit{\mbox{ for non-integer $z$.}} }$$
(20)

Item (20) means that given any positive constant M and a non-integer z then

$$\displaystyle{\vert f_{\epsilon }(z)\vert> M\quad \mbox{ for sufficiently small $\epsilon $.}}$$

Proof.

The fact that f ε is an entire function in E π+ε follows from its definition and estimating the size of | f(z) | for large | z |.

To see (20) write

$$\displaystyle{\begin{array}{lll} f_{\epsilon }(z)& =&\sum _{n=-\infty }^{\infty }f(n)\frac{\sin \pi (z-n)} {\pi (z-n)}\phi (\epsilon (z - n) \\ & =&\frac{\sin \pi z} {\pi } \sum _{n=1}^{\infty }(-1)^{n}f(n)\left \{ \frac{2n} {z^{2}-n^{2}} \varPhi _{n} + \frac{2z} {z^{2}-n^{2}} \varPsi _{n}\right \}.\end{array} }$$

where

$$\displaystyle{\varPhi _{n} = \tfrac{1} {2}\{\phi (\epsilon (z - n)) +\phi (\epsilon (z + n))\}\quad \text{and}\quad \varPsi _{n} = \tfrac{1} {2}\{\phi (\epsilon (z - n)) -\phi (\epsilon (z + n))\}.}$$

with the dependence of Φ and Ψ on z and ε suppressed for convenience.

Now use the fact that f(n) = (−1)n, n = 1, 2, … , and

$$\displaystyle{ \frac{2n} {z^{2} - n^{2}} = \frac{2z^{2}} {(z^{2} - n^{2})n} - \frac{2} {n}}$$

to write

$$\displaystyle{f_{\epsilon }(z) = f_{1,\epsilon }(z) + f_{2,\epsilon }(z) + f_{3,\epsilon }(z)}$$

where

$$\displaystyle{f_{1,\epsilon }(z) = \frac{\sin \pi z} {\pi } \sum _{n=1}^{\infty } \frac{2z^{2}} {(z^{2} - n^{2})n}\varPhi _{n}\;,}$$
$$\displaystyle{f_{2,\epsilon }(z) = -\frac{2\sin \pi z} {\pi } \sum _{n=1}^{\infty }\frac{1} {n}\varPhi _{n}\;,}$$

and

$$\displaystyle{f_{3,\epsilon }(z) = \frac{\sin \pi z} {\pi } \sum _{n=1}^{\infty } \frac{2z} {z^{2} - n^{2}}\varPsi _{n}\;.}$$

Since, for non-integer z, both

$$\displaystyle{\sum _{n=1}^{\infty } \frac{2z^{2}} {(z^{2} - n^{2})n}\quad \text{and}\quad \sum _{n=1}^{\infty } \frac{2z} {z^{2} - n^{2}}}$$

converge absolutely and lim ε → 0 Φ n = 1 while lim ε → 0 Ψ n = 0, it follows that

$$\displaystyle{ \lim _{\epsilon \rightarrow 0}f_{1,\epsilon }(z) = f(z)\quad \text{and}\quad \lim _{\epsilon \rightarrow 0}f_{3,\epsilon }(z) = 0. }$$
(21)

To estimate the size of | f 2,ε (z) | write

$$\displaystyle{\sum _{n=1}^{\infty }\frac{1} {n}\varPhi _{n} =\sum _{ n=1}^{N} \frac{1} {n} +\sum _{ n=1}^{N} \frac{1} {n}\{\varPhi _{n} - 1\} +\sum _{ n=N+1}^{\infty }\frac{1} {n}\varPhi _{n}}$$

where the value of N will be chosen later. First

$$\displaystyle{\begin{array}{lll} \varPhi _{n} - 1& =&\tfrac{1} {2}\{\phi {\bigl (\epsilon (z - n)\bigr )} - 1 +\phi (\epsilon (z + n)) - 1\} \\ & =&\frac{1} {2}\left \{\int _{0}^{\epsilon (z-n)}\phi \prime(\zeta )d\zeta +\int _{ 0}^{\epsilon (z+n)}\phi \prime(\zeta )d\zeta \right \} \end{array} }$$

where the integrals are taken along a straight line between the endpoints. The modulus of the first integral is no greater than Cε | z − n | where C is the maximum of ϕ′(ζ) on the strip \(\{\zeta: \vert \mathop{\mathrm{Im}}\nolimits \zeta \vert \leq \vert \mathop{\mathrm{Im}}\nolimits z\vert \}\) in the complex plane. A analogous bound is valid for the modulus of the second integral. Hence

$$\displaystyle{\vert \varPhi _{n} - 1\vert \leq C\epsilon \{\vert z\vert + n\}\quad \text{and}\quad \frac{\vert \varPhi _{n} - 1\vert } {n} \leq C\epsilon \{\vert z\vert /n + 1\}.}$$

It follows that

$$\displaystyle{\sum _{n=1}^{N}\frac{\vert \varPhi _{n} - 1\vert } {n} \leq C\epsilon \{\vert z\vert (1 +\log N) + N\}.}$$

Next

$$\displaystyle{\left \vert \sum _{n=N+1}^{\infty }\frac{1} {n}\varPhi _{n}\right \vert \leq \frac{C} {(N + 1)\epsilon }}$$

where we have used the inequalities

$$\displaystyle{\sum _{n=N+1}^{\infty }\frac{\vert \phi (\epsilon (z - n))\vert } {n} \leq \frac{1} {N + 1}\sum _{n=N+1}^{\infty }\vert \phi (\epsilon (z - n))\vert }$$

and, in view of [39, Property 4 on p. 150],

$$\displaystyle{\sum _{n=-\infty }^{\infty }\vert \phi (\epsilon (z - n))\vert \leq C\int _{ -\infty }^{\infty }\vert \phi (\epsilon \zeta )\vert d\zeta = C/\epsilon.}$$

Altogether we may conclude that there is a fixed constant C such that if N ≥ | z | (1 + logN) then

$$\displaystyle{\left \vert \sum _{n=1}^{N} \frac{1} {n}\{\varPhi _{n} - 1\} +\sum _{ n=N+1}^{\infty }\frac{1} {n}\varPhi _{n}\right \vert \leq C\left \{N\epsilon + \frac{1} {N\epsilon }\right \}.}$$

and hence, with the same constant C,

$$\displaystyle{\left \vert \sum _{n=1}^{\infty }\frac{1} {n}\varPhi _{n}\right \vert \geq \log N - C\{N\epsilon + \frac{1} {N\epsilon }\}.}$$

It follows that if N ≥ | z | (1 + logN) then

$$\displaystyle{\vert f_{2,\epsilon }(z)\vert \geq \frac{\vert \sin \pi z\vert } {\pi } \left \{\log N - C\{N\epsilon + \frac{1} {N\epsilon }\}\right \}.}$$

Now given any number M, if ε is positive and such that

$$\displaystyle{\log \frac{1} {2\epsilon } \geq M + 4C\quad \text{and}\quad \frac{1} {2\epsilon } \geq \vert z\vert \left (1 +\log \frac{2} {\epsilon } \right )}$$

and N is such that

$$\displaystyle{\frac{1} {2\epsilon } \leq N \leq \frac{2} {\epsilon } }$$

then

$$\displaystyle{\vert f_{2,\epsilon }(z)\vert \geq \frac{\vert \sin \pi z\vert } {\pi } M.}$$

Since z is not an integer and M is arbitrary, (20) follows.

Theorem 11 implies that there are functions f(z) in E π such that not only does f ε (z) fail to converge to f(z) as ε tends to 0 but that, for non-integer z, it simply fails to converge. The class of functions f(z) in E π for which f ε (z) converges as ε tends to 0 has not been characterized.

3.3 Extended Bernstein-Boas Regularization

The function ϕ in formula (14) need not be in E 1 for (14) to give rise to good regularizations or for appropriate variants of Theorem 10 to be valid. For example, the functions

$$\displaystyle{\phi (z) = e^{-z^{2} }\quad \text{and}\quad \phi (z) = (1 + z^{2})^{-2}}$$

give rise to good approximants. Indeed ϕ need not even be analytic and the dilates can be replaced by a family of function \(\{\phi _{\alpha }:\alpha \in \mathcal{I}\}\) where \(\mathcal{I}\) is an index set. However, properties of such families that are comprehensive enough to cover most of the interesting examples including the appropriate results are too cumbersome to formulate succinctly and are beyond the scope of this article. Instead, we consider a case that can be applied to Schoenberg’s spline summability method in Section 4.

In what follows we restrict our attention to the behavior of f(z) on the real axis, z = x and to families \(\{\phi _{\alpha }(x):\alpha \in \mathcal{I}\}\) of functions of the real variable x. More specifically, we assume that \(\{\phi _{\alpha }(x):\,\alpha \in \mathcal{I}\}\) is a family of functions in \(C^{2}(\mathbb{R})\) parameterized by \(\alpha \in \mathcal{I}\) where \(\mathcal{I}\) is an index set with a limit point. For simplicity we take the limit point to be 0 and the index set \(\mathcal{I}\) to be either the interval (0, 1] or the sequence {1, 1∕2, 1∕3, …}, namely

$$\displaystyle{\mathcal{I} =\{\alpha:\, 0 <\alpha \leq 1\}\quad \text{or}\quad \mathcal{I} =\{\alpha = 1/k: k = 1,2,3,\ldots \}.}$$

We also assume that the family {ϕ α (x)} enjoys the following properties:

$$\displaystyle{ \sup _{x\in \mathbb{R}}\sum _{n=-\infty }^{\infty }\vert x - n\vert \vert \phi _{\alpha }(x - n)\vert <\infty \quad \mbox{ for every $\alpha \in \mathcal{I}$,} }$$
(22)
$$\displaystyle{ \lim _{\alpha \rightarrow 0}\phi _{\alpha }(x) = 1\quad \mbox{ uniformly on compact subsets of $\mathbb{R}$,} }$$
(23)
$$\displaystyle{ \sup _{\alpha \in \mathcal{I}}\int _{-\infty }^{\infty }\vert \phi \prime_{\alpha }(x)\vert dx =\gamma _{ 1} <\infty, }$$
(24)
$$\displaystyle{ \sup _{\alpha \in \mathcal{I}}\int _{-\infty }^{\infty }\vert \phi \prime\prime_{\alpha }(x)\vert dx =\gamma _{ 2} <\infty, }$$
(25)
$$\displaystyle{ \sup _{\alpha \in \mathcal{I}}\int _{-\infty }^{\infty }\vert x\phi \prime\prime_{\alpha }(x)\vert dx =\gamma _{ 3} <\infty, }$$
(26)
$$\displaystyle{ \mbox{ For each $\alpha $, $\phi _{\alpha }(x)$ is an even function of $x$, that is}\quad \phi _{\alpha }(-x) =\phi _{\alpha }(x). }$$
(27)

Examples Suppose ϕ(z) is a function that satisfies the hypothesis of Theorem 10 or one of the examples mentioned in the first paragraph of this subsection. If ϕ α (x) = ϕ(αx) when restricted to the real axis, z = x, then the family {ϕ α (x)} satisfies all the desired properties.

Analogous examples can be constructed when ϕ(x) is any twice continuously differentiable even function that together with its derivatives decay sufficiently rapidly as x tends to ∞.

Of course such families need not consist of dilates of one function.

Theorem 12.

Suppose f(z) is a convergent cardinal sine series. Then for each α the series

$$\displaystyle{ f_{\alpha }(x) =\sum _{ n=-\infty }^{\infty }f(n)\frac{\sin \pi (x - n)} {\pi (x - n)}\phi _{\alpha }(x - n) }$$
(28)

converges absolutely and uniformly on compact subsets of \(\mathbb{R}\) and

$$\displaystyle{ \lim _{\alpha \rightarrow 0}f_{\alpha }(x) = f(x)\quad \mathit{\mbox{ uniformly on compact subsets of $\mathbb{R}$.}} }$$
(29)

Theorem 12 implies that the summability method suggested by (28) and (29) is regular. Of course generally (29) is valid for a much wider class of functions in E π than the class of convergent cardinal sine series. Sufficient conditions for (29) to be valid usually depend on the f(z) and the decay properties of the individual members of the family {ϕ α (x)}, such as those available in Theorem 15 in the next section. However, a more comprehensive discussion of such results is beyond the scope of this article.

4 Spline Type Sampling Series

4.1 Basic Setup

The class \(\mathcal{S}_{k}\) of cardinal splines of order 2k with knots at the integers and of no greater than polynomial growth consists of functions s(x) with the following properties:

  1. (i)

    s(x) is in \(C^{2k-2}(\mathbb{R})\)

  2. (ii)

    In each interval n ≤ x ≤ n + 1, n = 0, ±1, ±2, … , s(x) is a polynomial of degree ≤ 2k − 1.

  3. (iii)

    s(x) has no greater than polynomial growth as x → ±∞. In other words, | s k (x) | ≤ C(1 + | x | )m where C and m are constants independent of x.

Such splines are uniquely determined by their values on the integers. In other words, if s(x) is in \(\mathcal{S}_{k}\) for some k and s(n) = 0 for n = 0, ±1, ±2, … , then s(x) = 0 for all x.

Every spline s(x) in \(\mathcal{S}_{k}\) enjoys the representation

$$\displaystyle{ s(x) =\sum _{ n=-\infty }^{\infty }c_{ n}L_{k}(x - n) }$$
(30)

where c n = s(n) and L k (x) is the fundamental cardinal spline of order 2k that enjoys exponential decay as x → ±∞ and satisfies

$$\displaystyle{ L_{k}(n) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\mbox{ when $n = 0$}\\ 0\quad &\mbox{ when $n = \pm 1,\pm 2,\ldots \;$.} \end{array} \right. }$$
(31)

The spline defined by the sampling series (30) is said to interpolate the sequence of values {c n }. For convenient reference, we use the notation s k ({c n }, x) to denote it.

It has been known for some time that for certain classes of function f(z) in E π

$$\displaystyle{\lim _{k\rightarrow \infty }s_{k}(\{f(n)\},x) = f(x)\quad \mbox{ for all real $x$.}}$$

In particular,

$$\displaystyle{ \lim _{k\rightarrow \infty }L_{k}(x) = \frac{\sin \pi x} {\pi x} }$$
(32)

Schoenberg’s cardinal spline summability method [61, Definition 2, p. 106] is a natural consequence of these results and the exponential decay of L k (x). However the question of regularity has been settled only recently.

4.2 Regularity and More

The proof of regularity of the spline summability method consists of re-expressing (30) as

$$\displaystyle{ s_{k}(\{c_{n}\},x) =\sum _{ n=-\infty }^{\infty }c_{ n}\frac{\sin \pi x} {\pi x}Q_{k}(x) }$$
(33)

where for each k, k = 1, 2, … , the function Q k (x) is defined by the formula

$$\displaystyle{ Q_{k}(x) = \frac{\pi xL_{k}(x)} {\sin \pi x} \,, }$$
(34)

and showing that, the family \(\{\phi _{\alpha }(x):\,\alpha \in \mathcal{I}\}\) with \(\mathcal{I} = 1,1/2,1/3,\ldots \;\), α = 1∕k, and ϕ α (x) = Q k (x) satisfies the hypothesis of Theorem 1.

Theorem 13.

The function Q k (x) is well defined by (34) and if ϕ α (x) = Q k (x) with α = 1∕k then the family \(\{\phi _{\alpha }(x):\,\alpha \in \mathcal{I}\}\) with \(\mathcal{I} = 1,1/2,1/3,\ldots \;\) enjoys properties (22)- (27). Furthermore,

$$\displaystyle{ Q_{k}(0) = 1\,, }$$
(35)

there are positive constants, A k and a k , independent of x such that

$$\displaystyle{ \vert Q_{k}(x)\vert \leq A_{k}e^{-a_{k}\vert x\vert }\,, }$$
(36)
$$\displaystyle{ \sup _{x\in \mathbb{R}}\vert Q_{k}\prime(x)\vert \leq \frac{C} {k} \,, }$$
(37)

and

$$\displaystyle{ \sup _{x}\sum _{-\infty }^{\infty }\vert Q_{ k}(x - n)\vert ^{2} \leq C\,k\;. }$$
(38)

The constants C are independent of k.

In view of (33) the following regularity result for Schoenberg’s spline summability method is a corollary of Theorems 12 and 13.

Theorem 14.

Suppose f(z) is a convergent cardinal sine series. Then

$$\displaystyle{\lim _{k\rightarrow \infty }s_{k}(\{f(n)\},x) = f(x)\quad \mathit{\mbox{ uniformly on compact subsets of $\mathbb{R}$. }}}$$

The additional properties (35)– (38) give rise to further convergence results. For example, the exponential decay (36) implies that s k ({c n }, x) is well defined for any sequence of samples {c n } of no greater than polynomial growth for every k and leads to the following:

Theorem 15.

If f(z) is in E σ for some σ < π then

$$\displaystyle{\lim _{k\rightarrow \infty }s_{k}(\{f(n)\},x) = f(x)\quad \mathit{\mbox{ uniformly on compact subsets of $\mathbb{R}$. }}}$$

4.3 Generalizations

Sampling series that are in some sense analogous to (30) can be associated with various so-called shift invariant subspaces with one generator. These are spaces of functions s(x) of the form

$$\displaystyle{s(x) =\sum _{ n=-\infty }^{\infty }a_{ n}g(x - n)\;.}$$

Roughly speaking, these are spaces that consist of linear combinations of integer shifts of one function, that may be viewed as the generator; in the case that the generator is g(x), we denote and refer to the corresponding space as V (g).

Suppose the Fourier transform \(\widehat{g}(\xi )\) of g(x) decays sufficiently rapidly so that

$$\displaystyle{\widehat{G}(\xi ) = \frac{\widehat{g}(\xi )} {\sum _{n=\infty }^{\infty }\widehat{g}(\xi +2\pi n)}}$$

is well defined and its inverse Fourier transform G(x) is a continuous function. Then G(x) satisfies

$$\displaystyle{ G(n) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\mbox{ when $n = 0$}\\ 0\quad &\mbox{ when $n = \pm 1,\pm 2,\ldots \;$.} \end{array} \right. }$$
(39)

and is a member of V (g). The function G(x) is often referred to as a fundamental function of interpolation. In this case s(x) may be represented by the sampling series

$$\displaystyle{s(x) =\sum _{ -\infty }^{\infty }s(n)G(x - n)\;.}$$

If {g k (x): k = 1, 2, …} is a family of such generators and {G k (x): k = 1, 2, …} is the corresponding sequence of fundamental functions, then for every k

$$\displaystyle{ \sum _{-\infty }^{\infty }c_{ n}G_{k}(x - n) }$$
(40)

is a function in V (g k ). If {c n } is a fixed sequence then, as in the case of classical piecewise polynomial cardinal splines, one may ask what happens to (40) as k tends to ∞. The answer depends on the generators and the sequence of samples {c n }.

Examples: In what follows f ∗ g(x) denotes the convolution of f(x) and g(x),

$$\displaystyle{f {\ast} g(x) =\int _{ -\infty }^{\infty }f(x - y)g(y)dy.}$$

4.3.1 Successive Convolutions

Suppose g(x) is a function that is a tempered distribution such that \(\widehat{g}(\xi ) = p(\xi )h(\xi )\) where p(ξ) is 2π periodic and let g k (x) be the k-fold convolution

$$\displaystyle{g_{k}(x) =\mathop{\underbrace{ g {\ast}\cdots {\ast} g}}\limits _{k}(x)\;.}$$

(The function g k (x) can also be defined inductively as g 1(x) = g(x) and for k > 1, g k (x) = g ∗ g k−1(x).) Then

$$\displaystyle{\sum _{n=-\infty }^{\infty }\widehat{g}_{ k}(\xi -2\pi n) ={\bigl ( p(\xi )\bigr )}^{k}\sum _{ n=-\infty }^{\infty }{\bigl (h(\xi -2\pi n)\bigr )}^{k}}$$

and

$$\displaystyle{\widehat{G}_{k}(\xi ) = \frac{{\bigl (h(\xi )\bigr )}^{k}} {\sum _{n=-\infty }^{\infty }{\bigl (h(\xi -2\pi n)\bigr )}^{k}}\;.}$$

The last expression for \(\widehat{G}_{k}(\xi )\) suggests that the role of h(ξ) is critical in determining the behavior of (40) while p(ξ) can essentially be ignored.

We consider several examples of this scenario.

4.3.2 A Convenient Form

Using the notation established in 4.3.1 above, suppose that h(ξ) is a non-negative, strictly decreasing function of | ξ | that is integrable away from the origin; in other words, h(ξ) ≥ 0, h(ξ 1) > h(ξ 2) when | ξ 1 | < | ξ 2 |, and ∫ | ξ | > ε h(ξ)dξ is finite for every positive ε. It follows that h(ξ) is bounded away from the origin and

$$\displaystyle\begin{array}{rcl} & & \int _{\epsilon <\vert \xi \vert \leq \pi }\sum _{n=-\infty }^{\infty }{\bigl (h(\xi -2\pi n)\bigr )}^{k}d\xi =\sum _{ n=-\infty }^{\infty }\int _{ \epsilon <\vert \xi -2\pi n\vert \leq \pi }{\bigl (h(\xi )\bigr )}^{k}d\xi {}\\ & & \phantom{sgflsgdgsankarglfgfdgjh} \leq \int _{\vert \xi \vert>\epsilon }{\bigl (h(\xi )\bigr )}^{k}d\xi \leq {\bigl ( h(\epsilon )\bigr )}^{k-1}\int _{ \vert \xi \vert>\epsilon }h(\xi )d\xi <\infty. {}\\ \end{array}$$

Hence \(\sum _{n=-\infty }^{\infty }{\bigl (h(\xi -2\pi n)\bigr )}^{k}\) is a 2π periodic function that is integrable away from integer multiples of 2π. Assume that h(ξ) > 0 for | ξ | ≤ π. Then

$$\displaystyle{0 \leq \frac{{\bigl (h(\xi )\bigr )}^{k}} {\sum _{n=-\infty }^{\infty }{\bigl (h(\xi -2\pi n)\bigr )}^{k}} \leq 1}$$

and for n = ±1, ±2…

$$\displaystyle{\frac{h(\xi -2\pi n)} {h(\xi )} \quad \text{is}\quad \left \{\begin{array}{@{}l@{\quad }l@{}} <1\quad &\mbox{ if $\vert \xi \vert <\pi $,} \\ = 1\quad &\mbox{ if $\xi =\pi $ and $n = 1$ or $\xi = -\pi $ and $n = -1$,} \\> 1\quad &\text{otherwise.}\end{array} \right.}$$

In view of the fact that \(\widehat{G}_{k}(\xi )\) can be re-expressed as

$$\displaystyle{\widehat{G}_{k}(\xi ) = \left \{1 +\sum _{ _{n\neq 0}^{n=-\infty }}^{\infty }\left (\frac{h(\xi -2\pi n)} {h(\xi )} \right )^{k}\right \}^{-1}}$$

it follows that

$$\displaystyle{\lim _{k\rightarrow \infty }\widehat{G}_{k}(\xi ) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1 \quad &\mbox{ if $\xi \vert <\pi $,} \\ 1/2\quad &\mbox{ if $\xi \vert =\pi $,} \\ 0 \quad &\mbox{ if $\vert \xi \vert>\pi $.} \end{array} \right.}$$

We may conclude that

$$\displaystyle{\lim _{k\rightarrow \infty }G_{k}(x) = \frac{\sin \pi x} {\pi x}}$$

and that, with an appropriate sequence of samples {c n }, (40) converges to a function f(x) in E π .

Specific examples of this include the following:

4.3.2.1 Cardinal splines

Let

$$\displaystyle{g(x) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1 -\vert x\vert \quad &\mbox{ if $\vert x\vert \leq 1$}\\ 0 \quad &\mbox{ if $\vert x\vert> 1$,} \end{array} \right.}$$

whose Fourier transform is

$$\displaystyle{\widehat{g}(\xi ) = \frac{\sin \xi /2)} {\xi /2}.}$$

The Fourier transform of g k (x) is

$$\displaystyle{\widehat{g}_{k}(\xi ) = \left \{\frac{\sin (\xi /2)} {\xi /2} \right \}^{2k}\;.}$$

The Fourier transform of G k (x) is

$$\displaystyle{\widehat{G}_{k}(\xi ) = \frac{\xi ^{-2k}} {\sum _{n=-\infty }^{\infty }(\xi +2\pi n)^{-2k}}\;.}$$

The shift invariant subspace V (g k ) is essentially \(\mathcal{S}_{k}\), the class of cardinal splines of order 2k with knots at the integers, and some answers to the question raised after expression (40) can be found in Subsection 4.2. The generators g k (x) are known as B-splines [61] and G k (x) = L k (x) are the fundamental cardinal splines in \(\mathcal{S}_{k}\).

4.3.2.2 Gaussians

The Gaussian \(g(x) = e^{-x^{2} }\) is a classic example of the scenario described in 4.3.2 above. Its Fourier transform is

$$\displaystyle{\widehat{g}(\xi ) = \sqrt{\pi }e^{-(\xi /2)^{2} }.}$$

If we take \(p(\xi ) = \sqrt{\pi }\), then \(h(\xi ) = e^{-(\xi /2)^{2} }\) and

$$\displaystyle{{\bigl (h(\xi )\bigr )}^{k} = e^{-k(\xi /2)^{2} }.}$$

So the fundamental functions G k (x) follows the pattern described in 4.3.2. We will have more to say about this generator g(x) in 4.3.4 below.

4.3.2.3 Multiquadrics

The so-called multiquadric \(q(x) = \sqrt{1 + x^{2}}\) is a popular generator that does not decay as x tends to ±∞. However, if, following the example of piecewise polynomial splines, we make use of a difference, a symmetric fourth order difference in this case, we get

$$\displaystyle{g(x) = q(x - 2) - 4q(x - 1) + 6q(x) - 4q(x + 1) + q(x + 2)}$$

that is even and O( | x |−3) as x tends to ±∞. This generator is integrable so that as a k fold convolution g k (x) makes sense. The Fourier transform is

$$\displaystyle{\widehat{g}(\xi ) = \frac{-2(2\sin \xi )^{4}} {\vert \xi \vert } K_{1}(\vert \xi \vert )}$$

where K 1(z) is the modified Bessel function of the second kind, [11, 70]. Taking

$$\displaystyle{p(\xi ) = -2(2\sin \xi )^{4}\quad \text{and}\quad h(\xi ) = \frac{K_{1}(\vert \xi \vert )} {\vert \xi \vert } }$$

and using the representation

$$\displaystyle{K_{1}(r) = c\,r\int _{1}^{\infty }e^{-rt}(t^{2} - 1)^{1/2}dt,}$$

see [1, Formula 9.6.23, p. 376], it follows that h(ξ) is a strictly decreasing function of | ξ |. Hence this generator and corresponding fundamental functions G k (x) follow the pattern outlined in 4.3.2 above.

4.3.3 Other Forms

If the Fourier transform of g(x) cannot be expressed as p(ξ)h(ξ) with a 2π periodic p(ξ) and a function h(ξ) that is a decreasing function of | ξ | and is integrable away from the origin then, as outlined in 4.3.1, the fundamental functions G k (x) need not exist and, if they do, their behavior can vary depending on the nature of g(x) and, as illustrated by the observations found in [21], can lead to interesting and unexpected results. However, we do not consider such generators here.

4.3.4 Dilations

Another method of producing a family of generators g k (x) from g(x) is by dilation; namely, set

$$\displaystyle{g_{k}(x) = g(x/k).}$$

Of course, this naturally leads to the use of a continuous parameter. But, since that does not change the final outcome in any meaningful way, we’ll stick with the discrete parameter k, k = 1, 2, … .

The Fourier transform of g k (x) is

$$\displaystyle{\widehat{g}_{k}(\xi ) = k\,\widehat{g}(k\xi ).}$$

So, if Fourier transform of g(x) has the same form as that considered in 4.3.2, namely \(\widehat{g}(\xi ) = p(\xi )h(\xi )\) where p(ξ) is 2π periodic, etc., then kp(kξ) is still 2π periodic and hence

$$\displaystyle{\widehat{G}_{k}(\xi ) = \frac{h(k\xi ))} {\sum _{n=-\infty }^{\infty }h{\bigl (k(\xi -2\pi n)\bigr )}}\;.}$$

This leads to results that are somewhat different from those in 4.3.2.

4.3.4.1 Splines

We first consider the spline example in 4.3.2 where h(ξ) = 1∕ξ 2.

Since h(kξ) = k −2 h(ξ) = k −2 ξ −2, eliminating the factor k −2 from the top and bottom of the ratio of functions that define \(\widehat{G}_{k}(\xi )\) yields

$$\displaystyle{\widehat{G}_{k}(\xi ) = \frac{\xi ^{-2}} {\sum _{n=-\infty }^{\infty }(\xi -2\pi n)^{-2}} = \frac{\xi ^{-2}}{\bigl(\csc (\xi /2)\bigr)^{2}/4} = \left \{\frac{2\sin (\xi /2)} {\xi } \right \}^{2}.}$$

Hence,

$$\displaystyle{G_{k}(x) = g(x)\quad \mbox{ for $k = 1,2,\ldots \;$.}}$$

In other words, V (g k ) = V (g) for all k and all the spaces are equal to \(\mathcal{S}_{1}\).

An analogous conclusion is valid whenever g(x) is such that h(ξ) in the product representation \(\widehat{g}(\xi ) = p(\xi )h(\xi )\) can be chosen to be a homogeneous function.

4.3.4.2 Gaussians

If g(x) is the same Gaussian \(g(x) = e^{-x^{2} }\) as in 4.3.2, then \(h(k\xi ) = e^{-k^{2}(\xi /2)^{2} }\) and

$$\displaystyle{\widehat{G}_{k}(\xi ) = \frac{e^{-k^{2}(\xi /2)^{2} }} {\sum _{n=-\infty }^{\infty }e^{-k^{2}{\bigl ((\xi -2\pi n)/2\bigr )}^{2} }}.}$$

Hence, in this case G k (x), k = 1, 2, … , is a subsequence of the one in the case of the Gaussian in 4.3.3 and we may conclude that

$$\displaystyle{\lim _{k\rightarrow \infty }G_{k}(x) = \frac{\sin \pi x} {\pi x}.}$$
4.3.4.3 Multiquadrics

Suppose g(x) is the multiquadric, as 4.3.2. In this case, the fundamental functions G k (x) are significantly different from those defined via successive convolutions. Nevertheless, the exponential decay of the modified Bessel function K 1( | ξ | ) described by [1, Item 9.7.2, p. 378] leads to the conclusion that \(\lim _{k\rightarrow \infty }G_{k}(x) = \frac{\sin \pi x} {\pi x}\).

4.3.4.4 Remark

These examples give a sampling of the sort of behavior that can be expected when the family of generators g k (x) is derived from dilates of one function. Conditions on g(x) that imply that the G k (x) converge as k tends to ∞ have been formulated in [37, 38].

4.3.5 Other Schemes

There are other schemes for producing families of generators g k . For instance, appropriate differences of (1 + x 2)k−1∕2 result in a family reminiscent of the piecewise polynomial B-splines.

It should not go unmentioned that the scaling functions associated with various masks, scaling sequences, or subdivision algorithms give rise to important schemes for producing families of generators. However, the subject is far too rich and extensive to be given a brief treatment here that is adequate enough to be meaningful. The literature on the subject is vast; [19, Sec 6.5] or [18] provide a reasonably succinct summary of what is being referred to.

5 Appendix

5.1 Sampling Rates and the Paley-Wiener Theorem

There is a significant amount of literature involving varying sampling rates, often concerning bounds on the error between a continuous f(t), that is not necessarily frequency band limited, and its sampling series. Examples include [13, 16, 33–36, 52, 53, 60, 66].

A precise statement and proof of the distributional version of the Paley-Wiener Theorem can be found in [22] or [31].

5.2 Cardinal Sine Series

Succinct and accessible accounts can be found in [29] and [32].

Formulations and proofs of Theorems 1-8 can be found in [3–5]. Proofs of the corollary to Theorem 8 that don’t make use of Theorem 8 can be found in [3] and [44]; as can be expected, those arguments are more involved.

Properties of functions in E π that are also in \(L^{p}(\mathbb{R})\) on the real axis can be found in [43, 61, 63].

The entire function

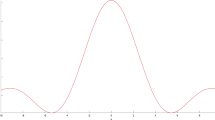
$$\displaystyle{ f(z) = \frac{\sin \pi z} {\pi } \sum _{n=2}^{\infty }\frac{1} {\log n}\, \frac{2z^{2}} {n(z^{2} - n^{2})} }$$
(41)

is an example of a member of E π with the property that for integers n, lim n → ±∞ f(n) = 0, and that fails to be a convergent cardinal sine series. In view of Theorem 3 on the real axis limsup x → ∞ | f(x) | > 0. Below are two plots of the graph of y = f(x): one with 0 ≤ x ≤ 30, the other with 1600 ≤ x ≤ 1630 (Figures 1 and 2).

Fig. 1
figure 1

Plot of y = f(x) in the range 0 ≤ x ≤ 30 where the sampling points (n, f(n)), n = 0, 1, …, 30, are indicated. The values f(x) are defined by (41).

Full size image
Fig. 2
figure 2

Plot of y = f(x) in the range 1600 ≤ x ≤ 1630 where the sampling points (n, f(n)), n = 1600, 1601, …, 1630, are indicated. The values f(x) are defined by (41). The dashed line is a plot of y = log(log(x)) − 1. 5. Note that the vertical scale in Fig. 2 is not the same as that in Fig. 1.

Full size image

For an example of an entire function f(z) in E π that is bounded and such that lim ε → 0 f ε (z) fails to exist for non-integer z see [8].

5.3 Regularization of Cardinal Sine Series

The regularization or summability of cardinal sine series has been treated in many works, including [13, 16, 23, 38, 52, 53, 60, 67, 73].

The Bernstein-Boas formula has also been adapted to irregular sampling, for example, [26, 43].

Plots of the function f(z) defined by (16) that is the subject of Theorem 11 can be found in [44].

5.4 Splines

In addition to [61], basic information on piecewise polynomial splines can be found in [20, 65]. The details to some of the limit theorems alluded to in [61] can be found in [62–64].

The class \(\mathcal{S}_{k}\) of cardinal splines of order 2k with knots at the integers can be defined more succinctly, with some abuse of notation, as the class of tempered distributions s(x) that satisfy

$$\displaystyle{s^{(2k)}(x) =\sum _{ n=-\infty }^{\infty }a_{ k}\delta (x - k),}$$

where {a n } is a sequence of coefficients and δ(x) is the unit Dirac measure at the origin, [46].

Proofs of Theorems 13 and 14 can be found in [45].

A formulation and proof of Theorem 15 that includes the convergence of the derivatives was originally recorded in [54]. A proof of the theorem, that is also valid in the case of more than one variable, can be found in [42].

5.5 Generalizations

Extensions of splines and sampling series to irregular samples can be found, for example, in [37, 40, 41, 43, 59].

The multiquadric, namely the function \(\phi (x) = \sqrt{1 + x^{2}}\) and its higher dimensional analogues, was introduced in geodesy and christened by Rolland L. Hardy, [28]. The study and use of its shifts in approximation and interpolation applications was apparently popularized by Richard Franke’s numerical study [27].

The dilates of the Gaussian and multiquadric have been thoroughly studied in, among others, [11, 38, 55–58, 70]. The so-called radial basis functions [11, 70] are yet another source of generators with a literature that is quite large. The term “shape parameter” in works on the subject often refers to a dilation parameter.

Extensions of sampling series to higher dimensions and various manifolds can be found in, among others, [2, 9, 11, 24, 25, 37, 47–51, 70].