Supervoxel-Based Segmentation of 3D Volumetric Images

Abstract

While computer vision has made noticeable advances in the state of the art for 2D image segmentation, the same cannot be said for 3D volumetric datasets. In this work, we present a scalable approach to volumetric segmentation. The methodology, driven by supervoxel extraction, combines local and global gradient-based features together to first produce a low level supervoxel graph. Subsequently, an agglomerative approach is used to group supervoxel structures into a segmentation hierarchy with explicitly imposed containment of lower level supervoxels in higher level supervoxels. Comparisons are conducted against state of the art 3D segmentation algorithms. The considered applications are 3D spatial and 2D spatiotemporal segmentation scenarios.

This work is partially supported by AFOSR under FA9550-15-1-0047.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The advent of big data and ease of access to computational resources has led to increasing interest in directly analyzing 3D data instead of merely relying on their 2D image projections. Consequently, 3D supervoxels which are a natural extension to 2D superpixels, play a key role as can be seen in many computer vision applications spanning spatiotemporal video and 3D volumetric datasets. For example, high dimensional data in the form of lightfields, RGBD videos and regular video data, particle-laden turbulent flow data comprising dust storms and snow avalanches and finally 3D medical images like MRIs are avenues for further development and application of 3D supervoxel estimation methods.

The popular ultrametric contour map (UCM) framework [1] has established itself as the state of the art in 2D superpixel segmentation. However, a direct extension of this framework has not been seen in the case of 3D supervoxels. The current popular frameworks in 3D segmentation start by constructing regions based on some kind of agglomerative clustering (graph based or otherwise) of single pixel data. However, the 2D counterparts of these methods on which they are founded are not as accurate as UCM. This is because the UCM algorithm does not begin by grouping pixels into regions. Instead it first computes a high quality boundary map which is subsequently utilized toward obtaining closed regions. The two step process in UCM is carried out by combining boundary organization with pixel clustering which leads to high quality segmentation results in 2D. Therefore, it follows that a natural extension of this two step process in the case of 3D should be a harbinger for success.

UCM derives its power from a combination of local and global cues which complement each other in order to detect highly accurate boundaries. However, all the other methods, with the exception of normalized cuts [2] (which directly obtains regions) are inherently local and do not incorporate global image information. In sharp contrast, UCM includes global image information by estimating eigenfunction scalar fields of graph Laplacians formed from local image features. Despite this inherent advantage, the high computational cost of UCM is a bottleneck in the development of its 3D analog. Recent work in [3] has addressed this issue in 2D by providing an efficient GPU-based implementation but the huge number of voxels involved in the case of spatiotemporal volumes remains an issue. The work in [4] provides an efficient CPU-only implementation by leveraging the structure of the underlying problem and provided a reduced order normalized cuts approach to solve the eigenvector problem. Consequently, this opens up a plausible route to 3D as a reduced order approach effectively solves the same globalization problem but at a fraction of the cost. Therefore, the main work of this paper is threefold: First, we design filters for 3D volumes (either space-time video or volumetric data) which provide local cues at multiple scales and at different orientations akin to the approach in 2D UCM. Second, we introduce a new method called as oriented intervening contour cue which extends the idea of the intervening contour cue in [5] for constructing the graph affinity matrix. Third, we solve the reduced order eigenvector problem by leveraging ideas from the approach in [4]. After this globalization step, the local and global fields are merged to obtain surface boundary fields. Subsequent application of a watershed transform yields supervoxel tessellations (represented as relatively uniform polyhedra that tessellate the region). The next step in this paper is to build a hierarchy of supervoxels. While 2D UCM merges regions based on their boundary strengths in its oriented watershed transform approach, we did not find this approach to work well in 3D. Instead, to obtain the supervoxel hierarchy, we follow the approach of [6] which performs a graph-based merging of regions using the method of internal variation [7].

In summary, our approach extends the popular and highly accurate gPb-UCM framework to 3D resulting in a highly scalable framework based on reduced order normalized cuts. To the best of our knowledge, there does not exist a surface detection method in 3D which uses graph Laplacian-based globalization for estimating supervoxels. Further, our results indicate that owing to the deployment of a high quality boundary detector as the initial step, our method maintains a distinction between the foreground and background regions by not causing unnecessary oversegmentation of the background at the lower levels of hierarchy.

Road map: The next section describes the related work on 2D and 3D segmentation which influenced our work. Section 3 describes how we extract supervoxels by extending the 2D gPb-UCM framework. Section 4 evaluates the proposed approach and other state of the art supervoxel methods on two different types of 3D volumetric datasets both qualitatively and quantitatively. Section 5 concludes by summarizing our contributions and also discusses the scope for future work. Throughout the paper, we use the term pixel and voxel interchangeably when referring to the basic “atom” of 2D/3D images.

2 Related Work

Normalized Cuts and gPb- UCM: Normalized cuts [2] gained immense popularity in 2D image segmentation by treating the image as a graph and computing hard partitions. The gPb-UCM framework [1] leveraged this approach in a soft manner to introduce globalization into their contour detection process. This led to a drastic reduction in the oversegmentation arising out of gradual texture or brightness changes in the previous approaches. Being a computationally expensive method, the last decade saw the emergence of several techniques to speed up the underlying spectral decomposition process in [1]. These techniques range from various optimization techniques like multilevel solvers [8, 9], to systems implementations exploiting GPU parallelism [3], and to approximate methods like reduced order normalized cuts [4, 10].

3D Volumetric Image Segmentation: Segmentation techniques applied to 3D volumetric images can be found in the literature of medical imaging (usually MRI) and 2D+time video sequence segmentation. In 3D medical image segmentation, unsupervised techniques like region growing [11] have been well studied. In [12], normalized cuts were applied to MRIs but gained little attention. Recent literature mostly focuses on supervised techniques [13, 14]. In video segmentation, there are two streams of works. On one hand, [15,16,17,18] are frame based that rely on segmenting each frame into superpixels in the first place. Therefore they are not applicable to general 3D volumes. On the other hand, a variety of other methods treat the video sequences as spatiotemporal volumes and try to segment them into supervoxels. Those methods are mostly extensions of popular 2D image segmentation approaches, including graph cuts [19, 20], SLIC [21], mean shift [22], graph-based methods [6] and normalized cuts [9, 23]. Besides these, temporal superpixels [24,25,26] are another set of effective approaches that extract high quality spatiotemporal volumes. A comprehensive review of supervoxel methods can be found in [27, 28]. All of this development in the area of 3D supervoxels has led to a general consensus in the video segmentation community that supervoxels have favorable properties which can be leveraged later in the pipeline. These characteristics include: (i) supervoxel boundaries should stick to the meaningful image boundaries; (ii) regions within one supervoxel should be homogeneous while inter-supervoxel differences should be substantially large; (iii) it’s important that supervoxels have regular topologies; (iv) a hierarchy of supervoxels is favorable as different applications have different supervoxel granularity preferences.

3 Supervoxel Extraction

Our work is a natural extension of the state of the art 2D superpixel method, the gPb-Ultrametric Contour Map framework (gPb-UCM) [1], henceforth referred to as 3D-UCM. The 2D gPb-UCM framework consists of three major parts: image gradient features detection, globalization and agglomeration. Analogously, the workflow in the 3D-UCM framework presented here is volume gradient features detection, globalization and supervoxel agglomeration. However, the voxel cardinality of 3D volumetric images far exceeds their 2D counterparts. Therefore, certain computational considerations force us to adopt reduced order eigensystem solvers. These approximations will become clear as we proceed. The upside is that the 3D-UCM algorithm becomes scalable to handle sizable datasets.

3.1 Volume Gradient Features Detection

We first require an edge detector to help quantify the presence of boundary-surfaces. Most gradient-based edge detectors in 2D [29, 30] can be extended to 3D for this purpose. We based our 3D edge detector on the mPb detector proposed in [1, 31] which has been empirically shown to have superior performance in 2D.

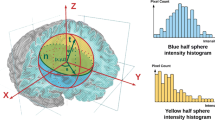
The building block of the 3D mPb gradient detector is an oriented gradient operator $G(x,y,z,\theta ,\varphi ,r)$ that is described in detail in Fig. 1. To be more specific, in a 3D volumetric intensity image, we place a sphere centered at each pixel to denote its neighborhood. An equatorial plane specified by its normal vector $\varvec{t}(\theta ,\varphi )$ splits the sphere into two half spheres. We compute the intensity histograms for both half spheres as $\mathbf {g}$ and $\mathbf {h}$. Then we define the gradient magnitude in the direction $\varvec{t}(\theta ,\varphi )$ as the $\chi ^{2}$ distance between g and h:

$$\begin{aligned} \chi ^{2}(\mathbf {g},\mathbf {h})=\frac{1}{2}\sum _{i}\frac{(g(i)-h(i))^{2}}{g(i)+h(i)}. \end{aligned}$$

(1)

In order to capture gradient information at multiple scales, this gradient value is calculated at different radius values r of the neighborhood sphere. Gradients obtained from different scales are then linearly combined together using

$$\begin{aligned} G(x,y,z,\theta ,\varphi )=\sum _{r}\alpha _{r}G(x,y,z,\theta ,\varphi ,r) \end{aligned}$$

(2)

where $\alpha _{r}$ weighs the gradient contribution at different scales. For multi-channel 3D images like video sequences, $G(x,y,z,\theta ,\varphi )$ are calculated separately from different channels and summed up using equal weights. Finally, the measure of boundary strength at (x, y, z) is computed as the maximum response among various directions $\varvec{t}(\theta ,\varphi )$:

$$\begin{aligned} mPb(x,y,z)=\max _{\theta ,\varphi }G(x,y,z,\theta ,\varphi ). \end{aligned}$$

(3)

In our experiments, $\theta$ and $\varphi$ take values in $\{0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4}\}$ and $\{-\frac{\pi }{4},0,\frac{\pi }{4}\}$ respectively and in one special case, $\varphi =\frac{\pi }{2}$. Therefore we compute local gradients in 13 different directions. Neighborhood values of 2, 4 and 6 voxels were used for r. Equal weights $\alpha _{r}$ were used to combine gradients from different scales. Also, as is standard, we always apply an isotropic Gaussian smoothing filter with $\sigma =3$ voxels before any gradient operation.

Fig. 1.

The oriented gradient operator $G(x,y,z,\theta ,\varphi ,r)$: At location (x, y, z), the local neighborhood is defined by a sphere with radius r. An equatorial plane $\varvec{n}$ (shaded green) along with its normal vector $\varvec{t}$ splits the sphere into two half spheres. The one above $\varvec{n}$ is shaded yellow and the one below is shaded blue. We histogram the intensity values of voxels that fall in the yellow and blue half spheres respectively. Finally we calculate the $\chi ^{2}$ distance between the yellow and blue histograms as the local gradient magnitude in the direction $\varvec{t}$ of scale r (Color figure online).

3.2 Globalization

The core aspect of the gPb-UCM algorithms is spectral clustering. It globalizes the local cues obtained from the gradient features detection phase and specifically focuses on the most salient boundaries in the image by analyzing the eigenvectors derived from the normalized cuts problem [2]. However, this approach depends on solving a sparse eigensystem at the scale of the number of pixels in the image. Thus as the size of the image grows large, the globalization step becomes the computational bottleneck of the whole process. This problem is even more severe in the 3D setting because the voxel cardinality far exceeds the pixel cardinality of our 2D counterparts. An efficient approach was proposed in [4] to reduce the size of the eigensystem while maintaining the quality of the eigenvectors used in globalization. We generalize this method to 3D so that our approach becomes scalable to handle sizable datasets.

In the following, we describe the globalization steps: (i) graph construction and oriented intervening contour cue, (ii) reduced order normalized cuts and eigenvector computation, (iii) scale-space gradient computation on the eigenvector image and (iv) the combination of local and global gradient information.

Fig. 2.

Left: Suppose we want to calculate the affinity value between voxels A and B. C is the voxel with maximal mPb value that lies on the line segment $\bar{AB}$. In the upper left case, A and B belong to one region. In the lower left case, A and B are in two different regions. But the intervening contour cue of UCM [1] gives the same affinity value in both cases, which is not very satisfactory. Obviously it would be better if we consider the direction $\varvec{t}$ of C’s mPb. Right: In our oriented intervening contour cue approach, when calculating affinity values, we always take the product of mPb(C) with the absolute value of the inner product $\langle \varvec{t},\varvec{n}\rangle$, where $\varvec{n}$ is the unit direction vector of line segment $\bar{AB}$. If A and B are on different sides of a boundary surface, $|\langle \varvec{t},\varvec{n}\rangle |$ will be large, leading to small affinity value and vice-versa.

Graph Construction and Oriented Intervening Contour Cue: In 2D, spectral clustering begins from a sparse graph obtained by connecting pixels that are spatially close to each other. gPb-UCM [1] constructs a sparse symmetric affinity matrix W using the intervening contour cue [5] that is the maximal value of mPb along a line connecting two pixels. However, this approach doesn’t utilize all the useful information obtained from the previous gradient features detection step. Figure 2 describes a potential problem and how we deal with it. To improve the accuracy of the affinity matrix, we take the direction vector of the maximum gradient magnitude into consideration when calculating the pixel-wise affinity value. We call this new variant as oriented intervening contour cue. For any spatially close voxels i and j, we use $\bar{ij}$ to denote the line segment connecting i and j. $\varvec{d}$ is defined as the unit direction vector of $\bar{ij}$. Assume P is a set of voxels that lie close to $\bar{ij}$. For any $p\in P$, $\varvec{n}$ is the unit direction vector associated with its mPb value. We define the affinity value $W_{ij}$ between i and j as follows:

$$\begin{aligned} W_{ij}=\exp (-\max _{p}\{mPb(p)|\langle \varvec{d},\varvec{n}\rangle |\}/\rho ) \end{aligned}$$

(4)

where $\langle \rangle$ is the inner product operator of the vector space and $\rho$ is a scaling constant. In our experiments, P contains the voxels that are at most 1 voxel away from $\bar{ij}$. $\rho$ is set to 0.1. In the affinity matrix W, each voxel is connected to voxels that fall in the $5\times 5$ cube centered at that voxel. So the graph defined by W is very sparse.

Reduced Order Normalized Cuts and Eigenvector Computation: At this point, the standard 2D gPb-UCM solves for the generalized eigenvectors of the sparse eigensystem

$$\begin{aligned} (D-W)\varvec{v}=\lambda D\varvec{v} \end{aligned}$$

(5)

where D is a diagonal matrix defined by $D_{ii}=\varSigma _{j}W_{ij}$. However, solving this eigenvalue problem is very computationally intensive. It becomes the bottleneck, both in time and memory efficiency, of the normalized cuts segmentation algorithms. To overcome this, an efficient and highly parallel GPU implementation was provided in [3]. However, this approach requires us to use GPU-based hardware and software suites—an unnecessary restriction. A clever alternative in [4, 10] builds the graph on superpixels instead of pixels to reduce the size of the eigensystem. We chose to generalize [4]’s approach to 3D as (i) the superpixel solution is more scalable than the GPU solution in terms of memory requirements, (ii) specialized GPU co-processors are not commonly available in many computing platforms like smart phones and wearable devices, and (iii) the approach in [10] is specifically designed for superpixels in each frame in video segmentation, thus not easily generalizable. Finally, the approach in [4] constructs a reduced order normalized cuts system which is easier to solve. The reduced order eigensystem is denoted by

$$\begin{aligned} (L^{T}(D-W)L)\varvec{x}=\lambda 'L^{T}DL\varvec{x} \end{aligned}$$

(6)

where $L\in \mathbb {R}^{m\times n},\varvec{x}\in \mathbb {R}^{m}$ and $L\varvec{x}=\varvec{v}$. The purpose of L is to assign each pixel to a superpixel/supervoxel. In our approach, the supervoxels are generated by a watershed transform on the mPb image obtained from the volume gradient features detection step. Obviously the number of supervoxels m is much smaller than the number of voxels n in the whole 3D volumetric image. In practice, there are usually two to three orders reduction in the size of the eigensystem (from millions voxels to a few thousands supervoxels). Therefore it is much more efficient to solve Eq. (6) than Eq. (5).

Fig. 3.

Upper Left: One slice of a brain MRI from the IBSR dataset [32]. Lower Left: One frame of a video sequence from the BuffaloXiph dataset [33]. Right: The corresponding slices/frames of the first 4 eigenvectors.

Scale Space Gradient Computation on the Eigenvector Image: We solve for the generalized eigenvectors $\{\varvec{x_{0}},\varvec{x_{1}},\ldots ,\varvec{x_{n}}\}$ of the system in (6) corresponding to the smallest eigenvalues $\{\lambda '_{0},\lambda '_{1},\ldots ,\lambda '_{n}\}$. As stated in [4], $\lambda _{i}$ in (5) will equal to $\lambda '_{i}$ and $L\varvec{x_{i}}$ will match $\varvec{v_{i}}$ modulo an irrelevant scale factor, where $\varvec{v_{i}}$ are the eigenvectors of the original eigensystem (5). Similar to the 2D scenario [1], eigenvectors $\varvec{v_{i}}$ carry surface information. Figure 3 shows several example eigenvectors obtained from two types of 3D volumetric datasets. In both cases, the eigenvectors distinguish salient aspects of the original image. Based on this observation, we apply the gradient operator mPb defined in (3.1) to the eigenvector images. The outcome of this procedure is denoted as ‘sPb’ because it represents the ‘spectral’ component of the boundary detector, following the convention established in [1]:

$$\begin{aligned} sPb(x,y,z)=\sum _{i=1}^{K}\frac{1}{\sqrt{\lambda _{i}}}mPb_{\varvec{v_{i}}}(x,y,z). \end{aligned}$$

(7)

Note that this weighted summation starts from $i=1$ because $\lambda _{0}$ always equals 0 and $\varvec{v_{0}}$ is a vanilla image. The weighting by $1/\sqrt{\lambda _{i}}$ is inspired by the mass-spring system in mechanics [1, 34]. In our experiments, we use 16 eigenvectors, i.e. $K=16$.

The Combination of Local and Global Gradient Information: The last step is to combine local cues mPb and global cues sPb. mPb tries to capture variations in every corner while sPb aims to obtain salient boundary surfaces. By linearly combining them together, we get a ‘globalized’ boundary detector gPb:

$$\begin{aligned} gPb(x,y,z)=\omega mPb(x,y,z)+(1-\omega )sPb(x,y,z). \end{aligned}$$

(8)

In practice, we use equal weights for mPb and sPb. After obtaining the gPb values, we apply a post-processing step of non-maximum suppression [29] to get thinned boundary surfaces when the resulting edges from mPb are too thick. Figure 4 shows some examples of mPb, sPb and gPb.

Fig. 4.

sPb augments the strength of the most salient boundaries in gPb.

3.3 Supervoxel Agglomeration

At this point, the 2D gPb-UCM algorithm proceeds with the oriented watershed transform (OWT) [1, 35, 36] to create a hierarchical segmentation of the image resulting in the ultrametric contour map. However, we find that the same strategy does not work well in 3D. The reasons are two-fold. First, because of the irregular topologies, it is more difficult to approximate the boundary surfaces with square or triangular meshes in 3D than to approximate the boundary curves with line segments in 2D. Second, in the merging process, following OWT, only the information of the pixels on the boundaries are used when the boundaries between superpixels are greedily removed. This is not a robust design especially considering that in 3D the boundary surfaces are frequently fragmented.

Due to the above considerations, we turn to the popular graph based image and video segmentation methods [6, 7] to create the segmentation hierarchy. We first apply a watershed transform to the gPb strengths obtained from the previous step to get an oversegmentation. Next we iteratively merge the adjacent segments starting from this oversegmentation. The output of this procedure is a segmentation hierarchy represented by a tree-structure whose lower level segments are always contained in higher level segments. As in [6], the merge rules run on a graph. The nodes of the graph are regions. First, for any two adjacent regions $R_{i}$ and $R_{j}$, we assign an edge $e_{ij}$ to connect them on the graph. The weight of $e_{ij}$ is set to the $\chi ^{2}$ distance between Lab space or intensity value histograms of $R_{i}$ and $R_{j}$ with 20 bins used. Also, for any region R, a quantity named the relaxed internal variation $\mathrm {RInt}(R)$ is defined:

$$\begin{aligned} \mathrm {RInt}(R):=\mathrm {Int}(R)+\frac{\tau }{|R|} \end{aligned}$$

(9)

where $\mathrm {Int}(R)$ is defined as the maximum edge weight of its minimum spanning tree (MST). For the lowest level regions, i.e. the regions of oversegmentation obtained from the watershed transform, $\mathrm {Int}(R)$ is set to 0. |R| is the voxel cardinality of region R. $\tau$ is a parameter to trigger the merging process and control the preferred granularity of the regions. In each iteration of merging, all the edges are traversed in ascending order. For any edge $e_{ij}$, we merge incident regions $R_{i}$ and $R_{j}$ if the weight of $e_{ij}$ is less than the minimum of the relaxed internal variation of the two regions. Thus the merging condition is written as

$$\begin{aligned} \mathrm {weight}(e_{ij})<\min \{\mathrm {RInt}(R_{i}),\mathrm {RInt}(R_{j})\}. \end{aligned}$$

(10)

In practice, we increase the granularity parameter $\tau$ by a factor of 1.1 in each iteration. This agglomeration process iteratively progresses until no edge meets the merging criteria. The advantage of graph based methods is that they make use of the information in all voxels in the merged regions. Furthermore, as shown in the experiments below, we see that it overcomes the weakness of fragmented supervoxels of graph based methods. This is because traditional graph based methods are built on voxel-level graphs.

Finally, we obtain a supervoxel hierarchy represented by a bottom-up tree structure. This is the final output of the 3D-UCM algorithm. The granularity of the segmentation is a user driven choice guided by the application.

4 Evaluation

We perform quantitative and qualitative comparisons between 3D-UCM and state of the art supervoxel methods on two different types of 3D volumetric datasets. Datasets and experimental results are presented in this section.

4.1 Experimental Setup

Datasets: The most typical use cases of 3D segmentation are medical images like MRIs and video sequences. We use the publicly available Internet Brain Segmentation Repository (IBSR) [32] for our medical imaging application. It contains 18 volumetric brain MRIs with their white matter, gray matter and cerebro-spinal fluid labeled by human experts. These represent cortical and subcortical structures of interest in neuroanatomy. For video segmentation applications, we use the dataset BuffaloXiph introduced by [33]. The 8 video sequences in the dataset have 69–85 frames and are labeled with semantic pixels. This allows us to examine whether the algorithms have the same perception as humans in the case of 2D+time segmentation.

Methods: A comprehensive comparison of current supervoxel and video segmentation methods is available in [27, 28]. Building on their approach, in our experiments, we will compare 3D-UCM to two state of the art supervoxel methods: (i) hierarchical graph based (GBH) [6] and (ii) segmentation by weighted aggregation (SWA) [8, 9, 37]. GBH is the standard graph based method for video segmentation and SWA is a multilevel normalized cuts solver that also generates a hierarchy of segmentations.

Fig. 5.

The level of segmentation hierarchy is chosen as similar to ground truth granularity. Left: IBSR dataset results. The white, gray and dark gray regions are white matter, gray matter and cerebro-spinal fluid (CSF) respectively. Right: BuffaloXiph dataset results.

Fig. 6.

The hierarchy of segmentation of all three methods of the same skating frame in Fig. 5. The leftmost column is the finest segmentation in each hierarchy.

4.2 Qualitative Comparisons

We present some example slices from both the IBSR and BuffaloXiph datasets in Fig. 5. Even a cursory examination shows us that all the three methods differ markedly in the kind of segmentations they obtain. However, it is hard to say which method performs best when compared to the ground truth. As can be noticed, GBH has a fragmentation problem in both the IBSR and BuffaloXiph datasets. A large number of small fragments of irregular shapes are visible in its results. On the other hand, SWA has a clean segmentation in IBSR but suffers from fragmentation in video sequences. In contrast, 3D-UCM has the most regular segmentation. This difference is clearer if we look at the whole hierarchy. Figure 6 shows the segmentation from fine to coarse of the same skating frame as in Fig. 5. Obviously, GBH and SWA generate unnecessary oversegmentations of the background at finer levels. This is because the first building blocks of the GBH and SWA hierarchies are single voxels. This makes them sensitive to local illumination or intensity value changes. 3D-UCM overcomes this problem by integrating global cues to obtain an initial set of supervoxels which leverage the strength of a high quality boundary detector. Hence, the basic building blocks of our hierarchy are these initial supervoxels and not the elementary voxels. It suffices to say that 3D-UCM generates meaningful and compact supervoxels at all levels of the hierarchy while GBH and SWA have a fragmentation problem at the lower levels.

Fig. 7.

Quantitative measures.

4.3 Quantitative Measures

As both the IBSR and BuffaloXiph datasets are densely labeled, we are able to compare the supervoxels methods on a variety of measures.

Boundary Quality: The precision-recall curve is the most recommended measure and has found widespread use in comparing image segmentation methods [1, 31]. This was introduced into the world of video segmentation in [16]. We use it as the boundary quality measure in our benchmarks. It measures how well the machine generated segments stick to ground truth boundaries. More importantly, it shows the tradeoff between the positive predictive value (precision) and true positive rate (recall). For a set of machine generated boundary pixels $S_{b}$ and human labeled boundary pixels $G_{b}$, precision and recall are defined as follows:

$$\begin{aligned} \mathrm {precision}=\frac{|S_{b}\cap G_{b}|}{|S_{b}|},\quad \mathrm {recall}=\frac{|S_{b}\cap G_{b}|}{|G_{b}|}. \end{aligned}$$

(11)

We show the precision-recall curves on IBSR and BuffaloXiph datasets in Fig. 7a and d respectively. 3D-UCM performs the best on IBSR and is the second best on BuffaloXiph. GBH does not perform well on BuffaloXiph while SWA is worse on IBSR. One limitation of 3D-UCM is that there is an upper limit of its boundary recall because it is based on supervoxels. GBH and SWA can have arbitrarily fine segmentations. Thus they can achieve a recall rate arbitrarily close to 1, though the precision is usually low in these situations.

Region Quality: Measures based on overlaps of regions such as Dice’s coefficients are widely used in evaluating region covering performances of voxelwise segmentation approaches [38, 39]. We use the 3D segmentation accuracy introduced in [27, 28] to measure the average fraction of ground truth segments that is correctly covered by the machine generated supervoxels. Given that $G_{v}=\{g_{1},g_{2},\ldots ,g_{m}\}$ are ground truth volumes, $S_{v}=\{s_{1},s_{2},...,s_{n}\}$ are supervoxels generated by the algorithms and V represents the whole volume, the 3D segmentation accuracy is defined as

$$\begin{aligned} \mathrm {3D\,\,segmentation\,\,accuracy}=\dfrac{1}{m}\sum _{i=1}^{m}\frac{\sum _{j=1}^{n}|s_{j}\cap g_{i}|\times \mathbf 1 (|s_{j}\cap g_{i}|\ge |s_{j}\cap \overline{g}_{i}|)}{|g_{i}|} \end{aligned}$$

(12)

where $\overline{g}_{i}=V\,\backslash \,g_{i}$. We plot the 3D segmentation accuracy against the number of supervoxels in Figs. 7b and e. GBH and SWA again perform differently in IBSR and BuffaloXiph datasets. But 3D-UCM consistently showed the best performance, especially when the number of supervoxels is low.

Supervoxel Compactness: Compact supervoxels of regular shapes are always favored because they benefit further higher level tasks in computer vision. The compactness of superpixels generated by a variety of image segmentation algorithms in 2D was investigated in [40]. It uses a measure inspired by the isoperimetric quotient to measure compactness. We use another quantity defined similarly to specific surface area in material science and biology. In essence, specific surface area and isoperimetric quotient both try to quantify the total surface area per unit mass or volume. Formally, given that $S_{v}=\{s_{1},s_{2},\ldots ,s_{n}\}$ are supervoxels generated by algorithms, the specific surface area to measure supervoxel compactness is defined as

$$\begin{aligned} \mathrm {specific\,\,surface\,\,area}=\dfrac{1}{n}\sum _{i=1}^{n}\frac{\mathrm {Surface}(s_{i})}{\mathrm {Volume}(s_{i})} \end{aligned}$$

(13)

where Surface() and Volume() count voxels on the surfaces and in the supervoxels respectively. Lower values of specific surface area imply more compact supervoxels. The compactness comparisons on IBSR and BuffaloXiph are shown in Figs. 7c and f. We see that 3D-UCM always generates the most compact supervoxels except at small supervoxel granularity on IBSR. GBH does not perform well in this measure because of its fragmentation problem, which is consistent with our qualitative observations.

Our quantitative measures cover boundary quality, region quality and supervoxel compactness that are the most important aspects of supervoxel qualities. 3D-UCM always performs the best or the second best in all measures on both IBSR and BuffaloXiph datasets. In contrast, GBH and SWA fail on some measures. In conclusion, we have empirically shown that 3D-UCM is a very competitive general purpose supervoxel method on 3D volumetric datasets with respect to the proposed measures albeit on a few datasets.

5 Discussion

In this paper, we presented the 3D-UCM supervoxel framework, an extension of the most successful 2D image segmentation technique, gPb-UCM, to 3D. Experimental results show that our approach outperforms the current state of the art in most benchmark measures on two different types of 3D volumetric datasets. Furthermore, we deployed a reduced order normalized cuts technique to overcome a computational bottleneck of the traditional gPb-UCM framework. This immediately allows our method to scale up to large datasets. When we jointly consider supervoxel quality and computational efficiency, we believe that 3D-UCM can become the standard bearer for massive 3D volumetric datasets. We expect applications of 3D-UCM in a wide range of vision tasks, including video semantic understanding, video object tracking and labeling in high-resolution medical imaging, etc.

Since this is a new and fresh approach to 3D segmentation, 3D-UCM still has several limitations from our perspective. First, because it is a general purpose technique, the parameters of 3D-UCM have not been tuned using supervised learning for specific applications. In immediate future work, we plan to follow the metric learning framework as in [1] to deliver higher performance. Second, since it is derived from the modular framework of gPb-UCM, 3D-UCM has numerous alternative algorithmic paths that can be considered. In image and video segmentation, a better boundary detector was proposed in [18], with different graph structures deployed in [17, 41, 42] followed by graph partitioning alternatives in [43, 44]. A careful study of these alternative options may result in improved versions of 3D-UCM going forward. Finally, 3D-UCM at the moment does not incorporate prior knowledge for segmentation [45, 46]. Prior information like object shape and optical flow motion cues could greatly improve segmentation performance. These represent interesting opportunities for future work.