Injection of Extreme Points in Evolutionary Multiobjective Optimization Algorithms

Abstract

This paper investigates a curious case of informed initialization technique to solve difficult multi-objective optimization (MOP) problems. The initial population was injected with non-exact (i.e. approximated) nadir objective vectors, which are the boundary solutions of a Pareto optimal front (PF). The algorithm then successively improves those boundary solutions and utilizes them to generate non-dominated solutions targeted to the vicinity of the PF along the way. The proposed technique was ported to a standard Evolutionary Multi-objective Optimization (EMO) algorithm and tested on a wide variety of benchmark MOP problems. The experimental results suggest that the proposed approach is very helpful in achieving extremely fast convergence, especially if an experimenter’s goal is to find a set of well distributed trade-off solutions within a fix-budgeted solution evaluations (SEs). The proposed approach also ensures a more focused exploration of the underlying search space.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Since the past two decades, the algorithmic techniques to solve multi-objective optimization problems (MOPs) have been developed mainly by the two communities independently. Centrally, by the classical numerical optimization practitioners and also by the Evolutionary Multi-objective Optimization (EMO) community. However, in many occasions, they both address the same problem in two completely different perspectives. For example, a canonical algorithm like Normal Boundary Intersection (NBI) [1] assumes that the bound (i.e. affine subspace of the lowest dimension that contains convex hull of individual minima or $\text {CHIM}_{+}$) of the Pareto-optimal front (PF) is already known, on the other hand, such assumption is not necessary in many standard EMO algorithms [2].

However, bounding/bracketing of the search space is the first step in many classical numerical optimization algorithms [3]. As EMO algorithms are stochastic global search algorithms, they do not require such a measure. Moreover, the concept of bound might not be understood as it has been done in the single function optimization problems. In MOPs, bounds can be considered as the set of boundary solutions beyond which the objective function is undefined (or in constrained problems, infeasible). However, if those bounding solutions are available before any EMO run, they will be very useful in finding the complete PF in a more efficient way. This paper will try to explore this possibility.

Interestingly, we can find some examples in the recent EMO literature where such bracketing techniques have been used. For example, in [4] the algorithm simultaneously searches for the boundary solutions and inserts them into the population on different stages. In another study [5], a high performance single objective search algorithm is used to seed the initial population with solutions to a scalarized version of the problem, and reported to be useful with standard EMO algorithms. From all these examples, there are some interesting questions that we think are not answered yet:

• Is it computationally feasible¹ to find the boundary solutions first and later use them in an EMO algorithm?

• Instead of only depending on random local search operations [4, 5, 7], can these boundary solutions be explicitly utilized in a more intuitive and deterministic way?

• How many bounding (or a minimum number of bounding) solutions are sufficient enough to be utilized efficiently?

In this paper, we would like to address these questions. The paper is organized as follows: in Sect. 2 we will review some basic definitions related to MOPs, then in Sect. 3 we will discuss two specific motivations for this study. After that we will describe our approach in Sect. 4. The proposed algorithm can explicitly construct (i.e. explores) the rest of the Pareto optimal solutions within (or, the vicinity of) the approximate bounding solutions through an intuitive heuristic. Moreover, our approach also improves the approximations using a careful update mechanism to ensure that they can reach to the true PF bounding points. By this way, we can facilitate a more informed exploration and save a huge number of solution evaluations. Our scheme is then applied to a standard EMO algorithms (i.e. NSGA-II [2]). Then we will discuss our experiment results on different benchmark MOP problem sets in Sect. 5 and then we conclude the paper in Sect. 6.

2 Preliminaries

We consider multi-objective optimization problems (MOPs) involving $m$ conflicting objectives $(f_i\, : \,\mathcal {S} \subset \mathbb {R}^n \rightarrow \mathcal {F} \subset \mathbb {R}^m)$ as functions of decision vector $\mathbf {x} \in \mathcal {S}$. We also assume that the readers are already familiar with the basic terminologies² concerning an MOP. Specific to this paper, we are more interested in the boundary of the set $\mathcal {F}$, the boundary can also be defined in terms of convex hull of finite point set [1]:

Definition 1

( Convex Hull of Inidividual Minima (CHIM) ). Given an ideal objective vector $\mathbf {z}^*= [f_1^*, f_2^*, \ldots , f_m^*]^T$, let us assume $\varPhi$ be an $m \times m$ matrix³ whose $i$-th column is $f_i^*$. Then the set of points in $\mathbb {R}^m$ which are convex combinations of $f_i^*$, i.e. $\varPhi \beta \, : \,\beta \in \mathbb {R}^m, \, \sum _{i=1}^n\beta _i = 1, \, \beta _i \ge 0$, are referred as the CHIM.

From the above definition, a PF can be understood in terms of so-called CHIM $_{+}$:

Definition 2

(CHIM $_{+}$ ). Let CHIM $_{\infty }$ be the affine subspace of the lowest dimension that contains the $\text {CHIM}$, i.e. the set $\{\varPhi \beta \, : \, \beta \in \mathbb {R}^m\,, \,\sum _{i=1}^m \beta _i = 1\}$. Moreover, denote $\delta \mathcal {F}$ as the boundary of the set $\mathcal {F}$. Then CHIM $_{+}$ is defined as the convex hull of the points in the set $\mathcal {F}\, \cap \, \textit{CHIM}_{\infty }$. More informally, if we extend (or withdraw) the boundary of the CHIM simplex to touch $\delta \mathcal {F}$; the “extension” of CHIM thus obtained is defined as CHIM $_{+}$.

Therefore, the Pareto-optimal front $\mathcal {PF}$ can also be defined as a set of intersection points found from the normals emanating from the CHIM $_{+}$ (towards the ideal objective vector $\mathbf {z}^*$) on to $\delta \mathcal {F}$. The bounding points of the PF is the end point solutions of CHIM $_{+}$, they can be approximated using either $\mathbf {z}^*$ or the nadir objective vector $\mathbf {z}^{\text {nad}}$.

As we have discussed before, the bounding points to the PF is a topic of special interest in the classical numerical optimization community since, in many cases, these points are the first step to model the PF. And therefore, it is the starting point of many non-stochastic MOP solvers [1, 10, 11]. Whereas in the EMO community, the bounding points are generally overlooked; just because: (i) bounding points do not represent the trade-off – being minimum at all objectives except one, (ii) they are not of much interest in Decision Maker’s (DM’s) perspective, (iii) since all EMO algorithms employ a population based parallel search, the bounds can be found out along with an EA run. As a result, finding boundary solutions⁴ is taken as granted. Or such points can be found with a careful change in the original algorithm [6].

In this paper, we will see how the performance of an EMO can be drastically improved if we first approximate such bounding solutions, inject them into the initial population and thereafter take necessary measures to improve the approximations to the true PF bounds. To approximate them, we will use classical optimization methods like Interior point method (IPM) [12] and generalized pattern-search (GPS) [13] approach by optimizing $m$ single objective achievement-scalarizing functions [14]. Given the function evaluations spent to find those bounding solutions, our approach demonstrates that it can still save a lot of computational effort compared to that of a standard EMO algorithms. Due to the space constraints, other relevant discussions and the results are included in the supplementary document [8] accompanied with this paper.

3 Motivations

The main motivating guide of this study stems from two aspects: (i) we wanted to take the advantages of the determinism in the classical numerical optimization methods and, (ii) we wanted to guide the search trajectory in a more non-skewed way so that all the trade-off regions will be explored with a similar pace.

3.1 Inspirations from the Classical Methods

In the classical numerical optimization discipline, the first thing we learn is the concept of bounding (or bracketing) of the minima (or maxima) [3]. Otherwise, the optimization algorithms will spend a lot of time figuring out a suitable place to start the actual search process.

The first example is the famous Normal Boundary Intersection (NBI) algorithm [1], where the primary theory is developed based on the assumption that we already have the end-point solutions of the CHIM $_{+}$. Another example is presented in [10], where the algorithm first finds the boundary solutions, then discretizes the PF using triangulation algorithm and then enumerates the entire PF. In [11], the idea is to find the $\mathbf {z}^\text {nad}$ (although the points are not referred as “nadir” objective vector in the paper), then construct the CHIM $_{+}$ from it. After that, the algorithms divides the space into smaller parts to find the rest of the solutions on the true PF. The authors mentioned that the approach is not suitable for more than 2 objectives. A more detailed survey on such non-population/stochastic MOP approaches to “bound first, then optimize” can be found in [15].

Unfortunately, in most cases the algorithms presented are not simple and easy to implement. Moreover, many examples of such strategies are specialized to a particular problem domain. According to [15], such approaches are termed as the first order approximation algorithms. In that sense, our approach can be considered as an example of such category, however simpler and more intuitive than the existing approaches. Moreover, our method is applicable to wide range of MOPs.

3.2 Search Trajectory Bias

Most of the standard EMO algorithms are elitist by design. They are also “opportunistic” in a sense that the population always try to converge to a particular portion of the PF which seems to be easier to solve at a particular moment. Therefore, they tend to generate more solutions on a certain portion of the objective space which is easier to explore. For example, we can see such bias when we try to solve the ZDT4 problem using NSGA-II. In this case, the first objective is easier to minimize than the second one. In ZDT4, reaching the actual PF is difficult because of the local fronts, however finding the weakly dominated solutions along the $f_2$ axis is comparatively easy. This kind of non-symmetric search behaviour, is what we think, impedes the optimization procedure – especially, if the goal is to find well-distributed solutions within a budgeted function evaluation. In addition, such bias might form in multiple spaces if the number of objective increases. Moreover, this can also lead to a stagnation on a locally optimal front.

4 The Algorithm Description

The algorithm works in two phases. The first phase approximates the boundary of the CHIM $_{+}$ using a fixed budget. In the next phase, an EMO algorithm will explore the entire PF. And most importantly, during the same time, the algorithm needs to successively update (or improve) the bounds, given the fact that the bounds found in the first phase might not be exact. Our approach nicely fits into a standard elitist EMO algorithm like NSGA-II [2].

4.1 Approximating the CHIM $_{+}$ Bounds

In $m$-dimensional objective space if the true PF is a surface, then it can have more than $m$ number of CHIM $_{+}$ end points. For example, in the three-objective DTLZ7 problem [16], CHIM $_{+}$ has eight end points. However, we do not want to trace all the solutions that encompasses the entire PF boundary (as it has been done in [10]), we are only interested in the CHIM $_{+}$ end-points. To find the bounds, we keep these criteria in mind:

• 1. Finding the exact PF bound is non-trivial, so the goal is to get an approximation that is “good enough”. Which is also difficult because, to measure the closeness, we need to know the true PF.

• 2. Use the “best possible” effort to approximate the PF bounds, by spending a fixed number (as small as possible) of solution evaluations⁵ (SEs).

• 3. Use a deterministic classical numerical single-objective optimization algorithm.

• 4. Try to approximate at most $m$ bounding solutions, but not more than that: running the single objective optimizer for at most $m$ times.

For a given EA run, let’s assume we start with $N_p$ individuals for $N_\text {gen}$ generations. Therefore, the total number of function evaluations will be $T_e = N_pN_\text {gen}$. For the fixed budget, we will allocate $T_b = T_e/4$ function evaluations for the bound search and $T_{ea} = 3T_e/4$ for the actual EA run. To approximate the bound, we will separately optimize $m$ objective functions, we will spend $T_b/m$ function evaluation for each bounding points.

The actual CHIM $_{+}$ bound computation algorithm was conducted in two steps – (i) given a particular objective function $f_i$, first we minimize it by spending $T_b/2m$ number of function evaluations and assume a solution $\mathbf {x}^{*}_i$ is found. Moreover, assume $\mathbf {z}^\text {ref} = \mathbf {f}(\mathbf {x}^{*}_i)$. This step is done as a “bootstrap” that will help us to reach close to the $f^*_i$. (ii) then we construct an Augmented Achievement Scalarizing Function (AASF) [14] by taking $\mathbf {z}^\text {ref}$ as a reference point:

$$\begin{aligned} f_{\text {aasf}} = \rho \sum _{j=1}^m w_j(f_j(\mathbf {x}) - z^\text {ref}_j) + \max _{j \in \{1, 2, \ldots , m\}} w_j(f_j(\mathbf {x}) - z^\text {ref}_j) \end{aligned}$$

(1)

and solve it again for $\frac{T_b}{2m}$ iterations. Here, we set $w_i = 0.9$, $w_{j \ne i} = \frac{1}{10(m-1)}$. We set $\rho = 0.0001$, the value of $\rho$ should be kept small enough so that we can avoid the weakly dominated solutions. For the single objective solver, we use classical methods like Interior Point Method (IPM) [12] or Generalized Pattern Search (GPS) [13] etc.

Fig. 1.

The illustration of Algorithm 1 while finding a bounding solution that minimizes $f_2$. The algorithm spends $T_b/2m$ function evaluations to find $\mathbf {z}^\text {ref}$ and another $T_b/2m$ function evaluations to approximate one of the CHIM $_{+}$ bounds. The figure also shows that the discovered solution $\mathbf {x}^*$ might not be the exact bounding point.

A basic listing for this routine is presented in Algorithm 1 and the concept is illustrated in the Fig. 1. It should be noted that, this algorithm does not always find the all the unique bounds correctly, especially when the problem is hard, or when the PF is composed of multiple disconnected fronts.

4.2 The Exploration Step

The basic exploration is conducted as follows: after estimating the CHIM $_{+}$ bounds, we will include the set $\mathcal {Z}^*_b$ into the initial population and then the EA execution will start. On each generation, we will select $25\%$ of the best (i.e. the first front) individuals from the current population, then we pick one arbitrary decision vector $\mathbf {x}_s$ (we call it source vector) from the selected $25\%$ solutions. Next we pick one random solution from $\mathcal {Z}^*_b$ as a target vector $\mathbf {x}_t$. Here, the decision vector $\mathbf {x}_t$ is the promising solution that we want to get close to. Given $\mathbf {x}_s$ and $\mathbf {x}_t \in \mathcal {Z}^*_b$, the variation operation is achieved using a simple linear translation –

$$\begin{aligned} \mathbf {x}_c= & {} \mathbf {x}_s + \mathbf {U}\left[ \left( \frac{3d}{4}, \frac{5d}{4}\right) \right] \circ \left[ \frac{\mathbf {x}_s - \mathbf {x}_t}{||\mathbf {x}_s - \mathbf {x}_t||}\right] \end{aligned}$$

(2)

Here, $\mathbf {U}[(l,u)]$ is a uniform random vector where each element is within the range $[l,u]$, $d = ||\mathbf {x}_s - \mathbf {x}_t||$ and $\circ$ is the Hadamard product. $\mathbf {x}_c$ is the generated solution. Basically, we are trying to generate a solution that is within an $n$-dimensional sphere with radius $d/4$ centered at $\mathbf {x}_t$.

In an ideal case, if the set $\mathcal {Z}^*_b$ contains the true CHIM $_{+}$ bounds, then the later operation will ensure a very fast (almost immediate) convergence. However this does not address the issue of so-called Search Trajectory Bias, to alleviate such a degeneracy, we will include more decision vectors in the set $\mathcal {Z}^*_b$. For this treatment, we will also include solutions with the maximal crowding distances from the current best front. If we compute the crowding distances as have been done in the NSGA-II algorithm, the extreme solutions will have the crowding distance of $\infty$ and the solutions that are rendered isolated within the current best front will have the maximal values. The gaps in the PF are enclosed by such isolated solutions.

Let us assume the solutions that reside on the edge of the gaps are denoted as $\mathcal {E}_g$ and the solutions with $\infty$ crowding distances are denoted as $\mathcal {E}_\infty$. Obviously, if we could generate more points to the vicinity of $\mathcal {E}_g$, the search trajectory bias could be repaired long before they become more severe. Therefore, we also include $\mathcal {E}_g$ in $\mathcal {Z}^*_b$ and we denote this set as $\mathcal {V}$, i.e. $\mathcal {V} = \{\mathcal {Z}^*_b \cup \mathcal {E}_g\}$. To do this, we will pick $m$ solutions with the maximal crowding distances (excluding the solutions in $\mathcal {E}_\infty$) from the current population, as $\mathcal {E}_g$. Moreover, this inclusion needs to be done in every generation, because we do not know if the current front is the PF or not. Furthermore, $\mathcal {E}_g$ is never identical across the generations.

Fig. 2.

The exploration step, i.e. the illustration of lines 9–12 in Algorithm 3. The right axes are the variable space and the left axes are the corresponding objective space. The point $\mathbf {x}_c$ is the child (black circle) and $\mathbf {x}_s$ is the source (white circle) decision vectors. The vectors $\mathbf {x}_t$ are the target points (grey circles). The operation will arbitrarily choose one of the directions denoted by $L_1$, $L_2$ or $L_3$. If $\mathbf {x}_c$ violates the variable bound then it is reverted back to the corresponding target point $\mathbf {x}_t$.

Fig. 3.

Different configurations and the relative positioning of the solutions in $\mathcal {V}$. The first two cases ((a), (b)) are ideal, since the target solutions can be retained in the set $\mathcal {V}$ by a simple non-dominated sorting. For the third case (c), a special swapping step (line 7–9, Algorithm 2) is required to maintain a solution set to encourage diversity.

Now, instead of taking the target decision vectors $\mathbf {x}_t$ from $\mathcal {Z}^*_b$, we will consider them from $\mathcal {V}$. We call all the solutions in $\mathcal {V}$ as “pivot points”. Along with the search trajectory bias corrections, we also consider the case when $\mathcal {Z}^*_b$ is not the true CHIM $_{+}$ bounds (in fact, this is the most likely case). Which follows that we need to improve the bounds in $\mathcal {Z}^*_b$ during the EA generations. This procedure is explained in the next section.

4.3 Successive Bound Correction

The procedure described in the previous section only considers an ideal case, where the positions of $\mathcal {Z}^*_b$, $\mathcal {E}_g$ and $\mathcal {E}_\infty$ never coincide with any other. However during the evolutionary runs, different configurations may arise –

• Case 1 (Ideal Case): where $\mathcal {Z}^*_b$ is close to (or coincident with) the true CHIM $_{+}$ bounds. The current front is far from the true PF, therefore $\mathcal {E}_g$ and $\mathcal {E}_\infty$ do not coincide with $\mathcal {Z}^*_b$. Refer to the Fig. 3a.

• Case 2 (Ideal Case): where $\mathcal {Z}^*_b$ is weakly dominated by the corresponding solutions in $\mathcal {E}_\infty$ (Fig. 3b). In this case, we need to discard the solution $\mathbf {x}_1$ and keep $\mathbf {x}_4$ in $\mathcal {V}$.

• Case 3 (Degenerate Case): where $\mathcal {Z}^*_b$ does not coincide with the true PF bound (or both non-dominated), and one of the solutions in $\mathcal {E}_\infty$ weakly dominates the corresponding solution in $\mathcal {Z}^*_b$ (Fig. 3c). In this case, we need to discard the solution $\mathbf {x}_4$ and keep $\mathbf {x}_1$ in $\mathcal {V}$. Because the solution $\mathbf {x}_1$ has the higher chance of extending the current/future front, so that it does not loose the diversity in terms of the objective function trade-off.

The above three configurations indicates that we also need to include $\mathcal {E}_\infty$ into the pivot set $\mathcal {V}$. In order to address the case 1 and 2, we first merge the sets $\mathcal {Z}^*_b\,\cup \,\mathcal {E}_\infty$ into $\mathcal {V}$ and apply non-dominated sorting. Then we will take out the non-dominated solutions $\mathcal {V}'$ from $\mathcal {V}$, i.e. $(\mathcal {V} - \mathcal {V}')$. After that, we will check if any point $\mathbf {x}_i \in (\mathcal {V} - \mathcal {V}')$ weakly dominates a point $\mathbf {x}_j \in \mathcal {V}'$. If yes, we will replace $\mathbf {x}_j$ by $\mathbf {x}_i$. This step will handle the case 3 as presented in the Fig. 3c. The procedural description of this step is presented in the Algorithm 2.

If we run Algorithm 2 in the case 1 (Fig. 3a), the resultant pivot set will be $\mathcal {V} = \{\mathbf {x}_1, \mathbf {x}_2, \mathbf {x}_5, \mathbf {x}_6\}$. In case 2 (Fig. 3b), it will be $\mathcal {V} = \{\mathbf {x}_2, \mathbf {x}_4, \mathbf {x}_5, \mathbf {x}_6\}$ and in the case 3 (Fig. 3c), the result will be $\mathcal {V} = \{\mathbf {x}_1, \mathbf {x}_2, \mathbf {x}_5, \mathbf {x}_6\}$, etc. Also, $|\mathcal {V}'| \le |\mathcal {V}|$ is trivially true. On the line 14 of Algorithm 2, it is always the case that $|\mathcal {V}| > m$. The integration into NSGA-II is straight-forward, which is discussed in the next section.

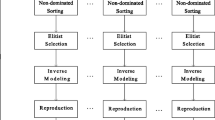
4.4 Integrating into an Elitist EMO Algorithm: NSGA-II

The integration listing is presented in the Algorithm 3. The only difference with NSGA-II is that we approximate the CHIM $_{+}$ bounds and inject them into the initial individual. Then we take $25\%$ of arbitrary individuals and project them on to the pivot solutions, and all these projected solutions will be merged into the child population on every generation. On the same iteration, the successive improvement on the bounds is done on line 7.

Moreover, upon generating the vector $\mathbf {x}_c$, if one of the variable values go beyond the variable bounds (i.e. $x_j > x_{j_H}$ or $x_j < x_{j_L}$), then we replace the overshot with the corresponding target vector value $y_j$, i.e. $y_j \in \mathbf {x}_t$. Therefore, if a certain vector $\mathbf {x}_c$ can’t make a successful translation, then $\mathbf {x}_c$ is reverted back to the vicinity of $\mathbf {x}_t$. Thus, we assure a local best estimated translation of the source vector $\mathbf {x}_s$. This process is done on the line 13 of the Algorithm 3, also explained in the Fig. 2. Again, if we look at the line 18, it may seem that the pivot points $\mathcal {V}$ are inserted into the current parent population on every generation. If the $\mathcal {Z}^*_b$ are true PF bounds, the line 18 will inject the same copies of solutions for multiple times. This can easily be avoided by keeping a global pointers to the solutions in $\mathcal {V}$. Another interesting aspect of this approach: it is “pluggable” – in a sense that this can be ported to any other elitist EMO algorithm.

5 Experiments and Comparisons

Before describing the main experimental results, in the following subsection we are going to review a special comparison technique called Relative Speed-up Ratio (RSR) that has been utilized in this study. We also see how the benchmark problems’ specifications are also modified in order to ensure a fair comparative analysis. The benchmark problems are taken from the existing EMO literature [16,17,18].

5.1 Performance Measure: The Relative Speed-Up Ratio (RSR)

In this experiment, we are interested to see if our approach can offer a better convergence speed while maintaining a good diversity in terms of objective trade-offs. For the spread and convergence measure, we have used the Hypervolume (HV) metric using the procedure discussed in [19]. For the speed, we have formulated a metric called Relative Speed-up Ratio (RSR), which also depends on the HV metric of the current front in each generation.

We ran the Algorithm 3 to solve a particular problem $P$ and then the same problem was solved using the original NSGA-II. At each generation, the HV measure was recorded from both algorithms and compared side by side. To understand the statistics, all the experiment data were collated from $31$ independent runs, therefore the HV metric is calculated as the mean of those $31$ runs at each generation.

Given a pair of EMO algorithms $A$ and $B$, that solve a particular problem $P$, the RSR measure is computed as follows:

$$\begin{aligned} \textit{RSR}(A,B)= & {} \frac{\text {SE}_A |_{\text {HV}_{A} \ge r \overline{\text {HV}}_{B_{\text {max}}}}}{\text {SE}_{B} |_{\overline{\text {HV}}_{B_{\text {max}}}}} \end{aligned}$$

(3)

In the above equation, $\text {SE}_A$ and $\text {SE}_B$ denotes the total number of solution evaluations (SE) for algorithms $A$ and $B$, respectively. And the subscripted expression after $|$ denotes the limit when the $\text {SE}$ values need to be recorded. $\overline{\text {HV}}_{B_{\text {max}}}$ denotes the maxmium mean-HV measure for the algorithm $B$ (in the convergence plot); and $r$ is a value $0.0 < r \le 1.0$. Hence, the above expression computes the ratio of two quantities –

• The total number of SE of algorithm $A$ to reach at-least a certain $r$-portion of the maximum of the mean-hypervolumes of $B$ and

• The total number of SE of algorithm $B$ to reach its maximum of the mean-hypervolumes.

Therefore, if the algorithm $A$ has a slower convergence rate than that of $B$, then $\textit{RSR}(A,B) > 0.0$, otherwise it will be equal to 0.0. For all the experiments, we have set the value of $r$ within $0.8 \le r \le 0.9$. All the benchmark test problems used in this paper are well defined and their shape of the PF is also known. Therefore, for a given reference objective vector $\mathbf {z}$, an ideal HV (IHV) is also computable analytically. For the RSR results (presented in Table 1), we have used the IHV values instead of $\overline{\text {HV}}_{B_{\text {max}}}$. So, in all our experiments, the RSR values are computed as:

$$\begin{aligned} \textit{RSR}_{\text {IHV}}(A,B) = \frac{\text {SE}_A |_{\text {HV}_{A} \ge r \text {IHV}}}{\text {SE}_B |_\text {IHV}} \end{aligned}$$

(4)

Table 1. The ideal HV (IHV), their corresponding reference points and $\text {RSR}_\text {IHV}$(NSGA-II, Algorithm 3) values.

5.2 Experiments with the Benchmark Problem Set

First we have tested the performance of Algorithm 3 on five $2$-objective problems [17], namely ZDT1, ZDT2, ZDT3, ZDT4 and ZDT6, and we have set NSGA-II results as the control groups. To maintain a fair comparison, we have compensated the extra solution evaluations by the Algorithm 1 for the NSGA-II runs, and compared NSGA-II and Algorithm 3 side by side. We are interested to see which algorithm can reach to a desired IHV within less solution evaluations (SE). For all the problems, we have seen our algorithm can demonstrate a very steep convergence to the true PF, given that the extra SE from Algorithm 1 are compensated for NSGA-II. The experiment with ZDT1 is illustrated in Fig. 4, here we can see that the Algorithm 1 takes up to around 2K of solution evaluations. Given that, NSGA-II still lags behind with a multiple factors to reach the desired PF, we have seen a similar effect on the problems ZDT2, ZDT4 and ZDT6; except for ZDT3, for which we saw some fluctuations due to the disconnected nature of the true PF. We only presented two of our results in the Fig. 5, due to the space constraint. To see the figures corresponding to the results of the rest of the problems, readers are referred to the accompanying supplementary material [8] with this paper.

Fig. 4.

The convergence test of Algorithm 3 vs. NSGA-II on problem ZDT1

Fig. 5.

These plots illustrates the comparative analysis of the convergence rates for different 2-objective problems, the curves are actually consisted of box-plots. Here Algorithm 3 denotes our algorithm and nsga2r is NSGA-II.

In the next experiment, we have carried out similar tests with the scalable problem sets – DTLZ1, DTLZ2, DTLZ3, DTLZ4, DTLZ5, DTLZ6 and DTLZ7 [16]. For all cases, we have considered $3$-objectives. Similarly, we compensate the measure by the extra SE spent to find bounds. All the results are collated from 31 independent runs. In DTLZ6, our approach shows a noticeable improvement, and also for DTLZ1 (Fig. 6). Figures for the results on other problems can be seen in [8]. There are some problems (i.e. DTLZ2, DTLZ4 and DTLZ5) for which the Algorithm 3 does not demonstrate any improvement. The reason behind this is that NSGA-II does not face much difficulty in reaching the true PF, as a result the outcome stays the same even if we introduce extreme points to guide the search. For example, DTLZ6 is harder than DTLZ5⁶, as a result, our approach shows even better speed-up in solving harder problems.

Fig. 6.

These plots illustrates the comparative analysis of the convergence rates for different 3-objective problems, the curves are actually consisted of box-plots. Here Algorithm 3 denotes our algorithm and nsga2r is NSGA-II.

6 Conclusions and Future Works

The main contribution of this paper is the utilization of the concept of bracketing in the MOP. Although in many classical optimization algorithms, they are assumed to be known. In EMO algorithms, the bounding solutions can play a very important step in the actual optimization run. Moreover, our approach does not assume that the initial approximations are true $\textit{CHIM}_{+}$ bounds. To overcome this limitation, it uses an intuitive and a simple way to improve the bounds during the evolutionary run – which is more intuitive than many approaches [4, 7] that use an archive or a population to improve/utilize the bounds.

Most importantly, our study has demonstrated that, even after spending a portion of the total allocated solution evaluations to find the $\textit{CHIM}_{+}$ bounds, they are so useful that the original EMO can achieve an extremely fast convergence. Our technique is also easy to implement and understand. We have also seen that the efficacy of our algorithm becomes more salient with the increasing level of problem difficulty. Even though we have carried out an extensive study of our model on a variety of benchmark problems, we did not conduct our study on many-objective cases yet. We hope to investigate along this line in the future.