Simple Approaches to Calculate Correlation Energy in Polyatomic Molecular Systems

Abstract

Ab initio calculation including electron correlation are still extremely costly, except for the smallest atoms and molecules. In this paper we present some simple semi-empirical methods to obtain correlation energy. These methods are based on the relation between energy and the off-diagonal density matrix elements, which represent the bonding between atoms in the molecule. The results of our previous studies are reported here and compared with the results obtained by using more accurate techniques.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

The terms ‘electron correlation’ and correlation energy was first used by Wigner [1] indicating an energy difference between the “exact” nonrelativistic molecular energy and energy obtained from a Hartree–Fock calculation, i.e.: $E_c = E_{\mathrm {exact,~nonrel}} - E_{\mathrm {HF}}$. Independent particle models, such as Hartree and Hartree–Fock methods, neglect this correlation at various level of approximation. In the Hartree model, there is an unphysical finite probability to find two electron in the same place, whereas the Hartree–Fock model electrons with parallel spin are prevented from overlapping but not those with antiparallel spin. Indeed, in the previous definition $E_c$ includes also the “basis set error” which is present in a simple HF calculation. For this reason some authors define the correlation energy $E_c$ as $E_c = E_{\mathrm {exact,~nonrel}} - E_{\mathrm {HF,~limit}}$, i.e., the energy difference with respect to a HF calculation with an “infinite” basis set. The value of $E_{\mathrm {HF}}$, limit can be obtained as limit value of various HF calculations on increasing the basis set.

Now, to account for electron correlation, several post-HF analytical techniques have been proposed, such as the Møller–Plesset perturbation theory (MP) [2], Configuration Interaction (CI) [3] or the Multi-configurational self-consistent field (MCSCF) [4] techniques, where the correlation is included at various levels within the HF calculation. Unfortunately, these methods are computationally very expensive even for small molecular systems.

Therefore, in the last 20 years alternative approaches to calculate the correlation energy have been developed. In these methods the electron correlation energy $E_c$ is related to some molecular properties, such as single- or two-particle electron density, bond order, bond distances, overlap populations, and so on. Some of these techniques are ‘semi-analytical’ methods, because they need an a priori empirical estimation of some parameters [5]. In general, the parameters are related to some atomic and atom–atom pair properties. It is worth to note how these methods are quite accurate, giving comparable results with respect to the analytical ones, and furthermore, they require lightweight computational efforts. The detailed exposition of these analytical or semi-analytical methods are beyond the scope of this paper. Therefore, in the following, we will expose in detail the methods that we have developed to calculate the correlation energy for simple or polyatomic molecules.

Methods

Correlation Energy versus Electron Number

Starting from a study of March and Wind [6], where the functional density theory (DFT) was used to explain the approximately linear variation in neutral atom correlation energy with atomic number Z, we have extended the model to treat some neutral diatomic molecules. As in Ref. [7], the starting point was to rewrite the correlation energy as:

$$\begin{aligned} E_c = \int \varepsilon _c (\mathbf{r}) \rho (\mathbf{r}) d\mathbf{r} , \end{aligned}$$

(20.1)

where $\varepsilon _c (\mathbf{r})$ is the correlation energy per electron (CEPE) at $\mathbf{r}$ and $\rho (\mathbf{r})$ is the electron density. Following the classical LCAO (Linear Combination of Atomic Orbitals) procedure, we expand the molecular wavefunction in an atomic basis set $\phi _\mu (\mathbf{r})$. So that we rewrite Eq. (20.1) as:

$$\begin{aligned} E_c = \sum _\mu ^A P_{\mu \mu } \int \varepsilon _c (\mathbf{r}) \phi _\mu ^2 (\mathbf{r}) d \mathbf{r} + \sum _\mu ^B P_{\mu \mu }&\int \varepsilon _c (\mathbf{r}) \phi _\mu ^2 (\mathbf{r}) d \mathbf{r} \nonumber \\&\quad + \sum _{\mu \ne \nu } P_{\mu \nu } \int \varepsilon _c (\mathbf{r}) \phi _\mu (\mathbf{r}) \phi _\nu (\mathbf{r}) d \mathbf{r} , \end{aligned}$$

(20.2)

where $P_{\mu \nu }$ are density matrix elements partitioned into atomic (A e B) and overlap terms. Assuming that the function $\varepsilon _c (\mathbf{r})$ varies in $\mathbf{r}$-space slowly with respect to $\phi _\mu ^2 (\mathbf{r})$, we can rewrite Eq. (20.2) as a sum of atomic and overlap contribution, i.e.:

$$\begin{aligned} E_c = E_c^{\mathrm {atomic}} + E_c^{\mathrm {overlap}} = \varepsilon _A \sum _\mu ^A P_{\mu \mu } + \varepsilon _B \sum _\mu ^B P_{\mu \mu } + \varepsilon _0 \sum _{\mu \ne \nu } P_{\mu \nu } S_{\mu \nu } . \end{aligned}$$

(20.3)

The first two terms refer to the atomic contribution, whereas the last refers to the interatomic one. In particular, $\varepsilon _A$, $\varepsilon _B$ and $\varepsilon _0$ are the CEPE for atom A and B (taken from experimental tabulated values [8]) and for the overlap terms represented by $S_{\mu \nu }$, the overlap matrix obtained from ab initio calculations. The assumption of Eq. (20.3) is to treat the overlap term at same level as for atoms, i.e., that correlation energy per electron for the overlap part is constant. This assumption is partially supported by the work of Gombas [9], who shows that $\varepsilon _c$ is not to strongly varying function of $\rho (\mathbf{r})$ which, in the overlap region, is a smoothly varying function of $\mathbf{r}$. Recalling the orthonormality of the atomic basis set, the term $\sum _{\mu \ne \nu } P_{\mu \nu } S_{\mu \nu }$ represents the total overlap population ($n^0 (AB)$), and the term $\sum _\mu ^A P_{\mu \mu }$ effective electron charge on the atom ($n^{\mathrm {eff}} (A)$). Then, we can rewrite Eq. (20.3) as:

$$\begin{aligned} E_c = \varepsilon _A n^{\mathrm {eff}} (A) + \varepsilon _B n^{\mathrm {eff}} (B) + \varepsilon _0 n^0 (AB) . \end{aligned}$$

(20.4)

Now, three different approaches have been taken in order to estimate the value of $\varepsilon _0$:

• (i) $\varepsilon _0 \simeq k_{(i)} N$, where N is the total number of electrons in the molecules. This assumption is based on the work of March and Wind [6], which shows that for atoms with small atomic number Z, the CEPE is nearly proportional to the total number of electrons; $k_{(i)}$ is a constant, calculated by the least square minimization procedure.

• (ii) $\varepsilon _0 \simeq (\varepsilon _A Z_A + \varepsilon _B Z_B )/2$. In this approach the overlap term of the CEPE is obtained as a mean value between total atomic correlation energy $E_A$ and $E_B$.

• (iii) $\varepsilon _0 \simeq k_{(iii)} n^0 (AB)$. At variance of (i) the overlap CEPE is proportional to the total overlap population, i.e., to the bond electron density. A detailed test of his assumption is showed in [10]. The constant $k_{(iii)}$ was also calculated by the least square minimization procedure.

Table 20.1 Experimental and calculated correlation energies for some diatomic molecules. In columns the experimental values, taken from [8], the calculated values with our methods (columns (i), (ii) and (iii)), Hollister and Sinanoglu (HS) [5], Savin et al. (SPP) [8], Langreth et al. (GCL) [8] and Perdew et al. (GCP) [8]

In Table 20.1 we have reported the experimental and calculated ones of the correlation energies for some diatomic molecules. Note that for method (i) the value of the constant $k_{(i)}$ was found to be equal to 12.5 mhartree/electron$^2$, whereas for method (iii) the value of the constant $k_{(iii)}$ is equal to 136.8 mhartree/electron$^2$.

Fig. 20.1

Correlation energy difference between the experimental $E_c$ and the calculated values for the various theoretical methods. Top figure the hydride systems (XH). Bottom figure the homonuclear systems (X$_2$). All values are in mhartree

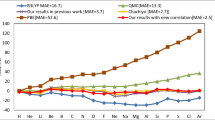
In Fig. 20.1 we report the difference (in mhartree) between the experimental $E_c$ values with respect to the various theoretical methods.

In particular, the top figure shows that for the hydride molecular systems better results are obtained with the more sophisticated methods as HS [5] or GCP. Whereas in homonuclear systems X$_2$ our methods appear to be more accurate.

It is noteworthy that in our method there is a direct relation between bond correlation energy and electron number of the molecular system. On the basis of this hypothesis and according to the work of Kais et al. [11], which expands the atomic $E_c$ in term of Z, we have shown [12] that this relation holds also for homonuclear diatomic systems.

Finally, we can infer that, despite the simplicity of the methods, our results reflect qualitatively the correct general trends of the correlation energy in diatomic molecules, and, for some systems, the difference found with respect to the experimental $E_c$ is smaller than those obtained by using more sophisticated methods reported in Table 20.1.

Correlation Energy and Bond Order

In order to treat molecular systems containing more than two atoms, following Cremer’s work [13], we define the correlation energy $E_c$ as:

$$\begin{aligned} E_c = E_S - E_{\mathrm {HF}} , \end{aligned}$$

(20.5)

where $E_{\mathrm {HF}}$ is the molecular Hartree–Fock energy and $E_S$ is the so called Schrödinger energy, which is obtained by the exact solution of the Schrödinger equation when vibrational, rotational and relativistic effects are excluded. This definition, as formerly stated, includes also than the “basis set error” which is present in a simple HF calculation.

Now, taking into account the formation reaction of a generic molecule,

$$\begin{aligned} A+B = C + \text{ binding } \text{ energy }, \end{aligned}$$

(20.6)

the molecular energy can be partitioned as follows:

$$\begin{aligned} E(C) =E(A) + E(B) - \text{ binding } \text{ energy } = E(A) + E(B) + E(AB) . \end{aligned}$$

(20.7)

The first step is to consider this Schrödinger molecular energy $E_S$ partitioned as follows:

$$\begin{aligned} E_S = \sum _{A=1}^N E_S (A) + \sum _{\mathrm {all}~AB} E_S (AB) , \end{aligned}$$

(20.8)

where N is the number of atoms in the molecule, $E_S(A)$ is the Schrödinger energy of the atom A and $E_S(AB)$ is the Schrödinger binding energy of the two bonded atoms A and B. Likewise, the total HF molecular energy can be written as:

$$\begin{aligned} E_{\mathrm {HF}} = \sum _{A=1}^N E_{\mathrm {HF}} (A) + \sum _{\mathrm {all}~AB} E_{\mathrm {HF}} (AB) . \end{aligned}$$

(20.9)

Molecular correlation energy is obtained subtracting Eq. (20.9) from Eq. (20.8), i.e.:

$$\begin{aligned} E_c = E_S - E_{\mathrm {HF}} = \sum _{A=1}^N E_c (A) + \sum _{\mathrm {all}~AB} E_c (AB). \end{aligned}$$

(20.10)

The Bond Order

In the framework of LCAO-MO theory (linear combination of atomic orbitals–molecular orbital), the definition of bond order in a polyatomic molecule was given first by Coulson [14] in the context of the Hückel MO approximation [15]. These bond orders are the off-diagonal elements $T_{\mu \nu }$ of the first-order density matrix T. More explicitly:

$$\begin{aligned} T_{\mu \nu } = \sum _{i=1}^{\mathrm {occ}} n_i c_{i\mu } c_{i\nu }^*, \end{aligned}$$

(20.11)

where $n_i$ is the occupation number of the ith MO, and $c_{i\mu }$ is the coefficient of the ith atomic orbital in the $\mu$th MO. This definition of bond order is applicable when the AOs (atomic orbitals) are mutually orthogonal and only one AO is considered for each atom. Various definitions for bond order have been proposed, e.g. Löwdin definition [16], which gives an orthogonal first-order density matrix Q by using the transformation:

$$\begin{aligned} Q = S^{1/2} T S^{1/2} , \end{aligned}$$

(20.12)

where S is the overlap matrix. In this framework the bond order $P_{AB}$ between the atoms A and B in a closed shell molecule is defined as:

$$\begin{aligned} P_{AB} = \sum _\mu ^A \sum _\nu ^B Q_{\mu \nu } Q_{\nu \mu } . \end{aligned}$$

(20.13)

More detailed treatments of the bond order for both closed shell and open shell systems is reviewed by Sannigrahi [17].

Bond Order Correlation Energy (BOCE)

The starting point is to relate the bond order population to the correlation energy, assuming that $E_c (AB)$ can be developed as series function of the bond order $P_{AB}$, we have:

$$\begin{aligned} E_c (AB) = \sum _m a_{m,AB} (P_{AB} )^m . \end{aligned}$$

(20.14)

The coefficient $a_{m,AB}$ are determined for a bond between two equal or different atom types (C−C, C−O, O−O, etc.), selecting a set of molecules containing the bond types reported in Table 20.2. Without loss of generality, we have retained only the first term of the expansion. Detailed procedure followed to obtain the bond parameters $a_{m,AB}$, and the selected molecular systems used in the best fit are reported in Refs. [18,19,20]. In Table 20.2 are reported the parameters $a_{1,AB}$ derived for the 6-31G** basis set.

Table 20.2 $a_{1,AB}$ (mhartree/electron) as defined by Eq. (20.14)

In the first paper, Ref. [18], the BOCE methods were applied to calculate the correlation energies of 20 molecules containing C, O, and H atoms. In the next work, Ref. [19], the method was applied to calculate the molecular dissociation energies ($D_0$) and heats of formation ($\varDelta H$). Finally in Ref. [20], the procedure was extended to calculate correlation energies in polyatomic molecules containing Si, F, and Cl atoms.

Table 20.3 Schrödinger and BOCE molecular energies (hartree) for some polyatomic molecules

In Table 20.3 we have reported the Schrödinger and the BOCE molecular energies, $E_{\mathrm {BOCE}} = E_{\mathrm {HF}} + E_c^{\mathrm {BOCE}}$, for some molecules containing the atoms of Table 20.2.

Fig. 20.2

Absolute relative energy difference between the Schrödinger and the calculated (BOCE) energy values for various molecular systems. In the top figure, molecular systems containing C, O and H atoms. In the bottom figure, molecular systems containing Si, F, Cl and H atoms

The very good agreement of the calculated energies using the BOCE techniques with respect to the Schrödinger ones, appears clearly form the values in Table 20.3. The highly accurate values of the correlation energy obtained using BOCE approach, for all molecules of the series, are confirmed from the calculated relative errors with respect to the Schrödinger energies, reported in Fig. 20.2.

However, it is important to add a comment: some calculated BOCE energies are lower than experimental (Schrödinger) energies. This is explained by taking into account that these values are obtained from various experimental data and any experimental measurement is subject to an error that, in general, is about $\pm 5$%. The BOCE results, for the molecular systems in the series, obtain values which are in the range of $\pm 0.007$% of the Schrödinger energy, which are much lower than the experimental error.

Finally, the good results obtained from BOCE technique in the molecular energy calculation is confirmed in the calculation of the molecular dissociation energy ($D_0$) as well as in the estimation of the molecular heat formation. Both molecular quantities were compared with experimental values and with the values calculated by using a very accurate, but computationally expensive, method (G2) [21], as shown in Ref. [20].

In conclusion, despite the simplicity of the BOCE approach, the results obtained by using this approach in the molecular energy calculation and other related molecular quantities are well comparable with the results obtained by using more accurate and very computationally expensive techniques.