Voronoi Diagram for Convex Polygonal Sites with Convex Polygon-Offset Distance Function

Abstract

The concept of convex polygon-offset distance function was introduced in 2001 by Barequet, Dickerson, and Goodrich. Using this notion of point-to-point distance, they showed how to compute the corresponding nearest- and farthest-site Voronoi diagram for a set of points. In this paper we generalize the polygon-offset distance function to be from a point to any convex object with respect to an m-sided convex polygon, and study the nearest- and farthest-site Voronoi diagrams for sets of line segments and convex polygons. We show that the combinatorial complexity of the nearest-site Voronoi diagram of n disjoint line segments is O(nm), which is asymptotically equal to that of the Voronoi diagram of n point sites with respect to the same distance function. In addition, we generalize this result to the Voronoi diagram of disjoint convex polygonal sites. We show that the combinatorial complexity of the nearest-site Voronoi diagram of n convex polygonal sites, each having at most k sides, is $O(n(m+k))$. Finally, we show that the corresponding farthest-site Voronoi diagram is a tree-like structure with the same combinatorial complexity.

M. De—Supported by DST-INSPIRE Faculty Grant (DST-IFA14-ENG-75).

1 Introduction

The Voronoi diagram is a very powerful tool which is widely used in diverse fields like epidemiology, ecology, computational chemistry, robot motion planning, and architecture, to name just a few. Being studied from as early as in the 17th century by Descartes [7], the topic has a vast literature. Many variations of Voronoi diagrams, differing by dimension, sites, measure of distance, etc., have been studied. To unify the concept, at least in two dimensions, Klein [11] introduced the notion of an abstract Voronoi diagram.

Chew and Drysdale [6] proposed a Voronoi diagram for point sites with respect to convex distance function (also known as Minkowski functionals [2, 9]), which is based on the notion of scaling of a convex polygon.

Barequet et al. [3] introduced the concept of convex polygon-offset distance function between two points. This function captures the distance according to the notion of shrinking or expanding a convex polygon along its medial axis. In the cited paper, the authors pointed out that polygon-offset distance functions are more natural than convex distance functions for many applications, e.g., manufacturing processes of physical three-dimensional objects, because a convex distance function varies, for the same underlying polygon, if different center (reference) points are used, which is not the case with polygon-offset distance function whose center is determined by the polygon. However, if the underlying polygon is not regular, the respective polygon-offset distance function does not satisfy the triangle inequality. In the same work, the authors also presented an algorithm for computing the Voronoi diagram for points with respect to this distance function.

In the current paper, we generalize the convex polygon-offset distance function to measure distances from a point to a convex object. This distance measure is useful, for example, to model the distribution of pollution expanded from an industrial zone to a residential area. Assume that an industrial zone $\mathcal P$ should be placed such that the pollution from $\mathcal P$ takes maximum time to reach any part of the residential area. Here, the residential area is described as a polygon set $\mathscr {S}$ and the (polygon-offset) distance is measured with respect to the industrial zone $\mathcal P$. The Voronoi vertices of the nearest-site Voronoi diagram are the candidates for the placement of the industrial zone. The vertex with the maximum distance to a site is the sought solution.

1.1 Related Work

The Voronoi diagram of point sites has been studied extensively in the literature. In the Euclidean metric, the combinatorial complexity of both the nearest- and farthest-site Voronoi diagram is O(n), where n is the number of point sites [8] or disjoint line segments [1, 16] in the diagram. These diagrams can be constructed in optimal $O(n\log n)$ time. For a set of k disjoint convex polygonal sites with total complexity n, the combinatorial complexity of the nearest-site Voronoi diagram in the Euclidean metric is also O(n) [10, 13, 17]. McAllister et al. [14] presented an algorithm to compute a compact representation of the diagram in $O(k\log n)$ time using only O(k) space. This compact representation can be used to answer closest-site queries in $O(\log n)$ time. Recently, Cheong et al. [5] showed that in the Euclidean metric, the combinatorial complexity of the farthest-site counterpart is also O(n), and the diagram can be computed in $O(n\log ^3 n)$ time. On a related note, Bohler et al. [4] introduced recently the notion of abstract higher-order Voronoi diagram and studied its combinatorial complexity.

With respect to the polygon-offset distance function, the combinatorial complexity of both nearest- and farthest-site Voronoi diagrams of a set of n points is O(nm) [3], where m is the complexity of the underlying convex polygon. Both diagrams can be computed in expected $O(n\log n\log ^2 m+m)$ time. Neither the combinatorial complexity nor the computation algorithm were investigated so far for sites which are disjoint line segments or convex polygons, with respect to the polygon-offset distance function.

1.2 Our Contribution

In this paper, we generalize the definition of the polygon-offset distance function $D_\mathcal{P}(p, S)$ to be from a point p to an object S (either a line segment or a convex polygon, rather than just to another point), where $\mathcal P$ is, as before, an m-sided convex polygon. Next, we study the properties and complexities of both nearest- and farthest-site Voronoi diagrams of disjoint line segments and convex polygons with respect to this distance function.

We show that the combinatorial complexity of the nearest-site Voronoi diagram of n disjoint line segments is O(nm), which is asymptotically the same as that of the nearest-site Voronoi diagram of n point sites. Next, we prove that the combinatorial complexity of the nearest-site Voronoi diagram of n polygonal sites, each having at most k sides, is $O(n(m+k))$. Finally, we show that the farthest-site Voronoi diagrams for both line segments and convex polygons are tree-like structures; they have the same combinatorial complexity as their nearest-site counterpart.

1.3 Organization

First, we give some relevant definitions and preliminaries in Sect. 2. Then, the nearest-site Voronoi diagrams of line segments and convex polygons are studied in Sect. 3. The farthest-site Voronoi diagram is studied in Sect. 4. We end in Sect. 5 with some concluding remarks.

2 Preliminaries

We begin with illustrating the process of offsetting a convex polygon, following closely the description of Barequet et al. [3]. Given a convex polygon $\mathcal P$, described by the intersection of m closed half-planes $\{H_i\}$, an offset copy of $\mathcal P$, denoted as $O_\mathcal{P,\varepsilon }$, is defined as the intersection of the closed half-planes $\{H_i(\varepsilon )\}$, where ${H_i(\varepsilon )}$ is the half-plane parallel to $H_i$ with bounding line translated by $\varepsilon$. Depending on whether the value of $\varepsilon$ is positive or negative, the translation is done outward or inward of P. See Fig. 3(a) for an illustration. The value of $\varepsilon _0 < 0$ for which the $O_\mathcal{P,\varepsilon _0}$ degenerates into a point c (or a line segment s) is the radius of $\mathcal P$, and the point c (or any point on s) is referred to as the center of $\mathcal P$.

Using the above concept, Barequet et al. [3] defined the polygon-offset distance function $D_\mathcal{P}$ between two points as follows.

Definition 1

(Point to point distance [3]). Let $z_1$ and $z_2$ be two points in $\mathbb {R}^2$ and $O_\mathcal{P,\varepsilon }$ be an offset of $\mathcal P$ such that a translated copy of $O_\mathcal{P,\varepsilon }$, centered at $z_1$, contains $z_2$ on its boundary. The offset distance is defined as $D_\mathcal{P}(z_1,z_2)= \frac{\varepsilon \,+\,|\varepsilon _0|}{|\varepsilon _0|}=\frac{\varepsilon }{|\varepsilon _0|}+1$.

Note that this distance function is not a metric since it is not symmetric. We generalize the offset distance function $D_\mathcal{P}$ to measure distance from any point z to any object o in $\mathbb {R}^2$ in a natural way, as follows.

Definition 2

(Point to object distance). Let z be any point, and let o be any object in $\mathbb {R}^2$. The offset distance $D_\mathcal{P}(z,o)$ is defined as $D_\mathcal{P}(z,o)=\min _{z'\in o}D_\mathcal{P}(z,z')$.

2.1 Properties of $D_\mathcal{P}$:

The following properties [3] also hold for the generalized distance function $D_\mathcal{P}$.

Property 1

[3, Sect. 3.1, Property 1]. The distance function $D_\mathcal{P}$ induces a Euclidean topology in the plane. In other words, each small neighborhood of a point contains an $L_2$-neighborhood of it, and vice versa.

Property 2

[3, Sect. 3.1, Property 2]. The distance between every pair of points is invariant under translation.

Property 3

[3, Theorem 6]. The distance function $D_\mathcal{P}$ is complete, and for each pair of points $z_1,z_3\in \mathbb {R}^2$, there exists a point $z_2 \notin \{z_1,z_3\}$ such that $D_\mathcal{P}(z_1,z_2)+ D_\mathcal{P}(z_2,z_3)=D_\mathcal{P}(z_1,z_3)$.

Property 4

[3, Theorem 7]. For each pair of points $z_1,z_2\in \mathbb {R}^2$, there exists a point $z_3 \ne z_2\}$ such that $D_\mathcal{P}(z_1,z_2)+ D_\mathcal{P}(z_2,z_3)=D_\mathcal{P}(z_1,z_3)$.

It is easy to observe the following property of $D_\mathcal{P}$.

Observation 1

Let z be a point and o be a convex object. Then, the function $D_\mathcal{P}(z,o)$ increases monotonically when z moves along a ray originating at a point on the boundary of o and never crossing it again.

2.2 Definitions of Voronoi Diagram

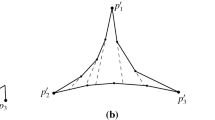
Under the convex polygon offset distance function, the bisector of two points (as defined originally [3]) can be 2-dimensional instead of 1-dimensional (see Fig. 1 for an illustration). This makes the Voronoi diagram of points unnecessarily complicated. To make it simple, as is also defined by Klein and Woods [12], we redefine the bisector and Voronoi diagram with respect to the offset distance function $D_\mathcal{P}$ as follows.

Fig. 1.

(a) Three different positions of the offset polygons from where both line segments are equidistant; (b) The bisector of two line segments according to the definition used in [3]; and (c) The bisector according to our definition.

Let z be a point, and $\varPi =\{\sigma _i\}$ a set of objects in the plane. In order to avoid 2-dimensional bisectors between two objects in $\varPi$, we define the index of the objects as the “tie breaker” for the relation ‘$\prec$’ between distances from z to the sites. That is,

$$ D_\mathcal{P}(z,\sigma _i) \prec D_\mathcal{P}(z,\sigma _j) $$

if $D_\mathcal{P}(z,\sigma _i) < D_\mathcal{P}(z,\sigma _j)$ or, in case $D_\mathcal{P}(z,\sigma _i) = D_\mathcal{P}(z,\sigma _j)$, if $i<j$.¹ Note that the relation ‘$\prec$’ does not allow equality if $i \ne j$. Therefore, the definition below uses the closure of portions of the plane in order to have proper boundaries between the regions of the diagram.

Definition 3

(Nearest-site Voronoi diagram). Let $\varPi =\{\sigma _1,\sigma _2,\ldots ,\sigma _n\}$ be a set of n sites in $\mathbb {R}^2$. For any $\sigma _i,\sigma _j\in \varPi$, we define the region of $\sigma _i$ with respect to $\sigma _j$ as $NV_\mathcal{P}^{\sigma _j}(\sigma _i)= \{z\in \mathbb {R}^2|D_\mathcal{P}(z,\sigma _i)\prec D_\mathcal{P}(z,\sigma _j)\}$. The bisecting curve $B_\mathcal{P}(\sigma _i,\sigma _j)$ is defined as $\overline{NV_\mathcal{P}^{\sigma _j}(\sigma _i)}\cap \overline{NV_\mathcal{P}^{\sigma _i}(\sigma _j)}$, where $\overline{X}$ is the closure of X. The region of a site $\sigma _i$ in the Voronoi diagram of $\varPi$ is defined as $NV_\mathcal{P}(\sigma _i)= { \{z\in \mathbb {R}^2|D_\mathcal{P}(z,\sigma _i) \prec D_\mathcal{P}(z,\sigma _j) \, \forall j\ne i\} }$. The nearest-site Voronoi diagram is the union of the regions: $NVD_\mathcal{P}(\varPi )=\mathop {\bigcup }\limits _{i}\text {NV}_\mathcal{P}(\sigma _i)$.

In other words, the diagram $\text {NVD}_\mathcal{P}(\varPi )$ is a partition of the plane, such that if a point $p\in \mathbb {R}^2$ has more than one closest site, then it belongs to the region of the site with the smallest index. The bisectors between regions are defined by taking the closures of the open regions. The farthest-site Voronoi diagram is defined analogously.

3 Nearest-Site Voronoi Diagram

3.1 Line Segments

Let $\mathscr {S}=\{s_1,s_2,\ldots , s_n\}$ be a set of n line segments in $\mathbb {R}^2$. First, we study the combinatorial complexity of the nearest-site Voronoi diagram $\text {NVD}_\mathcal{P}(\mathscr {S})$ with respect to $D_\mathcal{P}$, where $\mathcal P$ is an m-sided convex polygon. We use the abstract Voronoi diagram paradigm of Klein and Wood [12].

Theorem 2

 [12, Theorem 4.6]. If $D_\mathcal{P}$ satisfies Property 1, Property 3, and Property 4, then all Voronoi regions are simply connected.

As a result, we have the following.

Lemma 3

Every Voronoi region $NV_\mathcal{P}(s_i)$ in $NVD_\mathcal{P}(\mathscr {S})$ is simply connected.

Let $s_1,s_2$ be two line segments in the plane, and $B(s_1,s_2)$ and $B_\mathcal{P}(s_1,s_2)$ be the bisectors of $s_1$ and $s_2$ with respect to the Euclidean distance and the polygon-offset distance $D_\mathcal{P}$, respectively. In the sequel, we will use the term polyline to denote a piecewise-simple curve all of whose elements are described by low-degree polynomials, like line segments and parabolic arcs. It is well known, then, that $B(s_1,s_2)$ is a polyline. Let $N_t$ be the normal to the bisector $B(s_1,s_2)$ at a point t on the bisector. Now, observe the following.

Observation 4

If we move a point x from t along $N_t$ towards $s_1$, then $\mathcal{D}_\mathcal{P}(x, s_2)$ increases monotonically and $\mathcal{D}_\mathcal{P}(x, s_1)$ behaves like a convex function. At the minimum of $\mathcal{D}_\mathcal{P}(x, s_1)$, we have that $\mathcal{D}_\mathcal{P}(x, s_1)\le \mathcal{D}_\mathcal{P}(x, s_2)$ (see Fig. 3(b) for an illustration). A similar claim holds (with the roles of $s_1$ and $s_2$ exchanged) when we move x from t in the opposite direction along $N_t$ (towards $s_2$).

Fig. 2.

Illustration of Lemma 5.

Now, we prove the following.

Lemma 5

For any two line segments $s_1$ and $s_2$, the curve $B_\mathcal{P}(s_1,s_2)$ is monotone with respect to $B(s_1,s_2)$.

Proof

We need to show that for any point t on the Euclidean bisector $B(s_1,s_2)$, the normal $N_t$ to the bisector $B(s_1,s_2)$ at t intersects $B_\mathcal{P}(s_1,s_2)$ at most once. Assume to the contrary that there exist on $N_t$ two points $x_1$ and $x_2$, such that $\mathcal{D}_\mathcal{P}(x_1, s_1)=\mathcal{D}_\mathcal{P}(x_1, s_2)$ and $\mathcal{D}_\mathcal{P}(x_2, s_1)=\mathcal{D}_\mathcal{P}(x_2, s_2)$. Assume further, without loss of generality, that both $x_1$ and $x_2$ are closer to $s_2$ than to $s_1$ (see Fig. 2). Then, since both $B(s_1,s_2)$ and $B_\mathcal{P}(s_1,s_2)$ are continuous, there is a point $t_1$ on $B(s_1,s_2)$ for which the line $N_{t_1}$ is tangent to $B_\mathcal{P}(s_1,s_2)$, say, at point y. Thus, there exist a direction along which the two functions $\mathcal{D}_\mathcal{P}(x, s_1)$ and $\mathcal{D}_\mathcal{P}(x, s_2)$ are tangent but do not cross. This can happen only where both functions are monotone increasing or monotone decreasing. However, in light of Observation 4, this behavior cannot happen near the $\mathcal{D}_\mathcal{P}$-bisector, where one function decreases and the other increases (see Fig. 3(b)), which is a contradiction. The claim follows.    $\square$

Corollary 1

For any two line segments $s_1$ and $s_2$, the curve $B_\mathcal{P}(s_1,s_2)$ is unbounded.

Lemma 6

• (i) Let $s_1,s_2$ be two line segments in the plane. The bisecting curve $B_\mathcal{P}(s_1,s_2)$ is a polyline with O(m) arcs and line segments.

• (ii) Two different bisecting curves intersect O(m) times.

Fig. 3.

(a) Different offset copies of a polygon; (b) Illustration of Observation 4; and (c) Euclidean bisector of two line segments.

Proof

• (i) Let us swipe a point t along the bisector $B_\mathcal{P}(s_1,s_2)$ from end to end, and characterize every position of t by (a) which elements (vertices or sides) of the current offset of $\mathcal{P}$ (which now touches simultaneously $s_1$ and $s_2$) touch the two segments; and (b) the location of the touching points on the two segments (either one of the endpoints, or a point internal to the segment, in which case we also distinguish between the two sides of the segment). We call this characterization the status of the bisector at t; see Fig. 4(a) for an illustration. During this sweep, a new basic piece of the bisector is manifested by a change in the status. In between such changes, the bisector is a line segment or a parabolic arc, depending of the elements of the status. Estimating the complexity of the bisector boils down to setting an upper bound on the total number of such changes in the status.

  There are two crucial issues to observe. First, when t is swept along $B_\mathcal{P}(s_1,s_2)$, the offset-distance from $B_\mathcal{P}(s_1,s_2)$ to $s_1$ (or $s_2$) first decreases monotonically until a minimum point (or an interval of one minimum value, in the degenerate case in which the two segments are parallel and their mutual orthogonal projection is non-empty), and then it increases monotonically. This implies that $\mathcal{P}$ first shrinks continuously (a process in which sides only “disappear”) and then expands (the opposite process in which sides only “appear”). During this process, the touching point moves cyclically around $B_\mathcal{P}$. Hence, the status can change O(m) times due to changes of the touching element of $B_\mathcal{P}$. The fact that $B_\mathcal{P}$ first shrinks and then expands does not change this bound—it only implies that some elements of $\mathcal{P}$ are skipped without contributing to these changes.

  Second, the touching point on each segment also rotates about it. This means that each segment contributes an additional constant number of changes to the status.

  In conclusion, the total number of changes of the status during the sweep is O(m).

• (ii) Let $B_\mathcal{P}(s_1,s_2)$ and $B_\mathcal{P}(s_3,s_4)$ be the two bisectors (with respect to $D_\mathcal{P}$ of two pairs of segments $s_1,s_2$ and $s_3,s_4$. As we already know, the complexity of each one of them is O(m). Every pair of basic elements of the two bisectors may intersect at most two times (as they are partial polynomials of degree 1 or 2). Suppose that we advance along the two bisectors from end to end and detect one (or two) intersection(s) between the same basic pieces of the bisectors. It is crucial to observe that if we continue further along the one of the bisectors switching to another basic piece, and discover another intersection, this intersection must lie on a basic element which is further along the other bisector. This follows from the monotonicity of the polygon-offset distance functions. Indeed, as seen in Fig. 1(b), one can decompose the range of the parameter t into three intervals: One in which both functions decrease, one in which one increases and the other decreases, and one in which both functions increase. Hence, the number of intersections behaves like a merge between two ordered lists, each of complexity O(m): The complexity of the merged list is O(m) as well.    $\square$

Fig. 4.

Status configuration for (a) line segments, and (b) convex polygons.

Theorem 7

 [12, Theorem 2.5]. Assume that a distance function $D_\mathcal{P}$ induces the Euclidean topology in the plane. Furthermore, assume that each bisector consists of disjoint simple curves, and curves belonging to different bisectors can intersect only finitely often within each bounded area. Finally, assume that all possible Voronoi regions are connected sets. Then $NVD_\mathcal{P}(\mathscr {S})$, where $\mathscr {S}$ is a set of n sites, has n faces and O(n) edges and vertices.

Property 1, Lemma 3, and Lemma 6(i) ensure that all the assumptions in Theorem 7 are satisfied. As a corollary to the theorem above, and due to Lemma 6(ii), we have the following.

Theorem 8

For a set $\mathscr {S}$ of n line segments, the combinatorial complexity of the Voronoi diagram $NVD_\mathcal{P}(\mathscr {S})$ is O(nm), where m is the number of sides of $\mathcal{P}$.

Remark. The bound O(nm) on the complexity of the diagram is attainable. For example, put n line segments more or less aligned horizontally and well spaced, so that most of the bisector of every pair of consecutive segments is present in the diagram, for a total complexity of $\Omega (nm)$. Hence, we conclude that the complexity of the diagram is $\Theta (nm)$ in the worst case.

3.2 Convex Polygons

We can easily extend the sites from line segments to convex polygons. Let $\mathscr {Q}=\{p_1,p_2,\ldots , p_n\}$ be a set of n convex polygonal sites, each having at most k sides, and let $\text {NVD}_\mathcal{P}(\mathscr {Q})$ be the nearest-site Voronoi diagram of these sites with respect to the convex polygon-offset distance function $D_\mathcal{P}$, where $\mathcal P$ is an m- sided convex polygon. With similar arguments given for Lemmata 3 and 5 for the nearest-site Voronoi diagram of a set of line segments (with respect to $D_\mathcal{P}$), we can prove the following.

Lemma 9

Every Voronoi region $NV_\mathcal{P}(p_i)$ in the nearest-site Voronoi diagram $NVD_\mathcal{P}(\mathscr {Q})$ is simply-connected.

Lemma 10

For any convex polygons $p_1$ and $p_2$, the curve $B_\mathcal{P}(p_1,p_2)$ is monotone with respect to $B(p_1,p_2)$.

In the same manner, the following generalizes Lemma 6 to deal with polygonal sites.

Lemma 11

• (i) The bisecting curve $B_\mathcal{P}(p_1,p_2)$ of a pair of convex polygons $p_1,p_2$, each having at most k sides, is a polyline with $O(m+k)$ arcs and segments.

• (ii) Two such bisecting curves intersect $O(m+k)$ times.

The proof of the lemma above is identical to that of Lemma 6 with the following refinements.

• 1. The offset of $\mathcal{P}$ can touch any of the up to k corners and k sides of each of the sites.

• 2. When swiping the point t along the bisector, the touching points on the two sites move sequentially along their boundaries without turning back, therefore, decomposing the bisector according to the touching points contributes at most 4k additional pieces.

• 3. Except that, the proofs of the two parts of the lemmas are identical. Therefore, the complexity O(m) is replaced by $O(m+k)$.

Similarly to the argument in the proof of Theorem 8, in the polygonal case Property 1, Lemma 9, and Lemma 11 also ensure that all the assumptions in Theorem 7 are satisfied, and due to Lemma 11(ii), we have the following.

Theorem 12

For a set $\mathscr {Q}$ of n convex polygons, each having at most k sides, the combinatorial complexity of the Voronoi diagram $NVD_\mathcal{P}(\mathscr {Q})$ is $O(n(m+k))$, where m is the number of sides of $\mathcal{P}$.

4 Farthest-Site Voronoi Diagram

We are given a set $\mathscr {S}=\{\sigma _1,\sigma _2,\ldots ,\sigma _n\}$ of sites (line segments or convex polygons) in $\mathbb {R}^2$. In this section, following the framework of Mehlhorn et al. [15] (and generalizing the approach of Barequet et al. [3, Sect. 5]), we obtain the combinatorial complexity of the farthest-site Voronoi diagram of $\mathscr {S}$ with respect to the distance function $D_\mathcal{P}$, where $\mathcal P$ is a convex polygon with m sides.

Let $\sigma _i$, $\sigma _j$ be a pair of sites in $\mathscr {S}$. As in Sect. 2, we define $\text {NV}_\mathcal{P}^{\sigma _j}(\sigma _i)$ to contain all the points in the plane that are closer to $\sigma _i$ than to $\sigma _j$ with respect to $D_\mathcal{P}$. Let us also define the dominant set $M(\sigma _i,\sigma _j)$ to be equal to $\text {NV}_\mathcal{P}^{\sigma _j}(\sigma _i)$ except the bisecting curve $\delta M(\sigma _i,\sigma _j) = B_\mathcal{P}(\sigma _i,\sigma _j)$.

Consider the family $M=\{M(\sigma _i,\sigma _j)|1 \le i \ne j \le n \}$. The family M is a called a dominance system if for all $\sigma _i,\sigma _j\in S$, the following properties are satisfied:

• 1 $M(\sigma _i,\sigma _j)$ is open and non-empty;

• 2 $M(\sigma _i,\sigma _j)\cap M(\sigma _j,\sigma _i)=\emptyset$ and $\delta M(\sigma _i,\sigma _j) = \delta M(\sigma _j,\sigma _i)$; and

• 3 $\delta M(\sigma _i,\sigma _j)$ is homeomorphic to the open interval (0, 1).

Similarly to the argument given in the cited work [3, Theorem 16], we can prove the following.

Lemma 13

The family M is a dominance system.

Proof

We argue why the properties of a dominance system are satisfied.

• 1. $M(\sigma _i,\sigma _j)$ is open because $D_\mathcal{P}$ is monotone and continuous.

  Let $\ell$ be a line which splits the plane into two parts and separating between $\sigma _i$ and $\sigma _j$. Without loss of generality, assume that $\ell$ is vertical and that $\sigma _i$ is to the left side of $\ell$. In this situation, all the points which are further to the left of $\sigma _i$ belong to $M(\sigma _i,\sigma _j)$. Hence, $M(\sigma _i,\sigma _j)$ is always non-empty.

• 2. Centering $\mathcal{P}$ at any point $r\in \mathbb {R}^2$, if we “pump” $\mathcal{P}$ up, then either it hits $\sigma _i$ first, or $\sigma _j$ first, or hits simultaneously $\sigma _i$ and $\sigma _j$. In the first case, $r\in M(\sigma _i,\sigma _j)$; in the second case, $r\in M(\sigma _j,\sigma _i)$; and in the third case, if $D_\mathcal{P}(r,\sigma _i) \prec D_\mathcal{P}(r,\sigma _j)$ (that is, if $i < j$), then $r\in M(\sigma _i,\sigma _j)$, otherwise $r \in M(\sigma _j,\sigma _i)$. Hence, $M(\sigma _i,\sigma _j) \cap M(\sigma _j,\sigma _i)=\emptyset$. On the other hand, $\delta M(\sigma _i,\sigma _j)= B_\mathcal{P}(\sigma _i,\sigma _j) = \overline{\text {NV}_\mathcal{P}^{\sigma _j}(\sigma _i)} \cap \overline{\text {NV}_\mathcal{P}^{\sigma _i}(\sigma _j)}=B_\mathcal{P}(\sigma _j,\sigma _i) = \delta M(\sigma _j,\sigma _i)$.

• 3. $\delta M(\sigma _i,\sigma _j)$ is homeomorphic to the open interval (0, 1) since $B_\mathcal{P}(\sigma _i,\sigma _j)$ is a polyline (see Lemma 11(i)).    $\square$

A dominance system is admissible if it also satisfies the following properties.

• 4. Any two bisecting curves intersect finitely-many times.

• 5. For all non-empty subsets $S'$ of S, and for every reordering of indices in S,

  • (a) The (nearest neighbor) Voronoi cell of every sites $\sigma _i\in S'$ (with respect to $S'$) is connected and has a non-empty interior.

  • (b) The union of all the (nearest neighbor) Voronoi cells of all sites $\sigma _i\in S'$ (with respect to $S'$) is the entire plane.

A dominance system which satisfies only Properties 4 and 5(b) is called semi-admissible.

It is easy to verify from Lemmata 9 and 11(ii) that the family M is admissible. Thus, we have the following.

Theorem 14

The family M is admissible.

The fact that M is semi-admissible suffices for our purposes. Consider now the family $M^*$, the “dual” of M, in which the dominance relation as well as the ordering of the sites are reversed. From [15], we have the following theorem.

Theorem 15

[3, 15] If M is semi-admissible, then $M^*$ is semi-admissible too. Moreover, the farthest site Voronoi diagram that corresponds to $M^*$ is identical to the nearest site Voronoi diagram that corresponds to M.

As a consequence, we conclude the following.

Theorem 16

Let $\mathcal{P}$ be a convex polygon with m sides.

• (i) For a set of n line segments, the combinatorial complexity of the farthest-site Voronoi diagram (with respect to $D_\mathcal{P}$) is O(nm).

• (ii) For a set of n convex polygons, each having at most k sides, the combinatorial complexity of the farthest-site Voronoi diagram (with respect to $D_\mathcal{P}$) is $O(n(m+k))$.

As we could show that the farthest-site Voronoi diagram can be defined as a dominance system, we could benefit from all the results of [15] on this diagram, namely, that it is a tree.

5 Conclusion

We investigate the combinatorial complexity of the nearest- and farthest-site Voronoi diagram of line segments or convex polygons under a convex polygon-offset distance function. It would be interesting to see how fast one can compute these diagrams. Another important direction for future research is to investigate higher-order Voronoi diagram in this setting.