Abstract
This paper formulates strong permission in prescriptive causal models. The key features of this formulation are that (a) strong permission is encoded in causal models in a way suitable for interaction with functional equations, (b) the logic is simpler and more straightforward than other formulations of strong permission such as those utilizing defeasible reasoning or linear logic, (c) when it is applied to the free choice permission problem, it avoids paradox formation in a satisfactory manner, and (d) it also handles the embedding of strong permission, e.g. in conditionals, by exploiting interventionist counterfactuals in causal models.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Favoring Strong Permission
In a simplified version, the problem of free choice permission is a result of jointly holding the free choice inference (FCVE) and certain other intuitively attractive inferential principles such as (FCVI) and (FCCE); here, \(May(\varphi )\) stands for that \(\varphi \) is permitted.

Though many find that the application of FCVE acceptable (e.g. 1a, b), allowing simultaneous application of both FCVE and FCVI leads to unacceptable results (e.g. 2a, b): \(\varphi \) is permitted only if any \(\psi \) is permitted.
-
(1)
FCVE
-
a.
You may have tea or coffee.
-
b.
\(\therefore \)You may have tea and you may have coffee. (\(\surd \))
-
a.
-
(2)
FCVI+FCVE
-
a.
You may do your homework.
-
b.
\(\therefore \) You may play video games. (\(\times \))
-
a.
Among others, one of the main reasons to favor strong permission (rather than the weak permission defined as the dual of obligation) is that it aims to provide a logical framework which supports FCVE but rejects FCVI and FCCE, and so constitutes a semantic account for free choice permission without inducing paradox (cf. [2, 3]).
In this paper, I will first briefly outline the general idea of strong permission, including how FCCE can itself also lead to undesirable results if strong permission is not properly designed (Sect. 2). Some further examples will be used to show that the frameworks of strong permission in [2, 3], though they may properly handle the case of the free choice permission problem, are not yet equipped with the necessary tools to handle the practical aspect of strong permission (Sect. 3) and the embedding of strong permission in the context of conditionals (Sect. 4). It will also be indicated that, though counterfactual conditionals in causal modeling semantics (CMS) can be naturally extended to a framework for strong permission, the result does not actually do much better than previous approaches in handling the practical aspect and the embedding of strong permission (Sects. 5 and 6). Finally, a further extended causal modeling semantics, the prescriptive causal modeling semantics, will be introduced and shown to have various advantages over other approaches (Sect. 7).
2 General Constraints
The general idea to formalize strong permission is to make it one that differs from weak permission but also at the same time validates FCVE but rejects FCVI and FCCE. One strategy is to adopt some sort of deontic reduction strategy for deontic modalities (cf. [2, 3]). For example, one may adopt a specific sentence letter S to represent something like “the sanction occurs” or “not immune to sanction”, and then formulate standard obligation \(O(\varphi )\) by \(\lnot A \rightarrow S\), weak permission \(P_{w} (\varphi )\) by \(\lnot O(\lnot \varphi )\), and strong permission \(P(\varphi )\) by \(\varphi \rightarrow OK\), in which \(\rightarrow \) is some kind of conditional unspecified as of yet and OK is defined by \(\lnot S\) (cf. among others, [1,2,3]).
According to the above deontic reduction strategy, FCVE, FCVI, and FCCE have their correspondent formulations as follows, given the consequence relation \(\models _{?}\) of a certain sort.
-
(FCVE*) \((\varphi \vee \psi )\rightarrow OK \models _{?} (\varphi \rightarrow OK) \wedge (\psi \rightarrow OK)\)
-
(FCVI*) \(\varphi \rightarrow OK \models _{?} (\varphi \vee \psi )\rightarrow OK\)
-
(FCCE*) \((\varphi \wedge \psi )\rightarrow OK \models _{?} \varphi \rightarrow OK\)
Nonetheless, as indicated in [2]: 308, one substantive challenge to a framework of strong permission is to validate FCVE by validating the simplification of disjunctive antecedents (SDA) but without at the same time validating the substitution of equivalent antecedents (SEA), for otherwise the undesirable antecedent strengthening (AS) follows.

With the seemingly acceptable FCCE, AS leads to the unacceptable consequence that once \(\varphi \) is permitted, any \(\psi \) is permitted. So the problem of free choice permission surfaces again.
-
(3)
AS+FCCE
-
a.
You may invite John.
-
b.
\(\therefore \) You may invite Bill.Footnote 1 (\(\times \))
-
a.
It is then suggested that \(\rightarrow \) should be weaker than conditionals such as the standard Stalnaker-Lewis counterfactual (cf. [2]: 308), since it allows (SEA).
In the literature, logical frameworks for strong permission do not simply adopt a deontic reduction strategy paired with a “weak” sense of conditional, but also adopts a “weak” sense of consequence relation corresponding to the conditional used in the deontic reduction strategy. For a conditional in a “weak” sense, in [2] Asher & Bonevac suggest to use a defeasible framework and in [3] Barker suggests to use a linear logic framework for the implementation of strong permission, so that “\(\rightarrow \)” is respectively understood as a defeasible conditional paired with a defeasible consequence relation, and the linear conditional paired with a corresponding linear consequence relation. These two frameworks are roughly presented as follows.
2.1 The Defeasible Framework
According to [2], Asher & Bonevac’s deontic strategy implements strong permission \(May(\varphi )\) by \(\varphi > OK\), in which > is a defeasible conditional, so that \(\varphi >\psi \) roughly means if \(\varphi \) then normally \(\psi \). To implement the logical feature of FCVE by what they call C-disjunction, a defeasible consequence  is exploited.
is exploited.
-
(C-Disjunction)

FCVE is implemented by  , for
, for  is defeasible, in that it is non-monotonic by nature because it allows for inferences to be “defeated” by “counterexamples”, e.g. the fact that penguins do not fly defeats the conclusion that penguins fly follows from the defeasibility of the inference from the premises that birds fly and penguin are birds. [2] takes it that FCVE is only defeasible for the reason that the following is consistent.
is defeasible, in that it is non-monotonic by nature because it allows for inferences to be “defeated” by “counterexamples”, e.g. the fact that penguins do not fly defeats the conclusion that penguins fly follows from the defeasibility of the inference from the premises that birds fly and penguin are birds. [2] takes it that FCVE is only defeasible for the reason that the following is consistent.
-
(4)
You may have tea or coffee, but you may not have tea or you may not have coffee.
The reason for them to find (4) consistent is that the mere fact that you may have tea or coffee is compatible with it being the case that you may not have both (cf. [2]: 311). Nonetheless, the “reason” they provide is more suitably represented by the consistency of the following example.
-
(5)
You may have tea or coffee, but you may not have both tea and coffee.
Even if one finds (5) acceptable, it does not automatically follow that one will find (4) acceptable, unless one believes it to be the case that you may not have both tea and coffee implies (or is equivalent to) that you may not have tea or you may not have coffee.
-
(P-Dem) \(\lnot ((\varphi \wedge \psi )>OK)\equiv \lnot (\varphi>OK)\vee \lnot (\psi >OK)\)
It is unclear whether P-Dem is valid according to the semantics for > given in [2]. However, if there is no independent reason to motivate something like P-Dem, then using defeasible inference to model inference in free choice permission becomes less attractive. Moreover, in Sect. 4, I will give an example to show that it is better for P-Dem not to hold in a framework for strong permission.
In [2], FCVI and FCCE do not hold even in the defeasible sense. This satisfies the requirement for their proposal to be a solution for the problem of free choice permission. Besides, it also has the advantage of making modus ponens for > defeasible.
-
(Defeasible Modus Ponens)
-
 , but
, but -

If we only allow OK to defensibly follow from \(\varphi > OK\) and \(\varphi \), we can correctly avoid the inference from (6a) to (6b), which should not have followed:
-
(6)
a. The sanction occurs, and you pay compensation.
b. So, you may not pay compensation. ([2]: 307)Footnote 2
Any framework allow the inference from (6a) to (6b) is doomed to be inappropriate, for it can be inferred that once one violates some permission, he is no longer permitted to do anything else.
2.2 The Linear Logic Framework
In [3], Barker adopts a different sort of deontic reduction strategy. His strategy is differs in characters from [2] in two main aspects: strong permission is associated with linear-oriented operators and the linear consequence relation. Here, I will only illustrate the background idea in the linear logic metaphorically (and the metaphorical meaning can be read off from the sequent calculus for the linear logic) and refer readers to [3] for the formal details.
To begin with, consider the linear consequence \(\varphi \vdash _{L} \psi \), which means that the resource provided by \(\varphi \) is enough to produce the result or product \(\psi \). Notice that the resource in the linear consequence, once used, cannot be used again, meaning that a resource can be used only once, just as on a production line. The linear implication \(\varphi \multimap \psi \) means that the resource \(\varphi \) can bring you the product \(\psi \). When the linear implication is considered as a resource, meaning that it is located on the left hand side of the linear consequence, it means roughly that, continuing to use the production-line metaphor, the machine is adjusted in a manner so that \(\varphi \multimap \psi \). On the other hand, when an linear implication is situated on the right hand side of the linear consequence, it means roughly that some resource makes it so that \(\varphi \multimap \psi \).
According to [3], that it ought to be the case that \(\varphi \) is represented by \((\delta \multimap \varphi )\), where the sentence letter \(\delta \) roughly means that all required things are not violated.Footnote 3 \(\delta \multimap \varphi \) then means that if all required things are not violated, then \(\varphi \) is the case. Following this idea, a strong permission of \(\varphi \) is represented by \(\varphi \multimap \delta \), meaning that if \(\varphi \) is executed, all required things are not violated.
Two other operators are relevant to the consideration of free choice permission in linear logic.
-
(Additive Conjunction) & is the additive conjunction.
-
(i) \( \varphi \& \psi \vdash _{L} \chi \) means that at least one of \(\varphi \) and \(\psi \) is a sufficient resource for producing \(\chi \), and both of them are provided.
-
(ii) \( \chi \vdash _{L}\varphi \& \psi \) means that \(\chi \) is a sufficient resource for producing \(\varphi \) and \(\chi \) is also a sufficient resource for producing \(\psi \), but is not meant to produce both.
-
(Additive Disjunctive) \(\oplus \) is the additive disjunction.
-
(i) \(\varphi \oplus \psi \vdash _{L} \chi \) means that both \(\varphi \) and \(\psi \) are sufficient resources for producing \(\chi \), though only one of them is provided.
-
(ii) \(\chi \vdash _{L} \varphi \oplus \psi \) means that the resource \(\chi \) is sufficient for producing at least one of \(\varphi \) and \(\psi \).
Given the above notions, strong permission is formulated as follows in linear logic.
-
(Free Choice Permission) \( (\varphi \oplus \psi )\multimap \delta \vdash _{L} (\varphi \multimap \delta ) \& (\psi \multimap \delta )\). This means that, if the machine or the situation is adjusted in the manner that both \(\varphi \) and \(\psi \) are sufficient resources for producing \(\delta \) (given that only one of \(\varphi \) and \(\psi \) is provided), it follows that the machine or the situation is adjusted to one capable of making use of \(\varphi \) to produce \(\delta \) and making use of \(\psi \) to produce \(\delta \), though both cases need not hold.
At this point, we obtain the inference pattern FCVE in linear logic. Other logical operators are needed in order to present the corresponding invalid inference patterns for FCVI and FCCE.Footnote 4
3 Permissions as Prescriptive Norms
Both of the two proposals for strong permission I have discussed rely on two things: (a) the implementation of strong permission by using a conditional in a certain weak sense, and (b) the orchestration of a non-classical consequence relation. These proposals may successfully capture the required logical-inferential features of strong permission. Nonetheless, more remains to be done.
No matter whether we are concerned with strong permission or obligation, we care about their practical aspects, in the sense that permissions and obligations are prescriptive norms suitable for practical guidance. In order to be suitable for practical guidance, it is required that by following the prescriptive norms, we are certain to avoid sanctions. For example, when we execute a strong permission, we want the execution to bring us to a situation in which we will not be in danger of stepping on somebody’s toes, so that no sanction will result. However, the implementation of strong permission in both of the proposals does not capture this practical aspect appropriately. In [2], the defeasible conditional is excessively weak, so that the practice of strong permission does not guarantee that no sanction will occur (for it only promises that normally no sanction will occur). Similarly, since it is unclear how the linear implication can be understood in a way corresponding to a notion of prescriptive norm, it is also hard to see what is meant by a strong permission as formulated in Barker’s style. For example, how is a strong permission represented by \( (\varphi \multimap \delta ) \& (\psi \multimap \delta )\) meant to guide us, in any practical sense? Are we actually allowed to do \(\varphi \), and to do \(\psi \)?
Furthermore, the practical issue of strong permission in both proposals is even more vivid when we reconsider the orchestrated consequence relations designed for capturing the inference pattern FCVE. Since the consequence relations in both proposals are non-classical, it means that, given strong permission, what is non-classically implied is not guaranteed to be true, meaning that what is “implied” is not literally “true”. If so, the agent making the inference faces the worry of being in danger of inferring the “wrong” strong permission and thus in turn faces the danger of stepping on somebody’s toes (so that a sanction is activated). For example, when Asher & Bonevac claim in [2] that \((\varphi \vee \psi )> OK\) is compatible with \(\lnot (\varphi> OK) \vee \lnot (\psi >OK)\), an agent cannot safely execute either \(\varphi \) or \(\psi \) without facing the possibility that his action will activate a sanction. Strong permission, as a prescriptive norm, should not allow this to happen.
There are other practical aspects of prescriptive norms that I intend to capture, but earlier proposals do not pay much attention to. One is general counterfactual applicability, to be further illustrated later in Sect. 4, that prescriptive norms can survive in a range (though not in all) of situations. A logical framework that can represent this feature should be desirable. What concerns me more is specific counterfactual applicability: one is permitted (or not permitted) to \(\varphi \) in a situation s just in case one is permitted (or not permitted) to \(\varphi \) in another situation which is exactly like s except that \(\varphi \) is executed in it. This practical aspect is important, for we need, as will further elaborated in Sect. 4, for example, when \(\varphi \) is permitted, \(\varphi \) to be kept permitted if one were to execute \(\varphi \) (so that one’s \(\varphi \)-ing can be exempted from blaming); when \(\varphi \) is not permitted, \(\varphi \) should be kept not permitted even if one were to execute \(\varphi \) (so that one can still be blamed for his execution of \(\varphi \)).
Let us say that a strong permission is a prescriptive norm that promises us that when the permission is executed by an individual, the execution will bring the individual to a situation in which no sanction occurs or no obligations are violated. Let us also say that an inference to a strong permission reveals to us a different aspect of the permission encoded in the premises. The weak conditionals and non-classical consequence relations encoded in the previous two proposals, unfortunately, do not yield these aspects of permission, though the inference patterns they validate seem to capture the required inference patterns to solve the free choice permission problem.
4 Embedded Strong Permission
We say that a strong permission is one that when executed leads us to a situation in which no sanction occurs. We can go further. It is natural that some permission does not hold in the current situation, for the reason that even if the permission is executed, the execution may not bring us to a situation in which we are not susceptible to sanction. Nonetheless, it also happens that when the current situation has changed in a certain way, some previously non-applicable permission will be made applicable. I shall call this strong permission embedding, which is a case of general counterfactual applicability. Besides the suitable logical-inferential features to solve the free choice permission problem, I would also like to emphasize that a framework of strong permission should also properly capture the strong permission embedding. Let us look at some examples.
The sophisticated structure of prescriptive norms given in (Monty Hall) verifies various strong permission embeddings encoded by conditional permissions.
-
(Monty Hall) The guest is permitted to pick exactly one door from door 1, door 2, and door 3. Behind one door is a car and behind the other two are goats. After the guest chooses a door, the host Monty Hall is permitted to open a door which is not chosen by the guest and which has a goat behind it. After Monty Hall opens a door, the guest is permitted to change his choice.
There are some interesting features in this scenario of prescriptive norms. Consider some strong permissions to be derived from the norms in the scenario.
-
(7)
a. The guest may choose door 1, door 2, or door 3, but no more than one door.
b. If the guest were to choose door 1 and the car were to be behind the door 1, then it would be the case that Monty Hall may open door 2 or door 3.
c. If the guest were to choose door 1, the car were to be behind door 2, and Monty Hall were to open door 3, then it would be the case that the guest may change to door 2.
(7b, c) are examples of strong permission embeddings encoded under counterfactuals, which have the feature that the permissions in the consequents hold depending (or parasitic) on the actions and facts given in the antecedents. Not much about conditional permission is considered in the literature, since the conditional embedding gives rise to substantial complexity in a logic for strong permissions, concerning how strong permissions depend on other actions and facts.
A possible proposal is to embed defeasible permissions or linear strong permissions under Stalnaker-Lewis counterfactuals, e.g.  . Nonetheless, from the perspective of specific counterfactual applicability, this move will not avoid the challenges to the deontic reduction strategy in the previous two proposals arising from the prescriptive norms in (Monty Hall). Assume that the guest actually chose to open the door 2 and Monty Hall also opened the door 2. Given this situation, it is still the case that the guest may open the door 2, so that the guest cannot be blamed, and Monty Hall may (and should) not open the door 2, so that sanction should apply to Monty Hall. However, this is neither a situation in which no sanction occurs (so that the guest may open the door 2) nor a situation in which no obligation is violated (so that the guest may open the door 2). This problem for both proposals, on the face of it, arises from the fact that they apply the deontic notions ‘OK’ and \(\delta \) to the “whole” situation rather than specifically to the action to be executed.
. Nonetheless, from the perspective of specific counterfactual applicability, this move will not avoid the challenges to the deontic reduction strategy in the previous two proposals arising from the prescriptive norms in (Monty Hall). Assume that the guest actually chose to open the door 2 and Monty Hall also opened the door 2. Given this situation, it is still the case that the guest may open the door 2, so that the guest cannot be blamed, and Monty Hall may (and should) not open the door 2, so that sanction should apply to Monty Hall. However, this is neither a situation in which no sanction occurs (so that the guest may open the door 2) nor a situation in which no obligation is violated (so that the guest may open the door 2). This problem for both proposals, on the face of it, arises from the fact that they apply the deontic notions ‘OK’ and \(\delta \) to the “whole” situation rather than specifically to the action to be executed.
Similar conditional permissions also arise from examples like the following.
-
(Pain Killers) There are two kinds of pain killers, A and B. They each are effective for relieving John’s pain, so the doctor may use A and may use B. Though using both A and B is even more effective, some undesirable side effect will arise. A doctor’s treatment should not lead to an undesirable side effect.
The above scenario implicitly verifies conditional permissions such as (8), even if this conditional permission is not written specifically in the hospital working manual.
-
(8)
If the doctor were to use A, then it would be the case that he may not use B.
Furthermore, the following inference pattern seems to be reasonable.
-
(9)
a. If the doctor were to use both A and B, then the doctor’s treatment would lead to an undesirable side effect.
b. The doctor’s treatment may not lead to an undesirable side effect.
c. \(\therefore \) The doctor may not use both A and B.
It is unclear how a logic of strong permission validates the given inference from (9a, b) to (9c) based on the deontic reduction strategy, for the premise (9b) is formulated as a conditional rather than a plain non-conditional statement in the deontic reduction strategy. Moreover, the case and (9c) together constitute a straightforward case that P-Dem is unacceptable.
While previous attempts for a logic of strong permission focus on capturing a cluster of suitable inferential patterns, I would like to turn my attention to how we explicitly encode the structure of prescriptive norms in a semantics and make use of it for the truth conditions of strong permission. Given suitable logical-inferential features in a logical for strong permission, it does not follow directly that prescriptive norms are encoded properly in a given semantics. If we make a clear encoding of prescriptive norms and give the truth conditions of strong permission in a way based on that encoding, it will be more convincing that the given logic correctly captures the truth conditions of strong permission appropriately.
5 Causal Modeling Semantics
My plan is to use counterfactuals in the causal modeling semantics to formulate strong permission. To utilize causal modeling semantics (CMS), the formal framework is briefly introduced as follows (cf. [4, 6]).
Definition 1
(Causal Frame). A causal frame is a tuple \(\mathbb {F}=<U,V,R,E>\), in which U is a set of exogenous variables, V is a set of endogenous variables, R is a function assigning a set of values to each variable in \(U\cup V\), and E is a set of functional equations for every \(V_{i} \in V\) in the form of \(V_{i}=f_{V_{i}}(W_{1},...,W_{n})\) such that \(W_{1},...,W_{n} \in U\cup V\).
A causal graph generated from a causal frame is a directed graph \(G=<U\cup V, H>\) in which \(H=\{<X,Y>|\) \(Y=f_{Y}\) \((...,X,...)\}\). I shall restrict the attention to the recursive frames which lack loops in their corresponding graphs (a loop in a graph \(G=<U\cup V, H>\) is a sequence \(X_{1},...,X_{n}\) such that \(X_{1}=X_{n}\) and \(<X_{i},X_{i+1}>\in H\)). Formulas corresponding to causal frames are (a) atomic formulas in the form of \(X_{i}=\kappa _{i}\) in which \(X_{i} \in U \cup V\) and \(\kappa _{i} \in R(X_{i})\), (b) boolean combinations of formulas, and (c) counterfactual formulas in the form of  such that there is no occurrence of ‘
such that there is no occurrence of ‘ ’ in \(\varphi \) and \(\psi \).
’ in \(\varphi \) and \(\psi \).
Definition 2
(Causal Model). A causal model \(\mathbb {M}=<\mathbb {F},\mathbf f>\), where \(\mathbb {F}\) is a causal frame and f is a solution to the equations E in \(\mathbb {F}\).
If a frame \(\mathbb {F}\) in a model is recursive, it follows that every different solution to \(\mathbb {F}\) has at least some different value on their exogenous variables in the solutions (cf. [6]). To model counterfactuals in causal models, we need an extra piece of machinery called interventions.
Definition 3
(Intervention and Submodel). An intervention \(\varGamma \) is a set of atomic formulas, and no atomic formulas \(X_{i}=\kappa _{i}\) and \(X_{j}=\kappa _{j}\) in \(\varGamma \) such that \(X_{i}=X_{j}\) but \(x_{i}\not = x_{j}\) (so that \(\varGamma \) is called intervenable). \(\mathbb {M}^{\varGamma }=<U^{\varGamma },V^{\varGamma },R^{\varGamma },E^{\varGamma },\mathbf f ^{\varGamma }>\) is a submodel of (generated from intervention \(\varGamma \) on) \(\mathbb {M}=<U,V,R,E,\mathbf f>\), such that
-
1.
\(U^{\varGamma }=U \cup \{X_{i}|X_{i}=\kappa _{i} \in \varGamma \}\),
-
2.
\(V^{\varGamma }=V - \{X_{i}|X_{i}=\kappa _{i} \in \varGamma \}\),
-
3.
\(R^{\varGamma }=R\),
-
4.
\(E^{\varGamma }=E - \{f_{X_{i}}|X_{i}=\kappa _{i} \in \varGamma \}\),
-
5.
\(\mathbf f ^{\varGamma }\) is a solution to \(\mathbb {F}^{\varGamma }=<U^{\varGamma },V^{\varGamma },R^{\varGamma },E^{\varGamma }>\) that satisfies the conditions (a) \(\mathbf f ^{\varGamma }(X_{i})=\kappa _{i}\), if \(X_{i}=\kappa _{i}\in \varGamma \), and (b) \(\mathbf f ^{\varGamma }(X_{i})=\mathbf f (X_{i})\) if \(X_{i} \in U^{\varGamma }\) but \(X_{i} \not \in \{X_{i}|X_{i}=\kappa _{i} \in \varGamma \}\).
Simply speaking, intervention in a model by a formula \(X_{i}=\kappa _{i}\) generates a submodel by setting \(X_{i}\) as an exogenous variable and its value to \(\kappa _{i}\).
Definition 3 is designed for counterfactuals with antecedents only having the form of boolean conjunctions of atomic formulas. To extend to antecedents with any boolean antecedent but which still do not contain any counterfactual, we use the extension developed in [4].Footnote 5
Definition 4
(State and Fusion, [4] : 154).
-
1.
(Atomic State) For a variable X and \(x_{i} \in R(X)\), \(s_{X=x_{i}}\) is a state.
-
2.
(Fusion) For distinct variables \(X_{1},...X_{n}\) and \(x_{1}\in R(X_{1}), ..., x_{n} \in R(X_{n})\), \(s_{X_{1}=x_{1}}\sqcup ...\sqcup s_{X_{n}=x_{n}}\) is a state.
-
3.
(Empty State) There is an empty state \(\top \) such that for any state s, \(s\sqcup \top =s\).
-
4.
(Exclusion) For any \(s_{X_{i}=x_{i}}\) and \(s_{X_{i}=x_{j}}\) such that \(x_{i}\not = x_{j}\), \(... \sqcup s_{X_{i}=x_{i}} \sqcup ... \sqcup s_{X_{i}=x_{j}} \sqcup ...\) is not a state.
-
5.
(Equivalence) For any state s, \(... \sqcup s \sqcup ... \sqcup s \sqcup ...=s\).
Definition 5
(State Verification, [4]: 154–155).
-
1.
\(s \models X_{i}=\kappa _{i}\) if and only if \(s=s_{X_{i}=\kappa _{i}}\).
-
2.
\(s\models \lnot (X_{i}=\kappa _{i})\) if and only if \(s=s_{X_{i}=\kappa _{j}}\), where \(\kappa _{j} \in R(X_{i})\) and \(\kappa _{j}\not = \kappa _{i}\).
-
3.
\(s\models \lnot \lnot \varphi \) if and only if \(s\models \varphi \),
-
4.
\(s\models \top \) if and only if \(s=\top \),
-
5.
For any s,
 ,
, -
6.
(a) \(s \models \varphi \vee \psi \) if and only if \(s\models \varphi \) or \(s\models \psi \),Footnote 6
(b) \(s\models \lnot (\varphi \vee \psi )\) if and only if \(s=t\sqcup r\), in which \(t\models \lnot \varphi \) and \(r\models \lnot \psi \),
-
7.
(a) \(s \models \varphi \wedge \psi \) if and only if \(s=t\sqcup r\), in which \(t\models \varphi \) and \(r\models \psi \),
(b) \(s\models \lnot (\varphi \wedge \psi )\) if and only if \(s\models \lnot \varphi \) or \(s\models \lnot \psi \).
An intervention by any boolean formula can then be correspondingly defined as follows.
Definition 6
(Extended Intervention). Consider a function \(f_{s}\) that maps every \(s'=s_{X_{1}=\kappa _{i}}\sqcup ... \sqcup s_{X_{n}=\kappa _{n}}\) to a set \(\varGamma _{s'}=\{X_{1}=\kappa _{1},...,X_{n}=\kappa _{n}\}\). For a boolean formulas \(\varphi \), we define a set of submodels \(\mathbb {M}^{\varphi }=\{\mathbb {M}^{f_{s}(s')}|s'\models \varphi \}\) generated by intervention based on \(\varphi \) on \(\mathbb {M}\).
Based on the given definition of extended intervention, truth conditions for formulas are defined as follows.
Definition 7
(Truth Conditions). For a model \(\mathbb {M}=<\mathbb {F},\mathbf f>\), we define the truth conditions of formulas as follows.
-
1.
\(\mathbb {M}\models X_{i}=\kappa _{i}\) if and only if \(\mathbf f (X_{i})=\kappa _{i}\),
-
2.
\(\mathbb {M}\models \lnot \varphi \) if and only if
 ,
, -
3.
\(\mathbb {M}\models \varphi \wedge \psi \) if and only if \(\mathbb {M}\models \varphi \) and \(\mathbb {M}\models \psi \),
-
4.
 if and only if \(\forall \mathbb {M}_{i} \in \mathbb {M}^{\varphi }\), \(\mathbb {M}_{i}\models \psi \).
if and only if \(\forall \mathbb {M}_{i} \in \mathbb {M}^{\varphi }\), \(\mathbb {M}_{i}\models \psi \).
Given the truth definition, Facts 1–4 follow directly, in which \(\models \) is a classical consequence.
-
Fact 1 (SDA)

-
Fact 2 (DI Failure)

-
Fact 3 (CE Failure)

-
Fact 4 (AS Failure)

Though the causal modeling semantics for counterfactuals validates SDA, it does not follow that antecedent strengthening (AS) is valid, for the substitution of equivalent antecedent (SEA) is invalid, e.g.,  .
.
6 Strategy One
To utilize CMS for implementing strong permission, we may consider a deontic reduction strategy that adopts a new variable OK with two values 0, 1 in a causal model, and take \(OK=1\) to stand for “sanction occurs” and \(OK=0\) to stand for “no sanction occurs”. Based on the observed facts resulting from the truth definition in CMS, we have secured the following results suitable for a logic of free choice permission; here \(\models \) is simply classical consequence.
-
Fact 5 (FCVE)

-
Fact 6 (FCVI Failure)

-
Fact 7 (FCCE Failure)

-
Fact 8 (FCCI Failure)
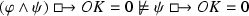
The above facts fit the required inference patterns for free choice permission. There are also some other advantages. Since the counterfactual conditional  validates modus ponens if its consequent involves no counterfactuals, it satisfies the need for the practical aspect of strong permission. Since the consequence relation of current concern is classical, the inferred strong permission is suitable to represent the permission encoded in the premises without the need to worry about the danger of stepping on somebody’s toes.
validates modus ponens if its consequent involves no counterfactuals, it satisfies the need for the practical aspect of strong permission. Since the consequence relation of current concern is classical, the inferred strong permission is suitable to represent the permission encoded in the premises without the need to worry about the danger of stepping on somebody’s toes.
Though the above facts seem to fit the required logical and practical features for a logic of strong permission, it is unclear how to present the functional equation for variable OK so that a direct coding for prescriptive norms can be achieved. For example, the following two permissions are true in (Monty Hall), which \(G=1\) means that the guest opens the door 1, \(C=2\) means that the car is behind the door 2, and \(M=1\) means that Monty Hall opens the door 1.
-
(10)
a.
 .
.b.
 .
.
The question is, how can we design a causal model that makes true both (10a, b), under the conditions (a) that the variable OK is a variable whose value is dependent on variables G, M, and C, and also (b) that G, C, M are mutually independent variables with respect to each other? Suppose the factual situation is \(G=1 \wedge C=2 \wedge M=1\), meaning that the guest did something permissible but Monty Hall did something impermissible. Ought we consider the equation for OK to output the value 0 or 1? If it is the former, (10b) turns out to be false; if it is the latter, (10a) turns out to be false. This problem arises from the simple reason that OK is a variable which evaluates the whole situation in a scenario, rather than evaluating whether a specific action is permitted. I will come back to this point in the next section.
(10a, b) looks just like a case of the failure of antecedent strengthening, so one may suspect that it should be understood as harmless for a logic of counterfactuals, even in the causal modeling semantics. However, it is not so. Given that the variable OK has only two values and that it deterministically has one of the two values, it can be shown that a model which verifies both (10a, b) can only be one in which \(\lnot (G=1 \wedge C=2 \wedge M=1)\). This result means that (10a, b) cannot both be true in a model in which \(G=1 \wedge C=2 \wedge M=1\). If this is the case, then we no longer have strong permissions as practically suitable prescriptive norms, for it is no longer suitable for Monty Hall to be condemned when he opened the door 1 under the situation that the guest opened the door 1. The specific counterfactual applicability that we desire is lost. One lesson to be learned is that a logical framework with correct logical features does not guarantee that framework being a suitable framework for strong permission, especially when we consider the practical aspect of strong permission. Alternative machinery may be worth considering.
7 Strategy Two
The situation described in examples (10a, b) fall into what I have called the specific counterfactual applicability of strong permission, in that (10a, b) is featured by their being applicable regardless of what the guest and Monty Hall have done. (10a, b) are also characterized by their general counterfactual applicability, in that they should be considered as true abstracting away from any action done (though not all permissions are true in this way), meaning that the truth of the permissions solely relies on how the causal frame is designed rather than what action is actually executed. This counterfactual applicability is important for the practical aspect, in that the strong permission does not just disappear when things are actually done. This is correct for any permissions true independent of any specific action actually executed, i.e. true by virtue of causal frames.
The view from counterfactual applicability also gives us a hint about how to provide a logic for strong permission but to escape from the deontic reduction strategy. If we take the deontic reduction strategy to be meant to capture the practical aspect of prescriptive norms, which in turn requires counterfactual applicability as an essential component, instead of considering whether an execution of an action leads to the situation OK = 1 or OK = 0, we can consider alternatively whether an execution of an action leads specifically to whether the action’s being executed is OK or not OK. The former takes OK to be a variable talking about the whole situation, but the latter makes OK a property attributed to a specific action’s being executed. Finally, the latter proposal means to capture OK as a property that directly observes the execution of actions.
This alternative proposal also implements strong permission by utilizing directly encoded prescriptive norms. To implement a direct encoding of prescriptive norms, we consider prescriptive causal models, a simple extension of causal models.
Definition 8
(Prescriptive Causal Models). A prescriptive causal model \(\mathbb {M}^{p}=<U,\) V, R, \(E,f,\varOmega>\) is one in which \(\mathbb {M}=<U,V,R,E,f>\) is a causal model, and \(\varOmega : SF \rightarrow \wp (\varPi )\) is a prescriptive function that explicitly assigns situations in which an action is permitted (so that no sanction occurs), where SF is the set of formulas that are either atomic formulas or boolean conjunction of atomic formulas, and \(\varPi \) is the set of functions \(\pi \) such that \(\pi \) maps every variable \(X_{i}\) in \(U\cup V\) to a value in \(R(X_{i})\).
The distinctive feature of prescriptive causal models is the function \(\varOmega \). Basically, \(\varOmega \) may be understood in this way: \(\varOmega \) maps a formula (an atomic formula or a conjunction of atomic formulas) to a set of situations (represented by a set of \(\pi \)) where the action (represented by the formula) is executed and is permissible. For example, in the case of (Monty Hall), we map \(G=1\) to any possible value combination for G, C, M in which \(G=1\), since \(G=1\) is permitted no matter what the agents involved in the scenario actually do.
To utilize the direct encoding of prescriptive norms in prescriptive causal models, I take OK to be a unary operator whose truth conditions are to be defined rather than a variable in causal models. Instead of interpreting a sentence “\(\varphi \) is permitted” as  , I interpret it as \(OK(\varphi )\) (and accordingly, “\(\varphi \) is obligated” is interpreted as \(O(\varphi )\)). The truth conditions for boolean connectives and counterfactuals in prescriptive causal models are defined as in standard causal models (so that the prescriptive functions are inert in those definitions). Strong permission and obligation are defined as follows.
, I interpret it as \(OK(\varphi )\) (and accordingly, “\(\varphi \) is obligated” is interpreted as \(O(\varphi )\)). The truth conditions for boolean connectives and counterfactuals in prescriptive causal models are defined as in standard causal models (so that the prescriptive functions are inert in those definitions). Strong permission and obligation are defined as follows.
Definition 9
(Strong Permission and Obligation). Let \(\mathbb {M}^{p}=<\mathbb {M},\varOmega>\) be a prescriptive causal model. For \(s'\models \varphi \) (that the state \(s'\) verifies the boolean formula \(\varphi \)), \(\omega =\bigwedge f_{s}(s')\) is a formula generated by the boolean conjunction on the set of atomic formulas \(f_{s}(s')\).
-
\(\mathbb {M}^{p}\models OK(\varphi )\) if and only if for any \(s'\models \varphi \), \(\pi \in \varOmega (\omega )\), where \(\omega =\bigwedge f_{s}(s')\) and \(\mathbb {M}^{f_{s}(s')}=<U,V,R,E,\pi>\).
-
\(\mathbb {M}^{p}\models O(\varphi )\) if and only if for any \(s'\models \lnot \varphi \), \(\pi \not \in \varOmega (\omega )\), where \(\omega =\bigwedge f_{s}(s')\) and \(\mathbb {M}^{f_{s}(s')}=<U,V,R,E,\pi>\).
Roughly, that \(OK(\varphi )\) is true in a model means that every possible execution \(\alpha \) of \(\varphi \) will lead to a \(\alpha \)-permitted situation; \(O(\varphi )\) being true in a model means that every possible execution \(\alpha \) of \(\lnot \varphi \) will lead to a \(\alpha \)-not-permitted situation. When weak permission is interpreted as the dual of obligation, saying that \(\varphi \) is weakly permitted is to say that not all possible executions of \(\lnot \varphi \) will lead to a \(\lnot \varphi \)-not-permitted situation. Strong permission is distinguished from weak permission, for example, if we can find some execution of \(\lnot \varphi \) which is permissible, but nonetheless not all executions of \(\varphi \) are permissible. For example, we should find that, in (Monty Hall), when the guest actually opens the door 1, \(OK(\lnot (C=1 \wedge M=1))\) fails, but \(\lnot O (C=1\wedge M=1)\) (so that \(\lnot (C=1\wedge M=1)\) is weakly permitted) holds. Strictly speaking, weak permission may not tell you what you are really permitted to do.
Given the truth conditions for operator OK, the following facts hold.
-
Fact 9 (FCVE) \(OK(\varphi \vee \psi ) \models OK(\varphi ) \wedge OK(\psi )\)
-
Fact 10 (FCVI Failure)

-
Fact 11 (FCCE Failure)

-
Fact 12 (FCCI Failure)

Given facts 9–12, we have a logic for strong permission suitable for the analysis of free choice permission. Moreover, the logic does not make use of deontic reduction to implement strong permission.
To show that prescriptive causal models are useful for directly encoded prescriptive norms, we present the prescriptive causal model for (Monty Hall) as follows. A model for (Pain Killer) can be constructed similarly.
-
\(\mathbb {M}_{MH}\) is a prescriptive causal model for (Monty Hall). \(\mathbb {M}_{MH}\) includes a causal frame \(\mathbb {F}_{MH}=<U,V,R,E>\) and a prescriptive function \(\varOmega \).
-
1.
\(U=<G,C,M>\) where the variables G, C, M stands for the guest’s choice of door 1, 2, or 3, C stands for the car’s location at door 1, 2, or 3, and M stands for Monty Hall’s action of choosing to open door 1, 2, or 3.
-
2.
\(V=\emptyset \).
-
3.
R: each variable is assigned with a set of three possible values {1, 2, 3}.
-
4.
\(E=\emptyset \), meaning that each variable is causally independent from others.Footnote 7
-
5.
-
(a)
\(\varOmega (G=1)=\{\) any variable assignment function \(\pi \) that assigns 1 to variable G \(\}\)
\(\vdots \)
-
(b)
\(\varOmega (M=1)=\{\) any \(\pi \) that does not assign 1 to either G or C \(\}\)
\(\vdots \)
-
(c)
\(\varOmega (C=1\wedge M=2)=\{\) any \(\pi \) that does not assign \(C=2\) \(\}\)
\(\vdots \)
-
(a)
-
1.
It should be not difficult to see that strong permissions, embedded or not, such as (7a, b, c), are true in \(\mathbb {M}_{MH}\).
In prescriptive causal models, we can further define the range of counterfactual applicability. For example, while the permission \(G=1\) is applicable in any variable-value combination of G, C, M, the permission of \(M=1\) is only applicable in those value assignments in which neither G nor C are assigned value 1. Formally, the counterfactually applicable situations of \(OK(\varphi )\) are those solutions in the models in which \(OK(\varphi )\) is true. Furthermore, we may state the following result: for any \(\mathbb {M}^{p}\), \(\mathbb {M}^{p}\models OK(\varphi )\) if and only if \((\mathbb {M}^{p})^{\varphi } \models OK(\varphi )\). The specific counterfactual applicability follows.
Finally, I remark on some desirable logical features for utilizing prescriptive causal models. First, it can be shown that \(\lnot OK(\varphi \wedge \psi )\) is not equivalent to \(\lnot OK(\varphi ) \vee \lnot OK(\psi )\). This allows for (4) being inconsistent but (5) consistent. This makes the free choice permission more practically sensible. Second, we should see that the inference from (6a) to (6b) is invalid. This invalidity comes from the feature that OK in prescriptive causal models is an operator applied to a specific action rather than representing a feature in the situation brought about by an execution of an action.
8 Concluding Remarks
In this paper, I argued that a logical framework for strong permission may capture the inferential patterns required for free choice permission without leading to paradox, but some important aspects of strong permission may still be missing. Proposals for strong permission in the literature are shown to lack the necessary means to capture the practical aspect of prescriptive norms and strong permission embedding. Prescriptive causal models are further provided to achieve the goal without exploiting the usual deontic reduction strategy for strong permission.
Notes
- 1.
By (AS), we infer \((p \wedge q) \rightarrow OK\) from \(p \rightarrow OK\). By (FCCE), it then follows that \(q \rightarrow OK\).
- 2.
Assume that modus ponens for the deontic reduction based on conditional \(\rightarrow \) is not defeasible, we show \(\lnot OK, p \models _{?} \lnot (p\rightarrow OK)\) to avoid inconsistency. Consider in some case that \(\lnot OK, p, p\rightarrow OK\) is consistent. If follows that \(\lnot OK\wedge OK\), which is inconsistent.
- 3.
In [3]: 11, \(\delta \) is understood as that all things are as required.
- 4.
[3] does not specifically address FCVI and FCCE. I suspect that, in linear logic, one might use the multiplicative operators (multiplicative conjunction \(\otimes \) and multiplicative disjunction
 , which have meanings close to the classical operators) to represent them, i.e.
, which have meanings close to the classical operators) to represent them, i.e. 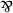 for the invalidity of FCVI, and \((\varphi \otimes \psi )\multimap \delta \not \vdash \varphi \multimap \delta \) for the invalidity of FCCE.
for the invalidity of FCVI, and \((\varphi \otimes \psi )\multimap \delta \not \vdash \varphi \multimap \delta \) for the invalidity of FCCE. - 5.
See also the original proposal in [5]: 233–235.
- 6.
In Briggs (2012), this principle is originally stated as \(s \models \varphi \vee \psi \) if and only if \(s\models \varphi \), \(s\models \psi \), or \(s\models \varphi \wedge \psi \). It will become clear in Sect. 6 that the original one does not suit our purpose for modeling strong permission.
- 7.
It is natural to think that which door the guest opens and which door the car locates have causal effect on which door Monty Hall opens. For example, given the guests choose the door 1 and the car is located at door 2, Monty Hall will open door 3. This causal concern is usefor for revealing the probabilistic dependency among variables under concern. When we construct prescriptive causal models, we assume that Monty Hall, one of the agents involved in the situation, are free to violated causal determination relations.
References
Anderson, A.: The formal analysis of normative systems. In: Rescher, N. (ed.) The Logic of Decision and Action, pp. 147–213. University of Pittsburgh Press, Pittsburgh (1966)
Asher, N., Bonevac, D.: Free choice permission is strong permission. Synthese 145, 303–323 (2005)
Barker, C.: Free choice permission as resource-sensitive reasoning. Semant. Pragmatics 3, 1–38 (2010)
Briggs, R.: Interventionist counterfactuals. Philos. Stud. 160, 139–166 (2012)
Fine, K.: Counterfactuals without possible worlds. J. Philos. CIX, 221–246 (2012)
Pearl, J.: Causality: Models, Reasoning and Inference. Cambridge University Press, Cambridge (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Wang, L. (2017). Strong Permission in Prescriptive Causal Models. In: Otake, M., Kurahashi, S., Ota, Y., Satoh, K., Bekki, D. (eds) New Frontiers in Artificial Intelligence. JSAI-isAI 2015. Lecture Notes in Computer Science(), vol 10091. Springer, Cham. https://doi.org/10.1007/978-3-319-50953-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-50953-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-50952-5
Online ISBN: 978-3-319-50953-2
eBook Packages: Computer ScienceComputer Science (R0)






 , but
, but
 ,
, ,
, if and only if
if and only if 






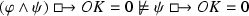
 .
. .
.


 , which have meanings close to the classical operators) to represent them, i.e.
, which have meanings close to the classical operators) to represent them, i.e. 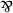 for the invalidity of FCVI, and
for the invalidity of FCVI, and