Multi-Sensor SLAM with Online Self-Calibration and Change Detection

Abstract

We present a solution for constant-time self-calibration and change detection of multiple sensor intrinsic and extrinsic calibration parameters without any prior knowledge of the initial system state or the need of a calibration target or special initialization sequence. This system is capable of continuously self-calibrating multiple sensors in an online setting, while seamlessly solving the online SLAM problem in real-time. We focus on the camera-IMU extrinsic calibration, essential for accurate long-term vision-aided inertial navigation. An initialization strategy and method for continuously estimating and detecting changes to the maximum likelihood camera-IMU transform are presented. A conditioning approach is used, avoiding problems associated with early linearization. Experimental data is presented to evaluate the proposed system and compare it with artifact-based offline calibration developed by our group.

1 Introduction

Autonomous platforms equipped with visual and inertial sensors have become increasingly ubiquitous. Generally these platforms must undergo sophisticated calibration routines to estimate extrinsic and intrinsic parameters to high degrees of certainty before sensor data may be interpreted and fused. Even once fielded, these platforms may experience changes in these parameters. Self-calibration addresses this by inferring intrinsic and/or extrinsic parameters pertaining to proprioceptive and exteroceptive sensors without using a known calibration mechanism or a specific calibration routine. The motivation behind self-calibration is to remove the explicit, tedious, and sometimes nearly impossible calibration procedure from robotic applications such as localization and mapping. By continuously estimating calibration parameters, no prior knowledge of calibration procedures is required. Furthermore, with the addition of statistical change detection on calibration parameters, long-term autonomy applications are greatly robustified.

Fig. 1.

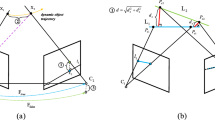
Example pose graph. Poses being estimated (blue) are conditioned on past poses (red) and landmark positions (stars). Both the fixed sliding window and the adaptive window are conditioned on previous poses. The candidate window is not conditioned since it does not make the assumption that previous poses are correctly estimated.

Most current techniques for vision-aided inertial navigation use filtering approaches [1,2,3] or a smoothing formulation. In either case the estimation is made constant-time by rolling past information into a prior distribution. Filtering methods present the significant drawback of introducing inconsistencies due to linearization errors of past measurements which cannot be corrected post hoc, particularly troublesome for non-linear camera models. Some recent work has tackled these inconsistencies; see, e.g. [4,5,6,7]. The state-of-the-art includes methods to estimate poses and landmarks along with calibration parameters, but these approaches do not output the marginals for the calibration parameters, which are desirable for long-term autonomy applications.

To address these considerations, we propose a method that avoids using any prior distribution; instead, a conditioning approach is used [8], coupled with selecting only highly informative segments of the trajectory [9]. The method discards segments capturing degenerate motions which provide little to no information for both camera intrinsic and camera-IMU extrinsic [1, 2] parameters. However, unlike the intrinsic parameters of a linear camera model [10], the convergence basin for the six degree of freedom camera-IMU transform is found to be very narrow. An initialization procedure similar to [11, 12] is employed to initialize the camera-IMU transform, which is then used in a maximum-likelihood estimator. The use of a maximum-likelihood formulation is especially useful as it provides the covariance matrix for the estimated parameters, which makes it possible to establish a fitness score for each segment of the trajectory.

We also propose an extension to the framework presented in [9], allowing for multiple sensors to be self-calibrated in an online setting, leveraging [1, 2] to disambiguate unobservable degrees of freedom. Note that while the global position of the IMU and the rotation axis about gravity are not observable, the following quantities are generally observable: (1) IMU roll and pitch with respect to the horizontal plane; (2) IMU position, orientation and velocity with respect to the initial IMU position; (3) feature position with respect to the initial IMU position; and (4) IMU-to-camera transformation. Finally, we introduce per-sensor candidate trajectory segments, which we find to be necessary to properly estimate each sensors’ relevant parameters online.

2 Formulation and Methodology

A keyframe-based [13] pose-and-landmark non-linear maximum likelihood estimation is performed for real-time map updates. The calibration parameters, including time-varying IMU biases, are also estimated alongside the pose and landmark parameters on the informative segments of the trajectory. The complete state vector is:

$$\begin{aligned} \varvec{X}= \left[ \begin{array}{ccc} \left\{ \begin{array}{cccc} \varvec{x}_{wp_n}&\varvec{v}_{w_n}&\varvec{b}_{g_n}&\varvec{b}_{a_n}\end{array}\right\}&\left\{ \rho _k\right\}&\left\{ \varvec{x}_{c}\right\} \end{array}\right] ^{T}, \end{aligned}$$

(1)

where $\varvec{x}_{wp_n} \in$ SE(3) is the transformation from the coordinates of the $n^\text {th}$ keyframe to world coordinates, $\varvec{v}_{w_n} \in \mathbb {R}^{3}$ is the velocity vector of the $n^\text {th}$ keyframe in world coordinates, and $\varvec{b}_{g_n}\in \mathbb {R}^{3}$ and $\varvec{b}_{a_n}\in \mathbb {R}^{3}$ are the gyroscope and accelerometer bias parameters for the $n^\text {th}$ keyframe respectively. $\left\{ \rho _{k}\right\}$ is the 1-D inverse-depth [14] parameter for the $k^{\text {th}}$ landmark and $\left\{ \varvec{x}_{c}\right\}$ are the calibration parameters. Note that $\varvec{x}_{wp_n}$ has 6 degrees of freedom: 3 for translation, and 3 for rotation. To avoid singularities arising from a minimal representation (e.g. using Euler angles), the rotation component of the transformation is represented as a quaternion, with the optimization lifted to the tangent space (at the identity) of the SO(3) manifold.

Measurements are formed by tracking image keypoints across frames. A landmark parameterized by inverse depth is projected onto an image forming a projected pixel coordinate $\varvec{p}_{proj}$ which is formulated via a transfer function $\varvec{T}$ as follows:

$$\begin{aligned} \nonumber \varvec{p}_{proj}&= \textit{T}\left( \varvec{p}_{r}, \varvec{T}_{wp_m}, \varvec{T}_{wp_r} \varvec{T}_{pc},\rho \right) \\&=\mathscr {P}\left( \varvec{T}_{pc}^{-1}\varvec{T}_{wp_{m}}^{-1}\varvec{T}_{wp_{r}}\varvec{T}_{pc}\mathscr {P}^{-1}\left( \varvec{p}_{r},\rho \right) \right) . \end{aligned}$$

(2)

where $\rho$ is the inverse depth of the landmark, $\varvec{T}_{wp_{r}}$ is the transformation from the coordinates of the reference keyframe (in which the landmark was first seen and initialized) to world coordinates, $\varvec{T}_{wp_{m}}$ is the transformation from the measurement keyframe to world coordinates, $\varvec{p}_{r}$ is the 2D image location where the original feature was initialized in the reference keyframe, $\varvec{p}_{m}$ is the measured 2D image location in the measurement keyframe, $\varvec{T}_{pc}$ is the transformation from the camera to the keyframe coordinates, $\mathscr {P}^{-1}$ is the 2D to 3D back-projection function and $\mathscr {P}$ is the 3D to 2D camera projection function which returns the predicted 2D image coordinates. The camera-to-keyframe transformation $\varvec{T}_{pc}$ is non-identity as the keyframe is collocated on the inertial frame (the frame in which inertial measurements are made), to simplify the inertial integration. $\varvec{T}_{pc}$ is the calibration parameter we have interest in estimating. The usual approach is to assume Gaussian noise and minimize a nonlinear least squares problem with the following residual function:

$$\begin{aligned} r_{\mathscr {V}_{m,k}} =&\Vert \varvec{e}_{\mathscr {V}_{m,k}}\Vert _{\varSigma _{\varvec{p}_{m,k}}}^{2} =\Vert \varvec{p}_{m,k}- \varvec{p}_{proj}\Vert _{\varSigma _{\varvec{p}_{m,k}}}^{2}. \end{aligned}$$

(3)

where $\varvec{p}_{m,k}$ is the measured 2D image location of the $k^\text {th}$ landmark in the $m^\text {th}$ keyframe with covariance $\varSigma _{\varvec{p}_{m,k}}$.

2.1 Initialization

As shown in [11, 12], having a good initial estimate can mean the difference between fast convergence and complete divergence. As such, we leverage the work from [1, 2, 11] which shows that with a minimum of three frames and five tracked features, it is possible to obtain the camera-to-IMU rotation. This initial rotation estimate can then be used to solve a linear system for an initial guess at the translation estimate.

We consider the scenario where enough (five or more) features are observed across at least three frames. The tracked features can be used to obtain the relative rotation between two camera frames i, j: $^{C}R_{ij}$ and integrating the IMU measurements to obtain the relative rotation: $^{B}R_{ij}$, where C represents the camera frame and B the body frame, which is defined without loss of generality as the IMU frame. The following equation relates the camera rotation to the body rotation:

$$\begin{aligned} ^{C}R_{ij} = {^{C}_{B}R} {^{B}R_{ij}} {^{B}_{C}R} \Rightarrow ^{C}R_{ij}{^{C}_{B}R} = {^{C}_{B}R}{^{B}R_{ij}}, \end{aligned}$$

(4)

where ${^{C}_{B}R}$ is the rotation of the body frame in the camera frame. In order to obtain ${^{C}_{B}R}$ we employ an error-state formulation to minimize a robustified over-constrained least squares problem.

In our experience we find that collecting more than 3 frames yielded more reliable estimates; therefore, we use 20 frames for the initial rotation estimate. Once the estimate on ${^{C}_{B}R}$ has converged, translation can be obtained by employing the method described in [11] by solving a linear system derived from transferring the 3D position of a landmark from the camera to the body frame.

2.2 Constant Time Self-Calibration

The constant time self-calibrating framework is briefly summarized here; for more details, refer to [10]. Due to the limited observability and high connectivity of calibration parameters in the SLAM graph, it is impractical to estimate these parameters in real-time applications using conventional filtering or smoothing approaches [3, 7, 15, 16]. Instead every segment of m frames in the trajectory is analyzed, and the n most informative segments are added to a priority queue, where m and n are tuning parameters dependent on the calibration parameters being estimated. In order to assess the informativeness of a segment, a score is computed based on the marginals of the calibration parameters estimated by a particular candidate segment.

If the candidate segment outperforms the worst-scoring window in the priority queue by a predefined margin, it is swapped in. Every time the priority queue is updated, a batch optimization over poses, landmarks and calibration parameters is run on all the segments in the queue to obtain a new set of calibration parameters. As such, the priority queue represents a rolling estimate of the n most informative segments in the trajectory. For estimating camera intrinsic parameters, such as focal length and principal point, only visual measurements are used in the candidate segment. When the camera-to-IMU transform is estimated, inertial residuals are added to the candidate window estimation. The priority queue optimization’s null space therefore requires careful treatment as it is carried out over several non-continuous segments of the trajectory with varying sensor data. Figure 1 shows the optimization windows over a sample set of poses. Figure 2 shows the proposed architecture for multiple sensors.

Fig. 2.

System architecture with two sensors. For new sensors to be added only the blue boxes need to be provided. Asynchronous Adaptive Conditioning and the Priority Queue boxes each run in their own thread (dotted regions). The main thread is only tasked with the maximum-likelihood estimator and analyzing candidate segments.

2.3 Change Detection

The priority queue posterior (with covariance $\varSigma ^\prime _{PQ}$) represents the uncertainty over the calibration parameters considering the top k segments in the trajectory. As these segments are usually not temporally consecutive, this distribution encodes the long term belief over the calibration parameters. Conversely, the candidate segment posterior (with covariance $\varSigma _{s}$) is calculated based on the most recent measurements and represents an instantaneous belief over the calibration parameters. If there is a sudden change in calibration parameters, for example if the camera is rotated or moved to a different location on the platform, then this will manifest as a difference in the means of the two posterior distributions. This task of comparing the means of two multivariate normal distributions with different covariances is known as the Multivariate Behrens-Fisher problem.

When the posterior of the priority queue and the candidate segment is over a set of calibration parameters that represent an SE(3) pose, special attention has to be given to comparing the means of these distributions, particularly with regards to the rotation. A minimal local parameterization is used for the rotation component of the 6 DOF SE(3) pose, so when comparing two posteriors over rotations in the $\mathfrak {so}(3)$ tangent space, one posterior must be transported to the tangent space of the other by means of the Adjoint map, which for SO(3) is:

$$\begin{aligned} {Ad}_{R} : \mathbb {R}^3 \rightarrow \mathbb {R}^3, \quad Ad_{R} = R, \end{aligned}$$

(5)

which allows moving the matrix exponential from the right-hand side to the left-hand side:

$$\begin{aligned} A\cdot exp(\widehat{x}\,) = exp(\widehat{Ad_{A} \cdot x})\cdot A, \end{aligned}$$

(6)

where if $q \in \mathfrak {so}(3)$ is in minimal 3-vector tangent representation, and $M^-_{3 \times 3}$ is the space of $(3 \times 3)$ skew-symmetric matrices, then the map $\widehat{(\cdot )} : q \rightarrow M^-_{3 \times 3}$.

By transporting the tangent space rotation posterior from the candidate segment to the tangent space of the priority queue posterior, the null hypothesis that the means are equal can be tested:

$$\begin{aligned} H_0 = \mu _{PQ} = \mu {s} \end{aligned}$$

(7)

The F distribution for the null hypothesis is as in [9].

2.4 Adaptive Asynchronous Conditioning

An adaptive asynchronous conditioning [8] solution is employed to avoid the use of a prior distribution on the sliding window SLAM. When conditioning is used instead of marginalization, current active parameters are conditioned on previous parameters, which are assumed to be correct. However since new information may alter the estimate for previous poses, a sliding window pose and landmark estimation is run on a separate thread. This sliding window can adaptively increase its size to alter previous poses based on new measurements. The criteria to increase the window is based on the “tension” of the conditioning residuals, explained as follows. Conditioning residuals are the residual terms connecting an active and inactive pose. For example, a landmark that has a reference frame in an inactive pose, but is seen in an active pose will have a conditioning visual residual. The window is expanded when the current estimate for a parameter falls outside of the expected estimate based on the conditioning residual. Since multiple sensor modalities are used, the Mahalanobis distance of each conditioning residual is thresholded in a $\chi ^2$ test to probabilistically determine when a residual is outside of its expected interval (inducing “tension” in that residual).

3 Experimental Results

In order to evaluate the proposed method, experiments were run on two sensor platforms known as “rigs.” Both rigs were equipped with a monocular camera and a commercial grade MEMS-based IMU. Rig A is a smartphone-like mobile device with an integrated global shutter camera with a wide field-of-view lens at $640\times 480$ resolution and a commercial MEMS IMU sampled at 120 Hz. Rig B is a Ximea MQ022CG-CM camera with a wide field-of-view lens at $2040 \times 1080$ resolution downsampled to $640 \times 480$ coupled with a LORD MicroStrain 3DM-GX3 MEMS IMU, sampled at 200 Hz. Cameras on both rigs capture images at 30 frames per second. In all experiments, the AAC system is comprised of a fixed-window estimator with a 10 keyframe window width and an asynchronous adaptive estimator (as per Sect. 2.4) with a minimum window size of 20 keyframes. As broached in Sect. 2.1, when both the camera intrinsic parameters and the camera-to-IMU transform are unknown, an initial batch optimization comprising all poses, landmarks and calibration parameters (but no IMU measurements) runs until its entropy falls below a predetermined threshold, at which point the camera intrinsic calibration is handed over to the self-calibration framework discussed in Sect. 2.2. At this point the IMU initialization procedure is engaged—first separately estimating rotation and translation by solving a linear system, then handing over initial estimates on the camera-to-IMU transform to a batch estimation for refinement. Once the batch camera-to-IMU estimation has fallen below a predetermined entropy, the estimation is passed on to the rolling self-calibrating framework for constant-time estimation.

Fig. 3.

Results of a reconstructed indoor dataset spanning 1200 keyframes and 2972 frames. The priority queue consisted of 5 segments with 30 poses in each segment. Camera-to-IMU translation and rotation estimates (solid blue line), with their 3 sigma bounds (dotted red line). The pseudo ground truth (solid black line), obtained by offline calibration procedures is shown to be close to the online estimates, with average sub-degree rotation error and centimeter-level translation error.

The first experiment was run on Rig A, with unknown camera and camera-to-IMU calibration parameters. The camera calibration was initialized to common values: focal lengths $f_x$ and $f_y$ were set to $90^\circ$ and the central points $c_x$ and $c_y$ were set to half the image width and height, respectively. The initial camera-to-IMU transform is set to identity, i.e. that the sensors are co-located. Figure 3 shows the results of camera-to-IMU estimation of the system running on a sample data-set, in which it can be seen that the priority queue is successfully tracking the offline estimates [17]. Of note are the limited observability of the rotation about the axis of gravity (yaw) and the relatively constant uncertainty. This is due to the fixed number of segments in the priority queue, which can be expanded to include more segments and approximate the batch estimate, at the cost of computational processing. Figure 4 shows the camera intrinsics on the same dataset.

A second experiment was performed on Rig B, where only the camera-to-IMU parameters were being estimated, but the position of the IMU was physically changed mid-dataset. This experiment’s results are show in Fig. 5.

Fig. 4.

Self-calibration camera intrinsic parameters. Neither camera intrinsic or camera-to-IMU extrinsic parameters were known. Even with total uncertainty on all calibration parameters at the start, convergence to offline values is observed for both camera intrinsic and extrinsic parameters.

Fig. 5.

Indoor dataset on Rig B, the IMU position was manually changed mid-dataset. Only the y component of translation was changed, all other parameters remained the same. as shown by the pseudo ground truth line (black line). The system automatically detected a change in mean and re-estimated all parameters.

4 Discussion

In Fig. 4, a sharp drop is witnessed in uncertainty on all intrinsic parameters around keyframe 820, where a particularly informative segment was swapped into the queue. The same behavior is not witnessed around keyframe 820 for the camera-to-IMU transform estimate in Fig. 3, which strongly suggests the need for different queues for different sensors. Supporting the initialization sequence used for SE(3) transform approximation, Fig. 5 demonstrates rapid convergence to new translation parameters when the sensors are moved with respect to one another on Rig B. The entropy of the priority queue increases temporarily until enough post-change segments are added.

Some discrepancies between the offline values and the estimates from the priority queue can be observed (such as on the rotation values in Fig. 3). This can be caused by a number of factors: (1) the offline calibration is only a pseudo-ground truth, and (2) lack of observability of these parameters, especially yaw, since we only use naturally occurring features. Note that the self-calibration sequence we suggest relies on non-degenerate motions that excite the appropriate degrees of freedom so as to render them observable, which we have found to occur naturally in experimental hand-held datasets.

A particular failure case is through slow changes of calibration parameters through a data collection. Changes in parameter values are currently induced as a step function; however, if a calibration parameter changes incrementally over time, it will not trigger a change event, as per Sect. 2.3. Instead, new segments with low entropy will be swapped into the priority queue, mixed with past segments that presented a different mean. Another failure case is related to the determinant-based scoring system, which could result in a very low uncertainty for an unobservable parameter. These drawbacks warrant further development of a more robust scoring system.

5 Conclusions and Future Work

This paper presents online, constant-time self-calibration and change detection with re-calibration for joint estimation of camera-to-IMU transform and camera intrinsic parameters, using only naturally occurring features. The system is evaluated with experimental data and shown to converge to offline calibration estimates with centimeter level accuracy for camera-to-IMU translation, and sub-degree accuracy for rotation. The statistical change detection framework presented in [9] and summarized in Sect. 2.3 has been extended to the camera-to-IMU transform, including a statistical comparison of distributions over candidate segments for a SE(3) pose.

The use of an adaptive conditioning window for re-estimation of past poses allows this framework to operate in long-term applications where the accumulation of linearization errors in a prior distribution would lead to significant drift. We presented a framework that supports adding additional sensors while maintaining online operation. To the authors’ best knowledge this is the first application of multi-sensor self-calibration with automatic change detection and re-estimation of parameters.