Higher Order Finite Element Methods

Abstract

The efficiency of numerical methods for wave propagation analysis is essential, as very fine spatial and temporal resolutions are required in order to properly describe all the phenomena of interest, such as scattering, reflection, mode conversion, and many more. These strict demands originate from the fact that high-frequency ultrasonic guided waves are investigated. In the current chapter, we focus on the finite element method (FEM) based on higher order basis functions and demonstrate its range of applicability. Thereby, we discuss the p-FEM, the spectral element method (SEM), and the isogeometric analysis (IGA). Additionally, convergence studies demonstrate the performance of the different higher order approaches with respect to wave propagation problems. The results illustrate that higher order methods are an effective numerical tool to decrease the numerical costs and to increase the accuracy. Furthermore, we can conclude that FE-based methods are principally able to tackle all wave propagation-related problems, but they are not necessarily the most efficient choice in all situations.

1 Higher Order Finite Element Methods: One-Dimensional Case

We already explained the basic idea of the finite element method (FEM) in Chap. 4 and derived the semi-discrete equations of motion, cf. Eq. (4.42). In this context, we also introduced the basis function matrices in Eqs. (4.43) and (4.44) without specifying the polynomial functions. In Sects. 6.1.1–6.1.3, different higher order FEM schemes are discussed. The only difference between these approaches lies in the choice of the type of basis functions.

Generally speaking, wave propagation problems require particularly accurate solutions [25], as they are very sensitive to numerical dispersion errors. In finite element simulations, the term dispersion error refers to the fact that the higher frequency components in a wave packet may exhibit a phase lead and accordingly propagate faster than they theoretically should (equivalent to the pollution effect in the frequency domain). This can cause unwanted interferences. Moreover, it can be proven that the pollution error increases with increasing frequency, and consequently, the number of finite elements per wavelength is also increasing to achieve a constant global error. However, in the following we demonstrate that the error is reduced if finite elements with higher order polynomials as basis functions are employed. Therefore, even today the task of simulating elastic waves is a highly demanding one.

One of the main challenges is to develop efficient numerical methods that reduce the computational effort resulting from very fine spatial and temporal discretizations [6, 34]. In our studies, we found that higher order methods are suitable to reduce the numerical costs significantly and that they are also applicable to all types of problems related to wave propagation [14, 55]. In this context, we make use of two advantages that higher order FEMs offer:

• 1. Anisotropic ansatz spaces, and

• 2. Free of locking phenomena.

The anisotropic ansatz space is important to represent shell-like structures using continuum elements [7, 15]. In such structures, locking is often encountered but can easily be avoided if the polynomial degree is chosen high enough, i.e. p ≥ 4 [15].

The content of the current chapter is essentially based on several PhD theses and related journal articles that have been published by the corresponding authors [1, 12, 20, 52, 53].

1.1 p-Version of the Finite Element Method

As mentioned before, all higher order FEMs that we discuss in Chap. 6 only differ in the choice of basis functions. The basis functions of the p-FEM are the normalized integrals of the Legendre polynomials. Following the methodology presented by Szabó and Babuška [49, 50], we demonstrate how hierarchical basis functions of arbitrary polynomial degree can be constructed.

In the one-dimensional case, the basis functions are defined on the reference element Ω _ref ¹ = (−1, 1), cf. Fig. 6.1. The internal degrees of freedom are not attached to the geometry because they do not retain a physical interpretation. They are only unknowns for the polynomial ansatz to describe the primary variables.

Fig. 6.1

A one-dimensional reference element with the numbering of the degrees of freedom. The illustration is based on the notion of hierarchical basis functions

The first two hierarchic basis functions associated with the two nodes 1 and 2 are the well-known linear basis functions given as

$$\displaystyle\begin{array}{rcl} N_{1}^{p\text{-}\mathrm{FEM}}(\xi _{ 1}) = \frac{1} {2}\left (1 -\xi _{1}\right ),& &{}\end{array}$$

(6.1)

$$\displaystyle\begin{array}{rcl} N_{2}^{p\text{-}\mathrm{FEM}}(\xi _{ 1}) = \frac{1} {2}\left (1 +\xi _{1}\right ).& &{}\end{array}$$

(6.2)

The higher order terms that are not associated with physical nodes are defined in terms of the normalized integrals of the Legendre polynomials

$$\displaystyle{ N_{n}^{p\text{-}\mathrm{FEM}}(\xi _{ 1}) = \frac{1} {\mathscr{L}_{n-2}}\int _{x_{1}=-1}^{\xi _{1} }L_{\text{e}_{n-2}}(x_{1})\mathrm{d}x_{1},\quad n = 3,\,4,\,\ldots,\,p + 1\;, }$$

(6.3)

where $\mathscr{L}_{n-2}$ denotes the norm of the Legendre polynomial

$$\displaystyle{ \mathscr{L}_{n-2} =\ \sqrt{ \frac{2} {2n - 3}}\;. }$$

(6.4)

The higher order basis functions N _n ^p-FEM are zero at the nodes 1 and 2 and can be computed by means of a simple recursion formula

$$\displaystyle{ N_{n}^{p\text{-}\mathrm{FEM}}(\xi _{ 1}) = \frac{1} {2}\mathscr{L}_{n-2}\left [L_{\text{e}_{n-1}}(\xi _{1}) - L_{\text{e}_{n-3}}(\xi _{1})\right ],\quad n = 3,\,4,\,\ldots,\,p + 1\;, }$$

(6.5)

with $L_{\text{e}_{i}}(\xi _{1})$ denoting the Legendre polynomial of order i. The Legendre polynomials belong to the class of orthogonal polynomials and are a special type of the Jacobi polynomials [48]. They satisfy the Legendre differential equation

$$\displaystyle\begin{array}{rcl} \left (1 - x_{1}^{2}\right )x_{ 2}'' - 2x_{1}x_{2}' + n\left (n + 1\right )x_{2} = 0,\quad n = 0,\,1,\,2,\,\ldots,\quad - 1 \leq x_{1} \leq 1.& &{}\end{array}$$

(6.6)

We can compute the Legendre polynomials either analytically by means of Rodriguez’ formula

$$\displaystyle{ L_{\text{e}_{n}}(x_{1}) = \frac{1} {2^{n}n!} \frac{\mathrm{d}^{n}} {\mathrm{d}x_{1}^{n}} \times \left (x_{1}^{2} - 1\right )^{n},\quad n = 0,\,1,\,2,\,\ldots,\quad - 1 \leq x_{ 1} \leq 1, }$$

(6.7)

or numerically using Bonnet’s recursion formula

$$\displaystyle\begin{array}{rcl} L_{\text{e}_{n}}(x_{1})& =& \frac{1} {n}\left [(2n - 1)x_{1}L_{\text{e}_{n-1}}(x_{1}) - (n - 1)L_{\text{e}_{n-2}}(x_{1})\right ]\;, \\ n& =& 2,\,3,\,4,\,\ldots,\quad - 1 \leq x_{1} \leq 1. {}\end{array}$$

(6.8)

The first two Legendre polynomials are needed to start the recursion process and are provided at this point by

$$\displaystyle\begin{array}{rcl} L_{\text{e}_{0}}(x_{1}) = 1\;,& &{}\end{array}$$

(6.9)

$$\displaystyle\begin{array}{rcl} L_{\text{e}_{1}}(x_{1}) = x_{1}\;.& &{}\end{array}$$

(6.10)

The roots of the Legendre polynomials are the integration points for the standard Gaussian quadrature scheme and therefore lie in the interval [−1,  1].

One important feature of this set of polynomials is their orthogonality with respect to the weight function w = 1

$$\displaystyle{ \int _{-1}^{1}L_{\text{e}_{ i}}(x_{1})L_{\text{e}_{j}}(x_{1})\mathrm{d}x_{1} = \left \{\begin{array}{@{}l@{\quad }l@{}} \frac{2} {2i+1}\quad &\mathrm{if}\quad i = j\;, \\ 0 \quad &\mathrm{if}\quad i\neq j\;. \end{array} \right. }$$

(6.11)

The orthogonality property of the Legendre polynomials also implies that the derivatives of the basis functions are orthogonal

$$\displaystyle{ \int _{-1}^{1}\frac{\mathrm{d}N_{n}^{p\text{-}\mathrm{FEM}}(\xi _{ 1})} {\mathrm{d}\xi _{1}} \frac{\mathrm{d}N_{m}^{p\text{-}\mathrm{FEM}}(\xi _{1})} {\mathrm{d}\xi _{1}} \mathrm{d}\xi _{1} =\delta _{nm},\quad n,\,m \geq 3\;. }$$

(6.12)

Because of this feature, the condition number of the (element) stiffness matrix is significantly decreased.

The first five basis functions corresponding to a polynomial degree of p = 4 are illustrated in Fig. 6.2. By means of a graphical representation, we can easily explain the concept of hierarchical basis functions. Generally speaking, in a hierarchic set of basis functions all lower order polynomials up to order ( p − 1) are contained in the set of basis functions of order p. Therefore, if the polynomial degree is elevated, we only need to add one new basis function without recomputing the lower order ones, cf. Fig. 6.2. This hierarchy also translates to the system matrices [15]. The behavior of nodal-based basis functions is fundamentally different in that regard.

Fig. 6.2

Hierarchic basis functions based on the normalized integrals of the Legendre polynomials: a solid black line denotes N ₁ ^p-FEM, a solid red (bright) line represents N ₂ ^p-FEM, a dashed black line stands for N ₃ ^p-FEM, a dashed red (bright) line marks N ₄ ^p-FEM, and N ₅ ^p-FEM is signified by a black line marked with filled squares

The derivatives of the Legendre polynomials that are required to compute the derivatives of the basis functions can also be expressed by means of the Legendre polynomials themselves

$$\displaystyle{ \frac{\mathrm{d}L_{\text{e}_{n}}(\xi _{1})} {\mathrm{d}\xi _{1}} = \frac{n} {\xi _{1}^{2} - 1}\left (\xi _{1}L_{\text{e}_{n}}(\xi _{1}) - L_{\text{e}_{n-1}}(\xi _{1})\right )\;. }$$

(6.13)

1.2 The Spectral Element Method

In the context of the spectral element method (SEM) , we typically use a polynomial expansion which is based on the Lagrange interpolation polynomials $L_{\text{a}_{n}}^{p}(\xi _{1})$. The presentation of this type of basis functions follows the explanations given in [27, 40]. Lagrange polynomials are also defined within the elemental reference region, cf. Fig. 6.3. However, this time all degrees of freedom retain their physical meaning and therefore we can assign each node also a physical location.

Fig. 6.3

A one-dimensional reference element with the numbering of the degrees of freedom. The illustration is based on the notion of nodal basis functions

The Lagrange polynomials of order p are based on a set of p + 1 nodal points ξ ₁ ^k which are chosen in advance? They can be distributed in an equidistant or non-equidistant fashion within the reference interval. For reasons, we will discuss later, it is preferable to choose a non-equidistant series of nodes. The basis functions for the SEM are generally given as

$$\displaystyle{ N_{n}^{\mathrm{SEM},p}(\xi _{ 1}) = L_{\text{a}_{n}}^{p}(\xi _{ 1}) =\prod \limits _{ k=1,\;k\neq n}^{p+1} \frac{\xi _{1} -\xi _{1}^{k}} {\xi _{1}^{n} -\xi _{1}^{k}}, }$$

(6.14)

where ξ ₁ ^k denotes the nodal points and ξ ₁ ⁿ represents the node corresponding to the nth basis function. In the current work, we use the Gauß–Lobatto–Legendre (GLL) points [28, 30, 51] which are defined as

$$\displaystyle{ \xi _{1}^{k} = \left \{\begin{array}{@{}l@{\quad }l@{}} -1 \quad &\mathrm{if}\;k = 1 \\ ^{k-1}\xi _{1}^{L_{\text{o}_{0}}^{p-1} }\quad &\mathrm{if}\;2 \leq k \leq p \\ +1 \quad &\mathrm{if}\;k = p + 1 \end{array} \right.\;. }$$

(6.15)

Here, $\boldsymbol{\xi }_{1}^{L_{\text{o}_{0}}^{p-1} }$ denotes the complete set of roots of the Lobatto polynomials of order p − 1. The Lobatto polynomials are the derivatives of the Legendre polynomials. Therefore, they can be analytically computed by

$$\displaystyle{ L_{\text{o}_{n}}(\xi _{1}) = \frac{1} {2^{n}n!} \frac{\mathrm{d}^{n+1}} {\mathrm{d}\xi _{1}^{n+1}} \cdot \left (\xi _{1}^{2} - 1\right )^{n},\quad n = 0,\,1,\,2,\,\ldots,\quad - 1 \leq \xi _{ 1} \leq 1. }$$

(6.16)

Figure 6.4 illustrates the basis functions for the polynomial degrees from p = 1 to p = 4. All basis functions have to be recomputed when increasing the polynomial degree as the set of functions is non-hierarchic.

Fig. 6.4

Spectral basis functions: a solid black line denotes N ₁ ^SEM, a solid red (bright) line represents N ₂ ^SEM, a dashed black line stands for N ₃ ^SEM, a dashed red (bright) line marks N ₄ ^SEM, and N ₅ ^SEM is signified by a black line marked with filled squares

The computation of the Lagrange polynomials by means of Eq. (6.14) is not very efficient and therefore we suggest a different approach [40]. First, an auxiliary polynomial is introduced as

$$\displaystyle{ \varTheta _{p+1}(\xi _{1}) =\prod \limits _{ k=1}^{p+1}\left (\xi _{ 1} -\xi _{1}^{k}\right )\,. }$$

(6.17)

Its first derivative with respect to ξ ₁ at ξ ₁ ⁿ is computed by means of the product rule of differentiation resulting in

$$\displaystyle{ \varTheta '_{p+1}(\xi _{1}^{n}) =\prod \limits _{ k=1,\;k\neq n}^{p+1}\left (\xi _{ 1}^{n} -\xi _{ 1}^{k}\right )\;. }$$

(6.18)

In a next step, we use the first derivative at ξ ₁ ⁿ to compute the barycentric weights c _n  by

$$\displaystyle{ c_{n} = \frac{1} {\varTheta '_{p+1}(\xi _{1}^{n})}\;. }$$

(6.19)

Fortunately, we can precompute them in order to increase the efficiency. The Lagrange basis functions can now be evaluated using

$$\displaystyle{ N_{n}^{\mathrm{SEM}}(\xi _{ 1}) = L_{\text{a}_{n}}^{p}(\xi _{ 1}) = \left \{\begin{array}{@{}l@{\quad }l@{}} c_{n}\frac{\varTheta _{p+1}(\xi _{1})} {\xi _{1}-\xi _{1}^{i}} \quad &\mathrm{for}\;\xi _{1}\neq \xi _{1}^{i} \\ 1 \quad &\mathrm{for}\;\xi _{1} =\xi _{ 1}^{i} \end{array} \right.\;. }$$

(6.20)

The first derivatives of the Lagrange polynomials are computed analogously and are given by

$$\displaystyle{ N_{n}^{{\prime}\mathrm{SEM}}(\xi _{ 1}) = L_{\text{a}_{n}}^{{\prime}p}(\xi _{ 1}) = \left \{\begin{array}{@{}l@{\quad }l@{}} L_{\text{a}_{n}}^{p}(\xi _{1})\sum \limits _{k=1,\;k\neq n}^{p+1} \frac{1} {\xi _{1}-\xi _{1}^{k}}\quad &\mathrm{for}\;\xi _{1}\neq \xi _{1}^{k} \\ \frac{c_{i}} {(\xi _{1}-\xi _{1}^{n})c_{k}} \quad &\mathrm{for}\;\xi _{1} =\xi _{ 1}^{k},\,n\neq k \\ \sum \limits _{k=1,\;k\neq n}^{p+1} \frac{1} {\xi _{1}-\xi _{1}^{k}} \quad &\mathrm{for}\;\xi _{1} =\xi _{ 1}^{k},\,n = k \end{array} \right.\;. }$$

(6.21)

A more detailed derivation of these formulae is given in the monograph by Pozrikidis [40] (see Chap. A.2).

In the remainder of the book, we use the GLL nodal distribution if not specified otherwise. In the context of seismic wave propagation problems, the Chebyshev–Gauß–Lobatto (CGL) grid is favored [35, 46, 47]

$$\displaystyle{ \xi _{1}^{k} = \left \{\begin{array}{@{}l@{\quad }l@{}} -1 \quad &\mathrm{if}\;k = 1 \\ -\cos \left (\frac{k\pi } {p}\right )\quad &\mathrm{if}\;2 \leq k \leq p \\ +1 \quad &\mathrm{if}\;k = p + 1 \end{array} \right.\;. }$$

(6.22)

The properties of the resulting numerical schemes are very similar in cases of other distributions, so that they are not considered here.

1.3 The Isogeometric Analysis

The isogeometric analysis (IGA) was developed to bridge the gap between finite element analysis (FEA) and computer-aided design [8, 23]. Typically nonuniform rational B-splines (NURBS) are deployed as basis functions [41]. Since B-splines are the building blocks of NURBS, we start with a brief definition of the univariate basis. For a detailed presentation of B-splines and NURBS, the interested reader is referred to the monograph by Piegl and Tiller [38].

1.3.1 B-Spline Curve

A B-spline basis of degree p is formed by a sequence of ascending values called knot vector Ξ ₁ = [ξ ₁ ¹, ξ ₁ ², …, ξ ₁ ^n+p+1]. Univariate B-spline basis functions can be computed using the Cox-de Boor recursion formula

$$\displaystyle{ N_{i}^{\mathrm{B},p}(\xi _{ 1}) = \frac{\xi _{1} -\xi _{1}^{i}} {\xi _{1}^{i+p} -\xi _{1}^{i}}N_{i}^{\mathrm{B},p-1}(\xi _{ 1}) + \frac{\xi _{1}^{i+p+1} -\xi _{1}} {\xi _{1}^{i+p+1} -\xi _{1}^{i+1}}N_{i+1}^{\mathrm{B},p-1}(\xi _{ 1}),\quad p \geq 0\;. }$$

(6.23)

The recursion starts with the piecewise constant ( p = 0) basis function

$$\displaystyle{ N_{i}^{\mathrm{B},0}(\xi _{ 1}) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\mathrm{if}\;\xi _{1}^{i} \leq \xi _{1} \leq \xi _{1}^{i+1} \\ 0\quad &\mathrm{otherwise} \end{array} \right.\;. }$$

(6.24)

If the knot vector Ξ ₁ has repeated entries, the smoothness of the B-spline is decreased at this location. A repeated knot of multiplicity k results in a C _p−k -continuous function at that location. With Eq. (6.23), the B-spline basis functions are given and we can build a B-spline curve by a linear combination of these basis functions

$$\displaystyle{ \mathbf{C}_{\mathrm{Bs}}(\xi _{1}) =\sum \limits _{ i=1}^{n}\mathbf{P}_{ i}N_{i}^{\mathrm{B},p}(\xi _{ 1})\;, }$$

(6.25)

where P _i denotes the coordinates of the control points. A piecewise linear interpolation of these points is referred to as control polygon.

In order to be able to compute the derivatives of a B-spline curve, we first need to define the derivative of an arbitrary B-spline basis function as [38]

$$\displaystyle{ \frac{\mathrm{d}N_{i}^{\mathrm{B},p}(\xi _{1})} {\mathrm{d}\xi _{1}} = \frac{p} {\xi _{1}^{i+p} -\xi _{1}^{i}}\;N_{i}^{\mathrm{B},p-1}(\xi _{ 1}) - \frac{p} {\xi _{1}^{i+p+1} -\xi _{1}^{i+1}}\;N_{i+1}^{\mathrm{B},p-1}(\xi _{ 1})\;. }$$

(6.26)

If we substitute Eq. (6.26) into Eq. (6.25), we obtain the first derivative of a B-spline curve with respect to ξ ₁

$$\displaystyle{ \frac{\mathrm{d}\mathbf{C}_{\mathrm{Bs}}(\xi _{1})} {\mathrm{d}\xi _{1}} =\sum \limits _{ i=1}^{n}\mathbf{P}_{ i}\frac{\mathrm{d}N_{i}^{\mathrm{B},p}(\xi _{1})} {\mathrm{d}\xi _{1}} \;. }$$

(6.27)

The set of B-spline basis functions is also a nonhierarchical one but it provides the advantage of higher inter-element continuity. Depending on the chosen polynomial degree p, these functions can be C _p−1-continuous. This aspect has advantages for dynamic problems as shown in [8, 53, 55].

1.3.2 Nonuniform Rational B-Spline Curve

In the one-dimensional case, NURBS are obtained from B-splines by a projection from the two-dimensional space [8]. Univariate NURBS basis functions N _i ^IGA,p are given by

$$\displaystyle{ N_{i}^{\mathrm{IGA},p}(\xi _{ 1}) = \frac{w_{i}N_{i}^{\mathrm{B},p}(\xi _{1})} {\sum \limits _{j=1}^{p}w_{j}N_{j}^{\mathrm{B},p}(\xi _{1})}\;, }$$

(6.28)

where N _i ^B,p(ξ ₁) are the polynomial B-spline basis functions and w _i denote the weights. The derivative of the NURBS basis functions can be computed straightforwardly by applying the quotient rule of differentiation in conjunction with Eq. (6.26).

Figure 6.5 illustrates the basis functions for the polynomial degrees from p = 1 to p = 4. To illustrate the higher order continuity of IGA basis functions, we show a domain consisting of two elements. The separation is indicated in the figure by a gray dashed line.

Fig. 6.5

Isogeometric basis functions: due to the higher continuity (C _p−1) of NURBS-based basis functions, two elements are depicted, separated by the gray dashed line. Depending on the location of the local maximum of these functions, the following colors have been chosen—black denotes that the maximum is in the first element, while red indicates that the maximum value occurs in the second element

The definition of suitable control points P _i and weights w _i can be done analytically in a straightforward manner only for simple geometries [38]. For more complex problems, they can be derived from CAD tools such as Rhino^®;.

2 Comparison of the Properties of Different Higher Order Finite Element Approaches

In principle, we have to note that all different higher order approaches span the same polynomial space. Nevertheless, there are specific advantages and disadvantages for the methods discussed in Sects. 6.1.1–6.1.3. Some of those features have already been mentioned but will be repeated at this point for the sake of completeness .

2.1 Hierarchic Basis Functions

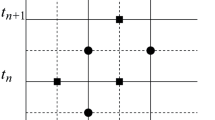
The advantages of hierarchic sets of basis functions over non-hierarchic ones is that only one basis function is added to a preexisting set when the polynomial degree is increased from p to p + 1 (p-adaptivity). In the case of non-hierarchic basis functions, we have to recompute the whole set of basis functions resulting in an increased numerical effort [12, 15, 49, 50]. This feature has also an immediate effect on the structure of the system matrices. Here, we also notice that the mass and stiffness matrices for the polynomial degree p are a subset of those corresponding to the polynomial degree p + 1. This behavior is illustrated in Fig. 6.6. The different shades of gray indicate the components of the matrices that belong to certain polynomial degrees.

Fig. 6.6

Hierarchic structure of the stiffness matrix and the load vector for p = 3

2.2 Nodal Basis Functions

Nodal basis functions that are used in the SEM (see Sect. 6.1.2) offer the advantage that each degree of freedom also corresponds to the primary variable at the location of the corresponding node [40]. Therefore, the degrees of freedom retain a physical meaning. The reason for this behavior lies in the Kronecker delta property of this type of basis functions. In the case of modal basis functions introduced in Sects. 6.1.1 and 6.1.3, the degrees of freedom only describe unknowns of the chosen ansatz. Consequently, we need an additional post-processing step to compute the primary variables.

Another advantage of nodal-based functions is that there are readily available mass-lumping techniques, see Sect. 4.6.3. Using a diagonal mass matrix, we can fully exploit the benefits provided by explicit time-integration schemes, see Sect. 4.6.1. Remembering that if we use a consistent mass matrix formulation, a system of equations has to be solved for each time step, while a diagonalized mass matrix results in a time-stepping scheme where only matrix-vector operations are required. Consequently, it is highly advantageous to be able to employ explicit time-marching schemes especially considering ultrasonic wave propagation analysis. Here, the time step is naturally limited by the high-frequency regime and therefore explicit time-stepping algorithms are the method of choice in these situations [9–11]. To our knowledge, suitable mass matrix diagonalization techniques for modal-based and/or hierarchic basis functions are currently not available.

The most important advantages and disadvantages of each type of basis functions are compiled in Table 6.1 [12, 55].

Table 6.1 Comparison of key features of the different basis function types (one-dimensional case)

3 Multivariate Basis Functions

In Sect. 6.1, we introduced the univariate basis functions for different higher order finite element approaches . In the present section, we want to generalize the one-dimensional case to multiple dimensions. As already mentioned in Sect. 4.4, the implementation of two- or three-dimensional basis functions is based on a quadrilateral or hexahedral element formulation. The reason for this choice is justified by the higher accuracy compared to triangular or tetrahedral element formulations [15]. In the book at hand, we only consider the tensor product space which consists of all polynomials spanned by the set of monomials

• ξ ₁ ⁱ ξ ₂ ^j(ξ ₃ ^k) with i = 0, 1, 2, …, p ₁, j = 0, 1, 2, …, p ₂, (k = 0, 1, 2, …, p ₃).

The terms in the round brackets denote a three-dimensional implementation. An alternative would be the trunk space (serendipity-type elements) which is commonly deployed in the p-version of the FEM [49, 50].

In the context of higher order FEMs, multivariate basis functions are defined by the tensor product of the univariate basis functions and therefore they are given by

$$\displaystyle\begin{array}{rcl} ^{2\text{D}}N_{ l}^{\mathrm{type,\mathbf{p}}}(\boldsymbol{\xi }) = N_{ i}^{\mathrm{type},p_{1} }(\xi _{1})N_{j}^{\mathrm{type},p_{2} }(\xi _{2})\;,& &{}\end{array}$$

(6.29)

$$\displaystyle\begin{array}{rcl} ^{3\text{D}}N_{ l}^{\mathrm{type,\mathbf{p}}}(\boldsymbol{\xi }) = N_{ i}^{\mathrm{type},p_{1} }(\xi _{1})N_{j}^{\mathrm{type},p_{2} }(\xi _{2})N_{k}^{\mathrm{type},p_{3} }(\xi _{3})\;.& &{}\end{array}$$

(6.30)

The polynomial degrees in the local coordinates are denoted by p _i . The superscript “type” indicates the type of basis functions that are being used: (1) p-FEM (see Sect. 6.1.1), (2) SEM (see Sect. 6.1.2), and (3) IGA (see Sect. 6.1.3); while the subscripts (i, j, k) specify the number of the one-dimensional shape functions. The index l stands for the number of the overall basis function

$$\displaystyle\begin{array}{rcl} i& =& 1,\,2,\,\ldots,\,p_{1} + 1\;, {}\\ j& =& 1,\,2,\,\ldots,\,p_{2} + 1\;, {}\\ k& =& 1,\,2,\,\ldots,\,p_{3} + 1\;, {}\\ l& =& 1,\,2,\,\ldots,\,(\,p_{1} + 1)(\,p_{2} + 1)(\,p_{3} + 1)\;. {}\\ \end{array}$$

A relation between the indices (i, j, k) and the basis function number l is defined separately according to the chosen numbering conventions.

4 Benchmark Problems

In the current section, one wave propagation-related problem is solved with each of the three different higher order FE approaches. In Sect. 6.4.1, we investigate the modal behavior of a piezoelectric disc actuator by means of the p-version of the FEM. Such a transducer is often used to excite ultrasonic guided waves in thin-walled structures. The second problem features a two-dimensional porous plate and is investigated in Sect. 6.4.2 deploying the SEM. Finally, in Sect. 6.4.3 we use the IGA to simulate the mode conversion behavior in a three-dimensional perforated plate.

The validation examples presented in Sects. 6.4.1–6.4.3 are taken from journal articles and PhD theses that have been published during the last 5 years in our research group. The chosen benchmark problems are of interest when dealing with the propagation of ultrasonic guided waves. Apart from the numerical problems that are discussed in the following, also other validation examples have been simulated confirming the performance of higher order FEMs in the context of high-frequency wave propagation analysis. For more information in that regard, the interested reader is referred to [12–14, 42, 53–55] and the references cited therein.

4.1 p-FEM: Modal Analysis of a Three-Dimensional Piezoelectric Disc

The first example is the modal analysis of a piezoelectric circular disc [12, 53], cf. Fig. 6.7. Here, we seek to compute the eigenfrequencies and the eigenmodes. The effect of a resonance on the wave field has been demonstrated by Pohl et al. [39] and Huang et al. [22]. Corresponding to the mode shape of the transducer, the wave field is distorted as well. Considering signal processing approaches, discussed in Chaps. 13–16, it is important that the propagating wave packets are not influenced by the excitation source itself. Therefore, it is necessary to take the dynamic behavior of the piezoelectric actuator into account.

Fig. 6.7

Geometry and electrical boundary conditions of the circular piezoelectric disc transducer. The diameter of the disc is d _pd = 0. 03 m and the thickness is t _pd = 0. 001 m. Depending on the state of the transducer (open or short-circuited electrodes), the electrical boundary conditions φ ₁ and φ ₂ are specified on the bottom and the top surface of the actuator

The influence of the electro-mechanical coupling is best seen when studying the analytical equations, i.e., Eq. (4.42). The mechanical boundary conditions are chosen to be free, while as electrical ones we examine the two limit cases:

• 1. Short-Circuited Electrodes, and

• 2. Open Electrodes.

In the first case, there is no coupling between the mechanical and electrical properties [37] and consequently the analytical solutions for a free circular plate can be used as a reference [17, 21]. The situation is different if we introduce a charge separation between the electrodes and hence an electric field is generated. This results in a stiffer behavior of the plate and thus higher eigenfrequencies compared to the purely elastic case are achieved.

4.1.1 Short-Circuited Electrodes

Considering short-circuited electrodes, the electric potential is controlled (Φ = 0). Consequently, we can directly solve the first row of the semi-discrete equations of motion in Eq. (4.42) as the electric potential is a priori known. This approach results in the following equation

$$\displaystyle{ \mathbf{M}_{\text{u}}\ddot{\mathbf{U}} + \mathbf{K}_{\text{u}}\mathbf{U} = \mathbf{f}_{\text{u}} -\mathbf{K}_{\text{u}\varphi }\boldsymbol{\varPhi }\;. }$$

(6.31)

The second term on the right-hand side of the system of equations represents the piezoelectric load. From Eq. (6.31), we can compute the mechanical displacements U and thereafter the electric charges f _φ are determined by inserting the results into the second row of Eq. (4.42). Another important result that follows immediately from the derived equation is that the eigenvalues of this system with short-circuited electrodes are identical to the elastic ones

$$\displaystyle{ \left (\mathbf{K}_{\text{u}} -\varLambda _{i}\mathbf{M}_{\text{u}}\right )\mathbf{U}_{i} = \mathbf{0}\;, }$$

(6.32)

where Λ _i is the square of the ith angular eigenfrequency $\omega _{ \text{R}_{i}}$ that can be computed in terms of the linear eigenfrequency $f_{\text{R}_{ i}}$

$$\displaystyle{ \varLambda _{i} =\omega _{ \text{R}_{ i}}^{2} = (2\pi f_{ \text{R}_{i}})^{2}\;. }$$

(6.33)

In Eq. (6.32), we note that all electro-mechanical coupling terms are neglected for short-circuited electrodes.

4.1.2 Open Electrodes

In contrast to short-circuited electrodes, open ones are specified by a charge boundary condition (f _φ = 0). In this case, we rearrange the second row of the semi-discrete equations of motion Eq. (4.42). According to Eq. (4.71) and the explanations given above, the electric potential is computed as

$$\displaystyle{ \boldsymbol{\varPhi }= \mathbf{K}_{\varphi }^{-1}\mathbf{K}_{\text{u}\varphi }^{T}\mathbf{U}. }$$

(6.34)

In the next step, we substitute the electric potential in the first row of Eq. (4.42) and obtain

$$\displaystyle{ \mathbf{M}_{\text{u}}\ddot{\mathbf{U}} + \left (\mathbf{K}_{\text{u}} + \mathbf{K}_{\text{u}\varphi }\mathbf{K}_{\varphi }^{-1}\mathbf{K}_{\text{u}\varphi }^{T}\right )\mathbf{U} = \mathbf{f}_{\text{u}}\;. }$$

(6.35)

By introducing the modified dynamic stiffness matrix $\tilde{\mathbf{K}}$ analogous to Eq. (4.72), we write the eigenvalue problem as

$$\displaystyle{ \left (\tilde{\mathbf{K}} -\varLambda _{i}\mathbf{M}_{\text{u}}\right )\mathbf{U}_{i} = \mathbf{0}\;. }$$

(6.36)

Therefore, the modified dynamic stiffness matrix depends on the electrical boundary conditions and the overall stiffness of the system is increased if the electrodes are left open [37]. Compared to the purely elastic case, the eigenfrequencies are raised but the mode shapes are identical since the coupling influences the whole structure homogeneously.

4.1.3 Eigenfrequencies and Mode Shapes of a Circular Disc

The piezoelectric actuator under investigation is made of the piezoceramic material PIC-151. The material constants are compiled in Table 6.2. Furthermore, Fig. 6.7 depicts the geometrical model of the transducer including the electrical boundary conditions.

Table 6.2 Material properties for PIC-151

The results we obtained by applying the p-version of the FEM are compared with an analytical solution for the elastic circular disc. Regarding the electro-mechanically coupled simulation, the commercial software Abaqus^®; is employed to compute a reference solution. The piezoelectric disc is discretized by means of fully integrated 20-noded hexahedral finite elements. Since we wish to obtain highly accurate results, a high-resolution finite element model is set up. To this end, the elements size is chosen as h _Abaqus = 1. 67 × 10⁻⁴ m. Using this element size, six quadratic elements are stacked over the thickness of the disc. In total, this results in 176,886 finite elements with 3,198,880 degrees of freedom.

The two special cases of boundary conditions have been numerically implemented by defining a zero potential for all electric degrees of freedom of the model in case of the short-circuited electrodes or by fixing the electric degrees of freedom of the top and bottom surfaces if open electrodes are of interest.

Considering the p-FEM solution, we decided for an element size of h _p-FEM = 2 × 10⁻³ m. The chosen element size results in a total of 224 finite elements with only one element layer over the thickness of the circular disc. The finite element discretizations for both models are shown in Fig. 6.8. The polynomial degree p is successively increased until the relative error in the eigenfrequencies reaches a value below 0. 1% which is considered to be very accurate from an engineering point of view. The smallest polynomial order to reach this error threshold is p = 3 (isotropic polynomial degree template [16]) for both cases—purely elastic and electro-mechanically coupled. Thus, the number of degrees of freedom amounts to n _dof = 33, 040. Even if we employ 27-noded quadratic p-elements, the error is already below 2. 1% for the first 10 eigenfrequencies (n _dof = 11, 148). For this benchmark problem, we observe highly accurate results of the p-extension. A sufficient accuracy, compared to the numerical or analytical reference solutions, is reached with a relatively low polynomial degree p = 3.

Fig. 6.8

Discretization of the circular piezoelectric disc. (a) Finite element mesh for the high-resolution model (Abaqus^®;). (b) Finite element mesh for the higher order FEM model (p-FEM)

In Table 6.3, we compiled the values of the first 10 nonzero eigenfrequencies. These results confirm what we have already deduced from the analytical equations. We generally observe a stiffening effect of the electro-mechanical coupling although the influence on certain mode shapes is more pronounced than on others. If only the boundary of the disc undergoes a considerable deformation (modes shape: 1, 3, 4, 6, and 9), the eigenfrequency is notably changed. However, if the interior of the domain is also affected by the deformation state (mode shape: 2, 5, 7, 8, and 10), the change in the eigenfrequency is more significant.

Table 6.3 Eigenfrequencies for the piezoelectric circular disc with open and short-circuited electrodes (first 10 nonzero eigenfrequencies)

We also notice from Table 6.3 that the mode shapes 4 and 5 are reversed. In the purely elastic case, the 5th mode shape has the smaller eigenvalue while in the electro-mechanically couple system mode shape 5 has the higher eigenfrequency.

Huang et al. [21] presented experimental and analytical results for the electro-mechanically coupled system. However, their results do not show a satisfactory agreement with FEM simulations and experiments. They used laser Doppler vibrometry (LDV) and amplitude-fluctuation electronic speckle pattern interferometry (AF-ESPI) to confirm the developed analytical theory. In contrast to Huang’s numerical results, our p-FEM and Abaqus^®; are in good agreement with the measurements.

4.2 Spectral Element Method: Wave Propagation Analysis in a Two-Dimensional Porous Plate

In the current section, we study the basic features of ultrasonic waves in thin-walled structures. To this end, we choose a two-dimensional system. The model geometry, including its boundary conditions and loads, is depicted in Fig. 6.9. Even in a two-dimensional system, important features such as wave scattering, transmission, reflection, and conversion are observed. In the context of wave propagation analysis, the specific advantage of the SEM is the option to compute lumped mass materices without simultaneously jeopardizing the convergence behavior. Consequently, the simulation is computationally very efficient as an explicit time-integration scheme can be deployed.

Fig. 6.9

Porous plate with 13 circular holes in the middle and 12 semi-circular cutouts on each side (top and bottom edge). The loading conditions (excitation forces) are also illustrated. The coordinates of the four measurement points are: P ₁ ($x_{1_{P_{ 1}}} = 100\,$ mm, $x_{2_{P_{ 1}}} = 2.5\,$ mm), P ₂ ($x_{_{1}P_{2}} = 163\,$ mm, $x_{2_{P_{ 2}}} = 0.0\,$ mm), P ₃ ($x_{1_{P_{ 3}}} = 167\,$ mm, $x_{2_{P_{ 3}}} = 0.0\,$ mm), and P ₄ ($x_{1_{P_{ 4}}} = 302\,$ mm, $x_{2_{P_{ 4}}} = 2.5\,$ mm) [26]

The porous plate, depicted in Fig. 6.9, is made of aluminum (material properties: Young’s modulus E = 70 GPa, Poisson’s ratio ν = 0. 33, and mass density ρ = 2700 kg/m³). Furthermore, we assume that the conditions of plane strain are fulfilled. The guided waves are excited by means of two time-dependent point forces acting in opposite directions. The excitation signal is a sine-burst which is often used in the context of ultrasonic waves. The time-dependent amplitude of the forces is given as

$$\displaystyle{ F(t) =\hat{ F}\sin (\omega _{\mathrm{ex}}t)\sin ^{2}\left ( \dfrac{\omega _{\mathrm{ex}}t} {2n_{\mathrm{cyc}}}\right ), }$$

(6.37)

where $\hat{F}$ is the amplitude, ω _ex = 2πf _ex denotes the central circular frequency, and n _cyc stands for the number of cycles determining the width of the excited frequency band around the central frequency f _ex.

In this example, we set $\hat{F} = 1\,\text{N}$, f = 200 kHz, and n = 5. Figure 6.10 shows the excitation force in the time and frequency domain. If the number of cycles in the signal is further increased, we can decrease the width of the main lobe and at the same time the amplitudes of the side lobes are also minimized.

Fig. 6.10

Excitation signal: Hann-window modulated sine-function. (a) Time domain. (b) Frequency domain

The loading conditions are chosen such that a mono-modal excitation of the fundamental symmetric Lamb wave mode S ₀ is facilitated. Since the perturbations of the plate-like structure are only symmetric with respect to its midplane, we do not expect any mode conversion to occur [1, 2].

Similar to the approach we followed in Sect. 6.4.1, we use the commercial software Abaqus^®; to compute reference solutions. In this case, both explicit and implicit simulations are conducted. By comparing the computational time for these two simulations, we already observe the advantages of an explicit time integration. The discretization of the porous plate is shown in Fig. 6.11. Generally speaking, the element size is a function of the wavelength and the polynomial degree of the basis function. The wavelength can be determined by means of a dispersion diagram. In our example, the excitation frequency is set to 200 kHz and the thickness of the plate is 5 mm. Therefore, we only expect the two fundamental Lamb wave modes, S ₀ and A ₀, to be present in the plate. Since we deploy a symmetric mono-modal excitation, only the S ₀-mode is observed in the simulated signal. As a rule of thumb, it is usually recommended to use 10 quadratic elements per wavelength, and at least 25 linear elements to achieve accurate results. Hence, the minimum element size can be estimated by

$$\displaystyle\begin{array}{rcl} h_{\mathrm{min}}^{\mathrm{quad}} = \frac{c_{\mathrm{p}}^{\mathrm{min}}} {10 \times f_{\mathrm{ex}}}\;,& &{}\end{array}$$

(6.38)

$$\displaystyle\begin{array}{rcl} h_{\mathrm{min}}^{\mathrm{lin}} = \frac{c_{\mathrm{p}}^{\mathrm{min}}} {25 \times f_{\mathrm{ex}}}\;,& &{}\end{array}$$

(6.39)

Fig. 6.11

Discretization of the porous plate. (a) Mesh for the explicit solver: Element size h _Abaqus ^explicit,lin = 1 × 10⁻⁴ m. (b) Mesh for the implicit solver: Element size h _Abaqus ^{implicit,quad} = 2 × 10⁻⁴ m. (c) Mesh for the SEM solver: Element size h _SEM = 5 × 10⁻⁴ m

with c _p ^min denoting the phase velocity of the slowest propagation mode that is present in the numerical model. We have to keep in mind that for higher frequencies the pollution error gets more pronounced and therefore more lower order finite elements are needed to ensure accurate results.

The phase velocities and the wavelengths in a 5 mm thick aluminum plate for the chosen excitation parameters are:

• S ₀ Lamb wave mode: $c_{\text{p}_{S_{ 0}}} = 5309\,$ m/s; $\lambda _{S_{0}} = 0.0265\,$ m, and

• A ₀ Lamb wave mode: $c_{\text{p}_{A_{ 0}}} = 2327\,$ m/s; $\lambda _{A_{0}} = 0.0116\,$ m.

The minimal element sizes estimated by Eqs. (6.38) and (6.39) are h _min ^quad = 2. 65 mm and h _min ^lin = 1. 06 mm. As the chosen element size are more than an order of magnitude smaller, accurate results can be expected.

As already mentioned, we use Abaqus^®; to compute the reference solutions. The discretization parameters for the different simulations are compiled in Table 6.4. The accuracy of the listed simulations is similar but the computational times are quite different. Here, we already observe the most important advantage of explicit time-integration methods concerning wave propagation analysis. Regarding explicit time-integration schemes, we exploit the fact that inversion of a diagonal mass matrix is trivial. Therefore, only matrix–vector operations are needed to advance in time. Furthermore, it is straightforward to parallelize explicit algorithms as it is possible to break all operations down to the element level. Considering implicit time-stepping techniques, we have to decompose the dynamic stiffness matrix first. This can be achieved by means of LU or Cholesky decompositions. Thus, we only need to perform a forward elimination and a backward substitution. If we save the result of the LU decomposition, the aforementioned processes are also only matrix–vector operations. Nonetheless, each time step is more costly compared to an explicit algorithm and therefore a significant reduction in computational time is achieved in comparison to an implicit solution scheme. Although implicit schemes are unconditionally stable, the time step is nonetheless limited by the physics of the problem, (typically around Δt ≈ 1 × 10⁻⁸ s) i.e., the high-frequency excitation that is required to generate ultrasonic guided waves. Therefore, in most SHM-related application cases the implicit time step is not significantly higher than the explicit one, which is determined by Eq. (4.79). Due to this fact, implicit time-integration methods are inefficient in this context and usually outperformed by explicit ones. Considering the example at hand, an explicit scheme needs roughly one hundredth of the computational time to reach the same accuracy as an implicit algorithm does.

Table 6.4 Discretization parameter

To get a first impression of the behavior of ultrasonic guided waves, contour plots for different time steps are shown in Fig. 6.12. We clearly observe the fundamental symmetric Lamb wave mode and its interaction with the obstacles in the structure. As predicted, only wave scattering and transmission take place. Even behind the perturbation, no antisymmetric mode is present in the plate.

Fig. 6.12

Contour plots of the displacement field in x ₂-direction at different time steps. (a) t = 3. 125 × 10⁻⁵ s. (b) t = 4. 375 × 10⁻⁵ s. (c) t = 5. 625 × 10⁻⁵ s. (d) t = 6. 875 × 10⁻⁵ s. (e) t = 8. 125 × 10⁻⁵ s

The displacement histories for the four measurement points computed using the FEM and the SEM are in excellent agreement. There is neither a notable phase shift nor a difference in the amplitudes. As a reference, we show the results at point P ₄ in Fig. 6.13.

Fig. 6.13

Comparison of the displacement in x ₁-direction at point P ₄

To further assess the accuracy of the SEM computations, we take a brief look at the group velocity of the S ₀-mode. By means of the Hilbert transform , we compute the envelope of the displacement history and evaluate the group velocity of the ultrasonic waves. The Hilbert transform is defined by

$$\displaystyle{ \mathscr{H}(u_{i}(t)) = \frac{1} {\pi } \int _{-\infty }^{\infty }u_{ i}(\tau ) \cdot \frac{1} {t-\tau }\;\mathrm{d}\tau \;. }$$

(6.40)

In the next step, we deploy the Hilbert transform of the time signal to compute the envelope

$$\displaystyle{ \mathscr{E}(t) = \sqrt{\mathscr{H}(u_{i } (t))^{2 } + u_{i } (t)^{2}}\;. }$$

(6.41)

If we now compute the centroids of the envelopes for two different points, we can also compute the group velocity as the distance between these measurement points is known. The corresponding time of flight between the two measurement points is computed by the absolute value of the difference of the two centroid values. The centroid is calculated using the static moment of the envelope signal as

$$\displaystyle{ t_{\mathrm{c}} = \frac{\int _{0}^{t_{\mathrm{e}}}\mathscr{E}(t) \cdot t\;\mathrm{d}t} {\int _{0}^{t_{\mathrm{e}}}\mathscr{E}(t)\;\mathrm{d}t} \;. }$$

(6.42)

In Fig. 6.14, we show the convergence of the relative error in the group velocity and the corresponding normalized computational time.

Fig. 6.14

Relative error in the group velocity (denoted by black squares) and normalized computational time (denoted by red triangles). The results are compiled for different SEM simulations (p = 1,  …,  4) and Abaqus^®; Implicit/Explicit ones

It follows from Fig. 6.14 that the results obtained by employing the SEM are highly accurate when a p-extension is performed. Moreover, due to the possibility of using a diagonal mass matrix the SEM is also computationally highly efficient. In comparison to Newmark-type solvers which are typically used in implicit dynamics, every time step in the SEM is less costly.

The benchmark problem of this section clearly demonstrated why the SEM is popular in the wave analysis community. It is very often used to compute both seismic and elastic waves [3, 4, 9–11, 18, 19, 29, 29–32, 36, 44, 46, 47, 56].

4.3 Isogeometric Analysis: Wave Propagation Analysis in a Three-Dimensional Perforated Plate

The third example features a three-dimensional plate structure that is perforated by a conical hole. In contrast to the example presented in Sect. 6.4.2, the perturbation of the plate-like structure is asymmetric with respect to the midplane.

Therefore, the excited wave mode(s) are not only scattered by the conical hole but also converted. That is to say an initially mono-modal wave packet still features both mode types after the interaction asymmetric (with respect to the midplane of the plate) perturbation of the palte structure.

The geometry of the model including its dimensions is given in Fig. 6.15. In the current example, the mono-modal excitation is executed by means of two collocated piezoelectric actuators that are driven in-phase. As only the fundamental symmetric Lamb wave mode is excited, a mode conversion to the fundamental antisymmetric mode is observed.

Fig. 6.15

Aluminum plate with a conical hole. Dimensions: a = 300 mm, b = 200 mm, c = 50 mm, d = 200 mm, r _a = 10 mm, r _i = 9 mm, and h = 2 mm (thickness of the plate); Material properties: Aluminum (Young’s modulus E = 70 GPa, Poisson’s ratio ν = 0. 33, and mass density ρ = 2700 kg/m³); Excitation: collocated transducers (r = 15 mm) at the origin of the coordinate system driven by a sine burst (cf. Eq. (6.37), f _ex = 175 kHz, n = 3). (a) Cross section. (b) Top view

The discretization is chosen according to the guidelines that have been proposed in [55]. Here, an anisotropic polynomial degree template is used with in-plane polynomial degrees of p ₁ = p ₂ = 3 and an out-of-plane polynomial degree of p ₃ = 4. To ensure the accuracy of the simulation results, the element size is determined by using 4.5 nodes/modes per wavelength. Corresponding to the wavelength at an excitation frequency of f _ex = 175 kHz, the element size is h _min = 0. 2828 mm (Fig. 6.16).

Fig. 6.16

Discretization of the three-dimensional perforated plate—dashed lines (bright yellow) indicate auxiliary planes used for the partitioning of the numerical model

In Fig. 6.17, we show contour plots of the x ₃-displacement at different time steps. The incident S ₀-wave packet is clearly seen in Fig. 6.17a where it interacts with the conical hole. Thus, the S ₀-mode is scattered, transmitted, and a mode conversion to the A ₀-mode takes place. In Fig. 6.17b, the existence of both modes can clearly be seen as well as the first signs of boundary reflections.

Fig. 6.17

Contour plot of the displacement field in x ₃-direction. The incident S ₀-wave packet is shown in part (a) of the figure. Parts (b) and (c) show the mode conversion from the S ₀-mode to an A ₀-mode as well as reflection and transmission of the incident S ₀-mode. (a) t ₁ = 0. 945 ⋅ 10⁻⁵ s. (b) t ₂ = 3. 420 ⋅ 10⁻⁵ s. (c) t ₃ = 5. 315 ⋅ 10⁻⁵ s

The reference solution is computed in Abaqus^®; Implicit by using a very fine mesh of 20-noded hexahedral elements (p = 2) with more than 50 nodes per wavelength (h _Abaqus ^{implicit,quad} = 1. 4 mm, n _dof ≈ 1. 5 × 10⁶). Furthermore, we exploited the symmetry of the structure and modeled only one half. The corresponding finite element grid is depicted in Fig. 6.16.

In Fig. 6.15, three measurement points have been defined where the displacement history is computed. The results are depicted in Fig. 6.18. The agreement between the reference solution and the IGA results is excellent. The time signals are virtually coincident. The relative error in the group velocity is below 0. 1% which is highly accurate from an engineering point of view. Therefore, we conclude that IGA provides very accurate results for wave propagation problems.

Fig. 6.18

Displacement history $(u_{x_{3}})$ at the three measurement points P ₁, P ₂, and P ₃. The IGA results are compared with solutions obtained by the commercial software Abaqus^®; Implicit

In various publications [8, 24, 53], the advantages of the so-called k-refinement is emphasized. k-refinement describes the opportunity to increase the inter-element continuity. In the case of the IGA, the elements typically exhibit a C _p−1-continuous approximation of the unknowns which benefits the accuracy of wave propagation problems. However, IGA suffers from the same drawback as the p-FEM:

• There is currently no suitable mass-lumping scheme available that provides accurate results over a wide range of frequencies [33].

Consequently, the SEM in conjunction with a diagonal mass matrix seems to be the most promising method for an efficient analysis of ultrasonic guided waves in the time domain.

5 Convergence Studies

Comprehensive convergence studies indicating the performance of different higher order FE schemes have been published by the authors and coworkers in [12, 14, 53, 55]. At this point, we only repeat the most important findings of these investigations and briefly outline the applied methodology.

5.1 Numerical Model

We use the system depicted in Fig. 6.19 as a benchmark problem for wave propagation analysis and conduct convergence studies showing the convergence properties of the higher order FEMs introduced in Sects. 6.1.1–6.1.3. To this end, we deploy a time-dependent excitation force with a central frequency f _ex = 477. 5 kHz and five cycles.

Fig. 6.19

Two-dimensional model including loads and boundary conditions for the convergence study. Two collocated point forces are employed to excite the structure. The time-dependent behavior of the load is given by Eq. (6.37). At the left boundary (x ₁ = 0), we apply symmetry boundary conditions. The dimensions of the aluminum (Young’s modulus E = 70 GPa, Poisson’s ratio ν = 0. 33, and mass density ρ = 2700 kg/m³) plate are: l _a = 100 mm, l _b = 200 mm, l _p = 500 mm, and d = 2 mm

Due to the collocated nature of the concentrated forces, we are capable of exciting a purely symmetric or antisymmetric Lamb wave mode. This procedure is favored as we want to study the behavior of these modes separately.

The main purpose of the convergence studies is to derive a general guideline concerning the necessary polynomial degree and element size to achieve a certain, predefined accuracy.

5.2 Signal Analysis

Similar to the approach taken in Sect. 6.4.2, we compute the time of flight of a wave packet between two measurement points P ₁ and P ₂, cf. Fig. 6.19, by means of the Hilbert transform and its envelope. From the time difference Δt _c, we can then determine the group velocity of the travelling wave packet. This procedure is illustrated in Fig. 6.20.

Fig. 6.20

Time of flight between two measurement points: difference in the location of the centroids

5.3 Polynomial Degree in x ₁

In the first step, we investigate the discretization in x ₁-direction. To eliminate the influence of the discretization in x ₂-direction, we fix the out-of-plane polynomial degree to $p_{x_{2}} = 6$ with one element layer over the thickness of the structure. Such a discretization provides highly accurate results independent of the discretization in x ₂-direction. For different in-plane polynomial degrees $(\,p_{x_{1}} = 2,\,3,\,\ldots,\,6)$, we perform a h-refinement and compute the relative error in the group velocity c _g. In the current example, we use the analytical solution as a reference value, cf. Sect. 3.2.3.4.

The results of the convergence study are depicted in Figs. 6.21 and 6.22. Here, the relative error in the group velocity is plotted over the number of nodes/modes per wavelength χ. This quantity can be determined in terms of the number of degrees of freedom n _dof, the out-of-plane polynomial degree $p_{x_{2}}$, the length of the plate l _p, and the wavelength of the propagating mode λ as

$$\displaystyle{ \chi _{S_{0}/A_{0}} = \frac{n_{\mathrm{dof}}} {2(\,p_{x_{2}} + 1)l_{\mathrm{p}}} \cdot \lambda _{S_{0}/A_{0}}\;. }$$

(6.43)

From an engineering point of view, an accuracy of 1% is sufficient and therefore the “optimal” polynomial degree in the in-plane direction can be determined at this threshold. A suitable discretization for a given wave propagation problem can therefore be determined with the help of Figs. 6.21 and 6.22.

Fig. 6.21

Convergence curves for the S ₀-mode ($p_{x_{1}}$): the relative error in the group velocity is plotted over the number of nodes/modes per wavelength

Fig. 6.22

Convergence curves for the A ₀-mode ($p_{x_{1}}$): the relative error in the group velocity is plotted over the number of nodes/modes per wavelength

The convergence curves of the p-FEM and the SEM exhibit kinks at distinct locations. This behavior is not severe and can be attributed to element resonances as reported in [42]. Furthermore, we note that an elevation of the in-plane polynomial degree automatically results in a faster convergence. Due to the higher continuity of isogeometric elements, higher convergence rates can be achieved [55]. The overall accuracy is, however, similar for all higher order approaches. For a detailed analysis of the numerical costs of the different approaches, the interested reader is referred to [12, 14, 53, 55].

5.4 Polynomial Degree in x ₂

In the second step, we investigate the discretization in x ₂-direction. To ensure that the discretization in x ₁-direction does not interfere with this study, we choose an element size that corresponds to at least 20 nodes/modes per wavelength and set the in-plane polynomial degree to $p_{x_{1}} = 6$. We now perform a p-refinement and again compute the relative error in the group velocity.

The results of these convergence studies are depicted in Figs. 6.23 and 6.24. The overall accuracy and the general convergence behavior are very similar for all higher order methods. The curves level off at an out-of-plane polynomial degree of $p_{x_{2}} = 4$ for the symmetric Lamb wave mode and at $p_{x_{2}} = 6$ for the antisymmetric one. Due to the flexural nature of the A ₀-mode, it is more demanding from a numerical point of view than the S ₀-mode that basically resembles a tensional mode.

Fig. 6.23

Convergence curves for the S ₀-mode ($p_{x_{2}}$): the relative error in the group velocity is plotted over the out-of-plane polynomial degree

Fig. 6.24

Convergence curves for the A ₀-mode ($p_{x_{2}}$): the relative error in the group velocity is plotted over the out-of-plane polynomial degree

Important meshing parameters such as the polynomial degrees in in-plane and out-of-plane directions and the element size can be inferred from the combined findings of Figs. 6.21, 6.22, 6.23, and 6.24. If a certain level of accuracy is prescribed, we can use these figures to construct a mesh that guarantees accurate results. In all cases, $p_{x_{1}} = 3$ and $p_{x_{2}} = 4$ would be a suitable polynomial degree template [55] that provides accurate results and minimizes the computational costs. The only thing left to do is to read the number of nodes/modes per wavelength from the diagram.

6 Industrial Applications

In this section, we compute the wave propagation in a structural section of an airplane and in a wind turbine rotor blade. Here, we apply the SEM since it offers the advantages of a lumped (diagonal) mass matrix and therefore explicit time-integration schemes can be deployed which reduces the numerical costs significantly.

6.1 Stiffened Composite Plate

The first example that we investigate is a curved carbon fiber reinforced plastic (CFRP) plate. To increase the stiffness of the structure, T-stringers have been bonded to the surface, cf. Fig. 6.25. The radius of curvature is r _curv = 3. 57 m. This radius corresponds to the width of an Airbus A380 fuselage. Since we want to highlight typical wave propagation phenomena in fiber reinforced materials, we assume that the structure consists of only one unidirectional layer (UD250) with the material data compiled in Table. 6.5. Such a material is transversely isotropic and therefore the wave velocity is directionally dependent.

Fig. 6.25

CAD model of the curved plate with three T-stringers

Table 6.5 Material properties of a UD250 layer at 0^∘

The thickness of the plate and the T-stringers is t = 2 mm. The three stringers are assembled with a distance of 200 mm from center to center. The plate itself is 800 mm long and 600 mm wide. The excitation is executed using a concentrated force with a time-dependent amplitude. The center frequency of the excitation signal is f _ex = 75 kHz with three periods, cf. Eq. (6.37). The force is placed between two stringers and is applied at the top surface of the plate. Due to the nature of the excitation, both the fundamental symmetric mode and the fundamental antisymmetric mode are present in the structure.

The curved plate is discretized using hexahedral finite elements with an element size of h = 2 mm resulting in 165, 000 finite elements and 3, 075, 090 degrees of freedom (p = 2). A detail view of the generated mesh is shown in Fig. 6.26.

Fig. 6.26

Detail view of the discretization of the curved plate with three T-stringers

This model demonstrates two distinct features of wave propagation in stiffened thin-walled structures made of CFRP. First, we notice that the wave front is not circular anymore, cf. Fig. 6.27. That is due to the anisotropy of the material properties, i.e., the material is considerably stiffer in the direction of the fibers and therefore the wave velocity is also increased in this direction. The second issue we notice is that the majority of the energy is reflected at the stiffener and is only partly transmitted. Due to the scaling of the color map, we primarily observe the A ₀-mode in Fig. 6.27. It can be seen that a significant amount of energy stays between the two stringers where also the excitation force is applied. Similar observations have been made by Schulte et al. [43–45]. Considering the symmetric guided wave mode, they have concluded that the mentioned behavior (energy is locked between the stringers) is not as pronounced. Due to the asymmetric placement of the stringers, also mode conversion takes place when the wave packet interacts with these structural elements of the shell-like structure. The mentioned features are discussed at length in [43–45].

Fig. 6.27

Contour plots of the guided waves at different time steps: curved plate with three T-stringers. (a) $u_{x_{1}}$: t ₁ = 3. 5 × 10⁻⁵ s. (b) $u_{x_{3}}$: t ₁ = 3. 5 × 10⁻⁵ s. (c) $u_{x_{1}}$: t ₂ = 1. 43 × 10⁻⁴ s. (d) $u_{x_{3}}$: t ₂ = 1. 43 × 10⁻⁴ s. (e) $u_{x_{1}}$: t ₃ = 2. 5 × 10⁻⁴ s. (f) $u_{x_{3}}$: t ₃ = 2. 5 × 10⁻⁴ s

Such a knowledge is very important if we want to design a robust SHM system. We can then a priori determine an optimal sensor and actuator placement which increases the detectability of damage events.

6.2 Rotor Blade of a Wind Turbine

As a geometrically complex example (features many stiffening elements in the wing box) which is also of practical interest, we analyze a rotor blade of the DTU 10 MW Reference Wind Turbine (offshore) [5]. A CAD model of the airfoil is depicted in Fig. 6.28. This device was designed by DTU Wind Energy in cooperation with Vestas Wind Systems during the research project Light Rotor. One of the objectives of the research was to design a wind energy plant with existing and established methods that are publicly available. Thus, the model can be used by persons, institutions, and companies that were not part of the project. As the name already suggests, the wind turbine should be a reference for future design ideas. The blade is made of CFRP/GFRP laminates with balsa wood as core material of the sandwich. The blade has a length of 86. 77 m and a mass of 41 t.

Fig. 6.28

CAD model of a wind turbine rotor blade—individual parts are highlighted with different colors

The analysis mesh consists of 8-noded layered shell elements and 20-noded hexahedral elements. The solid elements are only used to represent adhesive bonds in the model. For the sake of computational time, a mesh with 35,000 elements has been generated which amounts 61,600 degrees of freedom, cf. Fig. 6.29. For the wave propagation analysis, the blade was clamped at the left end (connection to the hub) and a pressure load with time-dependent amplitude Eq. (6.37) is prescribed to the surface as indicated in Fig. 6.30. The structure is excited at a frequency of f _ex = 2 kHz which is far below the otherwise used frequencies, with five signal periods. Due to the nature of the excitation, both the fundamental symmetric mode and the fundamental antisymmetric mode are present in the structure.

Fig. 6.29

Numerical model of a wind turbine rotor blade

Fig. 6.30

Numerical model of a wind turbine rotor blade including Dirichlet and Neumann boundary conditions

The results of the wave propagation analysis are shown in Fig. 6.31. In the left part of the figure, the out-of-plane displacements are shown, while the in-plane displacements are depicted in the right part. The symmetric guided wave mode is nicely seen through the in-plane displacements and the asymmetric mode is observed by the out-of-plane displacements. We basically notice the same properties as already discussed in Sect. 6.6.1. Again the main portion of the wave energy is shielded by the two webs which are inside the rotor blade. Therefore, the wave amplitudes in the leading edge of the blade are nearly decayed.

Fig. 6.31

Contour plots of the guided waves at different time steps (left: out-of-plane displacements; right: in-plane displacements): Rotor blade of a wind turbine. (a) $u_{x_{3}}$: t ₁ = 1. 75 × 10⁻³ s. (b) $u_{x_{1}}$: t ₁ = 1. 75 × 10⁻³ s. (c) $u_{x_{3}}$: t ₂ = 3. 5 × 10⁻³ s. (d) $u_{x_{1}}$: t ₂ = 3. 5 × 10⁻³ s. (e) $u_{x_{3}}$: t ₃ = 8. 5 × 10⁻³ s. (f) $u_{x_{1}}$: t ₃ = 8. 5 × 10⁻³ s

The current section demonstrates the applicability of the proposed methods to practical problems. The wavelength is approximately 0. 5 m and therefore the accuracy of detection would be quite poor. In this wavelength range, it would be also conceivable to deploy modal analysis approaches. By decreasing the wavelength, we are nonetheless able to monitor safety-relevant regions.

A detailed description of the material properties, the geometry and aeroelastic performance of the DTU 10 MW RWT can be found in [5].