Making Local Algorithms Wait-Free: The Case of Ring Coloring

Abstract

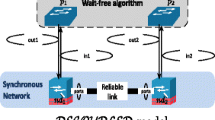
When considering distributed computing, reliable message-passing synchronous systems on the one side, and asynchronous failure-prone shared-memory systems on tyhe other side, remain two quite independently studied ends of the reliability/asynchrony spectrum. The concept of locality of a computation is central to the first one, while the concept of wait-freedom is central to the second one. The paper proposes a new $\mathcal{DECOUPLED}$ model in an attempt to reconcile these two worlds. It consists of a synchronous and reliable communication graph of n nodes, and on top a set of asynchronous crash-prone processes, each attached to a communication node.

To illustrate the $\mathcal{DECOUPLED}$ model, the paper presents an asynchronous 3-coloring algorithm for the processes of a ring. From the processes point of view, the algorithm is wait-free. From a locality point of view, each process uses information only from processes at distance $O(\log ^* n)$ from it. This local wait-free algorithm is based on an extension of the classical Cole and Vishkin vertex coloring algorithm in which the processes are not required to start simultaneously.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Locality in synchronous distributed computing. The standard synchronous message passing model (e.g. see [19, 20]) consists of a graph, whose vertices represent computational processes and whose edges represent bidirectional communication links. In each synchronous round, a process sends messages to its neighbors, then receives messages from them, and finally performs arbitrary computations. Failures are not considered: each message is received in the same round in which it was sent, and processes do not fail. The time complexity of a distributed algorithm in this model is the maximum number of rounds any process requires to terminate.

In sequential computing only the most trivial tasks can be solved in constant time. In contrast, there are many synchronous distributed algorithms that run in a number of rounds d which is constant (or nearly constant), independently of the number of vertices of the graph [23]. In such an algorithm, a process is able to collect information from others at most d links away, and hence we can think of the algorithm as a function that maps the d-neighborhood of a node to a local output, for each node. In synchronous distributed computing the focus is on locality, or to what extent a global property about the graph can be obtained from locally available data [16].

The study of the $\mathcal{LOCAL}$ synchronous model was initiated at the very early days of distributed computing [19], with problems such as coloring the vertices of a ring with 3 colors. This is a problem that depends globally on the ring, yet it can be solved locally. Cole and Vishkin [7] designed an algorithm that finds a 3-coloring of the vertices of a ring in $O(\log ^*n)$ rounds. Soon after, Linial proved that $\varOmega (\log ^*n)$ rounds are needed for 3-coloring a ring. For general graphs, only recently it was shown that $(\varDelta +1)$-coloring can be done in time $O(\varDelta )+\frac{1}{2}\log ^*n$, where $\varDelta$ is the largest degree in the graph [6]. Developments on what can or cannot be locally computed can be found in many papers (e.g., [4, 15, 16, 18] to cite a few; more references can be found in the survey [23]). This part of distributed computing is mainly complexity-oriented [11, 19], as every problem can be solved in d rounds, where d equal to the diameter of the graph.

Fault-tolerance in asynchronous distributed computing. At the same time that the $\mathcal{LOCAL}$ model began to be studied, ignoring asynchrony and failures, an orthogonal branch of distributed computing was beginning to focus on fault-tolerance, and disregarding the communication network topology [9, 13]. In an asynchronous crash-prone distributed computing model [21, 22], (i) there are communication links between every pair of processes, (ii) there are no bounds on message transfer delays and each process runs at its own arbitrary speed, which can vary along with time, and (iii) processes can fail by crashing. In this area, consensus is a fundamental problem, because, roughly speaking, it allows processes to agree on a function of their inputs, which can then be used by each process to individually perform a consistent computation. However, it was proved early on that there is no deterministic distributed asynchronous message-passing consensus algorithm even if only one process may crash [9]. Hence, computability questions are central in this part of distributed computing. Given assumptions about how many processes may fail, how severe the failures can be, and other assumptions about communication, one tries to identify the distributed problems that are solvable in a specific model.

Reliable message-passing synchronous systems and asynchronous failure-prone systems remain two quite independently studied poles of distributed computing.

Aim and content of the paper. In a distributed system failures and asynchrony are rarely coming from the hardware, but much more often from the software. Hence, it is natural to consider a model composed of two distinct layers, with distinct reliability and synchrony features, namely:

• A synchronous and reliable communication graph G with n nodes, and

• n asynchronous crash-prone processes, each one attached to a distinct node.

At each vertex of G there are two components: a failure-free synchronous node in charge of communicating with the nodes of its neighbors, and a failure-prone asynchronous process in charge of performing the actual computation. Notice that, in contrast to the $\mathcal{LOCAL}$ model, in the $\mathcal{DECOUPLED}$ model after d rounds of communication, a process can collect the local inputs of only a subgraph of its d-neighborhood, since processes can start at distinct times and run at different speeds. Thus, the new model is in principle more challenging than the $\mathcal{LOCAL}$ model.

To illustrate the $\mathcal{DECOUPLED}$ model approach, the paper considers a fundamental problem of failure-free synchronous distributed computing. It presents a 3-coloring algorithm for a ring, denoted WLC (for Wait-free Local Coloring), suited to the $\mathcal{DECOUPLED}$ model. This algorithm is based on the time-optimal Cole and Vishkin’s vertex coloring algorithm, which is denoted CV86 in the following [7]¹. The CV86 algorithm runs in $\log ^* n +3$ rounds² while the new algorithm runs in $\log ^* n +6$ rounds. From the processes point of view, the algorithm is fully asynchronous, wait-free, i.e., a process never waits for an event in another process. Yet the algorithm is local, in the sense that each process uses information only from processes at distance $O(\log ^* n)$ from it. Moreover, this amount of information is optimal due to Linial’s lower bound [16] and because in the absence of failures and asynchrony, the $\mathcal{DECOUPLED}$ model boils down to the $\mathcal{LOCAL}$ model.

The WLC algorithm for the $\mathcal{DECOUPLED}$ model is built in two stages. First an extension of CV86 is presented that may be interesting in itself. This extension, denoted AST-CV, is an implementation of CV86 in a synchronous system where reliable processes need not start at the very same round. The main idea of the first stage is to run CV86 within each segment of the ring that happens to wake up at precisely the same time. Then, adjacent endpoints of such segments fix their colors by giving priority to the segment that began earlier. Somewhat surprisingly this approach works even when all segments happen to consist of a single process. In the second stage it is shown how to derive the wait-free algorithm WLC from AST-CV. When a process starts (asynchronously with respect to other processes), it obtains information on the “current state” of the processes at distance at most $O(\log ^* n)$ from it; then, using the information obtained, the process executes alone a purely local simulation of AST-CV, at the end of which it obtains its final color.

The new algorithm shows how it is possible to extend the scope of a synchronous failure-free algorithm to run on asynchronous and crash-prone processes, without losing its fundamental locality properties, and at the cost of only a small constant number of rounds. Up to the best of our knowledge this is the first time the design of fault-tolerant asynchronous algorithms on top of a synchronous communication network is considered from the locality perspective. However this is certainly not the first work that relates synchronous and asynchronous systems, a few examples follow. From very early on the performance of asynchronous processes with access to a global clock has been considered [1]. The performance of wait-free algorithms running on top of partially synchronous, fully-connected systems has been of interest for some time, e.g. [10, 14]. The opposite problem, of running a synchronous algorithm in an asynchronous (failure-free) network was introduced in [2], and there are extensions even to the case where links are assumed to crash and recover dynamically [3]. In globally asynchronous locally-synchronous (GALS) design for microprocessor networks, the system is partitioned into synchronous blocks of logic which communicate with each other asynchronously [17]. An example of a reliable network infrastructure is provided by the highly popular Synchronous Optical Networking (SONET), which provides synchronous transport signals for fiber-optic based transmissions on top of which asynchronous algorithms may be deployed.

Roadmap. The remaining of the paper is organized as follows. Section 2 presents the first contribution, namely the $\mathcal{DECOUPLED}$ model. Section 3 presents first the distributed graph coloring problem and then a version of CV86 tailored for a ring. Section 4 presents the extension of CV86 which does not require simultaneous starting times, and Sect. 5 derives the algorithm WLC. Finally, Sect. 6 concludes the paper. Due to page limitations, the missing proofs can be found in [8].

2 The Two-Component-Based Model

Here the $\mathcal{DECOUPLED}$ model is presented, where asynchronous crash-prone processes running a wait-free algorithm are mounted on top of a reliable, synchronous network.

Communication component. The communication component is modelled by a connected graph G of n vertices. Its vertices represent nodes, $nd_1$, ..., $nd_n$. Each node $nd_i$ is a communication device connected with two types of entities. It is connected with its neighbor nodes in G, and to its local process $p_i$, in charge of running the wait-free algorithm. A node is connected to each of these entities through an input port and an output port.

Moreover, a node $nd_i$ is a device in charge only of transmitting messages (the actual computation of the wait-free algorithm is performed by the process $p_i$).

Each edge of G represents a reliable communication link, which does not corrupt, lose, create, nor duplicate messages. Similarly, nodes do not fail in any way. The communication component is synchronous. All its entities and message exchanges proceed in a lock-step manner. More precisely, there is a global clock which governs the progress of the communication component: at every clock tick³, each node $nd_i$ reads its input ports (from its neighbor nodes, and from its process $p_i$), composes a message from what it has read, and sends this message on all its output ports (to its neighbor nodes, and to $p_i$). Every message is received in the same clock tick as the one in which it was sent. Recall that the communication component is always active: at every clock tick, each node $nd_i$ sends and receives messages, independently of the behaviour of its associated process $p_i$.

Computing component. Each communication node $nd_i$ has an associated sequential process $p_i$. A process $p_i$ can communicate only with its node $nd_i$. A process is asynchronous, which means that it proceeds at its own speed, which can vary along with time, and is independent of the sped of other processes. Moreover, processes may crash, and when a process crashes it never recovers. As processes are asynchronous, they can wake up at arbitrary times to participate in an algorithm. Therefore, when a process wakes up, it may find messages from its input port waiting to be read, which were sent by its neighbors that started the algorithm before it, as described below.

Interaction between the components. The input and output ports connecting a process $p_i$ with its node $nd_i$ have two buffers (in our algorithms they are bounded). The one denoted $out_i$ is from $p_i$ to $nd_i$, while the one denoted $in_i$ is from $nd_i$ to $p_i$, initially empty. When a process starts, it writes in $out_i$ some value, which may depend on the problem being solved. At every communication step, node $nd_i$ first receives a message from each of its neighbors, and reads the local buffer $out_i$. Then, it packs the content of these messages and the current value of $out_i$ into a single message, sends it to its neighbors, and writes it in $in_i$. Notice that a process $p_i$, D time units after it started, can have information from processes in the graph at distance up to D from it.

The global ticks of the communication component govern when each communication step happens. In addition, each tick is associated to a global time. Given a process $p_i$, $ts_i$ is the global time at which $p_i$ wakes up and starts executing. Thanks to the underlying messages exchanged by the communication nodes at every clock tick (communication step), a process $p_i$ which started participating in the algorithm can know (a) which of its neighbors (until some predefined distance D) started the algorithm, and (b) at which time they started⁴. More precisely, considering a process $p_i$ that starts at time $st_i$, after D time units, $p_i$ can have information from processes in the graph at distance up to D from it.

Initial knowledge. Each of the n pairs made up of a communication node ($nd_i$) and a process ($p_i$) has a unique identity $id_i$. It is assumed that each identity can be encoded in $\log n$ bits. Initially, a process knows its identity, the value of n, and possibly the graph G. Moreover, while a process knows that no two processes have the same identity, it does not know the identities of the other processes.

Power of the model. The $\mathcal{DECOUPLED}$ model behaves exactly like the $\mathcal{LOCAL}$ model, in the absence of failures and presence of synchrony: all processes run in lock-step manner until decisions are made. Thus, if there is an algorithm solving a given problem in $\mathcal{DECOUPLED}$, then one can easily obtain an algorithm solving the corresponding problem in $\mathcal{LOCAL}$. The rest of the paper presents WLC, a 3-vertex coloring algorithm for a ring, showing that, in principle, the other direction is possible as well.

3 Distributed Graph Coloring and a Look at Cole and Vishkin’s Algorithm

In the 3-coloring problem, each vertex of a graph is assigned a color from a set of three possible colors, in such a way that no two adjacent vertices have the same color. In sequential computing, deciding if a graph can be 3-colored is a famous NP-complete problem [12].

3.1 Graph Coloring

In the context of synchronous systems, there is an $\varOmega (\log ^* n)$ rounds lower bound on the number communication rounds needed to 3-color the nodes of a ring [16], and the CV86 algorithm solves the problem in $\log ^* n +3$ rounds [7]. A monograph entirely devoted to distributed graph coloring can be found in [5].

The structure of Cole and Vishkin’s algorithm. This algorithm assumes that the underlying bi-directional communication graph has a logical orientation, such that each process has at most a single predecessor. It assumes that the processes have distinct identities, each consisting of $O(\log n)$ bits. The algorithm can be decomposed in two phases.

• Phase 1. From n colors to six colors. An original and clever bit-level technique is first used (see below), which allows the processes to be properly colored with six colors. Starting with colors encoded with $\log n$ bits (node identities), a sequence of synchronous communication steps is executed, such that in each step a process computes a new proper color whose size in bits is exponentially smaller than the previous one. This is repeated until attaining at most six colors, which requires $\log ^* n$ communication rounds.

• Phase 2. From six colors to three colors. The algorithm uses then a simple reduction technique to reduce the number of colors from six to three. This requires three additional rounds (each one eliminating a color).

Features of CV86. Those are the following: it is local, it’s time complexity is $\log ^* n +3$, time optimal [16], and deterministic. Combining the locality and determinism properties, it follows that the final color of a process depends only on the $\log ^* n +3$ identities of the processes on its predecessor path.

3.2 A Version of Cole and Vishkin’s Algorithm Suited to a Ring

A version of CV86 suited to a ring in Fig. 1. The two neighbors of a process $p_i$ are denoted $pred_i$ and $next_i$. The local variable $color_i$ contains initially the identity of $p_i$, using $\log n$ bits. Let $m=\lceil \log n\rceil -1$. The initial value of $color_i$ is a sequence of $(m+1)$ bits $b_m,b_{m-1},\cdots , b_1,b_0$, and no two processes have the same initial sequence of bits. We say that “$b_y$ is at position y”, i.e., the position of a bit in a color is defined by starting from position 0 and going from right to left.

Underlying principle. The aim is, from round to round, to compress as much as possible the size of the colors of the processes, while keeping invariant the property that no two neighbors have the same color. Basically, a process compares its current color with the one of its predecessor, to define its new color (using the logical orientation of the ring).

The two issues that have then to be solved are (i) how to compare current colors and how to compute a new shorter color (while maintaining adjacent processes with different colors), and (ii) how many iterations have to be executed to get to at most three colors.

Fig. 1.

Cole and Vishkin’s synchronous algorithm for a ring (code for $p_i$)

Description of the algorithm. Let r denote the current round number. Initialized to 1, it takes then the successive values 2, 3, etc. It is a global variable provided by the synchronous system, which can be read by all processes. Each process $p_i$ first defines its current color as the bit string representing its identity (line 01). As already indicated, it is assumed that each identity can be coded in $\log n$ bits. Then $p_i$ executes synchronous rounds until it obtains its final color (line 16). The total number of rounds that are executed is $\log ^* n+3$, which decompose into two parts.

The first $\log ^*n$ rounds (lines 03–08) allow each process $p_i$ to compute a color in the set $\{0,1,\cdots ,5\}$. Considering a round r, let k be an upper bound on the number of different colors at the beginning of round k, and m be the smallest integer such that $k\le 2^m$. Hence, at round r, the color of a process is coded on m bits. After a send/receive communication step (lines 04–05), a process $p_i$ compares its color with the one it has received from its predecessor ($color\_p$), and computes (starting at 0 from the right), the rightmost bit position x where they differ (line 06). Then (line 07), $p_i$ defines its new color as the bit sequence whose prefix is the binary encoding of x in $\log m$ bits and suffix is the first bit of its current color where both colors differ, namely $b_x$.

Consider two neighbor processes during a round r. If they have the same value for x, due to the bit suffix they use to obtain their new color, they necessarily obtain different new colors. If they have different values for x, they trivially have different new colors. It is easy to see that the round r reduces the number of colors from k to at most $2\lceil \log k\rceil \le 2m$. It is shown in [7] that, after at most $\log ^*n$ rounds, the binary encoding of a color requires only three bits, where the suffix $b_x$ is 0 or 1, and the prefix is 00, 10, or 01. Hence, only six color values are possible.

The second part of the algorithm consists of three additional rounds, each round eliminating one of the colors in $\{3,4,5\}$ (lines 10–15). Each process first exchanges its color with its two neighbors. Due to the previous $\log ^*n$ rounds, these three colors are different. Hence, if its color is 3, $p_i$ selects any color in $\{0,1,2\}$ not owned by its neighbors. This is then repeated twice to eliminate the colors 4 and 5.

Proofs of the algorithm correctness and its time complexity can be found in [7]. A simple way to go from a ring to a chain is described in [8].

4 Extending Cole and Vishkin’s Algorithm to Asynchronous Starting Times

This section presents an extension of CV86 for synchronous systems, where reliable processes may start at different rounds.

4.1 Asynchronous Starting Times and Unit-Segment

Asynchronous starting times. Let $st_i$ denote the round number at which process $p_i$ wakes up and starts participating in the algorithm. A process may start at any time, but when it starts, it does so at the beginning of a round, and then runs synchronously.

Notion of a unit-segment. A unit-segment is a maximal sequence of consecutive processes in the ring, $p_a$, $p_{next_a}$, $\cdots ,~p_{pred_z},~p_z$, that start the algorithm in the same round.

A unit-segment is identified by a starting time (round number), and any two contiguous unit-segments are necessarily associated with distinct starting times. It follows that, from an omniscient observer’s point of view, and at any time, the ring can be decomposed into a set of unit-segments, some of these unit-segments being contiguous, while others are separated by processes that have not yet started (or will never start, due to an initial crash). In the particular case where all processes start simultaneously, the ring is composed of a single unit-segment, and if all start at different times, it is composed of n unit-segments.

4.2 A Coloring Algorithm with Asynchronous Starting Times

This section presents the local algorithm AST-CV, which allows processes to start at different Each process executes $\varDelta =\log ^*n+6$ rounds. The algorithm is decomposed into four parts.

Starting round of the algorithm. The underlying synchronous system defines the first round ($r=1$) as being the round at which the first process(es) starts the algorithm. Hence, when such a process $p_i$ starts the algorithm, we have $st_i=1$. Then, the progress of r is managed by the system synchrony.

Part 1 and Part 2. These parts are described in Fig. 2. Considering a unit-segment (identified by a starting time st) they are a simple adaptation of CV86, which considers the behavior of any process $p_i$ belonging to this unit-segment.

Fig. 2.

Initialization, Part 1, and Part 2, of AST-CV (code for $p_i$)

A process $p_i$ executes first $\log ^* n$ synchronous rounds. During each round, it sends its current color to its neighbors, and receives their current colors. $msg\_pred=\bot$ if there is no message from $pred_i$ (line 04).

In line 05, $p_i$ can tell if its predecessor belongs to the same unit-segment from the st value received. If so, $p_i$ executes CV86. If its predecessor belongs to a different unit-segment or has not yet started the algorithm, $p_i$ considers a fictitious predecessor whose identity is the same as its own identity, except for the first bit, starting from the right (see the last paragraph of Annex Sect. 3.2). Lines 06–10 constitute the core of CV86, which exponentially fast reduces the bit size representation of $color_i$ at every round, to end up with a color in the set $\{0,1,\cdots ,5\}$ after $\log ^* n$ rounds.

Part 2 of AST-CV (lines 13–21) is the same as the part in CV86 that reduces the set of colors in each unit-segment from at most six to at most three [7], and hence, at the end of this part, the processes of the unit-segment identified by $st_i$ have obtained a proper color within their unit-segment. Moreover, if the process is internal to its unit-segment, it will have obtained its final color (after $\log ^* n+3$ rounds).

Fig. 3.

Part 3 and Part 4 of AST-CV (code for $p_i$)

Message management. Let us observe that, as not all processes start at the same round, it is possible that, while executing a round of the synchronous algorithm of Fig. 2, a process $p_i$ receives a message color $(0,st,-)$ with $st\ne st_i$ from its predecessor, or messages color $(j,-)$ (where $j\in \{1,2,3\}$, sent in Parts 3 or 4) from one or both of its neighbors. To simplify and make clearer the presentation, the reception of these messages is not indicated in Fig. 2. It is implicitly assumed that, when they are received during a synchronous round, these messages are saved in the local memory of $p_i$ (so that they can be processed later, if needed, at lines 25–28 and line 39 of Fig. 3).

Moreover, a process $p_i$ learns the starting round of $pred_i$ (resp., $next_i$) when it receives for the first time a message color $(0,st,-)$ from $pred_i$ (resp. $next_i$). To not overload the presentation, this is left implicit in the description of the algorithm.

Part 3 and Part 4. These parts are described in Fig. 3. If $p_i$ is a left end, or a right end, or both, of a unit-segment⁵, its color at the end of Part 2 is not necessarily its final color, because Part 1 and Part 2 color different unit-segments independently from each other. Hence, it is possible for two contiguous unit-segments to be such that the left end of one, say $p_i$, and the right end of the other, say $p_j$, have $color_i=color_j$.

The aim of Part 3 and Part 4 is to resolve these coloring conflicts. To this end, each process $p_i$ manages six local variables, denoted $color_i[j,nbg]$, where $j\in \{1,2,3\}$ and $nbg\in \{ pred_i, next_i\}$. They are initialized to $-1$ (no color).

Solving the conflict between neighbors belonging to contiguous unit-segments. A natural idea to solve a coloring conflict between two neighbor processes belonging to different unit-segments, consists in giving “priority” to the unit-segment whose starting time is the first.

Let $st_i[{pred_i}]$ (resp., $st_i[{next_i}]$) be the knowledge of $p_i$ on the starting time of its left (resp., right) neighbor. If $pred_i$ has not yet started let $st_i[{pred_i}]=+\infty$ (and similarly for $next_i$). Thanks to this information, $p_i$ knows if it is at the left (resp., right) end of a unit-segment: this is the case if $st_i\ne st_i[{pred_i}]$ (resp., if $st_i\ne st_i[{next_i}]$). Moreover, if $p_i$ is a left (resp., right) end of a unit-segment, it knows that it has not priority if $st_i > st_i[{pred_i}]$ (resp., $st_i> st_i[{next_i}]$). If such cases, $p_i$ may be required to change its color to ensure it differs from the color of its neighbor belonging to the priority contiguous unit-segment.

The tricky cases are the ones of the unit-segments composed of either a single process p or two processes $p_a$ and $p_b$. This is because, in these cases, it can be required that p (possibly twice, once as right end, and once as left end of its unit-segment), or once $p_a$ and once $p_b$ (in the case of a 2-process unit-segment), be forced to change the color they obtained at the end of Part 2, to obtain a final color consistent with respect to their neighbors in contiguous unit-segments. To prevent inconsistencies from occurring, it is required that (in addition to the previous priority rule) (a) first a left end process of a unit-segment modifies its color with respect to its predecessor neighbor (which belongs to its left unit-segment), and (b) only then a right end process of a unit-segment modifies its color if needed (this specific order is immaterial; the other order –first right, then left– would be equally fine).

Conflict resolutions rules summary. Let us consider a process $p_i$.

• If $p_i$ is inside a unit-segment (i.e., $st_i = st_i[{pred_i}]=st_i[{next_i}]$), or is the left end of a unit-segment and $pred_i$ began after it (i.e., $st_i < st_i[{pred_i}]$), or is the right end of a unit-segment and $next_i$ began after it (i.e., $st_i < st_i[{next_i}]$), then the color it obtained at the end of Part 2 is its final color.

• If $p_i$ is the left end of a unit-segment and $pred_i$ began before $p_i$ (i.e., $st_i > st_i[{pred_i}]$), then $p_i$ may be forced to change its color. This is done in Part 3. The color $p_i$ obtains at the end of Part 3 will be its final color, if it is not also the right end of its unit-segment and $next_i$ began before it (i.e., $st_i > st_i[{next_i}]$).

• This case is similar to the previous one. If $p_i$ is the right end of a unit-segment and $next_i$ began before it (i.e., $st_i > st_i[{next_i}]$), $p_i$ may be forced to change its color to have a final color different from the one of $next_i$. This is done in Part 4.

Recall that a process that is neither the left end, nor the right end of a unit-segment obtains its final color in Part 2. It follows that, during Part 3 and Part 4, such a process only needs to execute the sending of messages color $(j,-)$, $j \in \{1,2,3\}$ it lines 24,38, and 47 (the other statements cannot change its color).

Part 3. This part is composed of a single round (lines 22–35). A process $p_i$ sends first to its neighbors a message color(1, c) carrying the color c it has obtained at the end of Part 2. Then, according to the messages it received from them up to the current round, $p_i$ updates its local variables $color_i[j,pred_i]$ and $color_i[j,next_i]$ (lines 25–28).

Part 4. This part, composed of a single round (lines 36–46), is similar to the previous one. Due to the predicate of line 40, the lines 41–44 are executed only if $p_i$ is the right end of its unit segment. Their meaning is similar to the one of lines 30–33. Finally, $p_i$ sends (line 47) to its two neighbors the message color $(3,color_i)$ to inform them of its last color, in case it was modified in Part 4.

An execution of AST-CV and a proof of the following theorem are given in [8].

Theorem 1

If $p_i$ and $p_j$ wake up and are neighbors, their final colors are different and in the set $\{0,1,2\}$.

4.3 Properties of the Algorithm

AST-CV inherits the two most important properties from CV86: locality and determinism. A proof of the algorithm is given in [8].

• The locality property of CV86 states that a process obtains its final color by $\log ^* n+3$ rounds. In AST-CV, it obtains it $\log ^* n+6$ rounds after its starting round.

• In CV86, the determinism property states that the final color of a process depends only of the identities of the consecutive processes which are its $\log ^* n+3$ predecessors on the ring. In AST-CV, its final color depends only of the starting times and the identities of the consecutive processes which are its $\log ^* n+6$ predecessors on the ring.

5 From Asynchronous Starting Times to Wait-Freedom

This section presents the WLC (Wait-free Local Coloring) algorithm for the $\mathcal{DECOUPLED}$ model described in Sect. 2, which 3-colors the processes of a ring. This algorithm consists of two consecutive stages executed independently by each process $p_i$. The first stage is a communication stage during which $p_i$, whatever its starting time, obtains enough information to execute its second stage, which consists of a communication-free computation.

The following solvability notion incorporates asynchrony and failures, as needed by the $\mathcal{DECOUPLED}$ model. An algorithm wait-free solves m-coloring if for each of its executions: (1) Validity. The final color of any process is in $\{0,...,m-1 \}$. (2) Agreement. The final colors of any two neighbor nodes in the graph are different. (3) Termination. All processes that take an infinite number of steps decide a final color.

5.1 On the Communication Side

A ring structure for the synchronous communication network. The neighbors of a node $nd_i$ (or process $p_i$ with a slight abuse of language) are denoted as before, $pred_i$ and $next_i$.

On the side of the communication nodes. While each input buffer $in_i$ is initially empty, each output buffer $out_i$ is initialized to $\langle i,+\infty ,\bot \rangle$. When a process starts its participation in the algorithm, it writes the pair $\langle i,st_i, id_i\rangle$ in $out_i$, where $st_i$ is its starting time (as defined by the current tick of the clock governing the progress of the underlying communication component), and $id_i$ is its identity.

As already described, at every clock tick (underlying communication step), $nd_i$ first receives two messages (one from each neighbor), and reads the local buffer $out_i$. Then, it packs the content of these two messages and the content of $out_i$ (which can be $\langle i,+\infty ,\bot \rangle$ if $p_i$ has not yet started) into a single message, sends it to its two neighbors, and writes it in $in_i$ (full-information behavior of a node).

5.2 Wait-Free Algorithm: First a Communication Stage

Let $p_i$ be a process that starts the algorithm at time $st_i=t$. As previously indicated, this means that, at time t (clock tick defined by the communication component), $p_i$ writes $\langle i, t, id_i\rangle$ in its output buffer $out_i$. Then $p_i$ waits until time $t+\varDelta$ where $\varDelta = \log ^* n+5$. (⁶). At the end of this waiting period, and as far $p_i$ is concerned, the “dices are cast”. No more physical communication will be necessary. As we are about to see, $p_i$ obtained enough information to compute alone its color: the rest of the algorithm executed by $p_i$ is purely local (see below). This feature, and the fact that the starting time of a process depends only on it, makes the algorithm wait-free.

It follows from the underlying communication component that, at time $t+\varDelta$, $p_i$ has received information (i.e., a triplet $\langle j, st,id_j \rangle$) from all the processes at distance at most $\varDelta$ of it. If $st=t$, $p_i$ knows that $p_j$ started the algorithm at the same time as itself. If $st<t$ (resp., $st>t$), $p_i$ knows that $p_j$ started the algorithm before (resp., after) it. (If $st=+\infty$ –we have then $id_j=\bot$– and $p_j$ is at distance d from it, $p_i$ knows that $p_j$ did not start the algorithm before the clock tick $t+\varDelta -d$.)

5.3 Wait-Free Algorithm: Then a Local Simulation Stage of AST-CV

At the end of its waiting period, $p_i$ has information (triplets composed of an index, a starting time –possibly $+\infty$–, and a process identity –possibly $\bot$–) of all the processes at distance $\varDelta =\log ^* n+5$ from it, and also from the processes at distance k that started before $st_i+\varDelta -k$ (each triplet from process $p_j$ at distance k was propagated from it to a process $p_\ell$ at distance $\varDelta$ from $p_i$, and then from $p_\ell$ to $p_i$). More precisely, for each of these processes $p_j$, $p_i$ knows whether $p_j$ started before it ($st_j< st_i$), at the same time as it ($st_j=st_i$), or after it ($st_j>st_i$).

Simulation of AST-CV. It follows from the previous observation that, after its waiting period, $p_i$ has all the inputs (starting times and process identities) needed to simulate AST-CV and compute its final color, be it inside a unit-segment, the left end of a unit-segment, the right end of a unit-segment, or both ends of a unit-segment (a maximal sequence of consecutive processes that start the algorithm at the same time).

More precisely, the purely local simulation by a process $p_i$ is a follows. Starting from round 0, $p_i$ simulates $st_i+ \varDelta$ rounds of AST-CV, this simulation involving the processes from which it has the initial information $\langle j,st_j,id_j\rangle$ and are s.t. $st_j\le st_i$.

Notice that the crash of a process $p_j$ has no impact on the termination and the correctness of the coloring of other processes. This follows from the locality property of AST-CV, and the fact that as soon as a process has obtained a triplet $\langle j,st_j,id_j\rangle$ (where $st_j\le st_i$), it considers $p_j$ as competing for a color, whatever is its behavior after it started participating in the algorithm.

Optimality of WLC. When it executes WLC, each process waits during $O(\log ^* n)$ time units, which occurs during the communication phase. This duration is asymptotically optimal as (1) $\varOmega (\log ^* n)$ is a lower bound on the number of time units needed to color the nodes of a ring with at most three colors [16] in $\mathcal{LOCAL}$, and (2) when there is neither asynchrony nor failures, $\mathcal{DECOUPLED}$ behaves like $\mathcal{LOCAL}$.

6 Conclusion

The paper proposed a model where communication and processing are decoupled, consisting of asynchronous crash-prone processes that run on top of a reliable synchronous network. This $\mathcal{DECOUPLED}$ model is weaker than the synchronous model (on the process side) and stronger than the asynchronous crash-prone model (on the communication side), while encompassing in a single framework two fundamental issues of distributed computing, locality [16] and wait-freedom [13].

A 3-coloring algorithm for a ring was derived for the $\mathcal{DECOUPLED}$ model. This algorithm uses as a subroutine a generalization of Cole and Vishkin’s algorithm [7]. A process needs to obtain initial information from processes at distance at most $O(\log ^* n)$ of it. As far as we know, this is the first wait-free local coloring algorithm, which colors a ring with at most three colors.

In contrast to $\mathcal{LOCAL}$, in the $\mathcal{DECOUPLED}$ model, after d rounds of communication, a process collects the initial inputs of only a subgraph of its d-neighborhood. The paper has shown that, despite this uncertainty, it is possible to combine locality and wait-freedom, as far as 3-coloring is concerned. The keys to this marriage were (a) the decoupling of communication and processing, and (b) the design of a synchronous coloring algorithm (AST-CV), where the processes are reliable, proceed synchronously, but are not required to start at the very same round, which introduces a first type of asynchrony among the processes. As we have seen, the heart of this algorithm lies in the consistent coloring of the border vertices of subgraphs which started at different times (unit segments).

It would be interesting if this methodology applies to other coloring algorithms, or even to other distributed graph problems which are solvable in the $\mathcal{LOCAL}$ model.