Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The asynchronous system model places no assumptions on message propagation delay or relative process speeds. This makes the model attractive for distributed algorithm research as the results obtained in the model are applicable to an arbitrary network and computer architecture. However, the fully asynchronous system model is not well suited for fault tolerance studies. An elementary problem of consensus, where processes have to agree on a single value, is unsolvable even if only one process may crash [11]: the asynchrony of the model precludes processes from differentiating a crashed and a slow process.

A failure detector [7] is a construct that enables the solution to consensus or related problems in the asynchronous system model. Potentially, a failure detector may be very powerful and, therefore, hide the solution to the problem within its specification. Conversely, the weakest failure detector specifies the least amount of synchrony required to implement consensus [6]. One such detector is OmegaFootnote 1.

Naturally, a failure detector may not be implemented in the asynchronous model itself. Hence, a lot of research is focused on providing the implementation of a detector, especially Omega, in the least restrictive communication model. These restrictions deal with timeliness and reliability of message delivery. Aguilera et al. [1] provide a remarkable Omega implementation which requires only a single process to have eventually timely channels to the other processes and a single process to have so called fair-lossy channels to and from all other processes. Aguilera et al. present what they call an efficient implementation where only a single process sends infinitely many messages. In their work, Aguilera et al. consider a direct channel as the sole means of message delivery from one process to another. In this paper, we consider a more general setting where a message may arrive to a particular process through several intermediate processes. Otherwise, we preserve model assumptions of Aguilera et al.

Our contribution. We study Omega implementation under the assumption that a message may come to its destination through other processes.

To motivate this multi-hop Omega implementation approach, we consider a fixed probability of channel timeliness and study the probability of leader existence in a classic single-hop and in multi-hop implementations. We prove that the probability of leader existence tends to zero for single-hop implementations and to one for multi-hop ones as network size grows. Moreover, the probability of leader persisting while the timeliness of channel changes tends to zero for single-hop and to infinity for multi-hop implementations.

We then consider deterministic algorithms and study three classes of Omega implementations: message efficient, packet efficient and super packet efficient. In a message efficient implementation all but finitely many messages are sent by a single process. In a packet efficient implementation, the number of packets in all but finitely many transmitted messages is linear w.r.t. the number of processes in the network. However, in a (simple) packet efficient implementation, packets of different messages may use different channels such that potentially all channels in the system are periodically used. In a super packet efficient implementation, the number of channels used in all but finitely many messages is also linear w.r.t. to the number of processes.

Our major results are as follows. If timeliness of one message does not correlate with the timeliness of another, i.e., there are no timely channels, we prove that any implementation of Omega has to send infinitely many messages whose number of packets is quadratic w.r.t. the number of processes in the network. This precludes a packet efficient implementation of Omega. If eventually timely and fair-lossy channels are allowed, we establish the necessary and sufficient conditions for the existence of a packet efficient implementation of Omega. We then prove that this eventuality of timely and channels precludes the existence of a super packet efficient implementation of Omega. We present an algorithm that uses these necessary conditions and provides a message and packet efficient implementation of Omega.

Related work. The implementation of failure detectors is a well-researched area [2, 3, 9, 13–19]. Refer to [1, 2] for detailed comparisons of work related to the kind of Omega implementation we are proposing. We are limiting our literature review to the most recent and closest to our studies.

Delporte-Gallet et al. [9] describe algorithms for recognizing timely channel graphs. Their algorithms are super packet efficient and may potentially be used to implement Omega. However, their solutions assume non-constant size messages and perpetually reliable channels. That is, Delporte-Gallet et al. deviate from the model of Aguilera et al. and the algorithms of Delporte-Gallet et al. do not operate correctly under fair-lossy and eventually timely channel assumptions.

A number of papers consider an Omega implementation under various modifications of Aguilera et al. model. Hutle et al. [13] implement Omega assuming a send-to-all message transmission primitive where f processes are guaranteed to receive the message timely. Fernandez and Raynal [2] assume a process that is able to timely deliver its message to a quorum of processes over direct channels. This quorum and channels may change with each message. A similar rotating set of timely channels is used by Malkhi et al. [16]. Larrea et al. [15] give an efficient implementation of Omega but assume that all channels are eventually timely. In their Omega implementation, Mostefaoui et al. [17] rely on a particular order of message interleaving rather than on timeliness of messages. Biely and Widder [3] consider message-driven (i.e., non-timer based) model and provide an efficient Omega implementation.

There are several recent papers on timely solutions to problems related to Omega implementation. Charron-Bost et al. [8] use a timely spanning tree to solve approximate consensus. Lafuente et al. [14] implement the eventually perfect failure detector using a timely cycle of processes.

2 Notation and Definitions

Model specifics. To simplify the presentation, we use an even more general model than what is used in Aguilera et al. [1]. The major differences are as follows. We use infinite capacity non-FIFO channels rather than single packet capacity channels. Our channel construct makes us explicitly state the packet fairness propagation assumptions that are somewhat obscured by the single capacity channels.

In addition, we do not differentiate between a slow process and a slow channel since slow channels may simulate both. Omega implementation code is expressed in terms of guarded commands, rather than the usual more procedural description. The operation of the algorithm is a computation which is a sequence of these command executions. We express timeouts directly in terms of computation steps rather than abstract or concrete time. This simplifies reasoning about them.

Despite the differences, the models are close enough such that all of the results in this paper are immediately applicable to the traditional Omega implementation model.

Processes and computations. A computer network consists of a set N of processes. The cardinality of this set is n. Each process has a unique identifier from 0 to \(n-1\). Processes interact by passing messages through non-FIFO unbounded communication channels. Each process has a channel to all other processes. That is, the network is fully connected. A message is constant size if the data it carries is in \(O(\log n)\). For example, a constant size message may carry several process identifiers but not a complete network spanning tree.

Each process has variables and actions. The action has a guard: a predicate over the local variables and incoming channels of the process. An action is enabled if its guard evaluates to true. A computation is a potentially infinite sequence of global network states such that each subsequent state is obtained by executing an action enabled in the previous state. This execution is a computation step. Processes may crash. Crashed process stops executing its actions. Correct process does not crash.

Messages and packets. We distinguish between a packet and a message. Message is particular content to be distributed to processes in the network. Origin is the process that initiates the message. The identifier of the origin is included in the message. Messages are sent via packets. Packet is a portion of data transmitted over a particular channel. A message is the payload of a packet. A process may receive a packet and either forward the message it contains or not. A process may not modify it: if a process needs to send additional information, the process may send a separate message. A process may forward the same message at most once. In effect, a message is transmitted to processes of the network using packets. A particular process may receive a message either directly from the origin, or indirectly possibly through multiple hops.

Scheduling and fairness. We express process synchronization in terms of an adversarial scheduler. The scheduler restrictions are as follows. We do not distinguish slow processes and slow packet propagation. A scheduler may express these phenomena through scheduling process action execution in a particular way. A packet transmission immediately enables the packet receipt action in the recipient process. A packet is lost if the receipt action is never executed. A packet is not lost if it is eventually received.

Timers. Timer is a construct with the following properties. A timer can be reset, stopped and increased. It can also be checked whether the timer is on or off. It has a timeout integer value and a timeout action associated with it. A timer is either a receiver timer or a sender timer. If a sender timer is on, the timeout action is executed once the computation has at most the timeout integer steps without executing the timer reset. If a receiver timer is on, the timeout action is executed once the computation has at least the timeout integer steps without executing the timer reset. Increasing the timer adds an arbitrary positive integer value to the timeout integer. An off timer can be set to on by resetting it.

Reliable and timely messages and packets. A packet is reliable if it is received. A message is reliable if it is received by every correct process; i.e. one that does not crash. A channel is reliable if every packet transmitted over this channel is reliable.

A channel is fair-lossy if it has the following properties. If there is an infinite number of packet transmissions over a particular fair-lossy channel of a particular message type and origin, then infinitely many are received. We assume that a fair-lossy channel is not type discriminating. That is, if it is fair-lossy for one type and origin, it is also fair-lossy for every pair of message type and origin.

Observe that if there is an infinite number of message transmissions of a particular message type and origin over a path that is fair-lossy, then infinitely many succeed. There converse is true as well: if there is an infinite number of successful message transmissions, there must be a fair-lossy path between the origin an the destination.

A packet is timely if it is received within a bounded number of computation steps. Specifically, there is a finite integer B such that the packet is received within B steps. Naturally, a timely packet is a reliable packet. A message is timely if it is received by every process via a path of timely packets. A channel is timely if every packet transmitted over this channel is timely. A channel is eventually timely if the number of non-timely packets it transmits is finite. Note that a channel that transmits a finite number of packets is always eventually timely.

The timely channel definition is relatively clear. The opposite, non-timely channel, is a bit more involved. A channel that occasionally delays or misses a few packets is not non-timely as the algorithm may just ignore the missed packets with a large enough timeout. Hence, the following definition.

A channel is strongly non-timely if the following holds. If there is an infinite number of packet transmissions of a particular type and origin over a particular non-timely channel, then, for any fixed integer, there are infinitely many computation segments of this length such that none of the packets are delivered inside any of the segments.

Similarly, the non-timeliness has to be preserved across multiple channels, a message may not gain timeliness by finding a parallel timely path, then, for example, the two paths may alternate delivering timely messages. Therefore, we add an additional condition for non-timeliness.

All paths between a pair of processes x and y are strongly non-timely if x sends an infinite number of messages to y, yet regardless of how the message is forwarded or what path it takes, for any fixed integer, there are infinitely many computation segments of this length such that none of the messages are delivered inside any of the segments. Unless otherwise noted, when we discuss non-timely channels and paths, we mean strongly non-timely channels and paths.

Communication models. To make it easier to address the variety of possible communication restrictions, we define several models. The dependable (channel) model allows eventually or perpetually reliable timely or fair-lossy channels. In the dependable model, an algorithm may potentially discover the dependable channels by observing packet propagation. The general propagation model does not allow either reliable or timely channels. Thus, one message propagation is not related to another message propagation.

Message propagation graph. Message propagation graph is a directed graph over network processes and channels that determines whether packet propagation over a particular channel would be successful. This graph is connected and has a single source: the origin process. This concept is a way to reason about scheduling of the packets of a particular message.

Each message has two propagation graphs. In reliable propagation graph R, each edge indicates whether the packet is received if transmitted over this channel. In timely propagation graph T each edge indicates whether the packet is timely if transmitted over this channel. Since a timely packet is a reliable packet, for the same message, the timely propagation graph is a subgraph of the reliable propagation graph. In general, a propagation graph for each message is unique. That is, even for the same source process, the graphs for two messages may differ. This indicates that different messages may take divergent routes.

If a channel from process x to process y is reliable, then edge (x, y) is present in the reliable propagation graph for every message where process x is present. In other words, if the message reaches x and x sends it to y, then y receives it. A similar discussion applies to a timely channel and corresponding edges in timely propagation graphs.

Propagation graphs are determined by the scheduler in advance of the message transmission. That is, the recipient process, depending on the algorithm, may or may not forward the received message along a particular outgoing channel. However, if the process forwards the message, the presence of an edge in the propagation graph determines the success of the message transmission. Note that the process forwards a particular message at most once. Hence, the propagation graph captures the complete possible message propagation pattern. A process may crash during message transmission. This crash does not alter propagation graphs.

Proposition 1

A message is reliable only if its reliable propagation graph R is such that every correct process is reachable from the origin through non-crashed processes.

Proposition 2

A message is timely only if its timely propagation graph T is such that every correct process is reachable from the origin through non-crashed processes.

Omega implementation and its efficiency. An algorithm that implements the Omega Failure Detector (or just Omega) is such that in a suffix of every computation, each correct process outputs the identifier of the same correct process. This process is the leader.

An implementation of Omega is message efficient if the origin of all but finitely many messages is a single correct process and all but finitely many messages are constant size. An implementation of Omega is packet efficient if all but finitely many messages are transmitted using O(n) packets.

An Omega implementation is super packet efficient if it is packet efficient and the packets of all but finitely many messages are using the same channels. In other words, if a packet of message \(m_1\) is forwarded over some channel, then a packet of another message \(m_2\) is also forwarded over this channel. The intent of a super packet efficient algorithm is to only use a limited number of channels infinitely often. Since a packet efficient algorithm uses O(n) packets infinitely often, a super packet efficient algorithm uses O(n) channels infinitely often.

3 Probabilistic Properties

In this section, we contrast a multi-hop implementation of Omega and a classic single-hop, also called direct channel, implementation. We assume each network channel is timely with probability p. The timeliness probability of one channel is independent of this probability of any other channel.

Leader existence probability. We assume that the leader may exist only if there is a process that has timely paths to all processes in the network. In case of direct channel implementation, the length of each such path must be exactly one.

As n grows, Omega implementations behave radically differently. Theorems 1 and 2 state the necessary conditions for leader existence and indicate that the probability of leader existence for direct channel implementation approaches zero exponentially quickly, while this probability for multi-hop implementation approaches one exponentially quickly. In practical terms, a multi-hop omega implementation is far more likely to succeed in establishing the leader.

Theorem 1

If the probability of each channel to be timely is \(p < 1\), then the probability of leader existence in any direct channel Omega implementation approaches zero exponentially fast as n grows.

Proof

Let \(D_x\) be the probability that some process x does not have direct timely channels to all processes in the network. This probability is \(\mathbb {P}(D_x) = 1-p^{n-1}\). For two distinct processes x and y, \(D_x\) and \(D_y\) are disjoint since channels are oriented. Thus, if \(p < 1\), the probability that no leader exists is \(\mathbb {P}(\bigcap _{x\in V}D_x) = (1-p^{n-1})^{n}\overset{n\rightarrow + \infty }{\rightarrow } 1\).    \(\square \)

Theorem 2

If the probability of each channel to be timely is \(p < 1\), then the probability of leader existence in any multi-hop Omega implementation approaches 1 exponentially fast as n grows.

Proof

A channel is bitimely if it is timely in both directions. The probability that there exists at least one process such that there exist timely paths from this process to all other processes is greater than the probability to reach them through bitimely paths. We use the probability of the latter as a lower bound for our result. If p is the probability of a channel to be timely, \(\tilde{p} = p^2\) is the probability that it is bitimely. Consider graph G where the edges represent bitimely channels. It is an Erdos-Renyi graph where an edge exists with probability \(\tilde{p}\). It was shown (see [12]) that \(\mathbb {P}(G\text { is connected}) \sim 1-n(1-\tilde{p})^{n-1}\overset{n\rightarrow + \infty }{\rightarrow } 1\).    \(\square \)

Leader stability. As in the previous subsection, we assume the leader has timely paths to all other processes in the network. If channel timeliness changes, this process may not have timely paths to all other processes anymore. Leader stability time is the expected number of rounds of such channel timeliness change where a particular process remains the leader.

Again, direct channel and multi-hop implementations of Omega behave differently. Direct channel leader stability time approaches zero as n increases and cannot be limited from below by fixing a particular value of channel timeliness probability. Multi-hop leader stability goes to infinity exponentially quickly. In a practical setting, a leader is significantly more stable in a multi-hop Omega implementation than in a direct channel one.

Theorem 3

In any direct channel Omega implementation, if the probability of each channel to be timely is \(p < 1\), leader stability time goes exponentially fast to 0 as n grows. If leader stability time is to remain above a fixed constant \(E > 0\), then the channel timeliness probability p must converge to 1 exponentially fast as n grows.

Proof

At a given time, a given process has timely channels to all other processes with probability \(p^{n-1}\). The number of rounds X a given process retains timely paths to all other processes follows a geometric distribution \(\mathcal {P}(X=r)=q^{r}(1-q)\), where \(q = p^{n-1}\). Thus, the expected number of rounds a process retains timely channels to all other processes is \(\frac{q}{1-q} = \frac{p^{n-1}}{1-p^{n-1}}\sim p^{n-1}\), which tends exponentially fast toward 0 if p is a constant less than 1.

Assume \(\mathbb {E}(X)\) converges towards a given fixed number E as n tends towards infinity. That is, we need \(\lim _{n\rightarrow \infty } \mathbb {P}(G\text { is connected}) = \frac{1}{E+1}\). Then, \(p^{n-1}\) tends to \(\frac{1}{E+2}\), which implies that p converges towards 1 exponentially fast.    \(\square \)

Theorem 4

In any multi-hop Omega implementation, if the probability of each channel to be timely is \(p < 1\), leader stability time goes to infinity exponentially fast as n grows. If leader stability time is to remain above a fixed constant \(E > 0\), then channel timeliness probability may converge to 0 exponentially fast as n grows.

Proof

If we fix \(\tilde{p}\), \(0<\tilde{p}<1\), we have \(\mathbb {P}(G\text { is connected}) \sim 1-n(1-\tilde{p})^{n-1}\) (see [10, 12]). Then, the expected number of rounds a given process retains timely paths to all other processes is asymptotically \(n^{-1}\left( \frac{1}{1-\tilde{p}}\right) ^{n}\), which increases exponentially fast.

Assume \(\mathbb {E}(X)\) converges towards a given fixed number E as n tends to infinity. This means that

$$\lim _{n\rightarrow \infty } \mathbb {P}(G\text { is connected}) = \frac{1}{E+1} = e^{-e^{-c}}$$

Using well-known results of random graph theory [4], we can take

$$\tilde{p}(n) = \frac{\ln {n}}{n} + \frac{c}{n}= \frac{\ln {n}}{n} - \frac{\ln \ln {(1+E)}}{n}$$

   \(\square \)

4 Necessity and Sufficiency Properties

We now explore the properties of a deterministic Omega implementation.

Model independent properties. The below Omega implementation properties are applicable to both general propagation and dependable channel model. Intuitively, Theorem 5 states that the leader needs to periodically inform other processes of its correctness or they will not be able to detect its crash.

Theorem 5

In an implementation of Omega, at least one correct process needs to send infinitely many timely messages.

Proof

Assume \(\mathcal {A}\) is an implementation of Omega where every correct process sends a finite number of timely messages. Start with a network where all but two processes x and y crash, wait till all timely messages are sent. Since \(\mathcal {A}\) is an implementation of Omega, eventually x and y need to agree on the leader. Let it be x. Since all timely messages are sent, the remaining messages may be delayed arbitrarily. If x now crashes, process y must eventually elect itself the leader. Instead, we delay messages from x to y. The crash and the delay are indistinguishable to y so it elects itself the leader. We now deliver messages in an arbitrary manner. Again, since \(\mathcal {A}\) implements Omega, x and y should agree on the leader. Let it be y. The argument for x is similar. We then delay messages from y to x forcing x to select itself the leader. We continue this procedure indefinitely. The resultant sequence is a computation of \(\mathcal {A}\). However at least one process, either x or y, oscillates in its leader selection infinitely many times. To put another way, this process never elects the leader. This means that, contrary to the initial assumption, \(\mathcal {A}\) is not an implementation of Omega. This proves the theorem.    \(\square \)

If single process sends an infinite number of messages in a message efficient implementation of Omega, this process must be the leader. Otherwise processes are not able to recognize the crash of the leader. Hence, the corollary of Theorem 5.

Corollary 1

In a message efficient implementation of Omega, the leader must send infinitely many timely messages.

General propagation model properties. The intuition for the results in this subsection is as follows. Since there are no channel dependability properties in the general propagation model, for timely delivery a message needs to be sent across every channel. Indeed, in case some channel is skipped, this may be the channel that contains the only timely path leading to some process. Skipping this channel precludes timely message delivery. It follows that \(\varOmega (n^2)\) packets are required to timely deliver a message in the general propagation model. Therefore, there does not exist a message and packet efficient implementation of Omega in this model.

Lemma 1

To timely deliver a message in the general propagation model, each recipient process needs to send it across every outgoing channel, except for possibly the channels leading to the origin and the sender.

Proof

Assume the opposite. There exists an algorithm \(\mathcal {A}\) that timely delivers message m from the origin x to all processes in the network such that some process y receives it timely yet does not forward it to some process \(z \ne x\).

Consider the propagation graph T for m to be as follows.

$$\begin{aligned} x \rightarrow y \rightarrow z \rightarrow \text {rest of the processes} \end{aligned}$$

That is, the timely paths to all processes lead from x to y then to z. If \(\mathcal {A}\) is such that x sends m to y, then, by assumption, y does not forward m to z. Therefore, no process except for y gets m through timely packets. By definition of the timely message, m is not timely received by these processes. If x does not send m to y, then none of the processes receive a timely message. In either case, contrary to the initial assumption, \(\mathcal {A}\) does not timely deliver m to all processes in the network.    \(\square \)

The below corollary follows from Lemma 1.

Corollary 2

It requires \(\varOmega (n^2)\) packets to timely deliver a message in the general propagation model.

Combining Corollary 2 and Theorem 5 we obtain Corollary 3.

Corollary 3

In the general propagation model, there does not exist a message and packet efficient implementation of Omega.

Proposition 3

There exists a message efficient implementation of Omega in the general propagation model where each correct process can send reliable messages to the leader.

The algorithm that proves the above proposition is a straightforward extension of the second algorithm in Aguilera et al. [1] where every process re-sends received messages to every outgoing channel.

Dependable channel model properties. Unlike the general propagation model where dependability properties of a channel cannot be established, if timely and reliable channels are allowed, packet and message efficient implementation of Omega is possible. However, the super-packet efficiency is not.

Lemma 2

In any message efficient implementation of Omega, each correct process must have a fair-lossy path to the leader.

Proof

Assume there is a message-efficient implementation \(\mathcal {A}\) of Omega where there is a correct process x that does not have a fair-lossy path to the leader. According to Corollary 1, x itself may not be elected the leader. Assume there is a computation \(\sigma _1\) of \(\mathcal {A}\) where process \(y \ne x\) is elected the leader. Note that fair-lossy channels are not type discriminating. That is, if x does not have a fair-lossy path to y, but has a fair lossy path to some other process z, then z does not have a fair-lossy path to y either. Thus, there must be a set of processes \(S \subset N\) such that \(x \in S\) and \(y \notin S\) that do not have fair-lossy paths to processes outside S.

Since \(\mathcal {A}\) is message efficient, processes of S only send a finite number of messages to y. Consider another computation \(\sigma _2\) which shares prefix with \(\sigma _2\) up to the point were the last message from processes of S is received outside of S. After that, all messages from y to processes in S and all messages from S to outside are lost. That is in \(\sigma _2\), y does not have timely, or every fair-lossy, paths to processes of S. It is possible that some other process w is capable of timely communication to all processes in the network. However, since \(\mathcal {A}\) is efficient, no other processes but y is supposed to send infinitely many messages.

Since all messages from S are lost, \(\sigma _1\) and \(\sigma _2\) are indistinguishable for the correct processes outside S. Therefore, they elect y as the leader. However, processes in S receive no messages from y. Therefore, they have to elect some other process u to be the leader. This means that \(\mathcal {A}\) allows correct processes to output different leaders. That is, \(\mathcal {A}\) is not an implementation of Omega.    \(\square \)

We define a source to be a process that does not have incoming timely channels.

Lemma 3

To timely deliver a message in the dependable channel model, each recipient needs to send it across every outgoing channel to a source, except for possibly the channels leading to the origin and the sender.

The proof of the above lemma is similar to the proof of Lemma 1. Observe that Lemma 3 states that the timely delivery of a packet requires n messages per source. If the number of sources is proportional to the number of processes in the network, we obtain the following corollary.

Corollary 4

It requires \(\varOmega (n^2)\) packets to timely deliver a message in the dependable channel model where the number of sources is proportional to n.

Theorem 6

In the dependable channel model, the following conditions are necessary and sufficient for the existence of a packet and message efficient implementation of Omega: (i) there is at least one process l that has an eventually timely path to every correct process (ii) every correct process has a fair-lossy path to l.

Proof

We demonstrate sufficiency by presenting, in the next section, an algorithm that implements Omega in the dependable channel model with the conditions of the theorem.

We now focus on proving necessity. Let us address the first condition of the theorem. Assume there is a message and packet efficient implementation \(\mathcal {A}\) of Omega in the dependable channel model even though no process has eventually timely paths to every correct process. Let there be a computation of \(\mathcal {A}\) where some process x is elected the leader even though x does not have a timely path to each correct process. According to Corollary 1, x needs to send infinitely many timely messages. According to Corollary 4, each such message requires \(\varOmega (n^2)\) packets. That is, \(\mathcal {A}\) may not be message and packet efficient. This proves the first condition of the theorem. The second condition immediately follows from Lemma 2.    \(\square \)

The below theorem shows that (plain) efficiency is all that can be achieved with the necessary conditions of Theorem 6. That is, even if these conditions are satisfied, super packet efficiency is not possible.

Theorem 7

There does not exist a message and super packet efficient implementation of Omega in the dependable communication model even if there is a process l with an eventually timely path to every correct process and every correct process has a fair-lossy path to l.

Proof

Assume the opposite. Suppose there exists a super packet efficient algorithm \(\mathcal {A}\) that implements Omega in the network where some process l has an eventually timely path to all correct processes and every correct process has fair-lossy paths to l.

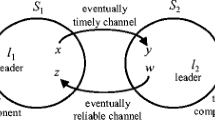
Without loss of generality, assume the number of processes in the network is even. Divide the processes into two sets \(S_1\) and \(S_2\) such that the cardinality of both sets is n/2. Refer to Fig. 1 for illustration. \(S_1\) is completely connected by timely channels. Similarly, \(S_2\) is also completely connected by timely channels. The dependability of channels between \(S_1\) and \(S_2\) is immaterial at this point.

Fig. 1.
figure 1

Network for \(\sigma _3\) computation of Theorem 7.

Full size image

Consider a computation \(\sigma _1\) of \(\mathcal {A}\) on this network where all processes in \(S_1\) are correct and all processes in \(S_2\) crashed in the beginning of the computation. Since \(\mathcal {A}\) is an implementation of Omega, one process \(l_1 \in S_1\) is elected the leader. Since \(\mathcal {A}\) is message efficient, only \(l_1\) sends messages infinitely often. Since \(\mathcal {A}\) is super packet efficient, only O(n) channels carry theses messages infinitely often. Since the network is completely connected, there are \((n/2)^2\) channels leading from \(S_1\) to \(S_2\). This is in \(O(n^2)\). Thus, there is least one channel (x, y) such that \(x \in S_1\) and \(y \in S_2\) that does not carry messages from \(l_1\) infinitely often.

Let us consider a computation \(\sigma _2\) of \(\mathcal {A}\) where all processes \(S_2\) are correct and all processes in \(S_1\) crash in the beginning of the computation. Similar to \(\sigma _1\), there is a process \(l_2 \in S_2\) that is elected the leader in \(\sigma _2\), and there is a channel (z, w) such that \(z \in S_2\) and \(w \in S_1\) that carries only finitely many messages of \(l_2\).

We construct a computation \(\sigma _3\) of \(\mathcal {A}\) as follows. All processes are correct. Channel dependability inside \(S_1\) and \(S_2\) is as described above. All channels between \(S_1\) and \(S_2\) are completely lossy, i.e., they lose every transmitted message. An exception is channel (x, y) that becomes timely as soon as it loses the last message it is supposed to transmit. Similarly, channel (z, w) becomes reliable as soon as it loses the last message.

To construct \(\sigma _3\), we interleave the actions of \(\sigma _1\) and \(\sigma _2\) in an arbitrary manner. Observe that to processes in \(S_1\) computations \(\sigma _1\) and \(\sigma _3\) are indistinguishable. Similarly, to processes in \(S_2\), the computations \(\sigma _2\) and \(\sigma _3\) are indistinguishable.

Let us examine the constructed computation closely. Sets \(S_1\) and \(S_2\) are completely connected by timely channels, and (x, y), connecting \(S_1\) and \(S_2\) is eventually timely. This means that \(l_1\) has an eventually timely path to every correct process in the network. Moreover, due to channel (z, w), every process has a fair-lossy path to \(l_1\). That is, the conditions of the theorem are satisfied. However, the processes of \(S_1\) elect \(l_1\) as their leader while the processes of \(S_2\) elect \(l_2\). This means that the processes do not agree on the single leader. That is, contrary to the initial assumption, \(\mathcal {A}\) is not an implementation of Omega. The theorem follows.    \(\square \)

Fig. 2.
figure 2

Message and packet efficient implementation of Omega \(\mathcal {MPO}\).

Full size image

5 \(\mathcal {MPO}\): Message and Packet Efficient Implementation of Omega

In this section we present an algorithm we call \(\mathcal {MPO}\) that implements Omega in the fair-lossy channel communication model. As per Theorem 6, we assume that there is at least one process that has an eventually timely path to every correct process in the network and every correct process has a fair-lossy path to this process. The code of the algorithm is shown in Fig. 2. The main idea of \(\mathcal {MPO}\) is for processes to attempt to claim the leadership of the network while discovering the reliability of its channels. Each process weighs each channel by the number of messages that fail to come across it. The lighter channel is considered more reliable. If a process determines that it has the lightest paths to all processes in the network, the process tries to claim leadership of the network.

The leadership is obtained in phases. First, the leader candidate sends startPhase message. Then, the candidate periodically sends alive message. In case an alive fails to reach one of the processes on time, the recipient replies with failed. The size of startPhase depends on the network size. The size of the other message types is constant.

The routes of the messages vary. Messages that are only sent finitely many times are broadcast: sent across every channel in the network. Once one process receives such a message for the first time, the process re-sends it along all of its outgoing channels. Specifically, startPhase, stopPhase and failed are broadcast. The leader sends alive infinitely often. Hence, for the algorithm to be packet efficient, alive has to be sent only along selected channels. Message alive is routed through the channels that the origin believes to be the most reliable.

Specifically, alive is routed along the channels of a minimum weight arborescence: a directed tree rooted in the origin reaching all other processes. The arborescence is computed by the origin once it claims leadership. It is sent in the startPhase that starts a phase. Once each process receives the arborescence, the process stores it in the arbs array element for the corresponding origin. After receiving alive from a particular origin, the recipient consults the respective arborescence and forwards the message to the channels stated there.

In addition to routing alive along the arborescence, each process takes turns sending the leader’s alive to all its neighbors. The reason for this is rather subtle: see Theorem 7 for details. Due to crashes and message losses, arbs for the leader at various processes may not reach every correct process. For example, it may lead to a crashed process. Thus, some processes may potentially not receive alive and, therefore, not send failed. Since failed are not sent, the leader may not be able to distinguish such a state from a state with correct arbs.

To ensure that every process receives alive, each process, in turn, sends alive to its every neighbor rather than along most reliable channels. Since only a single process sends to all neighbors a particular alive message, the packet complexity remains O(n).

Message failed is sent if a process does not receive a timely alive. This message carries the parent of the process which was supposed to send the alive. That is, the sender of failed blames the immediate ancestor in the arborescence. Once the origin of the missing alive, receives failed, it increments the weight of the appropriate edge in edges that stores the weights of all channels. If a process has timely outgoing paths to all processes in the network, its arborescence in edges convergences to these paths.

Action specifics. The algorithm is organized in five actions. The first is a timeout action, the other four are message-receipt actions.

The timeout action handles two types of timers: sender and receiver. Process p’s own timer (\(q=p\)) is a sender timer. It is rather involved. This timer is always on since the process resets it after processing. First, the process computes the minimum weight of the arborescence for each leader candidate. A process is considered a leader candidate if its timer is on. Note that since p’s own timer is always on, it is always considered.

The process with the minimum weight arborescence is the new leader. If the leadership changes (\(leader \ne newLeader\)), further selection is made. If p gains leadership (\(newLeader = p\)), then p starts a new phase by updating its own minimum-weight arborescence and broadcasting startPhase. If p loses leadership, it increments its phase and broadcasts stopPhase bearing the new phase number.

If the leadership persists (\(leader = newLeader\)) and p is the leader, it sends alive. Process p keeps track of whose turn it is to send alive to all its neighbors in the shout variable. The variable’s value rotates among the ids of all processes in the network.

The neighbor timer (\(q \ne p\)) is a receiver timer. If the process does not get alive on time from q, then p sends failed. In case the process sends failed, it also increases the timeout value for the timer of q thus attempting to estimate the channel delay.

For our algorithm, the timer integers are as follows. The sender timer is an arbitrary constant integer value TO. This value controls how often alive is sent. It does not affect the correctness of the algorithm. Receiver timers initially hold an arbitrary value. The timer integer is increased every time there is a timeout. Thus, for an eventually timely channel, the process is able to estimate the propagation delay and set the timer integer large enough that the timeout does not occur. For untimely channels, the timeout value may increase without bound.

The next four actions are message receipt handling. Note that a single process may receive packets carrying the same message multiple times across different paths. However, every process handles the message at most once: when it encounters it for the first time. Later duplicate packets are discarded.

The second action is startPhase handling. The process copies the arborescence and phase carried by the message, rebroadcasts it and then resets the alive receiver timer associated with the origin process. The third action is the receipt of stopPhase which causes the recipient to stop the appropriate timer.

The forth action is alive handling. If alive is the matching phase, it is further considered. If alive comes through the origin’s arborescence, the receiver sends alive to its children in the origin’s arborescence or broadcasts it. The process then resets the timer to wait for the next alive. If alive comes from elsewhere, that is, it was the sender’s turn to send alive to all its neighbors, then p just resets the timeout and waits for an alive to arrive from the proper channel. This forces the process to send failed if alive does not arrive from the channel of the arborescence.

The last action is failed handling. If failed is in response to an alive originated by this process (\(p=q\)) then the origin process increments the weight of the edge from the parent of the reporting process to the process itself according to the message arborescence. If failed is not destined to this process, p rebroadcasts it.

The algorithm’s correctness is summarized by the below theorem. Its detailed proof can be found here [5].

Theorem 8

Algorithm \(\mathcal {MPO}\) is a message and packet efficient implementation of Omega in the fair-lossy channel model.

6 Algorithm Extensions

We conclude the paper with several observations about \(\mathcal {MPO}\). The algorithm trivially works in a non-completely connected network provided that the rest of the assumptions used in the algorithm design, such as eventually timely paths from the leader to all correct processes, are satisfied. Similarly, the algorithm works correctly if the channel reliability and timeliness is origin-related. That is, a channel may be timely for some, not necessarily incident, process x, but not for another process y. Algorithm \(\mathcal {MPO}\) may be modified to use only constant-size messages. The only non-constant size message is startPhase. However, the message type is supposed to be timely. So, instead of sending a single large message, the modified \(\mathcal {MPO}\) may instead send a sequence of fixed-size messages with the content to be re-assembled by the receivers. If one of the constituent messages does not arrive on time, the whole large message is considered lost.