An Improved Method for Stock Market Forecasting Combining High-Order Time-Variant Fuzzy Logical Relationship Groups and Particle Swam Optimization

Abstract

Fuzzy forecasting approaches are mainly based on the modeling of fuzzy logical relationships of the historical data. In this paper, an improved model for forecasting stock market indices which combines the High-order Time-Variant Fuzzy Logical Relationship Groups (HV-FLRGs) and Particle Swarm Optimization (PSO) is presented. Firstly, HV-FLRGs are more effective to capture fuzzy relations on time series data than the conventional time-invariant fuzzy logical relationship groups. Secondly, PSO is employed to optimize the length of intervals by searching the space of the universe of discourse. To verify the effectiveness of the proposed model, the historical data of Taiwan Futures Exchange (TAIFEX) are examined. The simulation result shows that the proposed model outperforms the previous forecasting models based on the high-order fuzzy time series. These results are very promising for the future work on the development of fuzzy time series and PSO algorithm in real-world forecasting applications.

1 Introduction

In order to advance the decision-making process concerning future requirements, many researchers have focused on real-world problems to deal with various time series data, such academic enrolments [3–5, 7], temperature prediction [11], crop productions [10] and stock markets [12]. However, the conventional forecasting methods only refer to real numbers and fail to solve forecasting problems in which the historical data are represented by linguistic values. Fuzzy set theory was originally proposed by Zadeh [1] to handle human linguistic terms problems and successfully applied to time series forecasting in [2]. They introduced the time-invariant fuzzy time series and the time-variant time series model which use the max–min operations to forecast the enrolments of the University of Alabama. Unfortunately, their method had many drawbacks such as huge computation when the fuzzy rule matrix is large and lack of persuasiveness in determining the universe of discourse and the length of intervals. Therefore, Ref. [5] proposed the first-order fuzzy time series model by using simple arithmetic calculations instead of max-min composition operations [2–4] for better forecasting accuracy. Thereafter, the fuzzy time series methods have received increasing attention in many forecasting applications. To achieve better forecasting accuracy, Ref. [6] presented an effective approach which can properly adjust the lengths of intervals. Chen in [7] presented a new forecasting model based on the high-order fuzzy logical relationship groups to forecast the enrolments of the University of Alabama. Yu in [8] proposed a new model which refined the lengths of intervals during the formulation of fuzzy relationships, thus capturing the fuzzy relations more effectively. Singh in [10] presented a simplified and robust computational method for the forecasting rules based on one and various parameters as fuzzy relationships. Lee et al. in [13] presented method for forecasting the temperature and the TAIFEX based on fuzzy logic relation groups and genetic algorithm. They also used genetic algorithm and simulated annealing. Recently, Particle swarm optimization (PSO) technique has been successfully applied in many applications. Huang et al. in [16] proposed a new forecasting model based on two computational methods, fuzzy time series and PSO, for academic enrolments. Based on Chen’s model [5], Kuo et al. in [14] introduced a new hybrid forecasting model which combined fuzzy time series with PSO algorithm to find the proper length of each interval. Then, to improve method in [14], Kuo et al. in [15] presented a new hybrid forecast method to solve the TAIFEX forecasting problem based on fuzzy time series and PSO. Additionly, in [18] used a fuzzy relation matrix obtained also from PSO technique based on the high-order fuzzy time series. The above-mentioned researches showed that the lengths of intervals and fuzzy relations are two critical factors for forecasting accuracy. Therefore, we propose an improved forecasting method which combined the HV-FLRGs and PSO algorithm. Firstly, the proposed method fuzzifies the historical data into fuzzy sets to form high-order fuzzy logical relationships. Secondly, the PSO algorithm for the optimized lengths of intervals is developed to adjust interval lengths by searching the space of the universe of discourse. The case study with the data of TAIFEX shows that the performance of our model is better than those of any existing methods. The remainder of this paper is organized as follows. In Sect. 2, a brief review of the concepts of fuzzy time series and PSO algorithm are introduced. In Sect. 3, an improved forecasting model based on the HV-FLRGs and PSO is presented. Section 4, evaluates the forecasting performance of the proposed method with the existing methods on the historical data set of TAIFEX. Finally, some conclusions are discussed in Sect. 5.

2 Fuzzy Time Series and PSO Algorithm

2.1 Basic Concepts of Fuzzy Time Series

This section briefly summarizes the basic fuzzy and fuzzy time series concepts. The main difference between the fuzzy time series and traditional time series is that the values of the fuzzy time series are represented by fuzzy sets rather than real value. Let $U =\left\{ { u_1, u_2, \ldots , u_n}\right\}$ be an universal set; a fuzzy set A of U is defined as $A=\left\{ f_A (u_1)/u_1+ f_A (u_2)/u_2 +\ldots +f_A (u_n)/u_n\right\}$, where $f_A$ is a membership function of a given set A: $U \rightarrow [0,1],\, f_A(u_i)$ indicates the grade of membership of $u_i$ in the fuzzy set A. $f_A (u_i) \in [0,1]$, and $\ 1 \le i\le n$. General definitions of fuzzy time series are given as follows:

Definition 1

Fuzzy time series Let $Y(t) (t =\; ..,0,1,2 ..)$, a subset of R, be the universe of discourse on which fuzzy sets $f_i (t) (i = 1,2, \ldots )$ are defined and if F(t) be a collection of $f_1 (t),f_2 (t),\ldots$, then F(t) is called a fuzzy time series on $Y(t) (t \ldots , 0, 1,2 , \ldots ).$

Definition 2

Fuzzy logic relationships (FLRs) If there exists a fuzzy relationship R(t-1,t), such that $F(t) = F(t-1)*R(t-1,t)$, where “$*$” is an arithmetic operator, then F(t) is said to be caused by F(t-1). The relationship between F(t) and F(t-1) can be denoted by $F(t-1) \rightarrow F(t)$. Let $A_i = F(t)$ and $A_j = F(t-1)$, the relationship between F(t) and F(t-1) is denoted by fuzzy logical relationship $A_i \rightarrow A_j$ where $A_i$ and $A_j$ refer to the current state or the left - hand side and the next state or the right-hand side of fuzzy time series.

Definition 3

$\lambda$- Order Fuzzy Relations

Let F(t) be a fuzzy time series. If F(t) is caused by $F(t-1),F(t-2),\ldots ,F(t-\lambda +1) F(t-\lambda )$ then this fuzzy relationship is represented by $F(t-\lambda ),\ldots ,F(t-2),F(t-1) \rightarrow F(t)$ and is called an $\lambda$- order fuzzy time series.

Definition 4

Fuzzy Relationship Group (FLRG)

Fuzzy logical relationships, which have the same left-hand sides, can be grouped together into fuzzy logical relationship groups. Suppose there are relationships such that

$$\begin{aligned} A_i&\rightarrow A_k \\ A_i&\rightarrow A_m \\&\cdot \cdot \cdot \cdot \end{aligned}$$

So, based on [5], these fuzzy logical relationship can be grouped into the same FLRG as : $A_i \rightarrow A_k, A_m \ldots$

Definition 5

Time-Variant Fuzzy Relationship Group (TV-FLRG)

The fuzzy relationship is determined by the relationship of $F(t-1){\ss }F(t)$. If, let $F(t)= A_i (t)$ and $F(t-1)= A_j (t-1)$, we will have the relationship $A_j (t-1) \rightarrow A_i (t)$. At the time t, we have the following fuzzy relationships: $A_j (t-1) \rightarrow A_i (t), A_j (t1-1) \rightarrow A_{i_1} (t1),\ldots ,A_j (tp-1) \rightarrow A_{i_p} (tp)$ with $t1,t2,\ldots ,tp \le$ t. It means that if the fuzzy relationship took place before $A_j (t-1)\rightarrow A_i (t)$, we can group the fuzzy logic relationship to be $A_j (t-1) \rightarrow A_{i_1} (t1), A_{i_2} (t2), A_{i_p} (tp), A_i (t)$. It is called time-variant fuzzy logic relationship group

2.2 PSO Algorithm

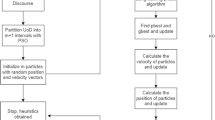
PSO was first introduced by Eberhart and Kannedy in 1995. It belongs to a population-based evolutionary algorithm that can efficiently search a nearly optimal or optimal solution for optimization problems. Most population-based approaches are motivated by evolution as seen in nature. The development of PSO algorithm [14–16] was inspired by the social behaviour of animals, such as fish schooling, birds flocking and the swarm theory. The PSO algorithm applies a cooperative particle swarm to find the best solution from all feasible solutions. Each particle is randomly initialized and then allowed to move in the virtual searching space. At each step of optimization, each particle evaluates its own fitness and the fitness of its neighbouring particles. Each particle can remember its own best solution, which results in the best fitness, as well as see the candidate solution for the best performing particle in its neighbourhood. A moving particle, indexed by id, adjusts its candidate solution according to the following formulas:

$$\begin{aligned} V_{id}^{k+1} = \omega ^k* V_{id}^k+ C_1* Rand()* (Pbest_{id}-X_{id}^k )+C_2* Rand()* ( G_{best}-X_{id}^k) \end{aligned}$$

(1)

$$\begin{aligned} X_{id}^{k+1}= X_{id}^k + V_{id}^{k+1} \end{aligned}$$

(2)

$$\begin{aligned} \omega ^k= \omega _{max} -k*( \omega _{max} - \omega _{min})/(iter_{max}) \end{aligned}$$

(3)

where, $X_{id}^k$ is the current position of a particle id in $^k th$ iteration; $V_{id}^k$ is the velocity of the particle id in $k^{th}$ iteration, and is limited to $[-V_{max},V_{max}]$ where $V_{max}$ is a constant pre-defined by user. Pbest is the position of the particle that experiences the best fitness value. $G_{best}$ is the best one of all personal best positions of all particles within the swarm. Rand() is the function can generate a random real number between 0 and 1 under normal distribution. $C_1$ and $C_2$ are acceleration values which represent the selfcondence coefficient and the social coefficient, respectively.

The steps for the standard PSO are presented in Algorithm 1.

3 An Improved Forecasting Model Based on the HV-FLRGs and PSO Algorithm

Based on Kuo et al. in [14], a new forecasting model which combined the HV-FLRGs and PSO algorithm is introduced. In the proposed model, three key aspects have been applied to approach the lengths of intervals and fuzzy relations on time series data to increase forecasting accuracy. First, original historical data are used instead of the variations of historical data in our forecasting model. Second, the HV-FLRGs are derived from the time-variant fuzzy relationship groups and calculate the forecasting output based on the fuzzy sets on the right-hand side of the HV-FLRGs. Third, the PSO algorithm is developed to adjust the interval lengths to obtain the optimal partition. A detailed explanation of the proposed model in Subsect. 3.1 follow.

3.1 Forecasting Model Based on HV-FLRGs

To verify the effectiveness of the proposed model, the empirical data for the TAIFEX [13] (Historical data of the TAIFEX under 8/3/1998 – 8/31/1998) are used to illustrate the high - order fuzzy time series forecasting process. The step-wise procedure of the proposed model is detailed as follows:

Step 1: Define the universe of discourse U Assume Y(t) be the historical data of TAIFEX on date t. The university of discourse is defined as $U=\left[ \beta _{min}- N_1,\beta _{max} + N_2\right]$ where $\beta _{min}$, $\beta _{max}$ are The minimum and maximum data of Y(t); $N_1$, and $N_2$ are two proper positive integers to tune the lower bound and upper bound of the U. From the historical data shown in [13], we obtain $\beta _{min}=6566$ and $\beta _{max}=7560$. Thus, the universe of discourse is defined as U= $\left[ 6500,7600\right]$ with $N_1= 66$ and $N_2= 40$.

Step 2: Partition U into appropriate intervals

Divide U into equal length intervals. Compared to the previous models in [5, 8], we cut U into seven intervals, $u_1,u_2,\ldots ,u_7$, respectively. The length of each interval is $l= \left( \beta _{max} + N_2 - \beta _{min} + N_1\right) \div 7 = \left( 7600-6500\right) \div 7 \approx 157.$ Thus, the seven intervals are: $u_1 = \left( 6500, 6657\right] , u_2 = \left( 6657,6814\right] , \ldots , u_6 = \left( 7285,7442\right] , u_7 = \left( 7442, 7600\right]$.

Step 3: Define the fuzzy sets.

Each interval in Step 2 represents a linguistic variable of “stock market” in [15]. For seven intervals, there are seven linguistic values which are , , , , , , and to represent different regions in the universe of discourse on U, respectively. Each linguistic variable represents a fuzzy set $A_i (1\le i\le 7)$ and its definition is described in (4).

$$\begin{aligned} A_i =\sum \limits _{i=1}^{7}\frac{a_{ij}}{u_j} = {\left\{ \begin{array}{ll} 1\;&{}\text {if} \;i==j \\ 0.5\; &{}\text {if} \; j==i-1\; or\; j=i+1 \\ 0\;&{}\text {otherwise} \\ \end{array}\right. } \end{aligned}$$

(4)

where $a_{ij}\in [0,1], 1 \le i \le 7, 1 \le j \le 7$ and $u_j$ is the $^jth$ interval of u. The value of $a_{ij}$ indicates the grade of membership of $u_j$ in the fuzzy set $A_i$.

Step 4: Fuzzy all historical data In order to fuzzify all historical data, it’s necessary to assign a corresponding linguistic value to each interval first. The simplest way is to assign the linguistic value with respect to the corresponding fuzzy set that each interval belongs to with the highest membership degree. For example, the historical data on date 8/3/1998 is 7552, and it belongs to interval $u_7$ because 7552 is within (7442, 7600]. So, we then assign the linguistic value “excellent” (eg. the fuzzy set $A_7$) corresponding to interval $u_7$ to it. Consider two time serials data Y(t) and F(t) on date t, where Y(t) is actual data and F(t) is the fuzzy set of Y(t). According to formula (4), the fuzzy set $A_7$ has the maximum membership value at the interval $u_7$. Therefore, the historical data time series on date Y(8/3/1998) is fuzzified to $A_7$. The completed fuzzified results of the TAIFEX are listed in Table 1.

Table 1. The results of fuzzification

Step 5: Create all $\lambda$-order fuzzy relationships

Based on Definition 3. To establish a $\lambda$-order fuzzy relationship, we should find out any relationship which has the $F(t-\lambda ),F(t-\lambda +1),...,F(t-1) F(t)$, where $F(t-\lambda ),F(t-\lambda +1),\ldots ,F(t-1)$ and F(t) are called the current state and the next state, respectively. Then, a $\lambda$ - order fuzzy relationship is got by replacing the corresponding linguistic values. For example, supposed $\lambda =3$, a fuzzy relationship $A_7,A_7,A_7 \rightarrow A_7$ is got as $F(8/3/1998),F(8/4/1998) F(8/5/1998) \rightarrow F(8/6/1998).$ So, from Table 1. we get $^3rd$-order fuzzy relationships are shown in Table 2.

Table 2. Fuzzy logical relationships

Step 6: Establish all $\lambda$-order fuzzy relationships groups

By [5, 14], all the fuzzy relationship having the same fuzzy set on the left-hand side or the same current state can be put together into one fuzzy relationship group. But, according to the Definition 5, we need to consider the appearance history of the fuzzy sets on the right-hand side too. Therefore, only the element on the right hand side appearing before the left-hand side of the relationship group is taken into the same fuzzy logic relationship groups. Thus, from Table 2 and based on Definition 5, we can obtain 20 fuzzy logical relationship groups shown in Table 3.

Table 3. $^3rd$-oder Fuzzy logical relationship groups

Step 7: Calculate the forecasting output

In this step, we create all forecast outputs for fuzzy logical relationship groups based on fuzzy sets on the right-hand or next state within the same group. For each group in Table 3, we divide each corresponding interval of each next state into p sub-regions with equal size, and create a forecasted value for each group according to equal (5).

$$\begin{aligned} forecasted = \frac{1}{n} \sum \limits _{j=1} ^{n}\frac{\left( m_{kj} + subm_{kj}\right) }{2} \end{aligned}$$

(5)

where;

- n is the total number of next states or the total number of fuzzy sets on the right-hand side within the same group

- $m_{kj}$ $\left( 1\le j \le n\right)$ is the midpoint of interval $u_{kj}$ corresponding to $^jth$ fuzzy set on the right-hand side where the highest level of fuzzy set $A_{kj}$ takes place in these intervals, $u_{kj}$.

- $subm_{kj}$ is the midpoint of one of p sub-regions corresponding to $^jth$ fuzzy set on the right-hand side where the highest level of $A_{kj}$ takes place in this interval. Based on equal (5) and the data in Table 1, we obtain forecasted results for TAIFEX from 8/3/1998 to 9/1/1998 based on $^3rd$-order fuzzy time series model with seven intervals are listed in Table 4.

Table 4. The complete forecasted outputs based on $^3rd$-oder fuzzy time series model

To calculate the forecasted performance of proposed method in the fuzzy time series, the mean square error (MSE) are used as an evaluation criterion to represent the forecasted accuracy. The MSE value is computed according to (6) as follows

$$\begin{aligned} MSE= \frac{1}{n}\sum \limits _{i=\lambda }^{n}\left( Fo_i-Ac_i\right) ^2 \end{aligned}$$

(6)

Where, $Ac_i$ denotes actual data on date i, $Fo_i$ is forecasted value on date i, n is number of the forecasted data, $\lambda$ is order of the fuzzy relationships

3.2 Forecating Method Based on the HV-FLRGs and PSO

To improve forecasted accuracy of the proposed, the effective lengths of intervals and time-variant fuzzy relationship groups which are two main issues presented in this paper. A novel method for forecasting TAIFEX is developed to adjust the length each of intervals in the universe of discourse without increasing the number of intervals by minimizing the MSE value. In our model, each particle exploits the intervals in the universe of discourse of historical data Y(t). Let the number of the intervals be n, the lower bound and the upper bound of the universe of discourse on historical data Y(t) be $p_0$ and $p_n$, respectively. Each particle is a vector consisting of n-1 elements $p_i$ where $1\le i\le n-1$ and $p_i \le p_{\left( i+1\right) }$. Based on these n-1 elements, define the n intervals as $u_1 = \left[ p_0, p_1\right] , u_2 = \left[ p_1, p_2\right] ,\cdot \cdot \cdot , u_i = \left[ p_{(i-1)}, p_i \right] ,\cdot \cdot \cdot , u_n= \left[ p_{(n-1)}, p_n \right]$ respectively. When a particle moves to a new position, the elements of the corresponding new vector need to be sorted to ensure that each element $p_i (1\le i\le n-1)$ arranges in an ascending order. The step-wise procedure of the proposed method is illustrated in Algorithm 2.

4 Computational Results

4.1 Preliminary Data

In this paper, we apply the proposed method to forecast TAIFEX index with the whole historical data [13], from 8/3/1998 to 9/30/1998 are used to perform comparative study in the training phase. The essential parameters of proposed model for forecasting TAIFEX are listed in Table 5.

Table 5. Parameters used for forecasting TAIFEX

4.2 Computational Results

In order to verify the forecasting effectiveness of the proposed model with the high-order FLRGs and different numbers of intervals, six FTS models in C96 [5], H01b [6], L06 [9], L08 [13], HPSO [14] and the NPSO [15], are examined and compared. The forecasted accuracy of the proposed method is estimated using the MSE technique in (6). The simulation result is expressed in Table 5. Our proposed model is executed 10 runs, and the best result of runs is taken to be the final result. A comparison of the fitness accuracy (i.e. the MSE value) with various orders and different number of intervals among the proposed model, the C96 model, H01b model, the L06 model, the L08 model, the HPSO model and the NPSO model are listed in Table 6.

Table 6. A comparison of the forecasted results of the proposed method with the existing models based on high – order fuzzy time series under number of intervals = 16

From Table 6, it is obvious that our model has a smaller MSE value than the other fuzzy forecasting models. The MSE value is calculated according to equal (6) following:

$$\begin{aligned} MSE=\frac{1}{40}\sum \limits _{i=7}^{40}{(7329.78-7330)^2+\cdot \cdot \cdot +(6785.24-6787)^2} = {18.49} \end{aligned}$$

In addition, we also perform five more runs with different orders and 16 intervals of the universe set of discourse to be compared with other models such as L08 in [13] (based on GA), HPSO in [14] (based on PSO), and NPSO [15] (also based on PSO). The detail of comparison is shown in Table 7. The forecasting trend is depicted in Fig. 1 for clearer illustration.

Table 7. A comparison of the forecasted results of the proposed method with the existing models based on high – order fuzzy time series under number of intervals = 16

During the simulation, the number of intervals is kept for the existing models and our model. A comparing of MSE value is listed in Table 7. In Table 7, it can be seen that the accuracy of the proposed model is improved significantly. Particularly, our model gets the lowest MSE value of 18.49 with 7th-order fuzzy relation and the average MSE value of the proposed model is 24.22, which is smallest among four forecasting models. In addition, we also rebuilt NPSO model [14] is considered to be quite effective in recent years and compare the forecasting accuracy of this model with the proposed model on the same historical data of the TAIFEX with different number of samples as 15, 20, 25, 30, 35, 40, 45 and 47. The detail is presented in Table 8

Fig. 1.

A comparison of the MSE value between our model and the previous methods: L08, HPSO, NPSO based on high –order FTS with number of intervals =16.

Table 8. The comparison(MSE) between the proposed model and NPSO model on the same historical data set but different in the numbers of sampling values

From Table 8, it can be seen that our proposed model gives remarkably better forecasting accuracy with MSE values compared to NPSO model with the different number of samples

5 Conclusion and Discussion

Stock market indices are very volatile time series in nature and it has difficult to make the potential relationship as a mathematical model. So, fuzzy time series has shown good performances for these real world problems. In order to improve the forecasting accuracy of the NPSO model, we consider the appearance history of the fuzzy sets on the right-hand side of the same fuzzy relation to create time–variant fuzzy logic relationship groups. Also we consider more information within all next states of all fuzzy relationships to calculate the forecasting output for these fuzzy relationship groups. Then, a novel hybrid forecasting model based on an aggregated HV-FLRGs and PSO is developed to adjust the length of each interval in the universe of discourse. After applying the proposed forecasting method for the real world datasets of TAIFEX, we found that our approach shows better forecasting accuracy than previous ones. The detail of comparison was presented in Tables 6, 7 and 8. The main contributions of this paper are illustrated in the following. First, we show the forecasted accuracy is affected by calculating the forecasting rules from time-variant fuzzy relationship groups. Second, the computational results show that the proposed model gets highest forecasted accuracy for with seven - order FTS model. Actually, as listed in Table 7, the minimal MSE value for the proposed model is 18.49 which is the lowest forecasting accuracy among the models as shown in Table 6. Finally, our forecasting method is general enough for different kinds of time series and can be used in various applications efficiently.