Keywords

1 Introduction

A quality of production depends on the stability and absence of changes in a technological process. Therefore, it is important to identify timely the reasons of dysfunction of technological process and the signals corresponding to them. If the process is carried out in normal conditions then the scattering of parameters, which characterize the properties and quality of a product, depends only on the influence of random variables. The possible dispersion of parameters (their standard deviations) are usually standardized in the normalized conditions.

A stability control of results is based on a series of control procedures. In this case a number of observations and the intervals between them have to be established on the basis of relations between the rates of changes of measured statistical characteristics under the influence of different random variables. This should be realized in such a way that the influence of deviations in carrying out the technological process could be neglected.

As proven practice the control charts are widely used for the statistical control of stability and quality of processes. This method was developed by Shewhart [1]. The main idea of control charts is to divide observations in subgroups, in which variations due to random causes are only permitted. The differences between these subgroups may not only be caused by random specific causes and this must be identified by control charts [2]. For this purpose, a reference value is established. The deviations from this value are detected as observations.

Depending on a control algorithm, the warning and action signals are selected and the control limits are calculated. A warning signal is an event which testifies a confidence level greater than (0.95 … 0.99) about the withdrawal of process from the statistically controlled conditions and about the requirement of technological process correction. An action signal is an event, which indicates to withdraw the process from the statistically controlled conditions with a confidence level of 0.997. The monitored results of a process are presented on the control charts after recording each current observation on them.

The practice of using charts for the control of process has shown that acceptable results are obtained when a number of elements in the subgroups is not more than 4 to 5. The number of elements has to be identical in the assumption of their normal distribution. Under this condition, the coefficients for calculating the control limits are derived. Since the control limits are used as empirical criteria for decision-making, it is allowed to ignore small deviations from normality.

If the volumes of experimental data are larger (n > 10) then the standard deviation (SD) adequately displays a scattering of results. It characterizes a stability of the controlled process. When the samples of small volume are considered then a sample range R n (the absolute difference between the highest and lowest values of subgroup sample) gives better estimate of the scattering of results than the standard deviation and it is calculated more quickly [1]. In addition, for the evaluation of process stability it allows to have only two observations in each subgroup. That should often be enough due to a dynamics of process or an economic feasibility.

The sample range R n and standard deviation σ is statistically connected. For normal distribution it is [3]

$$ M\left( {\frac{{R_{n} }}{\sigma }} \right) = \alpha_{n}, $$
(1)

where: α n – tabulated value depending on a number of elements n in sample, R n - range of n-element sample.

Due to these statistics the mean value of R n can be identified as

$$ M\left( {R_{n} } \right) = \alpha_{n} \sigma . $$
(2)

In addition, as it can be seen from the expression (1), α n is an unbiased estimate, and consequently, also, an unbiased estimate M (R n ) is important and it may be taken as the centre of possible scattering of inspection results.

The range of possible values of ratio R n /σ at a fixed value of n due to the influence of random variables and the limited sample size is also tabulated. Thus, there is a relationship

$$ var\left( {\frac{{R_{n} }}{\sigma }} \right) = \beta_{n} , $$
(3)

which allows, for a given σ, to set the possible values of scattering amplitude R n with respect to M (R n ) in the form

$$ var\left( {R_{n} } \right) = \beta_{n} \sigma . $$
(4)

The most common charts in the monitoring of process stability are:

  • average value (\( \overline{X} \)-chart) and range (\( \overline{R} \)-chart) or sample standard deviation s,

  • individual measured values (X-chart) and moving range (R-chart).

2 Average Value \( \overline{X} \) Control Chart and Range \( \overline{R} \) Control Chart

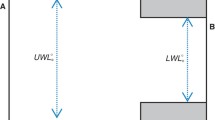
The control chart of average values \( \overline{X} \) is used to demonstrate what the average value of process is and what its stability is. Moreover, it allows identifying variations between subgroups that cannot be explained only by the influence of random variables and their relation to the total variation of the mean. If this type of control has to be reliable, the samples should be stable for a time period between repeated measurements.

Range control chart \( \overline{R} \) identifies any undesirable variation within a subgroup and it is an indicator of variability of a controlled process. If \( \overline{R} \) – chart shows that the variation within a subgroup are not changed then it informs about the uniformity of process. It is necessary to analyze \( \overline{R} \) – chart prior to the analysis of \( \overline{X} \) – chart.

Since the average value \( \overline{X} \) control chart and the range \( \overline{R} \) control chart (sample or standard deviations) reflect the state of process through the spread (variability from unit to unit) and through the centre of location (the average value of process), they are always used inseparably. Thus, to ensure the stability of process is necessary, firstly, to monitor the changes of σ in time which can be caused by an influence of random variables and a dysfunctional process.

By using the expressions (2) and (3) one can determine the absolute value of the variation quantile span R n as

$$ M\left( {R_{n} } \right)\,{ \pm }\,k\left( P \right)\text{var} \left( {R_{n} } \right), $$
(5)

where: \( k\left( P \right) \) – coefficient depending on a value of confidence interval.

If the range is positive number then for the left quantile the condition should be satisfied

$$ \left[ {M\left( {R_{n} } \right) - k\left( P \right)\text{var} \left( {R_{n} } \right)} \right] > 0. $$
(6)

These relations form the basis for the construction of Shewhart control charts. To make a decision on the stability of technological process, there are introduced precautionary warning limits k(P) = 2 and action limits k(P) = 3. It corresponds to the probability of decision P = 95% and R = 99.7%.

When a range control chart \( \overline{R} \) is constructed a tabulated value α n is used as a centre line which in the standard [4] is indicated as d 2. For example: when n = 2 in accordance with [3] d 2 = 1.128 and M(R n ) = 1.128σ is taken as a centre line CL. The action limits in the \( \overline{R} \) control chart must be separated from the centre line by ±3var(R n ). For example, the upper action limit is

$$ UCL_{a} \left( n \right) = d_{2} \sigma + 3d_{3} \sigma = D_{2} \sigma , $$
(7)

where: d 3 corresponds to the value where β n , taken from the same table, for n = 3, d 3 = 0.853.

Thus, calculated values D 2 = (d 2 + 3d 3) are provided in the table [4]. Similarly, one can obtain for the lower action limit

$$ LCL_{a} = d_{2} \sigma - 3d_{3} \sigma , $$
(8)

or

$$ LCL_{a} = D_{1} \sigma , $$
(9)

where D 1 = d 2 − 3d 3.

After analyzing the relation (6) one can conclude that for k(P) = 3 it will be executed if n ≥ 7 only. For n < 7 as the lower action limit of Shewhart chart is taken zero line.

To calculate the upper and lower warning limits, one can use the expressions (5) and (6). For example, if k(P) = 2

$$ UCL_{w} = D_{ 2} \left( 2 \right)\sigma $$
(10)

where:\( D_{ 2} \left( 2 \right) = d_{2} + 2d_{3} \),

$$ LCL_{w} = D_{ 1} \left( 2 \right)\sigma $$
(11)

where: \( D_{ 1} \left( 2 \right) = d_{2} - 2d_{3} \).

In this case Eq. (6) will only be carried out when n ≥ 4. In other cases the numerical value of the lower warning limit is absent – it is replaced by 0.

The calculated values for the centre line CL = d 2 σ, upper and lower action limits LCL a = D 1 σ, as well as upper and lower warning limits and LCL w = D 1(2), respectively, are used to build the Shewhart charts.

In Fig. 1 an example of construction \( \overline{R} \) – charts is presented. The ordinate axis represents the value of magnitude and on the horizontal axis are a number of observations of subgroup.

Fig. 1.
figure 1

Example of construction – Shewhart chart

Full size image

The values of coefficients used to determine the control limits of Shewhart charts are presented in Table 1 [4]. The coefficients for calculating the warning limits are derived according to formulas

$$ D_{ 1} \left( 2 \right) = d_{2} \, - \,2d_{3} , $$
(12)
$$ D_{ 2} \left( 2 \right) = d_{2} + 2d_{3} . $$
(13)
Table 1. The values of coefficients to determine the limit values of Shewhart charts
Full size table

Assessing the bias stability of technological process should be carried out on \( \overline{X} \) – chart using a standard sample with a SD value of μ. As mentioned before, a requirement is the invariance of its characteristics in time. A monitoring is carried out with a standard sample several times (n ≥ 2) and average \( \bar{x}_{i} \) is calculated for each subgroup.

In this case as the centre line in the construction of the \( \overline{X} \) – chart is used CL = μ, in relation to which changes \( \bar{x}_{i} \) are considered in i-subgroups. The warning and action limits of are defined as

$$ UCL = \mu + k\left( P \right)\frac{\upsigma}{\sqrt n }, $$
(14)
$$ LCL = \mu - k\left( P \right)\frac{\upsigma}{\sqrt n }, $$
(15)

where: σ – standard deviation (normalized value) of estimated results in the control due to the influence of random variables.

3 Individuals X Control Chart and Moving Range R Control Chart

In some cases for practical or economic reasons there is no possibility to carry out the multiple observations and n = 1. In such situation, the moving range R i may be used to monitor the stability of process. The μ value of standard sample does not need to be known accurately. However, the values of the samples must be stable. So-called initial “reference” measurement of performance of standard sample is realized with the result y 0. Then, there is the difference between the result of the first measurements y 1 and y 0, i.e. it is calculated the first implementation of bias (offset) results \( \hat{\delta }_{i} = y_{1} - y_{0} \). Subsequently, the offset is determined as the difference values obtained in the current and previous times. Thus, the moving range of i-th control chart estimated as

$$ R_{i} = |\hat{\delta }_{i} - \hat{\delta }_{i - 1} |. $$
(16)

A fragment of the moving range R-chart with the results of calculations [5] using the standard object with μ = 10.29 is presented in Table 2.

Table 2. Data to build the charts of moving range R
Full size table

Since the centre line CL at moving range R chart is the zero line then the previously received formula to calculate the action and warning limits should be modified. The starting point is known and the SD value of the process \( \sigma_{I} = 0.06645 \) is used. Then the action limits and warning limits are defined as

$$ \begin{aligned} UCL_{a} = + 3\sigma_{\text{I}} = 0.1994,\quad LCL_{a} = - 3\sigma_{I} = - 0.1994, \hfill \\ UCL_{w} = + 2\sigma_{I} = 0.1329,\quad LCL_{w} = - 2\sigma_{I} = - 0.1329. \hfill \\ \end{aligned} $$

In this case unlike the \( \overline{R} \) – charts, lower warning and action limits cannot be equal to zero because deviation from μ value can be positive or negative.

The centre line \( M(\hat{\delta }) = 0 \) is taken as the zero line to create the X-chart. Symmetrically in relation to it, the upper and lower warning limits are determined with factor k(P) = 2 and upper and lower action limits with factor k(P) = 3. Further actions and solutions taken for X-chart are similar as for R-chart. The Shewhart chart for the example from Table 2 is presented in Fig. 2 a,b.

Fig. 2.
figure 2

Shewhart control charts for: (a) assessment of displacement \( \hat{\delta } \) stability (b) current dispersion of results

Full size image

4 Display of Process Instability

As it is presented in Fig. 2, there are some periods of time when the bias of process and the changes of range are low. There are other periods where results indicate an increased instability. This situation requires the identification of reasons that caused an increase of process instabilities over a certain period although the current values of the parameters are within the required limits.

When creating a control chart it is assumed that during monitoring the change in the X value (the dispersion of sample means as an estimate of bias) results from the influence of random factors and the limited sample size. In this case, the value outside ±3σ is an low probable event. Its appearance indicates the presence of systematic influence, which leads to a process dysfunction and a change of its control. Based on practical experience in [4] is recommended to pay attention to “… any unusual structure of data points, which may indicate about a manifestation of the special (non-random) reasons”. Such an event corresponds to the probability of 0.003 [4]. The observed situation can be attributed as “critical” which constitutes a violation of the conditions of process.

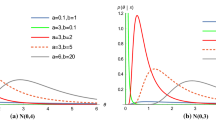
Figure 3 presents the probability of getting the results displayed in control zones A, B and C. It characterizes the relationship between σ and the number of observations n.

Fig. 3.
figure 3

The probability of getting the results into control zones A, B, C

Full size image

An indication of the influence of random variables is chaotic incidence of subgroups results in all areas A, B and C of the Shewhart chart. Tracking the emergence of a systematic trend in a distribution of points corresponding to the mean values of samples (bias estimate) can be used as evidence of the trend of mean value of controlled process parameter.

The trends on the control chart, which emerged under the influence of special causes, can lead to a breakdown of process. They will be called as series criteria. In this case, the manifestation of a systematic influence on the background of random dispersion is to find a sequence of a certain number of points on the control chart in one of zones or in area covering several zones. This approach allows to justify theoretically that the incidence of trend reports at an early stage about the possibility of violation of a correct process. In this way a sequence of control points on the chart located within the warning or action limit, the probability of which is less than 0.003, can be regarded as a manifestation of joint influence of random and systematic reasons. This property can be used as the basis for the creation of preventive warning criteria. It would allow to adjust the progress of process without waiting for situation when it could be disordered that the results would be outside the control limits.

Checkpoints should be sufficiently distant from each other in time and space that the effect of autocorrelation cannot be included [7]. In accordance with the multiplication theorem for independent events the probability of getting a normally distributed random variable in area A, B, C is equal to the product of individual probabilities

$$ P\left( {A_{1} ,A_{2} , \ldots ,A_{s} } \right) = P\left( {\prod\limits_{i = 1}^{s} {P\left( {A_{i} } \right)} } \right). $$
(17)

During analysis the criteria were established. According to them it can be found the probability of several independent, consecutive values in a particular field of control chart. It may indicate a trend of dysfunctional process. For example if we assume that the average value (bias estimate) of consecutive subgroups are independent random variables then the probability of getting the result for any subgroup above (or below) the centre line in each of zones A, B, C is 0.4986 approximately 0.5 (Fig. 3). Probability, that two consecutive sample values are e.g. above the centre line, is equal to 0.5 ∙ 0.5 = 0.25.

It is necessary to find out what the minimum number of successive results, arranged in a row on one side of the center line of the control chart, corresponds to the probability of 0.003 (0.0027). It is the probability that a single sample value is not within the control limits ±3σ. It turns that this condition can be fulfilled by a sequence of nine points, i.e. probability that a series of nine control chart points will be on one side of central line is 0.00195. If this criterion is satisfied then a change in average value of the overall process can be considered.

Similar reasoning can be made for the possible sequences of points, which are located in corresponding zones of the control chart with a certain probability. One can define a set of preventive criteria when a dysfunctional process begins but results still do not go outside the warning limits or action limits. An example would be a situation when finding 15 consecutive results in a completely “safe” zones ±C cannot cause concern. However, the emergence of the next 16-th result in this zone corresponds to the probability 0.0023, which exceeds the value of 3σ. Therefore, this criterion is also “critical” as shown in Fig. 4.

Fig. 4.
figure 4

The probability of warning signals and symptoms of the action

Full size image

With the use of similar analysis one can define a number of simple criteria shown in Table 3, which demonstrate that the mean value of controlled process is biased.

Table 3. Examples criteria that indicate the shift of mean value of controlled process variable
Full size table

5 Conclusions

In evaluating the stability of process it is possible an very early detection of trends leading to dysfunction of the process.

The considered approach and the resulting criteria for identifying trends can be treated as the basis of sequential analysis and the identification of the “critical” situation for the controlled process, depending on a location of area and a number of points in their sequence on the control chart.

The established laws for the control of individual sections of the X chart allow to introduce corrective actions rapidly, without waiting for the actual dysfunction of process parameters.

This area of research is promising and requires further detailed development and formalization of the results in the form of adaptive decision-making algorithms.