Robust Control for Asynchronous Switched Nonlinear Systems with Time Varying Delays

Abstract

In this article a novel robust controller for the control of switched nonlinear systems with asynchronous switching is proposed considering state delays. The proposed approach improves the actual methodologies found in literature in which the disturbance rejection properties of these two methodologies consider a disturbance equal to zero but the proposed robust controller considers any kind of disturbances that makes this strategy to surpass other similar methodologies. The main objective is that the robust controller stabilizes the studied system in matched and unmatched modes considering the dwell time in order to obtain an exponentially stable closed loop system. Another characteristic of the proposed control strategy is that a conmutative control law in both matched and unmatched cases is designed with a linear part, where the gain matrices for the linear part are obtained by linear matrix inequalities LMI’s along with a nonlinear controller part.

abstract environment.

1 Introduction

Asynchronous switched control of linear and nonlinear systems have been studied in recent years in which there are several interesting results, considering that an asynchronous switching occurs when the modes of the controller and the system are differents. Some of these studies found in literature are related to linear systems such as [3] where the control of the studied system with average dwell time is proposed for the synchronous and asynchronous cases. Another interesting study can be found in [5] where a $H_{\infty }$ controller [15] of switched delayed system with average dwell time is evinced. In [1] there is another example for the stabilization of time delayed linear systems [9] under asynchronous switching, a robust $H_{\infty }$ controller is implemented following a similar procedure as the previous study. In [2] an asynchronous finite time $H_{\infty }$ controller with mode dependent dynamic state feedback is shown so the controller is designed implementing its disturbance rejection properties. Lyapunov-Krasovskii functionals for the design of asynchronous switched controller for nonlinear systems can be found in [4] in order to test and ensure the closed loop exponential stability, implementing an average dwell time. In [6] the average dwell time is implemented again for the exponential stability proof and in the case of the nonlinear controller, this includes delays in the states. In [7] a $L_{\infty }$ robust asynchronous controller like the proposed system in this article is shown, where as similar to the previous study the switched system consists of a linear and nonlinear part and the delays are considered only in the linear part. In the case of intelligent controllers to solve this kind of problems there are several studies such as [8] where an asynchronous fuzzy controller for switched nonlinear systems via switching Lyapunov functions implementing a Takagi-Sugeno model is used to estimate each subsystem, so the average dwell time is used obtaining the gain matrices solving the LMI’s. There are other approaches such as sliding mode control [10, 12, 14] and intelligent control techniques [13] that can be implemented for the stabilization of this kind of systems in future studies. In this article a novel asynchronous robust controller for switched nonlinear time delayed systems is proposed. The objective of this study is to design a conmutative controller in the presence of disturbances, contrary to other control approaches for nonlinear systems in which the disturbance is considered as zero $w=0$ [7]. Another contribution of this article is that the time delays are considered not only in the linear states these are also considered in the nonlinear states something that is not found in the literature as far as the author knowledge so with these results the outcomes obtained in other studies are significantly improved. The design procedure consists in selecting appropriated Lyapunov-Krasovskii functionals in order to consider the delayed states in the linear and nonlinear parts, dividing the problem in two parts the matched case and unmatched case so the Lyapunov functions derivatives are obtained to corroborate the closed loop exponential stability. The robust conmutative control laws are obtained for both switching cases, the matched and unmatched cases, so the controller consists of two parts one linear state feedback part, obtaining the gain matrices solving the required LMI’s [16] and a nonlinear feedback control law obtained for each switching case. The article is divided in three sections; Sect. 2 shows the problem formulation, in the following section, the robust controller design is shown, in Sect. 4 a simulation is evinced, and in the last section the conclusions of this study are presented.

2 Problem Formulation

Consider [7]

$$\begin{aligned} \dot{x}(t)=A_{\sigma (t)}x(t) + A_{d\sigma (t)}x(t-d(t)) + f_{\sigma (t)}(x(t),x(t-d(t))) + B_{\sigma (t)}u(t) \nonumber \\ +\; G_{\sigma (t)}w(t). \end{aligned}$$

(1)

Where

$x(t) \in \mathbb {R}^{n}$, $u(t) \in \mathbb {R}^{m}$, $w(t) \in \mathbb {R}^{p}$, $x(t_{0} + \theta )=\varphi (\theta )$ and $\theta \in [-\tau ,0]$ and $0 \le d(t) \le \tau$, $\dot{d}(t) \le \eta < 1$ and $max_{w}(w(t))=\gamma$

In order to design the proposed controller is important to define the following switching instances of the system as found in [3, 7]

$$\begin{aligned} \sigma :{(t_{0},\sigma (t_{0})),(t_{1},\sigma (t_{1})) ... (t_{k},\sigma (t_{k})) } \end{aligned}$$

(2)

and the controller switching instance are defined as [3, 7]

$$\begin{aligned} \sigma :{(t_{0},\sigma (t_{0})),(t_{1} + \varDelta _{1},\sigma (t_{1})) ... (t_{k} + \varDelta _{k},\sigma (t_{k})) } \end{aligned}$$

(3)

where $0<\varDelta _{k}<inf_{k \ge 1}(t_{k+1} - t_{k})$. Apart from these equations it is important to define the average dwell time and chattering bound [4, 6, 7].

Definition 1

For any $0< t \le T$ define $N_{\sigma (t)}(T,t)$ be the number of switching numbers over (t, T). So $N_{\sigma (t)}(T,t)\le N_{0} + \frac{T- t}{\tau _{a}}$ is met for $\tau _{a}>0$ and $N_{0} \ge 0$ then $\tau _{a}$ is the average dwell time and $N_{0}$ is the chattering bound.

With these definitions the proposed approach could be designed following the required design procedure.

3 Robust Asynchronous Controller Design for Nonlinear Switched Systems with Time Varying Delays

The results of this article are explained in this section, so to derive the proposed approach the problem must be divided in the matched and unmatched cases. The following theorem depicts the asynchronous robust controller design for the studied system. It is important to remark that the asynchronous robust control law is divided into a linear part (state feedback) and a nonlinear part, obtaining the gains solving the required LMI’s.

Theorem 1

An asynchronous robust controller is obtained if the following LMI’s are solved for ( $K_{i\sigma (t)}, K_{j\sigma (t)}$ ).

(4)

with $\tau _{a}$

$$\begin{aligned} \tau _{a}>\tau _{a}^{*}=\frac{(\alpha + \beta )T_{max} + ln(\mu )}{\alpha }. \end{aligned}$$

(5)

Proof

Consider the case when $t \in [t_{k-1}+\varDelta _{k-1},t_{k}]$ by selecting the following Lyapunov functional [7] where $P_{i}>0$ and $Q_{i}>0$ are diagonal matrices:

$$\begin{aligned} V_{i1}=x^{T}(t)P_{i}x(t) + \int _{t-d(t)}^{t}e^{-\alpha (t-s)}x^{T}(s)Q_{i}x(s)ds. \end{aligned}$$

(6)

Taking the time derivative of (6) and substituting system (1)

$$\begin{aligned} \dot{V}_{i1}\le 2x^{T}(t)P_{i}A_{\sigma (t)}x(t) + 2x^{T}(t)P_{i}A_{d\sigma (t)}x(t-d(t)) + 2x^{T}(t)P_{i}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +\; 2x^{T}(t)P_{i}B_{\sigma (t)}u(t) + 2x^{T}(t)P_{i}G_{\sigma (t)}w(t) + x^{T}(t)Q_{i}x(t) \nonumber \\ -\; x^{T}(t- \tau )Q_{i}x(t -\tau )(1-\eta )e^{-\alpha \tau } - \alpha \int _{t-d(t)}^{t}e^{-\alpha (t-s)}x^{T}(s)Q_{i}x(s)ds. \end{aligned}$$

(7)

Making $\overline{x}=[x^{T}(t),x^{T}(t-d(t))]$ and defining a control law with a nonlinear part $u_{nl\sigma (t)}$

$$\begin{aligned} U(t)= K_{i\sigma (t)}x(t) + u_{nl\sigma (t)}. \end{aligned}$$

(8)

Then

$$\begin{aligned} \dot{V}_{i1}\le \overline{x}^{T}\varPhi \overline{x} + 2x^{T}(t)P_{i}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +\; 2x^{T}(t)P_{i}B_{\sigma (t)}u_{nl\sigma (t)}(t) + 2x^{T}(t)P_{i}G_{\sigma (t)}w(t) \nonumber \\ -\; \alpha V_{i1}. \end{aligned}$$

(9)

where

$$\begin{aligned} \varPhi =\begin{bmatrix} 2P_{i}A_{\sigma (t)} + \alpha P_{i} + 2P_{i}B_{\sigma (t)}K_{\sigma (t)} + Q_{i}&2P_{i}A_{d\sigma (t)} \\ 0&-Q_{i}e^{-\alpha \tau } \end{bmatrix}<0. \end{aligned}$$

(10)

The following property is important to obtain the asynchronous robust control law

Property 1

The nonlinear part of system (1) has the following property

$$\begin{aligned} f_{\sigma (t)}(x(t),x(t-d(t))) -f_{\sigma (t)}(x(t),x(t-\tau )) \cong 0. \end{aligned}$$

(11)

To obtain the robust control law is necessary to implement [11]

$$\begin{aligned} inf_{u \in u(y,t)}sup_{x \in Q(y,t)}sup_{w \in W}[L_{f}V_{i1}(x,u,w,t) + \alpha _{v}(x,t)]<0. \end{aligned}$$

(12)

Defining $\alpha _{v}(x,t)=x^{T}(t)x(t)$, substituting (9) in (12) and implementing Property 1 yields

$$\begin{aligned} =2x^{T}(t)P_{i}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +~2x^{T}(t)P_{i}B_{\sigma (t)}u_{nl\sigma (t)}(t) + 2x^{T}(t)P_{i}G_{\sigma (t)}w(t) \nonumber \\ -~\alpha V_{i1} + x^{T}(t)x(t). \end{aligned}$$

(13)

Implementing Property 1 the following nonlinear control law is obtained

$$\begin{aligned} u_{nl\sigma (t)}=-B^{-1}_{\sigma (t)}f_{\sigma (t)}(x(t),x(t-\tau )) -B^{-1}_{\sigma (t)}G_{\sigma (t)}\gamma _{v} - \frac{1}{2}B^{-1}_{\sigma (t)}P^{-1}_{i}x(t) \end{aligned}$$

(14)

where $\gamma _{v} \in \mathbb {R}^{p}$ is a constant vector that is used to satisfy the following condition in order to meets the robust stability requirements

$$\begin{aligned} sup_{\gamma }sup_{w}[2x^{T}(t)P_{i}G_{\sigma (t)}w(t) - 2x^{T}(t)P_{i}G_{\sigma (t)}\gamma _{v}]\cong 0. \end{aligned}$$

(15)

so substituting the nonlinear robust control law (14) in (13) the Lyapunov function derivative obtained is:

$$\begin{aligned} \dot{V}_{i\sigma (t)}= \left\{ \begin{array}{rcl} 0 &{} \left\| x \right\| =0\\ -\alpha V_{i\sigma (t)} &{} \left\| x \right\| >0 \end{array}\right. \end{aligned}$$

(16)

with the following conmutative controller

$$\begin{aligned} U(t)=\nonumber \\ \left\{ \begin{array}{rcl} K_{i\sigma (t)}x(t) &{} \left\| x \right\| =0\\ -B^{-1}_{\sigma (t)}f_{\sigma (t)}(x(t),x(t-\tau )) -B^{-1}_{\sigma (t)}G_{\sigma (t)}\gamma _{v} - \frac{1}{2}B^{-1}_{\sigma (t)}P^{-1}_{i}x(t) &{} \left\| x \right\| >0 \end{array}\right. \end{aligned}$$

(17)

When $t\in [t_{k},t_{k} + \varDelta _{k}]$ the following Lyapunov-Krasovskii functional is implemented [7] $P_{j}>0$ and $Q_{j}>0$ are diagonal matrices

$$\begin{aligned} V_{j1}=x^{T}(t)P_{j}x(t) + \int _{t-d(t)}^{t}e^{\beta (t-s)}x^{T}(s)Q_{j}x(s)ds. \end{aligned}$$

(18)

Taking the time derivative of (18) and substituting (1)

$$\begin{aligned} \dot{V}_{j1}\le 2x^{T}(t)P_{j}A_{\sigma (t)}x(t) + 2x^{T}(t)P_{j}A_{d\sigma (t)}x(t-d(t)) + 2x^{T}(t)P_{j}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +~2x^{T}(t)P_{j}B_{\sigma (t)}u(t) + 2x^{T}(t)P_{j}G_{\sigma (t)}w(t) + x^{T}(t)Q_{j}x(t) \nonumber \\ -~x^{T}(t- \tau )Q_{j}x(t -\tau )(1-\eta )e^{\beta \tau } + \beta \int _{t-d(t)}^{t}e^{\beta (t-s)}x^{T}(s)Q_{j}x(s)ds. \end{aligned}$$

(19)

Making $\overline{x}=[x^{T}(t),x^{T}(t-d(t))]$ and defining a control law with a nonlinear part $u_{nl\sigma (t)}$

$$\begin{aligned} U(t)= K_{j\sigma (t)}x(t) + u_{nl\sigma (t)} \end{aligned}$$

(20)

Then

$$\begin{aligned} \dot{V}_{j1}\le \overline{x}^{T}\varPhi \overline{x} + 2x^{T}(t)P_{j}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +~2x^{T}(t)P_{j}B_{\sigma (t)}u_{nl\sigma (t)}(t) + 2x^{T}(t)P_{j}G_{\sigma (t)}w(t) \nonumber \\ +~\beta V_{j1}. \end{aligned}$$

(21)

where

$$\begin{aligned} \varPhi = \begin{bmatrix} 2P_{j}A_{\sigma (t)} - \beta P_{j} + 2P_{j}B_{\sigma _{t}}K_{j\sigma (t)} + Q_{j}&2P_{j}A_{d\sigma (t)} \\ 0&-e^{\beta \tau }Q_{j} \end{bmatrix} < 0 \end{aligned}$$

(22)

with (12) the asynchronous robust control law is obtained, with $\alpha _{v}(x,t)=x^{T}(t)x(t)$, yielding

$$\begin{aligned} =2x^{T}(t)P_{j}f_{\sigma (t)}(x(t),x(t-d(t))) \nonumber \\ +~2x^{T}(t)P_{j}B_{\sigma (t)}u_{nl\sigma (t)}(t) + 2x^{T}(t)P_{j}G_{\sigma (t)}w(t) \nonumber \\ +~\beta V_{j1} + x^{T}(t)x(t). \end{aligned}$$

(23)

Implementing Property 1 the following nonlinear control law is obtained

$$\begin{aligned} u_{nl\sigma (t)}=-B^{-1}_{\sigma (t)}f_{\sigma (t)}(x(t),x(t-\tau )) -B^{-1}_{\sigma (t)}G_{\sigma (t)}\gamma _{v} - \frac{1}{2}B^{-1}_{\sigma (t)}P^{-1}_{j}x(t) \end{aligned}$$

(24)

where $\gamma _{v} \in \mathbb {R}^{p}$ is a constant vector that is used to satisfy the following condition in order to meets the robust stability requirements

$$\begin{aligned} sup_{\gamma }sup_{w}[2x^{T}(t)P_{j}G_{\sigma (t)}w(t) - 2x^{T}(t)P_{j}G_{\sigma (t)}\gamma _{v}]\cong 0 \end{aligned}$$

(25)

so substituting the nonlinear robust control law (24) in (23) the Lyapunov function derivative obtained is:

$$\begin{aligned} \dot{V}_{j\sigma (t)}= \left\{ \begin{array}{rcl} 0 &{} \left\| x \right\| =0\\ \beta V_{j\sigma (t)} &{} \left\| x \right\| >0 \end{array}\right. \end{aligned}$$

(26)

with the following conmutative controller

$$\begin{aligned} U(t)=\nonumber \\ \left\{ \begin{array}{rcl} K_{j\sigma (t)}x(t) &{} \left\| x \right\| =0\\ -B^{-1}_{\sigma (t)}f_{\sigma (t)}(x(t),x(t-\tau )) -B^{-1}_{\sigma (t)}G_{\sigma (t)}\gamma _{v} - \frac{1}{2}B^{-1}_{\sigma (t)}P^{-1}_{j}x(t) &{} \left\| x \right\| >0 \end{array}\right. \end{aligned}$$

(27)

Now to test the exponential stability the following steps must be implemented [6]: considering that

$$\begin{aligned}{}[\tau _{l},\tau _{l+1}]=T\uparrow (\tau _{l},\tau _{l+1}) \bigcup T\downarrow (\tau _{l},\tau _{l+1}) \end{aligned}$$

(28)

where $T\uparrow (\tau _{l},\tau _{l+1})$ and $T\downarrow (\tau _{l},\tau _{l+1})$ represents the increasing and decreasing intervals of the Lyapunov functionals. Considering (16) and (26) over all the interval $[\tau _{l},\tau _{l+1}]$ and using the following property

Property 2

The Lyapunov functional for different switching instants has the following property

$$\begin{aligned} V_{k}(x_{\tau _{l}})<\mu V_{l}(x_{\tau _{l}}) \end{aligned}$$

(29)

where $\sigma (\tau _{l})=l$ and $\sigma (\tau ^{-}_{l})=m$

Therefore

$$\begin{aligned} V_{\sigma (t)}(x_{t}) \le e^{-\alpha T\downarrow (\tau _{l},\tau _{l+1}) + \beta T\uparrow (\tau _{l},\tau _{l+1})}V_{\sigma (\tau _{l})}(\tau _{l}) \end{aligned}$$

(30)

$$\begin{aligned} \le e^{-\alpha [T\uparrow (t - \tau _{l}) + T\downarrow (t - \tau _{l})]}.e^{\alpha T \uparrow (t - \tau _{l}) }.e^{\beta T \uparrow (t - \tau _{l}) }V_{\sigma (\tau _{l})}(\tau _{l}) \end{aligned}$$

(31)

$$\begin{aligned} \le e^{-\alpha (t-\tau _{l})} e^{(\alpha + \beta ) T \uparrow (t - \tau _{l}) }V_{\sigma (\tau _{l})}(\tau _{l}) \end{aligned}$$

(32)

Considering Definition 1 and Property 2

$$\begin{aligned} \le e^{-\alpha (t- \tau _{0})} e^{N_{\sigma }(\alpha + \beta )T_{max}}\mu ^{N_{\sigma }}V_{\sigma (t_{0})}(t_{0}) \end{aligned}$$

(33)

where $T_{max}=max_{l} T\uparrow (\tau _{l + 1} - \tau _{l})$ for any switching instant $\tau _{1},\tau _{2}, ... ,\tau _{l}$. Rearranging (33) yields

$$\begin{aligned} \le e^{(N_{\sigma }(\alpha + \beta )T_{max} + N_{\sigma }ln \mu )}e^{-(t-t_{0})[\alpha - (\alpha + \beta )\frac{T_{max}}{\tau _{a}} - \frac{ln \mu }{\tau _{a}}]}V_{\sigma (t_{0})}(t_{0}) \end{aligned}$$

(34)

$$\begin{aligned} \le e^{(N_{\sigma }(\alpha + \beta )T_{max} + N_{\sigma }ln \mu )}e^{-(t-t_{0})\lambda } V_{\sigma (t_{0})}(t_{0}) \end{aligned}$$

(35)

where

$$\begin{aligned} \lambda =\alpha - (\alpha + \beta )\frac{T_{max}}{\tau _{a}} - \frac{ln \mu }{\tau _{a}}>0 \end{aligned}$$

(36)

So the system is exponentially stable with the following condition

$$\begin{aligned} \tau _{a}>\tau _{a}^{*}=\frac{(\alpha + \beta )T_{max} + ln \mu }{\alpha } \end{aligned}$$

(37)

This completes the proof.

Fig. 1

Switching modes

4 Simulation Example

The following problem is solved to test the theoretical results obtained in this article. The following matrices and nonlinear functions for system (1) are used for these purposes:

$$\begin{aligned} A_{2}&=\begin{bmatrix} -0.32&0.0 \\ 0.0&-0.43 \end{bmatrix},A_{d1}=\begin{bmatrix} -0.4&0.0 \\ 0.0&-0.5 \end{bmatrix},A_{d2}=\begin{bmatrix} -0.43&0.0\\ 0.0&-0.52 \end{bmatrix}\nonumber \\ B_{1}&=\begin{bmatrix} 0.8&0.0\\ 0.0&0.9 \end{bmatrix},B_{2}=\begin{bmatrix} 0.89&0.0 \\ 0.0&0.91 \end{bmatrix}, G_{1}=\begin{bmatrix} -0.3&0.0 \\ 0.0&-0.2 \end{bmatrix}, G_{2}=\begin{bmatrix} -0.31&0.0\\ 0.0&-0.21 \end{bmatrix} \nonumber \\ f_{1}&=\begin{bmatrix} x_{1}(t)e^{-2x_{2}(t)} + x_{1}(t-d(t))^{2}\\ x_{2}(t) + exp^{-3x_{2}(t - d(t))} \end{bmatrix}, f_{2}=\begin{bmatrix} 1.4x_{1}e^{-2.7x_{2}(t)} + x_{1}(t- d(t))^{2} \\ 0.6x_{2} + 0.9e^{-3x_{2}(t-d(t))} \end{bmatrix} \end{aligned}$$

(38)

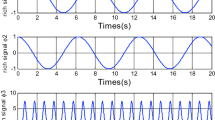
And the matrices $P_{i}=P_{j}=Q_{i}=Q_{j}=I$ where I is the identity matrix for $i=1,2$ and a step disturbance $w(t)=[step(0.00001),step(0.00001)]$ The stabilized variables are shown in Fig. 2 with the switching modes shown in Fig. 1 showing that the system is clearly stabilized.

$$\begin{aligned} K_{1matched}=K_{1unmatched}=\begin{bmatrix} 1.6&0.0 \\ 0.0&1.8; \end{bmatrix} \end{aligned}$$

(39)

$$\begin{aligned} K_{2matched}=K_{2unmatched}=\begin{bmatrix} 1.78&0.0 \\ 0.0&1.82; \end{bmatrix} \end{aligned}$$

(40)

Fig. 2

variable $x_{2}$

5 Conclusion

In this article an asynchronous robust controller for switched nonlinear system with state delays is shown. The results yielded in this study improves the outcomes obtained in studies found in literature. A conmmutative controller for the matched and unmatched cases are implemented to stabilize the system and these theoretical results are corroborated in the numerical simulation section.