Elastic and Inelastic Analysis of Frames with a Force-Based Higher-Order 3D Beam Element Accounting for Axial-Flexural-Shear-Torsional Interaction

Abstract

When one of the dimensions of a structural member is not clearly larger than the two orthogonal ones, engineers are usually compelled to simulate it with refined meshes of shell or solid finite elements that typically impose a large computational burden. The alternative use of classical beam theories, either based on Euler-Bernoulli or Timoshenko’s assumptions, will in general not accurately capture important deformation mechanisms such as shear, warping, distortion, flexural-shear-torsional interaction, etc. However, higher-order beam theories are a still largely disregarded avenue that requires an acceptable computational demand and simultaneously has the potential to account for the above mentioned deformation mechanisms, some of which can also be relevant in slender members. This chapter starts by recalling the main theoretical features of a recently developed higher-order beam element, which was combined for the first time with a force-based formulation. The latter strictly verifies the advanced form of beam equilibrium expressed in the governing differential equations. The main innovative theoretical aspects of the proposed element are accompanied by an illustrative application to members with linear elastic behaviour. In particular, the ability of the model to simulate the effect of different boundary conditions on the response of an axially loaded member is addressed, which is then followed by an application to a case where flexural-shear-torsional interaction takes place. The beam performance is assessed by comparison against refined solid finite element analyses, classical beam theory results, and approximate numerical solutions. Finally, with a view to a future extension to earthquake engineering, an example of the element behaviour with inelastic response is also carried out.

1 Introduction

Many structures are modelled with beam elements since it is well-known that the latter typically provide reliable simulation results when one of the dimensions of the member (the one along its longitudinal axis) is considerably larger than its two other orthogonal dimensions. In such circumstances, the use of other structural mechanics’ theories that involve less assumptions with respect to the three-dimensional problem are often not justified as they require a finer discretisation of the structure and a comparatively much larger number of degrees of freedom (and hence computational time).

However, classical beam theories such as Euler-Bernoulli’s and Timoshenko’s are often not sufficiently accurate to predict the global member response and its internal stress-strain state. For instance, in the Timoshenko beam theory (TBT), the shear strain distribution is incorrectly assumed to be constant throughout the beam height; e.g., considering a simple rectangular cross-section, such hypothesis does not respect the zero shear strain and stress boundary conditions at its top and bottom. Therefore, a shear correction factor is required to accurately determine the strain energy of deformation, which has deserved the attention of researchers since the 1950s up to the present day [9, 10, 14, 16]. Within the framework of this chapter, classical beam theories are considered to be of the first-order, i.e., those in which the displacement fields inside the cross-section are linear functions on each of the cross-sectional coordinates. Shear deformation effects are best considered through higher-order beam theories (HOBTs), wherein the displacement field inside the cross-section is represented by a power series expansion in the cross-sectional coordinates, thus relaxing the constraint in the cross-sectional warping. Therefore, out-of-plane warping displacements of the cross-sectional points are allowed by using shape functions for the cross-sectional displacements which are at least quadratic in one coordinate or bilinear in both. Moreover, in-plane deformations of the cross-section are also directly considered.

Many HOBTs have been proposed over the past decades for both planar and spatial beams; a brief review of some of the most relevant contributions is presented in Correia et al. [8]. The points on which they differ include the order of the theory, the number and definition of the cross-sectional displacement modes, the approach used to derive the corresponding beam governing equations, and the chosen finite element formulation. Regarding this latter issue, the so-called stiffness or displacement-based methods (DB, as they will be henceforth called, see Bathe [4]), which make use of compatible displacement interpolation functions along the element length and the principle of virtual work (or virtual displacements), are still the most commonly used. They are also known as pure compatibility models in the literature [18], and are popular since the inter-element continuity of the displacement field is trivially satisfied. On the other hand, the latter is difficult to enforce in flexibility or force-based formulations (FB, as they will be henceforth called), which are built on the derivation of self-equilibrated stress interpolation functions and the principle of complementary virtual work (or virtual forces). These approaches are also known as pure equilibrium models, and within their framework it is possible to find an exact solution to the beam equilibrium differential equations. Hence, the main advantage of FB beam-column formulations, over the more common DB counterparts, is that equilibrium is always strictly verified. Such property holds even when a material nonlinear response takes place, explaining why flexibility methods have been progressively adopted by the structural engineering community for the inelastic analysis of frame members. Another advantage of FB formulations is that no shear-locking phenomena exist, contrary to what occurs in DB approaches. Although frame finite elements based on force interpolation functions alone have been in use for many decades [6, 15], the development of efficient and stable state determination algorithms, wherein nodal compatibility is respected, is more recent [17, 20].

Comparative studies between FB and DB formulations can be found elsewhere [1, 17]. Of further interest are considerations on the bounding of the solution associated with these two different types of formulation, which are carried out in Almeida et al. [2]. Equally fundamental is to understand the relationship between DB and FB approaches, as they have been herein described, and energy principles. Such comparison should be carried out not just at the theoretical level, but also regarding numerical implementation and computational performance. While the application of the Hu-Washizu three-field functional seems to be a promising avenue [11], trade-offs between classical DB methods and mixed methods are far from being completely clarified [12]. The merit of FB beam models is however clearly undisputed [13], and the beam element of the present work relies on it.

To the authors’ knowledge, pure equilibrium (FB) approaches have only been used, up to now, in association with classical beam theory. In other words, the finite elements that have been developed within the context of the HOBTs are, in their essence, displacement-based formulations. A higher-order beam element developed within the framework of a pure force-based formulation has been proposed, for the first time, by Correia et al. [8]. Following a short review on the main theoretical aspects of this latter approach, the present chapter presents new numerical applications that evidence the ability of the model to simulate physical effects, such as axial-flexural-shear-torsional interaction, which typically can only be reproduced by refined meshes of shell or solid finite elements.

2 Theoretical Features of the Force-Based Higher-Order Beam Element

Following the basic idea from Vlassov [23], the distinctive trace in all beam theories is the assumption of a displacement field composed of cross-sectional displacement modes defined a priori and multiplied by functions of the beam coordinate axis only. In other words, the beam displacement field u (whose vector components are u _x , u _y , and u _z ) can be separated into a component function of the axis x of the beam and another varying in the cross-section (whose coordinate axes are y and z):

$$ {\mathbf{u}}\left( {x,y,z} \right) = {\mathbf{U}}\left( {y,z} \right){\mathbf{d}}(x) $$

(1)

where U(y,z) is the matrix of the displacement interpolation functions over the cross-section (the cross-sectional displacement modes), and d(x) is the vector of weights associated to the interpolation functions, also called generalised displacements. For the HOBT of the present work, which is derived for a solid rectangular cross-section of dimensions h (height) × b (width), the previous expression takes the form:

$$ {\mathbf{u}}\left( {x,y^{ * } ,z^{ * } } \right) = \sum\limits_{{\varvec{i} = 0}}^{\varvec{n}} {\sum\limits_{{\varvec{j} = 0}}^{\varvec{n}} {{\mathbf{U}}^{{ * ,\varvec{ij}}} \left( {y^{ * } ,z^{ * } } \right)\varvec{d}^{{ * ,\varvec{ij}}} (x) = {\mathbf{U}}^{\varvec{*}} \left( {y^{\varvec{*}} ,z^{\varvec{*}} } \right){\mathbf{d}}^{\varvec{*}} (x)} } $$

(2)

where the normalized cross-sectional coordinates $y^{\varvec{*}} = 2y/b$ and $z^{\varvec{*}} = 2z/h$ are adopted, the cross-sectional interpolation functions are defined as

$$ {\mathbf{U}}^{{\varvec{*},\varvec{ij}}} \left( {y^{\varvec{*}} ,z^{\varvec{*}} } \right) = \left[ {\begin{array}{*{20}c} {P_{i} (y^{\varvec{*}} )P_{j} (z^{\varvec{*}} )} & 0 & 0 \\ 0 & {P_{i - 1} (y^{\varvec{*}} )P_{j} (z^{\varvec{*}} )} & 0 \\ 0 & 0 & {P_{i} (y^{\varvec{*}} )P_{j - 1} (z^{\varvec{*}} )} \\ \end{array} } \right] $$

(3)

and $\varvec{d}^{{\varvec{*},\varvec{ij}}} (x) = \left[ {\begin{array}{*{20}c} {u_{x}^{{\varvec{*},ij}} } & {u_{y}^{{\varvec{*},ij}} } & {u_{z}^{{\varvec{*},ij}} } \\ \end{array} } \right]^{\varvec{T}}$ are the normalised generalised displacements. They replace the classical beam theory generalised displacements $\varvec{d}^{{\varvec{ij}}} (x) = \left[ {\begin{array}{*{20}c} {u_{x}^{ij} }\; & {u_{y}^{ij} }\; & {u_{z}^{ij} } \\ \end{array} } \right]^{\varvec{T}}$, for reasons that are apparent below.

In Eq. (3), $P_{n} (s)$ represents Legendre polynomials for $\textit{n}\,{ = }\,0,1,2, \ldots$, which are nth-degree polynomials that can be expressed using Rodrigues’ formula:

$$ P_{n} (s) = \frac{1}{{2^{n} n!}}\frac{{d^{n} }}{{ds^{n} }}\left[ {\left( {s^{2} - 1} \right)^{n} } \right] $$

(4)

The latter form a complete orthogonal set in the interval $- 1 \le s \le 1$, which is a fundamental property in the development of the current finite element since it enables the definition of generalised stress-resultants that are not only independent but also orthogonal to one another. This leads to an unambiguous definition of the generalised stress-resultants and to a minimisation of the coupling between the resulting equilibrium equations. The use of $y^{ * }$ and $z^{ * }$ defined above, instead of y and z, is related to the interval where the orthogonality property holds. Note that any set of orthogonal displacement functions could be used instead of Legendre polynomials. The application of a Gram–Schmidt orthogonalisation procedure to a set of independent base functions would produce such orthogonal set, and further it could be applied in order to extend this formulation to different cross-sectional geometries.

From Eq. (3), it can be observed that the transverse displacements have a one degree lower polynomial function than the axial displacements. This results in the same degree of approximation for the shear strain fields, considering the contributions of both the axial and transverse displacements in each set of modes ij.

The number of terms and the combination of indices ij adopted in the present beam-column model was based on a balance between intended accuracy and computational cost: all terms ${\mathbf{U}}^{{ * ,\varvec{ij}}} \left( {y^{ * } ,z^{ * } } \right)$ up to the fourth-order in one coordinate and first-order in the other were considered. As demonstrated in the application examples of Sects. 3 to 5, the selected terms are sufficient to retrieve the intended axial-flexural-shear-torsional interaction. Figure 1 represents all 16 terms considered for the longitudinal displacement u _x in a Pascal triangle type of representation. The transverse displacements u _y and u _z contain 11 terms each, with one degree less in $y^{ * }$ and $z^{ * }$ respectively than the corresponding terms in u _x , resulting in a total of 38 displacement terms.

Fig. 1

Polynomial terms considered for the longitudinal displacement u _x

The matrix ${\mathbf{U}}^{ * } \left( {y^{ * } ,z^{ * } } \right)$ in Eq. 2 is a (3 × 38) matrix which is not depicted due to space limitations, while the normalised generalised displacements ${\mathbf{d}}^{ * } \left( x \right)$ is the following (38 × 1) vector:

$$ {\mathbf{d}}^{ * } \left( x \right) = \begin{array}{*{20}l} {[u_{x0}^{*}\; u_{y0}^{*}\; u_{z0}^{*}\; \theta_{x}^{*}\; \theta_{y}^{*}\; \theta_{z}^{*}\; \eta^{*} \gamma^{*} u_{x}^{*,20}\; u_{y}^{*,20}\; u_{x}^{*,02}\; u_{z}^{*,02}\; u_{x}^{*,21}\; u_{y}^{*,21}\; u_{z}^{*,21} } \hfill \\ { \ldots u_{x}^{*,12}\; u_{y}^{*,12}\; u_{y}^{*,12}\; u_{z}^{*,12}\; u_{x}^{*,30}\; u_{y}^{*,30}\; u_{x}^{*,03}\; u_{z}^{*,03}\; u_{x}^{*,31}\; u_{y}^{*,31}\; u_{z}^{*,31}\; u_{x}^{*,13} } \hfill \\ { \ldots u_{y}^{*,13}\; u_{z}^{*,13}\; u_{x}^{*,40}\; u_{y}^{*,40}\; u_{x}^{*,04}\; u_{z}^{*,04}\; u_{x}^{*,41}\; u_{y}^{*,41}\; u_{z}^{*,41}\; u_{x}^{*,14}\; u_{y}^{*,14}\; u_{z}^{*,14} ]^{T} } \hfill \\ \end{array} $$

(5)

It is noted that there is a compatibility matrix which converts the classical generalised displacements vector ${\mathbf{d}}\text{(}x\text{)}$ (38 × 1) into the previous normalized generalised displacements vector ${\mathbf{d}}^{ * } \left( x \right)$ (38 × 1). Considering common engineering reasoning, the meaningful classical generalised displacements are those of the first-order ${\mathbf{d}}^{1st\; order} \left(x \right) = \left[{u_{x0}\; u_{y0}\; u_{z0}\; \theta_{x}\; \theta_{y}\; \theta_{z}\; \upeta\,\;\gamma } \right]$; hence, the components of vector ${\mathbf{d}}\left( x \right)$ related to the higher-order generalised displacements are considered here to be identical to the corresponding normalised generalised displacements. The complete set of cross-sectional displacement shapes for a square section, which will be used in the numerical applications of Sects. 3 to 5, is included in Fig. 2. Each mode is defined by a column of the matrix ${\mathbf{U}}\left( {y,z} \right)$ in Eq. (1). The first-order modes 1 through 8 are composed of the six modes corresponding to classical Timoshenko beam theory, followed by two related to warping and distortion. The remaining 30 higher-order displacement modes are defined in Eq. (3) based on normalised Legendre polynomials and therefore reflect a product of polynomials of different degree along the two orthogonal cross-sectional coordinate axes.

Fig. 2

Complete set of cross-sectional displacement modes for a square cross-section

In the process of derivation of the beam compatibility equations, Legendre polynomials and their derivatives appear in the definition of the generalised strains. However, those derivatives are not orthogonal either to the Legendre polynomials or between each other. Consequently, the generalised strains thus obtained would be independent from one another but they would not constitute an orthogonal set. Such lack of orthogonality would lead to a dubious definition for the generalised stress-resultants and to a large coupling of the equilibrium equations. This is undesirable in a FB approach since it would become extremely complex to obtain the self-equilibrated interpolation functions for the generalised stress-resultants. Moreover, the nodal boundary conditions (BCs) would also be coupled, which would unnecessarily increase the model’s complexity. Hence, in order to have a unique definition for the generalised stress-resultants and to reduce the coupling of the equilibrium equations and boundary conditions to a minimum, those derivatives may and should be decomposed on the basis of Legendre polynomials. Every single generalised strain will then be associated to a unique Legendre polynomial in each direction. The derivation of the first and higher-order compatibility equations can be found in Correia et al. [8].

In order to obtain power-conjugated generalised stress-resultants, the beam equilibrium equations are obtained through a projection of the classical local equilibrium equations on the functional space of the cross-sectional displacement modes defined in Eq. (3) [21]. Such operation may also be regarded as weighting the residuals of the classical local equilibrium equations, where the cross-sectional displacement modes are taken as weighting functions. The complete beam equilibrium equations are a highly indeterminate system of differential equations represented by a (38 × 57) differential equilibrium operator (adjoint to the differential compatibility operator), a (38 × 1) vector of normalised distributed loads, and the following (57 × 1) vector of normalised generalised stress-resultants ${\mathbf{s}}^{ * }$:

$$ {\mathbf{s}}^{ * } \left( x \right) = \begin{array}{*{20}c} {\left[ {N\; M_{y}^{ * }\; M_{z}^{ * }\; B^{ * }\; {\mathbf{N}}^{ * ,ij} \;\left( {12 \times 1} \right)\; {\mathbf{N}}_{y}^{ * ,ij} \;\left( {6 \times 1} \right)\; {\mathbf{N}}_{z}^{ * ,ij} \;\left( {6 \times 1} \right)}\; \right.} \\ { \ldots V_{y} T^{ * } \;\left. {Q^{ * } \;{\mathbf{V}}_{y}^{ * ,ij}\; \left( {9 \times 1} \right)\; V_{z}\; {\mathbf{V}}_{z}^{ * ,ij}\; \left( {9 \times 1} \right)\; V_{yz}\; {\mathbf{V}}_{yz}^{ * ,ij}\; \left( {6 \times 1} \right)} \right]^{T} } \\ \end{array} $$

(6)

where the first-order components ${\mathbf{s}}^{ * ,1st\,order} \left( x \right) = \left[ {N\; V_{y}\; V_{z}\; T^{ * } M_{y}^{ * }\; M_{z}^{ * }\; B^{ * }\; Q^{ * }\; V_{yz} } \right]^{T}$ relate to the classical generalised stress-resultants ${\mathbf{s}}^{ * ,1st\,order} \left( x \right) = \left[ {N\; V_{y}\; T\; M_{y}\; M_{z}\; B\; Q\; V_{yz} } \right]^{T}$, and conversely, through:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {M_{y}^{ * } = \frac{2}{h}M_{y} } \hfill \\ {M_{z}^{ * } = \frac{2}{b}M_{z} } \hfill \\ {B^{ * } = \frac{4}{bh}B} \hfill \\ {Q^{ * } = Q\left( {\frac{1}{b} + \frac{1}{h}} \right) + T\left( {\frac{1}{b} - \frac{1}{h}} \right)} \hfill \\ {T^{ * } = Q\left( {\frac{1}{b} - \frac{1}{h}} \right) + T\left( {\frac{1}{b} + \frac{1}{h}} \right)} \hfill \\ \end{array} } \right.} & {\left\{ {\begin{array}{*{20}c} {M_{y} = \frac{h}{2}M_{y}^{*} } \\ {M_{z} = \frac{b}{2}M_{z}^{*} } \\ {B = \frac{bh}{4}B^{*} } \\ {Q = Q^{*} \left( {\frac{b}{4} + \frac{h}{4}} \right) + T^{*} \left( {\frac{b}{4} - \frac{h}{4}} \right)} \\ {T = Q^{*} \left( {\frac{b}{4} - \frac{h}{4}} \right) + T^{*} \left( {\frac{b}{4} + \frac{h}{4}} \right)} \\ \end{array} } \right.} \\ \end{array} $$

(7)

and the higher-order components are given by:

$$ \begin{array}{*{20}c} {\left. {\begin{array}{*{20}c} {N^{ * ,ij} = \int\limits_{A} {P_{i} \left( {y^{ * } } \right)P_{j} \left( {z^{ * } } \right)\sigma_{x} da\;\;\left( {12\,terms} \right)} } \\ {N_{y}^{ * ,ij} = \int\limits_{A} {P_{i - 2} \left( {y^{ * } } \right)P_{j} \left( {z^{ * } } \right)\sigma_{y} da\;\;\left( {6\,terms} \right)} } \\ {N_{z}^{ * ,ij} = \int\limits_{A} {P_{i} \left( {y^{ * } } \right)P_{j - 2} \left( {z^{ * } } \right)\sigma_{z} da\;\;\left( {6 terms} \right)} } \\ \end{array} } \right\}\,for\, i \ge 2 \,or \,j \ge 2} \\ {\left. {\begin{array}{*{20}c} {V_{y}^{ * ,ij} = \int\limits_{A} {P_{i - 1} \left( {y^{ * } } \right)P_{j} \left( {z^{ * } } \right)\tau_{xy} da\;\;\left( {9\,terms} \right)} } \\ {V_{z}^{ * ,ij} = \int\limits_{A} {P_{i} \left( {y^{ * } } \right)P_{j - 1} \left( {z^{ * } } \right)\tau_{xz} da\;\;\left( {9\,terms} \right)} } \\ \end{array} } \right\}\,for\, i \ge 1\, or \,j \ge 1} \\ {V_{yz}^{ * ,ij} = \int\limits_{A} {P_{i - 1} \left( {y^{ * } } \right)P_{j - 1} \left( {z^{ * } } \right)\tau_{yz} da\;\;\left( {6\,terms} \right)\,for \,i \ge 1 \,and \,j \ge 1} } \\ \end{array} $$

(8)

The compatibility and equilibrium boundary conditions can be found in Correia et al. [8]. It is noted that $V_{yz}$, ${\mathbf{N}}_{y}^{ * ,ij}$, ${\mathbf{N}}_{z}^{ * ,ij}$, and ${\mathbf{V}}_{yz}^{ * ,ij}$ are related to the stress components $\sigma_{y}$, $\sigma_{z}$, and $\tau_{yz}$, which are not applied in the cross-section of the beam. Consequently, these 19 generalised stress-resultants do not appear in the static boundary conditions at the beam element ends.

As previously stressed, a FB formulation is employed in this work. Hence, the field of generalised stress-resultants should respect the beam local equilibrium conditions. In order to determine the complementary solution of the homogeneous equilibrium equations, and since there are a total of 38 local equilibrium equations involving 57 unknown generalised stress-resultants, a few assumptions have to be made concerning the functions describing the evolution of some generalised stress-resultants. Given that the differential equations of equilibrium require only one boundary condition each (as they involve only first derivatives), a total of 38 BCs are needed for this purpose. On the other hand, there are 38 × 2 = 76 available BCs at both extremities of the beam, corresponding to the nodal values of the 38 generalised stress-resultants related to the cross-sectional stresses $\sigma_{x}$, $\tau_{xy}$, and $\tau_{xz}$. Moreover, six of these nodal values are dependent on the remaining ones since they are related to the six rigid-body motions of the beam. Hence, from the remaining 76 − 6 = 70 BCs, there are 32 which will not be used to solve the equations of equilibrium and that may be applied instead for defining a priori an assumed variation for the 19 generalised stress-resultants related to the stresses $\sigma_{y}$, $\sigma_{z}$, and $\tau_{yz}$. Such assumed variation is not unique, which means that different self-equilibrated approximations can be envisaged. In the current formulation, the field of those 19 generalised stress-resultants is approximated by the simplest possible polynomial functions, namely linear and constant ones, and the necessary assumptions on their variations are briefly indicated in Appendix B of Correia et al. [8]. The latter reference also depicts the compact expression of the solution corresponding to such self-equilibrated higher-order stress-resultants.

With the above mentioned approximation, equilibrium in the domain and at the boundary is automatically satisfied. However, compatibility in the domain and at the boundary has to be likewise satisfied. So as to maintain power-conjugacy, the domain compatibility equations are verified in a weighted form using the generalised stress-resultants’ interpolation matrix as weighting functions. Finally, it is possible to derive the corresponding incremental equations required for nonlinear constitutive behaviour, including the beam tangent flexibility matrix. Although the complete theoretical developments of the present FB higher-order element cannot be included in the current chapter due to space limitations, they can be found in Correia et al. [8].

The first applications of the current model can be seen in the work by Almeida et al. [2], including: a cantilever subjected to a tip lateral load / imposed torsional rotation, and a simply supported beam with distributed loads. The following Sect. 3 illustrates the ability of the model to simulate the interaction between the different strain and stress components when a member is subjected to an imposed axial displacement. Section 4, on the other hand, includes a first example wherein a simultaneous flexural-shear-torsional loading is applied, while Sect. 5 shows the influence of material inelastic behaviour in such response. The structural analysis code SAGRES (Software for Analysis of GRadient Effects on Structures), developed by the authors and implemented in the MATLAB platform [22], was used to run the analyses.

3 Effect of Boundary Conditions on the Response of an Axially Loaded Member

In classical theories (Euler-Bernoulli or Timoshenko), stress-resultants and boundary conditions are of straightforward understanding and definition. However, in a higher-order model, the large number of generalised stress- and strain-resultants—well beyond the six classical ones—are much less intuitive from the engineering standpoint; they relate with the also large number of element nodal displacements and forces that are controlled by appropriate BCs. As observed by other researchers [5, 19], HOBTs are subjected to specific effects that require careful interpretation and a study of their influence on the accuracy of the results. These so-called higher-order boundary effects—which also show up in displacement-based formulations, although with distinct traits—play a relevant role in the response. They are intrinsically related to the boundary conditions assumed, which for this model consist of a combination of imposed generalised nodal displacements and/or forces, in a total of 76 (38 at each extremity), as discussed above. The special nature of such effects when applied together with a flexibility formulation naturally requires a careful analysis, which was carried out by Almeida et al. [2] to expose this yet undisclosed behaviour. Therein, the uncommon effects that the higher-order boundary conditions can cause on the stress-strain distributions—particularly near the member extremities—were highlighted, and an appropriate interpretation of the physical meaning of the generalised stress-resultants was made.

On the other hand, the number of BCs and stress-resultants also reflect the significant adaptability of the model in simulating physical phenomena that would pass unnoticed with traditional beam theories, even for very simple loading cases as the one that follows. This first numerical application analyses the response of a structural member subjected to an imposed end-node axial displacement, focusing on the comparison between the results of a refined mesh of solid finite elements, a classical beam theory, and the proposed higher-order one.

Five different member lengths L are analysed: 0.125, 0.25, 0.5, 1, and 5 (m). Additionally, a square cross-sectional geometry with unitary area 1 × 1 (m × m) is assumed and a linear elastic isotropic constitutive model was assigned, with Young’s modulus $E = 200 \times 10^{9} \,\left( {{\text{N}}/{\text{m}}^{ 2} } \right)$ and Poisson’s ratio $\nu = 0.3$. Regarding the solid finite element simulations [7], the meshes represented in Fig. 3 were employed, which had between 2178 and 18513 degrees of freedom (dof). All nodes in both member extremities were fully restrained and an axial displacement $\Delta_{axial} = 1 \times 10^{ - 3} \,\left( {\text{m}} \right)$ was applied to all nodes in one end. Concerning the frame models, a single element was used to model the member using both the classical beam theory (12 dof) and the proposed higher-order one (76 dof). Two sets of boundary conditions were considered for the higher-order element: (i) ‘Max. Fixity’: at each node all the 38 generalised displacements were restrained, while simultaneously an axial displacement $\Delta_{axial} = 1 \times 10^{ - 3} \,\left( {\text{m}} \right)$ was imposed at one node; this case corresponds to the maximum possible degree of fixity which is possible to assign to this higher-order beam model and is the one that better simulates the above mentioned joint restraints applied to the extremity nodes of the solid finite element mesh; (ii) ‘Min. Fixity’: at one node, only the six rigid-body displacements corresponding to the Timoshenko beam theory are restrained $\left( {u_{x0} = u_{y0} = u_{z0} = \theta_{x} = \theta_{y} = \theta_{z} = 0} \right)$, leaving the remaining 32 dof as force-controlled and equal to zero; at the other node, the 38 dof were also force-controlled and kept equal to zero, except the one corresponding to the dof of axial displacement, on which a value of $\Delta_{axial} = 1 \times 10^{ - 3} \,\left( {\text{m}} \right)$ was again imposed; this case corresponds to the minimum possible degree of fixity provided by the model. It is noted that the geometry and loading herein defined are not intended to be realistic and have the sole purpose of illustrating the qualitative features of the proposed beam theory. The results presented in the following, namely the distribution of stresses, thus only have a numerical meaning.

Fig. 3

Solid finite element mesh used to model the response for member lengths L equal to: a 0.125 (m); b 0.25 (m); c 0.5 (m); d 1 (m), and e 5 (m) [7]

Regarding the material properties, the HOBT model adopted the ones described above for the solid FE model, while the axial rigidity as used by classical beam theories (Timoshenko or Euler-Bernoulli) is equal to $\left( {EA} \right)_{classical} = 200 \times 10^{9} \,({\text{N}})$ and it is obviously independent of the member length L. However, for the HOBT and the solid FE model, the effect of fully restrained sections at the member extremities is expected to play a role in the increase of the equivalent axial rigidity, as computed by $\left( {EA} \right)_{equiv.} = F_{axial} /\left( {\Delta_{axial} /L} \right)$, where $F_{axial}$ is the reaction along the axial degree of freedom (for the HOBT), or the summation of all extremity joint reactions along the member axis (for the solid FE model). This physical effect is well-known, for instance, as a frictional confinement effect on the results of compression tests of concrete cylinder or cube specimens. Figure 4 shows the ratio of the equivalent axial rigidity (EA) _equiv. to the axial rigidity given by classical beam theory (EA) _classical , for the values of member length L indicated above. For the higher-order beam theory, both BCs ‘Max. Fixity’ and ‘Min. Fixity’ are analysed.

Fig. 4

Ratio of the equivalent axial rigidity (EA) _equiv. to the axial rigidity given by classical beam theory (EA) _classical , for the five distinct member lengths shown in Fig. 3

Taking the results obtained with the solid finite element mesh as the reference solution, it can be observed that for members with smaller lengths there is a significant increase in the equivalent axial rigidity due to the comparatively larger relevance of the boundary confining effects in the response with respect to longer members. Such increase is of around 15 % for a member length that is half the section side [i.e., L = 0.5 (m)], while for L = 0.125 (m) it goes up to close to 30 %.

Figure 4 also shows that the proposed HOBT, when the BCs ‘Max. Fixity’ are used, manages to capture accurately the increase of equivalent axial rigidity, closely reproducing the results from the solid finite element analyses. On the other hand, the BCs ‘Min. Fixity’ output the same results than classical beam theory, as the extremity sections are free to distort in their own plane. Other BCs corresponding to intermediate cases of fixity could have been considered as well, which would inevitably lead to estimations of the equivalent axial rigidity in-between those of the foregoing extreme scenarios.

Considering the BCs ‘Max. Fixity’, it is interesting to list the components of the stress-resultants ${\mathbf{s}}^{ * }$ that for this case influence the behaviour of the element, i.e., those that are non-negligible from a quantitative viewpoint: $N,N^{ * ,20} , N^{ * ,02} , N^{ * ,40} ,N^{ * ,04} ,N_{y}^{ * ,20} ,N_{z}^{ * ,02} ,N_{y}^{ * ,40} ,N_{z}^{ * ,04} ,V_{y}^{ * ,20} ,V_{z}^{ * ,02} ,V_{y}^{ * ,40} ,V_{z}^{ * ,04}$, see Eq. (8). The latter are all the variables that take part in the coupled differential equilibrium equations included in systems (1), (5) and (6) of Appendix A in Correia et al. [8]. System (1) corresponds simply to the differential equation from classical beam theory involving the axial force N. On the other hand, systems (5) and (6) involve the resultants $N^{ * ,ij}$ of the stress component $\sigma_{x}$ that are symmetric within the cross-section (namely $N^{ * ,20} , N^{ * ,02} , N^{ * ,40} ,N^{ * ,04}$, see also modes 9, 11, 29 and 31 in Fig. 2), which are expected to be non-null in view of the loading and geometric symmetry properties of the analysed problem. The additional presence, in the systems of coupled differential Eqs. (5) and (6), of some higher-order resultants of $\sigma_{y} , \sigma_{z} ,\tau_{xy}$ and $\tau_{xz}$ (namely $N_{y}^{ * ,20} ,N_{z}^{ * ,02} ,N_{y}^{ * ,40} ,N_{z}^{ * ,04} ,V_{y}^{ * ,20} ,V_{z}^{ * ,02} ,V_{y}^{ * ,40} ,V_{z}^{ * ,04}$), ensures that an advanced interaction between normal and shear stresses is considered in the proposed HOBT.

The extent to which the proposed element can also capture the distribution of stresses is now analysed. Figures 5 and 6 show the distribution of axial stresses at the extremity of the axially loaded member for L = 5 (m) and L = 0.125 (m) respectively. The results obtained with the solid finite element mesh are compared with those of the proposed higher-order element (again considering the BCs ‘Max. Fixity’); the legend colour code was adjusted so that it is approximately similar to that of the solid FE output.

Fig. 5

Distribution of axial stresses [× 10⁶ (N/m²)] for L = 5 (m): a along the member, from solid FE model [7]; At the extremity, from b solid FE model and c proposed HOBT

Fig. 6

Distribution of axial stresses [× 10⁹ (N/m²)] for L = 0.125 (m): a along the member, from solid FE model [7]; At the extremity, from b solid FEs and c proposed HOBT

Figure 5b, c show that, for L = 5 (m), the proposed FB higher-order beam element encouragingly manages to reproduce the general qualitative distribution of axial stresses obtained from the refined finite element analyses. From a quantitative viewpoint, the beam model is not able to recover the peak stress concentrations taking place at the four cross-sectional corners (the solid FE mesh outputs peak values of almost −64 × 10⁶ (N/m²), while the counterpart values given by the HOBT are of −45 × 10⁶ (N/m²)). A more enriched set of cross-sectional displacement modes would be required to better estimate such stress peaks. However, one should also note that FE mesh outputs at corners and other geometric or loading discontinuities oftentimes fail to produce realistic results. In fact, they output exaggerated peak stresses at those regions and require a much finer discretization or some output averaging to give results of practical significance. On the other hand, a better agreement is achieved for the stress values in the larger central part of the cross-section (−36.5 × 10⁶ (N/m²) from the solid FE analyses vs −38 × 10⁶ (N/m²) from the HOBT). It is noted that, both with a classical beam theory or the present HOBT using the BCs ‘Min. Fixity’, a constant value of $\sigma_{x} = - 40 \times 10^{6} \,\left( {{\text{N}}/{\text{m}}^{2} } \right)$ would be obtained throughout the entire cross-section, which is far off from the stress distribution occurring at the extremity sections. Finally, at the member mid-span, the referred constant stress profile is retrieved both with the solid FE model—see Fig. 5a—and with the HOBT (not represented).

The effects of the boundary conditions become predominant for smaller member lengths, which is apparent from contrasting Figs. 6a with 5a. Again, comparing the results of Fig. 6b with those of Fig. 6c, it is clear that the new beam formulation approximately reproduces the qualitative distribution of the axial stresses at the member extremities. Furthermore, the agreement now extends to a quantitative comparison as well: the refined solid FE model outputs a value of $\sigma_{x} = - 1.9 \times 10^{9} \,\left( {{\text{N}}/{\text{m}}^{2} } \right)$ for the central value in the four corner regions, vs $\sigma_{x} = - 1.8 \times 10^{9} \,\left( {{\text{N}}/{\text{m}}^{2} } \right)$ given by the HOBT. Around the cross-sectional geometrical centre, the solid FE model outputs an axial stress of −2.15 × 10⁹ (N/m²), while the current beam element indicates a value of −2.33 × 10⁹ (N/m²). Classical beam theory, or the current HOBT with BCs ‘Min. Fixity’, would provide a constant value of $\sigma_{x} = - 1.6 \times 10^{9} \,\left( {{\text{N}}/{\text{m}}^{2} } \right)$ throughout the entire cross-section.

4 Flexural-Shear-Torsional Interaction: Linear Elastic Behaviour

In this second group of examples, a member with the same mechanical and cross-sectional geometric characteristics of the previous Sect. 3 is subjected to a simultaneously imposed transversal displacement Δ and a torsional rotation θ at midspan (on a 1:1 ratio). Five different member lengths L are analysed: 0.25, 0.5, 1, 2, and 10 (m). Again, a comparison between a refined solid finite element mesh, the present HOBT, and results from classical beam theory and approximate solutions for the torsional constant is performed. Regarding the solid finite element simulations [7], the adopted meshes were resembling to those of Fig. 3 and had a total number of degrees of freedom ranging from 1782 to 3402. All the nodes at both member extremities were restrained. At each node at the midspan, a bidirectional (along y and z) translational displacement was assigned so that the imposed deformed shape combined the effects of the aforementioned imposed transverse displacement and torsional rotation. Concerning the frame models, four higher-order FB elements were used to model the member, in a total of 190 degrees of freedom. The boundary conditions corresponding to the previously discussed case ‘Max. Fixity’ were considered.

Figure 7 summarises the results of the analyses carried out, which are split into torsional and bending components and compared with the output of classical approaches. With regards to the latter, it is noted that whilst the second moment of the cross-sectional area I to compute the bending rigidity (EI) _classical is clearly defined, there are no exact analytical formulations for calculating the sectional torsion constant J. Approximate solutions have however been found for many shapes and the expression $J \approx 2.25a^{4}$ (a is the side length of a square section) was used to estimate the torsional rigidity (GJ) _{approxim. solution} , where $G = E/ \left[2\left( {1 + \nu } \right)\right]$ is the shear modulus. In particular, Fig. 7 (a) shows the ratio of the equivalent torsional rigidity (GJ) _equiv. —as derived both for the solid FE mesh and the HOBT—to the torsional rigidity given by the approximate solution mentioned above (GJ) _{approxim. solution} , for the considered values of member length L. Similarly, Fig. 7b shows the ratio of the equivalent bending rigidity (EI) _equiv. to the bending rigidity given by classical beam theory (EI) _classical . The equivalent torsional rigidity is computed as $\left( {GJ} \right)_{equiv.} = {T \times \left ({L/2} \right)} /\theta$, where T is the torsional moment at each member extremity, i.e., the reaction along the torsional degree of freedom (for the HOBT) or the summation of the torsional moments for every joint reaction using the appropriate lever arm (for the solid FE model). Analogously, the equivalent bending rigidity is computed as $\left( {EI} \right)_{equiv.} = {2 \times V \times L^{3} } /\left( {192 \times \Delta } \right)$, where V is the reaction shear force, i.e., the reaction along the transverse degree of freedom (for the HOBT) or the summation of the extremity joint reactions along that same direction (for the solid FE model).

Fig. 7

a Ratio of the equivalent torsional rigidity (GJ) _equiv. to the torsional rigidity given by available approximate solutions (GJ) _{approxim. solution} ; b Ratio of the equivalent flexural rigidity (EI) _equiv. to the flexural rigidity given by classical beam theory (EI) _classical

It is observed that the proposed higher-order theory closely follows the results of the solid finite element models. Figure 7a shows that the increase in torsional stiffness associated to the warping restraints provided at the member extremity sections, which assumes a particular relevance for the shorter members, is accurately simulated. On the other hand, Fig. 7b indicates that, as expected, the contribution of classical flexural beam-type deformations are very small for members with a short span; as the shear span increases, so does the relative contribution of these flexural deformations and, for L = 10 (m), the latter are roughly responsible for about 90–95 % of the overall deformations.

5 Flexural-Shear-Torsional Interaction: Multiaxial J2 Linear Plasticity

The present section expands the previous case-study [considering L = 10 (m)] to account for material nonlinear behaviour. Namely, the flexural-shear-torsional interaction is now assessed in the inelastic range, for the first time using the current FB higher-order beam element. The following ratios of torsional rotation θ to transversal displacement Δ at midspan were imposed: $\theta /\Delta = 0.5, 1, 2$, as well as the two bounds corresponding to the imposition of only θ and only Δ respectively. For this latter loading case, a classical FB Euler-Bernoulli beam theory (EBBT) is also employed for comparative purposes. It considers inelasticity through a cross-sectional discretisation by fibres to which one-dimensional nonlinear material models are assigned. As in the previous Sect. 3, the boundary conditions corresponding to ‘Max. Fixity’ were assigned to the HOBT model while, for the Euler-Bernoulli beam, the three translational displacements and the three rotations at each extremity were blocked.

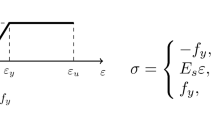
In order to validate the comparison between these beam theories, it should be possible to relate the distinct material models under specific states of stress and strain. On the other hand, to ease the interpretation of the results, the latter should be as simple as possible. Therefore, the following models were employed: (i) a one-dimensional plastic model with hardening, for the EBBT simulation, whose behaviour is defined by the Young’s modulus E, the uniaxial yield stress $\sigma_{y}^{uniaxial}$, and the strain hardening ratio $b = E_{p} /E$ (E _p stands for the plastic modulus); (ii) the multiaxial J2 linear plasticity model described by Auricchio and Taylor [3], for the HOBT simulation, which is based on linear evolutionary rules for both the plastic strain and the hardening mechanisms. The parameters that define this model are the isotropic and kinematic hardening (defined respectively by the parameters H _iso and H _kin ), the initial yield stress in the three-dimensional context $\sigma_{y,0}$, which relates to $\sigma_{y}^{uniaxial}$ through $\sigma_{y,0} = \sqrt {2/3}\; \sigma_{y}^{uniaxial}$, the shear modulus G, and the bulk modulus K. The last two parameters are herein obtained from the Young’s modulus E and the Poisson’s ratio ν.

In the present application, the following material parameters are considered for the one-dimensional material used in the force-based EBBT element: $\sigma_{y}^{uniaxial} = 500 \times 10^{6} \,\left( {{\text{N}}/{\text{m}}^{ 2} } \right)$, E = 200×10⁹ (N/m²), and b = 0.01. On the other hand, the analyses carried out with the proposed force-based HOBT element employ the following parameters for the multiaxial J2 linear plasticity: $\sigma_{y,0} = \sqrt {2/3} \times 500 \times 10^{6} \, \left( {{\text{N}}/{\text{m}}^{ 2} } \right)$, E = 200×10⁹ (N/m²), H _kin  = 1.34 × 10⁹, H _iso  = 0, and ν = 0.3.

For each of the four elements in the mesh, the numerical integration was carried out with a Gauss-Lobatto scheme with eight integration sections. Geometrical nonlinear effects are neglected. The cross-sectional area integration was performed with a grid of 16 × 16 quadrilaterals (along the height × along the width), each one featuring a total of 4 × 4 Gauss-Lobatto integration points. The midspan loads Δ and/or θ were applied through a suite of monotonic increments in order to trace the nonlinear response up to a level where the member is mainly responding plastically. Figure 8a, b depict the V−Δ and the T−θ curves respectively (where V stands for the reaction shear force and T for the reaction torsional moment), obtained for the different loading ratios and beam theories.

Fig. 8

a Reaction shear force vs imposed midspan displacement Δ, including the results for the EBBT; b Reaction torsional moment vs imposed midspan torsional rotation θ

The following main comments can be made to the several plots above. Firstly, the output of the proposed element and the EBBT in Fig. 8a, when subjected to an imposed midspan transversal displacement Δ (i.e., without torsion), show a very close match. Such expected outcome relates to the fact that, due to the long shear span of the analysed member, flexural deformations—which are appropriately simulated by the EBBT as well—are predominant. Further, they increase during the inelastic range of the response, heightening the aforementioned match. On the other hand, the role of the additional flexibility conferred by the enriched displacement modes accounted for in the HOBT is also clearly visible during the elastic behavioural phase (i.e., by the slightly lower initial stiffness due to shear deformability).

Secondly, the effects of the flexural-shear-torsional interaction in the inelastic range are clearly depicted. Figure 8a shows that the maximum member shear capacity is attained under bending without torsion, and that as the ratio of the imposed midspan torsional rotation to the transversal displacement at the midspan $\theta /\Delta$ increases (for 0.5, 1 and 2 respectively), the shear capacity progressively reduces. This lowered plateau of maximum shear force capacity is associated with the decrease of torsional stiffness with increased imposed torsional rotations, depicted in Fig. 8b. The same figure also shows that, as expected, the reduction of torsional stiffness is more pronounced for smaller ratios $\theta /\Delta$.

6 Conclusions

The present chapter started by recalling the theoretical framework of a recently developed higher-order force-based beam element that simulates the axial-flexural-shear-torsional interaction in three-dimensional frames. The explicit and direct interaction between three-dimensional shear and normal stresses is enabled by the considered set of higher-order deformation modes. In particular, cross-sectional displacement and strain fields are composed of independent and orthogonal modes, which results in unambiguously defined generalised cross-sectional stress-resultants and in a minimisation of the coupling between the equilibrium equations. On the basis of work-equivalency to three-dimensional continuum theory, dual one-dimensional higher-order equilibrium and compatibility equations are derived that govern an advanced form of beam equilibrium. The former are solved by using a force-based formulation, hence inherently avoiding shear-locking problems and allowing to account for the effects of span loads accurately. The proposed formulation is developed independently of the assumed constitutive behaviour (elastic or inelastic).

New numerical applications that capture a number of distinct physical phenomena were then presented. Firstly, the ability of the model in simulating the effect of different boundary conditions on the response of an axially loaded member under elastic response was addressed. The comparison against the results of solid finite element analyses showed the ability of the proposed formulation in adequately simulating the previous effect in the global response of members with different lengths, while using a total number of degrees of freedom one to two orders of magnitude smaller. Additionally, those examples showed that the proposed higher-order beam theory allows to simulate qualitatively the complex stress distribution occurring at the sectional level. From the quantitative viewpoint the matching is acceptable although the stress concentrations cannot be accurately reproduced, as expected. It is noted that the effects above cannot be simulated by classical beam theories. Secondly, an application to a case where flexural-shear-torsional interaction takes place was carried out. The beam performance was again assessed by comparison against refined solid finite element analyses, which confirmed the very good results of the present formulation for a wide range of member lengths wherein classical beam theory results and approximate numerical solutions are inadequate. Finally, the previous case was extended to account for inelastic material behaviour. Namely, the response of a relatively long member subjected to different ratios of imposed torsional rotation to transversal displacement at midspan was analysed. The current beam element simulated the progressive reduction of the shear force capacity due to larger torsional rotations, as well as the progressive decrease of torsional stiffness in the inelastic range. Moreover, the response of the member when only bending was applied closely matches the results of an Euler-Bernoulli force-based fibre beam approach with an equivalent inelastic uniaxial material model.