Abstract
In the design of probabilistic timed systems, requirements concerning behaviour that occurs within a given time or energy budget are of central importance. We observe that model-checking such requirements for probabilistic timed automata can be reduced to checking reward-bounded properties on Markov decision processes. This is traditionally implemented by unfolding the model according to the bound, or by solving a sequence of linear programs. Neither scales well to large models. Using value iteration in place of linear programming achieves scalability but accumulates approximation error. In this paper, we correct the value iteration-based scheme, present two new approaches based on scheduler enumeration and state elimination, and compare the practical performance and scalability of all techniques on a number of case studies from the literature. We show that state elimination can significantly reduce runtime for large models or high bounds.
This work was supported by the 3TU.BSR project, by CDZ project 1023 (cap), by the Chinese Academy of Sciences Fellowship for International Young Scientists, and by the National Natural Science Foundation of China (grant no. 61550110506).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Probabilistic timed automata (PTA, [17]) are a popular formal model for probabilistic real-time systems. They combine nondeterministic choices as in Kripke structures, discrete probabilistic decisions as in Markov chains, and hard real-time behaviour as in timed automata. We are interested in properties of the form “what is the best/worst-case probability to eventually reach a certain system state while accumulating at most b reward”, i.e. in calculating reward-bounded reachability probabilities. Rewards can model a wide range of aspects, e.g. the number of retransmissions in a network protocol (accumulating reward 1 for each), energy consumption (accumulating reward at a state-dependent wattage over time), or time itself (accumulating reward at rate 1 everywhere). Reachability probabilities for PTA with rewards can be computed by first turning a PTA into an equivalent Markov decision process (MDP) using the digital clocks semantics [17] and then performing standard probabilistic model checking [3].
The naïve approach to compute specifically reward-bounded reachability probabilities is to unfold [1] the state space of the model. For the example of time-bounded properties, this means adding a new clock variable that is never reset [17]. In the general case on the level of MDP [19], in addition to the current state of the model, one keeps track of the reward accumulated so far, up to b. This turns the reward-bounded problem into standard unbounded reachability. Unfolding blows up the model size (the number of states, or the number of variables and constraints in the corresponding linear program) and causes the model checking process to run out of memory even if the original (unbounded) model was of moderate size (cf. Table 1). For PTA, unfolding is the only approach that has been considered so far. A more efficient technique has been developed for MDP, and via the digital clocks semantics it is applicable to PTA just as well:
The probability for bound i depends only on the values for previous bounds \(\{\,i-r, \dots , i-1\}\) where r is the max. reward in the automaton. We can thus avoid the monolithic unfolding by sequentially computing the values for its “layers” where the accumulated reward is \(i=0\), 1, etc. up to b, storing the current layer and the last r result vectors only. This process can be implemented by solving a sequence of b linear programming (LP) problems no larger than the original unbounded model [2]. While it solves the memory problem in principle, LP is known not to scale to large MDP in practice. Consequently, LP has been replaced by value iteration to achieve scalability in the most recent implementation [14]. Value iteration is an approximative numeric technique to compute reachability probabilities up to a predefined error bound \(\epsilon \). When used in sequence, this error accumulates, and the final result for bound b may differ from the actual probability by more than \(\epsilon \). This has not been taken into account in [14].
In this paper, we first make a small change to the value iteration-based scheme to counteract the error accumulation. We then present two new ways to compute reward-bounded reachability probabilities for MDP (with a particular interest in the application to PTA via digital clocks) without unfolding (Sect. 3). Using either scheduler enumeration or MDP state elimination, they both reduce the model such that a reward of 1 is accumulated on all remaining transitions. A reward-bounded property in the original model corresponds to a step-bounded property in the reduced model. We use standard step-bounded value iteration [3] to check these properties efficiently and exactly. Observe that we improve the practical efficiency of computing reward-bounded probabilities, but the problem is Exp-complete in general [6]. It can be solved in time polynomial in the size of the MDP and the value of b, i.e. it is only pseudo-polynomial in b. Like all related work, we only present solutions for the case of nonnegative integer rewards.
The unfolding-free techniques also provide the probability for all lower bounds \(i < b\). This has been exploited to obtain quantiles [2], and we use it more generally to compute the entire cumulative (sub)distribution function (cdf for short) over the bound up to b at no extra cost. We have implemented all techniques in the mcsta tool (Sect. 4) of the Modest Toolset [10]. It is currently the only publicly available implementation of reward-bounded model checking for PTA and MDP without unfolding. We use it to study the relative performance and scalability of the previous and new techniques on six example models from the literature (Sect. 5). State elimination in particular shows promising performance.
Other Related Work. Randour et al. [18] have studied the complexity of computing reward-bounded probabilities (framed as percentile queries) for MDP with multiple rewards and reward bounds. They propose an algorithm based on unfolding. For the soft real-time model of Markov automata, which subsumes MDP, reward bounds can be turned into time bounds [13]. Yet this only works for rewards associated to Markovian states, whereas immediate states (i.e. the MDP subset of Markov automata) always implicitly get zero reward.
2 Preliminaries
\(\mathbb {N}\) is \(\{\, 0, 1, \dots \}\), the set of natural numbers. \(2^{S} \) is the powerset of S. \(\mathrm {Dom}({f}) \) is the domain of the function f.
Definition 1
A (discrete) probability distribution over a set \(\varOmega \) is a function \(\mu \in \varOmega \rightarrow [0, 1]\) such that  is countable and \(\sum _{\omega \in \mathrm {support}({\mu })}{\mu (\omega )} = 1\). \(\mathrm {Dist}({\varOmega }) \) is the set of all probability distributions over \(\varOmega \). \(\mathcal {D}(s) \) is the Dirac distribution for s, defined by \(\mathcal {D}(s) (s) = 1\).
is countable and \(\sum _{\omega \in \mathrm {support}({\mu })}{\mu (\omega )} = 1\). \(\mathrm {Dist}({\varOmega }) \) is the set of all probability distributions over \(\varOmega \). \(\mathcal {D}(s) \) is the Dirac distribution for s, defined by \(\mathcal {D}(s) (s) = 1\).
Markov Decision Processes. To move from one state to another in a Markov decision process, first a transition is chosen nondeterministically; each transition then leads into a probability distribution over rewards and successor states.
Definition 2
A Markov decision process (MDP) is a triple \(M =\langle S, T, s_ init \rangle \) where \(S \) is a finite set of states, \(T \in S \rightarrow 2^{\mathrm {Dist}({\mathbb {N} \times S})} \) is the transition function, and \(s_ init \in S \) is the initial state. For all \(s \in S \), we require that \(T (s)\) is finite and non-empty. M is a discrete-time Markov chain (DTMC) if \(\forall \,s \in S :|T (s)| = 1\).
We write  for \(\exists \,\mu \in T (s)\) and call it a transition. We write
for \(\exists \,\mu \in T (s)\) and call it a transition. We write  if additionally \(\langle r,s' \rangle \in \mathrm {support}({\mu }) \). \(\langle r,s' \rangle \) is a branch with reward r. If \(T \) is clear from the context, we write just
if additionally \(\langle r,s' \rangle \in \mathrm {support}({\mu }) \). \(\langle r,s' \rangle \) is a branch with reward r. If \(T \) is clear from the context, we write just  . Graphically, transitions are lines to an intermediate node from which branches labelled with reward (if not zero) and probability lead to successor states. We may omit the intermediate node and probability 1 for transitions into Dirac distributions, and we may label transitions to refer to them in the text. Figure 1 shows an example MDP \(M^e\) with 5 states, 7 (labelled) transitions and 10 branches. Using branch rewards instead of the more standard transition rewards leads to more compact models; in the example, we assign reward 1 to the branches back to s and t to count the number of “failures” before reaching v. In practice, high-level formalisms like Prism’s [15] guarded command language are used to specify MDP. They extend MDP with variables over finite domains that can be used in expressions to e.g. enable/disable transitions. This allows to compactly describe very large MDP.
. Graphically, transitions are lines to an intermediate node from which branches labelled with reward (if not zero) and probability lead to successor states. We may omit the intermediate node and probability 1 for transitions into Dirac distributions, and we may label transitions to refer to them in the text. Figure 1 shows an example MDP \(M^e\) with 5 states, 7 (labelled) transitions and 10 branches. Using branch rewards instead of the more standard transition rewards leads to more compact models; in the example, we assign reward 1 to the branches back to s and t to count the number of “failures” before reaching v. In practice, high-level formalisms like Prism’s [15] guarded command language are used to specify MDP. They extend MDP with variables over finite domains that can be used in expressions to e.g. enable/disable transitions. This allows to compactly describe very large MDP.
Definition 3
A finite path in \(M =\langle S, T, s_ init \rangle \) is defined as a finite sequence \(\pi _\mathrm {fin} = s_0\, \mu _0\, r_0\, s_1\, \mu _1\, r_1\, s_2 \dots \mu _{n-1}\, r_{n-1}\, s_n\) where \(s_i \in S \) for all \(i \in \{\, 0, \dots , n \}\) and  for all \(i \in \{\, 0, \dots , n - 1 \}\). Let
for all \(i \in \{\, 0, \dots , n - 1 \}\). Let  , and \(\mathrm {reward}(\pi _\mathrm {fin}) = \sum _{i=0}^{n-1} r_i\). \(\mathrm {Paths}_\mathrm {fin}(M)\) is the set of all finite paths starting with \(s_ init \). A path is an infinite sequence \(\pi = s_0\, \mu _0\, r_0\, s_1\, \mu _1\, r_1 \dots \) where \(s_i \in S \) and
, and \(\mathrm {reward}(\pi _\mathrm {fin}) = \sum _{i=0}^{n-1} r_i\). \(\mathrm {Paths}_\mathrm {fin}(M)\) is the set of all finite paths starting with \(s_ init \). A path is an infinite sequence \(\pi = s_0\, \mu _0\, r_0\, s_1\, \mu _1\, r_1 \dots \) where \(s_i \in S \) and  for all \(i \in \mathbb {N} \). \(\mathrm {Paths}(M)\) is the set of all paths starting with \(s_ init \). We define
for all \(i \in \mathbb {N} \). \(\mathrm {Paths}(M)\) is the set of all paths starting with \(s_ init \). We define  .
.
Definition 4
Given \(M =\langle S, T, s_ init \rangle \), \(\mathfrak {S}\in \mathrm {Paths}_\mathrm {fin}(M) \rightarrow \mathrm {Dist}({\mathrm {Dist}({\mathbb {N} \times S})}) \) is a scheduler for M if  . The set of all schedulers of M is \(\mathrm {Sched} (M)\). \(\mathfrak {S}\) is reward-positional if \(\mathrm {last}(\pi _1) = \mathrm {last}(\pi _2) \wedge \mathrm {reward}(\pi _1) = \mathrm {reward}(\pi _2) \) implies \(\mathfrak {S}(\pi _1) = \mathfrak {S}(\pi _2)\), positional if \(\mathrm {last}(\pi _1) = \mathrm {last}(\pi _2) \) alone implies \(\mathfrak {S}(\pi _1) = \mathfrak {S}(\pi _2)\), and deterministic if \(|\mathrm {support}({\mathfrak {S}(\pi )}) | = 1\), for all finite paths \(\pi \), \(\pi _1\) and \(\pi _2\), respectively. A simple scheduler is positional and deterministic. The set of all simple schedulers of M is \(\mathrm {SSched} (M)\).
. The set of all schedulers of M is \(\mathrm {Sched} (M)\). \(\mathfrak {S}\) is reward-positional if \(\mathrm {last}(\pi _1) = \mathrm {last}(\pi _2) \wedge \mathrm {reward}(\pi _1) = \mathrm {reward}(\pi _2) \) implies \(\mathfrak {S}(\pi _1) = \mathfrak {S}(\pi _2)\), positional if \(\mathrm {last}(\pi _1) = \mathrm {last}(\pi _2) \) alone implies \(\mathfrak {S}(\pi _1) = \mathfrak {S}(\pi _2)\), and deterministic if \(|\mathrm {support}({\mathfrak {S}(\pi )}) | = 1\), for all finite paths \(\pi \), \(\pi _1\) and \(\pi _2\), respectively. A simple scheduler is positional and deterministic. The set of all simple schedulers of M is \(\mathrm {SSched} (M)\).
Let  with
with  for \(\mathfrak {S}_\mathrm {s} \in \mathrm {SSched} (M)\). \({M}{\downarrow }_{\mathfrak {S}_\mathrm {s}} \) is a DTMC. Using the standard cylinder set construction [3], a scheduler \(\mathfrak {S}\) induces a probability measure \(\mathcal {P}^{\mathfrak {S}}_{M} \) on measurable sets of paths starting from \(s_ init \). We define the extremal values \(\mathcal {P}^{\mathrm {max}}_{M} (\varPi ) = \sup _{\mathfrak {S}\in \mathrm {Sched} (M)}\mathcal {P}^{\mathfrak {S}}_{M} (\varPi )\) and \(\mathcal {P}^{\mathrm {min}}_{M} (\varPi ) = \inf _{\mathfrak {S}\in \mathrm {Sched} (M)}\mathcal {P}^{\mathfrak {S}}_{M} (\varPi )\) for measurable \(\varPi \subseteq \mathrm {Paths}(M)\).
for \(\mathfrak {S}_\mathrm {s} \in \mathrm {SSched} (M)\). \({M}{\downarrow }_{\mathfrak {S}_\mathrm {s}} \) is a DTMC. Using the standard cylinder set construction [3], a scheduler \(\mathfrak {S}\) induces a probability measure \(\mathcal {P}^{\mathfrak {S}}_{M} \) on measurable sets of paths starting from \(s_ init \). We define the extremal values \(\mathcal {P}^{\mathrm {max}}_{M} (\varPi ) = \sup _{\mathfrak {S}\in \mathrm {Sched} (M)}\mathcal {P}^{\mathfrak {S}}_{M} (\varPi )\) and \(\mathcal {P}^{\mathrm {min}}_{M} (\varPi ) = \inf _{\mathfrak {S}\in \mathrm {Sched} (M)}\mathcal {P}^{\mathfrak {S}}_{M} (\varPi )\) for measurable \(\varPi \subseteq \mathrm {Paths}(M)\).
For an MDP M and goal states \(F \subseteq S \), we define the unbounded, step-bounded and reward-bounded reachability probabilities for \( opt \in \{\, \mathrm {max}, \mathrm {min} \}\):
-
 is the extremal probability of eventually reaching a state in F.
is the extremal probability of eventually reaching a state in F. -
 is the extremal probability of reaching a state in F via at most \(b \in \mathbb {N} \) transitions, defined as \(\mathcal {P}^{ opt }_{M} (\varPi ^\mathrm {T}_b)\) where \(\varPi ^\mathrm {T}_b\) is the set of paths that have a prefix of length at most b that contains a state in F.
is the extremal probability of reaching a state in F via at most \(b \in \mathbb {N} \) transitions, defined as \(\mathcal {P}^{ opt }_{M} (\varPi ^\mathrm {T}_b)\) where \(\varPi ^\mathrm {T}_b\) is the set of paths that have a prefix of length at most b that contains a state in F. -
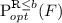 is the extremal probability of reaching a state in F with accumulated reward at most \(b \in \mathbb {N} \), defined as \(\mathcal {P}^{ opt }_{M} (\varPi ^\mathrm {R}_b)\) where \(\varPi ^\mathrm {R}_b\) is the set of paths that have a prefix \(\pi _\mathrm {fin}\) containing a state in F with \(\mathrm {reward}(\pi _\mathrm {fin}) \le b\).
is the extremal probability of reaching a state in F with accumulated reward at most \(b \in \mathbb {N} \), defined as \(\mathcal {P}^{ opt }_{M} (\varPi ^\mathrm {R}_b)\) where \(\varPi ^\mathrm {R}_b\) is the set of paths that have a prefix \(\pi _\mathrm {fin}\) containing a state in F with \(\mathrm {reward}(\pi _\mathrm {fin}) \le b\).
Theorem 1
For an unbounded property, there exists an optimal simple scheduler, i.e. one that attains the extremal value [3]. For a reward-bounded property, there exists an optimal deterministic reward-positional scheduler [12].
Continuing our example, let \(F^e = \{\, v \}\). We maximise the probability to eventually reach \(F^e\) in \(M^e\) by always scheduling transition a in s and d in t, so \(\mathrm {P}_{\!{\mathrm {max}}}({F^e}) = 1\) with a simple scheduler. We get  by scheduling b in s. For higher bound values, simple schedulers are no longer sufficient: we get
by scheduling b in s. For higher bound values, simple schedulers are no longer sufficient: we get  by first trying a then d, but falling back to c then b if we return to t. We maximise the probability for higher bound values n by trying d until the accumulated reward is \(n - 1\) and then falling back to b.
by first trying a then d, but falling back to c then b if we return to t. We maximise the probability for higher bound values n by trying d until the accumulated reward is \(n - 1\) and then falling back to b.
Probabilistic Timed Automata. Probabilistic timed automata (PTA [17]) extend MDP with clocks and clock constraints as in timed automata to model real-time behaviour and requirements. PTA have two kinds of rewards: branch rewards as in MDP and rate rewards that accumulate at a certain rate over time. Time itself is a rate reward that is always 1. The digital clocks approach [17] is the only PTA model checking technique that works well with rewards. It works by replacing the clock variables by bounded integers and adding self-loop edges to increment them synchronously as long as time can pass. The reward of a self-loop edge is the current rate reward. The result is (a high-level model of) a finite digital clocks MDP. All the algorithms that we develop for MDP in this paper can thus be applied to PTA. While time- and branch reward-bounded properties on PTA are decidable [17], general rate reward-bounded properties are not [4].
Probabilistic Model Checking. Probabilistic model checking for MDP (and thus for PTA via the digital clocks semantics) works in two phases: (1) state space exploration turns a given high-level model into an in-memory representation of the underlying MDP, then (2) a numerical analysis computes the value of the property of interest. In phase 1, the goal states are made absorbing:
Definition 5
Given \(M = \langle S, T, s_ init \rangle \) and \(F \subseteq S \), we define the F-absorbing MDP as \({M}{\downarrow }_{F} = \langle S, T ', s_ init \rangle \) with \(T '(s) = \{\,\mathcal {D}(\langle 1,s \rangle ) \}\) for all \(s \in F\) and \(T '(s) = T (s)\) otherwise. For \(s \in S \), we define \(M[s] = \langle S, T, s \rangle \).
An efficient algorithm for phase 2 and unbounded properties is (unbounded) value iteration [3]. We denote a call to a value iteration implementation by \(\texttt {VI}(V, {M}{\downarrow }_{F}, opt , \epsilon )\) with initial value vector \(V \in S \rightarrow [0,1]\) and \( opt \in \{\, \mathrm {max}, \mathrm {min} \}\). Internally, it iteratively approximates over all states s a (least) solution for
up to (relative) error \(\epsilon \). Let initially \(V = \{\, s \mapsto 1 \mid s \in F\} \cup \{\, s \mapsto 0 \mid s \in S \setminus F \}\). Then on termination of \(\texttt {VI}(V, {M}{\downarrow }_{F}, opt , \epsilon )\), we have \(V(s) \approx _\epsilon \mathrm {P}_{\!{ opt }}({F})\) in M[s] for all \(s \in S \). All current implementations in model checking tools like Prism [15] use a simple convergence criterion based on \(\epsilon \) that in theory only guarantees \(V(s) \le \mathrm {P}_{\!{ opt }}({F})\), yet in practice delivers \(\epsilon \)-close results on most, but not all, case studies. Guaranteed \(\epsilon \)-close results could be achieved at the cost of precomputing and reducing a maximal end component decomposition of the MDP [7]. In this paper, we thus write VI to refer to an ideal \(\epsilon \)-correct algorithm, but for the sake of comparison use the standard implementation in our experiments in Sect. 5.
For a step-bounded property, the call \(\texttt {StepBoundedVI}(V = V_0, {M}{\downarrow }_{F}, opt , b)\) with bound b can be implemented [3] by computing for all states
iteratively for \(i=1, \dots , b\). After iteration i, we have  in M[s] for all \(s \in S \) when starting with V as in the unbounded case above. Note that this algorithm computes exact results (modulo floating-point precision and errors) without any costly preprocessing and is very easy to implement and parallelise.
in M[s] for all \(s \in S \) when starting with V as in the unbounded case above. Note that this algorithm computes exact results (modulo floating-point precision and errors) without any costly preprocessing and is very easy to implement and parallelise.
Reward-bounded properties can naïvely be checked by unfolding the model according to the accumulated reward: we add a variable v to the model prior to phase 1, with branch reward r corresponding to an assignment \(v := v + r\). To check  , phase 1 thus creates an MDP that is up to b times as large as without unfolding. In phase 2, \(\mathrm {P}_{\!{ opt }}({F'})\) is checked using VI as described above where \(F'\) corresponds to the states in F where additionally \(v \le b\) holds.
, phase 1 thus creates an MDP that is up to b times as large as without unfolding. In phase 2, \(\mathrm {P}_{\!{ opt }}({F'})\) is checked using VI as described above where \(F'\) corresponds to the states in F where additionally \(v \le b\) holds.
3 Reward-Bounded Analysis Techniques
We describe three techniques that allow the computation of reward-bounded reachability probabilities on MDP (and thus PTA) without unfolding. The first one is a reformulation of the value iteration-based variant [14] of the algorithm introduced in [2]. We incorporate a simple fix for the problem that the error accumulation over the sequence of value iterations had not been accounted for and refer to the result as algorithm modvi. We then present two new techniques senum and elim that avoid the issues of unbounded value iteration by transforming the MDP such that step-bounded value iteration can be used instead.
From now on, we assume that all rewards are either zero or one. This simplifies the presentation and is in line with our motivation of improving time-bounded reachability for PTA: in the corresponding digital clocks MDP, all transitions representing the passage of time have reward 1 while the branches of all other transitions have reward 0. Yet it is without loss of generality: for modvi, it is merely a matter of a simplified presentation, and for the two new algorithms, we can preprocess the MDP to replace each branch with reward \(r > 1\) by a chain of r Dirac transitions with reward 1. While this may blow up the state space, we found that most models in practice only use rewards 0 and 1 in the first place: among the 15 MDP and DTMC models currently distributed with Prism [15], only 2 out of the 12 examples that include a reward structure do not satisfy this assumption. It also holds for all case studies that we present in Sect. 5.
For all techniques, we need a transformation \({}{\downarrow }_{\mathrm {R}} \) that redirects each reward-one branch to a copy \(s'_\mathrm {new}\) of the branch’s original target state \(s'\). In effect, this replaces branch rewards by branches to a distinguished category of “new” states:
Definition 6
Given \(M = \langle S, T, s_ init \rangle \), we define \({M}{\downarrow }_{\mathrm {R}} \) as \(\langle S \uplus S _\mathrm {new}, T ^\downarrow , s_ init \rangle \) with \(S _\mathrm {new} = \{\, s_\mathrm {new} \mid s \in S \}\),
and \( Conv (s, \mu ) \in \mathrm {Dist}({\mathbb {N} \times S \uplus S _\mathrm {new}}) \) is defined by \( Conv (s, \mu )(\langle 0, s' \rangle ) = \mu (\langle 0, s' \rangle )\) and \( Conv (s, \mu )(\langle 1, s'_\mathrm {new} \rangle ) = \mu (\langle 1, s' \rangle )\) over all \(s' \in S \).
For our example MDP \(M^e\) and \(F^e = \{\, v \}\), we show \({{M^e}{\downarrow }_{F^e}}{\downarrow }_{\mathrm {R}} \) in Fig. 2. Observe that \({M^e}{\downarrow }_{F^e} \) is the same as \(M^e\), except that the self-loop of goal state v gets reward 1. \({{M^e}{\downarrow }_{F^e}}{\downarrow }_{\mathrm {R}} \) is then obtained by redirecting the three reward-one branches (originally going to s, t and v) to new states \(s_\mathrm {new}\), \(t_\mathrm {new}\) and \(v_\mathrm {new}\).
All of the algorithm descriptions we present take a value vector V as input, which they update. V must initially contain the probabilities to reach a goal state in F with zero reward, which can be computed for example via a call to \(\texttt {VI}(V = V_F^0, {{M}{\downarrow }_{F}}{\downarrow }_{\mathrm {R}}, opt , \epsilon )\) with sufficiently small \(\epsilon \) and

3.1 Sequential Value Iterations

We recall the technique for model-checking reward-bounded properties of [2] that avoids unfolding. It was originally formulated as a sequence of linear programming (LP) problems \( LP _{\!\!i}\), each corresponding to bound \(i \le b\). Each \( LP _{\!\!i}\) is of the same size as the original (non-unfolded) MDP, representing its state space, but uses the values computed for \( LP _{\!\!i-r}, \dots , LP _{\!\!i-1}\) with r being the maximal reward that occurs in the MDP. Since LP does not scale to large MDP [7], the technique has been reconsidered using value iteration instead [14]. Using the transformations and assumptions introduced above, we can formulate it as in Algorithm 1. Initially, V contains the probabilities to reach a goal state with zero reward. In contrast to [14], when given an overall error bound \(\epsilon \), we use bound \(\frac{\epsilon }{b+1}\) for the individual value iteration calls. At the cost of higher runtime, this counteracts the accumulation of error over multiple calls to yield an \(\epsilon \)-close final result:
Consider \({{M}{\downarrow }_{F}}{\downarrow }_{\mathrm {R}} =\langle S, T, s_ init \rangle \) and \(f \in (S \rightarrow [0,1]) \rightarrow (S \rightarrow [0,1])\) with \(f = \lim _{i} f_{i}\) where for \(V\in S \rightarrow [0,1]\) it is \(f_0(V)(s) = V(s)\) and \(f_{i+1}(V)(s) = opt _\mu \sum _{s'} \mu (s') \cdot f_{i}(V)(s')\), i.e. f corresponds to performing an ideal value iteration with error \(\epsilon = 0\). Thus, performing Algorithm 1 using f would result in an error of 0. If we limit the error in each value iteration to \(\frac{\epsilon }{b+1}\), then the function we use can be stated as \(f' = f_n\) for n large enough such that \(|| f'(V) - f(V) ||_\mathrm {max} \le \frac{\epsilon }{b+1}\) for all V used in the computations. Let \(V_0\), \(V_0' = V_0 + \delta _0\) be the initial value vectors, \(\delta _0 < \frac{\epsilon }{b+1}\). Further, let \(V_i, V_i' \in S \rightarrow [0,1]\), \(i\in \{1,\ldots ,b\}\), be the value vectors after the i-th call to \(\texttt {VI}\) for the case without (\(V_i\)) and with error (\(V_i'\)). We can then show by induction that \(||V_i - V_i'||_\mathrm {max} \le (i+1) \frac{\epsilon }{b+1}\). Initially, we have \(V_0' = V_0 + \delta _0\). Therefore, we have \(V_1' = f'(V_0') = f(V_0') + \delta _1 = f(V_0) + \sum _{j=0}^0 \delta _j + \delta _1\) for some \(\delta _{1}\in S \rightarrow [0,1]\) with \(|| \delta _{1} ||_\mathrm {max} \le \frac{\epsilon }{b+1}\). Then, we have for some \(\delta _{j}\in S \rightarrow [0,1]\), \(j\in \{0, \ldots , i\}\), with \(|| \delta _{j} ||_\mathrm {max} \le \frac{\epsilon }{b+1}\):
where \(*\) holds by the induction assumption. Finally, \(||\sum _{j=0}^{i} \delta _{j}||_\mathrm {max} \le (i+1) \frac{\epsilon }{b+1}\), so \(||V_i - V_i'||_\mathrm {max} \le (i+1) \frac{\epsilon }{b+1}\), which is what had to be proved.
3.2 Scheduler Enumeration

Our first new technique, senum, is summarised as Algorithm 2. The idea is to replace the entire sub-MDP between a “relevant” state and the new states (that follow immediately after what was a reward-one branch before the \({}{\downarrow }_{\mathrm {R}}\) transformation) by one direct transition to a distribution over the new states for each simple scheduler. The actual reward-bounded probabilities can be computed on the result MDP \(M''\) using the standard step-bounded algorithm (line 7), since one step now corresponds to a reward of 1.
The relevant states, which remain in the result MDP \(M''\), are the initial state plus those states that had an incoming reward-one branch. We iterate over them in line 3. In an inner loop (line 4), we iterate over the simple schedulers for each relevant state. For each scheduler, ComputeProbs determines the distribution \(\mu \) s.t. for each new state \(s_\mathrm {new}\), \(\mu (s_\mathrm {new})\) is the probability of reaching it (accumulating 1 reward on the way) and \(\mu (\bot )\) is the probability of getting stuck in an end component without being able to accumulate any more reward ever. A transition to preserve \(\mu \) in \(M''\) is created in line 5. The total number of simple schedulers for n states with max. fan-out m is in \(\mathcal {O}(m^n)\), but we expect the number of schedulers that lead to different distributions from one relevant state up to the next reward-one steps to remain manageable (cf. column “avg” in Table 2).
ComputeProbs is implemented either using value iterations, one for each new state, or—since \({M'[s]}{\downarrow }_{\mathfrak {S}} \) is a DTMC—using DTMC state elimination [8]. The latter successively eliminates the non-new states as shown schematically in Fig. 3 while preserving the reachability probabilities, all in one go.
3.3 State Elimination
Instead of performing a probability-preserving DTMC state elimination for each scheduler as in senum, technique elim applies a new scheduler- and probability-preserving state elimination algorithm to the entire MDP. The state elimination algorithm is described by the schema shown in Fig. 4; states with Dirac self-loops will remain. Observe how this elimination process preserves the options that simple schedulers have, and in particular relies on their positional character to be able to redistribute the loop probabilities \(p_{c_i}\) onto the same transition only.
DTMC state elimination [8]

elim is shown as Algorithm 3. In line 3, the MDP state elimination procedure is called to eliminate all the regular states in \(S\). We can ignore rewards here since they were transformed by \({}{\downarrow }_{\mathrm {R}}\) into branches to the distinguished new states. As an extension to the schema of Fig. 4, we also preserve the original outgoing transitions when we eliminate a relevant state (defined as in Sect. 3.2) because we need them in the next step: In the loop starting in line 5, we redirect (1) all branches that go to non-new states to the added bottom state \(\bot \) instead because they indicate that we can get stuck in an end component without reward, and (2) all branches that go to new states to the corresponding original states instead. This way, we merge the (absorbing, but not eliminated) new states with the corresponding regular (eliminated from incoming but not outgoing transitions) states. Finally, in line 8, the standard step-bounded value iteration is performed on the eliminated-merged MDP as in senum. Figure 5 shows our example MDP after state elimination, and Fig. 6 shows the subsequent merged MDP. For clarity, transitions to the same successor distributions are shown in a combined way.
3.4 Correctness and Complexity
Correctness. Let \(\mathfrak {S}\)be a deterministic reward-positional scheduler for \({M}{\downarrow }_{F} \). It corresponds to a sequence of simple schedulers \(\mathfrak {S}_i\) for \({M}{\downarrow }_{F} \) where \(i \in \{\,b, \ldots , 0\}\) is the remaining reward that can be accumulated before the bound is reached. For each state s of \({M}{\downarrow }_{F} \) and \(i > 0\), each such \(\mathfrak {S}_i\) induces a (potentially substochastic) measure \(\mu _s^i\) such that \(\mu _s^i(s')\) is the probability to reach \(s'\) from s in \({{M}{\downarrow }_{F}}{\downarrow }_{\mathfrak {S}_i} \) over paths whose last step has reward 1. Let \(\mu ^0_s\) be the induced measure such that \(\mu _s^0(s')\) is the probability under \(\mathfrak {S}_0\) to reach \(s'\) without reward if it is a goal state and 0 otherwise. Using the recursion  with
with  , the value \(\overline{\mu }^b_s(s')\) is the probability to reach goal state \(s'\) from s in \({M}{\downarrow }_{F} \) under \(\mathfrak {S}\). Thus we have
, the value \(\overline{\mu }^b_s(s')\) is the probability to reach goal state \(s'\) from s in \({M}{\downarrow }_{F} \) under \(\mathfrak {S}\). Thus we have  and
and  by Theorem 1. If we distribute the maximum operation into the recursion, we get
by Theorem 1. If we distribute the maximum operation into the recursion, we get
and an analogous formula for the minimum. By computing extremal values w.r.t. simple schedulers for each reward step, we thus compute the value w.r.t. an optimal deterministic reward-positional scheduler for the bounded property overall. The correctness of senum and elim now follows from the fact that they implement precisely the right-hand side of (1): \(\overline{\mu }^0_s\) is always given as the initial value of V as described at the very beginning of this section. In senum, we enumerate the relevant measures \(\mu _s^{\cdot }\) induced by all the simple schedulers as one transition each, then choose the optimal transition for each i in the i-th iteration inside StepBoundedVI. The argument for elim is the same, the difference being that state elimination is what transforms all the measures into single transitions.
Complexity. The problem that we solve is Exp-complete [6]. We make the following observations about senum and elim: Let \(n_\mathrm {new} \le n\) be the number of new states, \(n_\mathrm {s} \le n\) the max. size of any relevant reward-free sub-MDP (i.e. the max. number of states reachable from the initial or a new state when dropping all reward-one branches), and \(s_\mathrm {s} \le m^n\) the max. number of simple schedulers in these sub-MDP. The reduced MDP created by senum and elim have \(n_\mathrm {new}\) states and up to \(n_\mathrm {new} \cdot s_\mathrm {s} \cdot n_\mathrm {s}\) branches. The bounded value iterations thus involve \(\mathcal {O}(b \cdot n_\mathrm {new} \cdot s_\mathrm {s} \cdot n_\mathrm {s})\) arithmetic operations overall. Note that in the worst case, \(s_\mathrm {s} = m^n\), i.e. it is exponential in the size of the original MDP. To obtain the reduced MDP, senum enumerates \(\mathcal {O}(n_\mathrm {new} \cdot s_\mathrm {s})\) schedulers; for each, value iteration or DTMC state elimination is done on a sub-MDP of \(\mathcal {O}(n_\mathrm {s})\) states. elim needs to eliminate \(n - n_\mathrm {new}\) states, with each elimination requiring \(\mathcal {O}(s_\mathrm {s} \cdot n_\mathrm {s})\) operations.
4 Implementation
We have implemented the three unfolding-free techniques within mcsta, the Modest Toolset’s model checker for PTA and MDP. When asked to compute  , it delivers all values
, it delivers all values  for \(i \in \{\,0, \dots , b\}\) since the algorithms allow doing so at no overhead. Instead of a single value, we thus get the entire (sub-)cdf. Every single value is defined via an individual optimisation over schedulers. However, we have seen in Sect. 3.4 that an optimal scheduler for bound i can be extended to an optimal scheduler for \(i+1\), so there exists an optimal scheduler for all bounds. The max./min. cdf represents the probability distribution induced by that scheduler. We show these functions for the randomised consensus case study [16] in Fig. 7. The top (bottom) curve is the max. (min.) probability for the protocol to terminate within the number of coin tosses given on the x-axis. For comparison, the left and right dashed lines show the means of these distributions. Note that the min. expected value corresponds to the max. bounded probabilities and vice-versa. As mentioned, using the unfolding-free techniques, we compute the curves in the same amount of memory otherwise sufficient for the means only. We also implemented a convergence criterion to detect when the result will no longer increase for higher bounds, i.e. when the unbounded probability has been reached up to \(\epsilon \). For the functions in Fig. 7, this happens at 4016 coin tosses for the max. and 5607 for the min. probability.
for \(i \in \{\,0, \dots , b\}\) since the algorithms allow doing so at no overhead. Instead of a single value, we thus get the entire (sub-)cdf. Every single value is defined via an individual optimisation over schedulers. However, we have seen in Sect. 3.4 that an optimal scheduler for bound i can be extended to an optimal scheduler for \(i+1\), so there exists an optimal scheduler for all bounds. The max./min. cdf represents the probability distribution induced by that scheduler. We show these functions for the randomised consensus case study [16] in Fig. 7. The top (bottom) curve is the max. (min.) probability for the protocol to terminate within the number of coin tosses given on the x-axis. For comparison, the left and right dashed lines show the means of these distributions. Note that the min. expected value corresponds to the max. bounded probabilities and vice-versa. As mentioned, using the unfolding-free techniques, we compute the curves in the same amount of memory otherwise sufficient for the means only. We also implemented a convergence criterion to detect when the result will no longer increase for higher bounds, i.e. when the unbounded probability has been reached up to \(\epsilon \). For the functions in Fig. 7, this happens at 4016 coin tosses for the max. and 5607 for the min. probability.
5 Experiments
We use six case studies from the literature to evaluate the applicability and performance of the three unfolding-free techniques and their implementation:
-
BEB [5]: MDP of a bounded exponential backoff procedure with max. backoff value \(K=4\) and \(H \in \{\,5, \dots , 10\}\) parallel hosts. We compute the max. probability of any host seizing the line while all hosts enter backoff \(\le b\) times.
-
BRP [9]: The PTA model of the bounded retransmission protocol with \(N \in \{\, 32, 64 \}\) frames to transmit, retransmission bound \( MAX \in \{\,6, 12\}\) and transmission delay \( TD \in \{\, 2, 4 \}\) time units. We compute the max. and min. probability that the sender reports success in \(\le b\) time units.
-
RCONS [16]: The randomised consensus shared coin protocol MDP as described in Sect. 4 for \(N \in \{\, 4, 6 \}\) parallel processes and constant \(K \in \{\, 2, 4, 8 \}\).
-
CSMA [9]: PTA model of a communication protocol using CSMA/CD, with max. backoff counter \( BCMAX \in \{\, 1, \dots , 4 \}\). We compute the min. and max. probability that both stations deliver their packets by deadline b time units.
-
FW [16]: PTA model (“Impl” variant) of the IEEE 1394 FireWire root contention protocol with either a short or a long cable. We ask for the min. probability that a leader (root) is selected before time bound b.
-
IJSS [14]: MDP model of Israeli and Jalfon’s randomised self-stabilising algorithm with \(N \in \{\,18, 19, 20\}\) processes. We compute the min. probability to reach a stable state in \(\le b\) steps of the algorithm (query Q2 in [14]). This is a step-bounded property; we consider IJSS here only to compare with [14].
Experiments were performed on an Intel Core i5-6600T system (2.7 GHz, 4 cores) with 16 GB of memory running 64-bit Windows 10 and a timeout of 30 min.
Looking back at Sect. 3, we see that the only extra states introduced by modvi compared to checking an unbounded probabilistic reachability or expected-reward property are the new states \(s_\mathrm {new}\). However, this was for the presentation only, and is avoided in the implementation by checking for reward-one branches on-the-fly. The transformations performed in senum and elim, on the other hand, will reduce the number of states, but may add transitions and branches. elim may also create large intermediate models. In contrast to modvi, these two techniques may thus run out of memory even if unbounded properties can be checked. In Table 1, we show the state-space sizes (1) for the traditional unfolding approach (“unfolded”) for the bound b where the values have converged, (2) when unbounded properties are checked or modvi is used (“non-unfolded”), and (3) after state elimination and merging in elim. We report thousands (k) or millions (M) of states, transitions (“trans”) and branches (“branch”). Column “avg” lists the average size of all relevant reward-free sub-MDP. The values for senum are the same as for elim. Times are for the state-space exploration phase only, so the time for “non-unfolded” will be incurred by all three unfolding-free algorithms. We see that avoiding unfolding is a drastic reduction. In fact, 16 GB of memory are not sufficient for the larger unfolded models, so we used mcsta ’s disk-based technique [11]. State elimination leads to an increase in transitions and especially branches, drastically so for BRP, the exceptions being BEB and IJSS. This appears related to the size of the reward-free subgraphs, so state elimination may work best if there are few steps between reward increments.
In Table 2, we report the performance results for all three techniques when run until the values have converged at bound value b (except for IJSS, where we follow [14] and set b to the 99th percentile). For senum, we used the variant based on value iteration since it consistently performed better than the one using DTMC state elimination. “iter” denotes the time needed for (unbounded or step-bounded) value iteration, while “enum” and “elim” are the times needed for scheduler enumeration resp. state elimination and merging. “#” is the total number of iterations performed over all states inside the calls to VI. “avg” is the average number of schedulers enumerated per relevant state; to get the approx. total number of schedulers enumerated for a model instance, multiply by the number of states for elim in Table 1. “rate” is the number of bound values computed per second, i.e. b divided by the time for value iteration. Memory usage in columns “mem” is mcsta ’s peak working set, including state space exploration, reported in mega- (M) or gigabytes (G). mcsta is garbage-collected, so these values are higher than necessary since full collections only occur when the system runs low on memory. The values related to value iteration for senum are the same as for elim. In general, we see that senum uses less memory than elim, but is much slower in all cases except IJSS. If elim works and does not blow up the model too much, it is significantly faster than modvi, making up for the time spent on state elimination with much faster value iteration rates.
6 Conclusion
We presented three approaches to model-check reward-bounded properties on MDP without unfolding: a small correction of recent work based on unbounded value iteration [14], and two new techniques that reduce the model such that step-bounded value iteration can be used, which is efficient and exact. We also consider the application to time-bounded properties on PTA and provide the first implementation that is publicly available, within the Modest Toolset at modestchecker.net. By avoiding unfolding and returning the entire probability distribution up to the bound at no extra cost, this could finally make reward- and time-bounded probabilistic timed model checking feasible in practical applications. As we presented the algorithms in this paper, they compute reachability probabilities. However all of them can easily be adapted to compute reward-bounded expected accumulated rewards and instantaneous rewards, too.
Outlook. The digital clocks approach for PTA was considered limited in scalability. The presented techniques lift some of its most significant practical limitations. Moreover, time-bounded analysis without unfolding and with computation of the entire distribution in this manner is not feasible for the traditionally more scalable zone-based approaches because zones abstract from concrete timing. We see the possibility to improve the state elimination approach by removing transitions that are linear combinations of others and thus unnecessary. This may reduce the transition and branch blowup on models like the BRP case. Going beyond speeding up simple reward-bounded reachability queries, state elimination also opens up ways towards a more efficient analysis of long-run average and long-run reward-average properties.
References
Andova, S., Hermanns, H., Katoen, J.-P.: Discrete-time rewards model-checked. In: Larsen, K.G., Niebert, P. (eds.) FORMATS 2003. LNCS, vol. 2791, pp. 88–104. Springer, Heidelberg (2004). doi:10.1007/978-3-540-40903-8_8
Baier, C., Daum, M., Dubslaff, C., Klein, J., Klüppelholz, S.: Energy-utility quantiles. In: Badger, J.M., Rozier, K.Y. (eds.) NFM 2014. LNCS, vol. 8430, pp. 285–299. Springer, Heidelberg (2014). doi:10.1007/978-3-319-06200-6_24
Baier, C., Katoen, J.P.: Principles of Model Checking. MIT Press, Massachusetts (2008)
Berendsen, J., Chen, T., Jansen, D.N.: Undecidability of cost-bounded reachability in priced probabilistic timed automata. In: Chen, J., Cooper, S.B. (eds.) TAMC 2009. LNCS, vol. 5532, pp. 128–137. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02017-9_16
Giro, S., D’Argenio, P.R., Ferrer Fioriti, L.M.: Partial order reduction for probabilistic systems: a revision for distributed schedulers. In: Bravetti, M., Zavattaro, G. (eds.) CONCUR 2009. LNCS, vol. 5710, pp. 338–353. Springer, Heidelberg (2009). doi:10.1007/978-3-642-04081-8_23
Haase, C., Kiefer, S.: The odds of staying on budget. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 234–246. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47666-6_19
Haddad, S., Monmege, B.: Reachability in MDPs: refining convergence of value iteration. In: Ouaknine, J., Potapov, I., Worrell, J. (eds.) RP 2014. LNCS, vol. 8762, pp. 125–137. Springer, Heidelberg (2014). doi:10.1007/978-3-319-11439-2_10
Hahn, E.M., Hermanns, H., Zhang, L.: Probabilistic reachability for parametric Markov models. STTT 13(1), 3–19 (2011)
Hartmanns, A., Hermanns, H.: A Modest approach to checking probabilistic timed automata. In: QEST, pp. 187–196. IEEE Computer Society (2009)
Hartmanns, A., Hermanns, H.: The Modest Toolset: an integrated environment for quantitative modelling and verification. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 593–598. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54862-8_51
Hartmanns, A., Hermanns, H.: Explicit model checking of very large MDP using partitioning and secondary storage. In: Finkbeiner, B., Pu, G., Zhang, L. (eds.) ATVA 2015. LNCS, vol. 9364, pp. 131–147. Springer, Heidelberg (2015). doi:10.1007/978-3-319-24953-7_10
Hashemi, V., Hermanns, H., Song, L.: Reward-bounded reachability probability for uncertain weighted MDPs. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 351–371. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49122-5_17
Hatefi, H., Braitling, B., Wimmer, R., Fioriti, L.M.F., Hermanns, H., Becker, B.: Cost vs. time in stochastic games and Markov automata. In: Li, X., Liu, Z., Yi, W. (eds.) SETTA 2015. LNCS, vol. 9409, pp. 19–34. Springer, Heidelberg (2015). doi:10.1007/978-3-319-25942-0_2
Klein, J., Baier, C., Chrszon, P., Daum, M., Dubslaff, C., Klüppelholz, S., Märcker, S., Müller, D.: Advances in symbolic probabilistic model checking with PRISM. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 349–366. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49674-9_20
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_47
Kwiatkowska, M.Z., Norman, G., Parker, D.: The PRISM benchmark suite. In: QEST, pp. 203–204. IEEE Computer Society (2012)
Kwiatkowska, M.Z., Norman, G., Parker, D., Sproston, J.: Performance analysis of probabilistic timed automata using digital clocks. FMSD 29(1), 33–78 (2006)
Randour, M., Raskin, J.-F., Sankur, O.: Percentile queries in multi-dimensional Markov decision processes. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 123–139. Springer, Heidelberg (2015). doi:10.1007/978-3-319-21690-4_8
Ummels, M., Baier, C.: Computing quantiles in Markov reward models. In: Pfenning, F. (ed.) FoSSaCS 2013. LNCS, vol. 7794, pp. 353–368. Springer, Heidelberg (2013). doi:10.1007/978-3-642-37075-5_23
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Hahn, E.M., Hartmanns, A. (2016). A Comparison of Time- and Reward-Bounded Probabilistic Model Checking Techniques. In: Fränzle, M., Kapur, D., Zhan, N. (eds) Dependable Software Engineering: Theories, Tools, and Applications. SETTA 2016. Lecture Notes in Computer Science(), vol 9984. Springer, Cham. https://doi.org/10.1007/978-3-319-47677-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-47677-3_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47676-6
Online ISBN: 978-3-319-47677-3
eBook Packages: Computer ScienceComputer Science (R0)







 is the extremal probability of eventually reaching a state in F.
is the extremal probability of eventually reaching a state in F. is the extremal probability of reaching a state in F via at most
is the extremal probability of reaching a state in F via at most 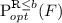 is the extremal probability of reaching a state in F with accumulated reward at most
is the extremal probability of reaching a state in F with accumulated reward at most 



