Abstract
We propose a way of reasoning about minimal and maximal values of the weights of transitions in a weighted transition system (WTS). This perspective induces a notion of bisimulation that is coarser than the classic bisimulation: it relates states that exhibit transitions to bisimulation classes with the weights within the same boundaries. We propose a customized modal logic that expresses these numeric boundaries for transition weights by means of particular modalities. We prove that our logic is invariant under the proposed notion of bisimulation. We show that the logic enjoys the finite model property which allows us to prove the decidability of satisfiability and provide an algorithm for satisfiability checking. Last but not least, we identify a complete axiomatization for this logic, thus solving a long-standing open problem in this field. All our results are proven for a class of WTSs without the image-finiteness restriction, a fact that makes this development general and robust.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Weighted transition systems (WTSs) are used to model concurrent and distributed systems in the case where some resources are involved, such as time, bandwidth, fuel, or energy consumption. Recently, the concept of a cyber-physical system (CPS), which considers the integration of computation and the physical world has become relevant in modeling various real-life situations. In these models, sensor feedback affects computation, and through machinery, computation can further affect physical processes. The quantitative nature of weighted transition systems is well-suited for the quantifiable inputs and sensor measurements of CPSs, but their rigidity makes them less well-suited for the uncertainty inherent in CPSs. In practice, there is often some uncertainty attached to the resource cost, whereas weights in a WTS are precise. Thus, the model may be too restrictive and unable to capture the uncertainties inherent in the domain that is being modeled.
In this paper, we attempt to remedy this shortcoming by introducing a modal logic for WTSs that allows for approximate reasoning by speaking about upper and lower bounds for the weights of the transitions. The logic has two types of modal operators that reason about the minimal and maximal weights on transitions, respectively. This allows reasoning about models where the quantitative information may be imprecise (e.g. due to imprecisions introduced when gathering real data), but where we can establish a lower and upper bound for transitions.
In order to provide the semantics for this logic, we use the set of possible transition weights from one state to a set of states as an abstraction of the actual transition weights. The logic is expressive enough to characterize WTSs up to a relaxed notion of weighted bisimilarity, where the classical conditions are replaced with conditions requiring that the minimal and maximal weights on transitions are matched. This logical characterization works for a class of WTSs that is strictly larger than the class of image-finite WTSs.
Our main contribution is a complete axiomatization of our logic, showing that any validity in this logic can be proved as a theorem from the axiomatic system. This solves a long-standing open problem in the field of weighted systems. Completeness allows us to transform any validity checking problem into a theorem proving one that can be solved automatically by modern theorem provers, thus bridging the gap to the theorem proving community. The completeness proof adapts the classical filtration method, which allows one to construct a (canonical) model using maximal consistent sets of formulae. The main difficulty of adapting this method to our setting is that we must establish both lower and upper bounds for the transitions in this model.
To achieve this result, we firstly demonstrate that our logic enjoys the finite model property. This property allows us not only to achieve the completeness proof, but also to address the problem of decidability of satisfiability. This is our second significant contribution in this paper: we propose a decision procedure for determining the satisfiability of formulae in our logic. This decision procedure makes use of the finite model property to automatically generate a finite model for any satisfiable formula.
Related Work. Several logics have been proposed in the past to express properties of quantified (weighted, probabilistic or stochastic) systems [5, 6, 12, 15, 17]. They typically use modalities indexed with real numbers to express properties such as “\(\varphi \) holds with at least probability b”, “we can reach a state satisfying \(\varphi \) with a cost at least r”, etc. While our logical syntax resemble these, our semantics is different in the sense that we argue not about one value (a probability or a cost), but about a compact interval of possible costs. For instance, in the aforementioned logics we have a validity of type \(\vdash \lnot L_r\phi \rightarrow M_r\phi \) saying that the value of the transition from the current state to \(\phi \) is either at least r or at most r; on the other hand, in our logic the formula \(\lnot L_r\phi \wedge \lnot M_r\phi \) might have a model since \(L_r\phi \) and \(M_r\phi \) express the fact that the lower cost of a transition to \(\phi \) is at least r and the highest cost is at most r respectively.
However, our completeness proof uses a technique similar to the one used for weighted modal logic [13] and Markovian logic [12, 16]. It is however different from these related constructions since our axiomatization is finitary, while the aforementioned ones require infinitary proof rules. Our axiomatic systems are related to the ones mentioned above and the mathematical structures revealed by this work are also similar to the related ones. This suggest a natural extension towards a Stone duality type of result on the line of [11], which we will consider in a future work.
Satisfiability results have been given for some related logics too, such as weighted modal logics [14] and probabilistic versions of CTL and the \(\mu \)-calculus [4]. However, the satisfiability problem is known to be undecidable for other related logics, in particular timed logics such as TCTL [1] and timed modal logic [8]. This fact suggests our logic as an interesting one which, despite its expressivity, remains decidable.
Our approach of considering upper and lower bounds is related to interval-based formalisms such as interval Markov chains (IMCs) [9] and interval weighted modal transition systems (WMTSs) [10]. Much like our approach, IMCs consider upper and lower bounds on transitions in the probabilistic case. WMTSs add intervals of weights to individual transitions of modal transition systems, in which there can be both may- and must-transitions. A main focus of the work both on IMCs and WMTSs have been a process of refinement, making the intervals progressively smaller until an implementation is obtained. However, none of these works have explored the logical perspective up to the level of axiomatization or satisfiability results, which is the focus of our paper.
2 Model
The models addressed in this paper are weighted transition systems, in which transitions are labeled with numbers to specify the cost of the corresponding transition. In order to specify and reason about properties regarding imprecision, such as “the maximum cost of going to a safe state is 10” and “the minimum cost of going to a halting state is 5”, we will abstract away the individual transitions and only consider the minimum and maximum costs from a state to another. We will do this by constructing for any two states the set of weights that are allowed from one to the other.
First we recap the definition of a weighted transition system. A WTS is formally defined as follows:
Definition 1
A weighted transition system (WTS) is a tuple \(\mathcal {M} = (S, \rightarrow , \ell )\), where
-
S is a non-empty set of states,
-
 is the transition relation, and
is the transition relation, and -
\(\ell : S \rightarrow 2^{\mathcal {AP}}\) is a labeling function mapping to each state a set of atomic propositions.
Note that we impose no restrictions on the state space S; it can be uncountable.
Consider now a WTS as in Fig. 1a. If this is a CPS, then the weights may have been obtained by measurements, simulations, or educated guesses, which may be imprecise. However, it may be that we can establish 1 as a lower bound and 10 as an upper bound on the actual weight. We could then address this problem by making more measurements and adding the results as weights on transitions, as in Fig. 1b but as long as we only introduce finitely many new transitions, there will still be some imprecision. Instead, we could add infinitely many transitions, for example one for each real or rational weight that lies between 1 and 10, as in Fig. 1c. However, then our WTS is no longer image-finite, so it no longer satisfies the Hennessy-Milner theorem [7].
In this paper, we will address this problem by abstracting away the individual transitions, and instead consider the set of weights between a state and a set of states.
Definition 2
For arbitrary WTS \(\mathcal {M} = (S,\rightarrow ,\ell )\) the function  is defined for any state \(s \in S\) and set of states \(T \subseteq S\) as
is defined for any state \(s \in S\) and set of states \(T \subseteq S\) as

Thus \(\theta _{\mathcal {M}}\left( s\right) \left( T\right) \) is the set of all possible weights of going from s to a state in T. We will sometimes refer to \(\theta \left( s\right) \left( T\right) \) as the image from s to T or simply as an image set.
Next, we introduce the notion of an image-compact WTS, which imposes a requirement on the image sets. This notion is very closely related to that of compactly branching introduced by van Breugel [3].
Definition 3
Let \(\mathcal {M} = (S,\rightarrow ,\ell )\) be a WTS. We say that \(\mathcal {M}\) is image-compact if for any \(s \in S\) and \(T \subseteq S\), \(\theta _{\mathcal {M}}\left( s\right) \left( T\right) \) is a compact set, i.e. a closed and bounded set.
Intuitively, one can think of a WTS being image-compact if each state can not take transitions with arbitrarily large weights and whenever a state can take transitions with weights arbitrarily close to some real number x it can also take a transition with exactly the weight x. We will drop the subscript \(\mathcal {M}\) from \(\theta \) unless we wish to differentiate between the image sets of two different WTSs. For the bisimulation invariance theorem that we will discuss later, it will be necessary to restrict ourselves to only considering image-compact WTSs. However, this will be the only place in the paper where this restriction is needed.
Consider a state s that can take a transition with weight \(\frac{1}{2^i}\) for any  to some state in a set T. We then have
to some state in a set T. We then have  which is clearly not a closed set, since \(\frac{1}{2^i} \xrightarrow {i \rightarrow \infty } 0\) and \(0 \not \in \theta \left( s\right) \left( T\right) \), hence it is non-compact. Consider now a state \(s'\) that has the same outgoing transitions as s except that also \(s' \xrightarrow {0} t\) for some \(t \in T\). We then have
which is clearly not a closed set, since \(\frac{1}{2^i} \xrightarrow {i \rightarrow \infty } 0\) and \(0 \not \in \theta \left( s\right) \left( T\right) \), hence it is non-compact. Consider now a state \(s'\) that has the same outgoing transitions as s except that also \(s' \xrightarrow {0} t\) for some \(t \in T\). We then have  which is a closed and bounded set, hence it is compact.
which is a closed and bounded set, hence it is compact.
Note that any image-finite WTS is also image-compact, since any finite set is compact. However, an image-compact WTS is not always image-finite. In the rest of the paper, we will use the notation \(\theta ^{-} \left( s\right) \left( T\right) = \inf \theta \left( s\right) \left( T\right) \) and \(\theta ^{+} \left( s\right) \left( T\right) = \sup \theta \left( s\right) \left( T\right) \) with the convention that \(\inf \emptyset = - \infty \) and \(\sup \emptyset = \infty \). Note that this convention is the opposite of the one usually adopted.
Example 4
Figure 2 shows a simple model of a robot vacuum cleaner that can be in a waiting state, a cleaning state, or a charging state. This is an example of a cyber-physical system where the costs of transitions are necessarily imprecise. The time it takes to recharge the batteries depends on the condition of the batteries as well as that of the charger; the time it takes to clean the room depends on how dirty the room is, and how free the floor is from obstacles; and the time it takes to reach the charger depends on where in the room the robot is when it needs to be recharged. By constructing the image sets, we can abstract away from the individual transitions. For example, we have \(\theta \left( s_2\right) \left( \{s_1\}\right) = \{5,10,15\}\), so \(\theta ^{-} \left( s_2\right) \left( \{s_1\}\right) = 5\) and \(\theta ^{+} \left( s_2\right) \left( \{s_1\}\right) = 15\).
We will now establish some useful properties of image sets. We first show that the transition function is monotonic with respect to set inclusion, meaning that if \(T_1\) is a subset of \(T_2\) then, the image from any state s to \(T_1\) is also a subset of the image from s to \(T_2\).
Lemma 5
(Monotonicity of \(\theta \) ). Let \(\mathcal {M} = (S,\rightarrow ,\ell )\) be a WTS and let \(T_1\) and \(T_2\) be subsets of S. If \(T_1 \subseteq T_2\), then \(\theta \left( s\right) \left( T_1\right) \subseteq \theta \left( s\right) \left( T_2\right) \).
Next, we show that union and intersection over image sets distribute as usual.
Lemma 6
Let \(\mathcal {M} = (S,\rightarrow ,\ell )\) be a WTS. For any \(s \in S\) and \(T_1,T_2 \subseteq S\), it holds that
-
1.
\(\theta \left( s\right) \left( T_1 \cup T_2\right) = \theta \left( s\right) \left( T_1\right) \cup \theta \left( s\right) \left( T_2\right) \) and
-
2.
\(\theta \left( s\right) \left( T_1 \cap T_2\right) = \theta \left( s\right) \left( T_1\right) \cap \theta \left( s\right) \left( T_2\right) \).
As usual we would like some way of relating model states with equivalent behavior. To this end we define the notion of a bisimulation relation. The classical notion of a bisimulation relation for weighted transition systems [2], which we term weighted bisimulation, is defined as follows.
Definition 7
Given a WTS \(\mathcal {M} = (S, \rightarrow , \ell )\), an equivalence relation \(\mathcal {R} \subseteq S \times S\) on S is called a weighted bisimulation relation iff for all \(s,t \in S\), \(s \mathcal {R} t\) implies
-
(Atomic harmony) \(\ell (s) = \ell (t)\),
-
(Zig) if \(s \xrightarrow {r} s'\) then there exists \(t' \in S\) such that \(t \xrightarrow {r} t'\) and \(s' \mathcal {R} t'\), and
-
(Zag) if \(t \xrightarrow {r} t'\) then there exists \(s' \in S\) such that \(s \xrightarrow {r} s'\) and \(s' \mathcal {R} t'\).
We say that \(s,t \in S\) are weighted bisimilar, written \(s \sim _W t\), iff there exists a weighted bisimulation relation \(\mathcal {R}\) such that \(s \mathcal {R} t\). Weighted bisimilarity, \(\sim _W\), is the largest weighted bisimulation relation. Note that we could replace the zig-zag conditions by the condition that \(\theta \left( s\right) \left( T\right) = \theta \left( t\right) \left( T\right) \) for all \(\mathcal {R}\)-equivalence classes \(T \subseteq S\).
Since it is our goal to abstract away from the exact weights on the transitions, the bisimulation that we will now introduce does not impose the classical zig-zag conditions [2] of a bisimulation relation, but instead require that bounds be matched for any bisimulation class.
Definition 8
Given a WTS \(\mathcal {M} = (S, \rightarrow , \ell )\), an equivalence relation \(\mathcal {R} \subseteq S \times S\) on S is called a generalized weighted bisimulation relation iff for all \(s,t \in S\), \(s \mathcal {R} t\) implies
-
(Atomic harmony) \(\ell (s) = \ell (t)\),
-
(Lower bound) \(\theta ^{-} \left( s\right) \left( T\right) = \theta ^{-} \left( t\right) \left( T\right) \), and
-
(Upper bound) \(\theta ^{+} \left( s\right) \left( T\right) = \theta ^{+} \left( t\right) \left( T\right) \)
for any \(\mathcal {R}\)-equivalence class \(T \subseteq S\).
Given \(s,t \in S\) we say that s and t are generalized weighted bisimilar, written \(s \sim t\), iff there exists a generalized weighted bisimulation relation \(\mathcal {R}\) such that \(s \mathcal {R} t\). Generalized weighted bisimilarity, \(\sim \), is the largest generalized weighted bisimulation relation.
In what follows, we will use bisimulation to mean generalized weighted bisimulation and bisimilarity to mean generalized weighted bisimilarity. We now show the relationship between \(\sim \) and \(\sim _W\).
Example 9
Consider the WTS depicted in Fig. 3. It is easy to see that \(\{s',t'\}\) is a \(\sim \)-equivalence class, and in fact it is the only \(\sim \)-equivalence class with ingoing transitions. Since \(\theta ^{-} \left( s\right) \left( \{s',t'\}\right) = \theta ^{-} \left( t\right) \left( \{s',t'\}\right) = 1\) and \(\theta ^{+} \left( s\right) \left( \{s',t'\}\right) = \theta ^{+} \left( t\right) \left( \{s',t'\}\right) = 3\) we must have \(s \sim t\), but because \(s \xrightarrow {2} s'\) and  it cannot be the case that \(s \sim _W t\).
it cannot be the case that \(s \sim _W t\).
Theorem 10
Generalized weighted bisimilarity is coarser than weighted bisimilarity, i.e.
This result is not surprising, as our bisimulation relation only looks at the extremes of the transition weights, whereas weighted bisimulation looks at all of the transition weights.
3 Logic
In this section we introduce a modal logic. Our aim is that our logic should be able to capture the notion of bisimilar states as presented in the previous section, and as such it must be able to reason about the lower and upper bounds on transition weights.
Definition 11
The formulae of the logic \(\mathcal {L}\) are induced by the abstract syntax
where  is a non-negative rational number and \(p \in \mathcal {AP}\) is an atomic proposition.
is a non-negative rational number and \(p \in \mathcal {AP}\) is an atomic proposition.
\(L_r\) and \(M_r\) are modal operators. An illustration of how L and M are interpreted can be seen in Fig. 4. Intuitively, \(L_r \varphi \) means that the cost of transitions to where \(\varphi \) holds is at least r (see Fig. 4a), and \(M_r \varphi \) means that the the cost of transitions to where \(\varphi \) holds is at most r (see Fig. 4b).
We now give the precise semantics interpreted on WTSs.
Definition 12
Given a WTS \(\mathcal {M} = (S, \rightarrow , \ell )\), a state \(s \in S\) and a formula \(\varphi \in \mathcal {L}\), the satisfiability relation \(\,\models \,\) is defined inductively as:

where \(\left[ \!\left[ \right. \right. \varphi \left. \left. \right] \!\right] _{\mathcal {M}} = \left\{ s \in S \mid \mathcal {M},s \,\models \, \varphi \right\} \).
We will omit the subscript \({\mathcal {M}}\) from \(\left[ \!\left[ \right. \right. \varphi \left. \left. \right] \!\right] _{\mathcal {M}}\) whenever the model is clear from the context. If \(\mathcal {M},s \,\models \, \varphi \) we say that \(\mathcal {M}\) is a model of \(\varphi \). A formula is said to be satisfiable if it has at least one model. We say that \(\varphi \) is a validity and write \(\,\models \, \varphi \) if \(\lnot \varphi \) is not satisfiable. In addition to the operators defined by the syntax of \(\mathcal {L}\), we also have the derived operators such as \(\bot \), \(\rightarrow \), etc. defined in the usual way.
The formula \(L_0 \varphi \) has special significance in our logic, as this formula means that there exists some transition to where \(\varphi \) holds. In fact, it follows in a straightforward manner from the semantics that \(\mathcal {M}, s \,\models \, L_0 \varphi \) if and only if \(\theta \left( s\right) \left( \left[ \!\left[ \right. \right. \varphi \left. \left. \right] \!\right] \right) \ne \emptyset \).
Example 13
Consider again our model of a robot vacuum cleaner depicted in Fig. 2. Perhaps we want a guarantee that it takes no more than one time unit to go from a waiting state to a charging state. This can be expressed by the formula \(\mathtt{waiting} \rightarrow M_1\mathtt{charging}\), but since we know the only waiting state in our model is \(s_1\) this can be simplified to simply checking whether \(\mathcal {M},s_1 \,\models \, M_1\mathtt{charging}\). We thus have to check that \(\theta ^{+} \left( s_1\right) \left( \left[ \!\left[ \right. \right. \mathtt{charging} \left. \left. \right] \!\right] \right) \le 1\). We do this by constructing the image set \(\theta \left( s_1\right) \left( \left[ \!\left[ \right. \right. \mathtt{charging} \left. \left. \right] \!\right] \right) \). Since \(\left[ \!\left[ \right. \right. \mathtt{charging} \left. \left. \right] \!\right] = \{s_3\}\), we have \(\theta \left( s_1\right) \left( \{s_3\}\right) = \{1,2\}\). Hence \(\theta ^{+} \left( s_1\right) \left( \left[ \!\left[ \right. \right. \mathtt{charging} \left. \left. \right] \!\right] \right) = 2 \not \le 1\), so  .
.
Next we show that our logic \(\mathcal {L}\) is invariant under bisimulation, which is also known as the Hennessy-Milner property.
Theorem 14
(Bisimulation invariance). For any image-compact WTS \(\mathcal {M} = (S, \rightarrow , \ell )\) and states \(s,t \in S\) it holds that
The proof strategy follows a classical pattern: The left to right direction is shown by induction on \(\varphi \) for \(\varphi \in \mathcal {L}\). The right to left direction is shown by constructing a relation \(\mathcal {R}\) relating those states that satisfy the same formulae and showing that this relation is a bisimulation relation.
4 Metatheory
In this section we propose an axiomatization for our logic that we prove not only sound, but also complete with respect to the proposed semantics.
4.1 Axiomatic System
Let  . Then the deducibility relation \(\vdash \subseteq 2^{\mathcal {L}} \times \mathcal {L}\) is a classical conjunctive deducibility relation, and is defined as the smallest relation which satisfies the axioms of propositional logic in addition to the axioms given in Table 1. We will write \(\vdash \varphi \) to mean \(\emptyset \vdash \varphi \), and we say that a formula or a set of formulae is consistent if it can not derive \(\bot \).
. Then the deducibility relation \(\vdash \subseteq 2^{\mathcal {L}} \times \mathcal {L}\) is a classical conjunctive deducibility relation, and is defined as the smallest relation which satisfies the axioms of propositional logic in addition to the axioms given in Table 1. We will write \(\vdash \varphi \) to mean \(\emptyset \vdash \varphi \), and we say that a formula or a set of formulae is consistent if it can not derive \(\bot \).
Axiom A1 captures the notion that since \(\bot \) is never satisfied, we can never take a transition to where \(\bot \) holds. Axiom A2 says that if we know some value is the lower bound for going to where \(\varphi \) holds, then any lower value is also a lower bound for going to where \(\varphi \) holds. Axiom A2\('\) is the analogue for upper bounds. Axioms A3–A4 show how \(L_r\) and \(M_r\) distribute over conjunction and disjunction. The version of axiom A4 where \(L_r\) is replaced with \(M_r\) is also sound, but it can be proven from the other axioms. Axioms A5 and A5\('\) say that if it is not possible to take a transition to where \(\psi \) holds, then requiring that \(\psi \) also holds does not change the bounds. Axioms A6 and A7 show the relationship between \(L_r\) and \(M_r\). In particular, A6 ensures that all bounds are well-formed. Notice also that the contrapositive of axiom A2 and A7 together gives us that \(\lnot L_0 \varphi \) implies \(\lnot L_r \varphi \) and \(\lnot M_r \varphi \) for any  . The axioms R1 and R1\('\) give a sort of monotonicity for \(L_r\) and \(M_r\), and axiom R2 says that if \(\psi \) follows from \(\varphi \), then if it is possible to take a transition to where \(\varphi \) holds, it is also possible to take a transition to where \(\psi \) holds.
. The axioms R1 and R1\('\) give a sort of monotonicity for \(L_r\) and \(M_r\), and axiom R2 says that if \(\psi \) follows from \(\varphi \), then if it is possible to take a transition to where \(\varphi \) holds, it is also possible to take a transition to where \(\psi \) holds.
 .
.Theorem 15
(Soundness)
4.2 Finite Model Property and Completeness
With our axiomatization proven sound we are now ready to present our main results, namely that our logic has the finite model property and that our axiomatization is complete.
To show the finite model property we will adapt the classical filtration method to our setting. Starting from an arbitrary formula \(\rho \), we define a finite fragment of our logic, \(\mathcal {L}[\rho ]\), which we then use to construct a finite model for \(\rho \). The main difference from the classical filtration method is that we must find an upper and a lower bound for the transitions in the model. For an arbitrary formula \(\rho \in \mathcal {L}\) we define the following based on \(\rho \):
-
Let
 be the set of all rational numbers
be the set of all rational numbers  such that \(L_r\) or \(M_r\) appears in the syntax of \(\rho \).
such that \(L_r\) or \(M_r\) appears in the syntax of \(\rho \). -
Let \(\varSigma _{\rho }\) be the set of all atomic propositions \(p \in \mathcal {AP}\) such that p appears in the syntax of \(\rho \).
-
The granularity of \(\rho \), denoted as \(gr(\rho )\), is the least common denominator of all the elements in \(Q_{\rho }\).
-
The range of \(\rho \), denoted as \(R_{\rho }\), is defined as
$$R_{\rho } = {\left\{ \begin{array}{ll} \emptyset &{} \text{ if }\; Q_{\rho } = \emptyset \\ I_\rho \cup \{0\} &{} \text{ otherwise } , \end{array}\right. }$$where
 . Note that we need to add 0 to \(R_{\rho }\) whether or not \(\rho \) actually contains 0 in any of its modalities. This is because, as we have pointed out before, formulae involving \(L_0\) have special significance in our logic.
. Note that we need to add 0 to \(R_{\rho }\) whether or not \(\rho \) actually contains 0 in any of its modalities. This is because, as we have pointed out before, formulae involving \(L_0\) have special significance in our logic. -
The modal depth of \(\rho \), denoted as \(md(\rho )\), is defined inductively as:

Since all formulae are finite, the modal depth is always a non-negative integer.
The language of \(\rho \), denoted by \(\mathcal {L}[\rho ]\), is defined as
Because all formulae are finite, \(\mathcal {L}[\rho ]\) must also be finite (modulo logical equivalence), and as we shall see, it contains all the formulae that are necessary to construct a model for \(\rho \).
In order to define the model, we need the notion of filters and ultrafilters.
Definition 16
A non-empty subset F of \(\mathcal {L}[\rho ]\) is called a filter on \(\mathcal {L}[\rho ]\) iff
-
\(\bot \not \in F\),
-
\(\varphi \in F\) and \(\vdash \varphi \rightarrow \psi \) implies \(\psi \in F\), and
-
\(\varphi \in F\) and \(\psi \in F\) implies \(\varphi \wedge \psi \in F\).
Intuitively, one can think of a filter as a consistent set of formulae closed under conjunction and deduction.
Definition 17
A filter \(F \in \mathcal {F}\) is called an ultrafilter iff for all formulae \(\varphi \in \mathcal {L}\) either \(\varphi \in F\) or \(\lnot \varphi \in F\).
The ultrafilters on \(\mathcal {L}[\rho ]\) correspond to the maximal consistent sets of \(\mathcal {L}[\rho ]\). We let \(\mathcal {U}[\rho ]\) denote the set of all ultrafilters on \(\mathcal {L}[\rho ]\). Since \(\mathcal {L}[\rho ]\) is finite \(\mathcal {U}[\rho ]\) is also finite and consequently, any ultrafilter \(u \in \mathcal {U}[\rho ]\) must be a finite set of formulae. Hence the formula obtained by taking the conjunction over all the formulae of u tells us exactly what formulae u contains.
For any set of formulae \(\varPhi \subseteq \mathcal {L}[\rho ]\), the characteristic formula of \(\varPhi \), denoted  , is defined as
, is defined as  . Note that
. Note that  is a finite formula, and that if \(u \in \mathcal {U}[\rho ]\), then
is a finite formula, and that if \(u \in \mathcal {U}[\rho ]\), then  .
.
We will now construct a (finite) model, \(\mathcal {M}_{\rho }\), for \(\rho \). In order to define the transition relation \(\rightarrow _\rho \subseteq \mathcal {U}[\rho ] \times \mathbb {R}_{\ge 0} \times \mathcal {U}[\rho ]\), we consider any two ultrafilters \(u,v \in \mathcal {U}[\rho ]\) and define two functions \(L,M : \mathcal {U}[\rho ] \times \mathcal {U}[\rho ] \rightarrow 2^{R_{\rho }}\) as

The following lemma establishes a relationship between L and M, that we will need to define the transition relation. The lemma is a straightforward consequence of axiom A7.
Lemma 18
Given any ultrafilters \(u,v \in \mathcal {U}[\rho ]\), it can not be the case that \(L(u,v) = \emptyset \) and \(M(u,v) \ne \emptyset \).
We can now define the transition relation in terms of L(u, v) and M(u, v). In Fig. 5, we have illustrated the different cases that we must consider. For any of the arches in the figure, we have the following correspondence with \(L_r\) and \(M_r\).
-
If a number r on the real line is contained within the arch, then we have
 and
and 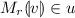 .
. -
If a number r on the real line is to the left of the arch, then we have
 and
and  .
. -
If a number r on the real line is to the right of the arch, then we have
 and
and  .
.
In case (a), we therefore have \(L(u,v) \ne \emptyset \) and \(M(u,v) \ne \emptyset \), so we have all the information we need to define the transition. In case (b) and (f), we have \(L(u,v) \ne \emptyset \) and \(M(u,v) = \emptyset \), so we have enough information to define the minimum transition, but we do not know what the maximum transition is. Note that we can not simply say that the maximum transition is \(\max Q_\rho \), because that would imply  , but we know that \(M(u,v) = \emptyset \). Hence we need to pick a number that is to the right of \(\max Q_\rho \) as the maximum. In case (d), we have both \(L(u,v) = \emptyset \) and \(M(u,v) = \emptyset \). This implies that
, but we know that \(M(u,v) = \emptyset \). Hence we need to pick a number that is to the right of \(\max Q_\rho \) as the maximum. In case (d), we have both \(L(u,v) = \emptyset \) and \(M(u,v) = \emptyset \). This implies that  , which means that there should be no transition from u to v. In case (c) and (e), we have \(L(u,v) = \emptyset \) and \(M(u,v) \ne \emptyset \), but according to Lemma 18 these cases can never occur.
, which means that there should be no transition from u to v. In case (c) and (e), we have \(L(u,v) = \emptyset \) and \(M(u,v) \ne \emptyset \), but according to Lemma 18 these cases can never occur.
When constructing a transition from u to v, we will only have information about what happens in the region \(R_\rho \) (which always includes 0). The line represents the non-negative real line and the arches represent the transitions that would be possible in a full model (i.e. one not restricted to \(\mathcal {L}[\rho ]\)). The dashed part of the arches represent the part of the transition that we do not have information about.
We therefore distinguish the following three cases in order to define the transition relation:
-
1.
If \(L(u,v) \ne \emptyset \) and \(M(u,v) \ne \emptyset \), then we add the two transitions \(u \xrightarrow {r_1} v\) and \(u \xrightarrow {r_2} v\) where \(r_1 = \max L(u,v)\) and \(r_2 = \min M(u,v)\).
-
2.
If \(L(u,v) \ne \emptyset \) and \(M(u,v) = \emptyset \), then we add the two transitions \(u \xrightarrow {r_1} v\) and \(u \xrightarrow {r_2} v\) where \(r_1 = \max L(u,v)\) and \(r_2 = \max Q_\rho + \frac{1}{gr(\rho )}\).
-
3.
If \(L(u,v) = \emptyset \) and \(M(u,v) = \emptyset \), then there is no transition from u to v.
Finally we define the labeling function \(\ell _\rho : \mathcal {U}[\rho ] \rightarrow 2^{\mathcal {AP}}\) for any \(u \in \mathcal {U}[\rho ]\) as \( \ell _\rho (u) = \{p \in \mathcal {AP} \mid p \in u\} \). We then have a model \(\mathcal {M}_\rho = (\mathcal {U}[\rho ], \rightarrow _\rho , \ell _\rho )\), and it is not difficult to prove that \(\mathcal {M}_\rho \) is a WTS. The following lemma shows that any formula \(\varphi \) in the language of \(\rho \) that is contained in some ultrafilter u must be satisfied by the state u in the finite model \(\mathcal {M}_{\rho }\).
Lemma 19
(Truth lemma). If \(\rho \in \mathcal {L}\) is a consistent formula, then for all \(\varphi \in \mathcal {L}[\rho ]\) and \(u \in \mathcal {U}[\rho ]\) we have \(\mathcal {M}_\rho ,u \,\models \, \varphi \) iff \(\varphi \in u\).
To prove the truth lemma, we first establish the following two theorems.
The proof then proceeds by induction on the structure of \(\varphi \). For the only-if-case of \(\varphi = L_r \psi \), it is easy to see that \(\left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \ne \emptyset \). We then partition the ultrafilters \(v \in \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \) by \(\left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] = E \cup N\) where \(E = \{ v \in \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \mid L(u,v) = \emptyset \}\) and \(N = \{ v \in \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \mid L(u,v) \ne \emptyset \}\). Because u is an ultrafilter, we have  , which we prove implies \(L_r \psi \in u\). For the if-case, it is straightforward to show by contradiction that \(\theta ^{-} \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) \ge r\), if we know that \(\theta \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) \ne \emptyset \). To show this, assume towards a contradiction that \(\theta \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) = \emptyset \). Then
, which we prove implies \(L_r \psi \in u\). For the if-case, it is straightforward to show by contradiction that \(\theta ^{-} \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) \ge r\), if we know that \(\theta \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) \ne \emptyset \). To show this, assume towards a contradiction that \(\theta \left( u\right) \left( \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \right) = \emptyset \). Then  for all \(v \in \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \), which we can enumerate as
for all \(v \in \left[ \!\left[ \right. \right. \psi \left. \left. \right] \!\right] \), which we can enumerate as  . This can then be shown to imply \(\lnot L_r \psi \in u\), which is a contradiction.
. This can then be shown to imply \(\lnot L_r \psi \in u\), which is a contradiction.
Having established the truth lemma, we can now show that any consistent formula is satisfied by some finite model.
Theorem 20
(Finite model property). For any consistent formula \(\varphi \in \mathcal {L}\), there exists a finite WTS \(\mathcal {M} = (S, \rightarrow , \ell )\) and a state \(s \in S\) such that \(\mathcal {M},s \,\models \, \varphi \).
We are now able to state our main result, namely that our axiomatization is complete.
Theorem 21
(Completeness). For any formula \(\varphi \in \mathcal {L}\), it holds that
We have thus established completeness for our logic. There is also a stronger notion of completeness, often called strong completeness, which asserts that \(\varPhi \,\models \, \varphi \) implies \(\varPhi \vdash \varphi \) for any set of formulae \(\varPhi \subseteq \mathcal {L}\). Completeness is a special case of strong completeness where \(\varPhi = \emptyset \). In the case of compact logics, strong completeness follows directly from completeness. However, our logic is non-compact.
Theorem 22
Our logic is non-compact, meaning that there exists an infinite set \(\varPhi \subseteq \mathcal {L}\) such that each finite subset of \(\varPhi \) admits a model, but \(\varPhi \) does not.
Proof
Consider the set \( \varPhi = \{L_q \varphi \mid q < r \} \cup \{\lnot L_r \varphi \} \). For any finite subset of \(\varPhi \), it is easy to construct a model. However, if \(\mathcal {M},s \,\models \, L_q \varphi \) for all \(q < r\) where  , then by the Archimedean property of the rationals, we also have \(\mathcal {M},s \,\models \, L_r \varphi \). Hence there can be no model for \(\varPhi \). \(\square \)
, then by the Archimedean property of the rationals, we also have \(\mathcal {M},s \,\models \, L_r \varphi \). Hence there can be no model for \(\varPhi \). \(\square \)
5 Satisfiability
The finite model property gives us a way of deciding in general whether there exists a WTS and a state in that WTS that satisfies a given formula. We do so by constructing a model \(\mathcal {M}_{\rho }\) such that if \(\rho \) is satisfiable there exists a state \(\varGamma \) in \(\mathcal {M}_{\rho }\) such that \(\mathcal {M}_{\rho }, \varGamma \,\models \, \rho \). The model construction closely mimics the finite model construction in Sect. 4.2. We will not go into the details of the construction here, but instead point out where the construction differs from that in Sect. 4.2.
Given an arbitrary formula \(\rho \in \mathcal {L}\), we construct the language of \(\rho \), \(\mathcal {L}[\rho ]\), in the same way as we did in Sect. 4.2. In this section we will not use ultrafilters as states in our model, but rather their semantic counterpart which we term maximal sets of formulae.
Definition 23
We say that a set \(\varGamma \subseteq \mathcal {L}[\rho ]\) of formulae is propositionally maximal if it satisfies the following where \(\varphi , \psi \in \mathcal {L}[\rho ]\):
-
(P1): \(\forall \varphi \in \mathcal {L}[\rho ].\; \varphi \in \varGamma \;\text{ iff }\; \lnot \varphi \not \in \varGamma \)
-
(P2): \(\varphi \wedge \psi \in \varGamma \) implies \(\varphi \in \varGamma \) and \(\psi \in \varGamma \)
-
(P3): \(\varphi \vee \psi \in \varGamma \) implies \(\varphi \in \varGamma \) or \(\psi \in \varGamma \).
In addition to the conditions for propositional maximality listed in Definition 23, we also have another notion of maximality that we term quantitative maximality.
Definition 24
We say that a set \(\varGamma \subseteq \mathcal {L}[\rho ]\) of formulae is quantitatively maximal if it satisfies the following:
- (Q1)::
-
\(\lnot L_0 \bot \in \varGamma \)
- (Q2)::
-
\(L_{r+q} \varphi \in \varGamma \) implies \(L_r \varphi \in \varGamma \)
- (Q2\('\))::
-
\(M_r \varphi \in \varGamma \) implies \(M_{r+q} \varphi \in \varGamma \)
- (Q3)::
-
\(L_r \varphi \wedge L_q \psi \in \varGamma \) implies \(L_{\min \{r,q\}}(\varphi \vee \psi ) \in \varGamma \)
- (Q3\('\))::
-
\(M_r \varphi \wedge M_q \psi \in \varGamma \) implies \(M_{\max \{r,q\}}(\varphi \vee \psi ) \in \varGamma \)
- (Q4)::
-
\(L_r(\varphi \vee \psi ) \in \varGamma \) implies \(L_r \varphi \vee L_r \psi \in \varGamma \)
- (Q4\('\))::
-
\(M_r(\varphi \vee \psi ) \in \varGamma \) implies \(M_r \varphi \vee M_r \psi \in \varGamma \)
- (Q5)::
-
\(\lnot L_0 \psi \in \varGamma \) and \(L_r \varphi \in \varGamma \) implies \(L_r(\varphi \vee \psi ) \in \varGamma \)
- (Q5\('\))::
-
\(\lnot L_0 \psi \in \varGamma \) and \(M_r \varphi \in \varGamma \) implies \(M_r(\varphi \vee \psi ) \in \varGamma \)
- (Q6)::
-
\(L_{r+q} \varphi \in \varGamma \) implies \(\lnot M_r \varphi \in \varGamma \)
- (Q7)::
-
\(M_r \varphi \in \varGamma \) implies \(L_0 \varphi \in \varGamma \)
- (Q8)::
-
\(\varphi \rightarrow \psi \in \varGamma \) and \(((L_r \psi ) \wedge (L_0 \varphi )) \in \varGamma \) implies \(L_r \varphi \in \varGamma \)
- (Q8\('\))::
-
\(\varphi \rightarrow \psi \in \varGamma \) and \(((M_r \psi ) \wedge (L_0 \varphi )) \in \varGamma \) implies \(M_r \varphi \in \varGamma \)
- (Q9)::
-
\(\varphi \rightarrow \psi \in \varGamma \) and \(L_0 \varphi \in \varGamma \) implies \(L_0 \psi \in \varGamma \)
where \(\varphi ,\psi \in \mathcal {L}[\rho ]\) and \(r,q \in R_{\rho }\).
The conditions for quantitative maximality are semantic analogues of the axioms listed in Table 1. We will say that a set \(\varGamma \subseteq \mathcal {L}[\rho ]\) of formulae is maximal if it is both propositionally maximal and quantitatively maximal.
The transitions between states and their associated weights are derived in the same was as in Sect. 4.2. We can now formally define the WTS \(\mathcal {M}_{\rho }\).
Definition 25
Given a formula \(\rho \in \mathcal {L}\), we define the WTS \(\mathcal {M}_{\rho } = (S_{\rho }, \rightarrow _{\rho }, \ell _{\rho })\) as follows.
-
\(S_{\rho } = \left\{ \varGamma \in 2^{\mathcal {L}[\rho ]} \mid \varGamma \;\text{ is } \text{ maximal }\right\} \).
-
\(\rightarrow _{\rho } \subseteq S_{\rho } \times \mathbb {R}_{\ge 0} \times S_{\rho }\) is defined as: for any \(\varGamma , \varGamma ' \in S_{\rho }\), \(\varGamma \xrightarrow {x}_\rho \varGamma '\) if
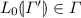 and either
and either-
1.
\(M(\varGamma , \varGamma ') = \emptyset \) and \(x \in \left\{ \max L(\varGamma , \varGamma '), \max Q_{\rho } + \frac{1}{gr(\rho )} \right\} \), or
-
2.
\(M(\varGamma , \varGamma ') \ne \emptyset \) and \(x \in \left\{ \max L(\varGamma , \varGamma '), \min M(\varGamma , \varGamma ') \right\} \).
-
1.
-
\(\ell _{\rho } : S_{\rho } \rightarrow 2^{\mathcal {AP}}\) is defined for any \(\varGamma \in S_{\varphi }\) as \(\ell _{\rho }(\varGamma ) = \left\{ p \in \mathcal {AP} \mid p \in \varGamma \right\} \).
The following lemma shows that any formula contained in a maximal set in the language of \(\rho \) has at least one model, namely the model \(\mathcal {M}_{\rho }\).
Lemma 26
For an arbitrary formula \(\varphi \in \mathcal {L}[\rho ]\) and maximal set of formulae \(\varGamma \in 2^{\mathcal {L}[\rho ]}\) it holds that \( \varphi \in \varGamma \quad \text { iff }\quad \mathcal {M}_{\rho }, \varGamma \,\models \, \varphi . \)
With the preceding result, we are now able to show that any formula in the language of \(\rho \) which has a model, must also be contained in a maximal set and vice versa.
Theorem 27
For any formula \(\rho \in \mathcal {L}\), the following two statements are equivalent:
-
1.
There exists a maximal set \(\varGamma \in 2^{\mathcal {L}[\rho ]}\) such that \(\rho \in \varGamma \).
-
2.
There exists a model \(\mathcal {M} = (S,\rightarrow ,\ell )\) and a state \(s \in S\) such that \(\mathcal {M},s \,\models \, \rho \).
A consequence of Theorem 27 is that if we can find a maximal set \(\varGamma \in 2^{\mathcal {L}[\rho ]}\) such that \(\rho \in \varGamma \), then \(\rho \) is satisfiable, and in particular it is satisfied by \(\varGamma \) in the WTS \(\mathcal {M}_{\rho }\). Also, if we can find no such maximal set, then \(\rho \) is not satisfiable. This gives a way of deciding satisfiability of a given formula. For any formula \(\varphi \in \mathcal {L}\), the following algorithm decides whether \(\varphi \) is satisfiable, and constructs a model if it is satisfiable.
Algorithm 28
-
1.
Construct the finite language \(\mathcal {L}[\varphi ]\).
-
2.
Construct the finite set \(2^{\mathcal {L}[\varphi ]}\) of all subsets of \(\mathcal {L}[\varphi ]\).
-
3.
Go through all elements \(\varGamma \in 2^{\mathcal {L}[\varphi ]}\) and check whether they satisfy the conditions for maximality. If they do not, remove them.
-
4.
Go through all the remaining maximal sets \(\varGamma \) and check whether \(\varphi \in \varGamma \). If there is no such \(\varGamma \), then \(\varphi \) is not satisfiable. If there is one such \(\varGamma \), then \(\varphi \) is satisfiable, and the finite model \(\mathcal {M}_\varphi \) is a model for \(\varphi \).
Example 29
Applying Algorithm 28 on the formula \(M_1 \mathtt{charging}\) yields a model \(\mathcal {M}_{M_1 \mathtt{charging}}\) with a state \(\varGamma \) such that \(\mathcal {M}_{M_1 \mathtt{charging}}, \varGamma \,\models \, M_1 \mathtt{charging}\), thus showing the satisfiability of the formula \(M_1 \mathtt{charging}\). We will not go through the construction here, but consider the WTS depicted in Fig. 6. It is easy to verify that \(\mathcal {M},s_1 \,\models \, M_1 \mathtt{charging}\).
6 Concluding Remarks
Our contributions in this paper have been to define a new bisimulation relation for weighted transition systems (WTSs), which relates those states that have similar behavior with respect to their minimum and maximum weights on transitions, as well as an accompanying modal logic to reason about the upper and lower bounds of weights on transitions. We have shown that this logic characterizes exactly those states that are bisimilar. This characterization holds for WTSs that we call image-compact, which is a weaker requirement than image-finiteness. Furthermore, we have provided a complete axiomatization of our logic, and we have shown that it enjoys the finite model property. Based on this finite model property, we have developed an algorithm which decides the satisfiability of a formula in our logic and constructs a finite model for the formula if it is satisfiable.
This work could be extended in different ways. Since our logic is non-compact, strong completeness does not follow directly from weak completeness, and hence it would be interesting to explore a strong-complete axiomatization of the proposed logic. Such an axiomatization would need additional, infinitary axioms. An example of such axioms would be \(\{L_q \varphi \mid q < r\} \vdash L_r \varphi \) and \(\{M_q \varphi \mid q < r\} \vdash M_r \varphi \), which are easily proven sound and describe the Archimedean property discussed in Theorem 22.
Although we have shown that our logic is expressive enough to capture bisimulation, it would also be of interest to extend our logic with a kind of fixed-point operator or standard temporal logic operators such as until in order to increase its expressivity, and hence its practical use. We envisage two ways in which such a logic could be given semantics: either by accumulating weights or by taking the maximum or minimum of weights. In the accumulating case in particular, one could also allow negative weights to model that the system gains resources.
References
Alur, R., Courcoubetis, C., Dill, D.: Model-checking in dense real-time. Inf. Comput. 104(1), 2–34 (1993)
Blackburn, P., van Benthem, J.F.A.K., Wolter, F.: Handbook of Modal Logic. Studies in Logic and Practical Reasoning. Elsevier Science, Amsterdam (2006)
Breugel, F.: Generalizing finiteness conditions of labelled transition systems. In: Abiteboul, S., Shamir, E. (eds.) ICALP 1994. LNCS, vol. 820, pp. 376–387. Springer, Heidelberg (1994). doi:10.1007/3-540-58201-0_83
Chakraborty, S., Katoen, J.P.: On the satisfiability of some simple probabilistic logics. In: LICS (2016 to appear)
Fagin, R., Halpern, J.Y.: Reasoning about knowledge and probability. J. ACM 41, 340 (1994)
Heifetz, A., Mongin, P.: Probability logic for type spaces. Games Econ. Behav. 35, 31 (2001)
Hennessy, M., Milner, R.: Algebraic laws for nondeterminism and concurrency. J. ACM 32, 137 (1985)
Jaziri, S., Larsen, K.G., Mardare, R., Xue, B.: Adequacy and complete axiomatization for timed modal logic. Electr. Notes Theor. Comput. Sci. 308, 183–210 (2014)
Jonsson, B., Larsen, K.G.: Specification and refinement of probabilistic processes. In: Proceedings of the Sixth Annual Symposium on Logic in Computer Science (LICS 1991) (1991)
Juhl, L., Larsen, K.G., Srba, J.: Modal transition systems with weight intervals. J. Log. Algebr. Program. 81, 408 (2012)
Kozen, D., Larsen, K.G., Mardare, R., Panangaden, P.: Stone duality for Markov processes. In: 2013 28th Annual IEEE/ACM Symposium on Logic in Computer Science (LICS), pp. 321–330, June 2013
Kozen, D., Mardare, R., Panangaden, P.: Strong completeness for Markovian logics. In: Chatterjee, K., Sgall, J. (eds.) MFCS 2013. LNCS, vol. 8087, pp. 655–666. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40313-2_58
Larsen, K.G., Mardare, R.: Complete proof systems for weighted modal logic. Theor. Comput. Sci. 546, 164 (2014)
Larsen, K.G., Mardare, R., Xue, B.: On decidability of recursive weighted logics. Soft Comput. 20, 1–18 (2016)
Larsen, K.G., Mardare, R., Panangaden, P.: Taking it to the limit: approximate reasoning for Markov processes. In: Rovan, B., Sassone, V., Widmayer, P. (eds.) MFCS 2012. LNCS, vol. 7464, pp. 681–692. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32589-2_59
Mardare, R., Cardelli, L., Larsen, K.G.: Continuous Markovian logics-axiomatization and quantified metatheory. Log. Meth. Comput. Sci. 8(4) (2012)
Zhou, C.: A complete deductive system for probability logic. J. Log. Comput. 19, 1427 (2009)
Acknowledgements
The authors would like to thank the anonymous reviewers for their useful comments and suggestions. This research was supported by the Danish FTP project ASAP: “Approximate Stochastic Analysis of Processes”, the ERC Advanced Grant LASSO: “Learning, Analysis, Synthesis and Optimization of Cyber Physical Systems” as well as the Sino-Danish Basic Research Center IDEA4CPS.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Hansen, M., Larsen, K.G., Mardare, R., Pedersen, M.R., Xue, B. (2016). A Complete Approximation Theory for Weighted Transition Systems. In: Fränzle, M., Kapur, D., Zhan, N. (eds) Dependable Software Engineering: Theories, Tools, and Applications. SETTA 2016. Lecture Notes in Computer Science(), vol 9984. Springer, Cham. https://doi.org/10.1007/978-3-319-47677-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-47677-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47676-6
Online ISBN: 978-3-319-47677-3
eBook Packages: Computer ScienceComputer Science (R0)





 is the transition relation, and
is the transition relation, and



 be the set of all rational numbers
be the set of all rational numbers  such that
such that  . Note that we need to add 0 to
. Note that we need to add 0 to 
 and
and 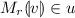 .
. and
and  .
. and
and  .
.
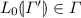 and either
and either