Keywords

1 Introduction

The analysis of the time series consists of a (usually mathematical) description of the movements that compose it, then building models using movements to explain the structure and predict the evolution of a variable over time [3, 4]. The fundamental procedure for the analysis of a time series is described below

  1. 1.

    Collecting data of the time series, trying to ensure that these data are reliable.

  2. 2.

    Representing the time series qualitatively noting the presence of long-term trends, cyclical variations, and seasonal variations.

  3. 3.

    Plot a graph or trend line length and obtain the appropriate trend values using the method of least squares.

  4. 4.

    When seasonal variations are present, obtain these and adjust the data rate to these seasonal variations (i.e., data seasonally).

  5. 5.

    Adjust the seasonally adjusted trend.

  6. 6.

    Represent the cyclical variations obtained in step 5.

  7. 7.

    Combining the results of steps 1–6 and any other useful information to make a prediction (if desired) and if possible discuss the sources of error and their magnitude.

Therefore the above ideas can assist in the important problem of prediction in the time series. Along with common sense, experience, skill and judgment of the researcher, such mathematical analysis can, however, be of value for predicting the short, medium, and long term.

As related work we can mention: Type-1 Fuzzy Neural Network (T1FNN) [15, 18, 19, 29] and Interval Type-2 Fuzzy Neural Network (IT2FNN) [13, 23–25, 44]; type-1 [1, 8, 16, 33, 45] and type-2 [11, 35, 41, 47] fuzzy evolutionary systems are typical hybrid systems in soft computing. These systems combine T1FLS generalized reasoning methods [18, 28, 34, 42, 43, 48, 51] and IT2FLS [21, 30, 46] with neural networks learning capabilities [12, 14, 18, 37] and evolutionary algorithms [2, 5, 9–11, 29, 35–37, 41] respectively.

This paper reports the results of the simulations of three main architectures of IT2FNN (IT2FNN-1, IT2FNN-2 and IT2FNN-3) for integrating a first-order TSK IT2FIS, with real consequents (A2C0) and interval consequents (A2C1), are used. Integration strategies to process elements of TSK IT2FIS are analyzed for each architecture (fuzzification, knowledge base, type reduction, and defuzzification). Ensemble architectures have three choices IT2FNN-1, IT2FNN-2, and IT2FNN-3. Therefore the output of the Ensemble architectures are integrated with a fuzzy system and the MFs of the fuzzy systems are optimized with PSO. The Mackey-Glass time series is used to test the performance of the proposed architecture. Prediction errors are evaluated by the following metrics: root mean square error (RMSE), mean square error (MSE), and mean absolute error (MAE).

In the next section, we describe the background and basic concepts of the Mackey-Glass time series, Interval type-2 fuzzy systems, Interval Type-2 Fuzzy Neural-Networks, and Particle Swarm Optimization. Section 3 presents the general proposed architecture. Section 4 presents the simulations and the results. Section 5 offers the conclusions.

2 Background and Basic Concepts

This section presents the basic concepts that describe the background in time series prediction and basic concepts of the Mackey-Glass time series, Interval type-2 fuzzy systems, Interval Type-2 Fuzzy Neural-Networks, and Particle Swarm Optimization.

2.1 Mackey-Glass Time Series

The problem of predicting future values of a time series has been a point of reference for many researchers. The aim is to use the values of the time series known at a point x = t to predict the value of the series at some future point x = t + P. The standard method for this type of prediction is to create a mapping from D points of a Δ spaced time series, is (x (t − (D − 1) Δ) … x (t − Δ), x (t)), to a predicted future value x (t + P). To allow a comparison with previous results in this work [11, 19, 29, 41] the values D = 4 and Δ = P = 6 were used.

Chaotic time series data used is defined by the Mackey-Glass [26, 27] time series, whose differential equation is given by Eq. (1)

$$x(t) = \frac{0.2x(t - \tau )}{{1 - x^{10} (t - \tau )}} - 0.1x(t - \tau )$$
(1)

For obtaining the values of the time series at each point, we can apply the Runge–Kutta method [17] for the solution of Eq. (1). The integration step was set at 0.1, with initial condition x(0) = 1.2, τ = 17, x(t) is then obtained for 0 ≤ t ≤ 1200, (Fig. 1) (we assume x(t) = 0 for t < 0 in the integration).

Fig. 1
figure 1

The Mackey-Glass time series

Full size image

2.2 Interval Type-2 Fuzzy Systems

Type-2 fuzzy sets are used to model uncertainty and imprecision; originally they were proposed by Zadeh [49, 50] and they are essentially “fuzzy–fuzzy” sets in which the membership degrees are type-1 fuzzy sets (Fig. 2).

Fig. 2
figure 2

Basic structure of the interval type-2 fuzzy logic system

Full size image

The basic structure of a type-2 fuzzy system implements a nonlinear mapping of input to output space. This mapping is achieved through a set of type-2 if-then fuzzy rules, each of which describes the local behavior of the mapping.

The uncertainty is represented by a region called footprint of uncertainty (FOU). When \(\mu_{{\widetilde{A}}} (x,u) = 1,\,\forall \,u \in l_{x} \subseteq [0,1]\); we have an interval type-2 membership function [5, 7, 20, 31] (Fig. 3).

Fig. 3
figure 3

Interval type-2 membership function

Full size image

The uniform shading for the FOU represents the entire interval type-2 fuzzy set and it can be described in terms of an upper membership function \(\bar{\mu }_{{\widetilde{A}}} (x)\) and a lower membership function \({\underline{\mu}}_{{\widetilde{A}}} (x).\)

A fuzzy logic systems (FLS) described using at least one type-2 fuzzy set is called a type-2 FLS. Type-1 FLSs are unable to directly handle rule uncertainties, because they use type-1 fuzzy sets that are certain [6, 7, 46]. On the other hand, type-2 FLSs are very useful in circumstances where it is difficult to determine an exact certainty value, and there are measurement uncertainties.

2.3 Interval Type-2 Fuzzy Neural Networks (IT2FNN)

One way to build interval type-2 fuzzy neural networks (IT2FNN) is by fuzzifying a conventional neural network. Each part of a neural network (the activation function, the weights, and the inputs and outputs) can be fuzzified. A fuzzy neuron is basically similar to an artificial neuron, except that it has the ability to process fuzzy information.

The interval type-2 fuzzy neural network (IT2FNN) system is one kind of interval Takagi–Sugeno–Kang fuzzy inference system (IT2-TSK-FIS) inside neural network structure. An IT2FNN is proposed by Castro [6], with TSK reasoning and processing elements called interval type-2 fuzzy neurons (IT2FN) for defining antecedents, and interval type-1 fuzzy neurons (IT1FN) for defining the consequents of rules.

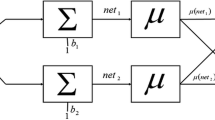
An IT2FN is composed by two adaptive nodes represented by squares, and two non-adaptive nodes represented by circles. Adaptive nodes have outputs that depend on their inputs, modifiable parameters, and transference function while non-adaptive, on the contrary, depend solely on their inputs, and their outputs represent lower \({\underline{\mu}}_{{\widetilde{A}}} (x)\) and upper \(\bar{\mu }_{{\widetilde{A}}} (x)\) membership functions (Fig. 4).

Fig. 4
figure 4

The MFs used for training the IT2FNN architecture

Full size image

The IT2FNN-1 architecture has five layers (Fig. 5), consists of adaptive nodes with an equivalent function to lower-upper membership in fuzzification layer (layer 1). Non-adaptive nodes in the rules layer (layer 2) interconnect with fuzzification layer (layer 1) in order to generate TSK IT2FIS rules antecedents. The adaptive nodes in consequent layer (layer 3) are connected to input layer (layer 0) to generate rules consequents. The non-adaptive nodes in type-reduction layer (layer 4) evaluate left-right values with KM algorithm [19–21]. The non-adaptive node in defuzzification layer (layer 5) average left-right values.

Fig. 5
figure 5

IT2FNN1 architecture

Full size image

The IT2FNN-2 architecture has six layers (Fig. 6 and uses IT2FN for fuzzifying inputs (layers 1–2). The non-adaptive nodes in the rules layer (layer 3) interconnect with lower-upper linguistic values layer (layer 2) to generate TSK IT2FIS rules antecedents. The non-adaptive nodes in the consequents layer (layer 4) are connected with the input layer (layer 0) to generate rule consequents. The non-adaptive nodes in type-reduction layer (layer 5) evaluate left-right values with KM algorithm. The non-adaptive node in defuzzification layer (layer 6) averages left-right values.

Fig. 6
figure 6

ITFNN2 architecture

Full size image

IT2FNN-3 architecture has seven layers (Fig. 7). Layer 1 has adaptive nodes for fuzzifying inputs; layer 2 has non-adaptive nodes with the interval fuzzy values. Layer 3 (rules) has non-adaptive nodes for generating firing strength of TSK IT2FIS rules. Layer 4, lower and upper values the rules firing strength are normalized. The adaptive nodes in layer 5 (consequent) are connected to layer 0 for generating the rules consequents. The non-adaptive nodes in layer 6 evaluate values from left-right interval. The non-adaptive node in layer 7 (defuzzification) evaluates average of interval left-right values.

Fig. 7
figure 7

IT2FNN3 architecture

Full size image

2.4 Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a metaheuristic search technique based on a population of particles (Fig. 8). The main idea of PSO comes from the social behavior of schools of fish and flocks of birds [22, 32]. In PSO, each particle moves in a D-dimensional space based on its own past experience and those of other particles. Each particle has a position and a velocity represented by the vectors \(x_{i} = \left( {x_{i1} ,x_{i2} , \ldots ,x_{iD} } \right)\) and \(V_{i} = \left( {v_{i1} ,v_{i2} , \ldots ,v_{iD} } \right)\) for the i-th particle. At each iteration, particles are compared with each other to find the best particle [32, 38]. Each particle records its best position as \(P_{i} = \left( {p_{i1} ,p_{i2} , \ldots ,p_{iD} } \right)\). The best position of all particles in the swarm is called the global best, and is represented as \(G = \left( {G_{1} ,G_{2} , \ldots ,G_{D} } \right)\). The velocity of each particle is given by Eq. (2).

$$V_{id} = wv_{id} + C_{1} \cdot {\text{rand}}_{1} \left( {} \right) \cdot (p{\text{best}}_{id} - x_{id} ) + C_{2} \cdot {\text{rand}}_{2} \left( {} \right) \ldots \cdot (g{\text{best}} - x_{id} )$$
(2)
Fig. 8
figure 8

Flowchart of the PSO algorithm

Full size image

In this equation, i = 1, 2, …, \(M,d\) = 1, 2, …,D, \(C_{1}\) and \(C_{2}\) are positive constants (known as acceleration constants), \({\text{rand}}_{1} ( )\) and \({\text{rand}}_{2} ( )\) are random numbers in [0,1], and w, introduced by Shi and Eberhart [39] is the inertia weight. The new position of the particle is determined by Eq. (3)

$$x_{id} = x_{id} + v_{id}$$
(3)

3 Problem Statement and Proposed Architecture

The general proposed architecture combines the ensemble of IT2FNN models and the use of fuzzy systems as response integrators using PSO for time series prediction (Fig. 9).

Fig. 9
figure 9

The general proposed architecture

Full size image

This architecture is divided into four sections, where the first phase represents the database to simulate in the Ensemble [40] of IT2FNN, which in this case is the historical data of the Mackey-Glass [26, 27] time series. From the Mackey-Glass time series we used 800 pairs of data points (Fig. 1), similar to [35, 36].

We predict x(t) from three past (delays) values of the time series, that is, x(t − 18), x(t − 12), and x(t − 6). Therefore the format of the training and checking data is

$$\left\lfloor {x(t - 18),x(t - 12),x(t - 6);x(t)} \right\rfloor$$
(4)

where t = 19–818 and x(t) is the desired prediction of the time series.

In the second phase, training (the first 400 pairs of data are used to train the IT2FNN architecture) and validation (the second 400 pairs of data are used to validate the ITFNN architecture) is performed sequentially in each IT2FNN, in this case we are dealing with a set of 3 IT2FNN (IT2FNN-1, IT2FNN-2, and IT2FNN-3) in the Ensemble. Therefore each IT2FNN architecture has three input variables \(\left( {x(t-18),\;x(t - 12),\;x(t - 6)} \right)\) and one output variable \((x(t))\) is the desired prediction.

In the fourth phase, we integrate the overall results of each Ensemble of IT2FNN which are (IT2FNN-1, IT2FNN-2, and IT2FNN-3) architecture, and such integration will be done by the fuzzy inference system (type-1 and interval type-2 fuzzy system) of Mamdani type; but each fuzzy integrators will be optimized with PSO of the MFs parameters. Finally the forecast output determined by the proposed architecture is obtained and it is compared with desired prediction.

3.1 Design of the Fuzzy Integrators

The design of the type-1 and interval type-2 fuzzy inference systems integrators are of Mamdani type and have three inputs (IT2FNN1, IT2FNN2, and IT2FNN3) and one output (Forecast), so each input is assigned two MFs with linguistic labels “Small and Large” and the output will be assigned three MFs with linguistic labels “OutIT2FNN1, Out IT2FNN2 and Out IT2FNN3” (Fig. 10) and have eight if-then rules. The design of the if-then rules for the fuzzy inference system depends on the number of membership functions used in each input variable using the system [e.g., our fuzzy inference system uses three input variables which each entry contains two membership functions, therefore the total number of possible combinations for the fuzzy rules is 8 (e.g., 2*2*2 = 8)], therefore we used eight fuzzy rules for the experiments (Fig. 11) because the performance is better and minimized the prediction error of the Mackey-Glass time series.

Fig. 10
figure 10

Structure of the type-1 FIS (a) and interval type-2 FIS (b) integrators

Full size image
Fig. 11
figure 11

If-then rules for the fuzzy integrators

Full size image

In the type-1 FIS integrators, we used different MFs (Gaussian, Generalized Bell, and Triangular) Fig. 12a and for the interval type-2 FIS integrators we used different MFs (igaussmtype2, igbelltype2, and itritype2) Fig. 12b [7] to observe the behavior of each of them and determine which one provides better forecast of the time series.

Fig. 12
figure 12

Type-1 MFs (a) and interval type-2 MFs (b) for the fuzzy integrators

Full size image

3.2 Design of the Representation for the Particle Swarm Optimization

The PSO is used to optimize the parameters values of the MFs in each of the type-1 and interval type-2 fuzzy integrators. The representation in PSO is of Real-Values and the particle size will depend on the number of MFs that are used in each design of the fuzzy integrators.

The objective function is defined to minimize the prediction error as follows in Eq. (5)

$$f(t) = \sqrt {\frac{{\sum\nolimits_{t = 1}^{n} {(a_{t} - p_{t} )^{2} } }}{n}}$$
(5)

where a, corresponds to the real data of the time series, p corresponds to the output of each fuzzy integrators, t is de sequence time series, and n is the number of data points of time series.

The general representation of the particles represents the utilized membership functions. The number of parameters varies according to the kind of membership function of the type-1 fuzzy system (e.g., two parameter are needed to represent a Gaussian MF’s are “sigma and mean”) Fig. 13a and interval type-2 fuzzy system (e.g., three parameter are needed to represent “igaussmtype2” MF’s are “sigma, mean1 and mean2”) Fig. 13b. Therefore the number of parameters that each fuzzy inference system integrator has depends of the MFs type assigned to each input and output variables.

Fig. 13
figure 13

Representation of the particles structure of the type-1 (a) and interval type (b) fuzzy integrators

Full size image

The parameters of particle swarm optimization used for optimizing the type-1 and interval type-2 fuzzy inference systems integrators are shown on Table 1.

Table 1 Parameters of PSO
Full size table

We performed experiments in time series prediction, specifically for the Mackey-Glass time series in ensembles of IT2FNN architectures using fuzzy integrators optimized with PSO.

4 Simulations Results

This section presents the results obtained through experiments on the architecture for the optimization of the fuzzy integrators in ensembles of IT2FNN architectures for time series prediction, which show the performance that was obtained from each experiment to simulate the Mackey-Glass time series.

The best errors were produced by the type-1 fuzzy integrator (using Generalized Bell MFs) with PSO are shown on Table 2. The RMSE is 0.035228102 and the average RMSE is 0.047356657, the MSE is 0.005989357 and the MAE is 0.056713089, respectively. The MFs optimized with PSO are presented in Fig. 14a, the forecasts in Fig. 14b, and the evolution errors in Fig. 14c are obtained for the proposed architecture.

Table 2 PSO results for the optimization of the fuzzy integrators
Full size table
Fig. 14
figure 14

Variables inputs/output MFs (a), forecast (b), and evolution errors of “65 iterations” (c), are generated for the optimized of the type-1 FIS integrator with PSO

Full size image

The best errors were produced by the interval type-2 fuzzy integrator (using igbelltype2 MFs) with PSO are shown on Table 2. The RMSE is 0.023648414 and the average RMSE is 0.024988012, the MSE is 0.00163873 and the MAE is 0.028366955 respectively. The MFs optimized with PSO are presented in Fig. 15a, the forecasts in Fig. 15b, and the evolution errors in Fig. 15c are obtained for the proposed architecture.

Fig. 15
figure 15

Variables inputs/output MFs (a), forecast (b), and evolution errors of “65 iterations” (c), are generated for the optimized of the interval type-2 FIS integrator with PSO

Full size image

5 Conclusion

Particle swarm optimization of the fuzzy integrators for time series prediction using ensembles of IT2FNN architecture was proposed in this paper.

The best result generated for the optimization the interval type-2 FIS (using igbelltype2 MFs) integrator is with a prediction error of 0.023648414 (98 %).

The best result generated for the optimization of type-1 FIS (using Generalized Bell MFs) integrator with a prediction error of 0.035228102 (97 %).

These results showed efficient results in the prediction error of the time series Mackey-Glass generated by proposed architecture.