A General Approach to the Linear Stability Analysis of Miscible Viscous Fingering in Porous Media

Abstract

We analyse the linear growth of the viscous fingering instability for miscible, non-reactive, neutral buoyant fluids using the non-modal analysis (NMA). The onset of instability is obscured due to the continually changing base state, and the normal mode analysis is not applicable to the non-autonomous linearized perturbed equations. Commonly used techniques such as frozen time method or amplification theory approach with random initial condition using transient amplifications yield substantially different results for the threshold of instability. We present the classical non-modal methods in the short-time limit using singular value decomposition of the propagator matrix. Using the non-modal approach we characterize the existence of a transition region between a domain exhibiting strong convection and a domain where initial perturbations are damped due to diffusion. Further, at the early times the algebraic growth of perturbations is possible which suggest that NMA could play an important role in describing the onset of instability in the physical phenomenon involving VF.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Flow of miscible fluids in a porous medium is found in a wide range of natural processes as well as industrial applications [5]. These displacement flows feature an interfacial instability that occurs when a less viscous fluid invades into the more viscous one. Finger like patterns are resulted at the interface, hence this is called viscous fingering (VF) instability. This hydrodynamic instability which is also known as Saffman–Taylor instability [14] has been a subject of many theoretical and experimental studies [3, 8, 10, 12] for many years. Stability analysis of VF has been performed extensively over the years [1, 5, 7, 11]. Traditionally, the modal analysis along with quasi-steady-state approximation (QSSA) has been used in different coordinate systems [7, 11]. Although, at the early times QSSA in a self-similar coordinate system successfully predicts the unconditional stability of perturbations, it fails to describe the early period dynamics of the disturbances [6]. Another approach which is more practical is the amplification theory (AT), in which the linear equations are solved as an initial value problem. However, this approach has a drawback of choosing the representative initial condition. In this article, using non-modal stability theory, we unify the frozen time method and AT to explore two important aspects of VF instability, namely the effect of non-normality of the governing non-autonomous linear operators and the optimal amplifications of the disturbances. The paper is organized as follows. In Sect. 2, the mathematical formulation of the physical model is presented. Section 3 describes the non-modal stability analysis and the numerical method to calculate the energy growth function G(t). In Sect. 4 we present the results and discussions. Finally, the conclusions are given in Sect. 5.

2 Mathematical Formulations

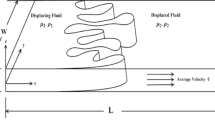
Consider a uniform rectilinear displacement of miscible fluids in a two-dimensional, homogeneous, porous medium with constant permeability [see Fig. 1]. The fluids are assumed to be incompressible, miscible, non-reactive, and neutrally buoyant and the dispersion is isotropic. The non-dimensional governing equations for the prescribed two-dimensional flow in a reference frame moving with velocity U are given by the following coupled nonlinear partial differential equations (PDEs) [5, 16]:

$$\displaystyle\begin{array}{rcl} \nabla \cdot \boldsymbol{ u} = 0,\ \nabla p = -\mu (c)(\boldsymbol{u} +\boldsymbol{ i}),\ \ \frac{\partial c} {\partial t} +\boldsymbol{ u} \cdot \nabla c = \nabla ^{2}c,& &{}\end{array}$$

(1)

where p is the dynamic pressure, $\boldsymbol{u} = (u,v)$ is the Darcy’s velocity, c is the concentration of the solvent, $\boldsymbol{i}$ is the unit vector along the x (downstream) direction, and μ(c) is the fluid viscosity which depends exponentially on the solute concentration, i.e., μ(c) = exp(Rc) [16]. Here R = ln(μ ₂∕μ ₁) is the log-mobility ratio, where μ ₁ and μ ₂ correspond to the viscosity of the less and more viscous fluid, respectively. The coupled PDEs (1) are provided with the following initial and boundary conditions in the moving frame of reference [5, 11]:

Fig. 1

Schematic of the flow configuration with coordinate system. Initially the interface is flat (dotted line) and then a wave like infinitesimal perturbation is applied

Initial conditions:

$$\displaystyle\begin{array}{rcl} \mathbf{u} = (0,0),\ \ \ c(x,y,t = 0) = \left \{\begin{array}{@{}l@{\quad }l@{}} 0,\quad &x \leq 0\\ 1,\quad &x> 0, \end{array} \right.\ \ \forall y.& &{}\end{array}$$

(2)

Boundary conditions:

$$\displaystyle\begin{array}{rcl} \mathbf{u} = (0,0),\ \ \ \ \ \ \ \ \ \frac{\partial c} {\partial x} = 0,\ \ \ \vert x\vert \rightarrow \infty,\mbox{ streamwise direction}& &{}\end{array}$$

(3)

$$\displaystyle\begin{array}{rcl} u\ \ \text{is arbitrary},\ \ \ \frac{\partial c} {\partial y} = 0 = \frac{\partial v} {\partial y},\ \ \ \forall x,\text{spanwise direction}& &{}\end{array}$$

(4)

The base state of the flow is assumed to be a pure diffusion of the concentration along the axial direction that can be written as

$$\displaystyle{ \boldsymbol{u}_{b} = (u_{b},v_{b}) =\boldsymbol{ 0},\;c_{b}(\xi ) = \frac{1} {2}\left [1 + \text{erf}\left ( \frac{\xi } {2}\right )\right ],\;\mu _{b} =\mu _{b}(\xi ), }$$

(5)

where $\text{erf}(z) = \frac{2} {\sqrt{\pi }}\int _{0}^{z}e^{-\eta ^{2} }\text{d}\eta$ is the error function and $\xi:= x/\sqrt{t}$ is the similarity variable transformation. Introducing the infinitesimal perturbations in terms of the Fourier modes of the form (u ^′, c ^′)(ξ, y, t) = (u ^′, c ^′)(ξ, t)e ^iky and using standard procedure of linear stability analysis along with central difference scheme to discretize the spatial variable, ξ, the nonlinear coupled PDEs (1) can be written as [6, 11]

$$\displaystyle{ \frac{\text{d}c^{{\prime}}} {\text{d}t} = \mathcal{A}(k,R,t)c^{{\prime}}, }$$

(6)

where k is the non-dimensional wave number and $\mathcal{A} = \mathcal{A}(k,R,t)$ is the stability matrix.

For such non-autonomous system [Eq. (6)], there are two distinct regions in the evolution of disturbances [15]. The first is the transient region, and the second is the asymptotic long time region. In mathematical sense, instability behaviors in the second region are determined by the eigenvalues of the stability matrix $\mathcal{A}$. In the first region, the transient growth may be quite substantial, such that the nonlinear region may be reached before the growth of eigenvalue mode. Thus, the eigenvalue approach is insufficient to study the stability analysis. For nonnormal and time independent matrices, $\mathcal{A}$, the stability analysis have explored by many researchers (see [15] and the references within). Recently, few works have discussed non-modal stability analysis (NMA) with unsteady base state flow [2, 4, 6, 13]. But in the case of VF, many aspects of stability matrix $\mathcal{A}(k,t)$ remained unexplored compared to its autonomous counterpart.

3 Transient Behaviors and Non-modal Analysis

In the framework of NMA, there are two major and broader aspects which are of ample interest, the responses to external excitations and the transient energy growth of initial conditions. Mathematically, the former can be studied from the structure of “ε-pseudospectra” [17] which is given by $\varLambda _{\epsilon }(\mathcal{A}) =\{ z \in \mathbb{C}\;:\;\sigma _{\text{min}}(z -\mathcal{A}) \leq \epsilon \}$, where $\sigma _{ \text{min}}(\mathcal{A})$ denotes the smallest singular value of $\mathcal{A}$, and 0 < ε ≪ 1. And the latter can be analysed from the energy growth function G(t) that identifies the optimal growth of energy at time t. In addition, it is often useful in hydrodynamic stability problem to know the initial growth rate of the energy growth function. This can be obtained from numerical abscissa of the stability matrix $\mathcal{A}$ [17]. Following [6, 13] G(t) can be described as

$$\displaystyle{ G(t) = G(t,k,R):=\max _{c_{0}^{{\prime}}}\|\varPhi (t_{0};t)c_{0}^{{\prime}}\|_{ 2} =\|\varPhi (t_{0};t)\| =\sup _{j}s_{j}(t), }$$

(7)

where Φ(t ₀; t) is the propagator matrix or matrizant satisfying the matrix differential equation

$$\displaystyle{ \frac{\text{d}} {\text{d}t}\varPhi (t_{0};t) = \mathcal{A}(k,R,t)\varPhi (t_{0};t), }$$

(8)

and it is related to the concentration perturbation field by c ^′(t) = Φ(t ₀; t)c ₀ ^′ with c ^′(t ₀) = c ₀ ^′ being an arbitrary function. Here, s _j ’s are the singular values of Φ(t ₀; t) and ∥ ⋅ ∥ ₂ is the standard Euclidean norm. It is important to note that the pseudospectra and the growth function are dependent on the definition of norm [17]. From mathematical and physical considerations, an appropriate measure of the disturbance is indispensable. In this article the standard Euclidean norm ∥ ⋅ ∥ ₂ and associated inner product have been used. Further, as the velocity perturbation is slaved to the concentration perturbation, the optimal amplification G(t) has been calculated only for the concentration perturbation c ^′ [4]. For stability analysis we consider the following quantities: the spectral abscissa and numerical abscissa are given by $\alpha (\mathcal{A}) \equiv \max \{\mathfrak{R}(\lambda (\mathcal{A}))\},\;\eta (\mathcal{A}) \equiv \max \{\lambda (\mathcal{A} + \mathcal{A}^{\mathcal{T}})/2\}$, respectively, where $\lambda (\mathcal{A})$ denotes the eigenspectrum of $\mathcal{A}$, $\mathfrak{R}$ denotes the real part, and $\mathcal{A}^{\mathcal{T}}$ denotes the transpose of the matrix $\mathcal{A}$. In the present paper, the computational domain has been chosen to be [−50, 50] with step size 0. 2. The initial value problem (8) is solved by Runge–Kutta fourth order method, and a matlab GUI EigTool [17] has been used to draw the pseudospectra of the stability matrix $\mathcal{A}$. The detail of the numerical procedure can be found in [6].

4 Results and Discussion

In stability analysis, the eigenspectrum $\lambda (\mathcal{A})$ is the principal aid to give an insight into how a system behaves. If the stability matrix $\mathcal{A}$ is non-normal (i.e., $\mathcal{A}\mathcal{A}^{\mathcal{T}}\neq \mathcal{A}^{\mathcal{T}}\mathcal{A}$), then the pseudospectra $\varLambda _{\epsilon }(\mathcal{A})$ are likely to explain the system behavior better than the eigenvalues, $\lambda (\mathcal{A})$. Thus, $\varLambda _{\epsilon }(\mathcal{A})$ will help us to understand the response to the external excitations in the parameter space k and R. Figure 2 shows the parabolic profile (the dashed line) of the numerical range, $W(\mathcal{A}) =\{ x^{\mathcal{T}}\mathcal{A}x:\| x\| = 1$, of the stability matrix $\mathcal{A}$. It is clearly visible that the boundary of $W(\mathcal{A})$ strictly contains the spectrum of $\mathcal{A}$. This reflects that $\mathcal{A}$ cannot be unitarily diagonalizable; or in other words, their eigenfunctions are not orthogonal. In the inset figures (Fig. 2), it is illustrated that the pseudospectra protrude strongly into the right half-plane, which imply that the evolution process will be susceptible to large transient effects. This is due to the non-normality of the stability matrix, and it signifies that the system is unstable, which is not captured by analysing the spectrum alone. This implies that at the initial time the energy of the disturbance is growing faster than what is anticipated from the spectral abscissa $\alpha (\mathcal{A})$. It can be conjectured that with increasing R, the boundary of numerical range becomes wider and the eigenvalues are more sensitive to the external forcing, as confirmed from the contours of pseudospectra.

Fig. 2

ε-pseudospectra of $\mathcal{A}$ for (a ) R = 1, k = 0. 08, t = 31, (b ) R = 4, k = 0. 3, t = 2. 5. Black dots (•): eigenvalues; black square (■): numerical abscissa; dashed line: boundary of the numerical range; solid lines: contours from innermost to outermost representing levels from ε = 10^−2. 5 to 10^−0. 5 with increment 10^−0. 5. λ _i , λ _r are the imaginary and real part of eigenvalues, respectively. Inset figure shows the numerical abscissa, $\eta (\mathcal{A})$ (■), and spectral abscissa, $\alpha (\mathcal{A})$(•)

Next, we present the optimal amplification of the perturbations to understand the transient effects. For this purpose we plot the energy growth function G(t) for (R, k) ∈ { (3, 0. 225), (4, 0. 3), (5, 0. 35)} in Fig. 3a. This figure shows that after a initial diffusion dominated period and each curve experiences a substantial energy growth. The onset of instability is the time when G(t) starts increasing (the first local minimum) and it is shown as black dot (•). Thus, NMA clearly distinguishes the domain where initial perturbations are damped or have no time to grow significantly due to diffusion, and a domain exhibiting strong convection. Further, to understand how the VF mechanism responses to external forcing, the spatial structures of the optimal input can be obtained from the singular value decomposition of the propagator matrix Φ(t ₀; t) [6, 13, 15]. Using matlab curve fitting tool (cftool), with 95 % confidence bounds, we found empirical relationships between the onset of instability, t _on, and R, as well as the critical wave number, k _c (the minimum wave number at which the instability sets in), and R. The obtained results are shown in Fig. 3b. It is shown that t _on ∼ R ^−1. 9, i.e., nearly a inverse square of R, whereas k _c  ∼ R ^0. 82. This empirical relationships are in good agreement with Tan and Homsy [16], who measured t _on ∼ R ⁻², and k _c  ∼ R, for a step-like initial concentration profile. The non-normality of the stability matrix $\mathcal{A}$ could be the source of observed difference between the two cases.

Fig. 3

(a ) Optimal amplification G(t) for different R and the corresponding critical wave numbers. The black dot denotes the onset t _on . (b ) The variation of the onset of instability t _on and the critical wave number k _c (inset), for different values of R determined from NMA. The circles (∘) are simulation data and continuous lines are fitted curves

5 Conclusion

A unified approach of linear stability analysis for the VF is presented. It is shown that at early times diffusion dominates, which causes the energy decay before it starts amplifying due to strong convection. For this purpose we have studied different components of the spectrum, such as the spectral abscissa, boundary of numerical range, and ε-pseudospectra. To understand the transient growth of energy, we studied the optimal amplification of disturbances for various flow parameters. It can be concluded that such approach not only presents a comprehensive stability analysis algorithm, but also explains the physical mechanism appropriately. It will be very interesting to apply this procedure for other unsteady base state problems such as VF in liquid chromatographic condition [12], analysing the effect of precipitation reactions in CO₂ sequestration techniques [10], or in understanding the effect of external forces, e.g., magnetic field [9] to VF to name a few.

6 Scientific Validation

This paper has been unanimously validated in a collaborative review mode with the following reviewers:

• Agota Toth, from University of Szeged

• Denis Grebenkov

• Soumya Banerjee, from Broad Institute of MIT and Harvard, Ronin Institute.