Fuzzy Quantified Structural Queries to Fuzzy Graph Databases

Abstract

This paper deals with fuzzy quantified queries in a graph database context. We study a particular type of structural quantified query and show how it can be expressed in the language FUDGE that we previously proposed. A processing strategy based on a compilation mechanism that derives regular (nonfuzzy) queries for accessing the relevant data is also described.

1 Introduction

Even though the concept of a graph database is not exactly new [2], it is only recently that the database community has started to show a strong interest in it, due in particular to the rise of linked data on the Web and the profusion of domains where networked objects have to be handled: social networks, genomics, cartographic databases, etc.

Simultaneously, the need for flexible querying has been acknowledged by database researchers, and many approaches to relational database preference queries have been proposed in the last decade, see e.g. [14]. However, the pioneering work in this domain dates back to the 70’s and is based on fuzzy set theory [15]. Since then, much effort has been made to come up with expressive and efficient flexible querying tools based on fuzzy logic, see e.g. [9]. In particular, fuzzy quantified queries have proved useful in a relational database context for expressing different types of imprecise information needs [4]. In a graph database context, such queries have an even higher potential since they can exploit the structure of the graph, beside the attribute values attached to the nodes or edges. Nevertheless, only one approach from the literature, described in [5], considered fuzzy quantified queries so far, and only in a limited way. In the present paper, we intend to integrate fuzzy quantified queries in a framework that we defined previously in [10, 11].

The remainder of the paper is organized as follows. Section 2 presents the different elements that constitute the context of the work. Section 3 is a refresher about fuzzy quantified statements. Section 4 discusses related work. In Sect. 5, we consider a specific type of fuzzy quantified structural query, we propose a syntactic format for expressing it in the FUDGE language defined in [10], and we describe its interpretation. Section 6 deals with query processing. Finally, Sect. 7 recalls the main contributions and outlines research perspectives.

2 Background Notions

In this section, we recall important notions about graph databases, fuzzy graph theory, fuzzy graph databases, and the query language FUDGE.

2.1 Graph Databases

A graph database management system enables managing data for which the structure of the schema is modeled as a graph (nodes are entities and edges are relations between entities), and data is handled through graph-oriented operations and type constructors. Different models of graph databases have been proposed in the literature (see [2] for an overview), including the attributed graph (aka. property graph) aimed to model a network of entities with embedded data. In this model, nodes and edges may contain data in attributes (aka. properties).

2.2 Fuzzy Graphs

A graph G is a pair $(V,\, R)$, where V is a set and R is a relation on V. The elements of V (resp. R) correspond to the vertices (resp. edges) of the graph. Similarly, any fuzzy relation $\rho$ on a set V can be regarded as defining a weighted graph, or fuzzy graph [13], where the edge $(x,\, y) \in V \times V$ has weight or strength $\rho (x,\, y) \in [0,\,1]$.

An important operation on fuzzy relations is composition. Assume $\rho _1$ and $\rho _2$ are two fuzzy relations on V. Thus, composition $\rho = \rho _1 \circ \rho _2$ is also a fuzzy relation on V s.t. $\rho (x,\,z) = \max _y\,\min (\rho _1(x,\,y),\,\rho _2(y,\,z)).$ The composition operation can be shown to be associative: $(\rho _1 \circ \rho _2) \circ \rho _3 = \rho _1 \circ (\rho _2 \circ \rho _3).$ The associativity property allows us to use the notation $\rho ^k = \rho \circ \rho \circ \ldots \circ \rho$ for the composition of $\rho$ with itself $k-1$ times. In addition, following [16], we define $\rho ^0$ to be s. t. $\rho ^0(x,\,y) = 0,\,\forall (x,\,y)$.

Useful notions related to fuzzy graphs are those of strength and length of a path. Their definition, drawn from [13], is given hereafter.

Strength of a path. — A path p in G is a sequence $x_0\,\rightarrow \,x_1\,\rightarrow \,\ldots \rightarrow \,x_n$ ($n \ge 0$) such that $\rho (x_{i-1},\,x_i) > 0,\,1 \le i \le n$ and where n is the number of links in the path. The strength of the path is defined as

$$\begin{aligned} ST(p) = \min _{i=1..n}\,\rho (x_{i-1},\,x_i). \end{aligned}$$

(1)

In other words, the strength of a path is defined to be the weight of the weakest edge of the path. Two nodes for which there exists a path p with $ST(p) > 0$ between them are called connected. We call p a cycle if $n \ge 2$ and $x_0 = x_n$. It is possible to show that $\rho ^k(x,\,y)$ is the strength of the strongest path from x to y containing at most k links. Thus, the strength of the strongest path joining any two vertices x and y (using any number of links) may be denoted by $\rho ^{\infty }(x,\,y)$.

Length and distance. — The length of a path $p = x_0\,\rightarrow \,x_1\,\rightarrow \,\ldots \rightarrow \,x_n$ in the sense of $\rho$ is defined as follows:

$$\begin{aligned} Length(p) = \sum _{i=1}^n \frac{1}{\rho (x_{i-1},\,x_i)}. \end{aligned}$$

(2)

Clearly $Length(p) \ge n$ (it is equal to n if $\rho$ is Boolean, i.e., if G is a nonfuzzy graph). We can then define the distance between two nodes x and y in G as

$$\begin{aligned} Distance(x,\,y) = \min _{all\, paths\, x\, to\, y}\,Length(p). \end{aligned}$$

(3)

It is the length of the shortest path from x to y. It can be shown that Distance is a metric [13], i.e., $Distance(x,\,x) = 0$, $Distance(x,\,y) = Distance(y,\,x)$, and $Distance(x,\,z) \le Distance(x,\,y) + Distance(y,\,z)\,\forall z$.

2.3 Fuzzy Graph Databases

We are interested in fuzzy graph databases where nodes and edges can carry data (e.g. key-value pairs in attributed graphs). So, we consider an extension of the notion of a fuzzy graph: the fuzzy data graph as defined in [11].

Definition 1

(Fuzzy data graph). Let E be a set of labels. A fuzzy data graph G is a quadruple $(V,\, R, \, \kappa , \, \zeta )$, where V is a finite set of nodes (each node n is identified by n.id), $R = \bigcup _{e \in E} \{\rho _e\,:\,V\,\times \,V\,\rightarrow \,[0,\,1] \}$ is a set of labeled fuzzy edges between nodes of V, and $\kappa$ (resp. $\zeta$) is a function assigning a (possibly structured) value to nodes (resp. edges) of G.

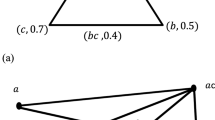
In the following, a graph database is meant to be a fuzzy data graph. Figure 1 is an example of a fuzzy data graph in which the degree associated with A -contributor- ${\small \texttt {>}}$ B is the proportion of journal papers co-written by ${\small \texttt {{A}}}$ and ${\small \texttt {{B}}}$, over the total number of journal papers written by ${\small \texttt {{B}}}$. The degree associated with J -domain- ${\small \texttt {>}}$ D is the extent to which the journal ${\small \texttt {{J}}}$ belongs to the research domain ${\small \texttt {{D}}}$.

Nodes are assumed to be typed. If n is a node of V, then Type(n) denotes its type. In Fig. 1, the nodes ${\small \texttt {{IJWS12}}}$, ${\small \texttt {{IJAR14}}}$, ${\small \texttt {{IJIS16}}}$, ${\small \texttt {{IJIS10}}}$ and ${\small \texttt {{IJUFK15}}}$ are of type journal, the nodes IJWS12-p, IJAR14-p, IJIS16-p, IJIS10-p, IJIS10-p1 and IJUFK15-p of type paper, and the nodes ${\small \texttt {{Andreas}}}$, ${\small \texttt {{Peter}}}$, ${\small \texttt {{Maria}}}$, ${\small \texttt {{Claudio}}}$, ${\small \texttt {{Michel}}}$, ${\small \texttt {{Bazil}}}$ and ${\small \texttt {{Susan}}}$ are of type author, the nodes named ${\small \texttt {{Database}}}$ are of type domain and the other nodes are of type impact_factor. For nodes of type journal, paper, author and domain, a property, called name, contains the identifier of the node and for nodes of type impact_factor, a property, called value, contains the value of the node. In Fig. 1, the value of the property name or value for a node appears inside the node.

Fig. 1.

Fuzzy data graph $\mathcal {DB}$

2.4 The FUDGE Query Language

FUDGE, based on the algebra described in [10], is an extension of the Cypher language [8], used in the Neo4j graph DBMS [1]. These languages are based on graph pattern matching, meaning that a query Q over a fuzzy data graph $\mathcal {DB}$ defines a graph pattern and answers to Q are its isomorphic subgraphs that can be found in $\mathcal {DB}$. More concretely, a pattern has the form of a subgraph where variables can occur. An answer maps the variables in elements of $\mathcal {DB}$.

A fuzzy graph pattern expressed à la Cypher consists of a set of expressions (n1:Type1)-[exp]- ${\small \texttt {>}}$ (n2:Type2) or (n1:Type1)-[e:label]- ${\small \texttt {>}}$ (n2:Type2) where ${\small \texttt {{n1}}}$ and ${\small \texttt {{n2}}}$ are node variables, ${\small \texttt {{e}}}$ is an edge variable, ${\small \texttt {{label}}}$ is a label of E, ${\small \texttt {{exp}}}$ is a fuzzy regular expression, and ${\small \texttt {{Type1}}}$ and ${\small \texttt {{Type2}}}$ are node types. Such an expression denotes a path satisfying a fuzzy regular expression ${\small \texttt {{exp}}}$ (that is simple in the second form ${\small \texttt {{e}}}$) going from a node of type ${\small \texttt {{Type1}}}$ to a node of type ${\small \texttt {{Type2}}}$. All its arguments are optional, so the simplest form of an expression is ()-[]- ${\small \texttt {>}}$ () denoting a path made of two nodes connected by any edge. Conditions on attributes are expressed on nodes and edges variables in a clause.

Example 1

We denote by $\mathcal {P}$ the fuzzy graph pattern:

This pattern “models” information concerning authors (${\small \texttt {{au2}}}$) who have, among their close contributors, an author (${\small \texttt {{au1}}}$) who published a paper (${\small \texttt {{ar1}}}$) in IJWS12 and also published a paper (${\small \texttt {{ar2}}}$) in a journal (${\small \texttt {{j2}}}$).    $\diamond$

Let us illustrate the way a selection query can be expressed in FUDGE, that embarks fuzzy preferences over the data and the structure specified in the graph pattern. Given a graph database $\mathcal {DB}$, a selection query expressed in FUDGE is composed of:

• 1. A list of clauses for fuzzy term declarations. If a fuzzy term ${\small \texttt {{fterm}}}$ corresponds to a trapezoidal function defined by the quadruple (A-a, ${\small \texttt {{A}}}$, ${\small \texttt {{B}}}$ and B+b), then the clause has the form . If ${\small \texttt {{fterm}}}$ is a decreasing function, then the clause has the form fterm ( $\delta$ , $\gamma$ ) meaning that the support of the term is $[0,\,\gamma ]$ and its core $[0,\,\delta ]$ (there is the corresponding clause for increasing functions).

• 2. A clause, which has the form that expresses the fuzzy graph pattern.

Example 2

Listing 1.2 is an example of a FUDGE query.

This pattern “models” information concerning authors (${\small \texttt {{au2}}}$) who have, among their close contributors (connected by a short path — — made of ${\small \texttt {{contributor}}}$ edges), an author (${\small \texttt {{au1}}}$) who published a paper (${\small \texttt {{ar1}}}$) in ${\small \texttt {{IJWS12}}}$ and also published a paper (${\small \texttt {{ar2}}}$) in a journal (${\small \texttt {{j2}}}$) which has a high impact factor (). The fuzzy terms short and high are defined on line 1.    $\diamond$

3 Refresher on Fuzzy Quantified Statements

In this section, we recall important notions about fuzzy quantifiers and present one of the approaches that have been proposed in the literature for interpreting fuzzy quantified statements.

3.1 Fuzzy Quantifiers

Zadeh [17] distinguishes between absolute and relative fuzzy quantifiers. Absolute quantifiers refer to a number while relative ones refer to a proportion. Quantifiers may also be increasing, as “at least half”, or decreasing, as “at most three”. An absolute quantifier $\mathcal {Q}$ is represented by a function $\mu _\mathcal {Q}$ from an integer range to $[0,\,1]$ whereas a relative quantifier is a mapping $\mu _\mathcal {Q}$ from $[0,\,1]$ to $[0,\,1]$. In both cases, the value $\mu _\mathcal {Q}(j)$ is defined as the truth value of the statement “$\mathcal {Q}\,X$ are A” when exactly j elements from X fully satisfy A (whereas it is assumed that A is fully unsatisfied for the other elements). Figure 2 gives two examples of monotonous decreasing and increasing quantifiers respectively.

Fig. 2.

Quantifiers “at most 2” (left) and “at least 3” (right)

Calculating the truth degree of the statement “$\mathcal {Q}\,X$ are A” raises the problem of determining the cardinality of the set of elements from X which satisfy A. If A is a Boolean predicate, this cardinality is a precise integer (k), and then, the truth value of “$\mathcal {Q}\,X$ are A” is $\mu _\mathcal {Q}(k)$. If A is a fuzzy predicate, this cardinality cannot be established precisely and then, computing the quantification corresponds to establishing the value of function $\mu _\mathcal {Q}$ for an imprecise argument.

3.2 Zadeh’s Interpretation

Let X be the usual (crisp) set {$x_1$, $x_2$, $\ldots$, $x_n$}. Zadeh [17] defines the cardinality of the set of elements of X which satisfy A, denoted by $\varSigma count(A)$, as:

$$\begin{aligned} \varSigma count(A) = \sum _{i=1}^n \mu _A(x_i) \end{aligned}$$

(4)

The truth degree of the statement “$\mathcal {Q}\,X$ are A” is then given by

$$\begin{aligned} \mu (\mathcal {Q}\,X\,are\,A) = {\left\{ \begin{array}{ll}\mu _\mathcal {Q}(\varSigma count(A)) \quad \text {(absolute)},\\[6pt] \mu _\mathcal {Q}\left( \dfrac{\varSigma count(A)}{n}\right) \text { (relative)}\end{array}\right. } \end{aligned}$$

(5)

where n denotes the cardinality of X.

As for quantified statements of the form “$\mathcal {Q}\,B\,X$ are A” (with $\mathcal {Q}$ relative), their interpretation is as follows:

$$\begin{aligned} \mu (\mathcal {Q}\,B\,X\,are\,A) = \mu _\mathcal {Q}\left( \dfrac{\varSigma count(A \cap B)}{\varSigma count(B)}\right) = \mu _\mathcal {Q}\left( \dfrac{\sum _{x \in X}\top (\mu _A(x),\,\mu _B(x))}{\sum _{x \in X}\mu _B(x)}\right) \end{aligned}$$

(6)

where $\top$ denotes a triangular norm (for instance the minimum).

4 Related Work

Fuzzy quantified queries have been thoroughly studied in a relational database context, see e.g. [4, 7] where they serve to express conditions about data values. In a graph database context, a new dimension can be exploited that concerns the structure of the graph. In [16], Yager briefly mentions the possibility of using fuzzy quantified queries in a social network database context, such as the question of whether “most of the people residing in western countries have strong connections with each other” and suggests to interpret it using an OWA operator. However, the author does not propose any formal language for expressing such queries.

A first attempt to extend Cypher with fuzzy quantified queries — in the context of a regular (crisp) graph database — is described in [5, 6]. In [5], the authors take as an example a graph database representing hotels and their customers and consider the following fuzzy quantified query:

looking for pairs of customers linked through almost 3 hops. The syntax ${\small \texttt {{**}}}$ is used for indicating what the authors call a fuzzy linker. However, the interpretation of such queries is not formally given. The authors give a second example that involves the fuzzy concept popular applied to hotels. They assume that a hotel is popular if a large proportion of customers visited it. First, they consider a crisp interpretation of this concept (large being seen as equivalent to at least n) and recall how the corresponding query can be expressed in Cypher:

Then, the authors switch to a fuzzy interpretation of the term popular and propose the expression:

In [6], the same authors propose an approach aimed to summarize a (crisp) graph database by means of fuzzy quantified statements of the form $\mathcal {Q}$ X are A, in the same spirit as what Rasmussen and Yager did for relational databases [12]. Again, they consider that the degree of truth of such a statement is obtained by a sigma-count (according to Zadeh’s interpretation) and show how the corresponding queries can be expressed in Cypher. More precisely, given a graph database G and a summary , the authors consider two degrees of truth of S in G defined by $truth_1(S) = \mu _\mathcal {Q} \left( count(distinct\, S) /count(distinct\,a)\right)$ and . They illustrate these notions using a database representing students who rent or own a house or an apartment. The degree of truth (in the sense of the second formula above) of the summary “S = student–[rent]–>apartment, most” — meaning “most of the students rent an apartment” (as opposed to a house) — is given by the membership degree to the fuzzy quantifier most of the ratio: (number of times a relationship of type rents appears between a student and an apartment) over (number of relations of type rents starting from a student node).

A limitation of this approach is that only the quantifier is fuzzy (whereas in general, in a fuzzy quantified statement of the form “$\mathcal {Q}$ B X are A”, the predicates A and B may be fuzzy too).

5 Fuzzy Quantified Queries in the FUDGE Language

In the following, we consider fuzzy quantified queries involving fuzzy predicates (beside the quantifier) over fuzzy graph databases. The fuzzy quantified statements considered are of the form “$\mathcal {Q}$ nodes, that are connected according to a certain pattern to a node x, satisfy a fuzzy condition $\varphi$”. An example of such a statement is: “most of the papers of which x is a main author, have been published in a renowned database journal”.

This type of statement rewrites “$\mathcal {Q}$ $Y_{P(x)}$ are $\varphi$” where the quantifier $\mathcal {Q}$ is represented by a fuzzy set and denotes either a relative quantifier (e.g., most) or an absolute one (e.g., at least three), $Y_{P(x)}$ designates the fuzzy set of nodes connected, according to the pattern P(x), to a node x in the graph, and $\varphi$, is represented also by a fuzzy set and denotes fuzzy (possibly compound) conditions. In a general setting, we have a statement of the form “$\mathcal {Q}$ B X are A” where B is the fuzzy condition “to be connected (according to the pattern P(x)) to a node x”, X is the set of nodes in the graph, and A is the fuzzy condition $\varphi$. In the particular case where the graph is crisp, we get a statement of the form “$\mathcal {Q}$ X are A” where the referential X is the (crisp) set of nodes connected to x.

Example 3

The query that consists in finding “most of the papers of which x is a main author, have been published in a renowned database journal” may be expressed in FUDGE as follows:

where the clause defines the fuzzy relative increasing quantifier most of Fig. 3(c), and the next clauses define the ascending fuzzy terms strong and high of Fig. 3(d) and (a).

Fig. 3.

Membership functions

We now consider a slightly more complex version of the above example by adding a fuzzy condition on the papers’ publication date: “most of the recent papers written by an important author x have been published in a renowned database journal”. The syntactic form of this query, denoted by $Q_{mostAuthors}$ in the following, is given in Listing 1.3.   $\diamond$

The general syntactic form of fuzzy quantified queries is given in the Listing 1.4.

It contains a list of clauses for the fuzzy quantifiers and the fuzzy terms declarations, a clause for fuzzy graph pattern selection, a clause for expressing the (possibly fuzzy) conditions on values, a clause for the fuzzy quantified statement definition, and a clause for specifying which elements should be returned in the resultset. ${\small \texttt {{P(x,y)}}}$ denotes the fuzzy graph pattern involving the nodes ${\small \texttt {{x}}}$ and ${\small \texttt {{y}}}$. $fc_1$ and $fc_2$ are fuzzy conditions.

Interpretation: From a conceptual point of view, its interpretation involves three derived queries (hereafter, the clauses are been omitted for the sake of simplicity). The first one, $Q_1$ (given in Listing 1.5), aims to retrieve the elements matching the variable ${\small \texttt {{x}}}$, for which we will then need to calculate a satisfaction degree. Query $Q_1$ is obtained by removing the and clauses from the initial query (one may also remove some useless parts of ${\small \texttt {{P(x,y)}}}$, as illustrated in Example 4 below).

The second derived query, denoted by $Q_2(e)$ (given in Listing 1.6), where e is an element returned by $Q_1$, is obtained by removing the and clauses from the initial query, integrating the fuzzy condition $fc_2$ and the condition ${\small \texttt {{x.name=e}}}$ in the clause and adding the clause . According to the semantics of a FUDGE query, its result, denoted by $A_{Q_2(x)}$, is a set of elements $\{(\mu _1/y_1), ... ,(\mu _n/y_n)\}$, where $\mu _i$ is the satisfaction degree associated with the element $y_i$.

The third derived query, denoted by $Q_3(e)$ (given in Listing 1.7), is the initial fuzzy query from the to the clause, adding the condition ${\small \texttt {{x.name=e}}}$ in the clause and the clause as follows:

The result of this query, denoted by $A_{Q_3(x)}$, takes the form of a set of elements $\{(\mu '_1/y_1) , ... ,(\mu '_m/y_m)\}$, where $\mu '_i$ is the satisfaction degree associated with the element $y_i$. Note that $Q_3$ only differs from $Q_2$ by its clause.

In accordance with the semantics of the projection, if the same value of $y_i$ appears in several instances in the resultset of $Q_2(x)$ or $Q_3(x)$, duplicates are eliminated and the final degree associated with $y_i$ in $A_{Q_2(x)}$ and $A_{Q_3(x)}$ is equal to the maximum degree associated with these occurrences.

Then, the results of the initial fuzzy relative quantified query Q (involving the fuzzy quantifier $\mathcal {Q}$) are results of the query $Q_1$ derived from Q, and the final satisfaction degree associated with each element e of these results is

$$\begin{aligned} \mu (e) = \mu _{\mathcal {Q}} \left( \frac{\sum _{(\mu _i/y_i) \in A_{Q_2(e)}}\mu _i}{\sum _{(\mu '_i/y_i) \in A_{Q_3(e)}} \mu '_i} \right) \end{aligned}$$

(7)

In case of a fuzzy absolute quantified query, the final satisfaction degree associated with each element e is $\mu (e) = \mu _{\mathcal {Q}} \left( \sum _{(\mu _i/y_i) \in A_{Q_2(e)}} \mu _i\right)$.

Example 4

Let us consider the query $Q_{mostAuthors}$ of Listing 1.3. We evaluate this query according to the fuzzy data graph $\mathcal {DB}$ of Fig. 1. In order to interpret $Q_{mostAuthors}$, we first evaluate the following query $Q_1$, derived from $Q_{mostAuthors}$, that retrieves “the authors (${\small \texttt {{x}}}$) who highly contributed to at least one recent paper (${\small \texttt {{p}}}$) published in a journal”.

$Q_1$ returns four results $X=\{{\small \texttt {{Peter}}}$, ${\small \texttt {{Maria}}}$, ${\small \texttt {{Claudio}}}$, ${\small \texttt {{Michel}}}$}. The authors ${\small \texttt {{Andreas}}}$, ${\small \texttt {{Susan}}}$ and ${\small \texttt {{Bazil}}}$ do not belong to the resultset of $Q_1$ because ${\small \texttt {{Susan}}}$ has not written a journal paper yet and ${\small \texttt {{Andreas}}}$ and ${\small \texttt {{Bazil}}}$ do not have a recent paper.

For each element x from the resultset X of $Q_1$, we process two queries $Q_2(x)$ and $Q_3(x)$. The query $Q_2(x)$, derived from $Q_{mostAuthors}$, aims to retrieve “the recent papers of which x is a main author, that have been published in a renowned database journal”. For instance, for the element ${\small \texttt {{Maria}}}$, the query $Q_2(Maria)$ is expressed as follows:

For a given x, we get a list of papers with their respective satisfaction degrees: $\mu (p)= \min ( \mu _{strong}(\rho _{author} (x,p)), \mu _{recent}(p), \mu _{high}(i))$. For the running example, we then have $A_{Q_2(Peter)} =$ {($\min$(0.5, 0, 0.92)/${\small \texttt {IJWS12\_{p}}}$), ($\min$(0.2, 0.33, 1)/${\small \texttt {IJAR14\_{p}}}$)} $=$ {(0/${\small \texttt {IJWS12\_{p}}}$), (0.2/${\small \texttt {IJAR14\_{p}}}$)}, $A_{Q_2(Maria)}=$ {(0.33/${\small \texttt {IJAR14\_{p}}}$), (0.33/${\small \texttt {IJIS16\_{p}}}$), (0/${IJIS10_p1}$)}, $A_{Q_2(Claudio)}= \{(0.33/{{\small \texttt {IJAR14\_p}}}), (0/{{\small \texttt {IJIS10\_p1}}}), (0.07/{{\small \texttt {IJUFK15\_p}}})\}$, $A_{Q_2(Michel)}= \{(0.07/{{\small \texttt {IJUFK15\_p}}})\}$.

Query $Q_3(x)$, derived from $Q_{mostAuthors}$, aims to retrieve “the recent papers of which x is a main author, that have been published in a journal”. For instance, for the element ${\small \texttt {{Maria}}}$, the query $Q_3(\textit{Maria})$ is expressed as follows:

For a given x, we get a set of papers written by x satisfying the conditions of query $Q_3(x)$ with their respective satisfaction degrees as follows: $\mu (p)= min(\mu _{strong}(\rho _{author} (x,p)), \mu _{recent}(p))$. For the running example, we then have $A_{Q_3(Peter)}=$ {(0/${\small \texttt {IJWS12\_p}}$), (0.2/${\small \texttt {{IJAR14\_p}}}$)}, $A_{Q_3(Maria)}=$ {(0.33/${\small \texttt {IJAR14\_{p}}}$), (0.6/${\small \texttt {IJIS16\_{p}}}$), (0/${\small \texttt {{IJIS10\_p1}}}$)}, $A_{Q_3(Claudio)}=$ {(0.33/${\small \texttt {IJAR14\_{p}}}$), (0/${\small \texttt {{IJIS10\_p1}}}$), (0.3/${\small \texttt {IJUFK15\_{p}}}$)}, $A_{Q_3(Michel)}=$ {(0.3/${\small \texttt {IJUFK15\_{p}}}$)}.

Lastly, the final result of the query $Q_{mostAuthors}$ evaluated on $\mathcal {DB}$, given by Formula 7, is {$\mu (\textit{Peter})= \mu _{most} (\frac{0.2}{0.2})= 1$, $\mu (\textit{Maria})= \mu _{most} (\frac{0.66}{0.93})= 0.82$, $\mu (\textit{Claudio})= \mu _{most}(\frac{0.4}{0.63})= 0.67$, $\mu (\textit{Michel})= \mu _{most}(\frac{0.07}{0.3})= 0$}.    $\diamond$

6 About Query Processing

The evaluation strategy we propose for these queries consists of a software add-on layer over the Neo4j graph DBMS. This software, called SUGAR, efficiently evaluates FUDGE queries that contain fuzzy preferences, but its initial version, described in [10, 11], does not support fuzzy quantified statements. We now consider the implementation of this functionality, based on the theoretical foundations defined in the previous section. The SUGAR software implements two modules, which interact with the embedded Neo4j crisp engine (see Fig. 4): The Transcriptor module, aimed to translate a FUDGE query requested by a user into a (crisp) cypher one (using the derivation principle presented in [9] in the context of relational databases), which is then sent to the crisp Neo4j engine, and The Score Calculator module, which calculates the satisfaction degree associated with each answer returned by the crisp engine, and ranks the answers.

Fig. 4.

SUGAR software architecture

The main process in our work is the quantified statement evaluation step which is described in Algorithm 1. For quantified queries of the type introduced in the previous section (i.e. using relative quantifiers), the principle is to first evaluate the fuzzy query $Q_1$. For each tuple x from the resulset of $Q_1$, we evaluate with SUGAR the fuzzy queries $Q_2(x)$ and $Q_3(x)$. The final satisfaction degree is given by Formula 7 according to $Q_2(x)$ and $Q_3(x)$ resultsets. Finally, we get as an output answers ranked by decreasing order of the satisfaction degree.

For a given x, queries $Q_2(x)$ and $Q_3(e)$ embed the same graph pattern (they only differ by their clause that is more restrictive for $Q_2$). This means that these queries could be processed together at evaluation time. Then one can see on Algorithm 1 that evaluating a fuzzy quantified query implies processing $x+1$ FUDGE queries where x is the number of elements that match the pattern declared in the clause of the initial query (without the quantified statement). The cost of the evaluation of a graph pattern query depends on the form of its pattern [3] and it has already been showed in [10] that a FUDGE query does not significantly increase the cost with respect to a crisp query in the case of selection graph pattern queries.

As a proof-of-concept of the proposed approach, the FUDGE prototype is available and downloadable at http://www-shaman.irisa.fr/fudge-prototype/.

7 Conclusion and Perspectives

In this paper, we have dealt with a specific type of fuzzy quantified queries, addressed to fuzzy graph databases. We have defined the syntax and semantics of an extension of the query language Cypher that makes it possible to express and interpret such queries. A query processing strategy based on the derivation of non-quantified fuzzy queries has also been proposed. As a future work, we first intend to carry out some experimentations in order to assess the performances of the evaluation method outlined here. We then plan to study other types of fuzzy quantified queries. An example of a fuzzy quantified statement that is out of the scope of the present approach is “find the authors x that had a paper published in most of the renowned database journals”. More generally, it would be interesting to study fuzzy quantified queries that aim to find the nodes x such that x is connected (by a path) to $\mathcal {Q}$ nodes reachable by a given pattern and satisfying a given condition C.