EPLA: Efficient Personal Location Anonymity

Abstract

A lot of researchers utilize side-information, such as map which is likely to be exploited by some attackers, to protect users’ location privacy in location-based service (LBS). However, current technologies universally model the side-information for all users. We argue that the side-information is personal for every user. In this paper, we propose an efficient method, namely EPLA, to protect the users’ privacy using visit probability. We selected the dummy locations to achieve k-anonymity according to personal visit probability for users’ queries. AKDE greatly reduces the computational complexity compared with KDE approach. We conduct comprehensive experimental study on the realistic Gowalla data sets and the experimental results show that EPLA obtains fine privacy performance and efficiency.

1 Introduction

In recent years, Location-based services (LBSs) are becoming more and more popular in our lives. While users benefit from the convenience of LBSs, they face problems caused by the privacy disclosure.

In a lot of applications, such as Meituan (www.meituan.com), LBS service providers aren’t completely trusted. They appeal to users to login by electronic coupons and discount, and then, they obtain the login information. Since LBS service providers have obtained login information, users’ are more fearful that their location information is collected by service providers. Once LBS service providers get users’ location information, they can precisely analyze the users and get their privacy information.

To protect users’ location privacy, a lot of scholars have proposed large amount of techniques including spatial cloaking technique [1, 2], pseudonyms technique [3, 4] and so on. Spatial cloaking technique is a very popular approach and it reduce the spatial resolution to obscure the real locations. Moreover, most of the current methods assumed that adversary don’t consider side-information, such as the location Semantics [5]. Therefore, some unlikely locations, such as lakes and mountains, are included to hide users’ real locations. As we know, the adversary can easily filter out the unlikely locations. Even though, a few literatures [4] make use of the side-information, researchers model them as universal model for all users. If location is the same one, the query probability is the same in [4] for every user. As we know, movement trajectories for everyone are personal. For instance, most of users travel around their residences and workplaces. So, the query probability of the same location is different for everyone. From the analysis, current methods are difficult to ensure the desired privacy degree.

To overcome the drawback of above methods, we present EPLA, an efficient personal location anonymity, to protect users’ location privacy. Differentiate from the current approaches, EPLA takes the users’ visited locations into account and selects dummy locations based on visit probabilities that are possibility visiting all locations. Since the visit probability is personal, we respectively model visit probability for each user in this paper. EPLA is a two-step method. In the first phase, we divided the space into cells and make sure the dummy locations candidate set P. And then, Approximate Kernel Density Estimation (AKDE) is utilized to compute the personal visit probability of each location $p_i$ in candidate dummy locations set P based on the sampling user’s visited locations. Computational complexity of the Kernel Density Estimation (KDE) [6] method is decreased from $O(|P|n^3)$ to O(|P|n) (where |P| is the number of elements in set P and n is the number of sampling user’s visited locations). In the second phase, we achieve k-anonymity via maximizing location information entropy and the area of cloaking region (CR).

The contributions made in this research are three-fold::

• 1. We proposed a new method, namely Approximate Kernel Density Estimation (AKDE) to compute the personal visit probability. AKDE greatly reduces the computational complexity compared with Kernel Density Estimation (KDE) from $O(|P|n^3)$ to O(|P|n).

• 2. We analyze the error between AKDE and KDE, and then, proof the error upper bound is $\frac{2}{(p!)^{1/2}}(\frac{3}{2q})^p$.

• 3. We conduct extensive experiments to evaluate the proposed method.

2 Related Work

Spatial cloaking technique [8] is a very popular method. Wang et al. [9] proposed a new model which can solve Location-aware Location Privacy Protection(L2P2) problem. ICliqueCloak [2] was proposed against location-dependent attacks.

Mix-zone [10] is one representative of Pseudonyms techniques, which enables users only to change their pseudonyms inside a special region where users do not report the exact locations. Guo et al. [11] combines a geometric transformation algorithm with a dynamic pseudonyms-changing mechanism and user-controlled personalized dummy generation to achieve strong trajectory privacy preservation. [12] exploited dummy locations to achieve anonymity.

Cryptography technique [13] is also one of the main approaches. Ghinita et al. [13] proposed a novel framework to support private location dependent queries, based on Private Information Retrieval PIR. Considering the insecure wireless net environment, [14] presented a k-anonymity algorithm using encryption for location privacy protection that can improve security of LBS system by encrypting the information transmitted by wireless. [15] designs a suite of novel fine-grained Privacy-preserving Location Query Protocol (PLQP) which allows different levels of location query on encrypted location information.

Differential privacy technique [16] is a new technique to protect location privacy. Andrés et al. [17] presented a mechanism for achieving geo-indistinguishability by adding controlled random noise to the users’ location with differential privacy.

3 Preliminaries

In our method, we adopt a client/server framework and pay close attention to location privacy when users dispatch snapshot queries in LBS.

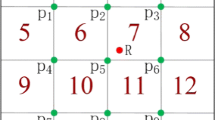
Our method firstly divides the space into $n\,\times \,n$ cells and select the $(n-1)\,\times \,(n-1)$ corners set $P'$ of inner cells. The user location of a user R is indicated as a corner $p_R$ which is closest to him. The candidate location anonymity set is $P=P'-p_R$. As shown in the Fig. 1, the space is divided into $4\,\times \,4$ cells and the set $P'$ is $\{p_1, p_2,\cdots , p_9\}$. The red location R is a real user’s location and it is close to $p_5$. Therefore, the candidate location anonymity set is $P=P'-\{p_5 \}$.

Fig. 1.

Candidate locations (Color figure online)

3.1 The Personal Visit Preference

To know the personal user’s visit preference, we conducted an analysis on the China Telecommunications data set which is collected in Shanghai. We randomly choose two different users from data. As Fig. 2 depicts, Their visit preference are different. The visited places of $U_1$ are centralized which the visited places of $U_2$ is dispersive. We can know the distribution over the distances between every pair of a user’s visited locations is also personal and it can reflect the user personal Preference.

Fig. 2.

Distributions of personal visited locations

3.2 Kernel Density Estimation of Distance Distribution

The analysis of Sect. 3.1 inspires us to use the distance distribution to research the personal visit preference. As we know, the form of the distance distribution is uncertain and we don’t get the parameters of the probability density function. In this paper, we use KDE to model the personal distance distribution because KDE can be used to model arbitrary distributions and don’t assume the form of the probability density function. There two steps in our method: sampling distances, and estimating distance distribution.

Sampling Distances. Firstly, we randomly sample some locations from the user’s visited locations. Then, we compute the Euclidean distance of every pair of sampling locations as distance sample. Since our method achieve anonymity in client and only use his visited locations, user can input some of his visited locations when he firstly uses our model.

Estimating Distance Distribution. We use D to denote the distance sample for a certain user, which is stem from the personal distance distribution density function f. $\hat{f}$ is KDE of f based on D, as follows:

$$\begin{aligned} \hat{f} (d) = \frac{1}{|D|\sigma } \sum _{d'\in D} K \left( \frac{d-d'}{\sigma } \right) \end{aligned}$$

(1)

where K(.) is the kernel function and $\sigma$ is the smoothing parameter, called the bandwidth. In our method, it is the normal kernel $K (x) = \frac{1}{\sqrt{2\pi }} e^{-\frac{x^2}{2}}$ and the bandwidth $\sigma = \left( \frac{4\hat{\sigma } ^5}{3|D|} \right) ^{1/5} \approx 1. 06\hat{\sigma } |D|^{-1/5}$ [6], where $\hat{\sigma }$ is the standard deviation of distance sample D.

3.3 Fast Gauss Transform

A Gaussian $e^{-(d_i-d')^2/2\sigma ^2}$ can be transformed to Hermite polynomials centered at $x_0$ by the Hermite expansion. And the fast Gauss Transform [18] is given by:

$$\begin{aligned} \begin{aligned} e^{-(d_i-d')^2/2\sigma ^2}&= \sum _{s=0} ^\infty \frac{1}{s!} (\frac{d'-d_0}{\sqrt{2}\sigma })^s h_s(\frac{d_i-d_0}{\sqrt{2}\sigma }) \\ {}&= \sum _{s=0} ^{p-1} \frac{1}{s!} (\frac{d'-d_0}{\sqrt{2}\sigma })^s h_s(\frac{d_i-d_0}{\sqrt{2}\sigma })+\varepsilon (p) \end{aligned} \end{aligned}$$

(2)

where $h_s(x) = (-1)^s\frac{d^s}{dx^s} (e^{-x^2})$ and $\varepsilon (p)$ is the error when we truncate the infinite series after p terms. When $d'$ is close to $d_0$, a small p is enough to guarantee that $\varepsilon (p)$ is negligible.

3.4 Metrics for Location Privacy

In this paper, entropy [4] and the area of CR [2] are used to measure the level of privacy and the location information entropy is a very popular metric. The entropy H is defined as:

$$\begin{aligned} H(x) = - \sum _{i=1} ^k p_i \cdot \log _2 p_i \end{aligned}$$

(3)

where $p_i$ is the probability which the location i is the user’s real location.

The area of CR is also an important metric. The higher privacy requirement demand the bigger area of CR. Since it is difficult to compute the area of polygon, we make use of an approximate method to substitute for it. Intuitively, the sum of the distances between pairs of locations in anonymity set $P^*$ can be used to substitute for it, which is $\sum _{i\not =j} d (P^*_i, P^*_j)$, where $d (P^*_i, P^*_j)$ denotes the distance between location $P^*_i$ and $P^*_j$ in anonymity set $P^*$.

4 Personal Visit Probability

In this section, we firstly calculate the personal visit probability by KDE, and then, an approximate method, namely AKDE, is proposed. Finally, we analyze the error between AKDE and KDE.

4.1 Exact Personal Visit Probability (EPVP)

In order to exactly compute the personal visit probability, We use KDE to estimate the personal distance distribution for every user U and compute the visit probability of any cell $p_j$ in candidate anonymity set P according to personal distance distribution. The user’s sampling visited locations is $L =\{ l_1, l_2, \cdots , l_n\}$. We can compute the Euclidean distance between every location $l_i$ in L and $p_j$, as follows:

$$\begin{aligned} d_{i} = \text{ distance } (l_i,p_j), \forall l_i\in L \end{aligned}$$

(4)

we can use Eq. (1) to compute a probability for each $d_{i}$ as follows:

$$\begin{aligned} \hat{f} (d_{i} ) = \frac{1}{|D|\sigma } \sum _{d'\in D} K \left( \frac{d_{i} -d'}{\sigma } \right) \end{aligned}$$

(5)

The probability which U visits a location $p_j$ can be computed as follows:

$$\begin{aligned} p(p_j) = \frac{1}{n} \sum _{i=1} ^n \hat{f} (d_{i})=\frac{1}{\sqrt{2\pi }n\sigma |D|} \sum _{i=1} ^n \sum _{d'\in D} e^{-\frac{(d_i-d')^2}{2\sigma ^2}} \end{aligned}$$

(6)

Eventually, we derive visit probability of any $p_j$ in candidate anonymity set P. As is show in Algorithm 1, the computational complexities of line 3 and line 4 are both $O(n^2)$. The computational complexity line 8 is $O(n^2)$. Since we should calculate all $p_j$ in P, the total computational complexity from line 8 to line 11 is $O(n^3)$. Therefore, the total computational complexity of from line 5 to line 14 is $O(|P|n^3)$. The total complexity of Algorithm 1 is $O(n^2)+O(n^2)+O(|P|n^3)=O(|P|n^3)$.

4.2 Approximate Personal Visit Probability

As we know, the computational complexity $O(|P|n^3)$ of EPVP grows rapidly with n increasing. In this part, we design an approximate method, namely APVP, to compute personal visit probability through the fast Gauss transform and three-sigma rule of Gaussian distribution. And we finally reduce the complexity of EPVP to O(|P|n).

For Eq. 6, the personal visit probability $p(p_j)$ that a user visits the location $p_j$ can be approximately calculated using Eq. 2. To reduce the error, we should not only select center, such as the mean of $d'$. And with the number of centers increasing, computational complexity increases.

Nearly all values of $d'$ in the distance sample D lie within interval $[\bar{d}-3\hat{\sigma }, \bar{d}-3\hat{\sigma }]$ according to three-sigma rule of Gaussian distribution. Where $\bar{d}$ is the mean of the sample D and $\hat{\sigma }$ is the standard deviation of the sample D. In order to facilitate the calculation, we evenly divide the interval $[\bar{d}-3\hat{\sigma }, \bar{d}-3\hat{\sigma }]$ into 2q small intervals set $I=\{I_1,I_2,\cdots ,I_{2q}\}=\{[\bar{d}-3\hat{\sigma }, \bar{d}-3\hat{\sigma } +\frac{3\hat{\sigma }}{q}], [\bar{d}-3\hat{\sigma } +\frac{3\hat{\sigma }}{q}, \bar{d}-3\hat{\sigma } +\frac{6\hat{\sigma }}{q}],\cdots ,[\bar{d}+3\hat{\sigma }-\frac{3\hat{\sigma }}{q}, \bar{d}+3\hat{\sigma }]\}$ and the distance sample D is divided into 2q small distance sample set $\{D_1,D_2,\cdots ,D_{2q}\}$ according to I. Where, $q=3k$ and $k\ge 1$. Each small distance sample $D_i$ is approximately shifted respectively by the fast Gauss transform and we select the middle value $\mu _i =\bar{d}-3\hat{\sigma } +\frac{3i\hat{\sigma }}{2q}$ of $I_i$ as transforming center of $D_i$. Based on the partition $D_i$ and three-sigma rule of Gaussian distribution, we have

$$\begin{aligned} \begin{aligned} \sum _{d'\in D} e^{-\frac{(d_i-d')^2}{2\sigma ^2}}&\approx \sum _{r=1} ^{2q} \sum _{d'\in D_{r}} \sum _{s=0} ^{p-1} \frac{1}{s!} (\frac{d'-\mu _r}{\sqrt{2}\sigma })^s h_s(\frac{d_i-\mu _r}{\sqrt{2}\sigma }) \\&= \sum _{r=1} ^{2q} \sum _{s=0} ^{p-1} \frac{1}{s!}\sum _{d'\in D_{r}} (\frac{d'-\mu _r}{\sqrt{2}\sigma })^s h_s(\frac{d_i-\mu _r}{\sqrt{2}\sigma }) \\&= \sum _{r=1} ^{2q} \sum _{s=0} ^{p-1} A(s,r) h_s(\frac{d_i-\mu _r}{\sqrt{2}\sigma }) \\ \end{aligned} \end{aligned}$$

(7)

where $A(s,r)= \frac{1}{s!}\sum _{d'\in D_{r}} (\frac{d'-\mu _r}{\sqrt{2}\sigma })^s$. We can transform the Eq. 6 according to Eq. 8, as follows:

$$\begin{aligned} p(p_j)=\frac{1}{\sqrt{2\pi }n\sigma |D|} \sum _{i=1} ^n \sum _{r=1} ^{2q} \sum _{s=0} ^{p-1} A(s,r) h_s(\frac{d_i-\mu _r}{\sqrt{2}\sigma }) \end{aligned}$$

(8)

As is show in Algorithm 2, the computational complexities of line 3 and line 4 are both $O(n^2)$. The complexities of line 5 and line6 are also both $O(n^2)$. Since the p and q are constant parameters and $|p|\gg n$, the computational complexity of from line 7 to line 13 is $O(pq|P|n)=O(|P|n)$. Therefore, the total complexity of Algorithm 2 is $O(n^2)+O(n^2)+O(n^2)+O(n^2)+O(|P|n)=O(|P|n)$.

4.3 Error Analysis

Theorem 1

(The upper bound of the error $\varepsilon$). By truncating the infinite series after p terms in Eq. 4 and dividing interval $[\bar{d}-3\hat{\sigma }, \bar{d}-3\hat{\sigma }]$ into 2q small intervals, Algorithm 2 guarantees that the upper bound of the error $\varepsilon$ satisfies $\frac{2}{(p!)^{1/2}}(\frac{3}{2q})^p$.

Proof. At first, according to Cramers inequality [21] $h_s(x) \le 2^{s/2}(s!)^{1/2}e^{-x^2/2}$ and $e^{-x^2/2} \le 1$, so $h_s(x)\le 2^{s/2}(s!)^{1/2}$

Hence,

$$\begin{aligned} \begin{aligned} | \varepsilon (p) |&\le \sum _{s=p} ^{\infty } \frac{1}{s!} |\frac{d'-d_0}{\sqrt{2}\sigma }|^s |h_s(\frac{d_i-d_0}{\sqrt{2}\sigma }|\\&\le \sum _{s=p} ^{\infty } \frac{1}{s!} |\frac{d'-d_0}{\sqrt{2}\sigma }|^s 2^{s/2}(s!)^{1/2}\\&= \sum _{s=p} ^{\infty } \frac{1}{(s!)^{1/2}} |\frac{d'-d_0}{\sigma }|^s \\&\le \frac{1}{(p!)^{1/2}}\sum _{s=p} ^{\infty } |\frac{d'-d_0}{\sigma }|^s \\ \end{aligned} \end{aligned}$$

(9)

As depicted in Sect. 4.2, every $d'$ in distance sample D is assigned to a small distance set $D_i$ whose transforming center is $\mu _i$. And we have $|d'-d_0|=|d'-\mu _i|\le \frac{3\sigma }{2q}$. Therefore,

$$\begin{aligned} \begin{aligned} | \varepsilon (p) |&\le \frac{1}{(p!)^{1/2}}\sum _{s=p} ^{\infty } (\frac{3}{2q})^s \\ \end{aligned} \end{aligned}$$

(10)

Moreover, $q\,{\ge }\,3$, Accordingly

$$\begin{aligned} \begin{aligned} | \varepsilon (p) |&\le \frac{1}{(p!)^{1/2}}(\frac{3}{2q})^p \frac{2q}{2q-3} \le \frac{2}{(p!)^{1/2}}(\frac{3}{2q})^p \\ \end{aligned} \end{aligned}$$

(11)

As depicted in Theorem 1, the upper bound of the error decreases faster than the exponential decay with the p and q increasing, as shown in Fig. 3.

5 Anonymity Set Selection (ASS)

In the process of dummy location selection, we consider two factor which are location information entropy and the area of CR to achieve anonymity. Therefore, the process of dummy selection can be formulated as MCDM model. Let $P^* = \{P^*_1, P^*_2, \cdots , P^*_k\}$ denote the location anonymity set in our scheme. The MCDM model can be described as:

$$\begin{aligned} Max\{-\sum _{i=1} ^k p(P^*_i) \cdot \log p(P^*_i), \sum _{k \not = j} d (P^*_i, P^*_j)\}. \end{aligned}$$

(12)

where $P^*_i, P^*_j\in P^*$, $p(P^*_i)$ and $p(P^*_j)$ denote the personal visit probabilities of $P^*_i$ and $P^*_j$ respectively.

For MCDM model, It is hard to find a location set to meet all requirements simultaneously. So, we use heuristic solution [4] to select the proper dummy location set. The process has two steps as follows: (1) maximizing location information entropy; (2) maximizing area, and Algorithm 3 depicts the process of dummy location selection.

Maximizing Location Information Entropy: A user whose location need to protect first input real location R. So, we can find the closest corner $p_R$ to R as Sect. 3.1 depicts. Secondly, our algorithm should get the user’s personal visit probabilities which are computed by Algorithm 2 and then sorts all locations in P based on the personal visit probabilities. Then, our algorithm selects 4k candidates locations set which contains the 2k locations before $p_R$ and the 2k locations after $p_R$ to ensure that they are as similar as possible to R. After that, our algorithm select m location set $S=\{S_1, S_2, \ldots , S_m\}$ from 4k candidates locations, each set containing the real location and $2k-1$ dummy location are contained. The $j^{th} (j \in [1, m])$ set can be denoted as $S_j = \{S_{j1}, S_{j2}, \ldots , S_{ji}, \ldots , S_{j2k} \}$. According to the personal visit probabilities, we should normalize visit probabilities. We denote them using $P_{j1}, P_{j2}, \ldots , P_{ji}, \ldots , P_{j2k}$ and $P_{ji} = \frac{p(S_{ji})}{\sum _{i=1} ^{2k} p(S_{ji})}$, where $p(S_{ji})$ is the personal visit probability of the location $S_{ji}$ and $\sum _{i=1} ^{2k} P_{ji}= 1$. So, the entropy $H_j$ of anonymity set $S_j$ can be derived based on Eq. 3. Finally, the location set $S'=\{S'_1, S'_2, \cdots , S'_j, \cdots , S'_{2k} \}$ whose entropy is maximum in S is selected.

Maximizing Area: In this process, we use greedy algorithm to get the final location anonymity set $P^*=\{P^*_1, P^*_2, \cdots , P^*_k\}$ from $S'$ based on $\sum _{i\not =j} d (S'_i, S'_j)$. Firstly, a set $P^*=\emptyset$ is constructed. The user’s real location is added into $P^*$ and removed from $S'$. Then, the next location $p^*$ is selected to be added into $P^*$ and to be removed from $S'$, when $\sum _{P^*_j\in P^*} d(p^*, P^*_j)$ is greatest. As lines 9–12 in Algorithm 3 depicts, ASS repeats this step $k-1$ times. Finally, we get the anonymity set $P^*$.

6 Performance Evaluation

6.1 Experiment Setup

In the experiments, we use the publicly available Gowalla [19] data set to instead of the users’ locations sample. The statistics of the data sets are shown in Table 1. We evaluate the privacy degree of our scheme by comparing three algorithms, namely dummy [12], DLS [4] and enhanced-DLS [4]. The dummy method is taken as baseline in this paper.

Moreover, we select $40\,\mathrm{km}\,\times \,40\,\mathrm{km}$ American region, and then, it is divided into $80\,\times \,80$ sells in our experiment. So the candidate locations anonymity set P includes $79\,\times \,79-1=6240$ locations. The personal visit probability is calculated by AKDE.

Table 1. Gowalla data set

Fig. 3.

Anonymity times vs. k

6.2 Evaluation of Privacy Degree

In the process, location information entropy and the sum of distance are used as metrics. Anonymity cost is also an important trait in LBS and we measure it using online time. Moreover, we compare the time costs of APVP and EPVP, and then, analyze the relationship between the time cost of APVP and the constant parameters (namely p and q).

Fig. 4.

$\varepsilon$ vs. k

Fig. 5.

Entropy vs. k

Fig. 6.

The sum of distances vs. k

Fig. 7.

The time cost vs. n

Entropy vs. k. Larger information entropy implies that it more difficult to ensure the user’s real location. As Fig. 4 depicts, the location information entropies of all methods increase following k. The entropy of dummy is terrible than other. Our scheme EPLA is optimal and provides better privacy level than DLS and enhanced-DLS.

Area of CR vs. k. The area of CR is focused on in location privacy domain. As we know, when the area is too small, attacker can know user’s real location. So, we should consider the area to evaluate the privacy level. As Fig. 5 depicts, the area of dummy method is biggest. EPLA method is slightly short of the other methods. From above analysis, we know every user’s zone of action is limited by a lot of factors and most of visit location is close to our residence and workplace.

The Time Cost vs. n. As we know, the different p and q will lead to the different time cost of APVP when n is the same. We select different p and q to test the time cost of APVP. In the Fig. 6, we fix p = 8 and we fix q = 8 in the Fig. 7. And the cost of APVP linearly grows with n increasing while the EPVP looks like exponential growth. Moreover, when p and n is fixed, the time cost is increasing with P increasing. And when q and n are fixed, the time cost is also increasing with q increasing. As Fig. 6 depict, the computational complexity of EPVP is far outweigh the computational complexities of APVP.

7 Conclusion

In this paper, we designed a new location privacy protection approach EPLA. Firstly, we used AKDE to compute personal visit probability of all sells. Then, the selection of dummy location set was modeled as MCDM and we use two factors to achieve the selection process. Experimental results showed the effectiveness of our method. In future work, we will consider the continuous query problem and try to solve the privacy protection in continuous query.