The Irreversibility Transition in Amorphous Solids Under Periodic Shear

Abstract

A fundamental problem in the physics of amorphous materials is understanding the transition from reversible to irreversible plastic behavior and its connection to the concept of yield. Currently, continuum materials modeling relies on the use of phenomenological yield thresholds, however, in many cases the transition from elastic to plastic behavior is gradual, which makes it difficult to identify an exact yield criterion . Recent work has shown that under periodic shear, amorphous solids undergo a transition from deterministic, periodic behavior to chaotic, diffusive behavior as a function of the strain amplitude. Furthermore, this transition has been related to a depinning-like transition in which cooperative avalanche events become system-spanning at the same point. Here we provide an overview of recent work focused on an understanding of the nature of yield in amorphous systems from a cooperative and dynamical point of view.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

11.1 Introduction

Amorphous solids such as plastics, window glass and amorphous metals are an important and ubiquitous form of matter. Industrial processing of such materials commonly involves plastic deformation . Although a microscopic mechanism of plastic deformation in these materials was identified [1–3], the collective behavior on the mesoscale is still being debated [4–7]. The main issues are the definition and nature of yield, how to describe the structural changes that occur during plastic deformation (this is related to the topics of ergodicity and entropy production which are some of the main issues in the general problem of the statistical mechanics description of glasses) and the role of long-range elastic interactions. As we will explain below, these issues play a role in the irreversibility transition discovered not long ago. Recent experiments and simulations on superconductor vortices , dilute colloidal dispersions and loosely packed granular materials show that these materials undergo a transition from reversible to irreversible diffusive behavior by varying the strength of an oscillatory external field [8–17]. These transitions have been ascribed to chaotic scattering [11] and/or to an absorbing phase transition [10].

11.2 Yield as an Irreversibility Transition

Recently, a similar transition was observed in amorphous solids under oscillatory shear, in simulations and experiments performed by several groups [8, 17–28]. These simulations and experiments studied highly condensed jammed materials (well above the jamming transition) under oscillatory shear and showed that for small strain amplitudes, after a transient, the system reaches a configuration which is completely reversible in the sense that particles return to the same position after one or more cycles (see Fig. 11.1). For large strain amplitudes, however, the particles are always diffusing (see Fig. 11.2). There have been several suggestions as to what causes this transition. One suggestion is that the transition from reversible to irreversible dynamics is an absorbing phase transition [24], which is a second order non-equilibrium phase transition , possibly of the directed percolation universality class [18]. The motivation behind this interpretation is that if one looks at the displacement of the particles from their positions before and after a cycle, at low strain amplitudes, one observes transient patches of moving particles which keep decreasing in size until one cannot observe any motion. This is very similar to the dynamics in directed percolation systems where below the percolation threshold there is random dynamics which stops after some time. The state where there is no dynamics is called the “absorbing phase” [29]. While this description is appealing, a closer look shows that there are states in which there is no overall diffusion but the particles do not return to their original positions after one cycle. However, after several cycles, the particles do return to their original positions and for that reason there is no overall diffusion. Furthermore, in all cases the dynamics during a cycle exhibits random particle rearrangements of considerable sizes [30, 31]. These rearrangements are dissipative and thus result in energy fluctuations, but they are completely repetitive (see Fig. 11.3). Therefore, the work being done on the material is transformed wholly into heat and structural rearrangements are reversible. Above a critical strain amplitude, the system does not settle into a limit cycle and the motion is chaotic with a positive maximal Lyapunov exponent. This allows us to define a yield point with a physical meaning. A yield point can be difficult to determine from a standard stress–strain curve since the behavior can be monotonic and there need not be a stress–peak as this depends on the way that the system is prepared. For example, the green curve in Fig. 11.6 was prepared by a fast quench compared to the blue curve in the inset which was prepared via a slow quench. Identifying and understanding the underlying dynamical behavior opens the possibility for a quantitative description of the structural changes in these systems after yield and their relation to the dynamics.

Fig. 11.1

(color online) Experimental evidence for the existence of irreversible states in a sheared colloidal suspension: dark colors represent areas that did not return to their original positions after a different number of cycles: a the first cycle of deformation with $\gamma _0=0.07$, b after 7 cycles, c cycles 1–3 and d cycles 10–12 (Taken from Keim et al. [17])

Fig. 11.2

Mean square displacement from simulations with different values of the maximal strain amplitude: $\gamma _{max}=0.07$ (dark blue circles), 0.08 (blue squares), 0.09 (greed diamonds), 0.1 (green down facing triangles), 0.12 (orange up facing triangles), and 0.14 (purple stars). The simulations were averaged over different runs with samples of $N=4000$ particles quenched from $T=0.466$ (closed symbols) and $T=1.0$ (open symbols). Note the transition between an arrested and diffusive regime as $\gamma _{max}$ is increased (Taken from Fiocco et al. [18])

Fig. 11.3

(color online) The potential energy as a function of cumulative strain during two cycles (red line marks the end of the first cycle)

Fig. 11.4

(color online) Transient behavior of the potential energy before reaching a limit-cycle for three different strain-amplitudes (strain amplitude growing from top to bottom). Red lines are the point at which periodic behavior begins

In all of the experiments and simulations that are mentioned, the strain is applied in a periodic manner: either in a “sawtooth” fashion or as a sinusoidal function [17]. For the “sawtooth” strain profile, the strain is applied in the following manner: First, positive strain steps are applied. When a maximal pre-decided strain $\epsilon _{max}$ is reached, the strain is reversed by applying strain steps in the opposite direction. This proceeds until the strain reaches the negative value of the maximal strain $-\epsilon _{max}$. At this point the strain steps are reversed until the system returns to zero strain, completing the elementary cycle of a specific maximal strain amplitude. The elementary cycle is then repeated and the response of the material per cycle is observed.

Different experiments and simulations [8, 17–24, 27, 28] have found that for small strain amplitudes these systems show random dynamics which gradually settles into a periodic limit-cycle (see Fig. 11.4). As the strain amplitude is increased, the transient times increase accordingly, until the transient time is so large that the system does not reach a limit cycle. Two main approaches have been suggested for describing the level of periodicity of the system. The first approach focuses on comparing the positions of particles before and after a limit-cycle. The long-time dynamics is than analysed by comparing how many particles changed their positions after a cycle [24], how much particles diffused and how the potential energy changed [18]. A limitation of this approach is that the dynamics inside the limit-cycle, which has interesting characteristics, as we will see below, is ignored. A different approach, is based on examining the dynamics inside the limit-cycle and comparing consecutive cycles in order to understand what happens as the system approaches the critical point [19]. In order to measure the time it takes for the system to reach a periodic limit cycle, a cycle decorrelation function was defined using the total potential energy of the system U(t):

$$\begin{aligned} R(n) = \int dt|U(t,n) - U(t,n-p)| . \end{aligned}$$

(11.1)

When $p=1$, this function compares the difference between potential energy fluctuations in two consecutive cycles (n is the number of cycles that the system underwent). For small strain amplitudes this function reaches a value close to zero after n cycles. However, in some cases the system reaches a limit cycle of periodicity p larger than one. Therefore, if periodic behavior is not observed p is increased by one and the function is recalculated. The process was repeated until a value of p for which the function reaches $R(n)=0$ for some n was reached. If periodicity smaller than $p=11$ was not observed p was set to its default value $p=1$. In all cases periodicity larger than $p=5$ was not observed. Figure 11.5 shows this function averaged over 30 different samples of size $N=16{,}384$, each prepared from a different initial condition in the liquid state and than quenched using the same protocol that was used to create the green curve in Fig. 11.6. One can observe that for the strain amplitudes $\gamma =0.06,0.07,0.75,0.85,0.88,0.09,0.093,0.095$ the function relaxes, after a transient time, to zero, while for larger strain amplitudes ($\gamma =0.12,0.15$) the function R(n) does not decay to zero but relaxes to some asymptotic finite value. In the inset to Fig. 11.7 we can see that the relaxation time , the time it takes the cycle-decorrelation function to go below $1\%$ of its initial value, follows a power-law with a critical point at $\gamma _c=0.11$. This critical strain amplitude is close to the yield strain as estimated from the blue linear stress–strain curve in the inset of Fig. 11.6, even though for the oscillatory shear that was used the faster quench protocol that corresponds to the green curve in Fig. 11.6. The transition from a repetitive to random behavior in a deterministic, dissipative system (no external noise is added) suggests that the transition might be a “transition to chaos” which is a well known phenomenon observed in various dynamical systems from the low-dimensional Lorenz system [32] to the high dimensional coupled chaotic maps [33] and involves a divergence (usually power-law) in the time it takes the system to reach periodic behavior as a parameter is varied. A transition to chaos might be associated with a phase transition as we will discuss below, though the connection between the two was not studied extensively, as much as we are aware. The main indication that a system exhibits chaotic behavior is sensitivity to initial conditions: trajectories starting from close-by initial conditions diverge exponentially [34, 35] (see Fig. 11.8). The sensitivity to initial conditions is estimated by measuring the maximal Lyapunov exponent $\lambda$ which describes the rate of growth of the distance between two phase-space trajectories (solutions of the equations of motion with different initial conditions) $\mathbf{x}(t)$ and $\mathbf{x}_{\epsilon }(t)$ which are initially separated by a diminishing distance $|\mathbf{x}(0)-\mathbf{x}_{\epsilon }(0)|=\epsilon$:

$$\begin{aligned} \lambda _{max}=\lim _{t\rightarrow \infty }\lim _{\epsilon \rightarrow 0}\frac{1}{t}\ln {\frac{|\mathbf{x}(t)-\mathbf{x}_{\epsilon }(t)|}{\epsilon }} . \end{aligned}$$

(11.2)

Fig. 11.5

Cycle decorrelation function as a function of the number of cycles, for system size $N=16{,}384$ particles for strain amplitudes $\gamma =0.06,0.07,0.75,0.85,0.88,0.09,0.093,0.095$ (from left to right). (inset) The same function for strain amplitudes $\gamma =0.12$ (blue), $\gamma =0.15$ (green)

Fig. 11.6

(color online) Stress–strain curve from molecular dynamics simulations for 16, 384 particles under quasi-static shear. Red dots represent the number of cycles, n, required to reach periodic behavior under oscillatory shear (scale is on the right side of the figure in red). The red line is the strain amplitude for which the time to reach reversible behavior diverges. Inset Stress–strain behavior for the same parameters as the green curve but with different initial particle configurations - the red line is the same as in the larger figure

Fig. 11.7

(color online) Slowing down: Accumulated strain to reach a limit-cycle as a function of the maximal strain amplitude minus the critical strain amplitude $\Gamma _{\mathrm {c}}=0.11$

Fig. 11.8

(color online) In a chaotic system, the distance between phase-space trajectories diverges exponentially fast

For a periodic system $\lambda _{max}=0$ whereas a chaotic system will have $\lambda _{max}>0$ [34]. There are different methods for calculating the maximal Lyapunov exponent. In [19] the method suggested by Kantz [35, 36] which extracts the largest Lyapunov exponent from a time-series of one of the observables (in our case the potential energy: $u_i=\{u_0,u_1,u_2,\ldots \}$) was used. The advantages of this method is that it has been widely tested, a highly tested code is available in the author’s website and that the results give a relatively clear distinction between chaotic and non-chaotic time-series, as we shall see below. Since we are analyzing a time-series, instead of looking at the distance between two different solutions of the equations of motion, we look for points in the time-series which are at some-point close to each other, i.e. $|u_i-u_k|<\epsilon$ and check how the distance grows over time $d_{\ell }=|u_{i+\ell }-u_{k+\ell }|$. However, since $u_i$ is a one dimensional function of the multi-dimensional phase-space, a simple measure of the distance between them does not reflect the actual distance of the phase-space coordinates that generated them. To overcome this we use Taken’s delay embedding theorem [37] which asserts that for an embedding dimension $m>2 D_A$ where $D_A$ is the dimension of the chaotic attractor (the part in phase-space at which the chaotic behavior occurs), a set of m variables generated by sampling the time-series at regular intervals $\tau \,m$:

$$\begin{aligned} (u_{n-(m-1)\tau },u_{n-(m-2)\tau },\ldots ,u_{n-\tau },u_n), \end{aligned}$$

(11.3)

will have an attractor with the same topological properties as the underlying attractor. As an example we show the reconstruction for the Lorenz system:

$$\begin{aligned} \frac{dx}{dt}= & {} \sigma (y-x)\,,\nonumber \\ \frac{dy}{dt}= & {} x(\rho -z)-y\,,\nonumber \\ \frac{dz}{dt}= & {} xy-\beta z. \end{aligned}$$

(11.4)

In Fig. 11.9 we show the dynamics as a function of all three coordinates which shows the famed Lorenz attractor which is chaotic for the parameters that we chose. To demonstrate reconstruction we take the time-series of one of the coordinates (Fig. 11.10) and construct three new coordinates using time-delay:

$$\begin{aligned} (x_{n-2\tau },x_{n-\tau },x_n), \end{aligned}$$

(11.5)

where we chose $m=3$ and an appropriate $\tau$. We now plot the new coordinates in Fig. 11.11. One can see the resemblance in the structure of the reconstructed attractor and the original one (Fig. 11.9).

Fig. 11.9

Phase space trajectory which is part of the “strange” attractor of the Lorenz system

Fig. 11.10

A representative time-series of the x-coordinate of the Lorenz system in the chaotic regime

Fig. 11.11

Attractor reconstructed from the x coordinate which shares the same topological structure as the original attractor

Typically, in a dissipative system, a chaotic attractor will have a smaller dimensionality than the phase space-dimension. Defining:

$$\begin{aligned} \mathbf{s}_n = (u_{n-(m-1)\tau },u_{n-(m-2)\tau },\ldots ,u_{n-\tau },u_n). \end{aligned}$$

(11.6)

as the delay-coordinates vector, for large enough $\tau$ and m, the distance $d=|\mathbf{s}_{i}-\mathbf{s}_{k}|$ will represent the actual phase-space distance and if the underlying dynamics is chaotic, $d_{\ell }=|\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }|$ will grow exponentially fast. The value of $\tau$ is usually taken to be the de-correlation time of the time-series ($\tau \approx 600$ in this case) but m is unknown since we do not know a-priori the dimension of the attractor. In order to find a numerical estimate of the largest Lyapunov exponent the algorithm calculates the finite-time maximal Lyapunov exponent for a trajectory starting at a point i:

$$\begin{aligned} \lambda ^i_{\ell }=\frac{1}{\ell }\ln {\frac{||\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }||}{\epsilon }} . \end{aligned}$$

(11.7)

where $||\mathbf{s}_{i}-\mathbf{s}_{k}||<\epsilon$ with respect to some norm ||..|| (the actual norm used in the algorithm is $||\mathbf{s}_{i}-\mathbf{s}_{k}|| = |u_{i}-u_{k}|$ for reasons explained in [35]). For each point $\mathbf{s}_i$ and a small distance $\epsilon$ a set of points $\mathbf{s}_k$ such that $||\mathbf{s}_{i}-\mathbf{s}_{k}||<\epsilon$ is gathered which allows to calculate the average distance from the point $\mathbf{s}_i$ as a function of $\ell$:

$$\begin{aligned} \lambda ^i_{\ell }=\frac{1}{\ell }\ln {\frac{1}{\mathcal {U}_i}\sum _k\frac{||\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }||}{\epsilon }} . \end{aligned}$$

(11.8)

where $\mathcal {U}_i$ is the total number of points $\mathbf{s}_{k}$ that are $\epsilon$ close to $\mathbf{s}_{i}$. The process is repeated for different initial points $\mathbf{s}_i$ which leads to further averaging. The actual function that we calculate is:

$$\begin{aligned} S_{\ell }=\frac{1}{\mathcal {\mathcal {W}}}\sum _i\ln {\left( \frac{1}{\mathcal {U}_i}\sum _k\frac{||\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }||}{\epsilon }\right) } . \end{aligned}$$

(11.9)

where $\mathcal {W}$ is the number of starting points i collected. Since this function describes the $\ln$ of the averaged growth of distances as a function of time, we expect that in a chaotic system ($\lambda _{max}>0$) $S_{\ell }$ will show linear behavior with a positive slope for large enough $\ell$. However, there are two caveats for this: the maximal Lyapunov exponent becomes dominant only after several time steps $\ell _0$:

$$\begin{aligned} ||\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }|| = \sum _i a_ie^{\lambda _i \ell }\approx _{_{\ell >\ell _0}} a_{_{max}}e^{\lambda _{_{max}} \ell } . \end{aligned}$$

(11.10)

The second caveat is that for large $\ell$ the distance $||\mathbf{s}_{i+\ell }-\mathbf{s}_{k+\ell }||$ can reach the size of the attractor and thus the trajectories start to fold back. When that happens $S_{\ell }$ saturates. In Fig. 11.12 one can see the function $S_{\ell }$ for a potential energy time-series of a system of size $N=4096$ sheared at maximal strain amplitudes $\gamma =0.12,0.15,0.2$ which are all above the critical amplitude [19]. Since the dimension of the attractor is not known a-priory all the values of m starting from $m=1$ were checked until the shape of $S_{\ell }$ did not change under further increase (remember that according to Takens theorem the delay coordinates should give the right result for any $m>2D_A$ where $D_A$ is the dimension of the attractor). For m values 5, 6, 6 respectively, the function $S_{\ell }$ shows a linear regime with a positive slope which indicates a positive maximal Lyapunov exponent.

Fig. 11.12

Estimation of Lyapunov exponents: The function $S_{\ell }$ of the time delay $\ell$ for a system of size $N=4096$ under oscillatory shear in different strain amplitudes larger than the critical amplitude. The straight lines are shown as a guide to the eye

In Fig. 11.13 we can see the result of applying the algorithm for one of the periodic limit-cycles with different values of m. One can see that the behavior is significantly different from that observed for the chaotic time-series: there is no linear regime and the values of $S_{\ell }$ are negative for large enough values of m. This function shows a distinct behavior when calculated for chaotic time-series: for an intermediate range of $\ell$ it will have a linear, positive slope where the value of the slope is the value of the Lyapunov exponent. In Fig. 11.12 we can see the function $S_{\ell }$ for a time-series of potential energy values for a system of size $N=4096$ sheared at maximal strain amplitudes $\gamma =0.12,0.15,0.2$ all above the critical amplitude. In all three cases the function shows linear behavior for intermediate values of $\ell$ indicating a positive Lyapunov exponent and hence chaotic behavior. These results are consistent with previous results for the maximal Lyapunov exponent for amorphous solids under linear shearing obtained in experiments [38] and simulations [39]. These results suggest that amorphous solids undergo a transition to chaos at a strain amplitude coincident with yield at least under oscillatory shear. One should note that a transition to chaos is not necessarily accompanied by a nonequilibrium phase transition and although it shows behavior similar to critical slowing down, it is not necessarily accompanied by critical fluctuations and a growing correlation length, which are expected in a non equilibrium phase transition such as directed percolation. However, it has been suggested that in high dimensional systems, such as fluid turbulence and ecological systems, a transition to chaos (or turbulence) can be accompanied and even be a result of, a non equilibrium phase transition such as directed percolation [40, 41]. Below we discuss how the transition to chaos is related to a different non equilibrium phase transition.

Fig. 11.13

The function $S_{\ell }$ applied for a periodic limit-cycle. The behavior is strikingly different than the one shown in Fig. 11.12 and includes negative values

11.2.1 Analysis of Periodic Behavior

As we explained above, for strain amplitudes smaller than the critical value, after a transient regime, the system shows fluctuating but periodic behavior. This resembles the reversible regime of dilute colloidal systems, of the types studied in [10, 11]. However, in these systems, the dynamics in a limit-cycle is quite trivial since the response becomes periodic only once the particles reach a configuration in which they do not touch each other during the cycle. On the contrary, in a highly condensed amorphous solid, particles change positions and rearrange in a non trivial manner, causing non affine deformation , even during a reversible limit cycle. Typically, this involves a large number of rearrangements of the T1 type (two next-nearest neighbours becoming nearest neighbors) which generate elastic-inclusion like displacement fields (see Fig. 11.14) and appear as energy drops in the potential energy time-series. The repetitive behavior can also be observed by following the trajectory of any single particle over consecutive cycles (blue and red lines in Fig. 11.15). The non-affine nature of the displacement of the particle is clearly seen in the figure. One should note that contrary to the usual notion the rearrangement events that are observed in the limit cycles are completely repetitive so that one can think of the dynamics inside a limit-cycle as a special form of non-linear elasticity rather than plasticity. It seems that the oscillatory loading reveals a distinction between plastic and nonlinear elastic rearrangements (for example, the phenomenon of super-elasticity in shape memory alloys [42–44]) which is somewhat subtle.

Fig. 11.14

Displacement field after a local particle rearrangement. Arrows indicate the direction and magnitude of displacement of each of the particles

Fig. 11.15

Two consecutive trajectories of one particle taken when the system is in a limit-cycle: blue is the first cycle and red is the one just after it. The trajectories are very similar

Fig. 11.16

(color online) Analysis of one limit cycle with a certain strain amplitude: Energy drops (rearrangement events ) are identified and marked as black lines on this curve

Fig. 11.17

(color online) A plot of the position of energy drops (marked as black dots) on the limit cycle as a function of the strain amplitude (x-axis) for one system of size $N=1024$. The y-axis is the time inside a limit-cycle

Fig. 11.18

Effect of thermal noise: System relaxes into a limit-cycle after initial overdamped dynamics (green). It is then subject to the same dynamics accompanied by a small Langevin noise. After some time it “hops” to another limit-cycle

Fig. 11.19

(color online) Periodic limit cycles with period 5 at strain amplitude $\gamma =0.09$. The green curve is the applied strain (not to scale). Red lines represent the start and the end of a cycle

In Fig. 11.16 energy drops (rearrangement events) are identified and marked as black lines. The points in the limit cycle where these drops occur are marked as black dots in the columns of Fig. 11.17 where time advances from bottom to top. The x-axis in Fig. 11.17 is the strain amplitude. This is repeated for different strain amplitudes with the same initial conditions. It was found that for small strain amplitudes limit-cycles that start from the same initial conditions are similar to each other and an increase of the strain amplitude changes the limit-cycle in a gradual manner. However, for large strain amplitudes small increments in the strain amplitude result in a completely different limit-cycle. This might be a manifestation of the coexistence of many different limit-cycles which occupy different parts of the state-space and of the existence of “riddled basins of attraction” where infinitesimally close initial points in state-space lead to completely different attractors [34, 45]. In Fig. 11.18 we can see the effect of applying Langevin noise to a system that is already in a limit-cycle (these simulations were performed using overdamped dynamics). After a few cycles the system escapes from the initial limit-cycle and settles in a different limit-cycle. This is another indication that there are a large number of nearby limit-cycles and also shows that a limit-cycle can survive a small level of thermal noise. While the limit cycle that is shown in Fig. 11.15 repeat themselves after one cycle, for large strain amplitudes cycles that repeat themselves after 2, 3, 4 and 5 cycles were observed (see Figs. 11.19, 11.20) which is a phenomenon observed in many dynamical systems and in some cases can lead to a transition from periodic to chaotic behavior. This can happen in systems that show “frequency locking” or “period doubling bifurcations”. In a system showing a transition to chaos due to period doubling , the period of the limit-cycle doubles for certain values of the control parameters. A succession of period doubling bifurcations (a period doubling cascade) leads to an infinite period and chaos. Below we will describe a possible explanation for the connection between the observed period doubling and the transition to chaos in amorphous solids.

Fig. 11.20

Limit cycles: Repetitive particle trajectories in a period-two limit-cycle. a shows the entire system, b shows local environment and the trajectories that each particle is undergoing and c shows the trajectory of one particle. d shows the strain applied using the Lees Edwards boundary conditions (purple arrows show how the Lees-Edwards boundaries move with respect to the simulation square when the system is sheared in the positive direction). Since the limit cycle has period two the trajectories repeat themselves only after two shearing cycles (the blue and green lines in d). The particle starts from the orange initial point and moves to the right on the blue trajectory, due to the external strain that shears the material to the right, then moves back to the center and to the right, when the strain is changed accordingly (blue curve on d). When the strain is set back to zero, the particle reaches the purple point. Then, when the strain is applied again to the right, the particle moves accordingly, but this time on the green trajectory. The particle then moves to the center and to the left due to the applied strain (green curve in d). Eventually the particle comes back to the orange point, the initial condition. The next two cycles repeat the same two trajectories, and the same for the following cycles

11.3 Ergodicity

The emergence of chaotic behavior can explain an important aspect of the physics of amorphous solids. In previous studies [46–48] it was shown that the effective or “fictive” temperature that describes the structure of an amorphous solid depends on the initial quench of the system. However, when the material is deformed, the effective temperature of systems that were quenched using different cooling protocols converge to the same steady-state value which depends on the work performed on the system (and on the thermal bath temperature, when it is larger than zero). This has been described as overaging or rejuvenation of the amorphous solid [46], depending on whether the effective temperature increases or decreases. We can understand this behavior in terms of the onset of chaos. The existence of a positive maximal Lyapunov exponent is an indication that the system is not only chaotic, but that the dynamics is ergodic on a chaotic attractor which occupies part of the state-space (this is different than ergodicity in Hamiltonian systems in which the entire state-space for a given energy is explored). Since every initial condition ends up on the attractor, and the dynamics on the attractor is ergodic, averaged observables will eventually show the same values independent of the initial configuration. In Fig. 11.21 we see three different limit cycles all simulated with the same system size and sub-yield strain amplitude but with different initial conditions. We observe that whereas the period is the same, the details of the cycles (energy fluctuations) depend on the initial configuration which indicates that the final state depends on the initial conditions, as we expect from a non-ergodic system . This dependence on initial conditions is clearly seen when one looks at the average potential energy as a function of the cumulative strain (Fig. 11.22 taken from Fiocco et al. [18]). One can observe that starting from two different initial quenches, with different potential energies, the final potential energy depends on the initial quench when the maximal strain amplitude is sub-yield and does not depend on the initial conditions when the maximal strain amplitude is above-yield which indicates that the system regains some kind of ergodicity above yield.

Fig. 11.21

(color online) Several different limit-cycles that were obtained using the same control parameters (number of particles, shearing steps, amplitude of shear) but different initial conditions

Fig. 11.22

Ergodicity breaking - Potential energy per particle E for zero-strain configurations, for different maximal strain amplitude $\gamma _{max}$ [0.07 (dark blue circles), 0.08 (blue squares), 0.09 (green diamonds), 0.1 (green down facing triangles), 0.12 (orange up facing triangles), and 0.14 (purple stars)], averaged over different runs with samples of $N=4000$ particles quenched from $T=0.466$ (closed symbols) and $T=1.0$ (open symbols). (Taken from Fiocco et al. [18])

Fig. 11.23

Reversible (repetitive) Avalanches. An avalanche in a sub-critical limit-cycle for a system with $N=16{,}384$ particles and maximal strain amplitude $\Gamma =0.1$. Even though the avalanche spans a large part of the system, it is repeated under repeating strain cycles of identical strain amplitude. The arrows mark the displacement during the avalanche and the colors represent the magnitude of the displacement (warm - large displacement, cold - small displacement)

11.4 Interactions and a Non-equilibrium Phase Transition

It is well known that solids under plastic deformation exhibit power-law noise due to large correlated plastic events which resemble avalanches [31, 49] (see Fig. 11.23). A connection between the avalanche statistics and the irreversibility transition was explored by studying the avalanche statistics for different maximal strain amplitudes and system sizes [30]. Since the simulations were athermal, potential energy drops were identified with plastic rearrangement events. For each simulation, all of the energy drops in the last shear cycle (to avoid transient effects), were extracted and used to create a histogram of the energy drops which was used to calculate the average energy drop for each maximal strain amplitude [30]. We observe in Fig. 11.24 a cusp in the average potential energy at the point at which the irreversibility transition occurs, followed by saturation to a value which depends on the system size, at large strain amplitudes. The cusp suggests that the irreversibility transition is related to a change in the avalanche dynamics, and the system size dependence of the saturation suggests that there is a saturating correlation length both indicative of critical behavior [50, 51].

Fig. 11.24

Mean energy drops. The mean energy drop as a function of the maximal strain amplitude for the largest system size. Note the distinct cusp at the irreversibility point

Fig. 11.25

Depinning theory in the amorphous plasticity context. a Depinning theory describes the motion of an elastic interface (here a one-dimensional front) in a random potential. The circles represent the (plastic) displacement of each point in the front. The front is subject to an applied force which causes it to move but elements of the front are pinned locally and need to overcome energy barriers. The different elements of the front are connected by springs so that if one pinned site overcomes the energy barrier it is pulling its nearest neighbors (and only them). b If the interactions are long range, different pinned elements of the front interact with distant elements and the actual structure of the front becomes immaterial. c In this case there is no real difference between the equations that describe a front and the equations that describe the interaction of some collection of pinning sites distributed in the material. A simple model of plasticity [52] that belongs to the depinning universality class, has been shown to describe the dynamics of an amorphous solid under shear where “shear transformation zones” or “weak spots” are dispersed in the material and affect each other with long-range elastic interactions

The avalanche statistics was interpreted using a simple model [52] that belongs to the same universality class as the theory of front depinning which was originally developed to explain the motion of an interface in a random media. This motion involves parts of an interface overcoming local energy barriers due to external forcing and neighbouring locations in the interface “pulling” the site back. The forward motion of the interface occurs in avalanches. In the case of long-range interactions, such as the ones that exist in elasto-plastic systems, the notion of a “front” becomes more abstract since sites that are far apart affect each other and the notion of locality becomes blurred (see Fig. 11.25 for illustration). This explains why the same equations can also describe avalanche behavior associated with the plasticity of amorphous solids in which the dynamics involves overcoming random energy barriers and long-range interactions , even if an actual front may not exist. The equations of motion describing the time evolution of the plastic displacement field $u(\mathbf{r},\mathbf{t})$ controlled by overdamped dynamics are [52]:

$$\begin{aligned}&\eta \frac{\partial u(\mathbf{r},\mathbf{t})}{\partial t} \nonumber = \\&F + \int d^2r' J(\mathbf{r}-\mathbf{r'})\, [\mathbf{u}(\mathbf{r'},\mathbf{t}) -\mathbf{u}(\mathbf{r},\mathbf{t})] - \mathbf{f}_\mathbf{R}(\mathbf{u},\mathbf{r}), \end{aligned}$$

(11.11)

where $\eta$ is the viscosity, F is an externally applied force, $\mathbf {r}$ is a position of a deformable region (Shear transformation zone ), $J(\mathbf {r}-\mathbf {r'})$ is the Green’s function for the elastic interaction between different “soft” regions located at points $\mathbf {r}$ and $\mathbf {r}'$ and $f_R(u,\mathbf {r})$ is a random pinning potential representing the structural disorder inherent to such systems. This model assumes that the nature of the structure (the distribution of the random pinning forces $f_R(u,\mathbf {r})$) does not change as a function of time. In amorphous solids the randomness is self-generated and can (and typically does) change under plastic deformation. However, when the system is at a steady-state under linear or cyclic shearing, one can assume that the disorder is fixed. Also, the scaling behavior of the model predictions do not change if the pinning stresses randomly change in time. This model exhibits a non-equilibrium phase transition between a pinned, static state and a flowing state as the stress is slowly increased past a critical force $F_{\mathrm {c}}$ [52]. The transition is a critical point involving correlated displacement jumps. These correlations are described in terms of a scaling theory, which was derived from a mean-field (infinite interaction range) approximation and renormalization group theory [52, 53]. This theory was indeed shown to give a good description of the statistics of avalanches during plastic deformation in crystals [54–57] and is now also being applied to amorphous solids [58–60]. For an applied external force, at zero velocity (quasi-static limit) it was found that at a critical force $F_{\mathrm {c}}$ the avalanche size distribution scales as:

$$\begin{aligned} D(\mathcal {S}) \sim \mathcal {S}^{-\tau }, \end{aligned}$$

(11.12)

where $\mathcal {S}$ is the avalanche size and $\tau$ is a universal critical exponent. Below $F_{\mathrm {c}}$ the distribution follows the same power law but with a maximal size (cutoff):

$$\begin{aligned} \mathcal {S}_{\mathrm {max}}\sim (F_{\mathrm {c}} - F)^{-1/\sigma }, \end{aligned}$$

(11.13)

where $\sigma$ is the cutoff exponent. Then the distribution function takes the form:

$$\begin{aligned} D(\mathcal {S},F) \sim \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S}/\mathcal {S}_{\mathrm {max}})\sim \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S}(F_{\mathrm {c}} - F)^{1/\sigma }), \end{aligned}$$

(11.14)

where $\mathcal {D}(x)\sim A\,e^{-Bx}$ is a universal cutoff scaling function but the constants A and B are system specific [52, 53].

11.4.1 Statistics Under Oscillatory Shear

The application of depinning theory for amorphous solids under oscillatory shear involves modifying the theory to take into account different factors that were not included in the theory described above which assumes a steady force. One issue is that the disorder in amorphous solids is not quenched which can affect the statistics. For example, there could be weakening effects during an avalanche event, where the same site can be triggered more than once. This has been addressed by Dahmen et al. [52] and was shown to affect the stress–strain curve but not the scaling exponents [53]. The second effect of having dynamic disorder is that the distribution which describes the random variable $f_R(u,\mathbf {r})$ can change during a cycle. This issue was avoided by performing statistics only for avalanches in “steady-state” cycles, when the avalanche statistics is stable. It is known that the exact distribution of the disorder does not affect the avalanche statistics so even if the disorder is different in different cycles, that should not change the scaling functions. Another issue is that the forcing is a “sawtooth”, periodic strain profile. In order to take that into account (11.14) was rewritten in terms of the strain and integrate over the different strain amplitudes. The relation between the stress and the strain shows hysteresis due to the nonlinear nature of plastic deformation. One immediate consequence of the existence of avalanches (and plastic events in general) is that the stress–strain curve becomes non-linear and exhibits hysteresis - the stress becomes a multivalued function of the strain (see Fig. 11.26). In principle, this nonlinearity can be deduced directly from the avalanche statistics. In the case of amorphous plasticity, however, in order to get an analytical solution certain approximation were needed as will be explained below. Since the forward and reverse straining branches of the hysteresis curve are statistically identical, we take into account only the forward direction. For the forward branch, we can model the relation between stress and strain using the scaling relation:

$$\begin{aligned} (\Sigma _{\mathrm {c}} - \Sigma ) \sim (\Gamma _{\mathrm {c}} - \Gamma )^{\delta } . \end{aligned}$$

(11.15)

where $\Gamma _{\mathrm {c}}$ is the critical strain and $\Sigma _{\mathrm {c}}$ is the critical stress which is related to the critical force $F_{\mathrm {c}}$ in a manner which will be explained below. The exponent $\delta$ was found to be $\delta = 1.25$ by fitting (see Fig. 11.27). The increment in plastic displacement $u_p$ due to an infinitesimal change in the force is [52]:

$$\begin{aligned} du_{\text {p}}\sim \langle \mathcal {S}\rangle _{\mathrm {F}} dF, \end{aligned}$$

(11.16)

for a small force increment ${ {dF}}$ over the current force F (the avalanche size $\mathcal {S}$ is the amount of slip or displacement in an avalanche event and $\langle \mathcal {S}\rangle _F$ is the average avalanche size for a constant applied force F). This can be translated to an equation for the force-displacement behavior, using the theoretical scaling law for $\langle \mathcal {S}\rangle _F$:

$$\begin{aligned} \frac{du_{\text {p}}}{dF} = \mathcal {C}\left( \frac{F_{\text {c}}}{F_{\text {c}}-F}\right) ^{\alpha } = \mathcal {C} f^{-\alpha }, \end{aligned}$$

(11.17)

where $\mathcal {C}$ is a constant with dimensions of length/force, $f=\frac{F_{\text {c}}-F}{F_{\text {c}}}$ and $\alpha$ is a critical exponent. When the avalanche size diverges, the behavior will be affected by finite size effects. If we assume that the irreversibility transition under oscillatory shear occurs at the same maximal strain amplitude as the non-equilibrium phase transition one can explain the finite-size dependence the results obtained by Fiocco et al. [18] which observed that the critical strain amplitude for the irreversibility transition decreases with system size: The maximal strain amplitude $\Gamma$ is related to the maximal displacement by $\Gamma = u/L$. If we integrate (11.17) directly, we expect to get $u_{\text {p}}\sim \ln L^{-1/\nu }$ when $F\rightarrow F_{\text {c}}$, where $\nu$ is the critical exponent associated with the correlation length since the correlation length $\xi \propto f^{-\nu }$ must be smaller than the system size L. This gives a system size dependence of the plastic critical strain amplitude:

$$\begin{aligned} \Gamma _{\text {p,c}}\sim \frac{\ln L}{L}. \end{aligned}$$

(11.18)

However, the total yield strain is the sum of the elastic $\Gamma _{\text {p,c}}$ and the plastic $\Gamma _{\text {e,c}}$ yield strains:

$$\begin{aligned} \Gamma _{\text {c}} = \Gamma _{\text {p,c}} + \Gamma _{\text {e,c}} \sim b\frac{\ln L}{L} + \Sigma _{\text {c}}/\mu \end{aligned}$$

(11.19)

such that for $L\rightarrow \infty$

$$\begin{aligned} \Gamma _{\text {c}}\rightarrow \Sigma _{\text {c}}/\mu , \end{aligned}$$

(11.20)

where $\mu$ is the shear modulus, b is a constant and $\Sigma _{\text {c}}$ is the critical stress for depinning. This prediction is compared in Fig. 11.28 to the transition to chaos points obtained from our simulations for three different system sizes. By fitting the critical strain was estimated to be $\Gamma _{\text {c}}\approx 0.11$ for infinite systems. This should also be compared with other theoretical results that predict a yield strain due to the appearance of a system spanning plastic event [61]. We substitute (11.15) into (11.14) and obtain a scaling relation for the avalanche size distribution as a function of the strain amplitude:

$$\begin{aligned} D(\mathcal {S},\Gamma ) \sim \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S} (\Gamma _{\mathrm {c}} - \Gamma )^{\delta /\sigma }), \end{aligned}$$

(11.21)

which would be expected to describe the avalanche statistics close to the critical strain amplitude. However, for oscillatory driving, the scaling function $D(\mathcal {S},\Gamma )$ requires corrections since the avalanche size distribution measured is a result of integration over a varying amount of applied strain. Since the strain increases and decreases periodically, the system spends time both below and above the critical strain amplitude. Because we are averaging over cycles, we need to integrate over the different strain amplitudes.

Fig. 11.26

Stress–strain curve exhibiting Hysteresis. Red and green branches are the relevant parts of the curve for the avalanche statistics. In the calculation we assume that they provide identical statistics

Fig. 11.27

Comparison of 30 stress–strain curves from simulations ($N=16{,}384$, $\Gamma =0.097$) with (11.5) in the main text, (thick dark-yellow curve) with a critical exponent $\delta =1.25$

Fig. 11.28

Finite size effects in the critical strain amplitude

Below the transition we get the equation:

$$\begin{aligned} P(\mathcal {S},\Gamma ) \sim \int _{-\Gamma }^{\Gamma } d\varepsilon \, \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S}(\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }), \end{aligned}$$

(11.22)

where $P(\mathcal {S},\Gamma )$ is the distribution of avalanche sizes at maximal strain amplitude $\Gamma$, and $\varepsilon$ is the instantaneous strain amplitude during a cycle $\varepsilon \in [-\Gamma ,\Gamma ]$.

By changing the variable of integration in (11.22), we get:

$$\begin{aligned} P(\mathcal {S},\Gamma )\sim & {} \int _{-\Gamma }^{\Gamma } d\varepsilon \, \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S}(\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }) \nonumber \\= & {} \int _{0}^{\Gamma } d\varepsilon \, \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S}(\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }) \nonumber \\+ & {} \int _{-\Gamma }^{0} d\varepsilon \, \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S} (\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }). \end{aligned}$$

(11.23)

Next, we make two simplifications: first, we perform the integral only in the forward shearing direction (the red part of the curve in Fig. 11.26) since the statistics are symmetric to the shearing direction, second, we neglect the second integral because for strain amplitudes that are away from the critical point (the blue parts of the curve in Fig. 11.26) the fluctuations are very small (the distribution function is an exponential). Substituting for $\mathcal {D}(x)$, we get:

$$\begin{aligned} P(\mathcal {S},\Gamma ) \sim \int _{0}^{\Gamma } d\varepsilon \, \mathcal {S}^{-\tau } \mathcal {D}(\mathcal {S} ( \Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }) \end{aligned}$$

(11.24)

$$\begin{aligned} = \int _{0}^{\Gamma } d\varepsilon \, \mathcal {S}^{-\tau } A e^{-B\mathcal {S}( \Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }} \end{aligned}$$

(11.25)

substituting

$$\begin{aligned} x=B\mathcal {S}( \Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma } \end{aligned}$$

(11.26)

$$\begin{aligned} \varepsilon = \Gamma _{\text {c}} - \left( \frac{x}{B\mathcal {S}}\right) ^{\sigma /\delta } \end{aligned}$$

(11.27)

we get:

$$\begin{aligned} P(\mathcal {S},\Gamma ) = -\mathcal {S}^{-\tau -\sigma /\delta } \frac{A\sigma /\delta }{B^{\sigma /\delta }}\int _{B\mathcal {S}( \Gamma _{\text {c}} )^{\delta /\sigma }}^{B\mathcal {S}( \Gamma _{\text {c}} - \Gamma )^{\delta /\sigma }} dx\, x^{\sigma /\delta -1} e^{-x} \end{aligned}$$

(11.28)

close to the critical point $\Gamma \rightarrow \Gamma _{\text {c}}$ the typical avalanche size $\mathcal {S}$ is very large. Therefore, we assume that taking the lower limit to infinity will contribute a negligible change to the result:

$$\begin{aligned} \sim -\mathcal {S}^{-\tau -\sigma /\delta } \frac{A\sigma /\delta }{B^{\sigma /\delta }}\int _{\infty }^{B\mathcal {S}( \Gamma _{\text {c}} - \Gamma )^{\delta /\sigma }} dx\, x^{\sigma /\delta -1} e^{-x} \end{aligned}$$

(11.29)

This gives the scaling function for the fluctuations below the critical point:

$$\begin{aligned} P(\mathcal {S},\Gamma ) \mathcal {S}^{\lambda } \sim \mathcal {F}(\mathcal {S}( \Gamma _{\mathrm {c}} - \Gamma )^{\chi }), \end{aligned}$$

(11.30)

where $\lambda = \tau +\sigma /\delta$ and $\chi = \delta /\sigma$. The scaling function is generally unknown. However, for mean-field depinning theory it was calculated to be $\mathcal {F}(x)=-\gamma (1/\chi ,-x)$, where $\gamma (a,x)$ is the complementary gamma function and seems to agree with the data collapse (see Figs. 11.29, 11.30). Avalanche sizes in plasticity are usually associated with the amount of slip, which is proportional to the stress drop. However, as was shown in refs [49, 62], in the steady-state the fluctuations of stress and potential energy drops are proportional due to a sum rule. This was assumed to apply here as well. If the maximal strain amplitude $\Gamma$ is larger than the critical value, we have to average over the statistics both below and above the critical strain amplitude. Due to the quasi-static forcing (zero strain-rate), for strains larger or equal to the critical strain amplitude, the system is expected to be exactly at criticality [63], and the avalanche statistics is expected to behave as a pure power-law:

$$\begin{aligned} D(\mathcal {S},\varepsilon \ge \Gamma _{\mathrm {c}}) \sim \mathcal {S}^{-\tau }. \end{aligned}$$

(11.31)

Substituting, we obtain:

$$\begin{aligned} P(\mathcal {S},\Gamma )\sim & {} \int _{0}^{\Gamma _{\mathrm {c}}} d\varepsilon \, \mathcal {S}^{-\tau } Ae^{-B\mathcal {S} (\Gamma _{\mathrm {c}} - \varepsilon )^{\delta /\sigma }} \nonumber \\+ & {} (\Gamma -\Gamma _{\mathrm {c}})\, \mathcal {S}^{-\tau }, \nonumber \end{aligned}$$

where we have performed the integral over the last term.

Fig. 11.29

Fluctuations: Energy drop distribution generated from log histograms for five different maximal strain amplitudes below the transition for strain amplitudes $\Gamma =0.05,0.07,0.08,0.085$ and 0.093

Fig. 11.30

Data collapse: Data collapse for five different maximal strain amplitudes below the transition compared to the mean-field scaling function $\mathcal {F}(x)=-\gamma (\sigma /\delta ,-x)$, where $\gamma (a,x)$ is the complementary gamma function (marked by a black line)

Fig. 11.31

Average energy drops versus stress drops for three different maximal strain amplitudes. The figure shows that the energy drops grow linearly with the stress drops

As demonstrated by Lerner et al. [62] and further developed by Salerno et al. [64] when the system is in a steady-state, there is a simple relation between an energy drop and the concurrent stress drop. The relation stems from the fact that at the steady-state, the work done on the system by the straining is balanced by the energy drops. Thus, they got the sum rule:

$$\begin{aligned} \frac{\langle \Sigma _{\text {s}}\rangle }{4\mu }\sum _{\text {i}} \Delta \Sigma _{\text {i}} = \sum _{\text {j}} \Delta \mathcal {U}_{\text {j}} \end{aligned}$$

(11.32)

where $\mu$ is the shear modulus, $\Delta \Sigma _{\text {i}}$ is a stress drop, $\Delta \mathcal {U}_{\text {j}}$ is an energy drop and we have assumed that there is a well-defined average stress $\langle \Sigma _s\rangle$ at the steady-state. Under oscillatory shear conditions the steady-state stress depends on the strain amplitude, but for a small strain interval this relation should still hold. Therefore, at the steady-state the sum of the energy drops is proportional to the sum of the stress drops. For large avalanches, which are dominant in determining the power-laws, this suggests that individual stress and energy drops are also proportional. This was confirmed in the simulations by Salerno et al. [64]. Indeed, this behavior was also observed for oscillatory shear where the stress and energy drops were found to be proportional (see Fig. 11.31).

Using (11.30), data collapse was found for five maximal strain amplitudes $\Gamma =0.05,0.07,0.08,0.085$ and 0.093 at system size $N=16{,}384$ (Figs. 11.29, 11.30) from which $\lambda$ and $\chi$ were extracted.

We expect to have data collapse only for intermediate strain amplitudes - for strain amplitudes smaller than $\Gamma =0.05$ the statistics are not good enough because there are not many energy drops (about 10 per cycle or less). Furthermore, far from the critical point the avalanche statistics is not expected to show the same behavior since the system is far from the singularity. For strain amplitudes that are too close to the critical point, finite size effects dominate. Close to the critical point we typically use the following expression:

$$\begin{aligned} g(f) = \xi ^{\alpha /\nu } g_0(L/\xi ) \end{aligned}$$

(11.33)

where $\xi =f^{-\nu }$ is the correlation length, $f=\frac{F-F_{\mathrm {c}}}{F_{\mathrm {c}}}$ is the rescaled force, g(x) is our scaling function, L is the system size, $\alpha$ and $\nu$ are the critical exponents ($\nu$ is the critical exponent of the correlation length) and $g_0(x)$ is the finite size scaling function who’s properties are:

$$\begin{aligned} g_0(x) \rightarrow x^{\alpha /\nu },\, x\rightarrow \infty \end{aligned}$$

(11.34)

and:

$$\begin{aligned} g_0(x) \rightarrow C,\, x\rightarrow 0 \end{aligned}$$

(11.35)

where C is a constant. Therefore, close to the critical point we get:

$$\begin{aligned} g(f) \sim L^{\alpha /\nu } \end{aligned}$$

(11.36)

which means that one cannot use the same function to describe the scaling behavior for maximal strain amplitudes in the intermediate range and close to the transition.

Using the estimate of $\delta$, the critical exponents values $\tau =1.04[0.26]$, $\sigma =0.59[0.04]$ were found from the data collapse. The exponents deviate from the exponents found using mean-field depinning theory, which are $\tau =1.5$ and $\sigma =0.5$. There are several possible reasons for that. The first possibility is that inertia effects are changing the exponents as was suggested by Salerno et al. [49], for simulations under direct shear (not alternating). This might be an issue since in [19, 30] the FIRE (Fast Inertial Relaxation Engine) algorithm was used to minimise the potential energy. Another possibility is that since the elastic interactions can be both positive and negative, contrary to the only positive interactions exhibited by most depinning models, the mean field is in a “marginal state” [65] which dictates different scaling behavior. The main caveat to this approach, as we see it, is that the theoretical predictions that assume such behavior, based on scaling arguments [66, 67] and analytic calculations for hard spheres at infinite dimensionality [68] does not show the behavior that we are observing here. We believe that the discrepancy from both depinning theory and marginal stability might be a result of having anisotropic interactions which causes the formation of plastic events in specific directions [69], something that as much as we are aware, is not been taken explicitly into account in both theories. Another possibility is that the upper critical dimension is higher in amorphous solids than in standard depinning and in that case one may have to take into account corrections to the critical exponents. We hope that further work will clarify these points.

11.4.2 Average Fluctuations

From the relevant critical exponents we can obtain the average energy fluctuations introduced in Fig. 11.24 using similar analysis as above. In order to calculate the average fluctuation size in a cycle we integrate over the same probability distributions but divide by the strain amplitude:

$$\begin{aligned} \langle \mathcal {S}^n\rangle _{\Gamma } \sim \int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\, \mathcal {S}^{n}\mathcal {S}^{-\tau }\frac{2}{\Gamma }\int _{0}^{\Gamma } d\varepsilon \, Ae^{-B\mathcal {S} (\Gamma - \varepsilon )^{\delta /\sigma }} \end{aligned}$$

(11.37)

for $\Gamma < \Gamma _{\text {c}}$ and:

$$\begin{aligned} \langle \mathcal {S}^n\rangle _{\Gamma } \sim \int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\, \frac{2}{\Gamma }\int _{0}^{\Gamma _{\text {c}}} d\varepsilon \,\mathcal {S}^{n}\mathcal {S}^{-\tau } Ae^{-B\mathcal {S} (\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }} \end{aligned}$$

(11.38)

$$\begin{aligned} +\int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\frac{2}{\Gamma }\int _{\Gamma _{\text {c}}}^{\Gamma }\,\mathcal {S}^{n}\mathcal {S}^{-\tau } \end{aligned}$$

(11.39)

for $\Gamma >\Gamma _{\text {c}}$. After integration:

$$\begin{aligned} \langle \mathcal {S}^n\rangle _{\Gamma } \sim \int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\, \frac{2}{\Gamma }\int _{0}^{\Gamma _{\text {c}}} d\varepsilon \,\mathcal {S}^{n}\mathcal {S}^{-\tau } Ae^{-B\mathcal {S} (\Gamma _{\text {c}} - \varepsilon )^{\delta /\sigma }} \end{aligned}$$

(11.40)

$$\begin{aligned} +\int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\,\mathcal {S}^{n}\mathcal {S}^{-\tau }\frac{(\Gamma -\Gamma _{\text {c}})}{\Gamma } \end{aligned}$$

(11.41)

$$\begin{aligned} \langle \mathcal {S}\rangle\sim & {} \int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\, \frac{2}{\Gamma }\int _{0}^{\Gamma _{\mathrm {c}}} d\varepsilon \,\mathcal {S}^{1-\tau } Ae^{-B\mathcal {S} (\Gamma _{\mathrm {c}} - \varepsilon )^{\delta /\sigma }}\nonumber \\+ & {} \frac{(\Gamma -\Gamma _{\mathrm {c}})}{\Gamma }\int _{0}^{\mathcal {S}_{\mathrm {co}}}d\mathcal {S}\,\mathcal {S}^{1-\tau }, \end{aligned}$$

(11.42)

where $\mathcal {S}_{\mathrm {co}}$ is a cutoff avalanche size which depends on the system size in an unknown way, and the integral was divided by $\Gamma$ in order to perform a cycle-average. The values of the critical exponents $\tau$ and $\sigma$ that where used where $\tau =1.04$ and $\sigma =0.59$ which were obtained from the data collapse shown in Figs. 11.29 and 11.30. For the critical maximal strain amplitude the values $\Gamma _{\mathrm {c}}=0.135$ for $N=1024$, $\Gamma _{\mathrm {c}}=0.12$ for $N=4096$ and $\Gamma _{\mathrm {c}}=0.115$ for $N=16{,}384$ were chosen since they correspond to the values found for the transition to chaos. The maximal cluster size $\mathcal {S}_{\mathrm {co}}$ was assumed to be proportional to a power-law of the system size since at the steady-state the correlations span the entire system ($\xi \sim L$):

$$\begin{aligned} \mathcal {S}_{\mathrm {co}} = \mathcal {K} N^{\Delta }. \end{aligned}$$

(11.43)

where $\mathcal {K}$ and $\Delta$ are constants. The parameter values $\mathcal {K}\sim 0.4$, $A\sim 4.547$, $B\sim 30.51$ and $\Delta \sim 0.482$ were found by minimising the normalised $L_{\text {2}}$ norm of (11.42) with respect to the data from simulations:

$$\begin{aligned} L_{\text {2}} = \frac{1}{N}\sqrt{\sum _i(\langle \Delta \mathcal {U}\rangle _{\text {sim,i}} - \langle \mathcal {S}\rangle _{\text {theory,i}})^2\,} \end{aligned}$$

(11.44)

the best fit resulted in $L_{\text {2}}\sim 0.114$. Note that the value of $\Delta \sim 0.482$ is approximately consistent with avalanches concentrated along a shear-band and thus proportional to the linear system size $L\sim N^{1/2}$. Figure 11.32 shows the first moment of the potential energy fluctuations $\langle \Delta \mathcal {U}\rangle$ obtained from the simulations as a function of the maximal strain amplitude $\Gamma$, compared to (11.42) for three different system sizes. The most obvious features of $\langle \Delta \mathcal {U}\rangle$ as a function of the maximal strain amplitudes is the crossover (cusp) in behavior at the critical point (Figs. 11.32, 11.33), which was mentioned above, and the system size dependent saturation of $\langle \Delta \mathcal {U}\rangle$ for very large strain amplitudes. As one can see in the figures, both of these features are described by the theory. The saturation, and dependence on system size can be explained by noting that for very large maximal strain amplitudes $\Gamma \rightarrow \infty$, the normalized distribution function converges to the usual power-law statistics $P(\mathcal {S}) \sim \mathcal {S}^{-\tau }$ and respectively $\langle \Delta \mathcal {U}\rangle \sim \langle \Delta \mathcal {S}\rangle \rightarrow \mathcal {S}_{\mathrm {co}}^{-\tau }$. One feature that was observed in the simulations that is not explained by the current theory is that $\Gamma _{\mathrm {c}}$ changes slightly with the strain amplitude due to structural rearrangements. In the theory (11.11), structural rearrangements will amount to a change in the properties of the distribution of the random pinning $f_R(u,t)$. However, this effect is small (changes in $\Gamma _{\mathrm {c}}$ are less than $5\%$) and was not taken into account when fitting the data to the theory. By analyzing the avalanche statistics using scaling forms predicted by depinning theory, it was shown that there is a critical point at a critical strain amplitude $\Gamma = \Gamma _{\mathrm {c}}$ which is the same strain amplitude at which the system undergoes an irreversibility transition. However, this raises the question of why the two occur at the same point. An explanation for this intriguing concurrency will be provided below.

Fig. 11.32

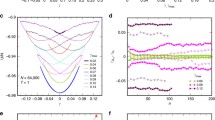
First moment: Average potential energy drops versus maximal strain amplitude for different system sizes: N $=$ 16,384, N $=$ 4096, N $=$ 1024. The yellow lines are the theoretical results (11.42) where the integral was calculated numerically. The red dashed line marks the transition to chaos point for N $=$ 16,384

Fig. 11.33

Transition point: Scaled up version of Fig. 11.32. Note the change in curvature at the critical points $\Gamma _{\mathrm {c}}=0.115,0.12,0.135$ for N $=$ 16,384, N $=$ 4096, N $=$ 1024 respectively. Yellow lines are theoretical results

Fig. 11.34

Nonlinear stability: a Tilted energy landscape - nonlinearly stable. b Tilted energy landscape - completely unstable. Chaotic behavior is possible in this scenario. c A simple example of an attractor: for a dissipative system, different initial conditions which are in the same basin of attraction result in trajectories (blue and green lines) which end-up in the same limit-cycle. d Below the critical strain amplitude, for each strain amplitude, the system finds, after a transient (arrow), a stable configuration (circles)

11.5 Connection Between Dynamics and Critical Behavior

The most interesting question that arises in view of the findings mentioned above is the connection between depinning and the observed dynamics in the reversible and irreversible regimes. The essence of this connection is that at depinning, the external force F suppresses all the energy barriers (see Fig. 11.34a, b) which changes the topology of the energy landscape - instead of a set of disconnected energy minima, we have a fully connected set of energy minima in terms of strain. This affects the dynamics and reversibility of the system (a related explanation was suggested for the dynamics of supercooled liquids, see [70]).

Limit cycles: Since the system is dissipative, it will always flow to an attractor occupying a limited part of phase-space (see Fig. 11.34c and [34]). This attractor will be composed of a finite or infinite set of configurations of the system connected to each other by elastic or plastic displacement (see Fig. 11.34d). For a system under linear shear, when the external forcing is below depinning, it is guaranteed that after some amount of strain the system will find a local minimum of the potential energy (will become pinned). For cyclic strain, if the maximal strain amplitude is below depinning, the system will find, after transient dynamics, a set of configurations all below the critical stress. Since the stress is lower than the critical depinning stress, this set of states is guaranteed to be linearly stable or nonlinearly stable. In the case that is nonlinearly stable, if the stress is increased, the system will overcome a close-by energy barrier but will “fall” into an adjunct energy barrier (see also Fig. 11.34a) which means that the next configuration in the attractor is separated by a finite energy barrier. Therefore, in this case, the attractor is not chaotic and it must be a limit-cycle (periodic). This situation is not so different to an absorbing phase transition, which was suggested as an explanation for similar phenomena [10, 24], although we suggest that depinning provides greater physical insight into the reason for the system to reach an absorbing state.

Chaotic attractor: When the stress is close to depinnig values, a small increase in stress, due to a strain step will supress all of the energy barriers (see Fig. 11.34b). In this case the system will be completely unstable, for a short time. In the quasi-static shearing scenario, the system will reach another minimum of the potential energy when the minimization algorithm or dissipation lowers the energy again but before that happens it will spend some time in boundless motion. Since there are effectively no energy barriers in this time, there are no retrieving forces and chaotic motion is possible (in some systems with quenched disorder and with a “no passing” property fulfilled [71], such as charge density waves and certain random magnets, chaotic motion is not possible and there always is a limit-cycle [72], but this is not the case in plasticity in amorphous solids in which disorder is not strictly quenched and for which the no passing rule is broken).

Period doubling: when the system is close but still not exactly at criticality, there are less and less stable “pinned” configurations. Therefore, the likelihood of the system being able to “construct” a limit-cycle that returns to the same point after one period is smaller and it may be required to have more than one cycle before the system can return to the initial configuration.

To summarize, if the strain amplitude is below depinning, the system can always self organize into cycles composed of states in which the stress fluctuations never reach depinning values. In that case the dynamics will always be bounded, either linearly or nonlinearly (overcoming one energy barrier). If the strain amplitude is large enough, there are always states in which the stress is very close to depinning. In that case small increase in the stress, due to straining, will generate stresses that are larger than the depinning value, and thus will cause unbounded motion which can lead to sensitivity to initial conditions and chaos.

11.5.1 Relaxation Dynamics

Depinning mean-field theory predicts that close to a depinning transition, the system will “slide” for a long time before it becomes pinned due to critical slowing-down. Therefore, the accumulated strain to reach a steady-state (the number of cycles times $4\Gamma$) is expected to diverge as function of the applied force:

$$\begin{aligned} \epsilon _{\text {acc}} \sim (F_{\mathrm {c}} - F)^{-z\nu } , \end{aligned}$$

(11.45)

with mean-field depinning theory, which was derived for linear shear, predicting a value of $z\nu =1$ [52]. Since the steady-state is a limit-cycle composed of a set of pinned states, we expect that also under oscillatory shear, the accumulated strain to reach a steady-state will scale in the same way as the strain needed to pin one state. Since the control parameters was the maximal strain amplitude, we obtain on substituting:

$$\begin{aligned} \epsilon _{\text {acc}} \sim (\Gamma _{\mathrm {c}} - \Gamma )^{-z\nu \delta } . \end{aligned}$$

(11.46)

The simulations found [30] power-law scaling with $z\nu \sim 2.4$ for a choice $\Gamma _{\mathrm {c}}=0.11$ (Fig. 11.7), and $z\nu \sim 1.38$ for a slightly smaller $\Gamma _{\mathrm {c}}=0.1$ for the largest system that was ($N=16{,}384$). The dynamical exponent $z\nu =1$ predicted by mean-field theory is in rough agreement with the scaling of the time to reach steady-state measured in the experiments of Nagamanasa et al. [24] on colloidal glasses which gave $z\nu \sim 1.1/\delta \sim 0.88$.

11.6 Summary

The recent discovery of a reversibility transition connected to yield has raised the possibility that yield is a result of a transition from periodic to chaotic behavior. However, a number of questions arise regarding the nature of the transition and the implications to ergodicity and entropy production in these systems. The results described in this chapter suggest that the critical behavior might be caused by a transition to chaos [19], a phenomenon well studied in dynamical systems theory, which seems to be a result of a change in the topology of the energy landscape [30]. Furthermore, it is suggested that the change in energy landscape topology may be a result of a depinning-like dynamical non-equilibrium phase transition.

The existence of an irreversibility transition is supported by several experimental results based on the shearing of colloidal suspensions [17, 20, 24]. Similarly, experiments on granular piles have also shown that the onset of irreversible behavior is associated with the appearance of system spanning events [12], consistent with our findings. Therefore, it appears that the existence of an irreversibility transition/transition to chaos in colloidal systems is reasonably well substantiated. However, it is still not clear what happens in the thermodynamic limit and in molecular amorphous solids, such as bulk metallic glasses. Furthermore, the existence and nature of a non-equilibrium critical point at yield is still under debate. There are suggestions that the transition is actually first-order in nature rather than showing critical behavior [73, 74]. It will be interesting to see if one can explain the irreversibility transition based on a first-order non equilibrium phase transition.