Scaled Test Stand Simulation for Studying the Behavior of Anti-lock Brake Systems on Bumpy Roads

Abstract

The paper presents a design concept for a scaled-down test stand that allows studying of various possible anti-lock brake system algorithms, by considering a quarter car model traveling over an uneven road surface (a bumpy road, or a road with continuous variable friction coefficient), represented by a rolling inertial tambour track, in contact with an articulated braking wheel. The concept is transposed in a CAD model simulation where motion analysis can be conducted. Also a software application is designed for generating a road surface profile (for the CAD model) and verifying it against the real motion of a smart servo motor. The combined simulation results prove the viability of the concept and encourage the authors to further develop this scaled test stand.

1 Introduction

A top priority for automotive engineers and researchers alike is to make vehicles and roads safer for everyone. One way is enhancing the ability to brake and steer safely in difficult road conditions, by having the anti-lock braking system installed.

The ABS is now available as standard equipment on all passenger vehicles with the main goal of improving vehicle steering ability during hard braking, by preventing wheel locking. This phenomenon can occur if the applied braking torque surpasses the value of the rolling friction force so that the tire stops rotating and starts sliding onto the road surface. Consequently the steering of the vehicle is almost impossible and also the stopping distance increases. The ABS system mitigates this aspect by alternating the pressure in the wheel’s brake caliper with a certain frequency and duty cycle by freeing-up the brake and allowing the wheel to roll and then re-applying maximum pressure and locking the wheel. This fast cycling of the pressure (5–10 times a second) tries to emulate a mean tire slip percentage of about 10–20 %, which is the interval where, for almost all types of road surface, the friction coefficient is at its highest values [1].

As an option to study and enhance the ABS algorithms the quarter car model of a car can be employed (Fig. 1) [2].

Fig. 1

Quarter car model

The present paper proposes the design of a scaled test stand based on this model that can be able to simulate braking of a wheel that travels over a bumpy road surface, so that different anti-lock algorithms can be employed to increase the braking-steering efficiency over an uneven road surface. Scaled test stands have been used in automotive industry for a long time and, for antilock brake systems, similar stands were approached before [3, 4] for testing braking algorithms on even road surfaces.

2 The Scaled Stand Design Concept

Figure 2 depicts a simplified CAD model of the scaled test stand, developed using SolidWorks. All elements are geometrically constrained in such a way that motion analysis can be applied upon the mechanism. Also the balancing weights are applied on the model (Figs. 2, 3) and a Dynamixel smart servo motor [5] was selected for road surface profile replication.

Fig. 2

Scaled stand CAD model

Fig. 3

Scaled stand equivalent schematic (inset perspective CAD model)

In order to observe both the vertical swing of the track-wheel assembly, an oscillating motion was imposed to the servo model’s output shaft with an angular range in the interval $\left[ {\frac{\pi }{2} \cdots \frac{3 \cdot \pi }{2}} \right]$, and another continuous rotational motion was applied to the track tambour.

For a better understanding of this application, a schematic equivalent of the stand in depicted in Fig. 3, where some of the dimensional constraints have been preset in order to facilitate the CAD model generation and further calculation of required values: a = b/2 = 20 mm, c ₁ = c ₂ = e ₂ = d = 120 mm, r ₁ = 70 mm, r ₂ = 100 mm, e ₃ = 40 mm. The decision of selecting certain dimensions from the start is due to some pieces of equipment being already available for building the physical scaled stand.

To be able to analyze the motion of the track tambour when imposing various angular values to the smart servo, two four bar linkage mechanisms are presented in Fig. 4 and the vertical stroke of point K is extracted.

Fig. 4

a Tambour oscillation equiv. mechanism; b contact point K oscillation equiv. mechanism

By considering the first four bar linkage ABCD (Fig. 4a) and its closed loop vector equation written in complex number form, the following results:

$$ l_{1} \cdot e^{i \cdot \varphi } + l_{2} \cdot e^{i \cdot \beta } = \left( {x_{D} + i \cdot y_{D} } \right) + l_{3} \cdot e^{i \cdot \psi } $$

(1)

The computation of the angle $\psi (\varphi )$ from the Eq. (1) follows by isolating of the term which contains the angle ϑ and by multiplication with its conjugate complex vector equation:

$$ \begin{aligned} l_{2} \cdot e^{i \cdot \vartheta } & = \left( {x_{D} + i \cdot y_{D} } \right) - l_{1} \cdot e^{i \cdot \varphi } + l_{3} \cdot e^{i \cdot \psi } \\ l_{2} \cdot e^{ - i \cdot \vartheta } & = \left( {x_{D} - i \cdot y_{D} } \right) - l_{1} \cdot e^{ - i \cdot \varphi } + l_{3} \cdot e^{ - i \cdot \psi } \\ \end{aligned} $$

(2)

The result of the multiplication is the transmission function of the first order of the considered four bar linkage:

$$ \begin{aligned} 0 & = x_{D}^{2} + y_{D}^{2} + l_{1}^{2} - l_{2}^{2} + l_{3}^{2} - 2 \cdot l_{1} \cdot x_{D} \cdot \,\cos \varphi + 2 \cdot i^{2} l_{1} y_{D} \cdot \,\sin \varphi \\ & \quad + 2 \cdot l_{3} \cdot x_{D} \cdot \,\cos \psi - 2 \cdot i^{2} \cdot l_{3} \cdot y_{D} \cdot \,\sin \psi - 2 \cdot l_{1} \cdot l_{3} \cdot \,\cos (\varphi - \psi ) \\ \end{aligned} $$

(3)

The computing of the transmission function $\psi (\varphi )$, having angle $\varphi$ placed in the selected quadrants, is accomplished by:

$$ \psi (\varphi ) = 2 \cdot atan\left( {\frac{{B1(\varphi ) - \sqrt {A1(\varphi )^{2} + B1(\varphi )^{2} - C1(\varphi )^{2} } }}{A1(\varphi ) - C1(\varphi )}} \right) $$

(4)

where: $A1\left( \varphi \right) = 2 \cdot l_{3} \cdot \left( {x_{D} - l_{1} \cdot \,\cos \varphi } \right)$; $B1\left( \varphi \right) = 2 \cdot l_{3} \cdot \left( {y_{D} - l_{3} \cdot \,\sin \varphi } \right)$; $C1\left( \varphi \right) = \left( {x_{D}^{2} + y_{D}^{2} } \right) + l_{1}^{2} - l_{2}^{2} + l_{3}^{2} - 2 \cdot l_{1} \cdot \left( {x_{D} \cdot \,\cos \varphi + y_{D} \cdot \,\sin \varphi } \right)$.

By considering another equivalent four bar linkage DO ₂ O ₁ E (Fig. 4b) and writing the closed loop vector equation referencing in point D:

$$ l_{31} \cdot e^{i \cdot \psi } + l_{4} \cdot e^{i \cdot \beta } = l_{5} \cdot e^{i \cdot \alpha } + i \cdot \left( {y_{E} - y_{D} } \right) $$

(5)

a similar procedure can be employed for computing the equiv. coupler angle β($\psi (\varphi )$):

$$ \beta (\psi \left( \varphi \right)) = 2 \cdot atan\left( {\frac{{B2\left( {\psi \left( \varphi \right)} \right) + \sqrt {A2(\psi \left( \varphi \right))^{2} + B2(\psi \left( \varphi \right))^{2} - C2(\psi \left( \varphi \right))^{2} } }}{A2(\psi \left( \varphi \right)) - C2(\psi \left( \varphi \right))}} \right) $$

(6)

where: $A2\left( {\psi (\varphi } \right)) = 2 \cdot l_{31} \cdot l_{4} \cdot \,\cos \psi (\varphi )$; $B2\left( {\psi (\varphi } \right)) = 2 \cdot l_{4} \cdot \left( {l_{31} \cdot \,\sin \psi (\varphi ) - y_{E} + y_{D} } \right)$; $C2\left( {\psi (\varphi } \right)) = \left( {y_{E} - y_{D} } \right)^{2} + l_{31}^{2} + l_{4}^{2} - l_{5}^{2} - 2 \cdot l_{31} \cdot \left( {y_{E} - y_{D} )\sin \psi (\varphi } \right)$

Knowing the oscillating angles ψ and β and accepting that the point K belongs to the equivalent coupler, the coordinates of the contact point K can be determined:

$$ \begin{aligned} x_{K} (\varphi ) & = l_{31} \cdot \,\cos \psi (\varphi ) + r_{2} \cdot \,\cos \beta (\psi (\varphi )) \\ y_{K} (\varphi ) & = l_{31} \cdot \,\sin \psi (\varphi ) + r_{2} \cdot \,\cos \beta (\psi (\varphi )) \\ \end{aligned} $$

(7)

By numerically solving the above expressions a total value y _K (φ) = 20 mm is obtained (approx. ±10 mm) which is appropriate for the scope of the scaled test stand.

3 Solution Implementation

The scaling of the system is achieved by conserving the volumetric density of an average vehicle traveling at a maximum constant speed of v _I  = 15 m/s. For this purpose a vehicle was selected, having an inertial mass of m _I  = 1400 kg (considered with 2 passengers and luggage), and overall outside dimensions of 4.2 × 1.8 × 1.5 m.

3.1 System Scaling

The scaling factor is dependent of the already existing equipment (the braking wheel, with an outer diameter of 140 mm) having a dimensional reducing proportionality K _S value of 4.6. The volumetric density of the full size vehicle, considering the values given above, is ρ = 123.5 kg/m³.

The virtual scaled vehicle should then have a mass of 14.38 kg resulting a virtual quarter car model inertial mass of m _IQ  = 3.59 kg, traveling at v _Q  = 3.26 m/s, as per Eq. (8).

$$ m_{Q} = \frac{{m_{I} }}{{4 \cdot K_{s}^{3} }}; v_{Q} = \frac{{v_{I} }}{{K_{S} }}. $$

(8)

Since the scaled stand concept consists of a rotating track tambour (the road surface) it means that the mass that needs to be stopped by the braking wheel is transferred as the inertial mass of the track tambour, m _D , rotating with the angular velocity ω. In order to obtain this mass a kinetic energy equilibrium must be enforced between the two components, E _K  = E _R :

$$ E_{K} = \frac{{m_{Q} \cdot v_{Q}^{2} }}{2}; E_{R} = \frac{{J \cdot \omega^{2} }}{2} $$

(9)

Considering a simplified approach where the track tambour is a disc with uniformly distributed mass and the rotating braking wheel (not braking it yet!) has non-slip contact with the track tambour (same peripheral velocity), the following assumptions can be made: the angular velocity of the track is $\omega = v_{Q} /r_{D}$ and the inertial moment of the disc is $J = m_{D} \cdot r_{D}^{2} /2$, where r _D is the tambour/disc radius (imposed at 100 mm). Then the energy equilibrium gives Eq. (10):

$$ \frac{{m_{Q} \cdot v_{Q}^{2} }}{2} = \frac{{m_{D} \cdot r_{D}^{2} \cdot v_{Q}^{2} }}{{4 \cdot r_{D}^{2} }}; m_{D} = 2 \cdot m_{Q} , $$

(10)

resulting that the track tambour mass must be m _D  = 7.18 kg. For an aluminum disc of r _D  = 100 mm this gives a tambour width of approx. 85 mm.

Further considering that a balancing mass of 12 kg applied at point M2 (Fig. 3) keeps the system in static equilibrium and that c ₁ = c ₂ = d = 120 mm, the necessary torque for accelerating the system with α = 4π rad/s² must be determined as per Eq. (11):

$$ \tau_{Q} = J_{S} \cdot \alpha ; \tau_{Q} = \mathop \sum \nolimits m_{S} \cdot r_{S}^{2} \cdot \alpha $$

(11)

where: m _S are the total inertial stand masses rotating about point D, in total approx. 24 kg; r _S is the inertial masses’ gyration radius, r _S  = c ₂ (Fig. 3) and τ _Q is the required inertial torque, τ _Q  = 4.34 Nm.

Then the necessary input torque T _S from the servo-motor can be expressed as:

$$ T_{S} = \tau_{Q} \cdot \frac{{\omega_{c2} }}{{\omega_{a} }} $$

(12)

where: ω _c2 is the angular velocity of the oscillating arm (c ₂ in Fig. 3); ω _a is the angular velocity of the servo shaft and T _S is the required servo torque, T _S  = 0.22 Nm.

Since the maximum torque developed by the selected servo motor is 2.5 Nm [5], it can be considered as perfectly suitable for this task.

3.2 Profile Generation

In order to be able for the motion analysis package of SolidWorks to reproduce a certain road surface profile, the servo shaft angular position values must be taken from a formatted data file [6].

This file is produced using a custom built software application where the user can graphically impose a longitudinal road profile with the desired dips and bumps (Fig. 5) in real time, by moving the slider on the right. Once the profile is considered complete it can be saved in a csv data file with a time base of 0.1 s.

Fig. 5

Road profile generation application

At this point the generated profile can be tested on the scaled test stand by connecting via a USB port the smart servo motor [7]. The servo will attempt to follow the profile and will return its actual position for the current time, which will be plotted over the user imposed graph.

The values returned from the servo can also be saved and used further, and it can be inspected if the motor lags behind the originally imposed values. The program also allows the user to manually move the servo and record its actual positions for further analysis or reference.

Upon saving the desired data file which contains the timestamp and angular position for each record, it can be transferred to the motion analysis package.

4 Simulation Results

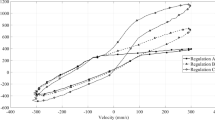
Once the profile data file has been imported as position values and the motion analysis has completed the vertical stroke of a point (K) from the model, this can be plotted and exported as another csv data file. Also the model is now animated following the virtual motion of the servo shaft angular positioning. The resulting values are graphically represented in Fig. 6. It can be noted that the resulting motion follows the imposed road profile, but having some deviations towards the angular limits, due to the non-linearity resulting from the angle dependencies $\psi (\varphi )$ and β(ψ).

Fig. 6

Simulation result of track tambour vertical movement

It can also be observed that the vertical stroke of the tambour is near ±10 mm, which is consistent with the numeric modelling and, considering the dimensional scaling factor of the stand, equates to an equivalent vertical motion of the full size vehicle of ±46 mm. This limit is acceptable since bumps or dips in the road surface having such an abrupt maximum height/depth are at the limit of driving, taking into account the imposed initial speed of 15 m/s.

5 Conclusions

Previous tests done on a similar scaled test stand demonstrate that this approach is a viable solution.

By adding the controlled vertical motion of the track tambour new ways of studying the behavior of anti-lock algorithms can be developed. Two distinct aspects are presented through this vertical motion: the simulation of a bumpy road or with a sudden dip or bump, and the simulation of a road surface with continuous variable friction coefficient (if the vertical travel of the braking wheel is restricted).

The results of the CAD model motion analysis enforces the viability of the concept and gives momentum for further developing the test stand, into a practical experimentation platform (for both research and didactical activities). Future work will concentrate on completing the building of the stand, following the presented concept and developing an integrated hardware-software design which should be able to combine and analyze wheel braking with the track vertical motion. Also a suspension component should be present to better simulate real conditions.