Parameter Selection in Particle Swarm Optimisation from Stochastic Stability Analysis

Abstract

Particle swarm optimisation is a metaheuristic algorithm which finds reasonable solutions in a wide range of applied problems if suitable parameters are used. We study the properties of the algorithm in the framework of random dynamical systems (RDS) which, due to the quasi-linear swarm dynamics, yields exact analytical results for the stability properties in the single particle case. The calculated stability region in the parameter space extends beyond the region determined by earlier approximations. This is also evidenced by simulations which indicate that the algorithm performs best in the asymptotic case if parameterised near the margin of instability predicted by the RDS approach.

1 PSO Introduction

Particle Swarm Optimisation (PSO, [13]) is a metaheuristic algorithm which is widely used to solve search and optimisation tasks. It employs a number of particles as a swarm of potential solutions. Each particles shares knowledge about the current overall best solution and also retains a memory of the best solution it has encountered itself previously. Otherwise the particles, after random initialisation, obey a linear dynamics of the following form

$$\begin{aligned} \mathbf {v}_{i,t+1}= & {} \omega \mathbf {v}_{i,t}+\alpha _{1} \mathbf {R}_{1}(\mathbf {p}_{i}-\mathbf {x}_{i,t})+\alpha _{2} \mathbf {R}_{2}(\mathbf {g}-\mathbf {x}_{i,t}) \\\mathbf {x}_{i,t+1}= & {} \mathbf {x}_{i,t}+\mathbf {v}_{i,t+1} \end{aligned}$$

(1)

Here $\mathbf {x}_{i,t}$ and $\mathbf {v}_{i,t}$, $i=1,\dots ,N$, $t=0,1,2,\dots$, represent, respectively, the d-dimensional position in the search space and the velocity vector of the i-th particle in the swarm at time t. The velocity update contains an inertial term parameterised by $\omega$ and includes attractive forces towards the personal best location $\mathbf {p}_{i}$ and towards the globally best location $\mathbf {g}$, which are parameterised by $\alpha _{1}$ and $\alpha _{2}$, respectively. The symbols $\mathbf {R}_{1}$ and $\mathbf {R}_{2}$ denote diagonal matrices whose non-zero entries are uniformly distributed in the unit interval. The number of particles N is quite low in most applications, usually amounting to a few dozens.

In order to function as an optimiser, the algorithm uses a nonnegative cost function $F:\mathbb {R}^d \rightarrow \mathbb {R}$. In many problems, where PSO is applied, also states with near-optimal costs can be considered as good solutions. The cost function is evaluated for the state of each particle at each time step. If $F(\mathbf {x}_{i,t})$ is better than $F(\mathbf {p}_{i})$, then the personal best $\mathbf {p}_{i}$ is replaced by $\mathbf {x}_{i,t}$. Similarly, if one of the particles arrives at a state with a cost less than $F(\mathbf {g})$, then $\mathbf {g}$ is replaced in all particles by the position of the particle that has discovered the new best solution. If its velocity is non-zero, a particle will depart even from the current best location, but can still return guided by the force terms in the dynamics (1).

In the next section we will consider an illustrative simulation of a particle swarm and move on to a standard matrix formulation of the swarm dynamics in order to describe some of the existing analytical work on PSO. In Sect. 3 we will argue for a formulation of PSO as a random dynamical system which will enable us to derive a novel exact characterisation of the dynamics of a one-particle system. In Sect. 4 we will compare the theoretical predictions with multi-particle simulations on a representative set of benchmark functions. Finally, in Sect. 5 we will discuss the assumption we have made in Sect. 3 based on the empirical evidence for our approach.

2 Swarm Dynamics

2.1 Empirical Properties

The success of the algorithm in locating good solutions depends on the dynamics of the particles in the state space of the problem. In contrast to many evolution strategies, it is not straight forward to interpret the particle swarm as following a landscape defined by the cost function. Unless the current best position $\mathbf {g}$ changes, the particles do not interact with each other and follow an intrinsic dynamics that does not even indirectly obtain any gradient information.

Fig. 1.

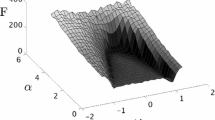
Typical PSO performance as a function of its $\omega$ and $\alpha$ parameters. Here a 25 particle swarm was run for pairs of $\omega$ and $\alpha$ values ($\alpha _1=\alpha _2=\alpha /2$). Cost function here was the $d=10$ non-continuous rotated Rastrigin function [15]. Each parameter pair was repeated 100 times and the minimal costs after 2000 iterations were averaged.

The particle dynamics depends on the parameterisation of the Eq. 1. To obtain the best result one needs to select parameter settings that achieve a balance between the particles exploiting the knowledge of good known locations and exploring regions of the problem space that have not been visited before. Although adaptive schemes are available [6, 9, 20], parameter values often need to be experimentally determined, and poor selection may result in premature convergence of the swarm to poor local minima or in a divergence of the particles.

Empirically we can execute PSO against a variety of problem functions with a range of $\omega$ and $\alpha _{1,2}$ values. Typically the algorithm shows performance of the form depicted in Fig. 1. The best solutions found show a curved relationship between $\omega$ and $\alpha =\alpha _1+\alpha _2$, with $\omega \approx 1$ at small $\alpha$, or $\alpha \gtrapprox 4$ at small $\omega$. Large values of both $\alpha$ and $\omega$ are found to cause the particles to diverge leading to results far from optimality, while at small values for both parameters the particles converge to a nearby solution which sometimes is acceptable. For other cost functions similar relationships are observed in numerical tests (see Sect. 4) unless no good solutions found due to problem complexity or runtime limits. For simple cost functions, such as a single well potential, there are also parameter combinations with small $\omega$ and small $\alpha$ will usually lead to good results. The choice of $\alpha _1$ and $\alpha _2$ at constant $\alpha$ may have an effect for some cost functions, but does not seem to have a big effect in most cases.

2.2 Matrix Formulation

In order to analyse the behaviour of the algorithm it is convenient to use a matrix formulation by inserting the velocity explicitly in the second equation (1).

$$\begin{aligned} \mathbf {z}_{t+1}=M \mathbf {z}_t + \alpha _1 \mathbf {R}_1 (\mathbf {p},\mathbf {p})^{\top }+ \alpha _2 \mathbf {R}_2 (\mathbf {g},\mathbf {g})^{\top } \end{aligned}$$

(2)

with $\mathbf {z}=(\mathbf {v},\mathbf {x})^{\top }$ and

$$\begin{aligned} M=\left( \begin{array}{cc} \omega \mathbf {I}_d &{} -\alpha _1 \mathbf {R}_1- \alpha _2 \mathbf {R}_2 \\ \omega \mathbf {I}_d &{} \mathbf {I}_d-\alpha _1 \mathbf {R}_1- \alpha _2 \mathbf {R}_2 \end{array}\right) , \end{aligned}$$

(3)

where $\mathbf {I}_d$ is the unit matrix in d dimensions. Note that the two occurrence of $\mathbf {R}_1$ in Eq. 3 refer to the same realisation of the random variable. Similarly, the two $\mathbf {R}_2$’s are the same realisation, but different from $\mathbf {R}_1$. Since the second and third term on the right in Eq. 2 are constant most of the time, the analysis of the algorithm can focus on the properties of the matrix M. PSO’s wide applicability has led to the analyses discussed in Sect. 2.3. These focused either on simplifying the algorithm to make it deterministic or on the expectation and variance values of the update matrix. Here we analyse the long term behaviour of the swarm considering both the stationary probability distribution of the particles within the z state space and the properties of the infinite product of the stochastic matrix.

2.3 Analytical Results

An early exploration of the PSO dynamics [12] considered a single particle in a one-dimension space where the personal and global best locations were taken to be the same. The random components were replaced by their averages such that apart from random initialisation the algorithm was deterministic. Varying the parameters was shown to result in a range of periodic motions and divergent behaviour for the case of $\alpha _1+ \alpha _2 \ge 4$. The addition of the random vectors was seen as beneficial as it adds noise to the deterministic search.

Control of velocity, not requiring the enforcement of an arbitrary maximum value as in Ref. [12], is derived in an analytical manner by [4]. Here eigenvalues derived from the dynamic matrix of a simplified version of the PSO algorithm are used to imply various search behaviours. Thus, again the $\alpha _1+\alpha _2\ge 4$ case is expected to diverge. For $\alpha _1+\alpha _2<4$ various cyclic and quasi-cyclic motions are shown to exist for a non-random version of the algorithm.

In Ref. [19] again a single particle was considered in a one dimensional problem space, using a deterministic version of PSO, setting $\mathbf {R}_{1}=\mathbf {R}_{2}=0.5$. The eigenvalues of the system were determined as functions of $\omega$ and a combined $\alpha$, which leads to three conditions: The particle is shown to converge when $\omega <1$, $\alpha >0$ and $2\omega -\alpha +2>0$. Harmonic oscillations occur for $\omega ^2+\alpha ^2-2\omega \alpha -2\omega -2\alpha +1<0$ and a zigzag motion is expected if $\omega <0$ and $\omega -\alpha +1<0$. As with the preceding papers the discussion of the random numbers in the algorithm views them purely as enhancing the search capabilities by adding a drunken walk to the particle motions. Their replacement by expectation values was thus believed to simplify the analysis with no loss of generality.

A weakness in these early papers stems from the treatment of the stochastic elements. Rather than replacing the $R_1$ and $R_2$ vectors by 0.5 the dynamic behaviour can be explored by considering their expectation values and variances. An early work doing this produced a predicted best performance region in parameter space similar to the curved valley of best values that is seen empirically [10]. The authors explicitly consider the convergence of means and variances of the stochastic update matrix. The curves they predict marks the locus of ($\omega ,\alpha$)-pairs they believed guaranteed swarm convergence, i.e. parameter values within this line will result in convergence. Similar approaches yielded matching lines [17] and utilised a weaker stagnation assumption [16]. Ref. [1] provides an extensive recent review of such analyses. We will refer to this locus as the Jiang line [10]. It is included for comparison with the curves derived here, see Fig. 2 below.

We show in this contribution that the iterated use of these random factors $\mathbf {R}_{1}$ and $\mathbf {R}_{2}$ in fact adds a further level of complexity to the dynamics of the swarm which affects the behaviour of the algorithm in a non-trivial way. Essentially it is necessary to consider both the stationary distribution of particles in the system’s state space and the properties of the infinite product of the stochastic update matrix. This leads to a loci of parameters leading to stable swarms that differs from previous solutions and depends upon the values of $\alpha _1$ and $\alpha _2$ used. All solutions lie outside the Jiang line [10]. We should note that they state that their solution is a guarantee of convergence but may not be its limit. Our analytical solution of the stability problem for the swarm dynamics explains why parameter settings derived from the deterministic approaches are not in line with experiences from practical tests. For this purpose we will now formulate the PSO algorithm as a random dynamical system and present an analytical solution for the swarm dynamics in a simplified but representative case.

3 Critical Swarm Conditions for a Single Particle

3.1 PSO as a Random Dynamical System

As in Refs. [12, 19] the dynamics of the particle swarm will be studied here as well in the single-particle case. This can be justified because the particles interact only via the global best position such that, while $\mathbf {g}$ (1) is unchanged, single particles exhibit qualitatively the same dynamics as in the swarm. For the one-particle case we have necessarily $\mathbf {p}=\mathbf {g}$, such that shift invariance allows us to set both to zero, which leads us to the following is given by the stochastic-map formulation of the PSO dynamics (2).

$$\begin{aligned} \mathbf {z}_{t+1}=M \mathbf {z}_t \end{aligned}$$

(4)

Extending earlier approaches we will explicitly consider the randomness of the dynamics, i.e. instead of averages over $\mathbf {R}_1$ and $\mathbf {R}_2$ we consider a random dynamical system with dynamical matrices M chosen from the set

$$\begin{aligned} \mathcal{M}_{\alpha ,\omega }=\left\{ \left( \begin{array}{cc} \omega \mathbf {I}_d &{} -\alpha \mathbf {R} \\ \omega \mathbf {I}_d &{} \mathbf {I}_d-\alpha \mathbf {R} \end{array}\right) \!,\,\, \mathbf {R}_{ij}=0 \text{ for } i\ne j \text{ and } \mathbf {R}_{ii}\in \left[ 0,1\right] , \right\} \end{aligned}$$

(5)

with $\mathbf {R}$ being in both rows the same realisation of a random diagonal matrix that combines the effects of $\mathbf {R}_1$ and $\mathbf {R}_2$ (1). The parameter $\alpha$ is the sum $\alpha _1 + \alpha _2$ with $\alpha _1,\alpha _2\ge 0$. As the diagonal elements of $\mathbf {R}_1$ and $\mathbf {R}_2$ are uniformly distributed in $\left[ 0,1\right]$, the distribution of the random variable $\mathbf {R}_{ii} = \frac{\alpha _1}{\alpha } \mathbf {R}_{1,ii} + \frac{\alpha _2}{\alpha } \mathbf {R}_{2,ii}$ in Eq. 4 is given by a convolution of two uniform random variables, namely

$$\begin{aligned} P_{\alpha _1,\alpha _2}(s)={\left\{ \begin{array}{ll} \frac{\alpha ^2 s}{\alpha _1 \alpha _2}&{}\text{ if } 0\le s\le \min \{\frac{\alpha _1}{\alpha },\frac{\alpha _2}{\alpha }\}\\ \frac{\alpha }{\max \{\alpha _1,\alpha _2\}} &{} \text{ if } \min \{\frac{\alpha _1}{\alpha },\frac{\alpha _2}{\alpha }\}<s\le \max \{\frac{\alpha _1}{\alpha },\frac{\alpha _2}{\alpha }\}\\ \frac{\alpha ^2 \left( 1-s\right) }{\alpha _1 \alpha _2} &{} \text{ if } \max \left\{ \frac{\alpha _1}{\alpha },\frac{\alpha _2}{\alpha }\right\} <s\le 1 \end{array}\right. } \end{aligned}$$

(6)

if the variable $s\in [0,1]$ and $P_{\alpha _1,\alpha _2}(s)=0$ otherwise. $P_{\alpha _1,\alpha _2}(s)$ has a tent shape for $\alpha _1=\alpha _2$ and a box shape in the limits of either $\alpha _1\rightarrow 0$ or $\alpha _2\rightarrow 0$. Thus, the selection of particular $\alpha _1$ and $\alpha _2$ parameters will determine the distribution for the random multiplier $\mathbf {R}_{ii}$ in Eq. 5.

We expect that the multi-particle PSO is well represented by the simplified version for $\alpha _2\gg \alpha _1$ or $\alpha _1\gg \alpha _2$, the latter case being irrelevant in practice. For $\alpha _1\approx \alpha _2$ deviations from the theory may occur because in the multi-particle case $\mathbf {p}$ and $\mathbf {g}$ will be different for most particles. We will discuss this as well as the effects of the switching of the dynamics at discovery of better solutions in Sect. 5.

3.2 Marginal Stability

As the PSO algorithm runs, the particles locate new and better solutions. These result in updates to the personal best locations of the particles, and sometimes to the swarm’s global best location. Typically, these updates become rarer over time. When the swarm is not discovering new and better solutions, the dynamics of the system is determined by an infinite product of matrices from the set $\mathcal {M}_{\alpha ,\omega }$ (5). Such products have been studied for several decades [7] and have found applications in physics, biology and economics. Here they provide a convenient way to explicitly model the stochasticity of the swarm dynamics such that we can claim that the performance of PSO is determined by the stability properties of the random dynamical system (4).

Since the equation (4) is linear, the analysis can be restricted to vectors on the unit sphere in the $(\mathbf {v},\mathbf {x})$ space, i.e. to unit vectors $\mathbf {a}=\left( \mathbf {x},\mathbf {v}\right) ^{\top }\!/\, \Vert \left( \mathbf {x},\mathbf {v}\right) ^{\top }\!\Vert$, where $\Vert \cdot \Vert$ denotes the Euclidean norm. Unless the set of matrices shares the same eigenvectors (which is not the case here) standard stability analysis in terms of eigenvalues is not applicable. Instead we will use tools from the theory of random matrix products in order to decide whether the set of matrices is stochastically contractive. The properties of the asymptotic dynamics can be described based on a double Lebesgue integral over the unit sphere $S^{2d-1}$ and the set $\mathcal {M}_{\alpha ,\omega }$ [14]. As in Lyapunov exponents, the effect of the dynamics is measured in logarithmic units in order to account for multiplicative action.

$$\begin{aligned} \lambda \left( \alpha ,\omega \right) =\int \! d\nu _{\alpha ,\omega }\left( \mathbf {a}\right) \!\int dP_{\alpha ,\omega }\left( M\right) \,\log \left\| M\mathbf {a}\right\| \end{aligned}$$

(7)

If $\lambda \left( \alpha ,\omega \right)$ is negative the algorithm will converge to $\mathbf {p}$ with probability 1, while for positive $\lambda$ arbitrarily large fluctuations are possible. While the measure for the inner integral (7) is given by Eq. 6, we have to determine the stationary distribution $\nu _{\alpha ,\omega }$ (called invariant measure in [14]) on the unit sphere for the outer integral. It tells us where (or rather in which sector) the particles are likely to be in the system’s state space. It is given as the solution of the integral equation

$$\begin{aligned} \nu _{\alpha ,\omega }\left( \mathbf {a}\right) =\int \! d\nu _{\alpha ,\omega }\left( \mathbf {b}\right) \int \! dP_{\alpha ,\omega }\left( M\right) \delta \left( \mathbf {a},M\mathbf {b} / \left\| M\mathbf {b}\right\| \right) ,\,\,\,\mathbf {a},\mathbf {b}\in S^{2d-1}, \end{aligned}$$

(8)

which represents the stationarity of $\nu _{\alpha ,\omega }$, i.e. the fact that under the action of the matrices from $\mathcal {M}_{\alpha ,\omega }$ the distribution of particles over sectors remains unchanged. Obviously, if the particles are more likely to reside in some part then this part should have a stronger influence on the stability, see Eq. 7.

The existence of the invariant measure requires the dynamics to be ergodic which is ensured if at least some of elements of $\mathcal {M}_{\alpha ,\omega }$ have complex eigenvalues, such as being the case for $\omega ^2 + \alpha ^2/4 - \omega \alpha - 2\omega - \alpha +1<0$ (see above, [19]). This condition excludes a small region in the parameters space at small values of $\omega$, such that there we have to take all ergodic components into account. There are not more than two components which due to symmetry have the same stability properties. It depends on the parameters $\alpha$ and $\omega$ and differs strongly from a homogenous distribution. Critical parameters are obtained from Eq. 7 by the relation

$$\begin{aligned} \lambda \left( \alpha ,\omega \right) =0. \end{aligned}$$

(9)

A similar goal was followed in Ref. [6], where, however, an adaptive scheme rather than an analytical approach was invoked in order to identify critical parameters. Solving Eq. 9 is difficult in higher dimensions, so we rely on the linearity of the system when considering the $(d=1)$-case as representative. In Fig. 2 critical loci of parameter values are plotted. Two lines are plotted in black: one (outer) derived for the case of $\alpha = \alpha _1+\alpha _2$, and $\alpha _1 = \alpha _2$, the other (inner) for the case of $\alpha = \alpha _2$, and $\alpha _1 = 0$. We also plot a line (in dark green) showing the earlier solution of swarm stability [10]. Inside the contour $\lambda \left( \alpha ,\omega \right)$ is negative, meaning that the state will approach the origin with probability 1. Along the contour and in the outside region large state fluctuations are possible. Interesting parameter values are expected near the curve where due to a coexistence of stable and unstable dynamics (induced by different sequences of random matrices) a theoretically optimal combination of exploration and exploitation is possible. For specific problems, however, deviations from the critical curve can be expected to be beneficial.

Fig. 2.

Solution of Eq. 9 representing a single particle in one dimension with a fixed best value at $\mathbf {g}=\mathbf {p}=0$. The curve that has higher $\alpha$-values on the right (solid) is for $\alpha _1=\alpha _2$, the other curve (dashed) is for $\alpha =\alpha _2$, $\alpha _1=0$. Except for the regions near $\omega =\pm 1$, where numerical instabilities can occur, a simulation produces an indistinguishable curve. In the simulation we tracked the probability of a particle to either reach a small region ($10^{-12}$) near the origin or to escape beyond a radius of $10^{12}$ after starting from a random location on the unit circle. Along the curve both probabilities are equal. For comparison the line of stability predicted by [10] is shown in green (the innermost line). (Color figure online)

4 Optimisation of Benchmark Functions

4.1 Experimental Setup

Metaheuristic algorithms are often tested in competition against benchmark functions designed to present different problem space characteristics. The 28 functions [15] contain a mix of unimodal, basic multimodal and composite functions. The domain of the functions in this test set are all defined to be $[-100, 100]^d$ where d is the dimensionality of the problem. Particles were initialised uniformly randomly within the same domain. We use 10-dimensional problems throughout. It may be interesting to consider higher dimensionalities, but $d=10$ seems sufficient in the sense that random hits at initialisation are already very unlikely. Our implementation of PSO performed no spatial or velocity clamping. In all trials a swarm of 25 particles was used. For the competition 50000 fitness evaluation were allowed which corresponds to 2000 iterations with 25 particles. Other iteration numbers (20, 200, 20000) were included here for comparison. Results are averaged over 100 trials. This protocol was carried out for pairs of $\omega \in [-1.1,1.1]$ and $\alpha \in [0,6]$. This was repeated for all 28 functions. The averaged solution costs as a function of the two parameters showed curved valleys similar to that in Fig. 1 for all problems. For each function we obtain different best values along (or near) the theoretical curve (9). There appears to be no preferable location within the valley.

4.2 Empirical Results

Using the 28 functions (in 10 dimensions) from the CEC2013 competition [15] we can run our unconstrained PSO algorithm for each parameter pairing. Randomly sampling of each problem is used to estimate its average value. This average is used to approximately normalise the PSO results obtained for each the function. We combined these results for 100 runs. The 5 % best parameter pairs are shown in Fig. 3 for different iteration budgets. As the iteration budget increases the best locations move out from the origin as we would expect. For 2000 iterations per run the best performing locations appear to agree well with the Jiang line [10]. It is known that some problem functions return good results even when parameters are well inside the stable line. Simple functions (e.g. Sphere) will benefit from early swarm convergence. Thus, our average performance may mask the full effects. Figure 3 also shows an example of a single function’s best performing parameter for 2000 iterations. This function now shows many locations beyond the Jiang line for which good results are obtained.

In Fig. 4 detailed explorations of two functions are shown. For these, we set $\omega =0.55$, while $\alpha$ is varied with a much finer granularity between 2 and 6. 2000 repetitions of the algorithm are performed for each parameter pairing. The curves shown are for increasing iteration budgets (20, 200, 2000, 20000). Vertical lines mark where the two predicted stable loci sit on these parameter space slices.

The best results lie outside the Jiang line for these functions. Our predicted stable limit appears to be consistent with these results. In other words, if the solution is to be found in a short time a more stable dynamics is preferable, because the particles can settle in a nearby optimum at smaller fluctuations. If more time is available, then parameter pairs more close to the critical curve lead to an increased search range which obviously allows the swarm to explore better solutions. Similarly, we expect that in larger search spaces (e.g. relative to the width of the initial distribution of the particles) parameters near the critical line will lead to better results.

Fig. 3.

Empirical cost function value results. (left) 5 % best parameter pair locations across all 28 functions plotted against our curve (black) and Jiang curve [10] (green). Iteration budgets are 20 (green circles), 200 (blue crosses), 2000 (red $\times$’s). (right) 5 % best parameter pair locations for function 21 plotted against our curve (black) and Jiang curve (green). Red dot is best location. (Color figure online)

5 Discussion

Our analytical approach predicts a locus of $\alpha$ and $\omega$ pairings that maintain the critical behaviour of the PSO swarm. Outside this line the swarm will diverge unless steps are taken to constrain it. Inside, the swarm will eventually converge to a single solution. In order to locate a solution precisely in the search space, the swarm needs to converge at some point, so the line represents an upper bound on the exploration-exploitation mix that a swarm manifests. For parameters on the critical line, fluctuations are still arbitrary large. Therefore, subcritical parameter values can be preferable if the settling time is of the same order as the scheduled runtime of the algorithm. If, in addition, a typical length scale of the problem is known, then the finite standard deviation of the particles in the stable parameter region can be used to decide about the distance of the parameter values from the critical curve. These dynamical quantities can be approximately set, based on the theory presented here, such that a precise control of the behaviour of the algorithm is in principle possible.

Fig. 4.

Detailed empirical cost function value results. Detailed PSO performance along the ($\omega =0.55$)-slice of parameter space for functions 7 (left) and 21 (right) [15]. Different iteration budgets are shown: 20 (red), 200 (yellow), 2000 (green) and 20000 (cyan) fitness evaluations. Vertical lines show our limit (black) and Jiang limit [10] (dark green). (Color figure online)

The observation of the distribution of empirically optimal parameter values along the critical curve, confirms the expectation that critical or near-critical behaviour is the main reason for success of the algorithm. Critical fluctuations are a plausible tool in search problem if apart from certain smoothness assumptions nothing is known about the cost landscape: The majority of excursions will exploit the smoothness of the cost function by local search, whereas the fat tails of the jump distribution allow the particles to escape from local minima.

The critical line in the PSO parameter space has been previously investigated and approximated by various authors [2, 8, 11, 17, 18]. Many of these approximations are compared alongside empirical simulation in [16]. As the authors of Ref. [3] note, the most accurate calculation of the critical line so far is provided by Poli in Refs. [17, 18], however, not without pointing out that the effects of the higher-order terms were actually ignored. In contrast, the method we present here uses an approach which does not exclude the effects of higher order terms. Thus, where our results differ from those previously published, we can conclude that the difference is a result of incorporating the effects of these higher order terms. Further, a second result is that these higher order terms do not have noticeable effect for $\omega$ values close to $\pm 1$, and thus in these regions of the parameter space both methods coincide.

The critical line (9) defines the best parameters for a PSO allowed to run for infinite steps. As the number of steps (and the size of the problem space) decrease, the best parameters move inwards, such that for e.g. 2000 steps the line proposed by Poli in Refs. [17, 18] provides a good estimate for good parameters.

The work presented here can be seen as a Lyapunov condition based approach to uncovering the phase boundary. Previous work considering the Lyapunov condition has produced rather conservative estimates for the stability region [8, 11] which is a result of the particular approximation used, while we avoid this by directly calculating the integral (7) for the one-particle case.

Equation 2 shows that the discovery of a better solution affects only the constant terms of the linear dynamics of a particle, whereas its dynamical properties are governed by the (linear) parameter matrices. However, in the time step after a particle has found a new solution the corresponding force term in the dynamics is zero (see Eq. 1) such that the particle dynamics slows down compared to the theoretical solution which assumes a finite distance from the best position at all (finite) times. As this affects usually only one particle at a time and because new discoveries tend to become rarer over time, this effect will be small in the asymptotic dynamics, although it could justify the empirical optimality of parameters in the unstable region for some test cases.

The question is nevertheless, how often these changes occur. A weakly converging swarm can still produce good results if it often discovers better solutions by means of the fluctuations it performs before settling into the current best position. For cost functions that are not ‘deceptive’, i.e. where local optima tend to be near better optima, parameter values far inside the critical contour (see Fig. 2) may give good results, while in other cases more exploration is needed.

A numerical scan of the $(\alpha _1, \alpha _2)$-plane shows a valley of good fitness values, which, at small fixed positive $\omega$, is roughly linear and described by the relation $\alpha _1+\alpha _2= \text{ const, }$ i.e. only the joint parameter $\alpha =\alpha _1+\alpha _2$ matters. For large $\omega$, and accordingly small predicted optimal $\alpha$ values, the valley is less straight. This may be because the effect of the known solutions is relatively weak, so the interaction of the two components becomes more important. In other words, if the movement of the particles is mainly due to inertia, then the relation between the global and local best is non-trivial, while at low inertia the particles can adjust their $\mathbf {p}$ vectors quickly towards the $\mathbf {g}$ vector such that both terms become interchangeable.

6 Conclusion

In previous approaches, inherent stochasticity of PSO was handled via various simplifications such as the consideration of expectation values, thus excluding higher order terms that were, however, included in the present approach. It was shown here that the system is more correctly understood by casting PSO as a random dynamical system. Our analysis shows that there exists a locus of ($\omega$,$\alpha$)-pairings that result in the swarm behaving in a critical manner. This plays a role also in other applications of swarm dynamices, e.g., the behaviour reported in Ref. [5] occurred as well in the vicinity of critical parameter settings.

A weakness of the current approach is that it focuses on the standard PSO [13] which is outperformed on benchmark sets as well as in practical applications by many of the existing PSO variants. Similar analyses are certainly possible and can be expected to be carried out for some of these variants.