Universality of 8-State Reversible and Conservative Triangular Partitioned Cellular Automata

Abstract

A partitioned cellular automaton (PCA) is a subclass of a standard CA such that each cell is divided into several parts, and the next state of a cell is determined only by the adjacent parts of its neighbor cells. This framework is useful for designing reversible CAs. Here, we investigate isotropic three-neighbor 8-state triangular PCAs where a cell has three parts, and each part has two states. They are called elementary triangular PCAs (ETPCAs). There are 256 ETPCAs, and they are extremely simple since each of their local transition functions is described by only four local rules. In this paper, we study computational universality of nine kinds of reversible and conservative ETPCAs. It has already been shown that one of them is universal. Here, we newly show universality of another. It is proved by showing that a Fredkin gate, a universal reversible logic gate, can be simulated in it. From these results and by dualities, we can conclude six among the nine are universal. We also show the remaining three are non-universal. Thus, universality of all the reversible and conservative ETPCAs is clarified.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A reversible cellular automaton (RCA) is a CA such that its global function is injective. Among various research topics on RCAs, computational universality of them is one of the important problems. Toffoli [12] first showed that a two-dimensional RCA is universal. Since then, studies on universality of one- and two-dimensional RCAs have been done extensively. As for two-dimensional RCAs, several very simple universal RCAs have been proposed. Margolus [4] presented a two-state universal block RCA with the Margolus neighborhood. Morita and Ueno [11] showed two kinds of 16-state universal RCAs using the framework of partitioned CAs (PCAs). Imai and Morita [3] gave a universal 8-state reversible triangular PCA (in the following sections it is denoted by $T_\mathrm{RU}$) that has an extremely simple local function. In all these models, computational universality is shown by giving a configuration that simulates a Fredkin gate, a 3-input 3-output universal reversible logic gate.

A triangular CA is a one such that each cell is triangular-shaped, and communicates with its three neighbor cells. Here, we use the framework of a triangular PCA (TPCA) to study reversible ones. It is a CA whose cell is divided into three parts. Each cell changes its state depending only on the three adjacent parts of its three neighbor cells, but not depending on the whole states of the three cells. This framework makes it easy to design reversible TPCAs. An elementary TPCA (ETPCA) is a TPCA where each part of a cell has only two states (hence a cell has eight states) and it is isotropic. ETPCAs are extremely simple, since each of their local transition functions is described by only four local rules.

In this paper, we investigate all the conservative (i.e., bit-conserving) and reversible ETPCAs (RETPCAs). There are nine conservative RETPCAs. It has been shown that one of them (denoted by $T_\mathrm{RU}$) is computationally universal [3]. Here, we newly show another one, denoted by $T_\mathrm{RL}$, is also universal. It is proved by showing that a Fredkin gate can be simulated in $T_\mathrm{RL}$. From these results, and by the dualities among ETPCAs under reflection and conjugation, we can see six of them are universal. We also show that three are non-universal. Hence, universality of all the nine conservative RETPCAs is clarified.

2 Preliminaries

In this section, we give definitions on elementary triangular partitioned cellular automata (ETPCAs), their reversibility, and conservativeness. We also explain a method for showing computational universality of a reversible PCA.

2.1 Triangular Partitioned Cellular Automata (TPCAs)

A partitioned cellular automaton (PCA) is a subclass of a standard CA, where a cell is divided into several parts, and each part has a state set. The next state of a cell is determined by the states of the adjacent parts of the neighbor cells. A two-dimensional three-neighbor triangular PCA (TPCA) is a special kind of a PCA such that a cell is triangular-shaped, and divided into three parts.

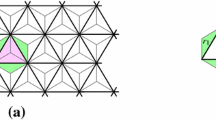
We first consider an example of a TPCA whose behavior is determined by the set of local transition rules shown in Fig. 1. Note that each of the three parts of a cell has the state set $\{0,1\}$, where 0 and 1 are represented by a blank and a particle (i.e., ). Hence, each cell has eight states. We assume this TPCA is isotropic (or rotation-symmetric). Namely, for each local rule, the rules obtained by rotating the both sides of it by a multiple of $60^{\circ }$ exist. Thus, the set of local rules in Fig. 1 specifies the local function f by which the next state of each cell is uniquely determined from the present states of the adjacent parts of the neighbor cells. Applying the local function f to all the cells in parallel, we obtain the global function F, which defines transition among configurations as in Fig. 2.

Fig. 1.

Example of local rules of an isotropic TPCA, which define a local function

Fig. 2.

Evolution of configurations by the global function F, which is induced by the local function shown in Fig. 1

We say a PCA is locally reversible if its local function is injective, and globally reversible if its global function is injective. It is known that global reversibility and local reversibility are equivalent (Lemma 1). Thus, such a PCA is simply called a reversible PCA (RPCA). Note that, in [10], the lemma is given for one-dimensional PCAs, but it is easy to extend it for two-dimensional PCAs.

Lemma 1

[10] A PCA A is globally reversible iff it is locally reversible.

By this lemma, to obtain a reversible CA, it is sufficient to give a locally reversible PCA. Thus, the framework of PCA makes it easy to design reversible CAs.

We can see that the local function defined by the set of local rules shown in Fig. 1 is injective, since there is no pair of local rules that have the same right-hand sides. Therefore, it is a reversible TPCA.

2.2 Elementary Triangular Partitioned Cellular Automata

An 8-state isotropic TPCA is called an elementary TPCA (ETPCA). Thus, each part of a cell has two states. ETPCAs are the simplest ones among two-dimensional PCAs. But, this class still contains many interesting PCAs as in the class of one-dimensional elementary CAs (ECAs) [13, 14].

Since ETPCA is isotropic, and each part of a cell has the state set $\{0,1\}$, its local function is defined by only four local rules. Hence, an ETPCA can be specified by a four-digit number wxyz, as shown in Fig. 3, such that $w,z \in \{0,7\}$ and $x,y \in \{0,1,\ldots ,7\}$. Thus, there are 256 ETPCAs. Note that w and z must be 0 or 7 because an ETPCA is deterministic and isotropic. The ETPCA with the number wxyz is denoted by $T_{wxyz}$. The ETPCA in Fig. 1 is $T_{0157}$.

Fig. 3.

Representing an ETPCA by a four-digit number wxyz, where $w,z \in \{0,7\}$ and $x,y \in \{0,1,\ldots ,7\}$. Vertical bars indicate alternatives of a right-hand side of a rule.

A reversible ETPCA is denoted by RETPCA. It is easy to see the following.

$$ \begin{array}{l} \text{ An } \text{ ETPCA }\ T_{wxyz}\ \text{ is } \text{ reversible } \text{ iff } \\ \ (w, z) \in \{(0,7),(7,0)\} \ \wedge \\ \ (x, y) \in \{1,2,4\}\!\times \!\{3,5,6\}\,\cup \,\{3,5,6\}\!\times \!\{1,2,4\} \end{array} $$

Let $T_{wxyz}$ be an ETPCA. We say $T_{wxyz}$ is conservative (or bit-conserving), if the total number of particles (i.e., ’s) is conserved in each local rule. Thus, the following holds.

$$ \begin{array}{l} \text{ An } \text{ ETPCA }\ T_{wxyz}\ \text{ is } \text{ conservative } \text{ iff } \\ \ w=0\ \wedge \ x \in \{1,2,4\}\ \wedge \ y \in \{3,5,6\}\ \wedge \ z=7 \end{array} $$

We can see that if an ETPCA is conservative, then it is reversible. This is because ETPCAs are isotropic. There are nine kinds of conservative RETPCAs.

Here, we give “aliases” to the nine conservative RETPCAs for the later convenience. Each of their local functions are shown in Fig. 4. Based on it, we denote a conservative RETPCA by $T_{XY}$, if its local function f is given by the set of local rules $\{ (0), (1X), (2Y), (3) \}$, where $X,Y \in \{\text{ L, } \text{ U, } \text{ R } \}$. For example, $T_\mathrm{RU} = T_{0157}$. Note that L, U, and R stand for left-, U-, and right-turns of particles, respectively. Namely, the rule (1L) ((1U), and (1R), respectively) can be interpreted as the one where a coming particle makes left-turn (U-turn, and right-turn). The rules (2L), (2U), and (2R) are also interpreted similarly.

Fig. 4.

Local function of a conservative RETPCA

2.3 Dualities in ETPCAs

We can define two kinds of dualities in ETPCAs. They are the duality under reflection, and the duality under conjugation, which are similarly defined as in the case of one-dimensional ECAs [13]. Dual ETPCAs are equivalent since they can simulate each other in a straightforward manner.

ETPCAs T and $T'$ are called dual under reflection, if their local functions are mirror image of each other. It is denoted by $T \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T'$. Evolution of configurations in T is simulated by the mirror images of them in $T'$ in an obvious way. We can see the following relations hold among nine conservative RETPCAs.

$$ T_\mathrm{RL} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T_\mathrm{LR}, \ T_\mathrm{RU} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T_\mathrm{LU}, \ T_\mathrm{UR} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T_\mathrm{UL}, \ T_\mathrm{RR} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T_\mathrm{LL}, \ T_\mathrm{UU} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ refl }}}\! T_\mathrm{UU}. $$

ETPCAs T and $T'$ are called conjugate (or dual under conjugation), if their local functions are $0\,-1$ exchange of the other (i.e., renaming of the states). It is denoted by $T \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T'$. Obviously, evolution of configurations in T is simulated by the complemented configurations in $T'$. We can see the following relations hold.

$$ \begin{array}{l} T_\mathrm{RU} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{UR}, \ T_\mathrm{UL} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{LU}, \ T_\mathrm{RL} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{LR}, \\ T_\mathrm{RR} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{RR}, \ T_\mathrm{LL} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{LL}, \ T_\mathrm{UU} \!\mathrel {\mathop {\longleftrightarrow }\limits _{\text{ conj }}}\! T_\mathrm{UU}. \end{array} $$

2.4 Turing Universality of RPCAs

An RPCA is called Turing universal, if any Turing machine is simulated in it. To prove Turing universality of an RPCA, it is sufficient to show any circuit composed of Fredkin gates [2] (Fig. 5) and delay elements is simulated in it. It is stated in Lemma 5.

Fig. 5.

Fredkin gate [2]. It is a 3-input 3-output reversible logic gate.

Lemma 5 can be derived, e.g., in the following way. First, any reversible sequential machine (RSM), in particular, a rotary element (RE), which is a 2-state 4-symbol RSM, is composed of Fredkin gates (Lemma 2). Next, any reversible Turing machine is constructed out of REs (Lemma 3). Finally, any (irreversible) Turing machine is simulated by a reversible one (Lemma 4). Thus, Lemma 5 follows. Note that the circuit that realizes a reversible Turing machine constructed by this method becomes an infinite (but ultimately periodic) circuit.

Lemma 2

[5, 7] Any RSM (in particular RE) can be simulated by a circuit composed of Fredkin gates and delay elements, which produces no garbage signals.

Lemma 3

[6] Any reversible Turing machine can be simulated by a garbage-less circuit composed only of REs.

Lemma 4

[1] Any (irreversible) Turing machine can be simulated by a garbage-less reversible Turing machine.

Lemma 5

An RPCA is Turing universal, if any circuit composed of Fredkin gates and delay elements is simulated in it.

In [3], it is shown that any circuit composed of Fredkin gates and delay elements is simulated in $T_\mathrm{RU}$ (see Fig. 1). From this, and the dualities in ETPCAs, we have the following theorem.

Theorem 1

[3] The conservative RETPCAs $T_\mathrm{RU}$, $T_\mathrm{LU}$, $T_\mathrm{UR}$, and $T_\mathrm{UL}$ with infinite (but ultimately periodic) configurations are Turing universal.

3 Universality of the RETPCA $T_\mathrm{RL}$

We prove Turing universality of $T_\mathrm{RL}$. Its local function is given in Fig. 6. In $T_\mathrm{RL}$, if one particle comes, it makes right-turn, and if two come, they make left-turns.

Fig. 6.

Local function of the conservative RETPCA $T_\mathrm{RL}$

It is easy to see that if the following elements and modules are implemented in $T_\mathrm{RL}$, then any circuit composed of Fredkin gates and delay elements can be realized in it: (1) Signal and transmission wire. (2) Delay module. (3) Signal crossing module. (4) Fredkin gate module.

In $T_\mathrm{RL}$ a signal is represented by a single particle, and a transmission wire is composed of blocks (Fig. 7). A block is a stable pattern consisting of six particles as in Fig. 7 (note that a pattern is a finite segment of a configuration). A signal travels along a sequence of blocks as shown in Fig. 7.

Fig. 7.

A signal, and a transmission wire composed of blocks in $T_\mathrm{RL}$. The signal travels along the wire. The number t ($1 \le t \le 68$) shows the position of the signal at time t.

To implement a delay module and a signal crossing module, we use a signal control module. It consists of a single particle that simply rotates (Fig. 8(a)), by which the trajectory of a signal can be altered as explained below. Since it is a pattern of period 6, a signal to be controlled must be given at a right timing.

Fig. 8.

(a) Signal control module, and (b) delay module of 2 steps in $T_\mathrm{RL}$

A delay module is a pattern for fine adjustment of signal timing. Putting a signal control module near a transmission wire as in Fig. 8(b), an extra delay of 2 steps is realized. On the other hand, a large delay is implemented by appropriately bending a transmission wire. Note that a delay of odd steps is not necessary by the following reason. Assume a signal is in an up-triangle ($\bigtriangleup$) at $t=0$. At $t=1$ it must be in a down-triangle ($\bigtriangledown$), then at $t=2$ it is in an up-triangle, and so on. Therefore, to interact two signals at a specified cell, they must be in the same type of triangles at $t=0$. Thus, if both of the signals visit the same cell, then the difference of their arriving time is even.

A signal crossing module is for crossing two signals in the two-dimensional space. It consists of two signal control modules and transmission wires (Fig. 9).

Fig. 9.

Signal crossing module in $T_\mathrm{RL}$. Trajectories of (a) signal x, and (b) signal y.

To simulate a Fredkin gate, we implement a switch gate and an inverse switch gate (Fig. 10(a) and (b)). Since a Fredkin gate is composed of switch gates and inverse switch gates as in Fig. 10(c) [2], we can obtain a pattern that simulates a Fredkin gate, from those of a switch gate and an inverse switch gate.

Fig. 10.

(a) Switch gate. (b) Inverse switch gate, where $c=y_1$ and $x=y_2 + y_3$ under the assumption $(y_2 \rightarrow y_1)\wedge (y_3 \rightarrow \overline{y_1})$. (c) Fredkin gate composed of them [2].

In $T_\mathrm{RL}$, a single cell works as a switch gate and an inverse switch gate as shown in Fig. 11. However, since it is not convenient to use one cell as a building unit for a larger circuit, we design a switch gate module and an inverse switch gate module from it. A gate module in the standard form is a pattern embedded in a rectangular-like region in the cellular space that satisfies the following (see Fig. 12): (1) It realizes a reversible logic gate. (2) Input ports are at the left end. (3) Output ports are at the right end. (4) Delay between input and output is constant.

Fig. 11.

A single cell of $T_\mathrm{RL}$ works as (a) a switch gate, and (b) an inverse switch gate

Fig. 12.

Gate module in the standard form

Figure 13 shows a switch gate module, and an inverse switch gate module, each of which contains a (modified) signal crossing module, and three delay modules. The cells that work as switch gate and inverse switch gate are indicated by bold lines. The delay between input and output is 126 steps.

Fig. 13.

(a) Switch gate module, and (b) inverse switch gate module in $T_\mathrm{RL}$

A Fredkin gate module is obtained by connecting two switch gate modules, two inverse switch gate modules, five signal crossing modules, and many delay modules to form the circuit shown in Fig. 10(c). The complete configuration is found in [9]. Its size is of $30 \times 131$, and the input-output delay is 744 steps.

By above, and by the duality in ETPCAs, we have the following.

Theorem 2

The conservative RETPCAs $T_\mathrm{RL}$ and $T_\mathrm{LR}$ with infinite (but ultimately periodic) configurations are Turing universal.

4 Non-universality of the RETPCAs $T_\mathrm{RR}$, $T_\mathrm{LL}$ and $T_\mathrm{UU}$

$T_\mathrm{RR}$ has the set of local rules $\{\text {(0), (1R), (2R), (3)}\}$ (see Fig. 4). We can interpret (1R), (2R) and (3) to be the ones where all particles make right-turn. Therefore, every configuration has period 6, and thus $T_\mathrm{RR}$ is trivially non-universal. By a similar argument, $T_\mathrm{LL}$ is also non-universal.

In $T_\mathrm{UU}$, we can interpret its local rules (1U), (2U) and (3) to be the ones where all particles make U-turn. Therefore, every configuration has period 2, and thus $T_\mathrm{UU}$ is again trivially non-universal.

Theorem 3

The RETPCAs $T_\mathrm{RR}, T_\mathrm{LL},$ and $T_\mathrm{UU}$ are not Turing universal.

5 Concluding Remarks

In this paper, nine conservative RETPCAs, which have extremely simple local functions, are studied. It was shown that $T_\mathrm{RL}$, and $T_\mathrm{LR}$ are Turing universal (Theorem 2), while $T_\mathrm{RR}, T_\mathrm{LL},$ and $T_\mathrm{UU}$ are not (Theorem 3). With Theorem 1 shown in [3], universality of all the nine conservative RETPCAs was clarified. Evolving processes of various configurations of $T_\mathrm{RL}$, $T_\mathrm{RU}$, and $T_\mathrm{UR}$ can be seen by movies in [9].

A non-conservative RETPCA $T_{0347}$ also exhibits interesting behavior. Recently, existence of a glider and glider guns in $T_{0347}$, and its universality were shown in [8]. Investigation of other ETPCAs is left for the future study.