The Stabilizing Virtues of Monetary Policy on Endogenous Bubble Fluctuations

Abstract

We explore the stabilizing role of monetary policy on the existence of endogenous fluctuations when the economy experiences a rational bubble. Considering an overlapping generations model, expectation-driven fluctuations are explained by a portfolio choice between three assets (capital, bonds and money), credit market imperfections and a collateral effect. They occur under a positive bubble on bonds. The key mechanism relies on the existence of gaps between the returns on assets due to financial distortions. Then, we study the stabilizing role of the monetary policy. Such a policy managed by a (standard) Taylor rule has no clear stabilizing virtues.

We would like to thank an anonymous referee for his comments. We also thank Stefano Bosi, Marion Davin, Takashi Kamihigashi, Carine Nourry and Alain Venditti for valuable suggestions. We also thank participants to the Conference in honor of Jean-Michel Grandmont held in Aix-Marseille University on June 2013, to the Conference 12th “Journées Louis-André Gérard-Varet”, to the Conference PET 2013 and to the 13th Annual SAET Conference. Any remaining errors are our own.

1 Introduction

In recent years, asset prices have experienced large fluctuations, and the financial sphere of the economy had strong effects on the real one, as illustrating during the last financial crisis. Some empirical contributions shed light on the excessive asset price volatility, and reveal that asset prices fluctuate more than their fundamental value (see Shiller 1981, 1989, and LeRoy and Porter 1981). One explanation for this excessive volatility is the existence and the fluctuations of asset bubbles.

A large body of theoretical literature explores the role of credit market imperfections in the existence and dynamics of rational bubbles (Farhi and Tirole 2012; Martin and Ventura 2012; Wang and Wen 2012). Despite the fact that most of these contributions deal with credit constraints at the level of entrepreneurs, some empirical studies highlight the existence of credit constraints faced by consumers underlying the role of collateral on their behavior (Campbell and Mankiw 1989; Jappelli 1990; Iacoviello 2004). Such types of credit market imperfections affect the portfolio choices between different existing assets, but also explain the gaps between their returns. We think that such credit market imperfections may be a main transmission channel between the financial and the real spheres. In this paper, we argue that credit constraints faced by consumer play a crucial role to explain expectation-driven fluctuations of speculative bubbles, as illustrated during the recent subprime crisis. This idea already appears in Bosi and Seegmuller (2010) and Clain-Chamosset-Yvrard and Seegmuller (2015).¹ They assume that the share of consumption financed by credit is positively correlated to a collateral. Because of this type of credit market distortions, the portfolio choices are no longer constant through time. A change in agents’ expectations generates a new trade-off between asset holdings promoting equilibrium indeterminacy, and thus the occurrence of expectation-driven fluctuations. We enrich these contributions by considering both capital and the stabilizing role of a monetary policy conducted through a Taylor rule.

Indeed, economic fluctuations based on consumer credit constraints open the door to new policy tools for stabilizing issues. A stabilizing policy must dampen or eliminate the mechanism source of indeterminacy. Since our explanation of expectation-driven fluctuations relies on a trade-off between different assets, namely capital, bonds and money, relevant stabilizing policies are those reducing the gaps between their returns. Monetary policy appears to be a natural policy tool, since it affects the opportunity cost of money holdings through the level of the nominal interest rate. In addition, contrary to most of the literature, we analyze the stabilizing role of the monetary policy when bubble fluctuations occur in an economy with both production and a positive bubble (Grandmont 1985, 1986; Bernanke and Woodford 1997; Benhabib et al. 2001; Sorger 2005; and Rochon and Polemarchakis 2006).

We consider a simple overlapping generations (OLG) model with capital accumulation to highlight the role of consumers’ credit market imperfections and collateral in an economy characterized by a rational bubble.² Households save through bonds, money and capital. Bonds are sold by the monetary authority to supply money. Because of a binding cash-in-advance (CIA) constraint, money is held by households to finance a share of their consumption in the second period of their life. Despite the fact that capital is used for the production, it also serves as a collateral: Holding more capital increases the amount of collateral, and thus allows each household to reduce the share of consumption financed through money. It is important to note that the three assets have different returns. Bonds have larger return than capital because this latter is used as a collateral to relax the consumers’ credit constraint, and also a larger return than money because we focus on equilibria with binding constraints. As a direct implication, the Fisher relationship is not satisfied.³ The violation of this relationship will induce some portfolio choices that promote indeterminacy, and therefore endogenous fluctuations.

We prove the existence of a steady state characterized by a positive rational bubble on bonds (Tirole 1985). In contrast to several existing papers (Farmer 1986; Benhabib and Laroque 1988; Rochon and Polemarchakis 2006), expectation-driven fluctuations occur in the neighborhood of such a steady state with a positive rational asset bubble under gross substitutability and reasonable values of input substitution, without requiring arbitrarily large increasing returns to scale (Cazzavillan and Pintus 2005). This result is obtained because of the role of collateral.

Since expectation-driven fluctuations are mainly driven by the portfolio choices between capital, money and bonds and the violation of the Fisher relationship, a policy may have a stabilizing virtue if it is able to reduce the gaps between the different returns on assets. Therefore, the monetary authority could play an active role in stabilizing the economy by manipulating the nominal interest rate. Following Bernanke (2010) who argues that a rule which responds to expected inflation is relevant to describe the US monetary policy, we consider that the nominal interest rate is determined according to a Taylor rule on expected inflation. We show however that the stabilizing results are mitigated. A weakly active policy can even promote endogenous fluctuations for some relevant parameter configurations. One explanation is that such a rule does not significantly modify the nominal interest rate, and therefore does not alter so much the portfolio choices. More generally, this result provides an adding argument emphasizing that standard policy tools are not so relevant in some circumstances. In our case, these circumstances are the existence of a bubble and consumers’ credit constraints affected by a collateral.

This paper is organized as follows. In the next section, we present the model. The intertemporal equilibrium is defined in Sect. 10.3. Section 10.4 is devoted to the steady state analysis. In Sect. 10.5, we analyze the occurrence of expectation-driven fluctuations when there is a positive bubble and the stabilizing role of monetary policy. Concluding remarks are provided in Sect. 10.6, and all the proofs are gathered in a final Appendix.

2 The Model

We consider an OLG model with production in discrete time ($t=0,1,...,+\infty$). This economy consists of identical two period-lived households, firms, a monetary authority and a government.

2.1 Households

There is no population growth, and at each date t, a generation of unit size is born and lives for two periods.

An household derives utility from consumption of final good when young $(c_t)$ and old $(d_{t+1})$. Her preferences are represented by an additively separable life-cycle utility function:

$$\begin{aligned} u\left( c_t\right) + \beta v\left( d_{t+1}\right) =\frac{c_t^{1-\varepsilon _u}}{1-\varepsilon _u}+\beta \frac{d_{t+1}^{1-\varepsilon _v}}{1-\varepsilon _v}\ , \,\,\beta >0 \end{aligned}$$

(10.1)

where $\varepsilon _{u}>0$ and $\varepsilon _{v}>0$ denote respectively the degrees of concavity of $u\left( c_t\right)$ and $v\left( d_{t+1}\right)$. We further note that $\varepsilon _v<1$ implies gross substitutability meaning that savings are an increasing function of the global return on portfolio.⁴

In her first period of life, the household is young and supplies one unit of labor inelastically remunerated at the wage $w_t$. With this wage, she can consume an amount $c_t$ of final good at price $p_t$, and save through a diversified portfolio of nominal balances $M_{t+1}$ needed for a transaction motive, productive capital per capita $k_{t+1}$ (with rental factor $R_{t+1}$)⁵ and nominal bonds $B_{t+1}$ (with nominal interest rate $i_{t+1}$). In our framework, bonds denote nominal debts issued by the monetary authority in order to inject money in the economy. In contrast to asset papers with no fundamental value considered as freely disposed of, these bonds can have a negative nominal value $(B_{t+1}<0)$.

In her second period of life, the household is old. She uses her remunerated savings and her monetary transfer $\Delta _{t+1}$ received from the monetary authority to purchase an amount $d_{t+1}$ of final good at price $p_{t+1}$. The first and second-period budget constraints are written as follows:

$$\begin{aligned} p_t c_t+M_{t+1}+B_{t+1}+p_t k_{t+1}\le & {} p_t w_t \end{aligned}$$

(10.2)

$$\begin{aligned} p_{t+1}d_{t+1}\le & {} M_{t+1}+\left( 1+i_{t+1}\right) B_{t+1}\nonumber \\&+p_{t+1} R_{t+1}k_{t+1} + \Delta _{t+1} \end{aligned}$$

(10.3)

The household has to pay cash a part of the second period consumption $d_{t+1}$: Her money demand is rationalized by a cash-in-advance (CIA) constraint. We use a constraint of the type introduced by Hahn and Solow (1995), i.e. $\gamma p_{t+1}d_{t+1}\le M_{t+1}$, but we extend it to capture the role of collateral:

$$\begin{aligned} \gamma (k_{t+1})p_{t+1}d_{t+1}\le & {} M_{t+1} \end{aligned}$$

(10.4)

A binding cash-in-advance constraint means that a share $\gamma (k_{t+1})\in (0,1)$ of her second-period consumption has to be paid cash, i.e. with nominal balances $M_{t+1}$. As underlined in Rochon and Polemarchakis (2006) and Clain-Chamosset-Yvrard and Seegmuller (2015), the household can consume the remaining share $1-\gamma (k_{t+1})$ of consumption on credit when old. Indeed, because she holds $B_{t+1}+p_{t+1}k_{t+1}$ in her portfolio when young, the household knows that she will have her remunerated savings from bonds and capital $(1+i_{t+1})B_{t+1}/p_{t+1}+ R_{t+1}k_{t+1}$ at the next period, in addition to the transfer from the monetary authority $\Delta _{t+1}/p_{t+1}$. As a result, she can consume on credit by borrowing from a bank or a financial institution an amount equal to $(1+i_{t+1})B_{t+1}/p_{t+1}+ R_{t+1}k_{t+1}+\Delta _{t+1}/p_{t+1}$, that she will pay back at the end of her second period of life. In the following, we refer to $1-\gamma (k_{t+1})$ as the credit share.

Furthermore, we assume that the credit share is increasing with the amount of physical capital held by a household. Through this assumption, we assert that capital acts as a collateral for the household. Since a collateral is by definition an asset that a household offers a bank or a financial institution to secure a loan, we argue that the value of physical capital $k_{t+1}$ can be pledged as a collateral, rather than the capital income $R_{t+1}k_{t+1}$. If the household fails to repay the loan, the financial institution can seize its physical capital to recover its losses, and thus become the owner of this capital. Since the financial institution takes less risk, it would be easier for the household to obtain credit from the bank or the financial institution by holding more capital in her portfolio, and thus to reduce her need of cash in her second period of life.

This is also in accordance with some empirical studies which, focusing on U.S data, underline the negative correlation between money holdings and wealth (see Wolff 1998). In our framework, $k_{t+1}$ can be seen as a proxy of household’s wealth. In any case, it is a simple way to introduce credit market imperfections and to capture the role of collateral on consumption behavior of the household as highlighted by empirical studies (among others, Campbell and Mankiw 1989; Iacoviello 2004).⁶

The following assumption summarizes the properties of the function $\gamma (k)$:

Assumption 1

$\gamma \left( k\right) \in \left( 0,1\right)$ is a continuous function defined on $\left[ 0,+\infty \right)$, $C^{2}$ on $\left( 0,+\infty \right)$, decreasing ($\gamma ^{\prime }\left( k\right) \le 0$).

For further references, we define the following elasticities:

$$\begin{aligned} \eta _{1}\left( k\right)\equiv & {} \frac{\left[ 1-\gamma \left( k\right) \right] ^{\prime } k}{ 1-\gamma \left( k\right) }=-\frac{\gamma ^{\prime }(k)k}{1-\gamma (k)}\ge 0, \end{aligned}$$

(10.5)

$$\begin{aligned} \eta _{2}\left( k\right)\equiv & {} -\frac{\left[ 1-\gamma \left( k\right) \right] ^{\prime \prime } k}{\left[ 1-\gamma \left( k\right) \right] ^{\prime } } =-\frac{\gamma ^{\prime \prime }(k)k}{\gamma ^{\prime }(k)} \end{aligned}$$

(10.6)

Example

The following function satisfies these properties:

$$\begin{aligned} \gamma (k)= & {} 1-\frac{a+bk^{\epsilon }}{1+ck^{\epsilon }}, \end{aligned}$$

(10.7)

with $a\in (0,1)$, $c>1$, $b\in (ac,c)$ and $\epsilon >0$. Using this example, $\eta _1(k)$ and $\eta _2(k)$ are given by:

$$\begin{aligned} \eta _1(k)= & {} \frac{b-ca}{a+bk^{\epsilon }}\frac{\epsilon k^{\epsilon }}{1+ck^{\epsilon }}\ge 0 \,\, and \,\, \eta _2(k)=1+\epsilon \left( \frac{2ck^{\epsilon }}{1+ck^{\epsilon }}-1\right) \end{aligned}$$

When collateral does not matter $(\eta _1\left( k_{t+1}\right) =0)$, and $\gamma$ tends to 0, money is no longer needed and the credit market distortion disappears, whereas when $\gamma >0$, there is a need of cash. When collateral matters $(\eta _1\left( k_{t+1}\right) >0)$, the households are aware of the credit share function: They are able to relax the CIA constraint by increasing capital holdings.

Using $\pi _{t+1}\equiv p_{t+1}/p_t$ and introducing the real variables $m_{t+1}\equiv M_{t+1}/p_{t+1}$, $b_{t+1}\equiv B_{t+1}/p_{t+1}$ and $\delta _{t+1}\equiv \Delta _{t+1}/p_{t+1}$, the constraints (10.2)–(10.4) can be rewritten as follows:

$$\begin{aligned} c_t+\pi _{t+1}m_{t+1}+\pi _{t+1}b_{t+1}+k_{t+1}\le & {} w_{t}\end{aligned}$$

(10.8)

$$\begin{aligned} d_{t+1}\le & {} m_{t+1}+\left( 1+i_{t+1}\right) b_{t+1} +R_{t+1}k_{t+1} +\delta _{t+1} \end{aligned}$$

(10.9)

$$\begin{aligned} \gamma \left( k_{t+1}\right) d_{t+1}\le & {} m_{t+1} \end{aligned}$$

(10.10)

An household derives her optimal consumption choice $(c_t,$ $d_{t+1})$ and her optimal portfolio choice $(k_{t+1}, m_{t+1}, b_{t+1})$ by maximizing her utility function (10.1) under her budget and cash-in-advance constraints (10.8)–(10.10).

Assumption 2

Let $\displaystyle \tilde{\varepsilon }_u\equiv \displaystyle c\frac{1+i}{\pi }\frac{i\eta _1\left( 1-\gamma \right) }{\eta _2 d\left( 1+i\gamma \right) ^{2}}$.⁷ For all $t\ge 0$, we assume $i_{t}>0$, $\eta _2 (k_t)>0$ and $\varepsilon _u>\tilde{\varepsilon }_u$.

Since the conditions in Assumption 2 rely on endogenous variables, as $i_t, \pi _t, \gamma (k_t)$, Assumption 2 can seem quite strong. Nevertheless, as we are interested in the occurrence of fluctuations in the vicinity of a steady state, Assumption 2 will be supposed satisfied at the steady state. By continuity, it will also hold in the neighborhood of this steady state. Note that we provide a numerical example satisfying $n_2(k_t)>0$ at the normalized steady state that we consider for the dynamic analysis. In addition, since $\varepsilon _u$ is a free preference parameter, Assumption 2 can always be satisfied.

We can derive the following Lemma⁸:

Lemma 1

Under Assumptions 1 and 2, constraints (10.8)–(10.10) are binding and the second-order conditions are satisfied.

Lemma 1 requires that the function of the credit share $1-\gamma (k_{t+1})$ is concave: Capital holdings increase, at a decreasing rate, the fraction of second-period consumption purchased on credit. Moreover, the CIA constraint is binding if the nominal interest rate $i_{t+1}$ is strictly positive ($i_{t+1}>0$).

Under Assumptions 1 and 2, the optimal households’ behavior is summarized by the following equations:

$$\begin{aligned} \frac{u^{\prime }(c_t)}{\beta v^{\prime }(d_{t+1})}= & {} \frac{1+i_{t+1}}{\pi _{t+1}}\frac{1}{1+i_{t+1}\gamma (k_{t+1})}\end{aligned}$$

(10.11)

$$\begin{aligned} R_{t+1}= & {} \frac{1+i_{t+1}}{\pi _{t+1}}-i_{t+1}\eta _1(k_{t+1})\frac{1-\gamma (k_{t+1})}{k_{t+1}} d_{t+1} \end{aligned}$$

(10.12)

When collateral does not matter $(\eta _1(k)=0)$, Eqs. (10.11) and (10.12) rewrite:

$$\begin{aligned} \frac{u^{\prime }(c_t)}{\beta v^{\prime }(d_{t+1})}=\frac{(1+i_{t+1})/\pi _{t+1}}{1+i_{t+1}\gamma } \end{aligned}$$

(10.13a)

and

$$\begin{aligned} R_{t+1}=\frac{1+i_{t+1}}{\pi _{t+1}} \end{aligned}$$

(10.13b)

We note that as $\gamma$ tends to 0, we obtain the intertemporal trade-off found in Diamond (1965) and Tirole (1985), in which there are no credit market distortions in the economy (see Eq. (10.13a)). As $\gamma >0$, a distortion exists: Old households now have to pay cash $\gamma$ in order to consume an additional unit of final good, and money entails an opportunity cost. Nevertheless, when collateral does not matter, capital and bonds are perfect substitutes (see Eq. (10.13b)).

When collateral matters ($\eta _1(k)>0$), capital and bonds are no longer perfect substitutes. Households can now decrease their need of cash by holding more capital in their portfolio. As a consequence, the return on capital is lower than the return on bonds.

The endogeneity of the credit share ensures the portfolio choices to be no longer constant through time. The trade-off between assets is endogenous and depends on the amount of collateral held by the households. A change in expected inflation generates a portfolio effect, i.e. a new trade-off between asset holdings. This portfolio effect is the key mechanism through which expectation-driven fluctuations may occur. Since the portfolio choices are the explanation for fluctuations, we will also focus on a stabilizing policy designed to dampen the portfolio effect by modifying the different returns on assets.

2.2 Firms

A representative competitive firm produces the final good using capital and labor under a constant returns to scale technology $f\left( K/L \right) L$. Using $k=K/L$, the intensive production function $f\left( k\right)$ satisfies:

Assumption 3

$f\left( k\right)$ is a continuous function defined on $\left[ 0,+\infty \right)$ and $C^{2}$ on $\left( 0,+\infty \right)$, strictly increasing ($f^{\prime }\left( k\right) >0$) and strictly concave ($f^{\prime \prime }\left( k\right) < 0$). Defining $\alpha (k)\equiv f^{\prime }(k)k/f(k)\in \left( 0,1\right)$ as the capital share in total income and $\sigma (k)\equiv \left[ \frac{f^{\prime }\left( k\right) k}{f\left( k\right) } -1\right] \frac{f^{\prime }\left( k\right) }{ kf^{\prime \prime }\left( k\right) }>0$ as the elasticity of capital-labor substitution, we further assume $f^{\prime }(1)<1$, $\lim _{k\rightarrow 0^{+}}f^{\prime }\left( k\right) >1$ and $\sigma (k)>1-\alpha (k)$.

Note that at the end of Sect. 10.4.2, we provide a numerical example that satisfies Assumption 3. The competitive firm takes the prices as given and maximizes the profits $f\left( K_{t}/L_{t}\right) L_{t}-w_{t}L_{t}-R_{t}K_{t}$:

$$\begin{aligned} R_{t}= & {} f^{\prime }\left( k_{t}\right) \equiv R\left( k_{t}\right) \end{aligned}$$

(10.14)

$$\begin{aligned} w_{t}= & {} f\left( k_{t}\right) -k_{t}f^{\prime }\left( k_{t}\right) \equiv w\left( k_{t}\right) \end{aligned}$$

(10.15)

Hence, the interest rate and wage elasticities are respectively equal to $\epsilon _R(k) \equiv R^{\prime }(k)k/R(k)=-(1-\alpha (k))/\sigma (k)$ and $\epsilon _w(k) \equiv w^{\prime }(k)k/w(k)=\alpha (k)/\sigma (k)$. The inequality $\sigma (k)>1-\alpha (k)$ involves capital income $R_tk_t$ being increasing with $k_t$, which is not a restrictive assumption.

2.3 Monetary Authority

For implementing monetary policy, the monetary authority (central bank) uses open market operations defined as the purchase or sale of bonds in exchange for nominal balances.⁹ At time t, the central bank creates nominal balances $M_{t+1}$, which offer liquidity at the next period $t+1$.¹⁰ The money growth factor $\mu _t =M_{t+1}/M_t$ can be written as follows:

$$\begin{aligned} \mu _t=\pi _{t+1}\frac{m_{t+1}}{m_t} \end{aligned}$$

(10.16)

In order to supply $M_{t+1}$ in the economy at $t+1$, the central bank buys bonds from old households, and pays for them in cash through open market operations. The profits made by central bank $\Delta _t$ at time t are given by:

$$\begin{aligned} \Delta _t = B_{t+1}+M_{t+1}-(1+i_t)B_t-M_t \end{aligned}$$

(10.17)

These profits are distributed as dividends to the old households at time t. The budget constraint of the monetary authority at time t is written as follows:

$$\begin{aligned} B_{t+1}+M_{t+1}=(1+i_t)B_t+M_t+\Delta _t=(1+i_t)(B_t+M_t) \end{aligned}$$

(10.18)

or in real terms:

$$\begin{aligned} \pi _{t+1}(b_{t+1}+m_{t+1})=(1+i_t)(b_t+m_t) \end{aligned}$$

(10.19)

Introducing the variable $\theta _t \equiv (1+i_t)(b_t+m_t)$, Eq. (10.19) can be rewritten as follows:

$$\begin{aligned} \pi _{t+1}\theta _{t+1}=(1+i_{t+1})\theta _t \end{aligned}$$

(10.20)

Note that if $\theta _t$ is positive at the equilibrium, then a part of bonds, which are purely unbacked public assets (intrinsically useless), has a positive value. Let $b_t=\bar{b}_t+\tilde{b}_t$, where $\bar{b}_t$ denotes the real counterpart of money, and $\tilde{b}_t$ the real value of unbacked public assets. As $\bar{b}_t+m_t=0$, $\theta _t=(1+i_t)(b_t+m_t)>0$ is equivalent to $\tilde{b}_t>0$. We can argue that there is a bubble on bonds when $\tilde{b}_t>0$. Therefore, $\theta _t>0$ pertains to a situation in which a positive bubble on bonds exists.¹¹ When $\theta _t=0$, all bonds are the counterpart of money. In this case, all money in the economy corresponds to inside money: No bubbles on bonds exist. When $\theta _t<0$, there is an excess of households’ debt.

In addition, the monetary authority chooses the nominal interest rate $i_{t+1}$ as the monetary instrument, and implements the following interest rate rule:

$$\begin{aligned} 1+i_{t+1}=\left( 1+i^{*}\right) \left( \frac{\pi _{t+1}}{\pi ^{*}}\right) ^{\phi }, \end{aligned}$$

(10.21)

where $\phi \ge 0$ is a measure of monetary policy responses to expected inflation. Furthermore, $i^{*}$ and $\pi ^{*}$ are respectively the stationary values of the nominal interest rate and the inflation of an existing stationary equilibrium chosen as the targets by the monetary authority.

When $\phi =0$, the central bank decides to fix the level of the nominal interest rate at its stationary level $i^{*}$. When $\phi >0$, Eq. (10.21) depicts a Taylor interest rate rule, which responds to expected inflation. Note that according to Bernanke (2010), a rule which responds to expected inflation is more relevant to describe the US monetary policy than a rule responding to observed inflation. For $\phi \in (0,1)$, the rule weakly reacts to expected inflation. An increase (decrease) in the inflation raises (depresses) the nominal interest rate less than proportionally, involving a decrease (increase) in the real interest rate. For $\phi >1$, the rule strongly reacts to expected inflation. An increase (decrease) in the inflation raises (depresses) the nominal interest rate more than proportionally, involving an increase (decrease) in the real interest rate. Following Benhabib et al. (2001), we define a rule with $\phi \in (0,1)$ as a passive one, and a rule with $\phi >1$ as an active one.

3 Intertemporal Equilibrium

At the intertemporal equilibrium, the budget and cash-in-advance constraints of households are given by:

$$\begin{aligned} c_t+\frac{\pi _{t+1}}{1+i_{t+1}}\theta _{t+1}+k_{t+1}= & {} w(k_t)\end{aligned}$$

(10.22)

$$\begin{aligned} d_{t+1}= & {} \theta _{t+1}+f^{\prime }(k_{t+1})k_{t+1} \end{aligned}$$

(10.23)

$$\begin{aligned} \gamma (k_{t+1})d_{t+1}= & {} m_{t+1} \end{aligned}$$

(10.24)

The budget constraints of the monetary authority is as follows:

$$\begin{aligned} \pi _{t+1}= & {} \left( 1+i_{t+1}\right) \frac{\theta _t}{\theta _{t+1}} \end{aligned}$$

(10.25)

Substituting Eq. (10.25) into the first-period budget constraint Eq. (10.22), we get:

$$\begin{aligned} c_t+ \theta _t+ k_{t+1}= & {} w(k_t) \end{aligned}$$

(10.26)

Using Eqs. (10.16), (10.24) and (10.25), we deduce the money growth factor:

$$\begin{aligned} \mu _t= & {} \left( 1+i_{t+1}\right) \frac{\theta _t}{\theta _{t+1}}\frac{\gamma (k_{t+1})}{\gamma (k_t)}\frac{\theta _{t+1}+f^{\prime }(k_{t+1})k_{t+1}}{\theta _t+f^{\prime }(k_t)k_t} \end{aligned}$$

(10.27)

Substituting Eqs. (10.22) and (10.26) into Eq. (10.11), and Eqs. (10.23) and (10.25) into Eq. (10.12), the consumers’ intertemporal trade-off and the no-arbitrage condition are respectively given by:

$$\begin{aligned}&\left\{ \begin{matrix} \displaystyle \theta _t\frac{u^{\prime }(f(k_t)-f^{\prime }(k_t)k_t-\theta _t-k_{t+1})}{\beta v^{\prime }(\theta _{t+1}+f^{\prime }(k_{t+1})k_{t+1})}= \frac{\theta _{t+1}}{1+i_{t+1}\gamma (k_{t+1})}\\ \\ \displaystyle \frac{\theta _{t+1}}{\theta _t}=\frac{1+i_{t+1}}{\pi _{t+1}}=f^{\prime }(k_{t+1})H_{t+1}(k_{t+1}, \theta _t), \end{matrix}\right. \end{aligned}$$

(10.28)

$$\begin{aligned}&with\,\, \,\,\displaystyle H_{t+1}(k_{t+1}, \theta _t)\equiv \frac{1+i_{t+1}\eta _1(k_{t+1})\left[ 1-\gamma (k_{t+1})\right] }{1-\theta _t i_{t+1}\eta _1(k_{t+1})\left[ 1-\gamma (k_{t+1})\right] /k_{t+1}} \end{aligned}$$

(10.29)

When collateral does not matter ($\eta _1(k)=0$), we obtain $H_{t+1}(k_{t+1},\theta _t)=1$. Therefore, the Fisher equation ($(1+i_{t+1})/\pi _{t+1}=f^{\prime }(k_{t+1})$) holds at the intertemporal equilibrium. This means that the return on real asset (capital) is equal to the return on nominal asset (bonds) deflated by the inflation factor. The role of collateral $(\eta _1(k)>0)$ implies the violation of the Fisher equation $(H_{t+1}(k_{t+1},\theta _t)>1)$. As capital serves as a collateral, its return becomes lower than the real return on bonds ($f^{\prime }(k_{t+1})<(1+i_{t+1})/\pi _{t+1})$). This violation of the Fisher equation will induce some portfolio choices that promote indeterminacy, a source of expectation-driven fluctuations.

Interestingly, the level of nominal interest rate can offset the collateral effect (see Eq. (10.29)). Hence, considering a monetary policy conducted through an usual interest rate rule, like a Taylor one, could a priori be relevant to stabilize macroeconomic fluctuations.

From the budget constraint of the monetary authority Eq. (10.25) and the monetary rule Eq. (10.21), we deduce that:

$$\begin{aligned} \frac{\pi _{t+1}}{\pi ^{*}}=\left( \frac{\theta _t}{\theta _{t+1}}\right) ^{\frac{1}{1-\phi }} \end{aligned}$$

(10.30)

Substituting Eq. (10.30) into Eq. (10.21), we obtain the nominal interest rate at the equilibrium:

$$\begin{aligned} i_{t+1}=\left( 1+i^{*}\right) \left( \frac{\theta _t}{\theta _{t+1}}\right) ^{a_{\phi }} - 1, \,\, where \,\, \displaystyle a_{\phi }\equiv \frac{\phi }{1-\phi } \in \left( -\infty ,-1\right) \cup \left[ 0,+\infty \right) \end{aligned}$$

(10.31)

Note that when $a_\phi \in (-\infty , -1)$, the monetary rule is active. When $a_\phi \in (0, +\infty )$, the rule is passive.

Definition 1

Under Assumptions 1–3, an intertemporal equilibrium with perfect foresight is a sequence $\left( k_{t}, \theta _t\right) \in \mathbb {R}_+\times \mathbb {R}$, $t=0,1,...,+\infty$, such that the dynamic system (10.28) is satisfied, where $H_{t+1}(k_{t+1}, \theta _t)$ is defined by (10.29), $i_{t+1}$ by Eq. (10.31), and $k_0>0$ is given.

Taking into account Eqs. (10.29) and (10.31), we note that $k_t$ is the only predetermined variable of the two-dimensional dynamic system (10.28). The intertemporal sequence of $k_t$ and $\theta _t$ enables us to determine all the other variables, namely $c_t$, $d_t$, $m_t$ and $b_t$.

4 Steady State Analysis

From the system (10.28), we deduce that two kinds of steady state exist: $\theta =0$ and $\theta \ne 0$. Since we are interested in fluctuations with a positive bubble, we will focus on steady states with $\theta >0$. A steady state with a positive bubble is a solution $(k,\theta ) \in \mathbb {R}^{2}_{++}$ that satisfies the following system:

$$\begin{aligned} \left\{ \begin{matrix} \displaystyle \frac{u^{\prime }(f(k)-f^{\prime }(k)k-k-\theta )}{\beta v^{\prime }(\theta +f^{\prime }(k)k)}&{}=&{} \displaystyle \frac{1}{1+i^{*}\gamma (k)}\\ \\ \displaystyle f^{\prime }(k)H(k,\theta )&{}=&{}1 \end{matrix}\right. \end{aligned}$$

(10.32)

$$\begin{aligned}&with\,\,H(k,\theta )=\displaystyle \frac{1+i^{*}\eta _1(k)\left[ 1-\gamma (k)\right] }{1-\theta i^{*}\eta _1(k)\left[ 1-\gamma (k)\right] /k} \end{aligned}$$

(10.33)

Under a constant credit share ($\eta _1(k)=0$), we see from the system (10.32) that the steady state is unique, and the monetary policy does not affect the production side. Indeed, the second equation of the system (10.32) reduces to $f^{\prime }(k)=1$. Under Assumption 3, this gives a unique stationary solution in k and superneutrality of money holds. When collateral matters ($\eta _1(k)>0$), the superneutrality of money is canceled. Because of collateral, the monetary sphere affects the real one.

4.1 Existence

From Eq. (10.32), a steady state with $\theta >0$ is a solution $k \in \mathbb {R}_{++}$ satisfying:

$$\begin{aligned} \left\{ \begin{matrix} \displaystyle \frac{u^{\prime }\left( c(k)\right) }{ \beta v^{\prime }\left( d(k)\right) }&{}=&{} \displaystyle \frac{1}{1+i^{*}\gamma (k)}\\ \\ \theta &{}=&{}\displaystyle \frac{1-f^{\prime }(k)\left\{ 1+i^{*}\eta _1(k)[1-\gamma (k)]\right\} }{i^{*}\eta _1(k)[1-\gamma (k)]/k} \end{matrix}\right. \end{aligned}$$

(10.34)

$$\begin{aligned} with \quad c(k)=f(k)-k-\displaystyle \frac{k[1-f^{\prime }(k)]}{i^{*}\eta _1(k)[1-\gamma (k)]}\text { and } d(k)=\displaystyle \frac{k[1-f'(k)]}{i^{*}\eta _1(k)[1-\gamma (k)]} \end{aligned}$$

From these equations, we deduce that $d(k)>0$ implies $f^{\prime }(k)<1$, and from Eqs. (10.25) and (10.27), $1+i^{*}=\pi =\mu >1$.

Assumption 4

$$\begin{aligned} \frac{1-f^{\prime }(k^{*})}{f^{\prime }(k^{*})}>i^{*}\eta _1(k^{*})\left[ 1-\gamma (k^{*})\right] \end{aligned}$$

(10.35)

Under Assumption 4, any bubble can be positive (see Eq. (10.34)). Note also that this assumption is satisfied by the example provided at the end of Sect. 10.4.2.

Proposition 1

Let $\displaystyle \overline{k}$ be defined by $\displaystyle c\left( \overline{k}\right) =0$ and $\underline{k}\in (0,\overline{k})$ by $f^{\prime }(\underline{k})=1$. Under Assumptions 1–4, there exists a steady state characterized by $k^{*}\in \left( \underline{k},\overline{k}\right)$ and $0<\theta ^{*}<f(k^{*})-k^{*}-f^{\prime }(k^{*})k^{*}$.

Proof

See Appendix “Proof of Proposition 1”.

Proposition 1 indicates that a steady state with a positive bubble exists. When collateral does not matter $(\eta _1(k)=0)$, we can see from Eq. (10.33) that the steady state is at the golden rule ($R(k)=1$). As the well-known result of Tirole (1985), a positive rational asset bubble crowds out capital. When collateral matters $(\eta _1(k)>0)$, this economy experiences an over-accumulation of capital at the steady state ($R(k)<1$). The existence of collateral incites households to hold more capital in their portfolio in order to relax the cash-in-advance constraint, and therefore, the capital return decreases.

Regarding the monetary policy, we recall that the central bank chooses the value of an existing steady state for its target. Since the steady state $k^{*}$ always exists, we assume that the central bank selects this steady state as a target, i.e. $\pi ^{*}=1+i^{*}$.¹²

4.2 Normalized Steady State

In order to facilitate the analysis of local dynamics (Sect. 10.5), we establish the existence of a normalized steady state $k^{*}=1$ (NSS). We follow the procedure introduced by Cazzavillan et al. (1998), and use the scaling parameter $\beta$ to give conditions for the existence of such a steady state.

Assumption 5

Let $\nu (\eta _1)=i^{*}\eta _1(1)\left[ 1-\gamma (1)\right]$, we assume:

$$\begin{aligned} f(1)>1+\frac{1-f^{\prime }(1)}{\nu (\eta _1)} \end{aligned}$$

Assumption 5 ensures that the first period consumption at the normalized steady state is positive (i.e. $c(1)>0$), and it is satisfied when the productivity is sufficiently large. Note that we show that a numerical example satisfies Assumption 5 at the end of Sect. 10.4.2.

Proposition 2

Under Assumptions 1–5, there exists a unique value $\beta ^{*}>0$ given by

$$\begin{aligned} \beta ^{*}= & {} \frac{u^{\prime }\left[ f(1) -1- (1-f^{\prime }(1))/\nu (\eta _1)\right] }{ v^{\prime }\left[ (1-f^{\prime }(1))/\nu (\eta _1)\right] }[1+i^{*}\gamma \left( 1\right) ] \end{aligned}$$

such that $k^{*}=1\in \left( \underline{k}, \overline{k}\right)$ is a steady state of the dynamic system (10.28). Moreover, there is a positive bubble $(\theta ^{*}>0)$ if $1-f^{\prime }(1)\left[ 1+\nu (\eta _1)\right] >0$.

Thereafter, we set $\beta =\beta ^{*}$ so that $k^{*}=1$. We further note $c^{*}\equiv c(1)$, $\gamma \equiv \gamma (1)$, $\eta _1\equiv \eta _1\left( 1\right)$, $\eta _2\equiv \eta _2\left( 1\right)$, $\psi \equiv f^{\prime }(1)$, $\alpha =\alpha (1)$ and $\sigma =\sigma (1)$.

To convince the reader that all our assumptions leading to our results are compatible, consider the following example:

Example

For a non-empty set of parameter values $(a, b, c,\epsilon , A, \alpha , \sigma )$, the function $\gamma (k)$ given by Eq. (10.7) in Sect. 10.2.1 and the production function $f(k)=A\left( \alpha k^{(\sigma -1)/\sigma }\right.$ $\left. +1-\alpha \right) ^{\sigma /(\sigma -1)}$ evaluated at the normalized steady state $k^{*}=1$ fit all the requirements imposed by Assumptions 2–5.

Indeed, there exist critical values $\underline{\sigma }$, $\bar{\alpha }$, $\underline{A}$ and $\bar{A}$ such that for $a<1$, $c>1$, $b\in (ac,c)$, $\epsilon >0$, $\sigma >\underline{\sigma }$, $\alpha \in (1-\sigma ,\bar{\alpha })$ and $A\in (\underline{A},\bar{A})$, the function $\gamma (k)$ and the production function f(k) evaluated at $k^{*}=1$ satisfy Assumptions 2–5.

Proof

See Appendix “Proof of Example in Section 10.4.2”.

5 Expectation-Driven Fluctuations and the Stabilizing Role of Monetary Policy

We now study the emergence of expectation-driven fluctuations with a speculative bubble and an interplay between the financial and the real spheres. We show that when no Taylor rule is implemented ($\phi =0$), local indeterminacy can occur in the neighborhood of the normalized steady state with a positive bubble under not restrictive conditions, namely gross substitutability and a not too weak input substitution, because of the credit market distortion. The violation of the Fisher relationship and the resulting portfolio choice between bonds, capital and money are the key ingredients to explain these fluctuations. When the Taylor rule is implemented ($\phi >0$), we analyze the stabilizing role of the monetary policy. We will see that it is quite mitigated.

To study the existence of local indeterminacy, we introduce the following additional assumption:

Assumption 6

Let $\bar{\eta }_1>0$ and $\bar{\eta }_2>0$.¹³ We assume $\eta _1<\bar{\eta }_1$ and $\eta _2>\bar{\eta }_2$.

Example

Note that $\eta _1=(b-ca)\epsilon /[(a+b)(1+c)]$ and $\eta _2= 1+\epsilon [2c/(1+c)-1]$ at the normalized steady state $k^{*}=1$. Recall that $a<1$, $c>1$, $b\in (ac,c)$ and $\epsilon >0$.

For b close to ca, $\eta _1$ is close to zero, and thus $\eta _1<\bar{\eta _1}$ is satisfied. As shown in Appendix “Proofs of Proposition 3, Corollaries 1 and 2” (see Eq. (10.54)), $\epsilon >\bar{\epsilon }$ is equivalent to $\eta _2>\bar{\eta _2}$. Thus, the function $\gamma (k)$ evaluated at $k^{*}=1$ satisfies Assumption 6.

To derive our different results, we start by linearizing the dynamic system (10.28) around the normalized steady state $k^{*}=1$, and obtain the following lemma¹⁴:

Lemma 2

Under Assumptions 1–6, the characteristic polynomial, evaluated at the steady state $k^{*}=1$, writes $P\left( X\right) \equiv X^{2}-T X+D=0$, where T and D are respectively the trace and the determinant of the associated Jacobian matrix. We have:

$$\begin{aligned} 1-T+D= & {} \varepsilon _{dk}\frac{1-\psi \left[ 1+\nu (\eta _1)\right] }{\xi _1}\frac{\varepsilon _v-\varepsilon _v^{s}}{\varepsilon _v-\bar{\varepsilon }_v}\end{aligned}$$

(10.36)

$$\begin{aligned} 1+T+D= & {} \frac{\xi _3}{\xi _1}\frac{\varepsilon _v-\varepsilon _v^{f}}{\varepsilon _v-\bar{\varepsilon }_v}\end{aligned}$$

(10.37)

$$\begin{aligned} 1-D= & {} \frac{\varepsilon _v-\varepsilon _v^{h}}{\varepsilon _v-\bar{\varepsilon }_v} \end{aligned}$$

(10.38)

where $\varepsilon _v \ne \bar{\varepsilon }_v$, and the expressions of $\xi _1\equiv \xi _1(a_\phi )$, $\xi _3\equiv \xi _3(a_\phi )$, $\bar{\varepsilon }_v\equiv \bar{\varepsilon }_v(a_\phi )$, $\varepsilon _v^{f}\equiv \varepsilon _v(a_\phi )$, $\varepsilon _v^{h}\equiv \varepsilon _v^{h}(a_\phi )$, $\varepsilon _v^{s}$ and $\varepsilon _{dk}$ are given in Appendix “Proofs of Proposition 3, Corollaries 1 and 2”.

We recall that when $1-T+D=0$, one eigenvalue is equal to 1. When $1+T+D=0$, one eigenvalue is equal to $-1$. When $1-T+D>0$, $1+T+D>0$ and $D=1$, the characteristic roots are complex conjugates with modulus equal to 1. All eigenvalues are inside the unit circle, when the following conditions are satisfied (i) $1-T+D>0$, (ii) $1+T+D>0$ and (iii) $D<1$. In other words, when conditions (i)-(iii) are satisfied, the steady state is a sink, i.e. locally indeterminate. The steady state is a saddle point when $1-T+D<0$ (resp. $>0$) and $1+T+D>0$ (resp. $<0$). It is a source otherwise.

A (local) bifurcation arises when at least one eigenvalue crosses the unit circle. Therefore, a bifurcation occurs when either (iv) $1-T+D=0$, or (v) $1+T+D=0$, or (vi) $1-T+D>0$, $1+T+D>0$ and $D=1$. According to a continuous change of $\varepsilon _v$, a pitchfork bifurcation emerges when $\varepsilon _v$ goes through $\varepsilon _v^{s}$, defined by $1-T+D=0$.¹⁵ A flip bifurcation occurs when $\varepsilon _v$ goes through $\varepsilon _v^{f}$, defined by $1+T+D=0$. Finally, a Hopf bifurcation arises, as $\varepsilon _v$ goes through $\varepsilon _v^{h}$, defined by $D=1$, but we still keep $1-T+D>0$ and $1+T+D>0$.

The next proposition summarizes the local dynamic properties of the model:

Proposition 3

Let $\varepsilon _v\ne \bar{\varepsilon }_v$, $\psi <1/(1+i^{*}\gamma )$ and Assumptions 1–6 hold.

• 1. When $\varepsilon _u\in \left( \tilde{\varepsilon }_u, \varepsilon _u^{s}\right)$, the following holds:

  • if $a_\phi \in (-\infty , \hat{a}_\phi )$, then the steady state is locally determinate for $\varepsilon _v<max \lbrace \varepsilon _v^{h},\varepsilon _v^{s} \rbrace$, undergoes a pitchfork (resp. Hopf) bifurcation for $\varepsilon _v=\varepsilon _v^{s}$ (resp. $\varepsilon _v=\varepsilon _v^{h}$), is locally indeterminate for $\varepsilon _v>max \lbrace \varepsilon _v^{h},\varepsilon _v^{s} \rbrace$.

  • if $a_\phi \in (\hat{a}_\phi , \bar{a}_\phi )$, then the steady state is locally indeterminate for $\varepsilon _v<\varepsilon _v^{f}$, undergoes a flip bifurcation for $\varepsilon _v=\varepsilon _v^{f}$, is locally determinate for $\varepsilon _v^{f}<\varepsilon _v<max \lbrace \varepsilon _v^{h},\varepsilon _v^{s} \rbrace$, undergoes a pitchfork (resp. Hopf) bifurcation for $\varepsilon _v=\varepsilon _v^{s}$ (resp. $\varepsilon _v=\varepsilon _v^{h}$), is locally indeterminate for $\varepsilon _v>max \lbrace \varepsilon _v^{h},\varepsilon _v^{s} \rbrace$.

  • if $a_\phi \in (\bar{a}_\phi , -1[$, then the steady state is locally indeterminate for $\varepsilon _v<\varepsilon _v^{s}$, undergoes a pitchfork bifurcation for $\varepsilon _v=\varepsilon _v^{s}$, is locally determinate for $\varepsilon _v^{s}<\varepsilon _v<max \lbrace \varepsilon _v^{f},\varepsilon _v^{h} \rbrace$, undergoes a flip (resp. Hopf) bifurcation for $\varepsilon _v=\varepsilon _v^{f}$ (resp. $\varepsilon _v=\varepsilon _v^{h}$), is locally indeterminate for $\varepsilon _v>max \lbrace \varepsilon _v^{f},\varepsilon _v^{h} \rbrace$.

  • if $a_\phi \in [0, \tilde{a}_\phi )$, then the steady state is locally indeterminate for $\varepsilon _v<\varepsilon _v^{s}$, undergoes a pitchfork bifurcation for $\varepsilon _v=\varepsilon _v^{s}$, is locally determinate for $\varepsilon _v\in (\varepsilon _v^{s}, \varepsilon _v^{f})$, undergoes a flip bifurcation for $\varepsilon _v=\varepsilon _v^{f}$, is locally indeterminate for $\varepsilon _v>\varepsilon _v^{f}$.

  • if $a_\phi \in (\tilde{a}_\phi , +\infty )$, then the steady state is locally indeterminate for $\varepsilon _v<\varepsilon _v^{s}$, undergoes a pitchfork bifurcation for $\varepsilon _v=\varepsilon _v^{s}$, is locally determinate for $\varepsilon _v> \varepsilon _v^{s}$.

• 2. When $\varepsilon _u>\varepsilon _u^{s}$, the steady state is locally determinate for $\varepsilon _v<max \lbrace \varepsilon _v^{f},\varepsilon _v^{h} \rbrace$, undergoes a flip (resp. Hopf) bifurcation for $\varepsilon _v=\varepsilon _v^{f}$ (resp. $\varepsilon _v=\varepsilon _v^{h}$), and is locally indeterminate for $\varepsilon _v>max \lbrace \varepsilon _v^{f},\varepsilon _v^{h} \rbrace$.

Proof

See Appendix “Proofs of Proposition 3, Corollaries 1 and 2”.

Fig. 10.1

The stabilizing role of monetary policy

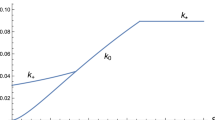
Figure 10.1 provides a qualitative illustration of the local dynamic properties of the model when $\varepsilon _v^{s}>0$. Under Assumptions 1–6, $\bar{\varepsilon }_v$, $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ are increasing functions of $a_\phi$, while $\varepsilon _v^{s}$ does not depend on $a_\phi$. Furthermore, $\bar{\varepsilon }_v$, $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\varepsilon _v^{s}$ intersect as indicated in Fig. 10.1 under some parameter conditions. Note that Fig. 10.1 is precisely constructed using Appendix “Proofs of Proposition 3, Corollaries 1 and 2”. From Lemma 2 and plotting the different critical and bifurcation values, $\bar{\varepsilon }_v$, $\varepsilon _v^{s}$, $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ in the plane $(a_\phi ,\varepsilon _v)$, we can determine the local indeterminacy regions corresponding to the grey areas in Fig. 10.1.

Proposition 3 provides general conditions for local dynamics. To clarify their significance, we start by considering the case where a Taylor rule is not implemented ($a_\phi =0$). This allows us to understand under which conditions expectation-driven fluctuations occur. In a second step, we will discuss the stabilizing role of a monetary policy managed by a Taylor rule ($a_{\phi }\in \left( -\infty ,-1\right) \cup \left( 0,+\infty \right)$).

From Proposition 3, we can derive the following corollary on the existence of expectation-driven fluctuations when $a_\phi =0$:

Corollary 1

Assuming $\varepsilon _v\ne \bar{\varepsilon }_v$ and Assumptions 1–6, the following holds when $a_\phi =0$:

• 1. When $\varepsilon _u\in \left( \tilde{\varepsilon }_u, \varepsilon _u^{s}\right)$, the steady state is locally indeterminate for $\varepsilon _v<\varepsilon _v^{s}<1$, undergoes a pitchfork bifurcation for $\varepsilon _v=\varepsilon _v^{s}$, is locally determinate for $\varepsilon _v\in \left( \varepsilon _v^{s}, \varepsilon _v^{f}\right)$, undergoes a flip bifurcation for $\varepsilon _v=\varepsilon _v^{f}$, and is locally indeterminate for $\varepsilon _v>\varepsilon _v^{f}$.

• 2. When $\varepsilon _u>\varepsilon _u^{s}$, the steady state is locally determinate for $\varepsilon _v<\varepsilon _v^{f}$, undergoes a flip bifurcation for $\varepsilon _v=\varepsilon _v^{f}$, and is locally indeterminate for $\varepsilon _v>\varepsilon _v^{f}$.

Proof

See Appendix “Proofs of Proposition 3, Corollaries 1 and 2”.

Corollary 1 shows the occurrence of persistent endogenous fluctuations around the steady state with a positive bubble under gross substitutability and a not too weak capital-labor substitution when no Taylor rule is implemented. Hence, this result extends Bosi and Seegmuller (2010) and Clain-Chamosset-Yvrard and Seegmuller (2015) to a model with both inside money and capital.¹⁶

When collateral does not matter ($\eta _1=0$), the local stability properties of the model correspond to Corollary 1.2. Endogenous fluctuations and two-period cycles occur only for a significant income effect, i.e. a large degree of concavity $\varepsilon _v$.¹⁷ More interestingly, when collateral matters ($\eta _1>0$), local indeterminacy also appears under gross substitutability, i.e. for a small degree of concavity $\varepsilon _v<\varepsilon _v^{s}<1$.

The basic mechanism for fluctuations under gross substitutability relies on a portfolio trade-off between the three assets. Because of the difference between the returns on physical and monetary assets, a reallocation between the assets takes place following a modification in agents’ expectations.

Economic intuition. If households expect an increase in inflation from period t to $t+1$, the return on bonds becomes less attractive compared to the return on capital. Because of the portfolio effect, households reallocate their savings towards capital. As a consequence, when $\varepsilon _v<\varepsilon _v^{s}<1$, the portfolio effect can accelerate capital accumulation. Households consume less by cash (see Eq. (10.24)). The real balances $m_{t+1}$ decrease, entailing a decrease in the return on money. An effective rise in inflation takes place, meaning that the initial expectations are self-fulfilling.

We focus now on the stabilizing role of the monetary policy managed by a Taylor rule. A policy is stabilizing in our framework as soon as it reduces the range of parameter values for which local indeterminacy, and thus expectation-driven fluctuations, emerge. Since the occurrence of fluctuations under gross substitutability is an interesting result, we ensure for the remainder of the paper that $\varepsilon _v^{s}>0$, assuming¹⁸:

Assumption 7

$\varepsilon _u<\varepsilon _u^{s}$.

Since $\varepsilon _u$ is a free preference parameter, Assumption 7 can always be satisfied and is in accordance with the numerical example provided at the end of Sect. 10.4.2.

We recall that since $a_\phi =\phi /(1-\phi )$, $a_\phi \in (-\infty , -1)$ ($\phi >1$) means that the monetary rule is active, while $a_\phi \in (0, +\infty )$ ($\phi \in (0,1)$) means that the rule is passive. Using these notations, we derive the next corollary from Proposition 3 and Fig. 10.1:

Corollary 2

Assuming $\varepsilon _v\ne \bar{\varepsilon }_v$, $\psi <1/(1+i^{*}\gamma )$ and Assumptions 1–7, the following holds:

• 1. If $a_{\phi }\in (-\infty , \hat{a}_{\phi }]$, increasing the responsiveness of the monetary rule $\phi$ does not affect or reduces the range of parameters for indeterminacy.

• 2. If $a_{\phi }\in (\hat{a}_{\phi },-1)$, increasing the responsiveness of the monetary rule $\phi$ reduces the range of parameters for local indeterminacy when $\varepsilon _v$ is large enough, but raises the range of parameters for local indeterminacy when $\varepsilon _v$ is small enough.

• 3. If $a_{\phi }\in [0,+\infty )$, increasing the responsiveness of the monetary rule $\phi$ reduces the range of parameters for local indeterminacy when $\varepsilon _v$ is large enough, but has no impact on the range of parameters for local indeterminacy when $\varepsilon _v$ is small enough.

Proof

See Appendix “Proofs of Proposition 3, Corollaries 1 and 2”.

Proposition 3, Corollary 2 and Fig. 10.1 highlight that a monetary policy managed by a Taylor rule has mitigated results concerning the stabilization of expectation-driven fluctuations. Comparing with the results of Corollary 1, a passive rule ($a_{\phi }\in (0,+\infty )$) stabilizes fluctuations occurring for a large level of $\varepsilon _v$ ($\varepsilon _v>\varepsilon _v^f$). However, it has no impact on fluctuations occurring for $\varepsilon _v<\varepsilon _v^{s}$. On the contrary, an active rule ($a_\phi \in (-\infty , -1)$) could stabilize endogenous fluctuations that occur for $\varepsilon _v<\varepsilon _v^{s}$, in particular if it is weakly active ($a_\phi$ sufficiently negative i.e. $\phi$ close to one). Nevertheless, with respect to the configuration without Taylor rule ($a_{\phi }=0$), an active rule destabilizes promoting indeterminacy for new ranges of parameter values. Indeed, under a weakly active rule ($a_{\phi }$ sufficiently negative), local indeterminacy occur for all $\varepsilon _v>\varepsilon _v^{s}$.

To sum, depending on households’ preferences ($\varepsilon _v$) and on the responsiveness of the monetary policy with respect to expected inflation ($a_{\phi }$), we may have opposite conclusions concerning the stabilizing role of the monetary policy. This is in contrast with several previous contributions, for instance Bernanke and Woodford (1997), Sorger (2005) or Clain-Chamosset-Yvrard and Seegmuller (2015).

Our explanation of these results is that the monetary authority manipulates the level of the elasticity of the nominal interest rate with respect to the expected inflation ($\phi$), which has not a sufficiently significant impact on the interest rate level to dampen or eliminate the impact of the credit market imperfection and the role of collateral. For instance, a weakly active rule has not a huge impact on the nominal interest rate, and therefore does not sufficiently modify the portfolio choices.

6 Concluding Remarks

We develop an overlapping generations model with capital accumulation, bonds and money, where the share of consumption purchased on credit depends on a collateral. We show the existence of expectation-driven fluctuations with a positive rational bubble on bonds. In addition, such endogenous fluctuations are in accordance with gross substitutability and a not too weak substitution between inputs. This is explained by a credit market imperfection and the role of a collateral. The basic mechanism for fluctuations relies on a portfolio trade-off between the three assets.

We further analyze the stabilizing role of the monetary policy. To consider an usual policy rule, we focus on a monetary policy fixed according to a Taylor rule on expected inflation. We show that the stabilizing role of such a policy is mitigated. In fact, no clear-cut conclusion on stabilisation is obtained. One reason is that such a policy does not alter sufficiently the portfolio choices. More generally, we think that our results provide an adding argument against the use of standard policy instruments in any circumstances. In this model, these circumstances are the existence of a bubble, a credit market imperfection and the collateral effect.

Appendix

1.1 Proof of Proposition 1

A steady state k is a solution of $h\left( k\right) =j\left( k\right)$, with:

$$\begin{aligned} h\left( k\right) \equiv \frac{u^{\prime }\left( c(k)\right) }{\beta v^{\prime }\left( d(k)\right) } \end{aligned}$$

(10.39a)

$$\begin{aligned} j\left( k\right) \equiv \frac{1}{1+i^{*}\gamma (k)} \end{aligned}$$

(10.39b)

where $\quad c\left( k\right) \equiv f(k)-k-d(k)$ and $d\left( k\right) \equiv$ $\displaystyle \frac{k[1-f^{\prime }(k)]}{i^{*}\eta _1(k)[1-\gamma (k)]}$.

We start by determining the admissible range of values for k. To ensure $d(k)>0$, we get at the steady state $f^{\prime }\left( k\right) <1$. Under Assumption 3, $f^{\prime }(k)$ is a decreasing function of k. Hence, $k>f^{\prime -1}\left( 1\right) =\underline{k}$.

Now, we want to determine the range of k such that $c(k)>0$. The decreasing returns on capital imply $f\left( \underline{k}\right) >\underline{k}f^{\prime }(\underline{k})$. Since $f^{\prime }(\underline{k})=1$, $c(\underline{k})=f(\underline{k})-\underline{k}>0$. In addition, as $d(k)>0$, we derive the following inequality:

$$\begin{aligned} \lim _{k\rightarrow +\infty }c\left( k\right)< & {} \lim _{k\rightarrow +\infty } f(k)-k=-\infty \end{aligned}$$

because $f^{\prime }(k)<1$ for k large enough. As a result, there exists one value $\overline{k}$ such that $\forall k<\overline{k}$, $c\left( \overline{k}\right) >0$. By construction, we have $\underline{k}< \overline{k}$, and therefore $(\underline{k}, \overline{k})$ is a nonempty subset.

To prove the existence of a stationary solution k, we use the continuity of $h\left( k\right)$ and $j\left( k\right)$. Using Eqs. (10.39a) and (10.39b), we determine the boundary values of $h\left( k\right)$ and $j\left( k\right)$:

$$\begin{aligned} \begin{array}{cc} \lim _{k\rightarrow \underline{k}}h\left( k\right) =\displaystyle \frac{u^{\prime }\left( c\left( \underline{k}\right) \right) }{\beta v^{\prime }(0)}=0^{+} &{} \lim _{k\rightarrow \overline{k}}h\left( k\right) =\displaystyle \frac{u^{\prime }\left( c\left( 0\right) \right) }{\beta v^{\prime }(d(\overline{k}))}=+\infty \\ \lim _{k\rightarrow \underline{k}}j\left( k\right) =\displaystyle \frac{1}{1+i(\underline{k})\gamma (\underline{k})}\in (0, 1] &{} \lim _{k\rightarrow \overline{k}}j\left( k\right) =\displaystyle \frac{1}{1+i(\overline{k})\gamma \left( \overline{k}\right) }\le 1 \end{array} \end{aligned}$$

We have $\lim _{k\rightarrow \underline{k}}h\left( k\right) <\lim _{k\rightarrow \underline{k}}j\left( k\right)$ and $\lim _{k\rightarrow \overline{k}}h\left( k\right) >\lim _{k\rightarrow \overline{k}}j\left( k\right)$. Therefore, there exists at least one value $k^{*} \in \left( \underline{k},\overline{k}\right)$ such that $h\left( k^{*}\right) =j\left( k^{*}\right)$.    $\blacksquare$

1.2 Proof of Example in Section 10.4.2

Let $\underline{\sigma } \equiv 1-\frac{1}{2+\nu (\eta _1)}$, $\bar{\alpha }\equiv \frac{1}{2+\nu (\eta _1)}$, $\underline{A}\equiv \frac{1+\nu (\eta _1)}{\alpha +\nu (\eta _1)}$ and $\bar{A} \equiv \frac{1/\alpha }{1+\nu (\eta _1)}$. For $a\in (0,1)$, $c>1$, $b\in (ac,c)$ and $\epsilon >0$, Assumption 2 is satisfied at the normalized steady state. Assumption 3 requires $A<1/\alpha$ and $\sigma >1-\alpha$. For $A>\underline{A}$, Assumption 5 is satisfied. Moreover, the bubble is positive at the normalized steady state when $A<\overline{A}$. As a consequence, the set $(\underline{A},\bar{A})$ must be non-empty. This is true for $\alpha <\bar{\alpha }$ and $\sigma >\underline{\sigma }$.

1.3 Proofs of Proposition 3, Corollaries 1 and 2

$$\begin{aligned} \text { Recall that } \psi= & {} f^{\prime }(1),\,\, \nu (\eta _1)= \eta _1i^{*}\left( 1-\gamma \right)>0,\,\, c^{*}= f(1) -1- \frac{1-\psi }{\nu (\eta _1)}>0, \\ a_\phi= & {} \phi /(1-\phi ) \in (-\infty , -1[\cup [0,+\infty ) \text { and let } \varepsilon _{dk}=\frac{\psi }{1-\psi } \frac{1-\alpha }{\sigma }+ \eta _2>0,\text { and } \nonumber \\ \eta _1^{\theta }= & {} \frac{1-\psi }{\psi }\frac{1}{i^{*}(1-\gamma )}\nonumber .\end{aligned}$$

(10.40)

First of all, we suppose for the rest of the proof that $\eta _1<\eta _1^{\theta }$, because $\forall$ $\eta _1<\eta _1^{\theta }$, $\theta >0$ (see condtion (10.35)).

From Lemma 2, the expressions of $1-T+D$, $1+T+D$ and $1-D$ can be written as follows:

$$\begin{aligned} 1-T+D= & {} \varepsilon _{dk}\frac{1-\psi \left[ 1+\nu (\eta _1)\right] }{\xi _1(a_\phi )}\frac{\varepsilon _v-\varepsilon _v^{s}}{\varepsilon _v-\bar{\varepsilon }_v}\end{aligned}$$

(10.41)

$$\begin{aligned} 1+T+D= & {} \frac{\xi _3(a_\phi )}{\xi _1(a_\phi )}\frac{\varepsilon _v-\varepsilon _v^{f}}{\varepsilon _v-\bar{\varepsilon }_v}\end{aligned}$$

(10.42)

$$\begin{aligned} 1-D= & {} \frac{\varepsilon _v-\varepsilon _v^{h}}{\varepsilon _v-\bar{\varepsilon }_v} \end{aligned}$$

(10.43)

$$\begin{aligned} \text { where } \varepsilon _v^{s}= & {} \frac{1-\psi }{\nu (\eta _1)}\frac{\nu (\eta _1)+\varepsilon _{dk}}{\varepsilon _{dk}} \frac{\varepsilon _u^{s}-\varepsilon _u}{c^{*}},\,\,\,\, \varepsilon _v^{f}=\frac{\xi _4(a_\phi )}{\xi _3(a_\phi )}\equiv \varepsilon _v^{f}(a_\phi ),\nonumber \\ \varepsilon _v^{h}= & {} \frac{\xi _5(a_\phi )}{\xi _1(a_\phi )}\equiv \varepsilon _v^{h}(a_\phi )\text { and } \bar{\varepsilon }_v=-\frac{\xi _2(a_\phi )}{\xi _1(a_\phi )}\equiv \bar{\varepsilon }_v(a_\phi ) \end{aligned}$$

(10.44)

$$\begin{aligned} \text {with }\varepsilon _u^{s}&= c^{*}\frac{\nu (\eta _1)}{1-\psi }\frac{1}{\nu (\eta _1)+\varepsilon _{dk}}\frac{\nu (\eta _1)}{1+i^{*}\gamma },\end{aligned}$$

(10.45)

$$\begin{aligned} \xi _1(a_\phi )&=-\psi \nu (\eta _1)\left( 1-\small {\frac{1-\alpha }{\sigma }}\right) \frac{1+i^{*}}{i^{*}} a_\phi +\left\{ 1-\psi \left[ 1+\nu (\eta _1)\right] \right\} \varepsilon _{dk}\nonumber \\&\quad -\frac{\psi }{1-\psi }\nu (\eta _1)\left( 1-\frac{1-\alpha }{\sigma }\right) ,\nonumber \\ \end{aligned}$$

(10.46)

$$\begin{aligned} \xi _2(a_\phi )&= \left( 1-\psi \right) \frac{1+i^{*}}{i^{*}}\left\{ -\frac{\varepsilon _u}{c^{*}}+\frac{\nu (\eta _1)}{1+i^{*}\gamma }\left[ 1+i^{*}\gamma \frac{\psi }{1-\psi }\left( 1-\frac{1-\alpha }{\sigma }\right) \right] \right. \nonumber \\&\left. -\varepsilon _{dk}\frac{i^{*}\gamma }{1+i^{*}\gamma }\right\} a_\phi -\psi \left[ 1+\nu (\eta _1)\right] \frac{\varepsilon _u}{c^{*}}+\nu (\eta _1)^{2}\frac{\psi }{1+i^{*}\gamma }+\nu (\eta _1)\psi \nonumber \\&\left( 1-\frac{1-\alpha }{\sigma }+\frac{1}{1+i^{*}\gamma }\right) -\left( 1-\psi \right) \varepsilon _{dk},\nonumber \\ \end{aligned}$$

(10.47)

$$\begin{aligned} \xi _3(a_\phi )&= -\psi \nu (\eta _1)\left( 1-\frac{1-\alpha }{\sigma }\right) \frac{1+i^{*}}{i^{*}} a_\phi +\left\{ 1-\psi \left[ 1+\nu (\eta _1)\right] \right\} \varepsilon _{dk}\nonumber \\&\quad -2\frac{\psi }{1-\psi }\nu (\eta _1) \left( 1-\frac{1-\alpha }{\sigma }\right) , \end{aligned}$$

(10.48)

$$\begin{aligned} \xi _4(a_\phi )&= 2 (1-\psi )\frac{1+i^{*}}{i^{*}}\left\{ \left( 1+\psi \frac{1-\alpha }{\sigma }\right) \frac{\varepsilon _u}{c^{*}}-\frac{i^{*}\gamma \nu (\eta _1)}{1+i^{*}\gamma }\left[ 1+ \frac{\psi }{1-\psi }\left( 1-\frac{1-\alpha }{\sigma }\right) \right] \right. \nonumber \\&\quad \left. +\frac{\varepsilon _{dk}i^{*}\gamma }{1+i^{*}\gamma }\right\} a_\phi +\left\{ 2\psi \left[ 1+\nu (\eta _1)+\frac{1-\alpha }{\sigma }\right] +\right. \nonumber \\&\quad \left. \frac{1-\psi }{\nu (\eta _1)}\left[ \nu (\eta _1)+\varepsilon _{dk}\right] \left\{ 1-\psi \left[ 1+\nu (\eta _1)\right] \right\} \right\} \frac{\varepsilon _u}{c^{*}}-\frac{\nu (\eta _1)^{2}\psi }{1+i^{*}\gamma }\nonumber \\&\quad -2\nu (\eta _1)\psi \left( 1-\frac{1-\alpha }{\sigma }\right) -\nu (\eta _1)\frac{1+\psi }{1+i^{*}\gamma }+2(1-\psi )\varepsilon _{dk},\end{aligned}$$

(10.49)

$$\begin{aligned} \xi _5(a_\phi )&=\left( 1-\psi \right) \frac{1+i^{*}}{i^{*}}\left\{ \left( 1-\psi \frac{1-\alpha }{\sigma }\right) \frac{\varepsilon _u}{c^{*}}-\frac{\nu (\eta _1)}{1+i^{*}\gamma }\right. \nonumber \\&\left. \quad \left[ 1+\frac{i^{*}\gamma \psi }{1-\psi }\left( 1-\frac{1-\alpha }{\sigma }\right) \right] +\frac{\varepsilon _{dk}i^{*}\gamma }{1+i^{*}\gamma }\right\} a_\phi +\psi \left[ 1+\nu (\eta _1)-\frac{1-\alpha }{\sigma }\right] \frac{\varepsilon _u}{c^{*}}-\frac{\nu (\eta _1)^{2}\psi }{1+i^{*}\gamma }\nonumber \\&\quad -\nu (\eta _1)\psi \left( 1-\frac{1-\alpha }{\sigma }+\frac{1}{1+i^{*}\gamma }\right) +(1-\psi )\varepsilon _{dk}\nonumber \\ \end{aligned}$$

(10.50)

We aim to determine the range of parameter values ($a_\phi$ and $\varepsilon _v$) for which local indeterminacy conditions (i)-(iii) are satisfied. To do this, we must analyze the functions $\varepsilon _v^{f}$, $\varepsilon _v^{h}$, $\bar{\varepsilon }_v$ and $\xi _i$ with $i=\lbrace 1,2,3,4,5 \rbrace$, then draw $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ in the plane $(a_\phi , \varepsilon _v)$.

We observe that $\xi _i$ with $i=\lbrace 1,2,3,4,5 \rbrace$ are linear functions of $a_\phi$, i.e. $\xi _i^{a} a_\phi +~\xi _i^{b}$. Note that $\xi _1^{a}<0$ and $\xi _3^{a}<0$. Furthermore, there exist $\eta _1^{\xi _1^{b}}>0$, $\eta _1^{\xi _2^{a}}>0$, $\eta _1^{\xi _2^{b}}>0$, $\eta _1^{\xi _3^{b}}>0$, $\eta _1^{\xi _4^{a}}>0$, $\eta _1^{\xi _4^{b}}>0$, $\eta _1^{\xi _5^{a}}>0$ and $\eta _1^{\xi _5^{b}}>0$ such that $\forall$ $\eta _1<min \lbrace \eta _1^{\xi _1^{b}}, \eta _1^{\xi _2^{a}}, \eta _1^{\xi _2^{b}}, \eta _1^{\xi _3^{b}}, \eta _1^{\xi _4^{a}}, \eta _1^{\xi _4^{b}}, \eta _1^{\xi _5^{a}}, \eta _1^{\xi _5^{b}} \rbrace \equiv \tilde{\eta }_1$, one has $\xi _1^{b}>0$, $\xi _2^{a}<0$, $\xi _2^{b}<0$, $\xi _3^{b}>0$, $\xi _4^{a}>0$, $\xi _4^{b}>0$, $\xi _5^{a}>0$ and $\xi _5^{b}>0$. Therefore, we deduce that $\xi _1(a_\phi )\ge 0$ when $a_\phi \le \frac{\xi _1^{b}}{\xi _1^{a}}$ and $\xi _1(a_\phi )<0$ otherwise. $\xi _2(a_\phi )\ge 0$ when $a_\phi \le \frac{\xi _2^{b}}{\xi _2^{a}}<0$ and $\xi _2(a_\phi )< 0$ otherwise. $\xi _3(a_\phi )\ge 0$ when $a_\phi \le \frac{\xi _3^{b}}{\xi _3^{a}}$ and $\xi _3(a_\phi )<0$ otherwise. $\xi _4(a_\phi )\le 0$ when $a_\phi \le \frac{\xi _4^{b}}{\xi _4^{a}}<0$ and $\xi _4(a_\phi )>0$ otherwise. $\xi _5(a_\phi )\le 0$ when $a_\phi \le \frac{\xi _5^{b}}{\xi _5^{a}}<0$ and $\xi _5(a_\phi )>0$ otherwise.

We analyze now $\varepsilon _v^{f}$, $\varepsilon _v^{h}$, $\varepsilon _v^{s}$ and $\bar{\varepsilon }_v$. Suppose that $\eta _1<min\lbrace \eta _1^{\theta },\tilde{\eta }_1\rbrace$.

First, $\varepsilon _v^{s}$ does not depend on $a_\phi$. Second, the different critical and bifurcation values ($\bar{\varepsilon }_v$, $\varepsilon _v^{f}$, $\varepsilon _v^{h}$) are homographic functions of $a_\phi$. $\varepsilon _v^{f}$ has a vertical asymptote at $a_\phi =\frac{\xi _3^{b}}{\xi _3^{a}}\equiv \tilde{a}_\phi >0$. $\bar{\varepsilon }_v$ and $\varepsilon _v^{h}$ have the same vertical asymptote at $a_\phi =\frac{\xi _1^{b}}{\xi _1^{a}}>\tilde{a}_\phi$. The first derivatives of $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ with respect to $a_{\phi }$ are given by:

$$ \frac{\partial \varepsilon _v^{f}}{\partial a_{\phi }}=\frac{\xi _4^{a}\xi _3^{b}-\xi _4^{b}\xi _3^{a}}{\xi _3(a_\phi )^{2}}>0,\frac{\partial \varepsilon _v^{h}}{\partial a_{\phi }}=\frac{\xi _5^{a}\xi _1^{b}-\xi _5^{b}\xi _1^{a}}{\xi _1(a_\phi )^{2}}>0 \text { and } \frac{\partial \bar{\varepsilon }_v}{\partial a_{\phi }}=-\frac{\xi _2^{a}\xi _1^{b}-\xi _2^{b}\xi _1^{a}}{\xi _1(a_\phi )^{2}}>0.$$

It would be useful to locate the different bifurcation and critical values ($\varepsilon _v^{f}$, $\varepsilon _v^{h}$, $\varepsilon _v^{s}$ and $\bar{\varepsilon }_v)$ when $a_\phi =0$. We can note that $\varepsilon _v^{f}>0$, $\varepsilon _v^{h}>0$ and $\bar{\varepsilon }_v>0$ when $a_\phi =0$. Moreover, $\varepsilon _v^{s}>0$ if and only if $\varepsilon _u\in (\tilde{\varepsilon }_u, \varepsilon _u^{s})$, where $\varepsilon _u>\tilde{\varepsilon }_u$ is required for the second-order conditions, with:

$$\begin{aligned} \tilde{\varepsilon }_u\equiv & {} c^{*}\frac{\nu (\eta _1)^{2}}{\eta _2\left( 1-\psi \right) \left( 1+i^{*}\gamma \right) ^{2}} \end{aligned}$$

(10.51)

The set ($\tilde{\varepsilon }_u, \varepsilon _u^{s}$) is nonempty if and only if

$$\begin{aligned} \eta _2(1-\psi )i^{*}\gamma> & {} \nu (\eta _1)\left( 1-\psi \right) +\psi \frac{1-\alpha }{\sigma } \end{aligned}$$

(10.52)

As $\nu (\eta _1)=i^{*}\eta _1\left( 1-\gamma \right)$, the condition (10.52) holds if

$$\begin{aligned} \eta _1 < \frac{1}{i^{*}\left( 1-\gamma \right) } \frac{\eta _2(1-\psi )i^{*}\gamma -\psi \left( 1-\alpha \right) /\sigma }{1-\psi }\equiv \overline{\overline{\eta }}_1\text { and }\eta _2 > \frac{\psi }{1-\psi }\frac{\left( 1-\alpha \right) /\sigma }{i^{*}\gamma }\equiv \bar{\eta }_2 \end{aligned}$$

(10.53)

Therefore, $\forall$ $\eta _1<\overline{\overline{\eta }}_1$ and $\eta _2>\bar{\eta }_2$, we have $\tilde{\varepsilon }_u<\varepsilon _u^{s}$. We suppose now that $\eta _1<\min \lbrace \eta _1^{\theta }, \tilde{\eta }_1, \overline{\overline{\eta }}_1\rbrace$ and $\eta _2>\bar{\eta }_2$. Note that using the function $\gamma (k)$ given by Eq. (10.7), $\eta _2>\bar{\eta }_2$ is equivalent to:

$$\begin{aligned} \epsilon >\frac{1+c}{c-1}\left( \frac{\psi }{1-\psi }\frac{1-\alpha }{\sigma i \gamma }-1\right) \equiv \bar{\epsilon } \end{aligned}$$

(10.54)

where $\gamma =1-(a+b)/(1+c)$.

We can show that $\varepsilon _v^{s}<1$. Since $\varepsilon _{dk}=\frac{\psi }{1-\psi }\frac{1-\alpha }{\sigma }+\eta _2$ and the condition (10.52) is satisfied, we have $\nu (\eta _1)<\left( 1+i^{*}\gamma \right) \varepsilon _{dk}$. Therefore, $\varepsilon _v^{s}= \frac{\nu (\eta _1)}{1+i^{*}\gamma }\frac{1}{\varepsilon _{dk}}-\frac{\varepsilon _u}{c^{*}} \frac{\nu (\eta _1)+\varepsilon _{dk}}{\varepsilon _{dk}}\frac{1-\psi }{\nu (\eta _1)}<~1$.

Furthermore, $\varepsilon _v^{h}<\bar{\varepsilon }_v$ and $\varepsilon _v^{h}>1$ for a sufficiently small $\eta _1$. Indeed $\varepsilon _v^{h}>1$ is equivalent to $\psi Q(\nu (\eta _1))>0$, where $Q(\nu (\eta _1))$ is a quadratic polynomial defined on $\mathbb {R}_{+}$ such that:

$$\begin{aligned} Q(\nu (\eta _1))=&-\frac{\nu (\eta _1)^{2}}{1+i^{*}\gamma } +\nu (\eta _1)\left[ \frac{\varepsilon _u}{c^{*}}-\left( 1-\frac{1-\alpha }{\sigma }+\frac{1}{1+i\gamma }\right) \right. \\&+ \left. \varepsilon _{dk}+\frac{1-(1-\alpha )/\sigma }{1-\psi }\right] +\left( 1-\frac{1-\alpha }{\sigma }\right) \frac{\varepsilon _u}{c^{*}} \end{aligned}$$

$Q(\nu (\eta _1))$ is a concave function with $Q(\nu (0))>0$. As a consequence, there is a threshold $\hat{\eta }_1>0$ such that $\forall \eta _1<\hat{\eta }_1$, $Q(\nu (\eta _1))>0$.

Concerning $\varepsilon _v^{f}$, we can show that $\bar{\varepsilon }_v<\varepsilon _v^{f}$ for $\eta _1$ small enough. Note that $\varepsilon _v^{f}>\xi _4^{b}/\xi _1^{b}$. $\xi _4^{b}/\xi _1^{b}>\bar{\varepsilon }_v$ is satisfied if $-\nu (\eta _1) \left[ \psi \left( 1-\frac{1-\alpha }{\sigma }\right) +\frac{1}{1+i^{*}\gamma }\right] +\left( 1-\psi \right) \varepsilon _{dk}>0$. Therefore, there exists $\underline{\eta }_1>0$ such that $\forall$ $\eta _1<\underline{\eta }_1$, this inequality is satisfied. Hence, $\forall$ $\eta _1<\underline{\eta }_1$, $\bar{\varepsilon }_v<\varepsilon _v^{f}$.

Therefore, $\forall$ $\eta _1<\min \lbrace \eta _1^{\theta }, \tilde{\eta }_1, \overline{\overline{\eta }}_1,\hat{\eta }_1,\underline{\eta }_1 \rbrace$, one has $\varepsilon _v^{s}<1<\varepsilon _v^{h}<\bar{\varepsilon }_v<\varepsilon _v^{f}$ when $a_\phi =0.$ Moreover, we can show that there exists $\eta _1^{\prime }>0$ such that $\forall$ $\eta _1<\eta _1^{\prime }$, $\varepsilon _v^{s}<\varepsilon _v^{h}<\bar{\varepsilon }_v<\varepsilon _v^{f}$ when $a_\phi =-1$. For the rest of the proof, we assume that $\eta _1<\min \lbrace \eta _1^{\theta }, \tilde{\eta }_1, \overline{\overline{\eta }}_1,\hat{\eta }_1,\underline{\eta }_1, \eta _1^{\prime }\rbrace$.

Recall that $a_\phi$ is defined on $(-\infty , -1) \cup [0, +\infty )$. At this stage of the proof, we can state by analyzing $1-T+D$, $1+T+D$ and $1-D$ given by Eqs. (10.41)–(10.43) that if $a_\phi \in (-\infty , -1)$, local indeterminacy occurs when $\varepsilon _v<min \lbrace \bar{\varepsilon }_v, \varepsilon _v^{f}, \varepsilon _v^{h}, \varepsilon _v^{s}\rbrace$ or when $\varepsilon _v> max \lbrace \bar{\varepsilon }_v, \varepsilon _v^{f}, \varepsilon _v^{h}, \varepsilon _v^{s}\rbrace .$ From the previous results, we deduce that if $a_\phi \in [0,\tilde{a}_\phi )$, local indeterminacy occurs when $\varepsilon _v<\varepsilon _v^{s}$ or when $\varepsilon _v>\varepsilon _v^{f}$. Finally, if $a_\phi >\tilde{a}_\phi$, local indeterminacy occurs when $\varepsilon <\varepsilon _v^{s}$. For the case $a_\phi \in (-\infty , -1)$, we should determine the location of $\varepsilon _v^{f}$, $\varepsilon _v^{h}$, $\varepsilon _v^{s}$ and $\bar{\varepsilon }_v$ in the plane $(a_\phi , \varepsilon _v).$

The functions $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ are continuous and monotone increasing on $a_\phi \in (-\infty , -1)$. We can show that the graph of these functions cross the horizonntal axis on $a_\phi \in (-\infty , -1)$. Let introduce the different following points $a_\phi ^{\xi _2}$, $a_\phi ^{\xi _4}$ and $a_\phi ^{\xi _5}$, which corresponds to the points at which $\bar{\varepsilon }_v$, $\varepsilon _v^{f}$ and $\varepsilon _v^{h}$ cross the horizontal axis. $a_{\phi }^{\xi _2}$ is defined by $\bar{\varepsilon }_v=0$ such that $a_\phi ^{\xi _2}=-\frac{\xi _2^{b}}{\xi _2^{a}}<0$. $a_\phi ^{\xi _4}$ is defined by $\varepsilon _v^{f}=0$ such that $a_\phi ^{\xi _4}=-\frac{\xi _4^{b}}{\xi _4^{a}}<0$. $a_\phi ^{\xi _5}$ is defined by $\varepsilon _v^{h}=0$ such that $a_\phi ^{\xi _5}=-\frac{\xi _5^{b}}{\xi _5^{a}}<0$.

After some algebra, we can show that since $\psi <1/(1+i^{*}\gamma )$, there exists $\eta _1^{a}>0$ such that $\forall$ $\eta _1<\eta _1^{a}$, $a_\phi ^{\xi _5}<a_\phi ^{\xi _2}$. Furthermore, either $a_\phi ^{\xi _2}<a_\phi ^{\xi _4}$ $\forall$ $\eta _1>0$ or there exists $\eta _1^{b}$ such that $\forall$ $\eta _1<\eta _1^{b}>0$, $a_\phi ^{\xi _2}<a_\phi ^{\xi _4}$. Hence, if $\eta _1<min \lbrace \eta _1^{a}, \eta _1^{b}, \eta _1^{\theta }, \tilde{\eta }_1, \overline{\overline{\eta }}_1,\hat{\eta }_1,\underline{\eta }_1, \eta _1^{\prime } \rbrace$, one has $a_\phi ^{\xi _5}<a_\phi ^{\xi _2}< a_\phi ^{\xi _4}<0$.

Let $\eta _1^{\prime \prime }=min \lbrace \eta _1^{a}, \eta _1^{b}, \eta _1^{\theta }, \tilde{\eta }_1, \overline{\overline{\eta }}_1,\hat{\eta }_1,\underline{\eta }_1, \eta _1^{\prime } \rbrace$. For the rest of the proof, we suppose that $\eta _1<\eta _1^{\prime \prime }$.

Since the functions $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ are continuous and monotone increasing on $(-\infty , -1) \cup [0, \tilde{a}_\phi )$, we can now locate $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ in the plane $(a_\phi , \varepsilon _v).$

Let $\hat{a}_\phi \equiv a_\phi ^{\xi _4}$. Since $\psi <1/(1+i^{*}\gamma ),$ $a_\phi ^{\xi ^{5}}<a_\phi ^{\xi _2}< \hat{a}_\phi$. Using the expressions of $1-T+D$, $1+T+D$ and $1-D$ given by Eqs. (10.41)–(10.43), we state that if $a_\phi \in (-\infty , \hat{a}_\phi )$, local indeterminacy occurs when $\varepsilon _v>max \lbrace \varepsilon _v^{f}, \varepsilon _v^{h}, \varepsilon _v^{s} \rbrace .$ If $a_\phi \in [\hat{a}_\phi , -1)\cup [0,\tilde{a}_\phi )$, local indeterminacy occurs when $\varepsilon _v<min\lbrace \varepsilon _v^{f}, \varepsilon _v^{s} \rbrace$ or when $\varepsilon _v>max \lbrace \varepsilon _v^{f}, \varepsilon _v^{h}, \varepsilon _v^{s} \rbrace .$

We have shown that $\varepsilon _v^{s}$ can be positive. In such a case, it would be useful to determine when $\varepsilon _v^{f}$, $\varepsilon _v^{h}$ and $\bar{\varepsilon }_v$ cross $\varepsilon _v^{s}$. Suppose that $\varepsilon _v^{s}>0$. $\varepsilon _v^{h}=\varepsilon _v^{s}$ when $a_\phi = - \left( \varepsilon _v^{s}\xi _1^{b}-\xi _5^{b}\right) /(\varepsilon _v^{s}\xi _1^{a}-\xi _5^{a})\equiv a_\phi ^{1} <0$, $\bar{\varepsilon }_v=\varepsilon _v^{s}$ when $a_\phi = -\left( \varepsilon _v^{s}\xi _1^{b}+\xi _2^{b}\right) /(\varepsilon _v^{s}\xi _1^{a}+\xi _2^{a})\equiv a_\phi ^{2}<0$, and $\varepsilon _v^{f}=\varepsilon _v^{s}$ when $a_\phi = -\left( \varepsilon _v^{s}\xi _3^{b}-\xi _4^{b}\right) /(\varepsilon _v^{s}\xi _3^{a}-\xi _4^{a})\equiv a_\phi ^{3}<0$.

Because $\psi <1/(1+i^{*}\gamma )$, we can show after some algebra that either $a_\phi ^{1}<a_\phi ^{2}$ $\forall$ $\eta _1>0$ or there exists $\eta _1^{e}>0$ such that $\forall$ $\eta _1<\eta _1^{e}$, $a_\phi ^{1}<a_\phi ^{2}$. It is difficult to determine the location of $a_\phi ^{3}$. Nevertheless, if $a_\phi ^{1}<a_\phi ^{3}<a_\phi ^{2}<0$ or if $a_\phi ^{3}<a_\phi ^{1}<a_\phi ^{2}<0$, we get $1-T+D<0,$ $1+T+D<0$ and $D>1$ for some values of $\varepsilon _v$. Since this is not feasible, we can eliminate these configurations. Therefore, if $\eta _1<min \lbrace \eta _1^{e}, \eta _1^{\prime \prime } \rbrace$, one has $a_\phi ^{1}<a_\phi ^{2}<a_\phi ^{3}<0$.

Let $\bar{\eta }_1=min \lbrace \eta _1^{e}, \eta _1^{\prime \prime } \rbrace$. All conditions on $\eta _1$ required in this proof are satisfied when $\eta _1<\bar{\eta }_1$. We can now derive the dynamic properties of the model. The properties of local dynamics are depicted by Fig. 10.1.¹⁹ Grey areas in Fig. 10.1 correspond to the different regions in which the steady state is a sink, in other words to the indeterminacy regions.

We deduce Proposition 3 and Corollary 1 from Fig. 10.1. Since $a_\phi =\phi /(1-\phi )$ is increasing with $\phi$, we can derive Corollary 2 from Proposition 3 and Fig. 10.1.    $\blacksquare$