Atlas-Based Reconstruction of 3D Volumes of a Lower Extremity from 2D Calibrated X-ray Images

Abstract

In this paper, reconstruction of 3D volumes of a complete lower extremity (including both femur and tibia) from a limited number of calibrated X-ray images is addressed. We present a novel atlas-based method combining 2D-2D image registration-based 3D landmark reconstruction with a B-spline interpolation. In our method, an atlas consisting of intensity volumes and a set of predefined, sparse 3D landmarks, which are derived from the outer surface as well as the intramedullary canal surface of the associated anatomical structures, are used together with the input X-ray images to reconstruct 3D volumes of the complete lower extremity. Robust 2D-2D image registrations are first used to match digitally reconstructed radiographs, which are generated by simulating X-ray projections of an intensity volumes, with the input X-ray images. The obtained 2D-2D non-rigid transformations are used to update the locations of the 2D projections of the 3D landmarks in the associated image views. Combining updated positions for all sparse landmarks and given a grid of B-spline control points, we can estimate displacement vectors on all control points, and further to estimate the spline coefficients to yield a smooth volumetric deformation field. To this end, we develop a method combining the robustness of 2D-3D landmark reconstruction with the global smoothness properties inherent to B-spline parametrization.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Good clinical outcomes of hip and knee arthroplasties demand the ability to plan a surgery precisely and measure the outcome accurately. In comparison with plain radiograph, CT-based three-dimensional (3D) planning offers several advantages. More specifically, CT has the benefits of avoiding errors resulting from magnification and inaccurate patient positioning. Additional benefits include the assessment in the axial plane, replacement of two-dimensional (2D) projections with 3D data, and the availability of information on bone quality including accurate differentiation between cortical and cancellous bone. The concern on 3D CT-based planning, however, lies in the increase of radiation dosage to the patients [1]. An alternative is to reconstruct a patient-specific 3D volume data from 2D X-rays (Fig. 1).

Depending on the output, 2D-3D reconstruction methods can be largely classified into two categories [2]: 3D surface model reconstruction methods [3, 4] and 3D volume reconstruction methods [5–9]. The methods in the former category compute 3D patient-specific surface models from one or multiple 2D X-ray images. No intensity information or information about cortical bone is available. The methods in the second category generate 3D patient-specific volumes from a limited number of X-ray images. When two or more C-arm/X-ray images are available, Yao and Tayor [5] and Sadowsky et al. [6] proposed an iterative registration process to estimate the pose, scale and modes of variation of a tetrahedral meshes-based Statistical Shape and Intensity Model (SSIM) by minimizing the difference between the simulated Digitally Reconstructed Radiographs (DRRs) and the real X-ray images. Mutual information was used as the similarity measure. With leave-one-out tests, an average registration error of 2.0 mm was reported in [6]. Zheng [8] proposed to reconstruct a patient-specific 3D volume by matching independent shape and appearance models that are learned from a set of training data to a limited number of C-arm/X-ray images. An intensity-based nonrigid 2D-3D registration algorithm was proposed to deformably fit the learned models to the input images. When two C-arm images were used, a mean reconstruction accuracy of 1.5 mm was reported in [8]. To the best knowledge of the authors, none of the above mentioned methods have been applied to reconstruct volumes of a complete lower extremity.

Fig. 1.

A schematic view of the present 2D-3D reconstruction pipeline.

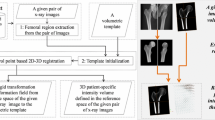
The contribution of this paper is an atlas-based approach for reconstructing 3D volumes of a complete lower extremity (including both femur and tibia) from a limited number of calibrated X-ray images. Figure 2 shows a schematic view of the present 2D-3D reconstruction method. Our method combines 2D-2D image registration-based 3D landmark reconstruction with a B-spline interpolation. In our method, an atlas consisting of intensity volumes and a set of pre-defined, sparse 3D landmarks, which are derived from the outer surface as well as the intramedullary canal surface of the associated anatomical structures, are used together with the input X-ray images to reconstruct 3D volumes of the complete lower extremity. Robust 2D-2D image registrations are first used to match digitally reconstructed radiographs (DRRs), which are generated by simulating X-ray projections of the intensity volumes, with the input X-ray images. The obtained 2D-2D non-rigid transformations are used to update the locations of the 2D projections of the 3D landmarks in the associated image views. Combining updated positions for all sparse landmarks and given a grid of B-spline control points, we can estimate displacement vectors on all control points, and further to estimate the spline coefficients to yield a smooth volumetric deformation field.

The paper is organized as follows. Section 2 presents the 2D-3D reconstruction techniques. Section 3 describes the 2D-3D reconstruction algorithm. Section 4 presents the experimental results, followed by the conclusions in Sect. 5.

2 2D-3D Reconstruction Techniques

Below we first present two 2D-3D reconstruction techniques that are used in our method. We assume that we are given a pair of calibrated X-ray images, one acquired from the Anterior-Posterior (AP) direction and the other from an oblique view (not necessary a Lateral-Medial (LM) view). All the images are calibrated and co-registered to a common coordinate system called c. As we would like to match a 3D intensity volume to the 2D calibrated X-ray images, we consider the 3D volume as the floating image ${\{ {\mathbf {I}}({{\mathbf {x}}_f})\} }$, where ${\mathbf {x}}_f$ is a point in the intensity volume, and the set of predefine landmarks as $\{ {\mathbf {l}}_f^i\} ,i = 1,2,...,L$. The floating volume is aligned to the X-ray reference space c by following forward mapping:

$$\begin{aligned} {\mathbf {I}}({{\mathbf {x}}_{\mathbf {c}}}\left( {{T_g},{T_d})} \right) = {\mathbf {I}}({T_g} \circ {T_d} \circ {{\mathbf {x}}_{\mathbf {f}}}) \end{aligned}$$

(1)

where $T_g$ is a similarity transformation and $T_d$ is a local deformation.

2.1 2D-2D Image Registration-Based 3D Landmark Reconstruction

The 2D-2D image registration-based 3D landmark reconstruction is conducted as follows.

• Step 1: DRR generation and landmark projection. Based on the current estimation of the registration transformation, we generate DRRs using Nvidias CUDA environment. At the same time, we transform all landmarks from the floating volume space to the X-ray reference space. We denote an arbitrary landmark with index i as ${\mathbf {l}}_{\mathbf {c}}^{i,t}$. After that, we do a forward projection of all transformed landmarks to the X-ray image reference space.

• Step 2: 2D-2D Intensity-based Image Registration. At this step, we conduct an intensity-based affine 2D-2D registration first, followed by a deformable B-spline 2D-2D registration of each DRR with the associated X-ray image. In both stages, we choose to use Mattes mutual information [10] as the similarity metric and the adaptive stochastic gradient descent optimization [11] as the optimization method. The estimated 2D-2D transformations are used to update the localizations of the 2D projections of all landmarks.

• Step 3: Triangulation-based Point Reconstruction. Given the updated 2D locations of the projections of a 3D landmark ${\mathbf {l}}_{\mathbf {c}}^{i,t}$, an updated 3D position ${\mathbf {l}}_{\mathbf {c}}^{i,t+1}$ can be reconstructed from those updated 2D locations via a triangulation strategy as shown in Fig. 2.

Fig. 2.

A schematic view of the 2D-2D image registration-based 3D landmark reconstruction. Left: triangulation-based 2D-3D reconstruction of a single landmark; right: reconstruction of all landmarks.

2.2 B-Spline Interpolation

Before we present the details of our 3D B-spline interpolation algorithm, we introduce here the notations first.

• $\{ \mathbf{c}_{l,m,n},\;l = - 1 \sim L + 1,\;m = - 1 \sim M + 1,\;n = - 1 \sim N + 1 \}$: To be computed B-spline coefficients.

• $\{ \mathbf{d}_{l,m,n} \}$: displacements at the positions of the B-spline control points are obtained with thin-plate spline interpolation from the sparse landmarks using the positions before and after triangulation-based landmark reconstruction.

• $( {S_x},{S_y},{S_z} )$: spacing of the B-spline lattice.

• $( {O_x},{O_y},{O_z} )$: origin of a volume data.

Given a volume space with a compact support $\varOmega = [ {{O_x},{X_{Upper}}} ] \times [ {{O_y},{Y_{Upper}}} ] \times [ {{O_z},{Z_{Upper}}} ] \subset {\mathbb {R} ^3}$, for any point $( {x,y,z} ) \in \varOmega$ and its deformed position $( {x',y',z'} ) \in \varOmega$, we can calculate the displacement $( {x'-x,y'-y,z'-z} )$ via a B-spline tensor product as follows:

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {x' - x}\\ {y' - y}\\ {z' - z} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\sum \limits _{r = 0}^3 {\sum \limits _{s = 0}^3 {\sum \limits _{t = 0}^3 {{B_r}( u ){B_s}( v ){B_t}( w ){\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^x} } } }\\ {\sum \limits _{r = 0}^3 {\sum \limits _{s = 0}^3 {\sum \limits _{t = 0}^3 {{B_r}( u ){B_s}( v ){B_t}( w ){\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^y} } } }\\ {\sum \limits _{r = 0}^3 {\sum \limits _{s = 0}^3 {\sum \limits _{t = 0}^3 {{B_r}( u ){B_s}( v ){B_t}( w ){\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^z} } } } \end{array}} \right) \end{aligned}$$

(2)

where

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {B_0}(s) = \frac{{- {s^3} + 3{s^2} - 3s + 1}}{6}\\ {B_1}(s) = \frac{{3{s^3} - 6{s^2} + 4}}{6}\\ {B_2}(s) = \frac{{- 3{s^3} + 3{s^2} + 3s + 1}}{6}\\ {B_3}(s) = \frac{{{s^3}}}{6} \end{array}} \right. \;\;\;\;\;\;( {0 \le s < 1} ) \end{aligned}$$

(3)

are the B-spline basis functions.

At the positions of the B-spline control points, it can be derived that ${u=v=w=0}$. Then, we have ${B_3}( u )={B_3}( v )={B_3}( w )=0$, and the tensor product at the positions of these B-spline control points can be written as

$$\begin{aligned} \mathbf{{d}}_{l,m,n} = \left( {\begin{array}{*{20}{c}} {{\mathop {\text{ d }}\nolimits } _{l,m,n}}\\ {{\mathop {\text{ d }}\nolimits } _{l,m,n}}\\ {{\mathop {\text{ d }}\nolimits } _{l,m,n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\sum \limits _{r = 0}^2 {\sum \limits _{s = 0}^2 {\sum \limits _{t = 0}^2 {{a_r}{a_s}{a_t}{\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^x} } } }\\ {\sum \limits _{r = 0}^2 {\sum \limits _{s = 0}^2 {\sum \limits _{t = 0}^2 {{a_r}{a_s}{a_t}{\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^y} } } }\\ {\sum \limits _{r = 0}^2 {\sum \limits _{s = 0}^2 {\sum \limits _{t = 0}^2 {{a_r}{a_s}{a_t}{\mathop {\text{ c }}\nolimits }_{l + r,m + s,n + t}^z} } } } \end{array}} \right) \end{aligned}$$

(4)

where ${{a_0} = {B_0}\left( 0 \right) = \frac{1}{6}}$, ${{a_1} = {B_1}\left( 0 \right) = \frac{2}{3}}$ and ${{a_2} = {B_2}\left( 0 \right) = \frac{1}{6}}$.

Equation 4 defines 3 sets of $\left( {L + 3} \right) \times \left( {M + 3} \right) \times \left( {N + 3} \right)$ equations with $3 \times \left( {L + 3} \right) \times \left( {M + 3} \right) \times \left( {N + 3} \right)$ unknowns. Each set of equations can be reformulated as a block-matrix style shown as below (without causing confusion, since now on we drop coordinate superscript).

$$\begin{aligned} {\left( {\begin{array}{*{20}{c}} {{a_1}\varLambda }&{}{{a_2}\varLambda }&{}0&{}0&{} \cdots &{}0&{}0\\ {{a_0}\varLambda }&{}{{a_1}\varLambda }&{}{{a_2}\varLambda }&{}0&{} \cdots &{}0&{}0\\ 0&{}{{a_0}\varLambda }&{}{{a_1}\varLambda }&{}{{a_2}\varLambda }&{} \cdots &{}0&{}0\\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots &{} \vdots \\ 0&{}0&{}0&{}0&{} \cdots &{}{{a_0}\varLambda }&{}{{a_1}\varLambda } \end{array}} \right) _{N + 3}}\left( {\begin{array}{*{20}{c}} {{\mathbf{{c}}_{-1}}}\\ {{\mathbf{{c}}_{0}}}\\ {{\mathbf{{c}}_{1}}}\\ \vdots \\ {{\mathbf{{c}}_{N + 1}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\mathbf{{d}}_{-1}}\\ {\mathbf{{d}}_{0}}\\ {\mathbf{{d}}_{1}}\\ \vdots \\ {\mathbf{{d}}_{N + 1}} \end{array}} \right) \end{aligned}$$

(5)

where $\varLambda$ has the tridiagonal structure as Eq. 5, while for the 3D case, the tridiagonal matrix $\varLambda '$ is nested in the structure of $\varLambda$:

$$\begin{aligned} \varLambda = {\left( {\begin{array}{*{20}{c}} {{a_1}\varLambda '}&{}{{a_2}\varLambda '}&{}0&{}0&{} \cdots &{}0&{}0\\ {{a_0}\varLambda '}&{}{{a_1}\varLambda '}&{}{{a_2}\varLambda '}&{}0&{} \cdots &{}0&{}0\\ 0&{}{{a_0}\varLambda '}&{}{{a_1}\varLambda '}&{}{{a_2}\varLambda '}&{} \cdots &{}0&{}0\\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots &{} \vdots \\ 0&{}0&{}0&{}0&{} \cdots &{}{{a_0}\varLambda '}&{}{{a_1}\varLambda '} \end{array}} \right) _{M + 3}} \end{aligned}$$

(6)

$$\begin{aligned} \varLambda ' = {\left( {\begin{array}{*{20}{c}} {{a_1}}&{}{{a_2}}&{}0&{}0&{} \cdots &{}0&{}0\\ {{a_0}}&{}{{a_1}}&{}{{a_2}}&{}0&{} \cdots &{}0&{}0\\ 0&{}{{a_0}}&{}{{a_1}}&{}{{a_2}}&{} \cdots &{}0&{}0\\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots &{} \vdots \\ 0&{}0&{}0&{}0&{} \cdots &{}{{a_0}}&{}{{a_1}} \end{array}} \right) _{L + 3}} \end{aligned}$$

(7)

3 2D-3D Reconstruction Algorithm

We independently match the femoral and the tibial intensity volumes of the atlas with the input X-ray images. Thus, the 2D-3D reconstruction algorithm as presented below is used for reconstructing both femoral and tibial volumes.

Algorithm (2D-3D Intensity Volume Reconstruction). The following two stages are executed until the convergence of the algorithm.

• Scaled-rigid registration stage: At this stage, at the tth iteration, after applying the 2D-2D image registration-based 3D landmark reconstruction, we will obtain two sets of 3D positions $\{ {\mathbf {l}}_f^i \}$ and $\{ {\mathbf {l}}_{\mathbf {c}}^{i,t+1} \}$ with known correspondences, which allows us to compute an updated 3D similarity transformation $T_g^{t + 1}$ [12].

• Non-rigid registration stage: At this stage, the same 2D-2D image registration-based 3D landmark reconstruction is used in each iteration to obtain two sets of 3D positions with known correspondences. The B-spline interpolation algorithm as described in Sect. 2.2 is used to compute the B-spline coefficients and to further compute a smooth volumetric deformation field $T_d^{t + 1}$ to warp the intensity volume at the atlas space to the X-ray image reference space.

4 Experiments and Results

After a local institution review board approval, we designed and conducted experiments on data of 11 cadaveric legs and 10 patients. For each cadaveric leg, we acquired CT data of the full leg with a voxel size of 0.78 mm $\times$ 0.78 mm $\times$ 1 mm. One of the CT data was randomly chosen to be the atlas for all the 2D-3D reconstruction experiments described in this paper. For the atlas CT data, both femoral and tibial intensity volumes were manually segmented from the associated CT data. We further manually extracted a set of sparse landmarks from the outer surface and the intramedullary canal surface of the associated anatomical structures (we extracted 641 landmarks for femur and 872 landmarks for tibia). For each CT data of the remaining 10cadaveric legs, we generated a pair of simulated X-ray images. The 2D-3D reconstruction of the first experiment was then conducted on the simulated X-ray images. The second experiment was conducted on the patients’ data. For each patient, we acquired a pair of X-ray images. The acquired X-ray images were calibrated using the method that we introduced in [13] where a device was designed to immobilize a patient’s knee joint and to have a calibration phantom rigidly attached. Additionally, in order to validate the reconstruction accuracy, CT scan around three local joint regions (hip, knee and ankle) are done in one common coordinate system for each patient.

Experiment on Simulated X-ray Images. In this experiment, we take data manually segmented from the associated CT data as the ground truth. We evaluated not only the average surface distance (ASD) but also the intramedullary canal surface distance (Canal ASD) between surface models segmented from the ground truth volumes and the reconstructed volumes. We also estimated the overall Dice overlap coefficients (DICE) between the ground truth volumes and the reconstructed volumes, and the DICE overlap coefficients of the cortical bone regions (Cortical DICE), which were manually segmented from the associated volumes. Measurement differences for functional parameters such as femoral antetorsion (AT) angle, femoral collodiaphyseal (CCD) angle, and leg mechanical axis were also recorded. The quantitative results are shown in Fig. 3, left. Figure 3, right shows a qualitative comparison of the reconstructed volumes with the associated ground truth volumes for both femur and tibia. Overall, the average reconstruction accuracy achieved by our 2D-3D reconstruction technique is 1.5 mm and 1.3 mm for femur and tibia, respectively.

Fig. 3.

Results of the experiment conducted on simulated X-ray images. Left: quantitative results; right: a qualitative comparison.

Experiment on 10 Patients’ Data. In this experiment, due to the fact that only CT data around three local regions (hip, knee and ankle joints) were available (see Fig. 4, left for an example), the reconstruction accuracies were evaluated by comparing the surface models extracted from the ground truth CT data with those extracted from the reconstructed volumes after rigidly align them together. Similar to what we did in the first experiment, we also computed the measurement differences on functional parameters. The results are shown in Fig. 4, right. Please keep it in mind that here we only evaluated the average surface distances for local regions such as proximal femur (PF ASD), distal femur (DF ASD), proximal tibia (PT ASD) and distal tibia (DT ASD), while in the first experiment, the reconstruction accuracy was evaluated for the complete femur and tibia. An overall reconstruction accuracy of 1.4 mm was found.

Fig. 4.

Results of the experiment conducted on 10 patients’ data. Left: an example showing red surface models extracted from ground truth CT data and the green surface models extracted from reconstructed volumes; right: quantitative results. (Color figure online)

5 Conclusions

In this paper, we presented an atlas-based approach for reconstructing 3D volumes of a complete lower extremity (including both femur and tibia) from a pair of calibrated X-ray images. Our method has the advantage of combining the robustness of 2D-3D landmark reconstruction with the global smoothness properties inherent to B-spline parametrization. To the best knowledge of the authors, this is probably the first attempt to derive 3D volumes of a lower extremity from a pair of calibrated X-ray images. Results of experiments conducted on both simulated data and patient data demonstrated the efficacy of the present method.