Massive MIMO in Small Cell Networks: Wireless Backhaul

Abstract

Dense small cell networks are expected to be deployed in the next generation wireless system to provide better coverage and throughput to meet the ever-increasing requirements of high data rate applications. As the trend toward densification calls for more and more wireless links to forward a massive backhaul traffic into the core network, it is critically important to take into account the presence of a wireless backhaul for the energy-efficient design of small cell networks. In this chapter, we develop a general framework to analyze the energy efficiency of a two-tier small cell network with massive MIMO macro base stations and wireless backhaul. Our analysis reveal that under spatial multiplexing, the energy efficiency of a small cell network is sensitive to the network load, and it should be taken into account when controlling the number of users served by each base station. We also demonstrate that a two-tier small cell network with wireless backhaul can be significantly more energy efficient than a one-tier cellular network. However, this requires the bandwidth division between radio access links and wireless backhaul to be optimally designed according to the load conditions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

The next generation of wireless communication systems targets a thousandfold capacity improvement to meet the exponentially growing mobile data demand, and the prospective increase in energy consumption poses urgent environmental and economic challenges [1, 2]. Green communications have become an inevitable necessity, and much effort is being made both in industry and academia to develop new network architectures that can reduce the energy per bit from current levels, thus ensuring the sustainability of future wireless networks [3–7].

3.1.1 Background and Motivation

Since the current growth rate of wireless data exceeds both spectral efficiency advances and availability of new wireless spectrum, a trend toward network densification is essential to respond adequately to the continued surge in mobile data traffic [8–10]. To this end, small cell networks are proposed to provide higher coverage and throughput by overlaying macro cells with a vast number of low-power small access points, thus offloading traffic and reducing the distance between transmitter and receiver [11, 12]. Forwarding a massive cellular traffic to the backbone network becomes a key problem when small cells are densely deployed, and a wireless backhaul is regarded as the only practical solution where wired links are hardly available [13–17]. However, the power consumption incurred on the wireless backhaul links, together with the power consumed by the multitude of access points deployed, becomes a crucial issue, and an energy-efficient design is necessary to ensure the viability of future small cell networks [18].

Various approaches have been investigated to improve the energy efficiency of small cell networks. Cell size, deployment density, and number of antennas were optimized to minimize the power consumption of small cells [19, 20]. Cognitive sensing and sleep mode strategies were also proposed to turn off inactive access points and enhance the energy efficiency [21, 22]. A further energy efficiency gain was shown to be attainable by serving users that experience better channel conditions, and by dynamically assigning users to different tiers of the network [23, 24]. Although various studies have been conducted on the energy efficiency of small cell networks, the impact of a wireless backhaul has typically been neglected. On the other hand, the power consumption of backhauling operations at small cell access points (SAPs) might be comparable to the amount of power necessary to operate macrocell base stations (MBSs) [25–27]. Moreover, since it is responsible to aggregate traffic from SAPs toward MBSs, the backhaul may significantly affect the rates and therefore the energy efficiency of the entire network. With a potential evolution toward dense infrastructures, where many small access points are expected to be used, it is of critical importance to take into account the presence of a wireless backhaul for the energy-efficient design of heterogeneous networks.

3.1.2 Approach and Main Outcomes

Our main goal in this chapter is to study the energy-efficient design of small cell networks with wireless backhaul. In particular, we consider a two-tier small cell network which consists of MBSs and SAPs, where SAPs are connected to MBSs via a multiple-input-multiple-output (MIMO) wireless backhaul that uses a fraction of the total available bandwidth. We undertake an analytical approach to derive data rates and power consumption for the entire network in the presence of both uplink (UL) and downlink (DL) transmissions and spatial multiplexing, which is a practical scenario that has not yet been addressed. Similar to the framework we developed in Chap. 2, we model the spatial locations of MBSs, SAPs, and UEs as independent homogeneous Poisson point processes (PPPs), and analyze the energy efficiency by combining tools from stochastic geometry and random matrix theory. The analysis enable us to take a complete treatment of all the key features in a small cell network, i.e., interference, load, deployment strategy, and capability of the wireless infrastructure components. With the developed framework, we can explicitly characterize the power consumption of the small cell network due to signal processing operations in macro cells, small cells, and wireless backhaul, as well as the rates and ultimately the energy efficiency of the whole network. The main contributions in this chapter are summarized below.

• We provide a general toolset to analyze the energy efficiency of a two-tier small -network with wireless backhaul. Our model accounts for both UL and DL transmissions and spatial multiplexing, for the bandwidth and power allocated between macro cells, small cells, and backhaul, and for the infrastructure deployment strategy.

• We combine tools from stochastic geometry and random matrix theory to derive the uplink and downlink rates of macro cells, small cells, and wireless backhaul. The resulting analysis is tractable and captures the effects of multiantenna transmission, fading, shadowing, and random network topology.

• Using the developed framework, we find that the energy efficiency of a small cell network is sensitive to the load conditions of the network, thus establishing the importance of scheduling the right number of UEs per base station. Moreover, by comparing the energy efficiency under different deployment scenarios, we find that such property does not depend on the infrastructure.

• We show that if the wireless backhaul is not allocated sufficient resources, then the energy efficiency of a two-tier small cell network with wireless backhaul can be worse than that of a one-tier cellular network. However, the two-tier small cell network can achieve a significant energy efficiency gain if the backhaul bandwidth is optimally allocated according to the load conditions of the network.

The remainder of this chapter is organized as follows. The system model is introduced in Sect. 3.2. In Sect. 3.3, we detail the power consumption of a heterogeneous network with wireless backhaul. In Sect. 3.4, we analyze the data rates and the energy efficiency, and we provide simulations that confirm the accuracy of our analysis. Numerical results are shown in Sect. 3.5 to give insights into the energy-efficient design of a HetNet with wireless backhaul. The chapter is concluded in Sect. 3.6.

Fig. 3.1

Illustration of a two-tier small cell network with wireless backhaul

3.2 System Model

3.2.1 Topology and Channel

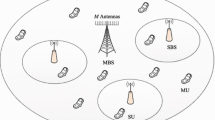
We study a two-tier small cell network which consists of MBSs, SAPs, and UEs, as depicted in Fig. 3.1. The spatial locations of MBSs, SAPs, and UEs follow independent PPPs $\varPhi _{\mathrm {m}}$, $\varPhi _{\mathrm {s}}$, and $\varPhi _{\mathrm {u}}$, with spatial densities $\lambda _{\mathrm {m}}$, $\lambda _{\mathrm {s}}$, and $\lambda _{\mathrm {u}}$, respectively. All MBSs, SAPs, and UEs are equipped with $M_\mathrm {m}$, $M_\mathrm s$, and 1 antennas, respectively, each UE associates with the base station that provides the largest average received power, and each SAP associates with the closest MBS. The links between MBSs and UEs, SAPs and UEs, and MBSs and SAPs are referred to as macro cell links, small cell links, and backhaul links, respectively. In light of its higher spectral efficiency [28], we consider spatial multiplexing where each MBS and each SAP simultaneously serve $K_{\mathrm {m}}$ and $K_{\mathrm {s}}$ UEs, respectively. In practice, due to a finite number of antennas, MBSs and SAPs use traffic scheduling to limit the number of UEs served to $K_{\mathrm {m}}\le M_\mathrm {m}$ and $K_{\mathrm {s}}\le M_\mathrm s$ [29]. Similarly, each MBS limits to $K_{\mathrm {b}}$ the number of SAPs served on the backhaul, with $K_{\mathrm {b}}M_\mathrm s \le M_\mathrm m$. The MIMO dimensionality ratio for linear processing on macrocells, small cells, and backhaul is denoted by $\beta _\mathrm {m} = \frac{K_{\mathrm {m}}}{M_{\mathrm {m}}}$, $\beta _\mathrm {s} = \frac{K_{\mathrm {s}}}{M_{\mathrm {s}}}$, and $\beta _\mathrm {b} = \frac{K_{\mathrm {b}}M_{\mathrm {s}}}{M_{\mathrm {m}}}$, respectively.

In this work, we consider a co-channel deployment of small cells with the macro cell tier, i.e., macro cells and small cells share the same frequency band for transmission.¹ In order to avoid severe interference which may degrade the performance of the network, we assume that the access and backhaul links share the same pool of radio resources through orthogonal division, i.e., the total available bandwidth is divided into two portions, where a fraction $\zeta _\mathrm {b}$ is used for the wireless backhaul, and the remaining $(1-\zeta _\mathrm {b})$ is shared by the radio access links (macro cells and small cells) [13, 15, 34, 35]. In order to adapt the radio resources to the variation of the DL/UL traffic demand, we assume that MBSs and SAPs operate in a dynamic time division duplex (TDD) mode [36, 37], where at every time slot, all MBSs and SAPs independently transmit in downlink with probabilities $\tau _{\mathrm {m}}$, $\tau _{\mathrm {s}}$, and $\tau _{\mathrm {b}}$ on the macro cell, small cell, and backhaul, respectively, and they transmit in uplink for the remaining time.² We model the channels between any pair of antennas in the network as independent, narrowband, and affected by three attenuation components, namely, small-scale Rayleigh fading, shadowing $S_{\mathrm {D}}$ and $S_{\mathrm {B}}$ for data link and backhaul link, respectively, and large-scale path loss, where $\alpha$ is the path loss exponent and the shadowing satisfies $\mathbb {E}[S_{\mathrm {D}}^{\frac{2}{\alpha }}] < \infty$ and $\mathbb {E}[S_{\mathrm {B}}^{\frac{2}{\alpha }}] < \infty$, and by thermal noise with variance $\sigma ^2$. We finally assume that all MBSs and SAPs use a zero forcing (ZF) scheme for both transmission and reception, due to its practical simplicity [38].³

3.2.2 Energy Efficiency

We consider the power consumption due to transmission and signal processing operations performed on the entire network, therefore energy-efficiency tradeoffs will be such that savings at the MBSs and SAPs are not counteracted by increased consumption at the UEs, and vice versa [4, 43]. To this end, we identify the three aspects as the major power consumption in the network, namely, the power spent on macro cells, small cells, and wireless backhaul. Consistent with previous work [43–46], we account for the power consumption due to transmission, encoding, decoding, and analog circuits.

Let $\mathscr {P} {[\frac{\text {W}}{\text {m}^2}]}$ be the total power consumption per area, which includes the power consumed on all links. We denote by $\mathscr {R} {[\frac{\text {bit}}{\text {m}^2}]}$ the sum rate per unit area of the network, i.e., the total number of bits per second successfully transmitted per square meter. The energy efficiency ${\eta =\frac{\mathscr {R}}{\mathscr {P}}}$ is then defined as the number of bits successfully transmitted per joule of energy spent [43, 47]. For the sake of clarity, the main notations used in this paper are summarized in Table 3.1.

Table 3.1 Notation summary

3.3 Power Consumption

In this section, we model in detail the power consumption of the small cell network with wireless backhaul.

To start with, notice that each UE associates with the base station, i.e., MBS or SAP that provides the largest average received power, the probability that a UE associates to a MBS or to a SAP can be respectively calculated as [48]

$$\begin{aligned} A_{\mathrm {m}} = \frac{\lambda _{\mathrm {m}}P_{\mathrm {mt}}^{\frac{2}{\alpha }}}{\lambda _{\mathrm {m}}P_{\mathrm {mt}}^{\frac{2}{\alpha }} + \lambda _{\mathrm {s}}P_{\mathrm {st}}^{\frac{2}{\alpha }}} \end{aligned}$$

(3.1)

and

$$\begin{aligned} A_{\mathrm {s}} = \frac{\lambda _{\mathrm {s}}P_{\mathrm {st}}^{\frac{2}{\alpha }}}{\lambda _{\mathrm {m}}P_{\mathrm {mt}}^{\frac{2}{\alpha }} + \lambda _{\mathrm {s}}P_{\mathrm {st}}^{\frac{2}{\alpha }}}. \end{aligned}$$

(3.2)

In the remainder of this chapter, we make the assumption that the number of UEs, the number of SAPs associated to a MBS, and the number of UEs associated to a SAP by constant values $K_{\mathrm {m}}$, $K_{\mathrm {b}}$, and $K_{\mathrm {s}}$, respectively, which are upper bounds imposed by practical antenna limitations at MBSs and SAPs.⁴

Fig. 3.2

Complementary cumulative distribution function (CCDF) of the number of UEs $N_\mathrm {m}$ associated to a MBS, where $K_{\mathrm {m}}$ is the maximum number of UEs that can be served due to antenna limitations

The assumption above is motivated by the fact that the number of UEs $N_\mathrm m$ served by a MBS has distribution [48]

$$\begin{aligned} \mathbb {P}(N_\mathrm m = n) = \frac{3.5^{3.5} \varGamma (n+3.5) \left( \frac{\lambda _{\mathrm {m}}}{A_\mathrm m \lambda _{\mathrm {u}}}\right) ^{3.5}}{ \varGamma (3.5) n! \left( 1 + 3.5 \lambda _{\mathrm {m}}/ \lambda _{\mathrm {u}}\right) ^{n+3.5} }, \end{aligned}$$

(3.3)

where $\varGamma (\cdot )$ is the gamma function. Let $K_\mathrm m$ be a limit on the number of users that can be served by a MBS, the probability that a MBS serves less than $K_\mathrm m$ UEs is given by

$$\begin{aligned} \mathbb {P}\left( N_\mathrm m < K_\mathrm m \right)&= \sum _{n=0}^{K_\mathrm m-1}\frac{3.5^{3.5} \varGamma (n+3.5)\left( \frac{\lambda _{\mathrm {m}}}{A_\mathrm m \lambda _{\mathrm {u}}}\right) ^{3.5}}{ \varGamma (3.5) n! \left( 1 + 3.5 \lambda _{\mathrm {m}}/ \lambda _{\mathrm {u}}\right) ^{n+3.5} } \nonumber \\&\le \left( \frac{2 \lambda _{\mathrm {m}}}{\lambda _{\mathrm {u}}}\right) ^{3.5} \sum _{n=0}^{K_\mathrm m-1}\frac{\varGamma (n+3.5) }{ n! } \frac{3.5^{3.5} }{ \varGamma (3.5)}, \end{aligned}$$

(3.4)

which rapidly tends to zero as $\frac{\lambda _{\mathrm {u}}}{\lambda _{\mathrm {m}}}$ grows. This indicates that in a practical network with a high density of UEs, i.e., where $\lambda _{\mathrm {u}}\gg \lambda _{\mathrm {m}}$, each MBS serves $K_\mathrm m$ UEs with probability almost one. Figure 3.2 shows the probability $\mathbb {P}(N_\mathrm m \ge K_{\mathrm {m}})$ that a MBS has at least $K_\mathrm m$ UEs to serve, where values of $\mathbb {P}(N_\mathrm m \ge K_{\mathrm {m}})$ are plotted for three UE–MBS density ratios $\lambda _{\mathrm {u}}/ \lambda _{\mathrm {m}}$, and for various numbers of scheduled users $K_{\mathrm {m}}$. It can be seen that $\mathbb {P}(N_\mathrm m \ge K_{\mathrm {m}}) \approx 1$ for moderate-to-high UE densities and low-to-moderate values of $K_{\mathrm {m}}$, therefore confirming that each MBS tends to serve a fixed number $K_{\mathrm {m}}$ of UEs with probability one. A similar approach can be used to show that $\mathbb {P}(N_\mathrm s < K_\mathrm s) \approx 0$ and $\mathbb {P}(N_\mathrm b < K_\mathrm b) \approx 0$ when $\lambda _{\mathrm {u}}\gg \lambda _{\mathrm {m}}$ and $\lambda _{\mathrm {s}}\gg \lambda _{\mathrm {m}}$, respectively, and therefore each SAP serves $K_\mathrm s$ UEs and each MBS serves $K_\mathrm b$ SAPs on the backhaul with probability almost one.

In the following, we use the power consumption model introduced in [43], which captures all the key contributions to the power consumption of signal processing operations. This model is flexible since the various power consumption values can be tuned according to different scenarios. We note that the results presented in this paper hold under more general conditions and apply to different power consumption models [52, 53].

Under the previous assumption, and by using the model in [43], we can write the power consumption on each macro cell link as follows

$$\begin{aligned} P_{\mathrm {m}}&= \tau _{\mathrm {m}}P_{\mathrm {mt}}+ \left( 1-\tau _{\mathrm {m}}\right) K_{\mathrm {m}}P_{\mathrm {ut}}+ \tau _{\mathrm {m}}K_{\mathrm {m}}\left( P_{\mathrm {me}} + P_{\mathrm {ud}}\right) R_{\mathrm {m}}^{\mathrm {DL}} \nonumber \\&\qquad + P_{\mathrm {mc}} + \left( 1-\tau _{\mathrm {m}}\right) K_{\mathrm {m}}\left( P_{\mathrm {md}} + P_{\mathrm {ue}}\right) R_{\mathrm {m}}^{\mathrm {UL}}, \end{aligned}$$

(3.5)

where $P_{\mathrm {mt}}$ and $P_{\mathrm {ut}}$ are the DL and UL transmit power from the MBS and the $K_{\mathrm {m}}$ UEs, respectively, $P_{\mathrm {mc}}$ is the analog circuit power consumption, $P_{\mathrm {me}}$ and $P_{\mathrm {md}}$ are encoding and decoding power per bit of information for MBS, while $P_{\mathrm {ue}}$ and $P_{\mathrm {ud}}$ are encoding and decoding power per bit of information for UE, and $R_{\mathrm {m}}^{\mathrm {DL}}$ and $R_{\mathrm {m}}^{\mathrm {UL}}$ denote the DL and UL rates for each MBS–UE pair. The analog circuit power can be modeled as [43]

$$\begin{aligned} P_{\mathrm {mc}}&= P_{\mathrm {mf}} + P_{\mathrm {ma}} M_{\mathrm {m}}+ P_{\mathrm {ua}} K_{\mathrm {m}}, \end{aligned}$$

(3.6)

where $P_{\mathrm {mf}}$ is a fixed power accounting for control signals, baseband processor, local oscillator at MBS, cooling system, etc., $P_{\mathrm {ma}}$ is the power required to run each circuit component attached to the MBS antennas, such as converter, mixer, and filters, $P_{\mathrm {ua}}$ is the power consumed by circuits to run a single-antenna UE. Under this model, the total power consumption on the macrocell can be written as

$$\begin{aligned}&P_{\mathrm {m}} = \tau _{\mathrm {m}}P_{\mathrm {mt}}\!+\! \left( 1 \!-\! \tau _{\mathrm {m}}\right) K_{\mathrm {m}}P_{\mathrm {ut}}\! +\! \tau _{\mathrm {m}}K_{\mathrm {m}}\!\left( P_{\mathrm {me}} \!+\! P_{\mathrm {ud}}\right) \! R_{\mathrm {m}}^{\mathrm {DL}} \nonumber \\&\!+\! P_{\mathrm {mf}} \!+\! P_{\mathrm {ma}} M_{\mathrm {m}}\!+\! P_{\mathrm {ua}} K_{\mathrm {m}}\!+\! \left( 1\!-\!\tau _{\mathrm {m}}\right) \!K_{\mathrm {m}}\! \left( P_{\mathrm {md}} \!+\! P_{\mathrm {ue}}\right) \! R_{\mathrm {m}}^{\mathrm {UL}}. \end{aligned}$$

(3.7)

Through a similar approach, the power consumption on each small cell and backhaul link can be written as

$$\begin{aligned} P_{\mathrm {s}}&= \tau _{\mathrm {s}}P_{\mathrm {st}}+ \left( 1-\tau _{\mathrm {s}}\right) K_{\mathrm {s}}P_{\mathrm {ut}}+ P_{\mathrm {sf}} + \tau _{\mathrm {s}}K_{\mathrm {s}}\left( P_{\mathrm {se}} + P_{\mathrm {ud}}\right) R_{\mathrm {s}}^{\mathrm {DL}} \nonumber \\&+ P_{\mathrm {sa}} M_{\mathrm {s}}+ P_{\mathrm {ua}} K_{\mathrm {s}}+ \left( 1-\tau _{\mathrm {s}}\right) K_{\mathrm {s}}\left( P_{\mathrm {sd}} + P_{\mathrm {ue}}\right) R_{\mathrm {s}}^{\mathrm {UL}} \end{aligned}$$

(3.8)

and

$$\begin{aligned}&P_{\mathrm {b}} = \tau _{\mathrm {b}} P_{\mathrm {mb}} + \left( 1-\tau _{\mathrm {b}}\right) K_{\mathrm {b}}P_{\mathrm {sb}} + \tau _{\mathrm {b}} K_{\mathrm {b}}K_{\mathrm {s}}\left( P_{\mathrm {me}} + P_{\mathrm {sd}}\right) R_{\mathrm {b}}^{\mathrm {DL}} \nonumber \\&+ P_{\mathrm {ma}} M_{\mathrm {m}}+ K_{\mathrm {b}}M_{\mathrm {s}}P_{\mathrm {sa}}+ \left( 1 - \tau _{\mathrm {b}} \right) K_{\mathrm {b}}K_{\mathrm {s}}\left( P_{\mathrm {md}} + P_{\mathrm {se}}\right) R_{\mathrm {b}}^{\mathrm {UL}}, \end{aligned}$$

(3.9)

respectively, the analog circuit power consumption in (3.9) accounts for power spent on out of band SAPs. In the above equations, $P_{\mathrm {st}}$ is the transmit power on a small cell, $P_{\mathrm {mb}}$ and $P_{\mathrm {sb}}$ are the powers transmitted by MBSs and SAPs on the backhaul, and $P_{\mathrm {sf}}$ and $P_{\mathrm {sa}}$ are the small-cell equivalents of $P_{\mathrm {mf}}$ and $P_{\mathrm {ma}}$. Moreover, $R_{\mathrm {s}}^{\mathrm {DL}}$ and $R_{\mathrm {s}}^{\mathrm {UL}}$ denote the DL and UL rates for each SAP–UE pair, and $R_{\mathrm {b}}^{\mathrm {DL}}$ and $R_{\mathrm {b}}^{\mathrm {UL}}$ denote the DL and UL rates for each wireless backhaul link.

With the above results, the average power consumption per area can be expressed as

$$\begin{aligned} \mathscr {P} = P_\mathrm m \lambda _{\mathrm {m}}+ P_\mathrm s \lambda _{\mathrm {s}}+ P_\mathrm b \lambda _{\mathrm {m}}, \end{aligned}$$

(3.10)

where $P_{\mathrm {m}}$, $P_{\mathrm {s}}$, and $P_{\mathrm {b}}$ are given, respectively, in (3.7), (3.8), and (3.9).

3.4 Rates and Energy Efficiency

In this section, we analyze the data rates and the energy efficiency of a small cell network with wireless backhaul. Particularly, we combine tools from stochastic geometry and random matrix theory to derive the uplink and downlink rates of macro cells, small cells, and wireless backhaul. The analytical expressions provided in this section are tight approximations of the actual data rates. For a better readability, proofs and mathematical derivations have been relegated to the Appendix.

To start with, we consider a typical DL transmission link between a typical UE located at the origin and served by its associated MBS. Note that under dynamic TDD [36, 37], the DL communication is corrupted by DL interference from other MBSs and SAPs, and by UL interference from UEs that associated with other MBSs and SAPs. Results from stochastic geometry indicates that the UL interference from UEs that associated with MBSs follow a homogeneous PPP with density $(1-\tau _{\mathrm {m}}) \lambda _{\mathrm {m}}K_{\mathrm {m}}$, and similarly, and similarly, the UL interference from UEs that associated with SAPs follow a homogeneous PPP with density $(1-\tau _{\mathrm {s}}) \lambda _{\mathrm {s}}{K_{\mathrm {s}}}$. The UL interference from UEs that associated with SAPs follow a homogeneous PPP with density $(1-\tau _{\mathrm {s}}) \lambda _{\mathrm {s}}{K_{\mathrm {s}}}$. Using composition theorem [54], we have the UL interfering UEs follow a PPP with density $\tilde{\lambda }_{\mathrm {u}} = (1-\tau _{\mathrm {m}}) \lambda _{\mathrm {m}}K_{\mathrm {m}}+ (1-\tau _{\mathrm {s}}) \lambda _{\mathrm {s}}{K_{\mathrm {s}}}$.

The large antenna array at MBS allows us to apply random matrix theory tools to obtain the DL rate on a macro cell link.

Lemma 3.1

The downlink rate on a macrocell is given by

$$\begin{aligned}&{R}_\mathrm {m}^{\mathrm {DL}} = (1 - \zeta _\mathrm b) \! \int _{0}^{\infty }\!\! \int _{0}^{\infty }\! \frac{e^{-\sigma ^2 z}}{z \ln 2} \, \left( 1 - e^{-z \nu _{\mathrm {m}}^{\mathrm {D}} }\right) \exp \left( - \frac{2 \pi ^2 \tilde{\lambda _\mathrm {u}} P_{\mathrm {ut}}^{ \delta } \mathbb {E}[S_{\mathrm {D}}^{ \delta }] z^{ \delta } }{\alpha \sin \left( \frac{2 \pi }{\alpha }\right) } \right) \nonumber \\&\times \! \exp \! \left( - \tau _{\mathrm {m}}a_{\mathrm {m}} \mathscr {C}_{\alpha , K_{\mathrm {m}}}\!\left( z P_{\mathrm {mt}}, t\right) \! \left( \frac{z P_{\mathrm {mt}}}{K_{\mathrm {m}}}\right) ^{ \delta } \!\!- \tau _{\mathrm {s}}a_{\mathrm {s}} \mathscr {C}_{\alpha , K_{\mathrm {s}}}\!\left( zP_{\mathrm {mt}}, t\right) \! \left( \frac{z P_{\mathrm {st}}}{K_{\mathrm {s}}}\right) ^{ \delta } \right) \! f_{L_\mathrm m}(t) dt dz, \end{aligned}$$

(3.11)

where $\delta = 2 / \alpha$, $a_\mathrm {m} = \lambda _{\mathrm {m}}\pi \mathbb {E}[S_{\mathrm {D}}^\delta ]$, $a_\mathrm {s} = \lambda _{\mathrm {s}}\pi \mathbb {E}[S_{\mathrm {D}}^\delta ]$, $\tilde{\lambda }_\mathrm {u} = (1-\tau _{\mathrm {m}})\lambda _{\mathrm {m}}K_{\mathrm {m}}+ (1-\tau _{\mathrm {s}})\lambda _{\mathrm {s}}K_{\mathrm {s}}$, while $\nu _{\mathrm {m}}^{\mathrm {D}}$, $f_{L_\mathrm m}(t)$, and $\mathscr {C}_{\alpha , K}\!\left( z, t\right)$ given as follows

$$\begin{aligned} \nu _{\mathrm {m}}^{\mathrm {D}}&= \frac{P_{\mathrm {mt}}\left( 1-\beta _{\mathrm {m}}\right) \left( G_\mathrm {m} \right) ^{\frac{\alpha }{2}}}{\beta _{\mathrm {m}} \varGamma \!\left( 1+\frac{\alpha }{2}\right) },\end{aligned}$$

(3.12)

$$\begin{aligned} f_{L_\mathrm m}(t)&= G_{\mathrm {m}} \delta x^{\delta - 1} \exp \left( - G_\mathrm {m} x^\delta \right) , \quad x \ge 0 \end{aligned}$$

(3.13)

$$\begin{aligned} \mathscr {C}_{\alpha , K}\!\left( z, t\right)&= \frac{2}{\alpha } \sum _{n=1}^K \begin{pmatrix}K \\ n\end{pmatrix} \left[ B\left( 1; K - n + \frac{2}{\alpha }, n - \frac{2}{\alpha }\right) \right. \nonumber \\&\qquad \qquad \qquad - \left. B\left( \left( 1 + \frac{s}{tK}\right) ^{-1}\!\!\!\!; K - n + \frac{2}{\alpha }, n - \frac{2}{\alpha }\right) \right] \end{aligned}$$

(3.14)

with $G_\mathrm m = a_\mathrm {m} + a_\mathrm {s} \left( {P_{\mathrm {st}}}/{P_{\mathrm {mt}}}\right) ^{\delta }$, and $B(x;y,z)=\int _0^x t^{y-1}(1-t)^{z-1}dt$ the incomplete Beta function.

Fig. 3.3

Comparison of the simulations and numerical results for macrocell downlink rate

The proof of this lemma is given in Appendix section “Proof of Lemma 3.1”. In Fig. 3.3, we provide a comparison between the simulated macrocell downlink rate and the analytical result obtained in Lemma 3.1 with different antenna numbers at the MBS. The downlink rate is plotted versus the transmit power at the MBSs. It can be seen that analytical results and simulations fairly well match, thus confirming the accuracy of Lemma 3.1.

We next deal with the analysis to the uplink achievable rate of an MBS UE. Note that in the downlink, due to the maximum received power association, interfering base station cannot be located closer to the typical user than the tagged base station, i.e., an exclusion region exists where the distance between a UE and the interfering base stations is bounded away from zero. However in the uplink, since PPP deployment assumption ignores a minimum inter-site distance between base stations, it can happen that an interfering base station locates arbitrarily close to a typical MBS, i.e., the distance between a MBS and the interfering base stations can be arbitrarily small. In the following, we treat the latter as a composition of three independent PPPs with different spatial densities. We then apply stochastic geometry to obtain the macrocell uplink rate as follows:

Lemma 3.2

The uplink rate on a macro cell is given by

$$\begin{aligned}&{R}^{\mathrm {UL}}_{\mathrm m} = (1-\zeta _\mathrm b) \int _0^\infty \!\! \int _0^\infty \frac{ \left( 1 - e^{- z \nu _{\mathrm {m}}^{\mathrm {U}} / t } \right) }{z e^{\sigma ^2 z} \ln 2} \exp \left\{ - \tilde{\lambda }_{\mathrm {u}} \pi \mathbb {E}[S_{\mathrm {D}}^{\delta }] \int _0^\infty \frac{1 - e^{ - G_\mathrm {m} u }}{1 + z^{-1} u^{\frac{1}{\delta }}/ P_{\mathrm {ut}}} du \right. \nonumber \\&- \left. \frac{ \varGamma \!\left( 1\!+\!\delta \right) \delta \pi ^2 z^\delta }{\sin (\delta \pi )} \left[ \frac{ \tau _{\mathrm {m}}a_\mathrm {m} P_{\mathrm {mt}}^\delta \prod _{i=1}^{K_{\mathrm {m}}-1} (i+\delta ) }{\varGamma (K_{\mathrm {m}}) K_{\mathrm {m}}^\delta } + \frac{ \tau _{\mathrm {s}}a_\mathrm {s} P_{\mathrm {st}}^\delta \prod _{i=1}^{K_{\mathrm {s}}-1} (i+\delta ) }{\varGamma (K_{\mathrm {s}}) K_{\mathrm {s}}^\delta }\right] \right\} f_{L_\mathrm {m}}(t) dt dz\qquad \end{aligned}$$

(3.15)

with $\nu _{\mathrm {m}}^{\mathrm {U}} = (1-\beta _{\mathrm {m}}) M_{\mathrm {m}}P_{\mathrm {mt}}$.

The proof is given in Appendix section “Proof of Lemma 3.2.”

In order to derive the downlink and uplink rate of an SAP UE, we apply similar trick as we used in the derivation of macrocell rate. However, unlike the macrocell, due to the relatively small number of antennas at the SAPs, random matrix theory tools cannot be employed to calculate the rate on a small cell. We therefore use the effective channel distribution as follows:

Lemma 3.3

The downlink rate on a small cell is given by

$$\begin{aligned}&R_{\mathrm s}^{\mathrm {DL}} = \int _0^\infty \!\! \int _0^\infty \! \frac{(1-\zeta _\mathrm b)}{z e^{\sigma ^2 z} \ln 2} \, \left( 1-\frac{1}{\left( 1+z P_{\mathrm {st}}t^{-1} / K_{\mathrm {s}}\right) ^{\varDelta _\mathrm s}}\right) \exp \left( - \frac{2 \pi ^2 \tilde{\lambda _\mathrm {u}} P_{\mathrm {ut}}^{\frac{2}{\alpha }} \mathbb {E}[S_{\mathrm {D}}^{\frac{2}{\alpha }}] z^{\frac{2}{\alpha }} }{\alpha \sin \left( \frac{2 \pi }{\alpha }\right) } \right) \nonumber \\&\times \exp \left( - \tau _{\mathrm {s}}a_\mathrm {s}\, \mathscr {C}_{\alpha , K_{\mathrm {s}}}\! \left( z P_{\mathrm {st}}, t \right) \left( \frac{z P_{\mathrm {st}}}{K_{\mathrm {s}}}\right) ^\delta - \tau _{\mathrm {m}}a_\mathrm {m}\, \mathscr {C}_{\alpha , K_{\mathrm {m}}}\! \left( z P_{\mathrm {st}}, t \right) \left( \frac{z P_{\mathrm {mt}}}{K_{\mathrm {m}}} \right) ^\delta \right) f_{L_\mathrm {s}}(t) dt dz, \end{aligned}$$

(3.16)

where $\varDelta _\mathrm s = M_{\mathrm {s}}- K_\mathrm s + 1$, and $f_{L_\mathrm s}(t)$ is given as

$$\begin{aligned} f_{L_\mathrm s}(t)&= G_\mathrm {s} \delta t^{\delta - 1} \exp \left( - G_\mathrm s t^\delta \right) ,~t \ge 0 \end{aligned}$$

(3.17)

with $G_\mathrm s = a_\mathrm {s} + a_\mathrm {m} \left( {P_{\mathrm {mt}}}/{P_{\mathrm {st}}}\right) ^{\delta }$.

Following a similar approach as the one in Lemma 3.2, we can obtain the uplink rate on a small cell.

Lemma 3.4

The uplink rate on a small cell is given by

$$\begin{aligned} R_{\mathrm s}^{\mathrm {UL}} =&\! \int _0^\infty \! \frac{(1-\zeta _\mathrm b)}{z e^{\sigma ^2 z} \ln 2} \left[ 1 - \int _0^\infty \!\!\!\! \frac{f_{L_{\mathrm {s}}}(t) dt}{\left( 1 \!+\! z P_{\mathrm {ut}}/ t\right) ^{\varDelta _\mathrm {s}}} \right] \exp \left\{ - \tilde{\lambda }_{\mathrm {u}} \pi \mathbb {E}[S_{\mathrm {D}}^{\delta }] \int _0^\infty \!\! \frac{1-e^{-G_\mathrm {s} z }}{1 + z^{-1} u^{\frac{1}{\delta }}/P_{\mathrm {ut}}} du \right. \nonumber \\&- \left. \frac{ \varGamma \left( 1+\delta \right) \delta \pi ^2 z^\delta }{\sin (\delta \pi )} \left[ \frac{ \tau _{\mathrm {s}}a_\mathrm {s} P_{\mathrm {st}}^\delta \prod _{i=1}^{K_{\mathrm {s}}-1} (i+\delta ) }{\varGamma (K_{\mathrm {s}}) K_{\mathrm {s}}^\delta } + \frac{ \tau _{\mathrm {m}}a_\mathrm {m} P_{\mathrm {mt}}^\delta \prod _{i=1}^{K_{\mathrm {m}}-1} (i+\delta ) }{\varGamma (K_{\mathrm {m}}) K_{\mathrm {m}}^\delta } \right] \right\} dz.\qquad \end{aligned}$$

(3.18)

The proof of Lemmas 3.3 and 3.4 can be found in [55].

Fig. 3.4

Comparison of the simulations and numerical results for macrocell downlink rate

Now, it remains to derive the downlink and uplink rates on the wireless backhaul. In the communication between MBS and SAP, each end of the transmission link involves multiple antennas. For this scenario, it has been shown that using block diagonalization (BD) is the optimal way to achieve capacity. However, there are no closed form expression is available for the rate achievable by BD. To this end, we treat each antenna of SAPs as an individual UE, and use ZF at the MBS to do the precoding/decoding. Although ZF is suboptimal compared to the BD, we will show by Fig. 3.4 that the rate gap between these two transmission schemes is limited, and that the rates under BD and ZF follow a similar trend. Therefore, our findings on the energy efficiency tradeoffs remain valid irrespective of the scheme used. In the following, we present the uplink and downlink rate of the wireless backhaul, and then show the simulation comparison to confirm the above claim.

Lemma 3.5

The downlink rate on the wireless backhaul is given by

$$\begin{aligned} R_\mathrm b ^{\mathrm {DL}}&= \frac{\zeta _\mathrm b M_\mathrm s}{K_\mathrm s} \int _0^\infty \! \int _0^\infty \frac{\left( 1 - e^{- z \nu _\mathrm {b}^{\mathrm {D}} }\right) }{z e^{\sigma ^2 z} \ln 2 } \exp \left( - \tau _{\mathrm {b}} a_\mathrm {b} \mathscr {C}_{\alpha , K_{\mathrm {b}} M_\mathrm {s} }\left( z P_{\mathrm {mb}}, t \right) \left( \frac{z P_{\mathrm {mb}}}{K_{\mathrm {b}}M_\mathrm {s}}\right) ^\delta \right) \nonumber \\&\times \exp \left( - \frac{\varGamma \left( 1+\delta \right) \delta \pi ^2 z^\delta P_{\mathrm {sb}}^\delta }{\sin (\delta \pi ) \varGamma (M_\mathrm {s}) M_{\mathrm {s}}^\delta } \mathbb {E}[S_{\mathrm {B}}^\delta ] (1-\tau _\mathrm {b}) \lambda _{\mathrm {s}}\!\! \prod _{i=1}^{M_\mathrm {s} - 1} (i+\delta ) \right) f_{L_\mathrm {b}}(t) dt dz, \end{aligned}$$

(3.19)

where $a_\mathrm {b} = \lambda _{\mathrm {m}}\pi \mathbb {E}[S_{\mathrm {B}}^{\delta }]$, $f_{L_\mathrm {b}}(t)$ and $\nu _{\mathrm {b}}^{\mathrm {D}}$ are given as

$$\begin{aligned} f_{L_\mathrm b}(t)&= a_\mathrm {b} \delta t^{\delta -1} \exp (- a_\mathrm {b} t^{\delta }),~t>0 \end{aligned}$$

(3.20)

$$\begin{aligned} \nu _{\mathrm {b}}^{\mathrm {D}}&= \frac{P_{\mathrm {mb}} (1-\beta _{\mathrm {b}}) a_{\mathrm {b}}^\delta }{\beta _\mathrm {b} \varGamma (1+ 1 / \delta ) }. \end{aligned}$$

(3.21)

Lemma 3.6

The uplink rate on the wireless backhaul is given by

$$\begin{aligned}&R_{\mathrm {b}}^{\mathrm {UL}} = \frac{\zeta _\mathrm b M_\mathrm s}{K_\mathrm s} \int _0^\infty \!\!\! \int _0^\infty \! \frac{\left( 1 - e^{-z \nu _{\mathrm {b}}^{\mathrm {U}} / t } \right) }{z e^{\sigma ^2 z} \ln 2} \exp \left\{ - \frac{\tau _{\mathrm {b}} a_{\mathrm {b}} \varGamma (1\!+\!\delta ) \delta \pi ^2 P_{\mathrm {mb}}^{\delta } z^{\delta } \prod _{i=1}^{K_{\mathrm {b}} M_{\mathrm {s}} - 1 }\! \left( i+\delta \right) }{\sin (\delta \pi ) \left( M_{\mathrm {s}} K_\mathrm {b} \right) ^{\delta } \varGamma \left( M_{\mathrm {s}} K_\mathrm {b} \right) } \right\} \nonumber \\&\times \exp \left\{ - \left( 1 \!-\! \tau _{\mathrm {b}}\right) a_{\mathrm {b}} K_{\mathrm {b}}\sum _{n=1}^{M_{\mathrm {s}}} \begin{pmatrix} M_{\mathrm {s}}\\ n\end{pmatrix} \! \int _0^\infty \! \frac{\left( {z u^{-1 / \delta } P_{\mathrm {sb}}}/{ M_{\mathrm {s}}} \right) ^n \left( 1 - e^{- a_{\mathrm {b}} u} \right) }{\left( 1 + {z u^{-1 / \delta } P_{\mathrm {sb}}}/{ M_{\mathrm {s}}} \right) ^{M_{\mathrm {s}}}} du \right\} f_{L_\mathrm {b}}(t) dt dz\qquad \end{aligned}$$

(3.22)

where $\nu _{\mathrm {b}}^{\mathrm {U}} = (1-\beta _{\mathrm {b}}) M_{\mathrm {m}}P_{\mathrm {sb}}$.

In Fig. 3.4 compares the rate on the wireless backhaul under BD and ZF, respectively, with different numbers of SAPs. It can be seen that although ZF achieves a lower rate than BD, the rate gap is limited as the antenna number grows, and the rates under BD and ZF follow a similar trend. Therefore, the conclusions drawn in this paper on the energy efficiency tradeoffs remain valid irrespective of the scheme used.

We can now write the data rate per area in a small cell network with wireless backhaul by combining results from above.

Lemma 3.7

The sum rate per area in a small cell network with wireless backhaul is given by

$$\begin{aligned} \mathscr {R}&= B \Big (K_\mathrm m \lambda _{\mathrm {m}}+ K_\mathrm s \lambda _{\mathrm {s}}\Big ) \Big \{ A_\mathrm m \Big [\tau _{\mathrm {m}}{R}^{\mathrm {DL}}_\mathrm m + (1-\tau _{\mathrm {m}}) {R}^{\mathrm {UL}}_\mathrm m \Big ] \nonumber \\&+ A_\mathrm s \Big [\tau _{\mathrm {s}}\min \Big \{ {R}_{\mathrm s}^{\mathrm {DL}}, {R}_{\mathrm b}^{\mathrm {DL}}\Big \} + (1-\tau _{\mathrm {s}}) \min \Big \{ {R}_{\mathrm s}^{\mathrm {UL}}, {R}_{\mathrm b}^{\mathrm {UL}}\Big \} \Big ]\Big \}, \end{aligned}$$

(3.23)

where B is the total available bandwidth, and ${R}^{\mathrm {DL}}_\mathrm m$, ${R}^{\mathrm {UL}}_\mathrm m$, ${R}_{\mathrm s}^{\mathrm {DL}}$, ${R}_{\mathrm s}^{\mathrm {UL}}$, ${R}_{\mathrm b}^{\mathrm {DL}}$, and ${R}_{\mathrm b}^{\mathrm {UL}}$ are given in (3.11), (3.15), (3.16), (3.18), (3.19), and (3.22), respectively.

Proof

See Appendix “Proof of Lemma 3.7”.

Note that the energy efficiency is obtained as the ratio between the data rate per area and the power consumption per area. We finally obtain the energy efficiency of a heterogeneous network with wireless backhaul, defined as the number of bits successfully transmitted per joule of energy spent.

Theorem 3.1

The energy efficiency $\eta$ of a heterogeneous network with wireless backhaul is given by

$$\begin{aligned} \eta&= \frac{ B \left( K_\mathrm m \lambda _{\mathrm {m}}+ K_\mathrm s \lambda _{\mathrm {s}}\right) }{P_{\mathrm {m}} \lambda _{\mathrm {m}}+ P_\mathrm {s} \lambda _{\mathrm {s}}+ P_\mathrm {b} \lambda _{\mathrm {m}}}\Big ( A_\mathrm m \Big [\tau _{\mathrm {m}}{R}^{\mathrm {DL}}_\mathrm m + (1-\tau _{\mathrm {m}}) {R}^{\mathrm {UL}}_\mathrm m \Big ] \nonumber \\&+ A_\mathrm s \Big [\tau _{\mathrm {s}}\min \Big \{ {R}_{\mathrm s}^{\mathrm {DL}}, {R}_{\mathrm b}^{\mathrm {DL}}\Big \} + (1-\tau _{\mathrm {s}}) \min \Big \{ {R}_{\mathrm s}^{\mathrm {UL}}, {R}_{\mathrm b}^{\mathrm {UL}}\Big \} \Big ]\Big ). \end{aligned}$$

(3.24)

Equation (3.24) quantifies how all the key features of a small cell network, i.e., interference, deployment strategy, and capability of the wireless infrastructure components, affect the energy efficiency when a wireless backhaul is used to forward traffic into the core network. Several numerical results based on (3.24) will be shown in Sect. 3.5 to give more practical insights.

3.5 Numerical Results

In this section, we provide numerical results to show how the energy efficiency is affected by various network parameters and to give insights into the optimal design of a small cell network with wireless backhaul. As an example, we consider two different deployment scenarios, namely, (i) femto cells that consist of a dense deployment of low-power SAPs with a small number of antennas, and (ii) pico cells that have a less dense deployment of larger and more powerful SAPs. We refer to light load and heavy load conditions as the ones of a network with $\beta _\mathrm m = \beta _\mathrm s = \beta _\mathrm b = 0.25$ and $0.9 \le \beta _\mathrm m$, $\beta _\mathrm s$, $\beta _\mathrm b < 1$, respectively. The network is considered to be operating at $2\, \text {GHz}$, with path loss exponent set to $\alpha = 3.8$ to model an urban scenario, the shadowing $S_{\text {B}}$ and $S_{\text {D}}$ are set to be lognormal distributed as $S_{\text {B}} = 10^{\frac{X_{\mathrm {B}}}{10}}$ and $S_{\text {D}} = 10^{\frac{X_{\mathrm {D}}}{10}}$, where $X_{\mathrm {B}} \sim N(0, \sigma _{\mathrm {B}}^2)$ and $X_{\mathrm {D}} \sim N(0, \sigma _{\mathrm {D}}^2)$, with $\sigma _{\mathrm {B}} = 3~\mathrm {dB}$ and $\sigma _{\mathrm {D}} = 6~\mathrm {dB}$, respectively [56]. In addition, we equal the backhaul transmit power to the radio access power, i.e., $P_\mathrm {mb}=P_\mathrm {mt}, P_\mathrm {sb} = P_\mathrm {st}$. All other system and power consumption parameters are set as follows: $P_{\mathrm {mt}}= 47.8~\mathrm {dBm}$, for pico cell SAPs $P_{\mathrm {st}}= 30~\mathrm {dBm}$, for femto cell SAP $P_{\mathrm {st}}= 23.7~\mathrm {dBm}$, $P_{\mathrm {ut}}= 17~\mathrm {dBm}$, $P_{\mathrm {ma}} = 1~\mathrm {W}$, for pico cell SAPs $P_{\mathrm {sa}} = 0.8~\mathrm {W}$, for femto cell SAP $P_{\mathrm {sa}} = 0.8~\mathrm {W}$, $P_{\mathrm {ua}} = 0.1~ \mathrm {W}$ [32]; $P_{\mathrm {mf}} = 225~\text {W}$, for pico cell SAPs $P_{\mathrm {sf}} = 7.3~\text {W}$, for femto cell SAPs $P_{\mathrm {sf}} = 5.2~ \text {W}$ [52, 53]; $P_{\mathrm {me}} = 0.1~\text {W}/\text {Gb}$, $P_{\mathrm {md}} = 0.8 \text {W}/\text {Gb}$, $P_{\mathrm {se}} = 0.2~\text {W}/\text {Gb}$, $P_{\mathrm {sd}} = 1.6~\text {W}/\text {Gb}$, $P_{\mathrm {ue}} = 0.3~\text {W}/\text {Gb}$, $P_{\mathrm {md}} = 2.4~\text {W}/\text {Gb}$ [43].

Fig. 3.5

Effect of network load on energy efficiency: a Energy efficiency of a small cell network that uses pico cells and femto cells, respectively, versus fraction of bandwidth $\zeta _\mathrm b$ allocated to the backhaul, under different load conditions; and b Optimal fraction of bandwidth to be allocated to the backhaul versus load on the backhaul, for various values of the number of UEs per SAP, $K_{\text {s}}$

Results from Fig. 3.5 illustrate the effect of network load on the energy efficiency. Particularly, we compare the energy efficiency of small cell networks that use pico cells and femto cells in Fig. 3.5a, under various load conditions and for different portions of the bandwidth allocated to the wireless backhaul. The figure shows that femto cell and pico cell deployments exhibit similar performance in terms of energy efficiency. Moreover, Fig. 3.5a shows that the energy efficiency of the network is highly sensitive to the portion of bandwidth allocated to the backhaul, and that there is an optimal value of $\zeta _\mathrm b$ which maximizes the energy efficiency. This optimal value of $\zeta _\mathrm b$ is not affected by the network infrastructure, i.e., it is the same for pico cells and femto cells. However, the optimal $\zeta _{\mathrm {b}}$ increases as the load on the network increases. In fact, when more UEs associate with each SAPs, more data need to be forwarded from MBSs to SAPs through the wireless backhaul in order to meet the rate demand. In summary, the figure shows that irrespective of the deployment strategy, an optimal backhaul bandwidth allocation that depends on the network load can be highly beneficial to the energy efficiency of a small cell network.

In Fig. 3.5b, we plot the optimal value $\zeta _\mathrm b^*$ for the fraction of bandwidth to be allocated to the backhaul as a function of the load on the backhaul $\beta _\mathrm b$. We consider femto cell deployment for three different values of the number of UEs per SAP, $K_{\text {s}}$. Consistently with Fig. 3.5a, this figure shows that the optimal fraction of bandwidth $\zeta _{\mathrm b}^*$ to be allocated to the wireless backhaul increases as $\beta _{\mathrm b}$ or $K_{\text {s}}$ increase, since the load on the wireless backhaul becomes heavier and more resources are needed to meet the data rate demand.

Fig. 3.6

Energy efficiency of a small cell network that uses pico cells and femto cells, respectively, versus power allocated to the backhaul, under different load conditions

In Fig. 3.6, the energy efficiency of the small cell network is plotted as a function of the MBS transmit power under different deployment strategies and load conditions. From the figure we can see that there is an optimal value for the transmit power, and this is given by a tradeoff between the data rate that the wireless backhaul can support and the power consumption incurred. Under spatial multiplexing, the data rate of the network is affected by the number of scheduled UEs per base station antenna, which we denote as the network load. As a consequence, the network load highly affects the data rate, and in turn affects the energy efficiency.

Fig. 3.7

Energy efficiency versus number of SAPs per MBS under various bandwidth allocation schemes

In Fig. 3.7, we plot the energy efficiency of the small cell network versus the number of SAPs per MBS. We consider four scenarios: (i) optimal bandwidth allocation, where the fraction of bandwidth $\zeta _{\mathrm b}$ for the backhaul is chosen as the one that maximizes the overall energy efficiency; (ii) proportional bandwidth allocation, where the fraction of bandwidth allocated to the backhaul is equal to the fraction of load on the backhaul, i.e., $\zeta _\mathrm b = \frac{K_{\mathrm {b}}K_{\mathrm {s}}}{K_{\mathrm {m}}+ K_{\mathrm {b}}K_{\mathrm {s}}}$ [35]; (iii) fixed bandwidth allocation, where the bandwidth is equally divided between macro- and small-cell links and wireless backhaul, i.e., $\zeta _\mathrm b = 0.5$; and (iv) one-tier cellular network, where no SAPs or wireless backhaul are used at all, and all the bandwidth is allocated to the macro cell link, i.e., $\zeta _\mathrm b = 0$. Figure 3.7 shows that in a two-tier small cell network there is an optimal number of SAPs associated to each MBS via the wireless backhaul that maximizes the energy efficiency. Such number is given by a tradeoff between the data rate that the SAPs can provide to the UEs and the total power consumption. This figure also indicates that a two-tier small cell network with wireless backhaul can be less energy efficient than a single tier cellular network if the wireless backhaul is not supported well. However, when the backhaul bandwidth is optimally allocated, the small cell network can achieve a significant gain over a one-tier deployment in terms of energy efficiency.

3.6 Concluding Remarks

In this chapter, we undertook an analytical study for the energy-efficient design of small cell network with a wireless backhaul. By combining stochastic geometry and random matrix theory, we developed a framework that is general and accounts for uplink and downlink transmissions, spatial multiplexing, and resource allocation between radio access links and backhaul. The framework allows to explicitly characterize the power consumption of the small cell network due to the signal processing operations in macro cells, small cells, and wireless backhaul, as well as the data rates and ultimately the energy efficiency of the whole network.

Our results revealed that, irrespective of the deployment strategy, it is critical to control the network load in order to maintain a high energy efficiency. Moreover, a two-tier small cell network with wireless backhaul can achieve a significant energy efficiency gain over a one-tier deployment, as long as the bandwidth division between radio access links and wireless backhaul is optimally designed.

Appendix

Proof of Lemma 3.1

The channel matrix between a MBS to its $K_{\mathrm {m}}$ associated UEs can be written as $\hat{\mathbf {H}} = \mathbf {L}^{\frac{1}{2}} \mathbf {H}$, where $\mathbf {L} = \text {diag}\{L_1^{-1}, \ldots , L_{K_\mathrm m}^{-1}\}$, with $L_i = r_i^\alpha / S_i$ being the path loss from the MBS to its ith UE, where $r_i$ is the corresponding distance and $S_i$ denotes the shadowing, $\mathbf {H} = [\mathbf {h}_1,\ldots ,\mathbf {h}_{K_\mathrm m}]^{\text {T}}$ is the $K_\mathrm m \times M_\mathrm m$ small-scale fading matrix, with $\mathbf {h}_i \sim {CN}\left( \mathbf {0}, \mathbf {I}\right)$. The ZF precoder is then given by $\mathbf {W} = \xi \hat{\mathbf {H}}^{*} ( \hat{\mathbf {H}}\hat{\mathbf {H}}^{*})^{-1}$, where $\xi ^2 = 1 / \text {tr}[ (\hat{\mathbf {H}}^{*}\hat{\mathbf {H}})^{-1}]$ normalizes the transmit power [56]. In the following, we use the notation $\varPhi ^{\mathrm {U}}$ as $\varPhi ^{\mathrm {D}}$ to denote the subsets of $\varPhi$ that transmit in uplink and downlink, respectively, we further denote $\mathscr {U}_x$ as the set of UEs that are associated with access point x, and denote $\hat{x}$ as the transmitter that locates closest to the origin. Since the locations of MBSs and SAPs follow a stationary PPP, we can apply the Slivnyark’s theorem [54], which implies that it is sufficient to evaluate the SINR of a typical UE at the origin. As such, by noticing that under dynamic TDD, every wireless link experiences interference from the downlink transmitting MBSs and SAPs, and from the uplink transmitting UEs, the downlink SINR between a typical UE at the origin and its serving MBS can be written as

$$\begin{aligned} \gamma _{\mathrm m}^{\text {DL}} = \dfrac{P_{\mathrm {mt}}\vert \mathbf {h}_{\hat{x}_{\mathrm {m}},o}^{*} \mathbf {w}_{\hat{x}_{\mathrm {m}},o} \vert ^2 L_{\hat{x}_{\mathrm {m}},o}^{-1} }{I_{\mathrm {oc}}^{\mathrm {mu}} + I_\mathrm u + \sigma ^2}, \end{aligned}$$

(3.25)

where $\mathbf {h}_{\hat{x}_{\mathrm {m}},o}$ is the small-scale fading, $\mathbf {w}_{\hat{x}_{\mathrm {m}},o}$ is the ZF precoding vector, $L_{\hat{x}_{\mathrm {m}},o}$ denotes the corresponding path loss, while $I_{\mathrm {oc}}^{\mathrm {mu}}$ is the aggregate interference from other cells to the MBS UE, and $I_\mathrm u$ denotes the interference from UEs, respectively given as follows:

$$\begin{aligned} I_{\mathrm {oc}}^{\mathrm {mu}}&= \sum \limits _{x_\mathrm {m} \in \varPhi _{\text {m}}^{\mathrm {D}} \setminus \hat{x}_{\mathrm {m}}} \dfrac{P_{\mathrm {mt}}g_{x_\mathrm {m},o}}{ K_\mathrm m L_{x_{\mathrm {m}},o}} + \sum \limits _{x_\mathrm {s} \in \varPhi _{\text {s}}^{\mathrm {D}}} \dfrac{P_{\mathrm {st}}g_{x_\mathrm {s},o}}{ K_\mathrm s L_{x_{\mathrm {s}},o} } \end{aligned}$$

(3.26)

and

$$\begin{aligned} I_\mathrm u&= \sum \limits _{x_{\mathrm {u}} \in \varPhi _{\text {u}}^{\mathrm {U}} } \dfrac{P_{\mathrm {ut}}\vert h_{x_{\mathrm {u}},o} \vert ^2}{L_{x_{\mathrm {u}},o} }, \end{aligned}$$

(3.27)

whereas $g_{x_\mathrm {m},o}$ and $g_{x_\mathrm {s},o}$ represent the effective small-scale fading from the interfering MBS $x_\mathrm {m}$ and SAP $x_\mathrm {s}$ to the origin, respectively, given by [57]

$$\begin{aligned} g_{x_\mathrm {m},o} = \sum _{u \in \mathscr {U}_{x_\mathrm {m}}} K_{\mathrm {m}}\vert \mathbf {h}_{x_\mathrm {m},o}^{*} \mathbf {w}_{x_\mathrm {m},u} \vert ^2 \sim \varGamma \left( K_{\mathrm {m}}, 1\right) \end{aligned}$$

(3.28)

and

$$\begin{aligned} g_{x_\mathrm {s},o} = \sum _{u \in \mathscr {U}_{x_\mathrm {s}}} K_{\mathrm {s}}\vert \mathbf {h}_{x_\mathrm {s},o}^{*} \mathbf {w}_{x_\mathrm {s},u} \vert ^2 \sim \varGamma \left( K_{\mathrm {s}}, 1\right) . \end{aligned}$$

(3.29)

By conditioning on the interference, when $K_{\mathrm {m}}, M_{\mathrm {m}}\rightarrow \infty$ with $\beta _{\mathrm m} = K_{\mathrm {m}}/ M_{\mathrm {m}}< 1$, the SINR under ZF precoding converges to [39]

$$\begin{aligned} \gamma _{\mathrm m }^{\text {DL}} \rightarrow \bar{\gamma }_{\mathrm m }^{\text {DL}} = \dfrac{P_{\mathrm {mt}}M_{\mathrm {m}}}{\left( I_{\mathrm {oc}}^{\mathrm {mu}} + I_\mathrm u + \sigma ^2\right) \sum _{j=1}^{K_{\mathrm {m}}} {e}_j^{-1}}, \,\,\, a.s. \end{aligned}$$

(3.30)

where ${e}_i$ is the solution of the fixed point equation

$$\begin{aligned} \dfrac{L_{\hat{x}_{\mathrm {m}},u_i}^{-1}}{{e}_i} = 1 + \dfrac{J}{M_{\mathrm {m}}},~i = 1, 2, \ldots , K_{\mathrm {m}}\end{aligned}$$

(3.31)

with $J = \sum _{j=1}^{K_{\mathrm {m}}} {L_{\hat{x}_{\mathrm {m}},u_j}^{-1}}{{e}_j^{-1}}$. By summing (3.31) over i we obtain

$$\begin{aligned} J = K_{\mathrm {m}}+ \frac{K_{\mathrm {m}}}{M_{\mathrm {m}}}J. \end{aligned}$$

(3.32)

Solving the equation above results in $J=K_{\mathrm {m}}M_{\mathrm {m}}/ (M_{\mathrm {m}}- K_{\mathrm {m}})$, and by substituting the value of J into (3.31) we can have

$$\begin{aligned} \dfrac{1}{\bar{e}_i} = \frac{M_{\mathrm {m}}}{M_{\mathrm {m}}-K_{\mathrm {m}}} \cdot L_{\hat{x}_{\mathrm {m}},u_i}, \end{aligned}$$

(3.33)

which substituted into (3.30) yields

$$\begin{aligned} \bar{\gamma }_{\mathrm m }^{\text {DL}} = \dfrac{ \left( 1 - \beta _{\mathrm m} \right) M_{\mathrm {m}}P_{\mathrm {mt}}}{\left( I_{\mathrm {oc}}^{\mathrm {mu}} + I_\mathrm u + \sigma ^2\right) \sum ^{K_{\mathrm {m}}}_{j=1} L_{\hat{x}_{\mathrm {m}},u_j}}.\qquad \end{aligned}$$

(3.34)

Notice that $\{L_{\hat{x}_{\mathrm {m}},u_j}\}_{j=1}^{K_{\mathrm {m}}}$ is an independent i.i.d. sequence with finite first moment, given by

$$\begin{aligned} \mathbb {E} \left[ L_{\hat{x}_{\mathrm {m}},u_j} \right] = \varGamma \left( 1 + \frac{1}{\delta }\right) G_\mathrm {m}^{-1} < \infty , \end{aligned}$$

by applying the strong law of large numbers (SLLN) to (3.34), we have

$$\begin{aligned} \bar{\gamma }_{\mathrm m }^{\text {DL}} \rightarrow \frac{ \left( 1 - \beta _{\mathrm m} \right) G_\mathrm {m}^{1/ \delta } P_{\mathrm {mt}}}{\beta _{\mathrm m} \varGamma \left( 1 + \frac{1}{\delta }\right) \left( I_{\mathrm {oc}}^{\mathrm {mu}} + I_\mathrm u + \sigma ^2\right) }, \quad a.s. \end{aligned}$$

(3.35)

As such, using the continuous mapping theorem and the lemma in [58], we can compute the ergodic rate as

$$\begin{aligned} \mathbb {E}\left[ \log _2\left( 1+\bar{\gamma }_{\mathrm m }^{\text {DL}}\right) \right]&= \frac{1}{\ln 2}\mathbb {E}\left[ \ln \left( 1+\frac{\nu _{\mathrm {m}}^{\mathrm {D}}}{I_{\mathrm {oc}}^{\mathrm {mu}} + I_\mathrm u + \sigma ^2}\right) \right] \nonumber \\&= \int _0^\infty \frac{e^{-\sigma ^2 z}}{z \ln 2} \left( 1 - e^{-\nu _\mathrm {m}^{\mathrm {D}} z} \right) \mathbb {E}\left[ e^{-z I_{\mathrm {u}}}\right] \mathbb {E}\left[ e^{-z I_{\mathrm {oc}}^{\mathrm {mu}}}\right] dz. \end{aligned}$$

(3.36)

Due to the composition of independent PPPs and the displacement theorem [59], the interference $I_{\text {u}}$ follows a homogeneous PPP with spatial density $\tilde{\lambda }_{\text {u}} = \left( 1-\tau _{\mathrm {m}}\right) \lambda _{\mathrm {m}} K_{\mathrm {m}}+ \left( 1-\tau _{\mathrm {s}}\right) \lambda _{\mathrm {s}}K_{\mathrm {s}}$, and the corresponding Laplace transform is given as [54]

$$\begin{aligned} \mathbb {E} \left[ e^{-z I_{\text {u}}} \right] = \exp \left( - \dfrac{2 \pi ^2 \tilde{\lambda }_{\text {u}} \mathbb {E}[S_{\mathrm {D}}^{\frac{2}{\alpha }}] P_{\mathrm {ut}}^{\frac{2}{\alpha }} z^{\frac{2}{\alpha }}}{\alpha \sin \left( \frac{2 \pi }{\alpha } \right) } \right) . \end{aligned}$$

(3.37)

As for the Laplace transform of $I_{\mathrm {oc}}^{\mathrm {mu}}$, the conditional Laplace transform on $L_{\hat{x}_{\mathrm {m}},o}$ can be computed as

$$\begin{aligned}&\mathbb {E}\left[ e^{-z I_{\mathrm {oc}}^{\mathrm {mu}}} | L_{\hat{x}_{\mathrm {m}},o} = t\right] \nonumber \\&= \exp \! \left( - \tau _{\mathrm {m}}a_\mathrm {m} \mathscr {C}_{\alpha , K_{\mathrm {m}}} \! \left( z P_{\mathrm {mt}}, t \right) \! \left( \frac{z P_{\mathrm {mt}}}{K_{\mathrm {m}}} \right) ^{\delta } \!\!- \tau _{\mathrm {s}}a_\mathrm {s} \mathscr {C}_{\alpha , K_{\mathrm {s}}} \! \left( z P_{\mathrm {mt}}, t \right) \! \left( \frac{z P_{\mathrm {st}}}{K_{\mathrm {s}}} \right) ^{\delta } \right) . \end{aligned}$$

(3.38)

Notice that $L_{\hat{x}_{\mathrm {m}},o}$ has its distribution given by (3.13), and the rate $R_{\mathrm {m}}^{\mathrm {DL}}$ given as

$$\begin{aligned} R_{\mathrm {m}}^{\mathrm {DL}} = \left( 1 - \zeta _{\mathrm {b}} \right) \mathbb {E}\left[ \log _2\left( 1+\bar{\gamma }_{\mathrm m }^{\text {DL}}\right) \right] , \end{aligned}$$

(3.39)

substituting (3.37) and (3.38) into (3.36), and decondition $L_{\hat{x}_{\mathrm {m}},o}$ with respect to (3.13) we have the corresponding result.

Proof of Lemma 3.2

Let us consider a UE transmitting in uplink to a typical MBS located at the origin, which employs a ZF receive filter $\mathbf {r}_{o,\hat{x}_{\mathrm {u}}}^* = \hat{\mathbf {h}}_{o,\hat{x}_{\mathrm {u}}}^* ( \sum _{u \in \mathscr {U}_o } \hat{\mathbf {{h}}}_{o,u} \hat{\mathbf {h}}_{o,u}^{*} )^{-1}$ [56], the SINR is then given by

$$\begin{aligned} \gamma _{\mathrm {m}}^{\text {UL}} = \dfrac{P_{\mathrm {ut}}L_{o,\hat{x}_\mathrm {u}}^{-1} \vert \mathbf {r}_{o,\hat{x}_\mathrm {u}}^{*} \mathbf {h}_{o,\hat{x}_\mathrm {u}} \vert ^2}{ \left( I_{\mathrm {oc}}^{\mathrm {mbs}} + I_\mathrm u + \sigma ^2 \right) \Vert \mathbf {r}_{o,\hat{x}_\mathrm {u}} \Vert ^2 }, \end{aligned}$$

(3.40)

where $I_{\mathrm {oc}}^{\mathrm {mbs}}$ denotes the interference from other cells received at the MBS. By conditioning on the interference, when $K_{\mathrm {m}}, M_{\mathrm {m}}\rightarrow \infty$ with $\beta _\mathrm m = K_{\mathrm {m}}/ M_{\mathrm {m}}< 1$, the SINR above converges to [39]

$$\begin{aligned} \gamma _{\mathrm m}^{\text {UL}} \rightarrow \bar{\gamma }_{\mathrm m}^{\text {UL}} = \frac{P_{\mathrm {ut}}M_{\mathrm {m}}(1-\beta _\mathrm m) L_{o,\hat{x}_{\mathrm {u}}}^{-1} }{I_{\mathrm {oc}}^{\mathrm {mbs}} + I_\mathrm u + \sigma ^2}, \quad a.s. \end{aligned}$$

(3.41)

By using the continuous mapping theorem [58], the uplink ergodic rate can be calculated as

$$\begin{aligned} \mathbb {E}\left[ \log _2\left( 1 + \bar{\gamma }_{\mathrm {m}}^{\mathrm {UL}} \right) \right]&= \frac{1}{\ln 2} \mathbb {E}\left[ \ln \left( 1 + \frac{\nu _{\mathrm {m}}^{\mathrm {U}} L_{o,x_\mathrm {u}}^{-1} }{ I_{\mathrm {oc}}^{\mathrm {mbs}} + I_{\mathrm {u}} + \sigma ^2 } \right) \right] \nonumber \\&= \int _0^\infty \!\!\! \int _0^\infty \frac{e^{-\sigma ^2 z}}{z \ln 2} \left( 1 - e^{-z \nu _{\mathrm {m}}^{\mathrm {U}}/t } \right) \mathbb {E}\left[ e^{- z I_{\mathrm {u}}} \right] \mathbb {E}\left[ e^{-z I_{\mathrm {oc}}^{\mathrm {mbs}} } \right] f_{L_{\mathrm {m}}}(t) dz dt. \end{aligned}$$

(3.42)

The Laplace transform of $I_{\mathrm {oc}}^{\mathrm {mbs}}$ can be computed as

$$\begin{aligned}&\mathbb {E}\left[ e^{-z I_{\mathrm {oc}}^{\mathrm {mbs}} } \right] \nonumber \\&= \exp \! \left( - \frac{ \varGamma \! \left( 1 \!+\! \delta \right) \delta \pi ^2 z^\delta }{\sin (\delta \pi )} \left[ \frac{ \tau _{\mathrm {m}}a_\mathrm {m} P_{\mathrm {mt}}^\delta \prod _{i=1}^{K_{\mathrm {m}}-1} (i\!+\!\delta ) }{\varGamma (K_{\mathrm {m}}) K_{\mathrm {m}}^\delta } \! + \! \frac{ \tau _{\mathrm {s}}a_\mathrm {s} P_{\mathrm {st}}^\delta \prod _{i=1}^{K_{\mathrm {s}}-1} (i\!+\!\delta ) }{\varGamma (K_{\mathrm {s}}) K_{\mathrm {s}}^\delta }\right] \right) . \end{aligned}$$

(3.43)

On the other hand, to consider the uplink interference from UEs, we use the result in [60] where the path loss from MBS UEs and SAP UEs are modeled as two independent inhomogeneous PPP with intensity measure being

$$\begin{aligned} \varLambda _{\mathrm {mu}}^{(\mathrm {m})}(dx)&= \delta a_{\mathrm {m}} x^{\delta -1} \left[ 1 - \exp \left( - G_{\mathrm {m}} x^\delta \right) \right] ,\end{aligned}$$

(3.44)

$$\begin{aligned} \varLambda _{\mathrm {su}}^{(\mathrm {m})}(dx)&= \delta a_{\mathrm {s}} x^{\delta -1} \left[ 1 - \exp \left( - G_{\mathrm {m}} x^\delta \right) \right] . \end{aligned}$$

(3.45)

The Laplace transform of the UE interference can then be calculated as

$$\begin{aligned} \mathbb {E}[e^{-z I_{\mathrm {u}}}]&= \exp \left( - (1-\tau _{\mathrm {m}}) K_{\mathrm {m}}\int _{0}^\infty \frac{\varLambda _{\mathrm {mu}}^{(\mathrm {m})}(dx)}{1 + z^{-1}x/P_{\mathrm {ut}}} - (1-\tau _{\mathrm {s}}) K_{\mathrm {s}}\int _{0}^\infty \frac{\varLambda _{\mathrm {su}}^{(\mathrm {m})}(dx)}{1 + z^{-1} x/P_{\mathrm {ut}}} \right) \nonumber \\&= \exp \left( - \tilde{\lambda }_{\mathrm {u}} \pi \mathbb {E}[S_{\mathrm {D}}^{\delta }] \int _0^\infty \frac{1 - e^{ - G_\mathrm {m} u }}{1 + z^{-1} u^{\frac{1}{\delta }}/P_{\mathrm {ut}}} du \right) . \end{aligned}$$

(3.46)

As such, noticing that

$$\begin{aligned} R_{\mathrm {m}}^{\mathrm {UL}} = \left( 1 - \zeta _{\mathrm {b}} \right) \mathbb {E}\left[ \log _2\left( 1 + \bar{\gamma }_{\mathrm {m}}^{\mathrm {UL}} \right) \right] \end{aligned}$$

(3.47)

the result follows by substituting (3.43) and (3.46) into (3.42).

Proof of Lemma 3.7

The average rate for a typical UE located at the origin is given by

$$\begin{aligned} R = A_\mathrm m R_\mathrm m + A_\mathrm s R_\mathrm s, \end{aligned}$$

(3.48)

where $R_\mathrm m$ and $R_\mathrm s$ are the data rates when the UE associates to a MBS and a SAP, respectively, given by

$$\begin{aligned} R_\mathrm m =\tau _{\mathrm {m}}{R}^{\mathrm {DL}}_\mathrm m + (1 - \tau _{\mathrm {m}}) {R}^{\mathrm {UL}}_\mathrm m \end{aligned}$$

(3.49)

and

$$\begin{aligned} R_\mathrm s = \tau _{\mathrm {s}}\min \left\{ {R}_{\mathrm s}^{\mathrm {DL}} , {R}_{\mathrm b}^{\mathrm {DL}} \right\} + (1 - \tau _{\mathrm {s}}) \min \left\{ {R}_{\mathrm s}^{\mathrm {UL}} , {R}_{\mathrm b}^{\mathrm {UL}} \right\} . \end{aligned}$$

(3.50)

As each MBS and each SAP serve $K_{\mathrm {m}}$ and $K_{\mathrm {s}}$ UEs, respectively, the total density of active UEs is given by $K_\mathrm m \lambda _{\mathrm {m}}+ K_\mathrm s \lambda _{\mathrm {s}}$. Let B be the available bandwidth, the sum rate per area is obtained as $\mathscr {R} = \left( K_\mathrm m \lambda _{\mathrm {m}}+ K_\mathrm s \lambda _{\mathrm {s}}\right) B R$. Lemma 3.7 then follows from Lemmas 3.1 to 3.6 and by the continuous mapping theorem.