Kinematics Analysis of a New Type 3T1R PM

Abstract

A new type of four degree of freedom (DOF) symmetric parallel mechanism (PM) with Schönflies motion is proposed based on the topological structure synthesis. The type synthesis process of the PM is carried out by using the theory of POC set. The new mechanism possesses the properties of folding characteristic, extensibility and large coverage of workspace in XY plane. The forward kinematics is solved by Sylvester’s dialytic elimination in Maple. This research has certain theoretical significance for the synthesis and analysis of the other PM.

1 Introduction

The PM has been widely concerned and studied since it is proposed, for the reasons that it has the characteristics of simple structure, high rigidity, high bearing capacity, high positioning accuracy and easy to control [1], and it is widely used in the field of assembly line, parallel machine tool, flight simulators and so on. The research of the PM is mainly focus on the process sectors of assembly line like high speed capture, precise positioning assembly and material handling. Therefore, some important efforts have been carried out in recent years on new type of 3T1R-PM. In 1999, a new kind of 3T1R PM suit for the industrial handling is proposed by L Rolland [2]. A new 3T1R PM is proposed by Jin Qiong [3] based on the theory of Single Open Chain. Another novel PM with Schönflies motion has been proposed high-speed pick-and-place manipulation in industrial lines in 2015 by Xie Fugui [4].

In this paper, a branch is added to the original Delta PM based on the theory of POC set to construct a novel 3T1R PM. The 3T1R PM proposed is different from the Delta PM which is invented by Clavel [5] in 1988, and can realize the Schönflies motion. The new PM possesses spatial folding characteristics and planar extensibility, and also it takes a small motion space in z direction.

The paper is organized as follows. The type synthesis of 3T1R PM is given in Sect. 2. The kinematic analysis is carried out in Sect. 3. The example analysis of the new mechanism’s forward kinematics is carried out in Sect. 4, and 4 real solutions of the example are obtained. Finally, conclusions are drawn in Sect. 5.

2 Type Synthesis of PM

2.1 Design Requirements and the Expected Output Matrix of PM

The expected motion, which the mechanism should realize, is a 4 DOF motion of three-dimension translation and one-dimension rotation, the POC set of the PM should be derived as $M_{{P_{a} }} = \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} } \\ \end{array} } \right]$. The methodology of position and orientation characteristic sets and its relevant definition in this paper can be referred to Ref. [6] (Fig. 1).

Fig. 1.

The mechanism sketch of 3T1R PM

2.2 The SOC Branches’ Structure Type of the PM

In order to achieve a PM with symmetric and simple structure, there is only one driving pair in each branch and all the branches set to be the same. The POC set of each SOC branch [7] is $M_{i} = \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right]_{i} ,\left( {i = 1,2,3,4} \right)$, according to the POC set theory [8], each branch consists of two revolute joints R _i1, R _i4, and a parallel quadrilateral connecting rod, which is equivalent as HSOC{-R _i1||R(−P ^(4R))||R _i4-}, then the branch combination scheme of 3T1R PM is denoted by 4-HSOC{-R ⁱ¹||R(−P ^(4R))||R _i4-}.

2.3 PM Synthesis with the Output Motion Characteristic Matrix

• 1) The POC sets of each branch end.

  The POC sets of SOC_i (i = 1,2,3,4) branch is $M_{i} = \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right]_{1}$

• 2) The POC sets of the PM.

  Substitute the POC matrix of each branch into formula $M_{{p_{a} }} = \cap_{i = 1}^{v + 1} M_{{b_{i} }}$ [9], then the POC sets of the PM is obtained.

  $$ M_{{P_{a} }} = \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right] \cap \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right] \cap \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right] \cap \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right] \Rightarrow \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} } \\ \end{array} } \right] $$

  Where the symbol ⇒ represents the POC set on the left side of the equation is to be obtained by intersection operation of all the POC sets on the right side of the equation.

2.4 The DOF Analysis of the PM

The POC set of the moving platform is constrained by the DOF (degrees of freedom) of the mechanism, so to analyze whether the DOF of the PM can meet the design demand (DOF = 4) is necessary.

• (1) The number of independent displacement equation ξ _{L i} .

  According to the formula [10] of the number of the independent loop ξ _Li, The first independent loop ξ _L1, which consists of branch I and II:

  $$ \xi_{{L_{i} }} = \dim_{\boldsymbol{\cdot}} \left\{ {\sum\limits_{i = 1}^{2} {M_{{b_{i} }} } } \right\} = \dim_{\boldsymbol{\cdot}} \left\{ {\left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right] \cup \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} (\parallel R)} \\ \end{array} } \right]} \right\} = \dim_{\boldsymbol{\cdot}} \left\{ {\left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{1} } \\ \end{array} } \right]} \right\} = 4 $$

  In the same way, ξ _L2 = 4, ξ _L3 = 4,

• (2) The calculation of the PM’s DOF.

  After the parallelogram mechanism in the PM has been equivalently transformed, there are 12 revolute joints and 4 translation pairs, the total number of the kinematic pairs is 16. There are three basic loops in the mechanism, The first one is the spatial loop -R ₁₁||R ₁₂(−P ^(4R))||R ₁₃ R ₂₁||R ₂₂(−P ^(4R))||R ₂₃-, the second and third branches can be denoted by -R ₃₁||R ₃₂(−P ^(4R))||R ₃₃-, and -R ₄₁||R ₄₂(−P ^(4R))||R ₄₃- respectively, so ξ _L1 = 4, ξ _L2 = 4 and ξ _L3 = 4. By using the formula of DOF [11], we can obtain:

  $$ F = \sum\limits_{i = 1}^{m} {f_{i} } - \sum\limits_{j = 1}^{v} {\xi_{{L_{j} }} } = 16 - 3 * 4 = 4 $$

  (1)

• Where m—the number of kinematic pairs

• f _i—the DOF of the ith kinematic pair

• v—the number of the independent loops

• ξ _Li—the number of the independent loop of the jth basic loop

According to the DOF analysis of the mechanism above, the degree of freedom of the 3T1R PM can meet the design requirement (Fig. 2).

Fig. 2.

The mechanism sketch of the equivalent 3T1R PM

2.5 Coupling Degree of the PM’s BKC

The coupling degree [12] indicates complexity of the kinematic and dynamic problem of multi-loop BKC, and it can be regarded as one of the indexes for selecting optimal structure type of topological design of mechanism, so the analysis of the PM’s coupling degree is given based on the formula [6]:

$$ \left\{ {\begin{array}{*{20}l} {\Delta_{j} = m_{j} - I_{j} - \xi_{{L_{j} }} } \hfill \\ {\kappa = \frac{1}{2}\min\nolimits_{\boldsymbol{\cdot}} \left\{ {\left( {\sum\limits_{j = 1}^{\nu } {\left| {\Delta_{j} } \right|} } \right)} \right\}} \hfill \\ \end{array} } \right. $$

(2)

• Where m _i—the number of the jth SOC’s kinematic pair

• f _i—the DOF of the ith kinematic pair

• I _j—the number of the jth SOC’s driving pair

• ξ _Li—the number of the independent loop of the jth basic loop

So, we can obtain that Δ₁ = 2>0, Δ₂ = −1 < 0, Δ₃ = −1 < 0. It means the first SOC can add the DOF of the PM by 2, while the second and third SOC can add a constraint to the PM respectively, and reduce the DOF of the PM by 1.

Substitute Δ_i of each SOC into Eq. (2) then we can obtain that κ = 2, so the kinematics and dynamics of the PM need to analyzed based on multi-loops.

2.6 Analysis of Folding Characteristic and Extensibility

In order to ensure that the PM has good spatial retractable characteristics and can be folded when it doesn’t work, the analysis of folding characteristic of the PM should be carried out. And to make sure that the mechanism has a large coverage of working space, the analysis of the mechanism’s extensibility is necessary.

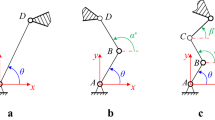
Since the axes of the four revolute joints R _i in the four branches are vertical to the base, and the 3T1R PM has the special geometric characteristics in its dimension, the PM has a spatial folding characteristic and planar extensibility, as is shown in Figs. 3 and 4. The structural sketch of the 3T1R PM in a folding state is shown in Fig. 3. The structural sketch of the 3T1R PM in an extension state is shown in Fig. 4.

Fig. 3.

The structural sketch of the 3T1R PM in a folding state

Fig. 4.

The structural sketch of the 3T1R PM in an extension state

3 Kinematic Analysis of 3T1R PM

3.1 The Establishment of Kinematic Equation

The static and moving coordinate systems are established respectively. The static coordinate system O-XYZ is attached to the base with the X-axis passing through the origin O of the static coordinate system and the center of the revolute joint R ₁₁, and the Y-axis passing through the origin O of the static coordinate system and the center of the revolute joint R ₂₁, The moving coordinate system o’-xyz is attached to the moving platform with the x-axis passing through the origin o’ of the moving coordinate system and the center of the revolute joint R ₁₄, and the y-axis passing through the origin O of the static coordinate system and the center of the revolute joint R ₂₄. The direction of Z-axis and z-axis can be determined by the right hand criterion. Suppose the rotation angle of the four revolute joints R ₁₁, R ₂₁, R ₃₁ and R ₄₁ in base can be denoted by θ _i(i = 1,2,3,4). As is shown in Fig. 6, the circumradius of the base and moving platform are denoted by R and r respectively, the center of revolute joints R _i1, R _i2, R _i3 and R _i4 are denoted by A _i, B _i, C _i and D _i, and the length of each linkage in each branch are denoted by a, b, c (Fig. 5).

Fig. 5.

The mechanism sketch of the 3T1R PM with the coordinate system

The vector expression of each point in the moving coordinate system can be transformed into the static coordinate system according to the transformation matrix of the static and moving coordinates.

$$ \begin{array}{*{20}l} {\overrightarrow {{OA_{i} }} = R\left[ {\begin{array}{*{20}c} {\cos (\tfrac{i - 1}{2}\pi )} \\ {\sin (\tfrac{i - 1}{2}\pi )} \\ 0 \\ \end{array} } \right],} \hfill & \begin{aligned} \overrightarrow {{OB_{i} }} & = \overrightarrow {{OA_{i} }} + \overrightarrow {{A_{i} B_{i} }} \\ & = \left[ {\begin{array}{*{20}c} {R\cos (\tfrac{i - 1}{2}\pi ) - a\cos (\tfrac{i - 1}{2}\pi - \theta_{i} )} \\ {R\sin (\tfrac{i - 1}{2}\pi ) - a\sin (\tfrac{i - 1}{2}\pi - \theta_{i} )} \\ 0 \\ \end{array} } \right], \\ \end{aligned} \hfill & \begin{aligned} \overrightarrow {{OC_{i} }} & = \overrightarrow {{OO^{{\prime }} }} + \overrightarrow {{O^{{\prime }} D_{i} }} + \overrightarrow {{D_{i} C_{i} }} \\ & = \left[ {\begin{array}{*{20}c} {X_{0}^{{\prime }} + r\cos (\alpha + \tfrac{i - 1}{2}\pi )} \\ {Y_{0}^{{\prime }} + r\sin (\alpha + \tfrac{i - 1}{2}\pi )} \\ {Z_{0} ' - c} \\ \end{array} } \right]. \\ \end{aligned} \hfill \\ \end{array} $$

Let $\varphi_{i} = \frac{i - 1}{2}\pi ,(i = 1,2,3,4)$, so that the subsequent derivation process can be simplified, and the vector expressions can be expressed as:

$$ \begin{array}{*{20}l} {\overrightarrow {{OA_{i} }} = R\left[ {\begin{array}{*{20}c} {\cos \varphi_{i} } \\ {\sin \varphi_{i} } \\ 0 \\ \end{array} } \right],} \hfill & {\overrightarrow {{OB_{i} }} = \left[ {\begin{array}{*{20}c} {R\cos \varphi_{i} - a\cos (\varphi_{i} - \theta_{i} )} \\ {R\sin \varphi_{i} - a\sin (\varphi_{i} - \theta_{i} )} \\ 0 \\ \end{array} } \right],} \hfill & {OC_{i} = \left[ {\begin{array}{*{20}c} {X_{0}^{{^{{\prime }} }} + r\cos (\alpha + \varphi_{i} )} \\ {Y_{0}^{{^{{\prime }} }} + r\sin (\alpha + \varphi_{i} )} \\ {Z_{0}^{{^{{\prime }} }} - c} \\ \end{array} } \right]} \hfill \\ \end{array} $$

The vector loop relationship of each branch can be established based on the geometry constraint relationship:

$$ \overrightarrow {{B_{i} C_{i} }} = \overrightarrow {{OC_{i} }} - \overrightarrow {{OB_{i} }} $$

(3)

Since $|\overrightarrow {{B_{i} C_{i} }} | = b$, then the kinematics equation can be expressed as:

$$ \begin{aligned} & & & (X_{0}^{{^{{\prime }} }} + r\cos (\alpha + \varphi_{i} ) - R\cos \varphi_{i} + a\cos (\varphi_{i} - \theta_{i} ))^{2} + (Y_{0}^{{^{{\prime }} }} + r\sin (\alpha + \varphi_{i} ) \\ & \quad & & - R\sin \varphi_{i} + a\sin (\varphi_{i} - \theta_{i} ))^{2} + (Z_{0}^{{^{{\prime }} }} - c)^{2} = b^{2} \\ \end{aligned} $$

(4)

3.2 Inverse Position Problem

The inverse position problem is to obtain the four revolute angle θ _i(i = 1,2,3,4) of driving pairs when the position and orientation parameters X ₀’, Y ₀’, Z ₀’, α are known [13].

Let $D_{i} = X_{0}^{{^{{\prime }} }} + r\cos \left( {\alpha + \varphi_{i} } \right) - R\cos \varphi_{i} ,\quad E_{i} = Y_{0}^{{^{{\prime }} }} + r\sin \left( {\alpha + \varphi_{i} } \right) - R\sin \varphi_{i} ,\quad F = Z_{0}^{{^{{\prime }} }} - c$, then Eq. (4) can be expressed as:

$$ \left( {D_{i} + a\cos (\varphi_{i} - \theta_{i} )} \right)^{2} + \left( {E_{i} + a\sin (\varphi_{i} - \theta_{i} )} \right)^{2} + F^{2} = b^{2} $$

(5)

Expand Eq. (5), then we can obtain:

$$ \begin{aligned} & D_{i}^{2} + E_{i}^{2} + F^{2} + a^{2} - b^{2} + 2aD_{i} \cos (\varphi_{i} - \theta_{i} ) + 2aE_{i} \sin (\varphi_{i} - \theta_{i} ) = 0 \\ & \theta_{i} = \varphi_{i} - 2\arctan \frac{{2aE_{i} \pm \sqrt {4a^{2} (E_{i}^{2} + D_{i}^{2} ) - \left( {D_{i}^{2} + E_{i}^{2} + F^{2} + a^{2} - b^{2} } \right)^{2} } }}{{2aD_{i} + 2aE_{i} }} \\ \end{aligned} $$

Where $D_{i} = X_{0}^{{^{{\prime }} }} + r\cos (\alpha + \varphi_{i} ) - R\cos \varphi_{i}$

$E_{i} = Y_{0}^{{^{{\prime }} }} + r\sin (\alpha + \varphi_{i} ) - R\sin \varphi_{i}$

$F = Z_{0}^{{^{{\prime }} }} - c$

$\varphi_{i} = \frac{i - 1}{2}\pi ,(i = 1,2,3,4),$

3.3 Forward Position Problem

The forward position problem is to obtain the position and orientation parameters X ₀′, Y ₀′, Z ₀′, α, when the four revolute angle θ _i(i = 1,2,3,4) of the driving pairs are known.

According to the projection relationship of the mechanism in the coordinate plane o’-xy, the position equation of the four DOF PM’s moving platform in any time can be obtained.

Let $p_{i} = - R\cos \varphi_{i} + a\cos (\varphi_{i} - \theta_{i} )$, $q_{i} = - R\sin \varphi_{i} + a\sin (\varphi_{i} - \theta_{i} )$, then Eq. (4) can be expressed as:

$$ \left( {X_{0}^{{^{{\prime }} }} + r\cos \left( {\alpha + \varphi_{i} } \right) + p_{i} } \right)^{2} + \left( {Y_{0}^{{^{{\prime }} }} + r\sin \left( {\alpha + \varphi_{i} } \right) + q_{i} } \right)^{2} + \left( {Z_{0}^{{^{{\prime }} }} - c} \right)^{2} = b^{2} $$

(6)

Then the four kinematics equations can be expressed as:

$$ (X_{0'} + r\cos (\alpha + \varphi_{1} ) + p_{1} )^{2} + (Y_{0'} + r\sin (\alpha + \varphi_{1} ) + q_{1} )^{2} + (Z_{0'} - c)^{2} = b^{2} $$

(7)

$$ (X_{0'} + r\cos (\alpha + \varphi_{2} ) + p_{i} )^{2} + (Y_{0'} + r\sin (\alpha + \varphi_{2} ) + q_{2} )^{2} + (Z_{0'} - c)^{2} = b^{2} $$

(8)

$$ (X_{0'} + r\cos (\alpha + \varphi_{3} ) + p_{3} )^{2} + (Y_{0'} + r\sin (\alpha + \varphi_{3} ) + q_{3} )^{2} + (Z_{0'} - c)^{2} = b^{2} $$

(9)

$$ (X_{0'} + r\cos (\alpha + \varphi_{4} ) + p_{4} )^{2} + (Y_{0'} + r\sin (\alpha + \varphi_{4} ) + q_{4} )^{2} + (Z_{0'} - c)^{2} = b^{2} $$

(10)

According to Eqs. (7)–(10), three independent linear equations are obtained by eliminating (Z _o’−c)² and b ² [14]:

$$ \left\{ {\begin{array}{*{20}c} {A_{1} \bullet X_{O'} + B_{1} \bullet Y_{O'} + C_{1} = 0} \\ {A_{2} \bullet X_{O'} + B_{2} \bullet Y_{O'} + C_{2} = 0} \\ {A_{3} \bullet X_{O'} + B_{3} \bullet Y_{O'} + C_{3} = 0} \\ \end{array} } \right. $$

(11)

Where $A_{1} = - 2p_{4} - 2r_{2} \sin \alpha + 2r_{2} \cos \alpha + 2p_{1}$

$A_{2} = 2p_{2} - 2p_{4} - 4r_{2} \sin \alpha$

$A_{3} = - 2p_{4} - 2r_{2} \sin \alpha - 2r_{2} \cos \alpha + 2p_{3}$

$B_{1} = - 2q_{4} + 2r_{2} \sin \alpha + 2r_{2} \cos \alpha + 2q_{1}$

$B_{2} = 4r_{2} \cos \alpha + 2q_{2} - 2q_{4}$

$B_{3} = - 2q_{4} - 2r_{2} \sin \alpha + 2r_{2} \cos \alpha + 2q_{3}$

$C_{1} = 2r_{2} q_{4} \cos \alpha + 2r_{2} p_{1} \cos \alpha - 2r_{2} p_{4} \sin \alpha + 2r_{2} q_{1} \sin \alpha + p_{1}^{2} + q_{1}^{2} - p_{4}^{2} - q_{4}^{2}$

$C_{2} = - 2r_{2} p_{4} \sin \alpha - 2r_{2} p_{2} \sin \alpha + 2r_{2} q_{4} \cos \alpha + 2r_{2} q_{2} \cos \alpha + p_{2}^{2} + q_{2}^{2} - p_{4}^{2} - q_{4}^{2}$

$C_{3} = 2r_{2} q_{4} \cos \alpha - 2r_{2} p_{3} \cos \alpha - 2r_{2} p_{4} \sin \alpha - 2r_{2} q_{3} \sin \alpha + p_{3}^{2} + q_{3}^{2} - p_{4}^{2} - q_{4}^{2}$

By using Sylvester’s dialytic elimination [15], a univariate nonlinear equation in α can be obtained from

$$ \left[ {\begin{array}{*{20}c} {A_{1} } & {B_{1} } & {C_{1} } \\ {A_{2} } & {B_{2} } & {C_{2} } \\ {A_{3} } & {B_{3} } & {C_{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{O'} } \\ {Y_{O'} } \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right] $$

$$ \Rightarrow \left| {\begin{array}{*{20}c} {A_{1} } & {B_{1} } & {C_{1} } \\ {A_{2} } & {B_{2} } & {C_{2} } \\ {A_{3} } & {B_{3} } & {C_{3} } \\ \end{array} } \right| = 0 $$

(12)

Expand Eq. (12) by using the software Maple, then use the half-angle transformation $t = \tan \frac{\alpha }{2},$ $\cos \alpha = \frac{{1 - t^{2} }}{{1 + t^{2} }},$ $\sin \alpha = \frac{2t}{{1 + t^{2} }},$ and multiply the equation by (1 + t ²)², a fourth-degree polynomial equation in s can be obtained:

$$ H_{4} t^{4} + H_{3} t^{3} + H_{2} t^{2} + H_{1} t + H_{0} = 0 $$

(13)

According to Ref. [16], Eq. (13) has a closed-form solution, after the revolute angle α of moving platform is solved, the output parameters of the moving platform can be solved then.

4 Examples Analysis of the Forward Kinematics

Example: as is shown in Fig. 6, the PM’s structure parameters are set as: R = 150 mm, r = 35 mm, a _i = 50 mm, b _i = 102.98 mm, c _i = 77.5 m. The input revolute angle of each drive pair is set as: θ ₁ = −58.16°, θ ₂ = 110.50°, θ ₃ = −10.71°, θ ₄ = −123.89° respectively.

Fig. 6.

The kinematic diagram of the branch

Following the analysis in above sections, 4 real solutions of the example is obtained and listed in Table 1. The 4 configurations corresponding to the real solutions are plotted in Fig. 7.

Table 1. The real solutions of the forward problem

Fig. 7.

Real configurations of the PM

5 Conclusion

• 1. A new type of 3T1R PM is proposed based on the POC set, it can realize the Schönflies motion and can meet the design demand.

• 2. The new 3T1R PM proposed in the paper possesses the properties of folding characteristic, extensibility and large coverage of workspace in XY plane.

• 3. By solving the kinematic equations of the PM, an example with 4 real solution of the forward kinematics are obtained. It provides a certain theoretical basis for the application of the PM in the practical production and processing.