Abstract
A project can be defined as a set of activities. Each activity needs a certain amount of time (that can be variable or even stochastic) and requires different type and quantity of resources (tools, personnel, money, etc.). Also, usually there are additional constraints that affect the scheduling of the activities, such as precedence constraints (for example, an activity cannot start until another one has finished), time constraints (do not start or finish before or later than a certain date) and simultaneously constraints (activities that cannot be done at the same time). In this chapter, different tools for project scheduling will be introduced: graph representation of time and precedence constraints; Gantt chart and load curves; and heuristic and exact algorithms for project scheduling considering different evaluation criteria. Then, a simple case of project scheduling is presented and solved using the described tools, allowing useful comparison between the graph-based approaches and the exact approach of a Mixed Integer Linear Programming (MILP) model implemented in IBM ILOG CPLEX. The implementation and verification procedure followed here allows the enlargement of project applications beyond commercial applications or open literature.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The development of large and complex projects requires specific tools for the planning, scheduling and coordination of a number of activities, tasks, and events, which usually present strong contingence relations among them.
The graph theory and related tools are very useful, namely, the Program Evaluation and Review Technique (PERT) whose key aim is to support activities planning and control, while project optimization is not directly addressed. PERT is often used in research projects where significant uncertainty about data arises. For example, to evaluate the probabilities of satisfying completion dates, to identify bottlenecks, to identify the activities requiring more care in order to maintain the program in time, to evaluate project changes and program alterations.
By other side, the Critical Path Method (CPM) identifies the sequence of activities that shall be strictly within the schedule otherwise the project terminates in tardiness. CPM allows balancing project costs and time slots, assuming the existence of accurate information about activities, their duration, and the inter-relations between activities and costs, therefore allowing project optimization. CPM is widely applied in projects for civil construction, maintenance programs, etc.
To better illustrate the described tools and discuss their application, a simple case of project scheduling is presented. The case is solved either using graph-related tools that are closely related with PERT and CPM methods, or using a MILP model that is computationally implemented. A useful comparison can thus be developed between these two approaches. This chapter is based on lectures, talks and computational lab sessions held during the triennial period 2012–2014, namely, Lusa (2012, 2013) and Miranda (2013, 2014), and so it is the case of project scheduling under analysis.
The structure of the chapter considers: in Sect. 2, basic notions on project scheduling are presented; in Sect. 3, a simple case of project scheduling is described along with the related solution procedures; in Sect. 4, the MILP model associated with the case at hand is presented and implemented in IBM ILOG CPLEX; in Sect. 5, the main conclusions and comments are presented.
2 Basic Notions on the Project Scheduling Problem
The general problem on project scheduling includes the time specification at which each of the activities in a given time horizon must be started. All activities have known or estimated durations, precedence relations and resource requirements.
The project scheduling objectives usually consider minimizing costs, minimizing all activity finishing times, or even balancing the use of the resources. Examples on real world are common, so as building a plant or a warehouse, developing a new product, devising IT projects, automating a production line, establishing new management software, reorganizing a company, and many others.
To improve the project management and control, scheduling priorities are taking in account, namely: establishing total project duration; estimating the resource requirements and when they will be needed; foreseeing financial and outsourcing needs; redistributing activities to balance resource load and consumption; monitoring and controlling time and money.
The project network is the graph representation of activities and events, including the related precedence relations and time constraints. Different types of project network can be developed accordingly with the edges and nodes attribution, in the current case activities are presented by nodes, while edges represent the relations between activities.
The construction of the project network requires information about activities, it is necessary to define completely each activity and the related attributes. They are commonly accepted: identification through a code and activity description; to know accurately the estimated duration, since the activity may be stochastic, or may depend on available resources; the precedence, time and simultaneously constraints; the required resources, their type and amount.
Some relations or constraints impose conditions on the execution of the all set of activities, and common techniques and schemes are applied, such as:
-
Precedence relations between activities, or inter-dependence due to technical factors on different activities are addressed by precedence constraints;
-
Earliest and latest starting dates of activities, due to commitments, to work force, etc., are treated through time constraints;
-
Activities that cannot be executed simultaneously, due to a critical resource or technical factors are represented by simultaneously constraints;
-
Resources availability on staff, technology, materials, money, or others, is emulated using resource constraints.
The precedence and time constraints are very important on project scheduling, since they directly define when activities take place. These constraints directly define the earliest and the latest start time for each activity, respectively:
-
Precedence constraints specify limitations with respect to other activities; for example, on a research project, testing can begin when the prototype is ready (minimum) and final polish must be completed four hours before the end of the thermal treatment (maximum);
-
Time constraints directly indicate minimum and maximum limitations with respect to a schedule; on an agrarian example, pruning cannot begin until 18 November (minimum) and grape picking must end before 15 October (maximum).
Various significant reasons arise to impose the integration of simultaneously constraints. In fact, it is necessary to incorporate information about those activities that need the same critical resource, e.g., activities A and B cannot be executed at the same time. In plus, sometimes activities are performed on the same part of a product or piece, other times activities need the product be put in a different way, e.g., one activity needs the product in one direction and the other in the opposite direction.
The minimum time required to perform all the activities is conditioned by the activities’ duration, and by their precedence, time and simultaneously constraints, as well as by resources’ availability. The representation of precedence constraints through graphs allows to define the time when all activities can end, the activities that are critical (i.e., those activities whose delay causes overall delays), and also the activities that are non-critical.
2.1 Graph Method
The formalization of precedence and time constraints considers the following parameters:
- ti :
-
i activity starting date;
- tj :
-
j activity starting date;
- fi :
-
date when activity i can begin;
- Fi :
-
date on which activity i must have already started;
- aij :
-
minimum time that must elapse between the start of i and the start of j;
- bij :
-
maximum time that can elapse between the start of i and the start of j;
- α:
-
the first node of the project network, the starting event;
- ω:
-
the last node of the project network, the final event.
The minimum time f i and the maximum time F i for the start of each activity i are defining a feasibility time-window for activity i (Fig. 1), but the time that can elapse between the start of activity i and the start of activity j shall be estimated too. In order to cope with the activities duration, the minimum time and the maximum time between the start of two consecutive activities is also necessary (Fig. 2).
From the prior estimates and conjugating with activities duration, the slack time between consecutive activities is calculated and the critical path for the project network is identified. The procedure follows the network forward, and then backward, to obtain orderly for each activity i:
-
Earliest Start Time (EST)—An activity’s EST is the longest path from α to the activity, and can be calculated with Dijkstra or Ford algorithms. In the case that no return edges nor negative values exist, the Ford algorithm gives the solution in just one iteration (EST is calculated from the first node, moving forward on the network and adding the activities duration time; in other words, EST is calculated by supposing the preceding activities are all done at their earliest time);
-
Latest Start Time (LST)—the activity’s LST is EST(ω) minus the longest path from the activity to ω (the final event, again, can be obtained by using the Ford algorithm); LST is calculated from the last node, moving backward and subtracting the duration time of the preceding activities; this means LST is the latest time for the activity start without provoking any delay in the project time completion.
The activity slack, Slack i , indicates the delay activity i can suffer without further implications in the project completion time. For activity i, the slack time is defined by the difference between the associated Latest Start Time and the Earliest Start Time:
Therefore, activities with null slack are critical for the project, because any delay will have implications on project completion time. The suggestion is to focus on the control of critical activities, but without forgetting about “sub-critical” activities.
The burden and the time necessary for these calculations, the large number of activities in the project and the related data, the current situation in modeling and solving large optimization problems, and the need to evaluate project schedules on a daily basis are making crucial the utilization of commercial software and formalized methods.
2.2 Heuristic Methods
Problems formulated with integer or binary variables have significant interest but large instances are very difficult to solve, then heuristics are very often applied to obtain admissible and near-optimal solutions. A heuristic is an approximation procedure, aiming at solutions of satisfactory quality that are obtained in a suitable execution time. However, it should be noted that the heuristic approach is to replace the problem exact solution for an alternative solution.
In comparison with exact methods, heuristic methods allow the treatment of very large problems; they rely on simple empiric concepts, as well as heuristics enable the direct use of problem information. However, heuristics do not guarantee solutions optimality and then the inherent deviation on sub-optimal solutions requires quantification.
In general, heuristics are classified accordingly their main purpose:
-
Constructive heuristics—the initial and inadmissible solution is conjugated with new elements to construct a possible solution;
-
Improvement heuristics—the target is to improve an existing possible solution, e.g., a solution (or group of solutions) that was already obtained by a construction method.
As example cited in Lusa (2012), consider the following pseudo-code for a heuristic method that addresses simultaneous constraints (pairs of activities that cannot be done at the same time and, thus, it must be decided, for each constraint, which activity must precede the other one):
Let N be the number of simultaneously constraints and n the number of already solved constraints;
While n < N do:
For each constraint and for each direction, calculate a lower bound* for T (time at which all activities have finished)
Take the constraint-direction with the largest lower bound and solve it in the opposite direction; n = n + 1
Update ESTi and LSTi values
End while
* Direction i → j: Lower bound = “longest path α-i” + di + “longest path j-ω” = ESTi + di + (T-LSTj) (being di the duration of the activity i)
Various types of construction heuristics can be observed:
-
Greedy heuristics, for example, when the best option in each iteration is selected, not taking into account the subsequent iterations;
-
Random construction, as designated, the solution is set at random; for instance, genetic algorithms consider random alterations as “solutions mutation”;
-
Construction by simplification, when the problem is separated into different modules or sub-problems, for which are either allowed well-known procedures or the special cases results.
A basic greedy heuristic may consist of a simulation in which activities are scheduled according to some priority rule as, for example the shortest duration or the shortest slack.
As example of improvement heuristics, the Burgess and Killebrew algorithm (1962) allows for distributing load and payments leveling. From the same authors, balance heuristic methods are firstly used to avoid overload, but these methods also level the use of resources. This resources attribute overpasses overload avoidance and the search of feasible solutions: when the starting point is already a solution with no overload on resources allocation, then a better and improved solution can be achieved in the feasible solutions space.
Let Δ be the total overload, \(\Delta = \sum\nolimits_{t = 1}^{{t_{\omega } }} {{ \hbox{max} }(0, Required\;resources - Available\;resources)}\)
Define;
Begin with the first activity;
Select the first activity that can be moved without pushing any other activity, and move it to the spot with the lowest Δ value and as far to the right as possible;
Go on to the next activity (after the last one, go back to the first one);
Repeat until Δ = 0 or until it is not possible to move more activities (in the latter case, increase the schedule’s total time —\(t_{\omega }\)— and start again).
Sometimes heuristics are not producing a feasible solution, therefore the integration of different aspects on solution search can be beneficial. Some examples of heuristic procedures that address precedence and resources constraints follow:
-
Use priority rules to build feasible solutions; for example, a greedy algorithm based on building the solution by simulating the execution of the project and selecting the activities to be scheduled (when there are not enough resources to schedule all the activities whose predecessors have finished) according to some priority rule (the shortest activity, the most critical, etc.);
-
Balance load by moving non-critical activities, either on an intuitive, by trial and error or using a formalized procedure such as the Burgess and Killebrew algorithm;
-
Start out with a solution and improve it by exploring new solutions; the current calculation methods make it possible to explore a large number of solutions in short time, and this type of local optimization methods are quite common nowadays.
In fact, Local Search (LS) is a basic tool that starts from a feasible solution, evaluates neighbor feasible solutions with similar structure, and then selects the best neighbor solution according with a specific evaluation function. LS is based on the principle that solutions near optimal solution present also near or similar structures, in despite of being worse solutions. In this method, beyond the definition of the neighborhood structure on search, the evaluation function, the strategy for solution alteration, also the stopping criterion shall be selected. The described LS method allows the introduction of variants, either in the neighborhood search, the alternatives evaluation, or the alterations to be made. The Iterated Local Search (ILS) method arises from the repeated iteration of LS method. ILS combines rapid generation of good solutions with asymptotic convergence to the optimum.
In addition, various alternatives to heuristic methods can be selected, in special if the problem dimension is not too large. For example:
-
To enumerate and evaluate all the combinations, and then to choose the best one; this alternative can be straightforward if the number of simultaneous constraints is small, but for project scheduling it is not the proper choice;
-
To try the Branch-and-Bound method (B&B); this is an enumeration method that guarantees optimality, that is, the exact solution is found when the method terminates (for details, see the contribution of Casquilho and Miranda in this book);
-
To formulate and solve an optimization MILP model; this option is developed later in Sect. 4, using the same case of Project Scheduling that is described in Sect. 3.
3 A Case of Project Scheduling
A simple case of project scheduling is presented based on Lusa (2012), the related data and the solution procedures are described. The application of basic rules and concepts on project scheduling, the description of some sample calculations, they are both supporting the daily utilization of commercial software and the computational implementation of exact algorithms.
The twelve activities (A–L) of a general project and the associated attributes are given in Table 1; For each activity: the duration in weeks; the preceding activities that must be completed before the activity starts; the people required to perform the activity jobs (renewable resources); and finally, the payments incurred in hundred of Euros (non-renewable resources) for each week (while the activity is being executed).
Noting that a person cannot do more than one activity at a time, then the renewable resources (people: AC, MP, RG, BC, RR) shall be strictly assigned to the activities set in non-overlapping mode.
The all set of procedures consider multiple steps, namely, to:
-
1.
Make the precedence’s graph. Compute the Earliest Start Time (EST), the Latest Start Time (LST) and the slack of each activity and determine the critical path.
-
2.
Draw the Gantt and load charts scheduling each activity at its EST.
-
3.
In case the prior schedule is not feasible within the renewable resources (people), determine a feasible schedule by using a heuristic method. Compute the total payment for each period.
-
4.
Modify the schedule found in point 3 with the objective of levelling the use of the non-renewable resources (payments) using the Burgess and Killebrew methods.
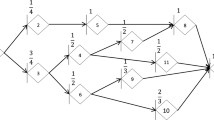
Addressing the first point, the precedence’s graph is constructed by direct observation of the three first columns on Table 1, and specifying the starting event as the network first node, α, at week 0. Thereafter, other nodes follow: activities A and D have no preceding activities; but before starting activity B, firstly activity A shall be completed and it takes 1 week; before starting activity C, activity B shall be completed too and it takes plus 6 weeks, meaning that EST for activity C sums 7 weeks. The same reasoning applies for activities E and I that are only able to start after B completion; and with this on mind the first two columns of Table 2 (the activities and related EST) can be filled in.
The final event or the last node of the project network, ω, occurs at week 23. Activity L has no immediate successors, 1 week duration, and its EST is 22; in plus, activity H also has no immediate successors, the related EST is 19, it takes 3 weeks to be completed, thus activity H is completed at week 22. This way, the project makespan is 23 weeks, corresponding to EST(ω) because activity L is being completed only at week 23.
The LST column is calculated backwards and starting from the network last node, ω, defining LST(ω) = EST(ω) = 23 and subtracting the duration of preceding activities. L duration is 1 week, then LST(L) is 22, but LST(H) is 20 because its duration is 3 weeks. From Table 1, L preceding activities are K, G, and D; their incumbent LST are LST(K) = 21, LST(G) = 19, and LST(D) = 4 because the related activities duration are, respectively, 1, 3, and 18 weeks. Following the same procedure, the LST values for all set of project activities are indicated in the third column of Table 2.
The slack for each activity can be directly calculated on Table 2 by the difference between LST and EST, the related slack times are indicated in the fourth column. The critical path is thus identified by the activities with zero slack, that is, the critical path considers the activities with equal EST and LST and, consequently, they are not tolerating any delay.
Graph representations are key tools for project scheduling because all the relationships between activities are placed in perspective, namely, activities duration, predecessor nodes for each activity, resources availability, that is, the all set of attributes is shown. Graphs and networks are often used to analyze projects and to support the development of PERT and CPM procedures (PERT puts the activities on the edges, while CPM put them on the nodes). The graph representation for the current project network, aggregating EST and LST values in “EST/LST”, and identifying the critical path on dashed line, follows on Fig. 3 (activities are put on the nodes).
Addressing the second point, each activity is scheduled at its EST time in the Gantt chart at Fig. 4. One row is allocated to each activity A–L, the starting and the finishing times the activities in the current project schedule are thus directly indicated. Duration times and the preceding relationships are also integrated, all set of activities attributes are taking in account and thus Gantt charts are very popular on practice.
Moreover, Gantt charts can also be used to evaluate resources’ load and payments schedule, that is, resources utilization can be fully appreciated. Activities overlapping, payments leveling, and further improvements on project scheduling can be supported from chart-based analysis, as described in the following text.
Reminding the definition of people as project’s renewable resource, one row is allocated to each person (AC, MP, RG, BC, RR) in Fig. 4, and the activities each person is required shall be verified from Table 1. For example:
-
Person AC is required in three activities (A, C, and E), and the related starting and finishing times for these activities are directly indicated in the chart; however, 2 activities (C and E) are overlapping weeks 7–9 as shown in the Gantt chart (Fig. 4), then this situation is presented in bold at Fig. 4.
-
Person MP is also required in three activities (A, F, and J), the related starting and finishing times are also indicated; by direct observation of the Gantt Chart, an overlapping situation also arises between 2 activities (F and J) at week 17, and bold line is applied once again.
-
Other overlapping situations are identified with the same verification procedure, namely, for person BC (week 21, activities H and K) and person RR (weeks 7–17, activities D and I).
Figure 4 allows the reader to identify two activities occurring at same time but each person cannot do more than one activity at a time. People unavailability means (renewable) resources unavailability, the identified activities cannot be performed, and the current project schedule is not feasible with the available resources.
Addressing the third point of the current case, a schedule with no overload in the use of the renewable resources (people) shall be established. Usually, a MILP model with the objective of minimizing the makespan is developed, this way avoiding the burden of trial-and-error and repetitive charts-based calculations.
A constructive heuristic aiming at finding a feasible solution can also be developed. The balancing heuristic method presented in Sect. 2.2 (Burgess and Killebrew 1962) is utilized and its reasoning is described in a colloquial manner. Based on a priority rule, the identified activities that need the same critical resource (activities C and E for person AC; activities F and J for person MP; activities H and K for person BC; and finally activities D and I for person RR) are selected; then overload elimination follows a trial-and-error approach that moves activities forward and backwards. For example, initiating the procedure with non-critical activities:
-
Activities C and E cannot be executed at the same time; moving EST(C) to week 10 then overload is avoided for person AC; activity C is not in the critical path and it will terminate at week 19; however the alteration of three weeks is over-passing C slack time (1 week), and the project completion time can be delayed;
-
Activities F and J cannot be executed at the same time; moving EST(J) to week 18 then overload is also avoided for person MP; since activity J is not in the critical path and this alteration of 1 week is equal to its slack time, then activity J becomes also a critical activity; in plus, activity C is preceding J, then J can start only after C is finished, that is, EST(J) is thus 20;
-
Overlapping activities H and K are causing overload for person BC, and this can be avoided by moving EST(K) to week 22; activity K is in the critical path and this alteration will cause 1 week delay on the project completion time;
-
However, activities D and I are overloading person RR, the project schedule becomes feasible by moving EST(I) from week 7 to week 18; activity I is also in the critical path, this alteration will cause a large delay (11 weeks) on the project schedule;
-
In fact, activity I is preceding activities K and L on the critical path and its duration is 14 weeks; activity I finishes at week 31, then EST(K) is 32 and EST(L) is 33.
The other non-critical activities can be accommodated in this larger time for project completion, 34 weeks, and the related Gantt chart with no overload on people is presented in Fig. 5. This project network corresponds to a feasible solution created through a priority rule that preferably selects non-critical activities, since moving critical activities will cause delay on project termination.
From the no overload project schedule on Fig. 5, and revisiting resources data (renewable and non-renewable) from Table 1, the chart on resources load and payment’s schedule is updated and presented in Fig. 6.
Finally addressing the case’s fourth point, the no overload schedule found in point 3 is modified with the objective of levelling the use of the non-renewable resources (payments). Note the feasible project schedule presented in Figs. 5 and 6 is created based on a non-feasible solution with people overload.
At now, an improvement heuristic considers balance load by moving the non-critical activities, either on an intuitive way or by trial and error. Even without overload to distribute, the Burgess and Killebrew procedure is useful since it allows payments levelling. Figure 6 shows larger payments during weeks 10–17, due to the simultaneous occurrence of three activities (C, D, and F). The payments evolution can be smoother, on average about 38.67 €, that is, the total payment (1315 €) divided by the makespan (34 weeks). For example, considering as a measure of payments overload the payments above the average value and from the observation of Figs. 5 and 6:
-
C and J are non-critical activities, and if they are moved forward it is not expected impact on project completion time; Activity C is preceding the activities sequence J, K, and L; then J activity is moved as far to the right as possible, on weeks 29–31 where the payments are at lower level;
-
Thus by the same rationale C can finish at week 28 and start at week 19;
-
H activity can also be moved to the spot with the lowest payments and as far to the right as possible, on weeks 29–31; in the same way, this alteration does not affect the project time;
-
G activity can be performed earlier and after preceding activity F is completed, at week 18 where a lower payment occurs; this alteration avoids that G is performed at same time as C and I, as presented in Fig. 7.
From the Gantt chart with payments leveling on Fig. 7, and revisiting again Table 1 for resources data, the chart on resources load and payment’s schedule is updated in Fig. 8.
Comparison between payment schedules follows in Fig. 9: while the initial approach in graph a presents larger alterations on payments, graph b shows a smoother evolution of payments along the project time horizon. In fact, the observed alterations on payments at graph b are of lower amplitude, and the lower variability is very important for finance planning.
Moreover, this solution concerning payments levelling can be also obtained in a two-steps procedure, by solving two MILP models in sequence: (i) Minimizing makespan; and (ii) Minimizing payments irregularities and ensuring the makespan from first step. Other MILP developments for project scheduling problems are treated by Artigues et al. (2013) and Koné et al. (2011).
4 Project Scheduling: MILP Model
In this section the implementation of a MILP model that focus the project scheduling case is addressed and we are using the implementation of exact algorithms on commercial software to solve it (Miranda 2013, 2014). The IBM ILOG environment is preferred due to its high performance and friendly utilization, and CPLEX solver is widely selected for Linear Programming (LP), Integer Programming (IP) and Constraint Programming (CP) implementations (IBM 2015a, b, c).
The MILP model is based on Pritsker et al. (1969) formulation, the associated nomenclature such as data, variables, and the model are described in below.
Data:
- N :
-
Number of activities to schedule
- Tmax :
-
Upper bound for T (time at which all activities have finished)
- d i :
-
Duration of activity i (i = 1,…,n)
- P i :
-
Set of immediate predecessors of activity i (i = 1,…,n)
- F :
-
Set of activities with no immediate successors
- L i , U i :
-
Lower and upper bound for the starting time of activity i (i = 1,…,n)
- R :
-
Set of types of resources
- A rt :
-
Quantity of resource r available at time t (r ∈ R, t = 1,…,Tmax)
- R ir :
-
Quantity of resource r necessary to perform activity i (r ∈ R, i = 1,…,n)
Variables:
- T :
-
Time at which all activities have finished
- t i :
-
Starting time of activity i (i = 1,…,n)
- y it ∈ {0,1}:
-
Takes value 1 if activity i starts at time t (i = 1,…,n, t = L i ,…,U i )
The objective function minimizes the project time horizon, that is, the time at which all activities have finished, T:
The project time horizon, T, shall consider the starting time, t, and the duration, d, of all the activities, i, with no immediate successors:
In a similar way, the starting times of each activity i shall consider the related starting times and the durations of all the activities j that are occurring immediately before activity i:
The logic-binary restriction on starting times t i is defining one time-value for each activity, i, between the associated lower bound, L i , and upper bound, U i , on starting times. The time-value t is an integer number as follows from the sum restriction:
For each activity i, the binary variables y are defined from a special ordered set with one single element equal to one (1), and all the other binary elements are zero (0). This restriction imposes that one and only one starting time is to be selected for activity i:
The model Project Scheduling is thus conjugating relations 2–6, it aims at the project time horizon minimization and simultaneously considers the restriction on total time, the restrictions set on starting times for all activities, the specification of one integer time-value for each activity, and the associated binary variables specification.
Model Project Scheduling:
subject to
The model can be improved by including other scheduling criteria and/or constraints (risk, uncertainty…) and also integrating other decisions (e.g., payments levelling). Some of these advanced topics are discussed in other parts of this handbook, namely, by Miranda and Casquilho or by Henriques and Coelho.
The implementation procedures are detailed in Miranda (2013, 2014) and the sequential steps are synoptically described in below (the code can be made available for the interested reader upon request).
-
1.
New OPL Project—opening a new workspace for the work at hand, saving dedicated memory and associated files;
-
2.
Create Project—automatically creating files in the workspace, such as, the MILP model, the problem data, and execution configurations; different data and models can be allowed under different execution configurations, for example on stochastic problems;
-
3.
Problem model—in the model file, firstly, sets and parameters are to be sequentially defined; then, in a second step, the positive variables are introduced; finally, after the initialization of all these attributes, the objective function and restrictions of the MILP model are included too;
-
4.
Problem data—in the data file, sets and parameters are specified, then the associated values are introduced; in the case at hand, the activities set, the set of immediate predecessors for each activity, the set of activities with no immediate successors, the upper bound for the project time, the activities duration, and additional data are required;
-
5.
Run the solver—the execution of CPLEX solver follows the default implementation, the usual model and data files are selected;
-
6.
Problem solution—with the proper instruction in the model file, the MILP solution is presented on screen (as in Fig. 10).
By direct observation of Fig. 10, the project completion time is confirmed (T = 23), so as the starting times (ST: activities in alphabetic order) for all the critical activities (in bold line, A-B-I-K-L) in the project schedule. This solution corresponds to the overload schedule presented in the first point of Sect. 3 (Fig. 3), allowing this way a better comparison between the computational procedures and the graphic approaches.
Resources restrictions shall apply during all the project period, and a logic-restrictions set on resources availability is usually included in MILP models. The resources restrictions consider the quantity of resource r necessary to perform activity i, R ir , the associated set of binary variables, y, and the sum of the required resources shall not overpass the quantity of resource available at time t, A rt :
With a sequence of MILPs, not only basic constraints are ensured but also other objectives and types of constraints can be considered. Next to the makespan minimization with no overload on resources (T = 34), a second MILP model is solved to minimize payments within such makespan. Therefore, the results in Fig. 6 and the related developments are also obtained by MILP solving.
5 Conclusions and Final Comments
A simple case of project scheduling is presented, graph-based and heuristics approaches are applied, such as a MILP model is implemented in IBM ILOG CPLEX. The former approaches allow the treatment of small size projects, real world applications on various fields, and they are widely used on practice.
To better provide larger applications, to address uncertainty on activities duration, or even to consider time-cost trade-offs, then commercial software is suggested. Computational implementation of LP or MILP models, friendly software environments, they allow to evaluate different scenarios, to update project data along its time horizon, and also to avoid the burden of step-by-step procedures.
In this sense, to implement a second MILP model to level resources utilization is a challenge that remains open, being the results provided on the final figures. This procedure is well-known, since the computational implementation of mathematical models and the results verification in the open literature allows readers to extend their capabilities beyond either the commercial applications or the bibliographic references.
References
Artigues, C., Brucker, P., Knust, S., Koné, O., Lopez, P., & Mongeau, M. (2013). A note on “event-based MILP models for resource-constrained project scheduling problems”. Computers & Operations Research, 40, 1060–1063.
Burgess, A. R., & Killebrew, J. B. (1962). Variation in activity level on a cyclical arrow diagram. Journal of Industrial Engineering, 13, 76–83.
Koné, O., Artigues, C., Lopez, P., & Mongeau, M. (2011). Event-based MILP models for resource-constrained project scheduling problems. Computers & Operations Research, 38, 3–13.
Lusa, A. (2012). Workshop on project development. In Erasmus Intensive Programme on “Optimization and DSS for SC”, Portalegre Polytechnics Institute, Portalegre, Portugal, July 01–15, 2012.
Lusa, A. (2013). Project development: Integrated aggregate planning. In Erasmus Intensive Programme on “Optimization and DSS for SC”, Portalegre Polytechnics Institute, Portalegre, Portugal, July 07–21, 2013.
Miranda, J. L. (2013). Workshop on Project Development—Lab Session. In Erasmus Intensive Programme on “Optimization and DSS for SC”, Portalegre Polytechnics Institute, Portalegre, Portugal, July 07–21, 2013.
Miranda, J. L. (2014). Workshop on project development. In Erasmus Intensive Programme on “Optimization and DSS for SC”, Portalegre Polytechnics Institute, Portalegre, Portugal, July 06–20, 2014.
IBM ILOG CPLEX Optimization Studio OPL Language User’s Manual. (2015a). © Copyright IBM Corporation 1987. http://www-01.ibm.com/support/knowledgecenter/SSSA5P_12.6.2/ilog.odms.studio.help/pdf/opl_languser.pdf?lang=en
IBM ILOG CPLEX Optimization Studio CPLEX User’s Manual. (2015b). © Copyright IBM Corporation 1987. http://www-01.ibm.com/support/knowledgecenter/SSSA5P_12.6.2/ilog.odms.studio.help/pdf/usrcplex.pdf?lang=en
IBM ILOG CPLEX Optimization Studio CP Optimizer User’s Manual. (2015c). © Copyright IBM Corporation 1987. http://www-01.ibm.com/support/knowledgecenter/SSSA5P_12.6.2/ilog.odms.studio.help/pdf/usrcpoptimizer.pdf?lang=en
Pritsker, A., Watters, L., & Wolfe, P. (1969). Multi-project scheduling with limited resources: A zero-one programming approach. Management Science, 16, 93–108.
Acknowledgments
Authors thank Universitat Politècnica de Catalunya (UPC) and Portalegre Polytechnics Institute (IPP). The presented works are partially developed with the CERENA/IST support on behalf of FCT project UID/ECI/04028/2013. We also thank Samuel Moniz (INESC/UP, CEG/IST/UL) for the support on IBM ILOG CPLEX lab sessions and the chapter reviewers for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this paper
Cite this paper
Lusa, A., de Miranda, J.L. (2017). An Introduction to the Resource Constrained Project Scheduling Problem Solving Techniques. In: Póvoa, A., Corominas, A., de Miranda, J. (eds) Optimization and Decision Support Systems for Supply Chains. Lecture Notes in Logistics. Springer, Cham. https://doi.org/10.1007/978-3-319-42421-7_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-42421-7_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42419-4
Online ISBN: 978-3-319-42421-7
eBook Packages: EngineeringEngineering (R0)