Keywords

1 Introduction

The Set Covering Problem (SCP) is a classic benchmark in the subject of combinatorial optimization that belongs to the NP-complete class of problems [19]. The purpose of the SCP is to find a set of solutions that cover a range of needs at the lowest possible cost. The SCP can be applied to many real-world problems, such are airline crew scheduling [14], network discovery [10], plant location [12], and service allocation [6] among others. Different algorithms have been developed to solve the classic SCP, ranging from classic exact methods to more recent bio-inspired metaheuristics. Exact methods can be applied to solve SCPs [1, 2], the main problem is when the instance size increases the algorithm is commonly unable to reach a solution in a reasonable amount of time. Approximate methods such as the well-known metaheuristics tackle this concern, being capable to generally provide good enough local optimums in a limited time interval. In this context a large list of metaheuristics have been proposed to solve the SCP [4, 5, 8, 9, 17, 20].

In this paper, a new approach for SCPs based on the black hole algorithm is presented. The Black Hole Algorithm (BHA) is a population-based metaheuristic based on the gravitational force that has a black hole to attract everything that is around it. The core of the BHA is enhanced with the incorporation of binarization through transfer and discretization functions in order to handle the binary nature of the SCP. Repairing operators are also employed to rapidly discard the unfeasible solutions and as a consequence to alleviate the search. We present promising results on 40 well-known pre-processed instances from the Beasley’s OR-Library, where a considerable amount of global optimums are reached.

This paper is organized as follows: In Sect. 2, we describe the SCP. Next section presents the BHA including binarization and repairing. Section 4 provides the experimental results, followed by conclusions and future work.

2 The Set Covering Problem

The Set Covering Problem consists in finding a set of solutions at the lowest possible cost to cover a set of needs. Formally, we define the problem as follows: Let \(A=(a_{ij})\) be a binary matrix with \(m\textendash rows \times n\textendash columns\), and let \(C=(c_j)\) be a vector representing the cost of each column j, assuming that \(c_j\) > 0 for \(\left( j \in N\right) \). So we can say that column \(\left( j \in N\right) \) cover a row i that exists in M if \(a_{ij} = 1\). The mathematical model is as follows:

$$\begin{aligned} min\left( z \right) = \sum _{j= 1}^{n}c_j X_j \end{aligned}$$

Subject to:

$$\begin{aligned} \sum _{j=1}^{n} a_{ij}x_j \ge 1 \,\,\,\,\,\,\, \forall i \in M ~~~~~~~~~~~~~~~~~~~~~ x_j = \left\{ \begin{array}{l} 1 \, j\in S\\ 0\,~ if\,~not \\ \end{array} \right. \forall \,j \in N \end{aligned}$$

3 The Black Hole Algorithm

A black hole is a region of space that has so much mass concentrated in it that there is no way for a nearby object to escape its gravitational pull [15]. Anything falling into a black hole, including light, cannot escape. The BHA is inspired on this phenomena [11].

Similar to other population-based metaheuristics, The BHA begins by randomly generating a population of candidate solutions, called stars, which are placed in the search space of some problem or function. After initialization, the fitness values of the population are evaluated and the best candidate, which has the best fitness values is introduced as black hole and the other solutions are selected as normal stars. Then, all the stars commence moving towards the black hole due of the power absorbing of the black hole.

The absorption of stars by the black hole is formulated as follows: \(x_{i} (t+1) = x_{i} + rand * (x_{bh} - x_{i}(t)) \ge 1~for~i = \{1,2,3,\dots ,N\}\). Where \(x_i(t+1)\) is the location of the \(i_{th}\) star at the iteration t+1, Rand is a random number between zero and one, \(x_{bh}\) is the location of the black hole in the search space, and N is the number of solutions (stars). In addition, there is a distance between stars and black hole, the stars that crosses the event horizon of the black hole will be absorbed by the black hole, in carrying out this event another candidate solution (star) is born and distributed randomly in the search space and starts a new iteration, this is known as probability of crossing the event horizon. This is done to keep the number of candidate solutions constant.

The radius of the event horizon in the black hole algorithm is calculated by using the following equation: \(E={f}_{BH} {}/ \sum _{i=1}^{N} {f}_{i}\). Where \(f_{bh}\) is the fitness value of the black hole, \(f_i\) is the fitness value of the \(i_{th}\) star, and N is the number of candidate solutions (stars). When the distance from the black hole with the star is less than the radio, or in other words when the difference in fitness between the black hole and the star is less than the radio, that star is swallowed by the black hole.

3.1 Binarization

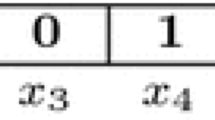
When the star moves toward the black hole, the algorithm generates a real number which must be transformed to a binary domain due to the nature of the problem treated. To this end, we firstly employ a transfer function, which map a real value to a [0, 1] real interval. As transfer function we employ the V-shaped-V4 (Eq. 1), which is was the best-performing one among the 8 tested transfer functions (4 S-shaped and 4 V-shaped) [8, 13]. Then, the resulting value from the transfer function is discretized via the half method depicted in Eq. 2 in order to obtain a binary value.

$$\begin{aligned} ~ T(x) = \left| \frac{2}{\pi } arctan \left( \frac{\pi }{2}x \right) \right| \end{aligned}$$
(1)
$$\begin{aligned} x_i(t+1) = \left\{ \begin{array}{ll} 1 &{} \mathrm {if\ } rand > 0.5 \\ \\ 0 &{} \mathrm {otherwise\ } \end{array} \right. \end{aligned}$$
(2)

3.2 Repairing

The BHA, as most metaheuristics do, generates a random population with solutions that violate the constraints, i.e., solutions holding uncovered rows. Repairing operators are responsible for turning unfeasible solutions on feasible ones. To this end, we incorporate a heuristic operator that achieves the generation of feasible solutions, and additionally eliminates column redundancy [3].

To make all feasible solutions we compute a ratio based on the sum of all the constraint matrix rows covered by a column \(c_j {}/ N_{uc}\), where \(N_{uc}\) is the amount of uncovered columns. The unfeasible solution are repaired by covering the columns of the solution that had the lower ratio. After this, a local optimization step is applied, where column redundancy is eliminated. A column is redundant when it can be deleted and the feasibility of the solution is not affected.

Table 1. Results obtained by BHA for the tested SCP instances.
Full size table

4 Experiment Results

The performance of the proposed black hole algorithm was experimentally evaluated by using 40 preprocessed instances of the SCP from the Beasley’s OR-LibraryFootnote 1. This algorithm has been implemented in Java and the experiments have been launched on a 2.3 Ghz Intel Core i3 with 4 GB RAM machine running Windows 7. We employ an initial population of 20 stars, 4000 iterations and 20 executions per instance. The results are given in Table 1 where column 1 shows the SCP instance, column 2 depicts the best known optimum for the instance, column 3 provides the best optimal value found by the algorithm, while columns 4 and 5 show average of results and the relative percentage deviation, respectively. The relative percentage deviation (RPD) is computed as follows: \( RDP = (Z - Z_{opt}) {}/ Z_{opt} \times 100\), where Z is the best optimum value found by the metaheuristic and \(Z_{opt}\) depicts the best known optimum value for the instance.

Table 2. Results obtained using BHA for instances SCP
Full size table
Table 3. Optimums reached for the 40 instances
Full size table

In Table 2, the proposed approach is compared with three recently reported metaheuristics for the SCP, namely, shuffled frog leaping algorithm (SFLA) [7], XOR-based artificial bee colony (xABC) [16], and a binary firefly algorithm (BFF) [8]. Table 3 depicts the amount of global optimums reached by each algorithm. BHA is able to reach 27 global optimums, while the results for the remaining 13 instances stay very near to the global optimum (RPDs around 1 %). The results also illustrate that BHA greatly outperforms its competitors, which were unable to reach more than 12 optimum values from the 40 tested instances. Let us also note the robustness of the proposed BHA, whose averages for 20 executions remain very close to the best optimum value found.

5 Conclusions

In this paper we have presented a new approach for solving SCPs based on the black hole algorithm. We have incorporated a transfer function and a discretization method in order to handle the binary nature of the problem. Repairing operators are also employed to avoid unfeasible solutions and column redundancy. We have tested 40 non-unicost instances from the Beasley’s OR-Library where the quality of results clearly outperform very recent reported metaheuristics for the SCP. The proposed approach is also robust able to provide averages very near to global optimums. As future work, we plan to test larger instances of the SCP as well as to incorporate adaptive capabilities to the BHA for performing parameter tuning during solving as exhibited in [18].