Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Assume we are given a data matrix \(\mathbf{X} \in \mathbb{R}^{n\times p}\) (n samples of a p-dimensional random variable) and a response vector \(\mathbf{Y} \in \mathbb{R}^{n}\). We assume a linear model for the data where Y = X β +ɛ for some regression coefficient \(\beta \in \mathbb{R}^{p}\) and ɛ i.i.d. mean-zero noise. Fitting a regression model by standard least squares or ridge regression requires \(\mathcal{O}(np^{2})\) or \(\mathcal{O}(\,p^{3})\) flops. In the situation of large-scale (n, p very large) or high dimensional ( p ≫ n) data these algorithms are not applicable without having to pay a huge computational price.

Using a random projection, the data can be “compressed” either row- or column-wise. Row-wise compression was proposed and discussed in [7, 15, 19]. These approaches replace the least-squares estimator

$$\displaystyle{ \mathop{\mathop{\mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{p}}\|\mathbf{Y} -\mathbf{X}\gamma \|_{ 2}^{2}\qquad \mbox{ with the estimator }\qquad \mathop{\mathop{\mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{p}}\|\boldsymbol{\psi }\mathbf{Y} -\boldsymbol{\psi }\mathbf{X}\gamma \|_{ 2}^{2}, }$$
(1)

where the matrix \(\boldsymbol{\psi }\in \mathbb{R}^{m\times n}\) (m ≪ n) is a random projection matrix and has, for example, i.i.d. \(\mathcal{N}(0,1)\) entries. Other possibilities for the choice of \(\boldsymbol{\psi }\) are discussed below. The high dimensional setting and ℓ 1-penalized regression are considered in [19], where it is shown that a sparse linear model can be recovered from the projected data under certain conditions. The optimization problem is still p-dimensional, however, and computationally expensive if the number of variables is very large.

Column-wise compression addresses this later issue by reducing the problem to a d-dimensional optimization with d ≪ p by replacing the least-squares estimator

$$\displaystyle{ \mathop{\mathop{\mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{p}}\|\mathbf{Y} -\mathbf{X}\gamma \|_{ 2}^{2}\qquad \mbox{ with the estimator }\qquad \boldsymbol{\phi }\;\mathop{\mathop{\mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{d}}\|\mathbf{Y} -\mathbf{X}\boldsymbol{\phi }\gamma \|_{ 2}^{2}, }$$
(2)

where the random projection matrix is now \(\boldsymbol{\phi }\in \mathbb{R}^{p\times d}\) (with d ≪ p). By right multiplication to the data matrix X we transform the data matrix to \(\mathbf{X}\boldsymbol{\phi }\) and thereby reduce the number of variables from p to d and thus reducing computational complexity. The Johnson–Lindenstrauss Lemma [5, 8, 9] guarantees that the distance between two transformed sample points is approximately preserved in the column-wise compression.

Random projections have also been considered under the aspect of preserving privacy [3]. By pre-multiplication with a random projection matrix as in (1) no observation in the resulting matrix can be identified with one of the original data points. Similarly, post-multiplication as in (2) produces new variables that do not reveal the realized values of the original variables.

In many applications the random projection used in practice falls under the class of Fast Johnson–Lindenstrauss Transforms (FJLT) [2]. One instance of such a fast projection is the Subsampled Randomized Hadamard Transform (SRHT) [17]. Due to its recursive definition, the matrix–vector product has a complexity of \(\mathcal{O}(\,p\log (\,p))\), reducing the cost of the projection to \(\mathcal{O}(np\log (\,p))\). Other proposals that lead to speedups compared to a Gaussian random projection matrix include random sign or sparse random projection matrices [1]. Notably, if the data matrix is sparse, using a sparse random projection can exploit sparse matrix operations. Depending on the number of non-zero elements in X, one might prefer using a sparse random projection over an FJLT that cannot exploit sparsity in the data. Importantly, using \(\mathbf{X}\boldsymbol{\phi }\) instead of X in our regression algorithm of choice can be disadvantageous if X is extremely sparse and d cannot be chosen to be much smaller than p. (The projection dimension d can be chosen by cross validation.) As the multiplication by \(\boldsymbol{\phi }\) “densifies” the design matrix used in the learning algorithm the potential computational benefit of sparse data is not preserved.

For OLS and row-wise compression as in (1), where n is very large and p < m < n, the SRHT (and similar FJLTs) can be understood as a subsampling algorithm. It preconditions the design matrix by rotating the observations to a basis where all points have approximately uniform leverage [7]. This justifies uniform subsampling in the projected space which is applied subsequent to the rotation in order to reduce the computational costs of the OLS estimation. Related ideas can be found in the way columns and rows of X are sampled in a CUR-matrix decomposition [12]. While the approach in [7] focuses on the concept of leverage, McWilliams et al. [15] propose an alternative scheme that allows for outliers in the data and makes use of the concept of influence [4]. Here, random projections are used to approximate the influence of each observation which is then used in the subsampling scheme to determine which observations to include in the subsample.

Using random projections column-wise as in (2) as a dimensionality reduction technique in conjunction with (ℓ 2 penalized) regression has been considered in [10, 11, 13]. The main advantage of these algorithms is the computational speedup while preserving predictive accuracy. Typically, a variance reduction is traded off against an increase in bias. In general, one disadvantage of reducing the dimensionality of the data is that the coefficients in the projected space are not interpretable in terms of the original variables. Naively, one could reverse the random projection operation by projecting the coefficients estimated in the projected space back into the original space as in (2). For prediction purposes this operation is irrelevant, but it can be shown that this estimator does not approximate the optimal solution in the original p-dimensional coefficient space well [18]. As a remedy, Zhang et al. [18] propose to find the dual solution in the projected space to recover the optimal solution in the original space. The proposed algorithm approximates the solution to the original problem accurately if the design matrix is low-rank or can be sufficiently well approximated by a low-rank matrix.

Lastly, random projections have been used as an auxiliary tool. As an example, the goal of McWilliams et al. [16] is to distribute ridge regression across variables with an algorithm called Loco. The design matrix is split across variables and the variables are distributed over processing units (workers). Random projections are used to preserve the dependencies between all variables in that each worker uses a randomly projected version of the variables residing on the other workers in addition to the set of variables assigned to itself. It then solves a ridge regression using this local design matrix. The solution is the concatenation of the coefficients found from each worker and the solution vector lies in the original space so that the coefficients are interpretable. Empirically, this scheme achieves large speedups while retaining good predictive accuracy. Using some of the ideas and results outlined in the current manuscript, one can show that the difference between the full solution and the coefficients returned by Locois bounded.

Clearly, row- and column-wise compression can also be applied simultaneously or column-wise compression can be used together with subsampling of the data instead of row-wise compression. In the remaining sections, we will focus on the column-wise compression as it poses more difficult challenges in terms of statistical performance guarantees. While row-wise compression just reduces the effective sample size and can be expected to work in general settings as long as the compressed dimension m < n is not too small [19], column-wise compression can only work well if certain conditions on the data are satisfied and we will give an overview of these results. If not mentioned otherwise, we will refer with compressed regression and random projections to the column-wise compression.

The structure of the manuscript is as follows: We will give an overview of bounds on the estimation accuracy in the following Sect. 2, including both known results and new contributions in the form of tighter bounds. In Sect. 3 we will discuss the possibility and properties of variance-reducing averaging schemes, where estimators based on different realized random projections are aggregated. Finally, Sect. 4 concludes the manuscript with a short discussion.

2 Theoretical Results

We will discuss in the following the properties of the column-wise compressed estimator as in (2), which is defined as

$$\displaystyle{ \hat{\beta }_{d}^{\boldsymbol{\phi }}\; =\;\boldsymbol{\phi }\;\mathop{\mathop{ \mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{d}}\|\mathbf{Y} -\mathbf{X}\boldsymbol{\phi }\gamma \|_{ 2}^{2}, }$$
(3)

where we assume that ϕ has i.i.d. \(\mathcal{N}(0,1/d)\) entries. This estimator will be referred to as the compressed least-squares estimator (CLSE) in the following. We will focus on the unpenalized form as in (3) but note that similar results also apply to estimators that put an additional penalty on the coefficients β or γ. Due to the isotropy of the random projection, a ridge-type penalty as in [11, 16] is perhaps a natural choice. An interesting summary of the bounds on random projections is, on the other hand, that the random projection as in (3) already acts as a regularization and the theoretical properties of (3) are very much related to the properties of a ridge-type estimator of the coefficient vector in the absence of random projections.

We will restrict discussion of the properties mostly to the mean-squared error (MSE)

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}\big[\mathbb{E}_{\varepsilon }(\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2})\big]. }$$
(4)

First results on compressed least squares have been given in [13] in a random design setting. It was shown that the bias of the estimator (3) is of order \(\mathcal{O}(\log (n)/d)\). This proof used a modified version of the Johnson–Lindenstrauss Lemma. A recent result [10] shows that the log(n)-term is not necessary for fixed design settings where Y = X β +ɛ for some \(\beta \in \mathbb{R}^{p}\) and ɛ is i.i.d. noise, centred \(\mathbb{E}_{\varepsilon }[\varepsilon ] = 0\) and with the variance \(\mathbb{E}_{\varepsilon }[\varepsilon \varepsilon '] =\sigma ^{2}I_{n\times n}\). We will work with this setting in the following.

The following result of [10] gives a bound on the MSE for fixed design.

Theorem 1 ([10])

Assume fixed design and Rank(X) ≥ d. Then

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}\big[\mathbb{E}_{\varepsilon }(\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2})\big]\; \leq \;\sigma ^{2}d + \frac{\|\mathbf{X}\beta \|_{2}^{2}} {d} +\mathop{ \mathrm{trace}}\nolimits (\mathbf{X}^{{\prime}}\mathbf{X})\frac{\|\beta \|_{2}^{2}} {d}. }$$
(5)

Proof

See Appendix.

Compared with [13], the result removes an unnecessary \(\mathcal{O}(\log (n))\) term and demonstrates the \(\mathcal{O}(1/d)\) behaviour of the bias. The result also illustrates the tradeoffs when choosing a suitable dimension d for the projection. Increasing d will lead to a 1∕d reduction in the bias terms but lead to a linear increase in the estimation error (which is proportional to the dimension in which the least-squares estimation is performed). An optimal bound can only be achieved with a value of d that depends on the unknown signal and in practice one would typically use cross validation to make the choice of the dimension of the projection.

One issue with the bound in Theorem 1 is that the bound on the bias term in the noiseless case (Y = X β)

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}\big[\mathbb{E}_{\varepsilon }(\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2})\big]\; \leq \frac{\|\mathbf{X}\beta \|_{2}^{2}} {d} +\mathop{ \mathrm{trace}}\nolimits (\mathbf{X}^{{\prime}}\mathbf{X})\frac{\|\beta \|_{2}^{2}} {d} }$$
(6)

is usually weaker than the trivial bound (by setting \(\hat{\beta }_{d}^{\boldsymbol{\phi }} = 0\)) of

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}\big[\mathbb{E}_{\varepsilon }(\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2})\big]\; \leq \|\mathbf{X}\beta \|_{ 2}^{2} }$$
(7)

for most values of d < p. By improving the bound, it is also possible to point out the similarities between ridge regression and compressed least squares.

The improvement in the bound rests on a small modification in the original proof in [10]. The idea is to bound the bias term of (4) by optimizing over the upper bound given in the foregoing theorem. Specifically, one can use the inequality

$$\displaystyle\begin{array}{rcl} & & \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\boldsymbol{\phi }(\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\boldsymbol{\phi })^{-1}\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\beta \|_{ 2}^{2}]]\; {}\\ & & \quad \leq \;\min _{\hat{\beta }\in \mathbb{R}^{p}}\;\mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\boldsymbol{\phi }\boldsymbol{\phi }^{{\prime}}\hat{\beta }\|_{ 2}^{2}]], {}\\ & & {}\\ \end{array}$$

instead of

$$\displaystyle\begin{array}{rcl} & & \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\boldsymbol{\phi }(\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\boldsymbol{\phi })^{-1}\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\beta \|_{ 2}^{2}]]\; {}\\ & & \quad \leq \; \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\boldsymbol{\phi }\boldsymbol{\phi }^{{\prime}}\beta \|_{ 2}^{2}]]. {}\\ \end{array}$$

To simplify the exposition we will from now on always assume we have rotated the design matrix to an orthogonal design so that the Gram matrix is diagonal:

$$\displaystyle{ \varSigma = \mathbf{X}^{{\prime}}\mathbf{X} = \text{diag}(\lambda _{ 1},\ldots,\lambda _{p}). }$$
(8)

This can always be achieved for any design matrix and is thus not a restriction. It implies, however, that the optimal regression coefficients β are expressed in the basis in which the Gram matrix is orthogonal, this is the basis of principal components. This will turn out to be the natural choice for random projections and allows for easier interpretation of the results.

Furthermore note that in Theorem 1 we have the assumption Rank(X) ≥ d, which tells us that we can apply the CLSE in the high dimensional setting p ≫ n as long as we choose d small enough (smaller than Rank(X), which is usually equal to n) in order to have uniqueness.

With the foregoing discussion on how to improve the bound in Theorem 1 we get the following theorem:

Theorem 2

Assume Rank(X) ≥ d, then the MSE (4) can be bounded above by

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2}]] \leq \sigma ^{2}d +\sum _{ i=1}^{p}\beta _{ i}^{2}\lambda _{ i}w_{i} }$$
(9)

where

$$\displaystyle{ w_{i} = \frac{(1 + 1/d)\lambda _{i}^{2} + (1 + 2/d)\lambda _{i}\mathop{ \mathrm{trace}}\nolimits (\varSigma ) +\mathop{ \mathrm{trace}}\nolimits (\varSigma )^{2}/d} {(d + 2 + 1/d)\lambda _{i}^{2} + 2(1 + 1/d)\lambda _{i}\mathop{ \mathrm{trace}}\nolimits (\varSigma ) +\mathop{ \mathrm{trace}}\nolimits (\varSigma )^{2}/d}. }$$
(10)

Proof

See Appendix.

The w i are shrinkage factors. By defining the proportion of the total variance observed in the direction of the ith principal component as

$$\displaystyle{ \alpha _{i} = \frac{\lambda _{i}} {\mathop{\mathrm{trace}}\nolimits (\varSigma )}, }$$
(11)

we can rewrite the shrinkage factors in the foregoing theorem as

$$\displaystyle{ w_{i} = \frac{(1 + 1/d)\alpha _{i}^{2} + (1 + 2/d)\alpha _{i} + 1/d} {(d + 2 + 1/d)\alpha _{i}^{2} + 2(1 + 1/d)\alpha _{i} + 1/d}. }$$
(12)

Analyzing this term shows that the shrinkage is stronger in directions of high variance compared to directions of low variance. To explain this relation in a bit more detail we compare it to ridge regression. The MSE of ridge regression with penalty term λ ∥ β ∥ 2 2 is given by

$$\displaystyle{ \mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\beta ^{\mathrm{Ridge}}\|_{ 2}^{2}] =\sigma ^{2}\sum _{ i=1}^{p}\Big( \frac{\lambda _{i}} {\lambda _{i}+\lambda }\Big)^{2} +\sum _{ i=1}^{p}\beta _{ i}^{2}\lambda _{ i}\Big( \frac{\lambda } {\lambda +\lambda _{i}}\Big)^{2}. }$$
(13)

Imagine that the signal lives on the space spanned by the first q principal directions, that is β i  = 0 for i > q. The best MSE we could then achieve is σ 2 q by running a regression on the first q first principal directions. For random projections, we can see that we can indeed reduce the bias term to nearly zero by forcing w i  ≈ 0 for i = 1, …, q. This requires d ≫ q as the bias factors will then vanish like 1∕d. Ridge regression, on the other hand, requires that the penalty λ is smaller than the qth largest eigenvalue λ q (to reduce the bias on the first q directions) but large enough to render the variance factor λ i ∕(λ i +λ) very small for i > q. The tradeoff in choosing the penalty λ in ridge regression and choosing the dimension d for random projections is thus very similar. The number of directions for which the eigenvalue λ i is larger than the penalty λ in ridge corresponds to the effective dimension and will yield the same variance bound as in random projections. The analogy between the MSE bounds (9) for random projections and (13) for ridge regression illustrates thus a close relationship between compressed least squares and ridge regression or principal component regression, similar to Dhillon et al. [6].

Instead of an upper bound for the MSE of CLSE as in [10, 13], we will in the following try to derive explicit expressions for the MSE, following the ideas in [10, 14] and we give a closed form MSE in the case of orthonormal predictors. The derivation will make use of the following notation:

Definition 1

Let \(\boldsymbol{\phi }\in \mathbb{R}^{p\times d}\) be a random projection. We define the following matrices:

$$\displaystyle\begin{array}{rcl} \boldsymbol{\phi }_{d}^{\mathbf{X}} =& \boldsymbol{\phi }(\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\boldsymbol{\phi })^{-1}\boldsymbol{\phi }^{{\prime}}\in \mathbb{R}^{p\times p}\quad \text{and}\quad T_{ d}^{\boldsymbol{\phi }} = \mathbb{E}_{\boldsymbol{\phi }}[\boldsymbol{\phi }_{ d}^{\mathbf{X}}] = \mathbb{E}_{\boldsymbol{\phi }}[\boldsymbol{\phi }(\boldsymbol{\phi }^{{\prime}}\mathbf{X}^{{\prime}}\mathbf{X}\boldsymbol{\phi })^{-1}\boldsymbol{\phi }^{{\prime}}] \in \mathbb{R}^{p\times p}.& {}\\ \end{array}$$

The next Lemma [14] summarizes the main properties of \(\boldsymbol{\phi }_{d}^{\mathbf{X}}\) and \(T_{d}^{\boldsymbol{\phi }}\).

Lemma 1

Let \(\boldsymbol{\phi }\in \mathbb{R}^{p\times d}\) be a random projection. Then

  1. (i)

    \((\boldsymbol{\phi }_{d}^{\mathbf{X}})^{{\prime}} =\boldsymbol{\phi }_{ d}^{\mathbf{X}}\) (symmetric),

  2. (ii)

    \(\boldsymbol{\phi }_{d}^{\mathbf{X}}\mathbf{X}^{{\prime}}\mathbf{X}\boldsymbol{\phi }_{d}^{\mathbf{X}} =\boldsymbol{\phi }_{ d}^{\mathbf{X}}\) (projection),

  3. (iii)

    if Σ = X ′ X is diagonal ⇒ \(T_{d}^{\boldsymbol{\phi }}\) is diagonal.

Proof

See Marzetta et al. [14].

The important point of this lemma is that when we assume orthogonal design then \(T_{d}^{\boldsymbol{\phi }}\) is diagonal. We will denote this by

$$\displaystyle{ T_{d}^{\boldsymbol{\phi }} =\mathrm{ diag}(1/\eta _{ 1},\ldots,1/\eta _{p}), }$$

where the terms η i are well defined but without an explicit representation.

A quick calculation reveals the following theorem:

Theorem 3

Assume Rank(X) ≥ d, then the MSE (4) equals

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2}]] =\sigma ^{2}d +\sum _{ i=1}^{p}\beta _{ i}^{2}\lambda _{ i}\Big(1 -\frac{\lambda _{i}} {\eta _{i}}\Big). }$$
(14)

Furthermore we have

$$\displaystyle{ \sum _{i=1}^{p}\frac{\lambda _{i}} {\eta _{i}} = d. }$$
(15)

Proof

See Appendix.

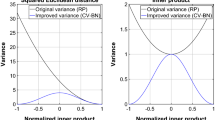
By comparing coefficients in Theorems 2 and 3, we obtain the following corollary, which is illustrated in Fig 1:

Fig. 1
figure 1

Numerical simulations of the bounds in Theorems 2 and 3. Left: the exact factor (1 −λ 1∕η 1) in the MSE is plotted versus the bound w 1 as a function of the projection dimension d. Right: the exact factor (1 −λ p ∕η p ) in the MSE and the upper bound w p . Note that the upper bound works especially well for small values of d and for the larger eigenvalues and is always below the trivial bound 1

Full size image

Corollary 1

Assume Rank(X) ≥ d, then

$$\displaystyle{ \forall i \in \{ 1,\ldots,p\}:\,\,\, 1 -\frac{\lambda _{i}} {\eta _{i}} \leq w_{i} }$$
(16)

As already mentioned in general we cannot give a closed form expression for the terms η i in general. However, for some special cases (26) can help us to get to an exact form of the MSE of CLSE. If we assume orthonormal design (Σ = CI p×p ), then we have that λ i ∕η i is a constant for all i and and thus, by (26), we have η i  = Cp∕d. This gives

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}^{\boldsymbol{\phi }}\|_{ 2}^{2}]] =\sigma ^{2}d + C\sum _{ i=1}^{p}\beta _{ i}^{2}\Big(1 -\frac{d} {p}\Big), }$$
(17)

and thus we end up with a closed form MSE for this special case.

Providing the exact mean-squared errors allows us to quantify the conservativeness of the upper bounds. The upper bound has been shown to give a good approximation for small dimensions d of the projection and for the signal contained in the larger eigenvalues.

3 Averaged Compressed Least Squares

We have so far looked only into compressed least-squares estimator with one single random projection. An issue in practice of the compressed least-squares estimator is its variance due to the random projection as an additional source of randomness. This variance can be reduced by averaging multiple compressed least-squares estimates coming from different random projections. In this section we will show some properties of the averaged compressed least-squares estimator (ACLSE) and discuss its advantage over the CLSE.

Definition 2

(ACLSE) Let \(\{\boldsymbol{\phi }_{1},\ldots,\boldsymbol{\phi }_{K}\}\, \in \mathbb{R}^{p\times d}\) be independent random projections, and let \(\hat{\beta }_{d}^{\boldsymbol{\phi }_{i}}\) for all i ∈ { 1, …, K} be the respective compressed least-squares estimators. We define the averaged compressed least-squares estimator (ACLSE) as

$$\displaystyle{ \hat{\beta }_{d}^{K}\;:= \frac{1} {K}\sum _{i=1}^{K}\hat{\beta }_{ d}^{\boldsymbol{\phi }_{i} }. }$$
(18)

One major advantage of this estimator is that it can be calculated in parallel with the minimal number of two communications, one to send the data and one to receive the result. This means that the asymptotic computational cost of \(\hat{\beta }_{d}^{K}\) is equal to the cost of \(\hat{\beta }_{d}^{\boldsymbol{\phi }}\) if calculations are done on K different processors. To investigate the MSE of \(\hat{\beta }_{d}^{K}\), we restrict ourselves for simplicity to the limit case

$$\displaystyle{ \hat{\beta }_{d} =\lim _{K\rightarrow \infty }\hat{\beta }_{d}^{K} }$$
(19)

and instead only investigate \(\hat{\beta }_{d}\). The reasoning being that for large enough values of K (say K > 100) the behaviour of \(\hat{\beta }_{d}\) is very similar to \(\hat{\beta }_{d}^{K}\). The exact form of the MSE in terms of the η i ’s is given in [10]. Here we build on these results and give an explicit upper bound for the MSE.

Theorem 4

Assume Rank(X) ≥ d. Define

$$\displaystyle{ \tau =\sum _{ i=1}^{p}\Big(\frac{\lambda _{i}} {\eta _{i}}\Big)^{2}. }$$

The MSE of \(\hat{\beta }_{d}\) can be bounded from above by

$$\displaystyle{ \mathbb{E}_{\boldsymbol{\phi }}[\mathbb{E}_{\varepsilon }[\|\mathbf{X}\beta -\mathbf{X}\hat{\beta }_{d}\|_{2}^{2}]] \leq \sigma ^{2}\tau +\sum _{ i=1}^{p}\beta _{ i}^{2}\lambda _{ i}w_{i}^{2}, }$$

where the w i ’s are given (as in Theorem  1 ) by

$$\displaystyle{ w_{i} = \frac{(1 + 1/d)\lambda _{i}^{2} + (1 + 2/d)\lambda _{i}\mathop{ \mathrm{trace}}\nolimits (\varSigma ) +\mathop{ \mathrm{trace}}\nolimits (\varSigma )^{2}/d} {(d + 2 + 1/d)\lambda _{i}^{2} + 2(1 + 1/d)\lambda _{i}\mathop{ \mathrm{trace}}\nolimits (\varSigma ) +\mathop{ \mathrm{trace}}\nolimits (\varSigma )^{2}/d}. }$$

and

$$\displaystyle{ \tau \in [d^{2}/p,d]. }$$

Proof

See Appendix.

Comparing averaging to the case where we only have one single estimator we see that there are two differences: First the variance due to the model noise ɛ turns into σ 2 τ with τ ∈ [d 2∕p, d], thus τ ≤ d. Second the shrinkage factors w i in the bias are now squared, which in total means that the MSE of \(\hat{\beta }_{d}\) is always smaller or equal to the MSE of a single estimator \(\hat{\beta }_{d}^{\boldsymbol{\phi }}\).

We investigate the behaviour of τ as a function of d in three different situations (Fig. 2). We first look at two extreme cases of covariance matrices for which the respective upper and lower bounds [d 2∕p, d] for τ are achieved. For the lower bound, let Σ = I p×p be orthonormal. Then λ i ∕η i  = c for all i, as above. From

$$\displaystyle{ \sum _{i=1}^{p}\lambda _{ i}/\eta _{i} = d }$$

we get λ i ∕η i  = d∕p. This leads to

$$\displaystyle{ \tau =\sum _{ i=1}^{p}(\lambda _{ i}/\eta _{i})^{2} = p\frac{d^{2}} {p^{2}} = \frac{d^{2}} {p}, }$$

which reproduces the lower bound.

Fig. 2
figure 2

MSE of averaged compressed least squares (circle) versus the MSE of the single estimator (cross) with covariance matrix Σ i, i  = 1∕i. On the left with σ 2 = 0 (only bias), in the middle σ 2 = 1∕40 and on the right σ 2 = 1∕20. One can clearly see the quadratic improvement in terms of MSE as predicted by Theorem 4

Full size image

We will not be able to reproduce the upper bound exactly for all d ≤ p. But we can show that for any d there exists a covariance matrix Σ, such that the upper bound is reached. The idea is to consider a covariance matrix that has equal variance in the first d direction and almost zero in the remaining p − d. Define the diagonal covariance matrix

$$\displaystyle{ \varSigma _{i,j} = \left \{\begin{array}{@{}l@{\quad }l@{}} 1,\quad &\text{if }\,i = j\text{ and }i \leq d \\ \epsilon, \quad &\text{if }\,i = j\text{ and }i > d \\ 0,\quad &\text{if }\,i\neq j\\ \quad \end{array} \right.. }$$
(20)

We show lim ε → 0 τ = d. For this decompose Φ into two matrices \(\varPhi _{d} \in \mathbb{R}^{d\times d}\) and \(\varPhi _{r} \in \mathbb{R}^{(\,p-d)\times d}\):

$$\displaystyle{ \varPhi = \left (\begin{array}{*{10}c} \varPhi _{d}\\ \varPhi _{r } \end{array} \right ). }$$

The same way we define β d , β r , X d and X r . Now we bound the approximation error of \(\hat{\beta }_{d}^{\varPhi }\) to extract information about λ i ∕η i . Assume a squared data matrix (n = p) \(\mathbf{X} = \sqrt{\varSigma }\), then

$$\displaystyle\begin{array}{rcl} \mathbb{E}_{\varPhi }[\mathop{\mathop{\mathrm{argmin}}\nolimits }\limits_{\gamma \in \mathbb{R}^{d}}\|\mathbf{X}\beta -\mathbf{X}\varPhi \gamma \|_{ 2}^{2}]& \leq & \mathbb{E}_{\varPhi }[\|\mathbf{X}\beta -\mathbf{X}\varPhi \varPhi _{ d}^{-1}\beta _{ d}\|_{2}^{2}] {}\\ & =& \mathbb{E}_{\varPhi }[\|\mathbf{X}_{r}\beta _{r} -\mathbf{X}_{r}\varPhi _{r}\varPhi _{d}^{-1}\beta _{ d}\|_{2}^{2}] {}\\ & =& \epsilon \mathbb{E}_{\varPhi }[\|\beta _{r} -\varPhi _{r}\varPhi _{d}^{-1}\beta _{ d}\|_{2}^{2}] {}\\ & \leq & \epsilon (2\|\beta _{r}\|_{2}^{2} + 2\|\beta _{ d}\|_{2}^{2}\mathbb{E}_{\varPhi }[\|\varPhi _{ r}\|_{2}^{2}]\mathbb{E}_{\varPhi }[\|\varPhi _{ d}^{-1}\|_{ 2}^{2}]) {}\\ & \leq & \epsilon C, {}\\ \end{array}$$

where C is independent of ε and bounded since the expectation of the smallest and largest singular values of a random projection is bounded. This means that the approximation error decreases to zero as we let ε → 0. Applying this to the closed form for the MSE of \(\hat{\beta }_{d}^{\varPhi }\) we have that

$$\displaystyle{ \sum _{i=1}^{p}\beta _{ i}^{2}\lambda _{ i}\Big(1 -\frac{\lambda _{i}} {\eta _{i}}\Big) \leq \sum _{i=1}^{d}\beta _{ i}^{2}\Big(1 -\frac{\lambda _{i}} {\eta _{i}}\Big) +\epsilon \sum _{ i=d+1}^{p}\beta _{ i}^{2}\Big(1 -\frac{\lambda _{i}} {\eta _{i}}\Big) }$$

has to go to zero as ε → 0, which in turn implies

$$\displaystyle{ \lim _{\epsilon \rightarrow 0}\;\sum _{i=1}^{d}\beta _{ i}^{2}\Big(1 -\frac{\lambda _{i}} {\eta _{i}}\Big) = 0, }$$

and thus lim ε → 0 λ i ∕η i  = 1 for all i ∈ { 1, …, d}. This finally yields a limit

$$\displaystyle{ \lim _{\epsilon \rightarrow 0}\;\sum _{i=1}^{p}\frac{\lambda _{i}^{2}} {\eta _{i}^{2}} = d. }$$

This illustrates that the lower bound d 2∕p and upper bound d for the variance factor τ can both be attained. Simulations suggest that τ is usually close to the lower bound, where the variance of the estimator is reduced by a factor d∕p compared to a single iteration of a compressed least-squares estimator, which is on top of the reduction in the bias error term. This shows, perhaps unsurprisingly, that averaging over random projection estimators improves the mean-squared error in a Rao–Blackwellization sense. We have quantified the improvement. In practice, one would have to decide whether to run multiple versions of a compressed least-squares regression in parallel or run a single random projection with a perhaps larger embedding dimension. The computational effort and statistical error tradeoffs will depend on the implementation but the bounds above will give a good basis for a decision (Fig. 3).

Fig. 3
figure 3

Simulations of the variance factor τ (line) as a function of d for three different covariance matrices and in lower bound (d 2∕p) and upper bound (d) (square, triangle). On the left (Σ = I p×p ) τ as proven reaches the lower bound. In the middle (Σ i, i  = 1∕i) τ reaches almost the lower bound, indicating that in most practical examples τ will be very close to the lower bound and thus averaging improves MSE substantially compared to the single estimator. On the right the extreme case example from (20) with d = 5, where τ reaches the upper bound for d = 5

Full size image

4 Discussion

We discussed some known results about the properties of compressed least-squares estimation and proposed possible tighter bounds and exact results for the mean-squared error. While the exact results do not have an explicit representation, they allow nevertheless to quantify the conservative nature of the upper bounds on the error. Moreover, the shown results allow to show a strong similarity of the error of compressed least squares, ridge and principal component regression. We also discussed the advantages of a form of Rao–Blackwellization, where multiple compressed least-square estimators are averaged over multiple random projections. The latter averaging procedure also allows to compute the estimator trivially in a distributed way and is thus often better suited for large-scale regression analysis. The averaging methodology also motivates the use of compressed least squares in the high dimensional setting where it performs similar to ridge regression and the use of multiple random projection will reduce the variance and result in a non-random estimator in the limit, which presents a computationally attractive alternative to ridge regression.