Need of Two-Dimensional Consideration for Modelling Urban Drainage

Abstract

The computation of unsteady free surface flow is essential in urban drainage systems to estimate values of various flow parameters like depth and velocity of flow in the different parts of a drain at different times of flow. Generally, 1-D governing equations of unsteady free surface flow (Saint-Venant equations) are solved for simulating storm water flow in drains. This gives acceptable result for turbulent flow in a channel of small width. However, for relatively larger channel width, flow parameters may vary significantly within a channel cross section and therefore, for proper analysis, 2-D simulation becomes essential. Need of using 2-D simulation for analyzing flow characteristic in a typical city drain is studied and presented in this paper. Comparison of 1-D and 2-D results has revealed that though both the models give same surface elevations along the drain at different times, flow velocity varies significantly across the channel in 2-D simulation. 2-D result shows higher velocity at middle of the channel and lower flow velocity near the bank, whereas, because of inherent limitation, the variation of flow velocity across the channel cross section never gets reflected in the result computed by 1-D analysis. Thus, the fact that a channel having low velocity near the bank may experience sediment deposition, might go unnoticed if it is analyzed by a 1-D model.

1 Introduction

The computation of unsteady free surface flow is essential in urban drainage systems to estimate values of various flow parameters like depth and velocity of flow in the different parts of a drain at different times of flow. Generally, 1-D governing equations of unsteady free surface flow (Saint-Venant equations) are solved for simulating storm water flow in drains. Many researchers (Jingxiang and Charles 1985; Khan 2000; Ramesh et al. 2000; Patricia and Raimundo 2005; Akbari and Firoozi 2010; Yong 2010) have been using the 1-D Saint-Venant’s equation for modelling channels. Though one-dimensional numerical model have been used extensively in this regards, in many situations, however, one-dimensional solution is not sufficient to describe the actual flow scenario. For example, to study the changes in different flow variables at different places of a same cross section in a channel, the computation of two-dimensional unsteady free surface flows becomes necessary. Due to this criterion, some investigators (Fennema and Chaudhry 1990; Weiming 2004; Schwanenberg and Harms 2004) have applied the 2-D Saint-Venant’s equations for modelling channels. From the survey of literature, it has been observed that though numerous models have been developed for simulation of water flow in channels in 1-D and 2-D, it appears that there is a scope of doing comparative study between 1-D and 2-D simulations of drains, for selecting the efficient one. In this paper, details of the study done on comparison of 1-D and 2-D unsteady open channel flow simulation for different shaped drains are presented.

2 Governing Equation

Saint-Venant equations describing unsteady free surface flows are composed of continuity and momentum equations. For prismatic channels having no lateral inflow or outflow the Saint-Venant equations in 1-D (Jingxiang and Charles 1985) are defined as

$$ \frac{\partial h}{\partial t} + D\frac{\partial u}{\partial x} + u\frac{\partial h}{\partial x} = 0 $$

(1)

$$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + g\frac{\partial h}{\partial x} = g(S_{O} - S_{\text{f}} ) $$

(2)

In Eqs. (1) and (2), h is flow depth; u is flow velocity; D = A/B is the hydraulic depth; A is flow area; B is top water surface width; $S_{O}$ is channel bottom slope; S _f  = (u ² × n ²)/h ^4/3 is friction slope; x is distance along the channel length; t is time and g is the acceleration due to gravity; n is Manning’s coefficient.

In 2-D form, the Saint-Venant equations with no lateral inflow and outflow in matrix form Fennema and Chaudhry (1990) are as follows:

$$ U_{t} + E_{x} + F_{y} + S = 0 $$

(3)

In Eq. (3),

$$ \begin{aligned} U & = \left( {\begin{array}{*{20}c} h \\ {hu} \\ {hv} \\ \end{array} } \right)\quad E = \left( {\begin{array}{*{20}c} {hu} \\ {hu^{2} + gh^{2}/2 } \\ {huv} \\ \end{array}} \right) \\ F & = \left( {\begin{array}{*{20}c} {hv} \\ {huv} \\ {hv^{2} + gh^{2} /2} \\ \end{array} } \right)\quad S = \left( {\begin{array}{*{20}c} 0 \\ { - gh(S_{ox} - S_{{{{f}}x}} )} \\ { - gh(S_{oy} - S_{{{{f}}y}} )} \\ \end{array} } \right) \\ \end{aligned} $$

where h is flow depth; u is flow velocity in x direction; v is the flow velocity in y direction; $S_{ox}$ is channel bottom slope in x direction; S _{f x}  = n ² u(u ² + v ²)^1/2/h ^4/3 is the friction slope in x direction and x is the distance along the channel length; $S_{oy}$ is channel bottom slope in y direction; S _{f y}  = n ² v(u ² + v ²)^1/2/h ^4/3 is friction slope in y direction; y is distance across the channel length; n is Manning’s coefficient; t is the time and g is the acceleration due to gravity.

3 Finite Difference Method

The governing equations are nonlinear first-order, hyperbolic partial differential equations for which closed-form solutions are not available. Therefore, these equations are solved numerically. One of the common numerical methods applied for the solution of these types of equation is finite difference method.

For 1-D case, the x direction is designated by the subscript i and the t direction is by subscript k. The time interval where the flow variable is known is denoted by subscript k and the unknown time level is by subscript k + 1. The increment in x direction is designated by Δx and Δt is the increment in the time direction.

Again for 2-D case, the x direction is designated by the subscript j, the y direction, by the subscript i and the t direction by the subscript k. The time interval where the flow variable is known is denoted by subscript k and the unknown time level is shown by subscript k + 1. Δx is the increment in the x direction, Δy is the increment in the y direction and Δt is the increment in the t direction.

4 Lax Diffusive Scheme

When a direct computation of the dependent variables can be made in terms of known quantities, the computation is said to be explicit. Lax diffusive finite difference scheme (Chaudhry 2008) is an explicit scheme. It is first-order accurate in time and second order accurate in space. Flow variables are known at time level k and their values are to be determined at time level k + 1.

The finite difference forms of the governing equations in one dimension are as follows,

$$ h_{i}^{k + 1} = \frac{1}{2}\left( {h_{i - 1}^{k} + h_{i + 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta x}}D_{i}^{*} \left( {u_{i + 1}^{k} - u_{i - 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta x}}u_{i}^{*} \left( {h_{i + 1}^{k} - h_{i - 1}^{k} } \right) $$

(4)

$$ u_{i}^{k + 1} = \frac{1}{2}\left( {u_{i - 1}^{k} + u_{i + 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta x}}g\left( {y_{i + 1}^{k} - y_{i - 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta x}}u_{i}^{*} \left( {u_{i + 1}^{k} - u_{i - 1}^{k} } \right) + g\Delta t\left( {S_{o} - S_{\text{f}}^{*} } \right) $$

(5)

The general formulation of this scheme in two dimensions is as follows:

$$ U_{i,j}^{k + 1} = \frac{1}{2}\left( {U_{i,j + 1}^{k} - U_{i,j - 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta x}}\left( {E_{i,j + 1}^{k} - E_{i,j - 1}^{k} } \right) - \frac{{\Delta t}}{{2\Delta y}}\left( {F_{i + 1,j}^{k} - F_{i - 1,j}^{k} } \right) -\Delta tS_{i,j}^{*} $$

(6)

From Eqs. (4)–(6), the dependent flow variables are computed at unknown time step.

5 Application of the Scheme

The above numerical schemes were then applied to solve the governing equations for studying the unsteady flow behaviour in different shaped drains by routing hydrographs through the drains. The details of the tests done for all the drains in 1-D and in 2-D and their results are presented below.

5.1 Drain Size Consideration

Test drain used for simulation was 200 m in length and 15 m in top width. Two different cross sections were taken under consideration. They are as follows:

• Trapezoidal shaped drain.

• Rectangular shaped drain.

The bottom widths of both the drains were 3 m. The total length of the drain was divided into 40 grids with Δx = 5 m for 1-D and 2-D considerations, whereas, for 2-D consideration the total width of the drain was divided into 5 grids with Δy = 3 m. The roughness of the drain was introduced by applying manning’s n. A classical value of 0.031 was applied over the whole computational domain for all the cases. The longitudinal bed slope of the drain was assumed to be 1:1000.

5.2 Initial and Boundary Condition

Initial values of all the dependent variables were applied on the drain as initial condition. Flow hydrographs were applied at the upstream as upstream boundary conditions. For the downstream boundary, all the dependent variables were extrapolated from the interior domain. For two-dimensional simulations the solid boundary was simulated by Reflective boundary condition technique (Fennema and chaudhry 1990). Figure 1 shows the upstream flow hydrograph.

Fig. 1

Upstream flow hydrograph

5.3 Stability of the Models

The Lax diffusive scheme is an explicit finite difference scheme and hence the model will be stable if Courant–Friedrichs–Lewy (CFL) criterion is satisfied. In one dimension according to CFL condition,

$$ \frac{{\left( {\left( {u + \sqrt {gh} } \right) \times\Delta t} \right)}}{{\Delta x}} \le 1 $$

And for two-dimensional cases the condition is

$$ \frac{{\left( {\left( {u + \sqrt {gh} } \right) \times\Delta t} \right)}}{{\Delta x}} \le 1\;{\text{and}} \frac{{\left( {\left( {v + \sqrt {gh} } \right) \times\Delta t} \right)}}{{\Delta y}} \le 1 $$

5.4 Results and Discussions

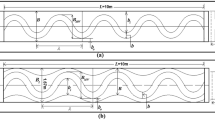
Using the above initial and boundary conditions, the governing equations of free surface flow (Saint-Venant’s equation) were solved by Lax diffusive scheme both in 1-D and 2-D for all the drains. To compare the performances of 1-D and 2-D simulations, surface elevations along the channel at different time steps were plotted. From the plots, same surface elevations along the channels between 1-D and 2-D results were observed, for both the drains. Figure 2 shows the water surface profiles after elapsing of 500 time steps from beginning for the trapezoidal drain. Figure 3 shows same for the rectangular drain. From the results of surface elevation profiles, the potential of 1-D modelling regarding computation of water depth in drains same as that of 2-D modelling can be evaluated.

Fig. 2

Water surface profiles after 500 time steps for trapezoidal drain

Fig. 3

Water surface profiles after 500 time steps for rectangular drain

The water velocities obtained from 1-D and 2-D models were also compared for both the drains to have an idea about the performances of the models in calculating water velocities. From the result of 2-D velocities, it was observed that velocities near the bank line are very lesser than the centreline velocities for both the drains, whereas in 1-D modelling since the values are averaged across the cross sections this difference velocity pattern cannot be observed. The lower velocity pattern near the banks establishes the possibilities of sedimentation on those less velocity areas. Figure 4 shows the comparison in velocities along the channel for one-dimensional and two-dimensional simulations for rectangular drain. Figure 5 shows the same for trapezoidal drain. The lower velocity pattern near the banks can also be observed from the velocity vector plotting of the drains in 2-D. Figure 6 shows the velocity vector plot for the trapezoidal drain.

Fig. 4

Water velocities after 500 time step for rectangular channel

Fig. 5

Water velocities after 500 time step for trapezoidal channel

Fig. 6

Velocity vector for trapezoidal drain

6 Conclusions

Lax diffusive finite difference explicit scheme has been applied for unsteady flow simulation in drains by solving the Saintt-Venant equation both in 1-D and 2-D forms. It has been found that 1-D modelling is sufficient for evaluating the correct water surface profiles. But, it has been observed that the flow velocity varies significantly across the channel in 2-D simulations for all the drains. Two-dimensional velocity results shows higher velocity at middle of the channel and lower flow velocity near the bank, whereas, because of inherent limitation, the variation of flow velocity across the channel cross section never gets reflected in the result computed by one-dimensional analysis. Thus, the fact that a channel having low velocity near the bank may experience sediment deposition, might go unnoticed if it is analyzed by a one-dimensional model. And hence, the present study facilitates the necessity of two-dimensional modelling in drain simulation problems.