Keywords

1.1 Introduction

Our intention in writing the following historical development is to provide our perspective on the evolution of nonparametric methodology (both finite and asymptotic). We will focus on a particular development based on ranks. We will show how beginning with simple rank tests in the 1940s, the area has grown into a coherent group of contemporary statistical procedures that can handle data from increasingly complex experimental designs. Two factors have been essential: theoretical developments especially in asymptotic theory, see Hettmansperger and McKean (2011), and in computational developments, see Kloke and McKean (2014). Statistical inference based on ranks of the data has been shown to be both statistically efficient relative to least squares methods as well as robust. Any history is bound to be selective. We have chosen a line of development that is consistent with the theme of this conference. There is a rich and extensive literature on nonparametric methods. We will confine ourselves to references that directly relate to the history as related to the topics of the conference.

When constructing tests for the median of a continuous population, the simplest nonparametric test is the sign test which counts the number of observations greater than the null hypothesized value of the median. The null and alternative distributions of the sign test statistic are both binomial. In the case of the null hypothesis, the binomial parameter is 0.5, and hence, the null distribution of the sign test statistic does not depend on the population distribution. We call such a test nonparametric or distribution free. The use of the sign test for dichotomous data was first proposed by Arbuthnott (1710).

The modern era for nonparametric or distribution free tests began with the work of Wilcoxon (1945) and Mann and Whitney (1947). Wilcoxon proposed the nonparametric Wilcoxon signed rank test for the median of a symmetric population, and the nonparametric Wilcoxon rank sum test for the difference in population medians. Mann and Whitney (1947) showed that the rank sum test is equivalent to the sign test applied to the pairwise differences across the two samples. Tukey (1949) showed the signed rank test is equivalent to the sign test applied to the pairwise averages from the sample (called the Walsh averages by Tukey). Hence, from the earliest time, we have a connection between rank based methods and the L 1 norm expressed through its derivative, the sign statistic. In what follows we will exploit this connection by considering a rank based norm and its relationship to the L 1 norm. In addition, we will need to include the L 2 norm and least squares for comparison in our discussion.

Noether (1955), based on earlier unpublished work by Pitman (1948), introduced Pitman efficiency for hypothesis tests. Then Hodges and Lehmann (1956, 1960) analyzed the efficiency of various rank tests relative to least squares tests (t- and F-tests) and proved the surprising result that the efficiency of the Wilcoxon tests relative to the t-tests is never less than 0.864, is 0.955 at the normal model, and can be arbitrarily large for heavy tailed model distributions. No longer was a rank test considered quick and dirty with low power. Rank tests now provided a serious alternative to least squares t tests.

Hodges and Lehmann (1963) next developed estimators based on rank test statistics (R-estimates) and showed that they inherit the efficiency of the rank tests that they were derived from. Because of the connection between the Wilcoxon test statistics and the L 1 norm, the Hodges-Lehmann estimate of location is the median of the pairwise averages and the estimate for the difference in locations is the median of the pairwise differences across the two samples. By the mid-sixties rank tests and estimates for location models, including the one-way layout, were available, and they share the excellent efficiency properties. Robustness was introduced during this time by Huber (1964) followed by the work of Hampel (1974). The basic tools of robustness include the influence function and break down point. Ideally we would like to have estimates that have bounded influence and positive breakdown. Indeed, Wilcoxon R-estimates enjoy precisely these good robustness properties in addition to the excellent efficiency properties mentioned above. For example the breakdown value for the Hodges-Lehmann estimate of location, the median of the pairwise averages, is 0.293 while the breakdown of the sample mean is 0.

Hájek and Šidák (1967) published a seminal work on the rigorous development of rank tests. This was followed many years later by a second edition, Hájek et al. (1999) which extends much of the theory and includes material on R-estimates.

Hence, during the 1960s nonparametric and distribution free rank tests and rank-based estimates for location models were well understood and provided excellent alternatives to least squares methods (means, t- and F-tests) from the point of view of both efficiency and robustness. Unfortunately the rank methods did not extend in a straight forward way to the two-way layout with interaction terms. For example, a quick check of text books on nonparametrics written before the mid-seventies did not reference a test for interaction in a two-way layout.

The next step involved the extension of rank methods to linear regression where the two-way layout could be formulated in regression terms and natural rank tests for regression parameters were easy to construct. The rank based statistical methods which require the estimation of nuisance parameters will then be asymptotically distribution free but no longer distribution free for finite samples. The tools for the development of rank regression were provided by Jurečková (1969, 1971) and Jaeckel (1972). Jurečková, in particular, provided the asymptotic theory and Jaeckel provided a rank based dispersion function that when minimized produced R-estimates. McKean (1975) developed corresponding rank tests along with the necessary asymptotic distribution theory for the linear model. In the next several sections we explicitly introduce the linear model and discuss the development of rank based methods and their efficiency and robustness properties. In subsequent sections, we discuss extensions of rank-based analyses to nonlinear models and models with dependent errors.

There is R software available to compute these rank-based analyses. In the examples presented, we discuss some of the R code for the computation of these analyses. The rank-based package for linear models, Rfit, (see Kloke and McKean 2012), can be downloaded at CRAN (http://cran.us.r-project.org/). Supplemental packages for the additional models discussed in the examples can be downloaded at the site https://github.com/kloke/.

1.2 Rank-Based Fit and Inference for Linear Models

In this section we will review the univariate linear model and present the rank based norm used to derive the rank based statistical methods along with the basic asymptotic tools. Then we will present the efficiency and robustness results that we mentioned in the introduction, but in more detail. We will also describe some of the rank based methods for residual analysis. For details of this development see Chaps. 3–5 of Hettmansperger and McKean (2011).

Let \(\boldsymbol{Y }\) denote the n × 1 vector of observations and assume that it follows the linear model

$$\displaystyle{ \boldsymbol{Y } =\boldsymbol{ 1}\alpha +\boldsymbol{ X}\boldsymbol{\beta } +\boldsymbol{ e}, }$$
(1.1)

where \(\boldsymbol{X}\) is an n × p full column rank matrix of explanatory variables, \(\boldsymbol{1}\) is an n × 1 vector of ones, \(\boldsymbol{\beta }\) is p × 1 vector of regression coefficients, α is the intercept parameter, and \(\boldsymbol{e}\) is the n × 1 vector of random errors. Letting \(\boldsymbol{x}_{i}^{{\prime}}\) denote the ith row of \(\boldsymbol{X}\), we have \(y_{i} =\alpha +\boldsymbol{x}_{i}^{{\prime}}\boldsymbol{\beta } + e_{i}\). For the theory cited in this section, assume that the random errors are iid with pdf f(x) and cdf F(x), respectively.

A score generating function is a nondecreasing square-integrable function φ(u) defined on the interval (0, 1) which, without loss of generality, satisfies the standardizing conditions

$$\displaystyle{ \int _{0}^{1}\varphi (u)\,du = 0\;\mbox{ and }\;\int _{ 0}^{1}[\varphi (u)]^{2}\,du = 1. }$$
(1.2)

We denote the scores by \(a(i) =\varphi [i/(n + 1)]\).

The basis of traditional analysis of most models in practice is the least squares (LS) fit of the model. This fit minimizes the squared-Euclidean distance between the vector of responses and the estimating region, (subspace if it is a linear model). In the same way, the basis for a rank-based analysis is the fit of the model except that a different norm is used other that the Euclidean norm. This norm leads to a robust fit. For a given score function φ(u), the norm is defined by

$$\displaystyle{ \|\boldsymbol{v}\|_{\varphi } =\sum _{ i=1}^{n}a_{\varphi }[R(v_{ i})]v_{i},\;\;\;\boldsymbol{v} \in R^{n}. }$$
(1.3)

Note that this is a pseudo-norm; i.e., it satisfies all properties of the norm except it is invariant to constant shifts, i.e., \(\|\boldsymbol{v} + a\boldsymbol{1}\|_{\varphi } =\|\boldsymbol{ v}\|_{\varphi }\) for all a, where \(\boldsymbol{1}\) is a vector of n ones. The counterpart in LS is the squared-Euclidean pseudo-norm \(\sum _{i=1}^{n}(v_{i} -\overline{v})^{2}\).

For convenience, we define the dispersion function \(D(\boldsymbol{\beta })\) in terms of the pseudo norm \(\|\cdot \|_{\varphi }\) as

$$\displaystyle{ D(\boldsymbol{\beta }) =\|\boldsymbol{ y} -\boldsymbol{ X}\boldsymbol{\beta }\|_{\varphi } =\sum _{ i=1}^{n}a[R(y_{ i} -\boldsymbol{ x}_{i}^{{\prime}}\boldsymbol{\beta })](y_{ i} -\boldsymbol{ x}_{i}^{{\prime}}\boldsymbol{\beta }) =\boldsymbol{ a}^{{\prime}}[R(\boldsymbol{y} -\boldsymbol{ X}\boldsymbol{\beta })](\boldsymbol{y} -\boldsymbol{ X}\boldsymbol{\beta }), }$$
(1.4)

where \(R(y_{i} -\boldsymbol{ x}_{i}^{{\prime}}\boldsymbol{\beta })\) denotes the rank of \(y_{i} -\boldsymbol{ x}_{i}^{{\prime}}\boldsymbol{\beta }\) among \(y_{1} -\boldsymbol{ x}_{1}^{{\prime}}\boldsymbol{\beta },\ldots,y_{n} -\boldsymbol{ x}_{n}^{{\prime}}\boldsymbol{\beta }\) and \(\boldsymbol{a}[R(\boldsymbol{y} -\boldsymbol{ X}\boldsymbol{\beta })]\) is the vector with ith component \(a[R(y_{i} -\boldsymbol{ x}_{i}^{{\prime}}\boldsymbol{\beta })]\). Note that ranks are invariant to constant shifts such as an intercept parameter. The rank-based estimator of \(\boldsymbol{\beta }\) is the minimizer

$$\displaystyle{ \hat{\boldsymbol{\beta }}= \mbox{ Argmin}\,D(\boldsymbol{\beta }). }$$
(1.5)

Let V f denote the full model subspace of R n; i.e., V f is the range (column space) of \(\boldsymbol{X}\). Then \(D(\hat{\boldsymbol{\beta }})\) is the minimum distance between the vector of responses \(\boldsymbol{Y }\) and the subspace V f in terms of the norm \(\|\cdot \|_{\varphi }\). For reference, we have

$$\displaystyle{ D(\hat{\boldsymbol{\beta }}) =\min _{\boldsymbol{\eta }\in V _{f}}\|\boldsymbol{Y } -\boldsymbol{\eta }\|_{\varphi }. }$$
(1.6)

Note that this minimum distance between \(\boldsymbol{Y }\) and V f is unique; i.e., the minimum distance does not depend on the basis matrix of V f .

Denote the negative of the gradient of \(D(\boldsymbol{\beta })\) by

$$\displaystyle{ \boldsymbol{S}(\boldsymbol{\beta }) = -\boldsymbol{\bigtriangledown } D(\boldsymbol{\beta }) =\boldsymbol{ X}^{{\prime}}\boldsymbol{a}[R(\boldsymbol{y} -\boldsymbol{ X}\boldsymbol{\beta })]. }$$
(1.7)

Then the estimator also satisfies \(\boldsymbol{S}(\hat{\boldsymbol{\beta }})\dot{ =}\boldsymbol{ 0}\). Generally, the intercept parameter is estimated by the median of the residuals; i.e.,

$$\displaystyle{ \hat{\alpha }= \mbox{ med}_{i}\{y_{i} -\boldsymbol{ x}_{i}^{{\prime}}\hat{\boldsymbol{\beta }}\}. }$$
(1.8)

Examples of scores functions include: \(\varphi (u) = \sqrt{12}[u - (1/2)]\), for Wilcoxon rank-based methods; \(\varphi (u) = \mbox{ sgn}[u - (1/2)]\), for L 1 methods; and \(\varphi (u) =\varPhi ^{-1}(u)\), where Φ(t) is the standard normal cdf, for normal scores methods. In Sect. 1.1, we pointed out that the nonparametric sign and Wilcoxon location estimators are based on minimizers of L 1-norms. This is true also in the regression case for the Wilcoxon and sign scores. First, if sign scores are used then the rank-based estimator of \(\boldsymbol{\beta }\) and α, as estimated by the median of the residuals, are the L 1 (least absolute deviations) estimators of α and \(\boldsymbol{\beta }\); see page 212 of Hettmansperger and McKean (2011). Secondly, for Wilcoxon scores we have the identity

$$\displaystyle{ \frac{4(n + 1)} {\sqrt{12}} \sum _{i=1}^{n}\sqrt{12}\left (\frac{R(u_{i})} {n + 1} -\frac{1} {2}\right )u_{i} =\sum _{ i=1}^{n}\sum _{ j=1}^{n}\vert u_{ i} - u_{j}\vert,\;\;\;\boldsymbol{u} \in R^{n}. }$$
(1.9)

That is, the Wilcoxon estimator of the regression coefficients minimizes the absolute deviations of the differences of the residuals.

In addition to the above defined rank-based estimator of \(\boldsymbol{\beta }\), we can also construct an hypothesis test of the general linear hypotheses

$$\displaystyle{ H_{0}:\;\boldsymbol{ M}\boldsymbol{\beta } =\boldsymbol{ 0}\mbox{ versus }H_{A}:\;\boldsymbol{ M}\boldsymbol{\beta }\not =\boldsymbol{0}, }$$
(1.10)

where \(\boldsymbol{M}\) is a q × p matrix of full row rank. Let V r denote the reduced model subspace; i.e., the subspace of V f subject to the null hypothesis. Let W be a n × (p − q) basis matrix of V r . Then we write the reduced model as \(\boldsymbol{Y } =\alpha \boldsymbol{ 1} +\boldsymbol{ W}\boldsymbol{\theta } +\boldsymbol{ e}\). Let \(\hat{\boldsymbol{\theta }}\) denote the rank-based estimator of this reduced model. Then the distance between \(\boldsymbol{Y }\) and the subspace V r is \(D(\hat{\boldsymbol{\theta }})\), which is the same for any basis matrix of V r .

The test statistic of the hypotheses (1.10) is the normalized version of the reduction in distance, \(D(\hat{\boldsymbol{\theta }}) - D(\hat{\boldsymbol{\beta }})\), given by:

$$\displaystyle{ F_{\varphi } = \frac{[D(\hat{\boldsymbol{\theta }}) - D(\hat{\boldsymbol{\beta }})]/q} {\hat{\tau }/2}, }$$
(1.11)

where \(\hat{\tau }\) is an estimator of the scale parameter

$$\displaystyle{ \tau ^{-1} =\int \varphi ^{{\prime}}(F(t))f^{2}(t)\,dt =\int f(t)\,d(\varphi (F(t)). }$$
(1.12)

Koul et al. (1987) developed a consistent estimator of τ. Note that the reduction in distance (dispersion) parallels the least squares reduction in sums of squares.

The approximating distributions of the estimator and the test statistic are determined by a linear approximation of the negative gradient of the dispersion and a quadratic approximation of the dispersion. Let \(\boldsymbol{\beta }_{0}\) denote the true parameter. Then the following approximations can be made asymptotically rigorous under mild regularity conditions:

$$\displaystyle\begin{array}{rcl} \frac{1} {\sqrt{n}}\boldsymbol{S}(\boldsymbol{\beta })& \asymp & \frac{1} {\sqrt{n}}\boldsymbol{X}^{{\prime}}\boldsymbol{\varphi }(F(\boldsymbol{y} -\boldsymbol{ X}\boldsymbol{\beta }_{ 0})) -\tau ^{-1} \frac{1} {n}\boldsymbol{X}^{{\prime}}\boldsymbol{X}\sqrt{n}(\boldsymbol{\beta }-\boldsymbol{\beta }_{ 0}) \\ D(\boldsymbol{\beta })& \asymp & D(\boldsymbol{\beta }_{0}) - (\boldsymbol{\beta }-\boldsymbol{\beta }_{0})^{{\prime}}\boldsymbol{S}(\boldsymbol{\beta }_{ 0}) + \frac{1} {2\tau }(\boldsymbol{\beta }-\boldsymbol{\beta }_{0})^{{\prime}}\frac{1} {n}\boldsymbol{X}^{{\prime}}\boldsymbol{X}(\boldsymbol{\beta }-\boldsymbol{\beta }_{ 0}).{}\end{array}$$
(1.13)

Based on these results the following asymptotic distributions can be obtained:

$$\displaystyle\begin{array}{rcl} \boldsymbol{S}(\boldsymbol{\beta }_{0})& \mbox{ is approximately }& MV N(\boldsymbol{0},\boldsymbol{X}^{{\prime}}\boldsymbol{X}) \\ \hat{\boldsymbol{\beta }}& \mbox{ is approximately }& MV N(\boldsymbol{\beta }_{0},\tau ^{2}(\boldsymbol{X}^{{\prime}}\boldsymbol{X})^{-1}){}\end{array}$$
(1.14)
$$\displaystyle\begin{array}{rcl} F_{\varphi }& \mbox{ is approximately }& \mbox{ $F(q,n - p - 1)$, under $H_{0}$};{}\end{array}$$
(1.15)

(qF φ  → χ 2-distribution with q degrees of freedom, under H 0).

Based on (1.14), an approximate (1 −α)100 % confidence interval for the linear function \(\boldsymbol{h}^{{\prime}}\boldsymbol{\beta }\) is

$$\displaystyle{ \boldsymbol{h}^{{\prime}}\hat{\boldsymbol{\beta }}\pm t_{\alpha,n-p}\hat{\tau }\sqrt{\boldsymbol{h}^{{\prime} } (\boldsymbol{X}^{{\prime} } \boldsymbol{X})^{-1 } \boldsymbol{h}}, }$$
(1.16)

where t α, n−p is the upper α∕2 quantile of a t-distribution with n − p degrees of freedom. The use of t-critical values and F-critical values for tests and confidence procedures is supported by numerous small sample simulation studies; see McKean and Sheather (1991) for a review of such studies.

1.2.1 Diagnostics

After fitting a model, a residual analysis is performed to check for quality of fit and anomalies. A standard diagnostic tool for a LS fit is the scatterplot of residual versus fitted values. A random scatter indicates a good fit, while patterns in the plot indicate a poor fit and, often, lead to the subsequent fitting of more adequate models. For example, suppose the true model is of the form

$$\displaystyle{ \boldsymbol{Y } =\boldsymbol{ 1}\alpha +\boldsymbol{ X}\boldsymbol{\beta } +\boldsymbol{ Z}\boldsymbol{\gamma } +\boldsymbol{ e}, }$$
(1.17)

where \(\boldsymbol{Z}\) is an n × q matrix of constants and \(\boldsymbol{\gamma }=\boldsymbol{\theta } /\sqrt{n}\), \(\boldsymbol{\theta }\not =\boldsymbol{0}\). We fit, though, Model (1.1) using LS; i.e., the model has been misspecified. A straight forward calculation yields

$$\displaystyle{\hat{\boldsymbol{Y }}_{LS} =\alpha \boldsymbol{ 1} +\boldsymbol{ X}\boldsymbol{\beta } +\boldsymbol{ H}\boldsymbol{e} +\boldsymbol{ H}\boldsymbol{Z}\boldsymbol{\gamma }\;\mbox{ and }\;\hat{\boldsymbol{e}}_{LS} =\boldsymbol{ e} -\boldsymbol{ H}\boldsymbol{e} + (\boldsymbol{I} -\boldsymbol{ H})\boldsymbol{Z}\boldsymbol{\gamma },}$$

where \(\boldsymbol{H}\) is the projection matrix onto the range of \(\boldsymbol{X}\). If \(\mbox{ range}(\boldsymbol{Z})\not\subset \mbox{ range}(\boldsymbol{X})^{\perp }\) then both the fitted values and residuals are functions of \(\boldsymbol{Z}\boldsymbol{\gamma }\) and, hence, there will be information in the plot concerning the misspecified model. Note that the function \(\boldsymbol{H}\boldsymbol{e}\) is unbounded; so, based on this representation, outliers in the random errors are diffused throughout the residuals and fitted values. This leads to distortions in the residual plot which, for example, may even mask outliers.

For the rank-based fit of Model (1.1) when Model (1.17) is the true model, it follows from the above linearity results that

$$\displaystyle{\hat{\boldsymbol{Y }}_{rb} =\alpha \boldsymbol{ 1} +\boldsymbol{ X}\boldsymbol{\beta } +\tau _{\varphi }\boldsymbol{H}\boldsymbol{\varphi }[F(\boldsymbol{e})] +\boldsymbol{ H}\boldsymbol{Z}\boldsymbol{\gamma }\;\mbox{ and }\;\hat{\boldsymbol{e}}_{rb} =\boldsymbol{ e} -\tau _{\varphi }\boldsymbol{H}\boldsymbol{\varphi }[F(\boldsymbol{e})] + (\boldsymbol{I} -\boldsymbol{ H})\boldsymbol{Z}\boldsymbol{\gamma }.}$$

Thus, as with LS, there is information in the residual plot concerning misspecified models. Note from the rank-based representation, the function \(\boldsymbol{H}\boldsymbol{\varphi }[F(\boldsymbol{e})]\) is bounded. Hence, the rank-based residual plot is less sensitive to outliers. This is why outliers tend to standout more in residual plots based on robust fits than in residual plots based on LS fits. Other diagnostic tools for rank-based fits are discussed in Chaps. 3 and 5 of Hettmansperger and McKean (2011). Among them are the Studentized residuals. Recall that the ith LS Studentized residual is \(\hat{e}_{LS,i}^{{\ast}} =\hat{ e}_{LS,i}/[\hat{\sigma }\sqrt{1 - (1/n) - h_{i}}]\), where h i is the ith diagonal entry of the projection matrix \(\boldsymbol{H}\) and \(\hat{\sigma }\) is the square root of MSE. Note that \(\hat{e}_{LS,i}^{{\ast}}\) is corrected for both scale and location. Rank-based Studentized residuals are discussed in Sect. 3.9.2 of Hettmansperger and McKean (2011). As with LS Studentized residuals, they are corrected for both location and scale. The usual outlier benchmark for Studentized residuals is ± 2, which we use in the examples below.

1.2.2 Computation

Kloke and McKean (2012, 2014) developed the R package Rfit for the rank-based fitting and analysis of linear models. This package along with its auxiliary package npsm can be downloaded from the site CRAN; see Sect. 1.1 for the url. The Wilcoxon score function is the default score function of Rfit but many other score functions are available in Rfit including the normal scores and the simple bent scores (Winsorized Wilcoxons). Furthermore, users can easily implement scores of their choice; see Chap. 3 of Kloke and McKean (2014) for discussion. In subsequent examples we demonstrate how easy Rfit is to use.

Analogous to least squares, the rank-based analysis can be used to conduct inference for general linear models, i.e., a robust ANOVA and ANCOVA; see Chaps. 3–5 of Hettmansperger and McKean (2011). As an illustration, we end this section with an example that demonstrates how easy the rank-based analysis can be used to test for interaction in a two-way design.

1.2.3 Example

Hollander and Wolfe (1999) provide an example on light involving a 2 × 5 factorial design; see, also, Kloke and McKean (2014) for discussion. The two factors in the design are the light regimes at two levels (constant light and intermittent light) and five different dosage levels of luteinizing release factor (LRF). Sixty rats were put on test under these ten treatments combinations (six repetitions per combination). The measured response is the level of luteinizing hormone (LH), nanograms per ml of serum in the resulting blood samples.

We chose Wilcoxon scores for our analysis. The full model is the usual two-way model with main and interaction effects. The right panel in Fig. 1.1 shows the mean profile plots based on the full model rank-based estimates. The profiles are not parallel indicating that interaction between the factors is present. These data comprise the serumLH data set in Rfit and hence is loaded with Rfit. The Rfit function raov, (robust ANOVA), obtains the rank-based analysis with one line of code as indicated below. The reduction in dispersion test, (1.11), of each effect is adjusted for all other effects analogous to Type III sums of squares in SAS; see Sect. 5.5 of Kloke and McKean (2014). Further, the design need not be balanced. Here is the code and resulting (with some abbreviation) rank-based ANOVA table:

Fig. 1.1
figure 1

Plots for the serum LH data

Full size image

> raov(serum~light.regime+LRF.dose+

       light.regime*LRF.dose, data=serumLH)

Robust ANOVA Table

                      DF        RD      F    p-value

light.regime           1 1642.3332  58.03844 0.00000

LRF.dose               4 3027.6734  26.74875 0.00000

light.regime:LRF.dose  4  451.4559   3.98850 0.00694

As the figure suggested, the factors light regime and LRF dose interact, p = 0. 00694. In contrast, the LS analysis fails to reject interaction at the 5 % level, p = 0. 0729. For this example, at the 5 % level of significance, the rank-based and LS analyses would lead to different interpretations. The left panel of Fig. 1.1 displays the q​ −​ q plot of the Wilcoxon Studentized residuals. This plot indicates that the errors are drawn from a heavy tailed distribution with numerous outliers, which impaired the LS analysis. The estimate of the ARE between the rank-based and least squares analyses is the ratio

$$\displaystyle{ \widehat{ARE} = \frac{\hat{\sigma }^{2}} {\hat{\tau }_{\varphi }^{2}} }$$
(1.18)

where \(\hat{\sigma }^{2}\) is the MSE of the full model LS fit. This is often thought of as a measure of precision. For this example, this ratio is 1.88. So, the rank-based analysis cuts the LS precision by a factor of \(1/1.88 = 0.53\).

In a two-way analysis when interaction is present often subsequent inference involves contrasts of interest. To demonstrate how easy this is accomplished using Rfit, suppose we consider the contrast between the expected response at the peak (factor LRF dose at 3, factor light at the intermittent level) minus the expected response at the peak (factor LRF dose at 3, factor light at the constant level). Of course this is after looking at the data, so we are using this in a confirmatory mode. Our confidence interval is of the form (1.16). Using the following code, it computes to 201. 16 ± 65. 63. The difference is significant.

#  full model fit

fitmod <- rfit(serum~factor(light.regime)+

   factor(LRF.dose)+ factor(light.regime)*

   factor(LRF.dose), data=serumLH)

#  hvec picks the contrast

hvec <- rep(0,60); hvec[27] <- -1; hvec[57] <- 1

# estimate of contrast

contr <- hvec%*%fitmod$fitted.values

# error in CI

se2 <- t(hvec)%*%mat%*%vc%*%t(mat)%*%hvec

# error term in the confidence interval.

err <- qt(.975,50)*sqrt(se2)

1.3 Efficiency and Optimality

In general, the relative efficiency of one statistical method to another, in estimating or testing, is the squared ratio of the slopes in their respective linear approximations. Restricting ourselves to the linear model, (1.1), and rank-based procedures, in light of the asymptotic linearity results, (1.13), such ratios involve the scale parameter τ. In particular, suppose we consider two rank-based methods using the respective score functions φ 1(u) and φ 2(u), and, hence, the norms \(\|\cdot \|_{\varphi _{1}}\) and \(\|\cdot \|_{\varphi _{2}}\). Then the aysmptotic efficiency of method 1 to method 2 is

$$\displaystyle{ e(\|\cdot \|_{\varphi _{1}},\|\cdot \|_{\varphi _{2}}) = \frac{\tau _{2}^{2}} {\tau _{1}^{2}}. }$$
(1.19)

Note by (1.14) that this is the same as the ratio of the asymptotic variances of the associated estimators of the regression coefficients. Values greater than 1 indicate that methods based on \(\|\cdot \|_{\varphi _{1}}\) are superior. The larger slope indicates a more sensitive method, where the slope is τ −1.

For LS, \(e(\|\cdot \|_{\varphi _{1}},\mbox{ LS}) =\sigma ^{2}/\tau _{1}^{2}\), where σ 2 is the variance of the random errors. For comparison with Wilcoxon methods, we already mentioned for location models that e(Wilcoxon, LS) is 0.955 when the error distribution is normal. Hence, e(Wilcoxon, LS) is the same for both linear and location models. Another striking result, due to Hodges and Lehmann (1956), shows that this efficiency is never less than 0.864 and may be arbitrarily large for heavy tailed distributions. In the case of the normal scores methods, the efficiency relative to least squares is 1 at the normal model and never less than 1 at any other model!

An optimality goal is to select a score function to minimize τ φ ; i.e., maximize τ φ −1. We can write expression (1.12) as

$$\displaystyle{ \tau ^{-1} =\int _{ 0}^{1}\varphi (u)\varphi _{ f}(u)\,du, }$$
(1.20)

where

$$\displaystyle{ \varphi _{f}(u) = -\frac{f^{{\prime}}[F^{-1}(u)]} {f[F^{-1}(u)]}. }$$
(1.21)

Recall that the scores have been standardized so that ∫ φ 2(u) du = 1. Hence τ −1 can be expressed as

$$\displaystyle\begin{array}{rcl} \tau ^{-1}& =& \frac{\int _{0}^{1}\varphi (u)\varphi _{ f}(u)\,du} {\sqrt{\int _{0 }^{1 }\varphi ^{2 } (u)\,du}\sqrt{\int _{0 }^{1 }\varphi _{f }^{2 }(u)\,du}}\left \{\sqrt{ \int _{0}^{1}\varphi _{f}^{2}(u)\,du}\right \} \\ & =& \rho \left \{\sqrt{\int _{0 }^{1 }\varphi _{f }^{2 }(u)\,du}\right \}. {}\end{array}$$
(1.22)

The first factor on the right in the first line is a correlation coefficient which we have indicated by ρ. Thus τ −1 is maximized if we select the score function to be φ f (u), (standardized form). This makes the correlation coefficient 1 and τ φ −1 equal to the term in the braces. This term, though, is the square-root of Fisher information. Therefore, by the Rao-Cramér lower bound, the choice of φ f (u) as the score function leads to an asymptotically efficient (optimal) estimator. For the score functions discussed in earlier sections, it follows that the optimal score function for normally distributed errors is the normal score function, for logistically distributed errors is the Wilcoxon score function, and for Laplace distributed errors is the sign score function.

Of course this optimality only can be accomplished provided that the form of f is known. Evidently, the closer the chosen score is to φ f , the more optimal the rank based analysis is. A Hogg-type adaptive scheme where the score function is selected based on initial (Wilcoxon) residuals has proven to be effective; see Sect. 7.6 of Kloke and McKean (2014). McKean and Kloke (2014) successfully modified this scheme for fitting a family of skewed normal distributions.

1.3.1 Monte Carlo Study

To illustrate the optimality discussed above, we conducted a small simulation study of a proportional hazards model. Consider a response variable T with a p × 1 vector of covariates \(\boldsymbol{x}\). Assume T has a Γ(1, ζ) distribution where \(\zeta =\exp \{\boldsymbol{ x}{\prime}\boldsymbol{\beta }\}\) and \(\boldsymbol{\beta }\) is a p × 1 vector of parameters. It follows that

$$\displaystyle{ \log T =\boldsymbol{ x}^{{\prime}}\beta +\epsilon, }$$
(1.23)

where ε has an extreme-valued distribution; see Chaps. 2 and 3 of Hettmansperger and McKean (2011). The optimal scores for this model are the log-rank scores generated by \(\varphi (u) = -1 -\log (1 - u)\).

We simulated this model for the following situation: sample size is n = 20; the covariates are (1, x i ), where \(x_{i} = i/21\); and \(\alpha = -2\) and β = 5. The methods involved are LS and the three rank-based methods: optimal scores (log-rank), Wilcoxon scores, and normal scores. These scores are intrinsic to Rfit. The simulation size is 10,000. To show how simple the coding is, here is the gist of the program’s loop portion for a simulation:

   mu <- exp(alpha + beta*x)

   y <- rgamma(20,1,1/mu); ly <- log(y);

   fitw <- rfit(ly~x)                        # Wil.

   fitly <- rfit(ly~x,scores=logrankscores)  # opt.

   fitns <- rfit(ly~x,scores=nscores)        # ns

   fitls <- lm(ly~x)                         # LS

Table 1.1 presents the empirical relative efficiencies (ratios of mean square errors) for the parameter β. The efficiencies are relative to the optimal rank-based score procedure. The log-rank score procedure is most efficient followed by the normal scores procedure and then the Wilcoxon. Least squares (LS) performed the worst.

Table 1.1 Empirical AREs of estimators of the slope parameter β relative to the rank-based estimator based on the optimal log-rank scores
Full size table

1.4 Influence and High Breakdown

1.4.1 Robustness Properties

In the 1960s and 1970s new tools to assess robustness properties of estimators were developed beginning with Huber (1964) and Hampel (1974). The breakdown value of a location estimator is the (limiting) proportion of the data that must be contaminated in order to carry the value of the estimator beyond any finite bound. In the one sample location model with score function φ +(u), the breakdown for the rank based estimator is ε where

$$\displaystyle{\int _{0}^{1-\epsilon }\varphi ^{+}(u)\,du = \frac{1} {2}\int _{0}^{1}\,\varphi ^{+}(u)\,du.}$$

A simple computation shows that the least squares estimate, the mean, has 0 breakdown point, worst possible. The median has breakdown 0.5, the best possible. The median of the pairwise averages (Wilcoxon score) has breakdown 0.293, while the normal scores estimate has breakdown 0.239.

Another robustness tool, the influence function, is a measure of how fast the estimator changes when an outlier is moved out beyond the edges of the sample. It is provided by the linear approximation of the negative gradient, \(\boldsymbol{S}(\boldsymbol{\beta })\), (1.7). Consider the linear model (1.1). For the rank-based estimator, using the score function φ(u), the influence function is given by:

$$\displaystyle{\varOmega (\boldsymbol{x},y) =\tau \left ( \frac{1} {n}\boldsymbol{X}'\boldsymbol{X}\right )^{-1}\varphi (F(y))\boldsymbol{x},}$$

where \((\boldsymbol{x},y)\) is the value at which we evaluate the influence. When the score function is bounded the influence is bounded in the \(\boldsymbol{y}\)-space. However, note that influence is unbounded in factor space. In the case of the location model, the influence functions for the median and the median of the pairwise averages are both bounded. Note also that least squares estimators have unbounded influence functions in both the \(\boldsymbol{y}\)- and the \(\boldsymbol{X}\)-spaces.

For most designed experiments and for designs with predictors which are well behaved, the rank-based estimators offer a robust and highly efficient alternative to LS for fitting and analyzing linear models. In the case of messy predictors, though, a robust alternative with bounded influence in factor space and positive breakdown is most useful. In fact a primary use of such fits is to highlight the difference between its fit and that of a highly efficient robust fit and, thus, alerting the user to possible anomalies in factor space. We next discuss a high breakdown rank-based (HBR) fit and its accompanying diagnostics which serve this purpose.

1.4.2 High-Breakdown and Bounded Influence Rank-Based Estimates

For the linear model, Chang et al. (1999) developed a rank-based estimator that has bounded influence and can achieve a 50 % breakdown point. It is a weighted version rank-based Wilcoxon fit. By the identity (1.9), the Wilcoxon estimator minimizes the least absolute deviations of the differences of the residuals. Let {b ij } be a set of nonnegative weights. Consider estimators which minimize

$$\displaystyle{ \hat{\boldsymbol{\beta }}= \mbox{ Argmin}\sum _{i<j}b_{ij}\vert (y_{i} -\boldsymbol{ x}_{i}'\boldsymbol{\beta }) - (y_{j} -\boldsymbol{ x}_{j}'\boldsymbol{\beta })\vert. }$$
(1.24)

If the weights are all 1, then this is the Wilcoxon estimator.

Chang et al. (1999) proposed weights which are both functions of factor space and residual space. For factor space, it uses robust distances based on the high breakdown minimum covariance determinant (MCD) which is an ellipsoid in p-space that covers about half the data. For residual space, it uses the high breakdown least trim squares (LTS) fit for an initial fit. See Rousseeuw and Van Driessen (1999).

A brief description of the weights are given next. These are the weights defined for the R function hbrfit which are in the R package npsmReg2 and are discussed in Sects. 7.2 and 7.3 of Kloke and McKean (2014). This package can be downloaded at the github site indicated at the end of Sect. 1.1.

Let \(\hat{\boldsymbol{e}}_{0}\) denote the residuals from the initial LTS fit. Let \(\boldsymbol{V }\) denote the MCD with center \(\boldsymbol{v}_{c}\). Define the function ψ(t) by \(\psi (t) = 1,\;t,\;\;\mbox{ or}\;\; - 1\) according as t ≥ 1, − 1 < t < 1, or t ≤ −1. Let σ be estimated by the initial scaling estimate \(\mbox{ MAD} = 1.483\;\mbox{ med}_{i}\vert \hat{e}_{i}^{(0)} -\mbox{ med}_{j}\{\hat{e}_{j}^{(0)}\}\vert \;\). Letting \(Q_{i} = (\boldsymbol{x}_{i} -\boldsymbol{ v}_{c})^{{\prime}}\boldsymbol{V }^{-1}(\boldsymbol{x}_{i} -\boldsymbol{ v}_{c})\), define

$$\displaystyle{m_{i} =\psi \left ( \frac{b} {Q_{i}}\right ) =\min \left \{1, \frac{b} {Q_{i}}\right \}.}$$

Consider the weights

$$\displaystyle{ \hat{b}_{ij} =\min \left \{1, \frac{c\hat{\sigma }} {\vert \hat{e}_{i}^{(0)}\vert } \frac{\hat{\sigma }} {\vert \hat{e}_{j}^{(0)}\vert }\min \left \{1, \frac{b} {\hat{Q}_{i}}\right \}\min \left \{1, \frac{b} {\hat{Q}_{j}}\right \}\right \}, }$$
(1.25)

where b and c are tuning constants. We set b at the upper χ . 05 2(p) quantile and c is set as

$$\displaystyle{c = [\mbox{ med}\{a_{i}\} + 3MAD\{a_{i}\}]^{2},}$$

where \(a_{i} =\hat{ e}_{i}^{(0)}/(MAD \cdot Q_{i})\). From this point-of-view, it is clear that these weights downweight both outlying points in factor space and outlying responses. Note that the initial residual information is a multiplicative factor in the weight function. Hence, a good leverage point will generally have a small (in absolute value) initial residual which will offset its distance in factor space.

In general, the HBR estimator has a 50 % breakdown point, provided the initial estimates used in forming the weights have 50 % breakdown. Further, its influence function is a bounded function in both the Y and the \(\boldsymbol{x}\)-spaces, is continuous everywhere, and converges to zero as the point \((\boldsymbol{x}^{{\ast}},Y ^{{\ast}})\) gets large in any direction. The asymptotic distribution of \(\hat{\boldsymbol{\beta }}_{HBR}\) is asymptotically normal. As with all high breakdown estimates, \(\hat{\boldsymbol{\beta }}_{HBR}\) is less efficient than the Wilcoxon estimates but it regains some of the efficiency if the weights depend only on factor space.

McKean et al. (1996) developed diagnostics to detect differences in highly efficient and high breakdown robust fits. Their diagnostic TDBETA measures the total difference in fits of the regression coefficients, standardized by the variance-covariance of the Wilcoxon fit. The benchmark is similar to the classic diagnostic DFFITS. A second diagnostic CFITS measures the difference of predicted values at each case. This diagnostic is useful for data sets where TDBETA exceeds its benchmark. Section 7.3 of Kloke and McKean (2014) give a full discussion of these diagnostics with examples. McKean et al. (1999) extended these diagnostics to differences between robust and LS fits. Next, we present an example which illustrates HBR fits and these diagnostics.

1.4.2.1 Stars Data

This data set is drawn from an astronomy study on the star cluster CYG OB1 which contains 47 stars; see Chap. 3 of Hettmansperger and McKean (2011) for discussion. The response is the logarithm of the light intensity of the star while the predictor is the logarithm of the temperature of the star. The scatterplot of the data is in the left panel of Fig. 1.2. Four of the stars, called giants, form a cluster of outliers in factor space while the rest of the stars fall in a point cloud. The panel includes the overlay plot of the Wilcoxon and HBR linear fits. The four giants form a cluster of high leverage points, exerting a strong influence on the Wilcoxon fit while having a minor influence on the HBR fit. The diagnostic TDBETAS between the Wilcoxon and HBR fits has the value 67.92 which exceeds the benchmark of 0.340, indicating a large difference in the fits. The right panel of Fig. 1.2 shows the values of the diagnostic CFITS versus case. The benchmark for this diagnostic is 0.34. The four largest values are the four giant stars. Hence, for this data set, the diagnostics work. The diagnostic TDBETAS alerts the user to the large difference between the fits and CFITS indicates the major points contributing to this difference. The next two largest CFITS values are of interest to astronomers, also. These are stars between the giants and the main sequence stars. Although not shown, the least squares fit is similar to the Wilcoxon fit. The fits and diagnostics can be computed with the following code:

Fig. 1.2
figure 2

The left panel displays the scatterplot of the log of light intensity versus the temperature of the star, overlaid with the Wilcoxon and HBR fits. The right panel displays the values of CFITS versus the case numbers. The horizontal line is the benchmark value

Full size image

fitw <- rfit(lintensity ~ temp)

fith <- hbrfit(lintensity ~ temp)

fitls <- lm(y ~ x)

fitsdiag <- fitdiag(temp,lintensity,est=c("WIL",

                    "HBR"))

1.5 Extensions to Mixed and Nonlinear Models

In the past 20 years, there have been extensions of the rank-based analysis to many other models. This includes nonlinear models and models with dependency among the responses. In this section, we briefly discuss a few of these models, ending with an example involving a mixed model.

For traditional least squares-based methods for these models, the geometry essentially remains the same in that least squares estimation is based on minimizing the squared-Euclidean distance between the vector of responses and the region of estimation. This is true of the rank-based approach, also, except that the rank-based norm, (1.3), replaces the squared-Euclidean norm.

1.5.1 Multivariate Linear Models

Davis and McKean (1993) extended the linear model rank-based procedures for general score functions to the multivariate linear model. They developed asymptotic theory for the estimators and tests of linear hypotheses of the form \(\boldsymbol{A}\boldsymbol{\beta }\boldsymbol{K}\) for the matrix of regression coefficients \(\boldsymbol{\beta }\). See Sect. 6.6 in Hettmansperger and McKean (2011) for discussion and examples. These are component wise estimators, so computations can be based on the package Rfit; see the web site indicated at the end of Sect. 1.1 to download a preversion of the package Rfitmult. These methods are regression equivariant but they are not affine invariant. Oja (2010) and his collaborators developed affine invariant rank-based procedures for Wilcoxon scores using a transformation retransformation procedure. Nordhausen and Oja (2011) developed the R package MNM, downloadable at CRAN, to compute these affine procedures.

1.5.2 Nonlinear Linear Models

For responses y i , consider a nonlinear model of the form \(y_{i} = g(\boldsymbol{\theta },\boldsymbol{x}_{i}) + e_{i}\), i = 1, …, n, where g is a specified nonlinear function, \(\boldsymbol{\theta }\) is a k × 1 vector of unknown parameters, and \(\boldsymbol{x}_{i}\) is a p × 1 vector of predictors. Let \(\boldsymbol{y}\) and \(g(\boldsymbol{\theta },\boldsymbol{x})\) denote the corresponding n × 1 vectors. Given a rank score function φ(u), the associated rank-based estimator of \(\boldsymbol{\theta }\) is

$$\displaystyle{\hat{\boldsymbol{\theta }}_{\varphi } = \mbox{ Argmin}\|\boldsymbol{y} - g(\boldsymbol{\theta },\boldsymbol{x})\|_{\varphi },}$$

where \(\|\cdot \|_{\varphi }\) is the norm defined in expression (1.3). Abebe and McKean (2007) obtained asymptotic theory for \(\hat{\boldsymbol{\theta }}_{\varphi }\) for the case of Wilcoxon scores. The efficiency properties of the Wilcoxon estimator are the same as in the linear model case; so, the estimator is highly efficient for the nonlinear model. Abebe and McKean (2013) extended this development to high breakdown rank-based nonlinear estimators of \(\boldsymbol{\theta }\) which have bounded influence in both the response and factor spaces. The R package npsmReg2 contains the R function wilnl which computes these estimators; see Chap. 7 of Kloke and McKean (2014) for further discussion.

1.5.3 Time Series Models

Consider the autoregressive model of order p, Ar(p):

$$\displaystyle\begin{array}{rcl} X_{i}& =& \phi _{0} +\phi _{1}X_{i-1} +\phi _{2}X_{i-2} + \cdots +\phi _{p}X_{i-p} + e_{i} \\ & =& \phi _{0} +\boldsymbol{ Y }_{i-1}'\boldsymbol{\phi } + e_{i},\;\;\;i = 1,2,\ldots,n {}\end{array}$$
(1.26)

where p ≥ 1, \(\boldsymbol{Y }_{i-1} = (X_{i-1},X_{i-2},\ldots,X_{i-p})'\), \(\boldsymbol{\phi }= (\phi _{1},\phi _{2},\ldots,\phi _{p})'\), and \(\boldsymbol{Y }_{0}\) is an observable random vector independent of \(\boldsymbol{e}\). Let \(\boldsymbol{X}\) and \(\boldsymbol{Y }\) denote the corresponding n × 1 vector and the n × p matrix with components X i and \(\boldsymbol{Y }_{i-1}^{{\prime}}\), respectively. For the score function φ(u), the rank-based estimator of \(\boldsymbol{\phi }\) is given by

$$\displaystyle{\hat{\boldsymbol{\phi }}_{\varphi } = \mbox{ Argmin}\|\boldsymbol{X} -\boldsymbol{ Y }'\boldsymbol{\phi }\|_{\varphi },}$$

where \(\boldsymbol{Y }\) is the matrix with rows \(\boldsymbol{Y }_{i-1}^{{\prime}}\). Koul and Saleh (1993) developed the asymptotic theory for these rank-based estimates. Because of the structure of the AR(p) model, outliers in the random errors become ensuing points of high leverage. As a solution to this problem, Terpstra et al. (2000, 2001) proposed estimating \(\boldsymbol{\phi }\) using the HBR estimators of Sect. 1.4. They obtained the corresponding asymptotic theory for these HBR estimators and showed their validity and empirical efficiency in several large simulation studies. Section 7.8 of Kloke and McKean (2014) discusses the computation of these estimates using the R package Rfit.

1.5.4 Cluster Correlated Data

Frequently in practice data are collected in clusters. Common examples include: repeated measures on subjects, experimental designs involving blocks, clinical studies over multiple centers, and hierarchical (nested) designs. Generally, the observations within a cluster are dependent.

For discussion, suppose we have m such clusters. Let y ki denote the ith response within the kth cluster, for i = 1, …, n k and k = 1, …, m, and let \(\boldsymbol{x}_{ki}\) denote the corresponding p × 1 vector of covariates. For cluster k stack the n k responses in the vector \(\boldsymbol{y}_{k}\) and let \(\boldsymbol{X}_{k}\) denote the n k × p matrix with rows \(\boldsymbol{x}_{ki}^{{\prime}}\). Assume a linear model of the form

$$\displaystyle{ \boldsymbol{y}_{k} =\beta _{0}\boldsymbol{1}_{n_{k}} +\boldsymbol{ X}_{k}\boldsymbol{\beta } +\boldsymbol{ e}_{k},\;\;\;k = 1,\ldots,m, }$$
(1.27)

where \(\boldsymbol{e}_{k}\) follows a n k -multivariate distribution and the vectors \(\boldsymbol{e}_{1},\ldots,\boldsymbol{e}_{m}\) are independent. We then stack the vectors \(\boldsymbol{y}_{k}\) and matrices \(\boldsymbol{X}_{k}\) into the vector \(\boldsymbol{Y }\) and matrix \(\boldsymbol{X}\), respectively.

There are several rank-based analyses available for these models. Abebe et al. (2016) develop a rank-based analysis for a general estimating equations (GEE) model which includes models of the form (1.27). This allows for very general dependency structure. For a general score function φ(u), Kloke et al. (2009) developed the asymptotic theory for the rank-based estimator defined in expression (1.5), i.e., the minimizer of the norm \(\|\boldsymbol{Y } -\boldsymbol{ X}\boldsymbol{\beta }\|_{\varphi }\). Their development includes consistent estimators of standard errors and consistent test statistics of general linear hypotheses. The theory requires the additional assumption that the univariate marginal distributions of \(\boldsymbol{e}_{k}\) are the same. This is true for many of the usual models in practice such as simple mixed models (compound symmetry covariance structure) and stationary times series models for the clusters.

The R package jrfit computes the analysis developed by Kloke et al. (2009); see Chap. 8 of Kloke and McKean (2014) for discussion and examples. This includes the fit and several options for the estimation of the covariance structure, including compound symmetry and two general estimators, (a sandwich-type estimator and a general nonparametric estimator). We conclude this discussion with an example which illustrates the use of jrfit on cluster data.

1.5.4.1 Example

For an example, we consider the first base study presented in Hollander and Wolfe (1999). This study investigated three methods of rounding first base for baseball players who are running from home plate to second base. The response is the player’s total running time. The three methods are narrow angle (NA), round out (RP), and wide angle (WA); see Hollander and Wolfe for details. Twenty-two ball players participated in the study and each ran six times, two repetitions for each method. The average time of the two repetitions are the response times available. The data can be found in the firstbase data set in the R package npsmReg2; see Chap. 8 of Kloke and McKean (2014).

Let y ij denote the running time for the jth player on method i and consider the randomized block design given by

$$\displaystyle{ y_{ij} =\mu +\alpha _{i} + b_{j} +\epsilon _{ij}, }$$
(1.28)

where α i denotes the ith treatment fixed effect; b j denotes the random effect for the jth player; and e ij denotes the random error. We assume that the random errors are iid and the random effects are iid with different distributions. We further assume that the random errors and the random effects are independent.

Although, finite variance is not required for the asymptotic theory, for the discussion, we assume finite variances. The variance-covariance structure of Model (1.28) is compound symmetric. Besides fixed effects analyses, we are interested in the estimation of the variance components given by σ b 2 the variance of b j , σ ε 2 the variance of ε ij , and the intraclass correlation coefficient \(\rho =\sigma _{ b}^{2}/(\sigma _{b}^{2} +\sigma _{ \epsilon }^{2})\). Kloke et al. (2009) provided robust estimates of these components based on the rank-based fit of Model (1.28). These estimates have been incorporated into the package jrfit.

The null hypothesis for the fixed effects is \(H_{0}:\alpha _{1} =\alpha _{2} =\alpha _{3} = 0\). The traditional nonparametric test of this hypothesis is based on Friedman’s test statistic, which for this example results in the value of 11.14 with p-value 0. 003. The comparative rank-based analysis is the Wald-type test on the rank-based fit. As shown below, the value of the test statistic is 19.31 with a p-value of 0.0001. As with the Friedman test, the Wald-type test is highly significant. An experimenter, though, wants a much more in depth analysis than just this test of the fixed effects. The left panel of Fig. 1.3 displays the comparative boxplots of the methods. Note that, based on this plot, it appears that the wide-angle method results in the quickest times. Such a judgement is easily confirmed by considering the estimates and confidence intervals for the three pairwise comparisons. These are shown in Table 1.2 based on the rank-based fit. They do confirm that the wide-angle method results in significantly faster times than the other two methods. Furthermore, the estimated effects provide the experimenter with an estimate of how much faster the wide-angle method is than the other two methods.

Fig. 1.3
figure 3

The left panel displays the comparative boxplots for the three methods of rounding first base, while the right panel shows the q​ −​ q plot of the rank-based Studentized residuals

Full size image
Table 1.2 Rank-based estimates of fixed effects and variance components, firstbase data
Full size table

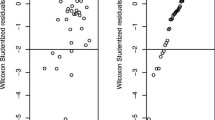
Table 1.2 also displays the robust estimates of the variance components. Note that the estimate of the intraclass correlation coefficient is 0.715 indicating a strong correlation among the times of a runner. The right panel of Fig. 1.3 shows the normal q​ −​ q plot of the Studentized residuals of the rank-based fit. The horizontal lines at ± 2 are the usual benchmark for potential outliers. This plot confirms the outliers in the boxplots and indicates a heavy tailed error structure. The three largest positive outliers correspond to Runner 22 who had the slowest times in all three methods.

The results in Table 1.2 and Fig. 1.3 are based on computations using the package jrfit. Some of the code for the computations is given by:

# The data are in the data set firstbase in the

# package npsmReg2. More discussion of the

# computations can be found in Chapter 8

# of Kloke McKean (2014).

#

# times is the vector of running times; player is

# the indicator of the player; method is the

# indicator of the method.

xmat <- model.matrix(~as.factor(method))[,2:3]

fit <- jrfit(xmat,times,player)

stud <- rstudent(fit) #Studentized residuals

vee(fit$resid,fit$block,method=’mm’) #Var comp.

h1 <-c(0,1,0); h2<-c(0,0,1); hmat<-rbind(h1,h2)

mid <- solve(hmat%*%fit$varhat%*%t(hmat))

tst <- t(hmat%*%fit$coef)%*%mid%*%hmat%*%fit$coef

19.31442

1-pchisq(tst,2)

6.396273e-05

1.6 Conclusion

As we indicated in Sect. 1.1, the rank tests for simple location problems were initially used because of their quick calculation in the pre computer age. These methods were further found to be highly efficient and robust by Hodges and Lehmann in the mid 1950s. The traditional t-tests for these problems, though, are based on least squares (LS) fitting which easily generalizes to much more complicated models, including linear, nonlinear, and models with dependent error structure. For all such models, the LS fitting is based on minimizing the squared-Euclidean distance between the vector (or matrix) of responses and the region (space) of estimation. Further, LS testing of general linear hypotheses is based on a comparison of distances between the vector of responses and full and reduced model subspaces. Also, there are ample diagnostic procedures to check the quality of the LS fit of a model. As in the location problems, though, LS procedures are not robust. Hence, a generalization was needed for the robust nonparametric methods.

As briefly outlined in Sect. 1.2, the extension of nonparametric methods to linear models came about in the late 1960s and early 1970s, with the robust estimation procedures developed by Jurečková and Jaeckel. In particular, as shown by McKean and Schrader (1980), Jaekel’s estimation involves minimizing a distance between the responses and the full model subspace. This distance is based on the norm defined in expression (1.3). For general linear hypotheses, McKean and Hettmansperger (1976) developed an accompanying analysis based on a comparison of distances between the vector of responses and full and reduced model spaces where distance is based on the norm (1.3). Diagnostics for this rank-based analysis were developed by McKean et al. (1990). This rank-based analysis is as general as the traditional LS analysis. As with LS, for any linear model, it offers a complete procedure including fitting, diagnostic checking of the fit, confidence regions, and tests of general linear hypotheses. Details of this analysis are discussed in Chaps. 3–5 of Hettmansperger and McKean (2011).

As discussed in Sect. 1.3, the rank-based analysis is highly efficient. For example, the rank-based procedure based on Wilcoxon scores has efficiency 0.955 relative to LS procedures when the random errors are normally distributed and is much more efficient when the distribution of the random errors has heavy tails. Further, if the form of the error distribution is known, then optimal scores can be used which results in fully asymptotically efficient procedures. Rank-based procedures based on minimizing the norm (1.3) are robust in response space but, similar to LS procedures, are not robust in factor space. A simple weighting scheme, based on robust distances in factor space and residuals from an initial robust fit, leads to a robust rank-based procedure which is robust in both response and factor space as well as having a 50 % breakdown point.

As reviewed in Sect. 1.5, these rank-based procedures have been extended to nonlinear models and models in which the errors have dependencies. For these models, LS fitting is still based on minimizing squared-Euclidean distance between the responses and the space of estimation. In the same way, the rank-based fitting of these models is obtained by minimizing the distance based on the norm (1.3). In recent years, asymptotic theory has been developed for these rank-based procedures. Hence, besides linear models, robust rank-based procedures exist for diverse models, including nonlinear models, autoregressive times series models, multivariate regression models, mixed models, and hierarchical models.

The easy computation of rank-based analyses is performed with R software. For linear models, the package Rfit offers a complete computation for the rank-based analysis. A wide variety of scores functions are intrinsic to the package with an option for user-supplied scores. For models other than linear there are accompanying R packages for computations. We have discussed the computation based on these packages throughout this paper. See Kloke and McKean (2014) for discussion of these packages.