Graph-Theoretic Modelling and Sensitivity Analysis of Dynamic Systems

Abstract

In this paper, a graph-theoretic formulation is presented that can be used to generate governing equations for dynamic systems in a flexible, automated and efficient fashion. Furthermore, a modified formulation is presented to demonstrate the applicability of graph-theoretic methods to generate the sensitivity equations for dynamic systems. An example is provided, in which the new graph-theoretic formulation is used to generate the governing and sensitivity equations simultaneously from the linear graph representation of the systems.

1 Introduction

One of the first uses of a linear graph was done by the famous mathematician Leonhard Euler in 1736 [1]. Later, researchers like Koenig et al. [2] extended the use of a linear-graph as a unified system modelling theory. Subsequently, graph-theoretic formulations have been successfully applied to model electrical circuits [3], mechanical/mechatronics systems [4], hydro-mechanical [5] and electro-chemical systems [6]. In this paper, a graph-theoretic formulation will be presented for automated generation of governing and sensitivity equations. First, basics of graph-theoretic modelling methods and analytical sensitivity studies will be introduced. Next, the process of graph-theoretic generation of governing equations and sensitivity equations will be presented. Finally, the theory presented in this paper will be further clarified using an example problem.

1.1 Graph-Theoretic Modelling of Dynamic Systems

To present the process of graph-theoretic modelling and sensitivity analysis, it is necessary to define certain key concepts. Figure 1 shows a simple spring-mass-damper system and the corresponding linear graph representation. The linear graph is comprised of nodes (G and A) and edges (k, c, m, F, and s). For multibody systems, nodes represent frames of reference. In Fig. 1, the node G represents the frame of reference fixed to the ground, whereas the node A refers to the frame of reference fixed to the center of the mass of the body. For other systems, (e.g. electrical circuits, hydraulic circuits), the nodes represent specific points in the system where measurements are made.

Fig. 1

Spring-mass-damper system and the corresponding linear graph

The edges of a linear graph represent various measurements, and their arrow directions denote the positive directions for those measurements. Depending on the nature of these quantities they are divided into two broad categories called through variables (e.g. current, flow rate, force, and torque) and the across variables (e.g. voltage difference, pressure difference, position, velocity, acceleration etc.). Functionally, these measurements are often associated with various components that constitute the system. In the linear graph shown above, the edge k corresponds to the spring, the edge m corresponds to inertia, c refers to the damper, F refers to the applied force, and the edge s corresponds to the slider joint.

In multibody systems, the edges are associated with through and across variables from both translational and rotational domains. On the other hand, for scalar systems (e.g. electrical circuits), the edges are usually associated with one through variable (current) and one across variable (voltage difference).

To continue this presentation, a few key terms need to be introduced. In the linear graph G shown in Fig. 1, which has e = 5 edges and n = 2 nodes, the following terms are defined.

A tree of a linear graph G is a connected sub-graph of G that contains all the nodes of G and has only one unique path between any two nodes. Edges of the tree are known as branches. A tree in G can have w = n − 1 branches. In Fig. 1, one possible tree selection could be the edge m. A cotree is the part of the graph G which remains after removing the tree. The edges of a cotree are called chords. In Fig. 1, if edge m is selected as the tree, the edges k, c, F, and s will become chords. In any graph, there can be u = e – n + 1 chords in the cotree.

A cutset is a subset of the graph G, which when removed from G, divides it into two parts in such a way that no subset of it can exist. An f-cutset is a cutset that contains exactly one branch and a unique set of chords. In any graph G, there can be ‘w’ f-cutsets.

A circuit is a sub-graph of G where every pair of nodes has exactly two distinct paths between them. In Fig. 1, the edges m and c form a circuit. An f-circuit is a circuit in G, which contains exactly one chord and a unique set of branches. In any graph G, there can be ‘u’ f-circuits.

The f-cutsets and the f-circuits are dependent on the choice of the tree branches. In the tree structure shown in Fig. 1 in bold lines, there is one f-cutset (the edges [m, k, c, F, s]) and four f-circuits (the edges [k, m], [c, m], [F, m], [s, m]).

Using these properties of a linear graph, a graph-theoretic method can be formulated to capture the topology of any dynamic system and derive both the governing and sensitivity equations for it.

1.2 Sensitivity Analysis of Dynamic Systems

Sensitivity analysis refers to the study of changes in system behavior brought in by the changes in entities inherent to the system. Mathematically, it is a problem of finding the derivatives of the state variables of a system with respect to the system parameters. It is routinely used in many engineering applications like design and optimization of physical systems, model simplification, and optimal control. For complex and/or large scale systems, however, this process can become complicated.

For models where symbolic equations are available, sensitivity analysis can be performed by the direct differentiation method. In this method a set of sensitivity equations are derived from the governing equations by symbolic differentiation. By solving these sensitivity equations, the corresponding sensitivity information is obtained as functions of time.

Direct differentiation sensitivity analysis is portable, easy to implement, stable, and produces results that are numerically exact. This method has been used to perform sensitivity analysis for systems governed by kinematic equations [7], differential equations [8–10] and also differential-algebraic equations [11].

Since it requires the solution of an increased number of equations, this method can become intractable for systems with a large number of parameters, especially if the size of the system is also large. To address this drawback, a graph-theoretic framework has been developed by Banerjee and McPhee [12]. In this formulation, the sensitivity equations are generated directly from the linear graph of the system using the very procedure used to generate the governing equations.

The graph-theoretic formulation uses direct differentiation as the underlying method, but instead of symbolically differentiating the governing equations after the fact, it stores the pre-formed expressions of the derivatives as sensitivity constitutive equations and evaluates them as needed. Figures 2 and 3 summarize the difference between direct differentiation and the proposed graph-theoretic sensitivity analysis. The following sections will illustrate the process of generation of the governing equations and the sensitivity equations.

Fig. 2

Direct differentiation method

Fig. 3

Graph-theoretic method

2 Generation of Governing and Sensitivity Equations

The graph-theoretic formulation presented by Banerjee and McPhee [12] uses two topologically identical linear graphs G₁ and G₂ (vide Fig. 1) to generate the required equations. The through variables associated with the edges of the graph G₁ are the forces/torques acting between the two frames of reference (G and A) whereas the associated across variables are the position, velocity, and acceleration (both translational and rotational) of frame A with respect to frame G. The through and across variables associated with the edges of graph G₂ (sensitivity graph) are defined to be the derivatives of the variables associated with G₁ with respect to the desired model parameter. A complete list of translational through and across variables are given in Table 1, where the subscripts used in the variable names denote the differentiation with respect to the model parameter appearing as a subscript.

Table 1 Translational through and across variables for G₁ and G₂

In any dynamic system, two types of equations govern these through and across variables. These can be either topological equations, which are equations that describe how through variables (or across variables) of different edges are related to each other, or constitutive equations, which are equations that describe how the through variables are related to the across variables. Functionally, the topological equations describe the connectivity of the different components of the system and can be readily derived from the linear graph of the system, whereas the constitutive equations describe the physical nature of the components and must be specified prior to the derivation.

To derive a compact form of equations, this paper will use a branch-chord formulation, where the first step is the selection of two trees for the graphs G₁ and G₂. For this demonstration, the edge m is selected as the tree for both trees and for both translational and rotational domains (bold line). This formulation uses a particular form of topological equations known as the f-cutset equations (for through variables) and f-circuit equations (for across variables). For the graph shown in Fig. 1, the translational f-cutset equations for the graphs G₁ and G₂ are shown in Eq. (1).

$$\begin{array}{*{20}l} {{\text{G}}_{ 1} {:}\; \bar{F}^{m} + \bar{F}^{k} + \bar{F}^{c} + \bar{F}^{F} + \bar{F}^{s} = 0,} \hfill \\ {{\text{G}}_{ 2} {:}\;\bar{F}_{k}^{m} + \bar{F}_{k}^{k} + \bar{F}_{k}^{c} + \bar{F}_{k}^{F} + \bar{F}_{k}^{s} = 0.} \hfill \\ \end{array}$$

(1)

These equations describe how the different through variables are related to each other, as constrained by the topology of the system. Similar equations governing the across variables are known as f-circuit equations. The translational f-circuit equations are shown in Eq. (2).

$$\begin{array}{*{20}l} {{\text{G}}_{ 1} {:}\,\left\{ { - \bar{r}^{m} + \bar{r}^{i} = 0} \right\}\left\{ { - \dot{\bar{r}}^{m} + \dot{\bar{r}}^{i} = 0} \right\}\left\{ { - \ddot{\bar{r}}^{m} + \ddot{\bar{r}}^{i} = 0} \right\}\quad i = k,\,c,\,F,\,s,} \hfill \\ {{\text{G}}_{ 2} {:}\,\left\{ { - \bar{r}_{k}^{m} + \bar{r}_{k}^{k} = 0} \right\}\left\{ { - \dot{\bar{r}}_{k}^{m} + \dot{\bar{r}}_{k}^{k} = 0} \right\}\left\{ { - \ddot{\bar{r}}_{k}^{m} + \ddot{\bar{r}}_{k}^{k} = 0} \right\}\quad i = k,\,c,\,F,\,s.} \hfill \\ \end{array}$$

(2)

The main benefit of using a branch-chord formulation is that it makes it possible to express the branch through variables in terms of the chord through variables (using f-cutset equations) and to express the chord across variables in terms of the branch across variables (using f-circuit equations). This opens up the possibility of reducing, by substitution, the number of unknowns in the generated equations. Further details are provided by Banerjee [13].

As mentioned before, the constitutive equations for the system must be specified prior to the derivation process. These equations govern how the through variables are related to the across variables depending on the nature of the associated components. For multibody systems, it is necessary to define these equations for both translational and rotational domains. A list of the translational constitutive equations for the graph G₁ is given in Eq. (3).

$$\begin{array}{*{20}l} {\bar{F}^{m} = - m\ddot{\bar{r}}^{m} } \hfill & {\bar{F}^{F} = F(t)\,\hat{i}} \hfill & {\bar{r}^{m} = x\left( t \right)\hat{i},} \hfill \\ {\bar{F}^{c} = - c\dot{\bar{r}}^{c} } \hfill & {\bar{F}^{k} = - k\left( {\bar{r}^{k} - l_{0} \hat{i}} \right)} \hfill & {\bar{F}^{s} = 0.} \hfill \\ \end{array}$$

(3)

For graph-theoretic sensitivity analysis the equations associated with G₂ is defined as the derivatives of those from G₁ with respect to the model parameter. Assuming the spring constant k as the model parameter the constitutive equations can be written down as shown in Eq. (4), (subscripts refer to derivatives).

$$\begin{array}{*{20}l} {\bar{F}_{k}^{m} = - m\ddot{\bar{r}}_{k}^{m} } \hfill & {\bar{F}_{k}^{F} = 0} \hfill & {\bar{r}_{k}^{m} = x_{k} \left( t \right)\hat{i},} \hfill \\ {\bar{F}_{k}^{c} = - c\dot{\bar{r}}_{k}^{c} } \hfill & {\bar{F}_{k}^{k} = - \left( {\bar{r}^{k} - l_{0} \hat{i}} \right) - k\bar{r}_{k}^{k} } \hfill & {\bar{F}_{k}^{s} = 0.} \hfill \\ \end{array}$$

(4)

Apart from the constitutive equations, to capture the nature of the constraint the joints enforce on the system, it is also necessary to specify the motion spaces and the reaction spaces for the joints. The motion space of a joint is defined as the span of directions along which motions are allowed by that joint and the reaction spaces are the span of directions along which the joint does not allow motion to take place and offer reactive forces and torques. For example, in an ideal prismatic joint, the translational motion space is the sliding direction, and the rotational motion space is null. At the same time, its translational reaction space contains the two directions normal to the slider direction and the rotational reaction space contains all three of the principal directions.

To generate the equations using graph-theoretic formulation, the first step is the substitution of the constitutive equations into the f-cutset equations obtained from the rigid bodies or joints present in the tree and the projection (scalar product) of the resulting equations on to the corresponding motion spaces. The projected equations are shown in Eq. (5). Since the rotational motion space is null, the rotational f-cutset equations do not generate any new equation in this step.

$$\begin{array}{*{20}l} {{\text{G}}_{ 1} :\,\left( { - m\ddot{\bar{r}}^{m} - k\left( {\bar{r}^{k} - l_{0} \hat{i}} \right) - c\dot{\bar{r}}^{c} + F(t)\,\hat{i} = 0} \right) \cdot \hat{i},} \hfill \\ {{\text{G}}_{ 2} :\,\left( { - m\ddot{\bar{r}}_{k}^{m} - \left( {\bar{r}^{k} - l_{0} \hat{i}} \right) - k\bar{r}_{k}^{k} - c\dot{\bar{r}}_{k}^{c} = 0} \right) \cdot \hat{i}.} \hfill \\ \end{array}$$

(5)

The next step is the elimination of the secondary variables (i.e. branch through variables and chord across variables). Using the equations shown in (1)–(2), the chord across variables (i.e. across variables from the edges k, c, F, and s) are replaced with the branch across variables (i.e. across variables from the edge m). This results in the equations shown in Eq. (6).

$$\begin{array}{*{20}l} {{\text{G}}_{ 1} :\,\left( { - m\ddot{\bar{r}}^{m} - k\left( {\bar{r}^{m} - l_{0} \hat{i}} \right) - c\dot{\bar{r}}^{m} + F(t)\,\hat{i} = 0} \right) \cdot \hat{i},} \hfill \\ {{\text{G}}_{ 2} :\,\left( { - m\ddot{\bar{r}}_{k}^{m} - {\kern 1pt} \left( {\bar{r}^{m} - l_{0} \hat{i}} \right) - k\bar{r}_{k}^{m} - c\dot{\bar{r}}_{k}^{m} = 0} \right) \cdot \hat{i}.} \hfill \\ \end{array}$$

(6)

Using the constitutive equations one more time, Eq. (6) can be readily simplified into two second-order ordinary differential equations as shown in equation

$$\begin{array}{*{20}l} {{\text{G}}_{ 1} :\, - m \ddot{\textit{x}} - k\left( {x - l_{0} } \right) - c\dot{x} + F(t) = 0 \Rightarrow m\ddot{\textit{x}} + k\left( {x - l_{0} } \right) + c\dot{x} = F(t),} \hfill \\ {{\text{G}}_{ 2} :\, - m\ddot{\textit{x}} _{k} - \left( {x - l_{0} } \right) - kx_{k} - c\dot{x}_{k} = 0 \Rightarrow m\ddot{\textit{x}} _{k} + \left( {x - l_{0} } \right) + k{\kern 1pt} x_{k} + c\dot{x}_{k} = 0.} \hfill \\ \end{array}$$

(7)

The second equation in (7) is the sensitivity equation of the system with respect to the model parameter k. This demonstrates that the presented graph-theoretic formulation can generate the governing equations and the sensitivity equations directly from the linear graph simultaneously. If sensitivities with respect to a second parameter is required, a third graph G₃ can be defined to generate the corresponding equations. Further details of this process can be found in reference [12].

3 Example Problem

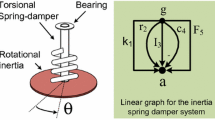
Figure 4 shows a simple mechanism with its linear graph representation. It constitutes two rigid bodies of masses m₁ = 1 kg and m₂ = 5 kg, connected by a revolute joint that includes a torsional damper with damping coefficient ξ = 10 N m s/rad. The parameters L = 1 m and r = 0.03 m represent the length and radius of cross-section of the pendulum. The sliding block is allowed to move along a prismatic joint and is connected to a linear spring of spring constant k = 50 N/m and unstretched length s₀ = 0.50 m. The gravity g = 9.81 m/s² acts in the downward direction. The nodes A and C represent the frames of reference fixed to the two centers of mass, G refers to the ground, and B refers to the frame of reference fixed to the body m₂ at the hinge point of the pendulum. The edges m₅, m₆ correspond to the inertia, j₁ refers to the slider joint, h₂ is the revolute joint, r₃ and r₄ are body fixed vectors.

Fig. 4

Slider-pendulum with linear graph

In branch-chord formulation, the choice of tree determines the state variables of the system. For the system shown in Fig. 4, if the edges m₅, m₆, r₃, and r₄ are selected as branches (for both translational and rotational domain), the equations are generated in terms of the absolute coordinates (i.e. position and orientation of the two bodies), but if the edges j₁, h₂, r₃ and r₄ are selected as branches (both translational and rotational), the equations are generated in terms of the slider displacement s and the revolute joint angle.

For this example the latter choice is used for the equation generation. By using the formulation presented in this paper, the governing equations are generated for this system as shown in Eq. (8).

$$\begin{array}{*{20}c} {m_{{{\mkern 1mu} 2}} \left( {{{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } 4}} \right. \kern-0pt} 4} + {{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } 3}} \right. \kern-0pt} 3}} \right)\ddot{\theta } + m_{{{\mkern 1mu} 2}} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\cos \theta \, \ddot{\textit{s}} + m_{{{\mkern 1mu} 2}} g\left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\sin \theta + \xi \dot{\theta } = 0,} \\ {m_{2} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\cos \theta \,\ddot{\theta } + \left( {m_{1} + m_{2} } \right) \ddot{\textit{s}} - m_{2} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\sin \theta \,\dot{\theta }^{{{\mkern 1mu} 2}} + k\left( {s - s_{0} } \right) = 0.} \\ \end{array}$$

(8)

By selecting the parameter L for sensitivity analysis the sensitivity graph G₂ results in the equations shown in Eq. (9).

$$\begin{array}{*{20}l} {m_{2} \left( {{\mkern 1mu} {{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } 4}} \right. \kern-0pt} 4} + {{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } 3}} \right. \kern-0pt} 3}} \right)\ddot{\theta }_{L} + \frac{{m_{2} {\mkern 1mu} }}{2}\left( {\cos \theta - L\sin \theta {\mkern 1mu} \theta_{L} {\mkern 1mu} } \right) \ddot{\textit{s}} + m_{2} {\mkern 1mu} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\cos \theta \, \ddot{\textit{s}} _{L} + \varUpsilon_{3} = 0} \hfill \\ {m_{1} {\mkern 1mu} \ddot{\textit{s}} _{L} + m_{2} \left( {\ddot{\textit{s}} _{L} + {\mkern 1mu} \left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\cos \theta \,\ddot{\theta }_{L} + \varUpsilon_{1} } \right) + ks_{L} = 0} \hfill \\ \end{array}$$

(9)

$$\begin{aligned} \varUpsilon_{3} & = 2m_{2} \left( {{L \mathord{\left/ {\vphantom {L 3}} \right. \kern-0pt} 3}} \right)\ddot{\theta } + \left( {{{m_{2} } \mathord{\left/ {\vphantom {{m_{2} } 2}} \right. \kern-0pt} 2}} \right)g\sin \theta + m_{2} g\left( {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0pt} 2}} \right)\cos \theta \,\theta_{L} + \xi \dot{\theta }_{L} \\ \varUpsilon_{1} & = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\left( {\cos \theta - L\sin \theta \,\theta_{L} } \right)\ddot{\theta } - \left( {L\sin \theta {\mkern 1mu} \dot{\theta }} \right)\dot{\theta }_{L} - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\left( {\sin \theta + L\cos \theta \,\theta_{L} } \right)\dot{\theta }^{\,2}. \\ \end{aligned} $$

(10)

It can be readily verified that the equations shown in (9) are the symbolic derivatives of the governing equations shown in Eq. (8). The initial conditions for the combined Eqs. (8) and (9) are shown in Eq. (11). The rest of the state variables are initiated at zero. The Runge-Kutta-Fehlberg method was used for numerical simulation.

$$\begin{array}{*{20}c} {s\left( 0 \right) = 0.5\;{\text{m}}} & {\dot{s}\left( 0 \right) = 1} \\ \end{array} \;{\text{m}}/{\text{s}} .$$

(11)

Figures 5 and 6 clearly identify the response of the system and validate the solution of the generated sensitivity equations. Figure 5 shows that the values of s(t) and θ(t) settles after initial oscillations, which is expected for the damped system. The behavior of s_L(t) can also be explained by considering the structure of the system. By considering the configuration of the system, it can be clearly seen that for different values of the parameter L, the resulting output of s(t) always approaches the same datum level s₀ asymptotically. As a result the sensitivity of s(t) with respect to the parameter L also oscillates and then settles to zero. To validate the sensitivity results the solution of the sensitivity equations were compared with those obtained by finite difference formulation. The comparison, as shown in Fig. 6, validates the sensitivity results obtained through the presented graph-theoretic formulation.

Fig. 5

Simulation results

Fig. 6

Sensitivity s_L versus time

4 Conclusions

A graph-theoretic formulation is presented in this paper that can be used to generate governing equations for dynamic systems in an automated and algorithmic fashion. The graph-theoretic method has been demonstrated to be able to derive equations from a pictorial description of the system called the linear graph. The method has been demonstrated in details using the example of a spring-mass-damper system. Concurrently, a graph-theoretic framework is presented that can be used to perform symbolic sensitivity analysis of dynamic systems. This framework is capable of generating symbolic sensitivity equations for the systems using the same algorithmic steps used in traditional graph-theoretic modelling techniques. The simultaneous generation of governing and sensitivity equations have been presented using an example of a sliding pendulum.