Perspectives of Model Transformation Reuse

Abstract

Model Transformations have been called the “heart and soul” of Model-Driven software development. However, they take a lot of effort to build, verify, analyze, and debug. It is thus imperative to develop good reuse strategies that address issues specific to model transformations. Some of the effective reuse strategies are adopted from other domains, specifically, programming languages. Others are custom developed for models. In this paper, we survey techiques from both categories.

Specifically, we present two techniques adoped from the PL world: subtyping and mapping, and then two techniques, lifting and aggregating, that are novel in the modeling world. Subtyping is a way to reuse a transformation for different - but similar - input modelling languages. Mapping a transformation designed for single models reuses it for model collections, such as megamodels. Lifting a transformation reuses it for aggregate representations of models, such as product lines. Aggregating reuses both transformation fragments (during transformation creation) and partial execution results (during transformation execution) across multiple transformations.

We then point to potential new directions for research in reuse that draw on the strengths of the programming and the modeling worlds.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Model-Driven Engineering (MDE) is a powerful approach used in industry for managing the complexity of large scale software development. MDE helps manage this complexity by using models to raise the level of abstraction at which developers build and analyze software and transformations to automate the various engineering tasks that apply to models. Model Transformations have been called the “heart and soul” of Model-Driven software development [30], and they are used to perform various manipulations on models, such as adding detail, refactoring, translating to a different formalism, generating code, etc. They have certain particular characteristics: (1) They are aimed, at least in principle, to accomplish a well-defined one-step “task” with a specific intent. Transformations are often chained together to form more complex tasks, much like pipelining processes in Unix. (2) They are also strongly typed, by the types of models they take as input and produce as output. (3) Since models are essentially typed graphs, transformations are often implemented using specialized languages that allow easy manipulation of graphs.

Because transformations are central to success of MDE, it is imperative to develop good reuse strategies for them. Since transformations are specialized programs, any attempt to study transformation reuse must answer the question: how is transformation reuse different from or similar to program reuse? This implies two perspectives of model transformation reuse. On the one hand, we can approach it as a problem of adapting, generalizing and/or “reinventing” techniques already understood in the context of program reuse. On the other hand, we can identify areas in which the MDE setting provides opportunities for creating novel reuse techniques, specific to the kinds of abstractions and usage scenarios found in modelling.

In this paper, we attempt to study transformation reuse from both of these perspectives, by illustrating examples of reuse mechanisms in each one. We show two examples of techniques, namely subtyping and mapping, that are adapted from program reuse. Specifically: (1) subtyping is a way to reuse a transformation for different – but similar – input modelling languages; and (2) mapping a transformation designed for single models reuses it for model collections, such as specialized model collections used in MDE called megamodels. We then show two MDE-specific reuse techniques, namely, lifting and aggregating that leverage the unique way in which MDE represents variability. Specifically: (3) lifting a transformation reuses it for aggregate representations of models, such as product lines; and (4) aggregating reuses both transformation fragments (during transformation creation) and partial execution results (during transformation execution) across multiple transformations. To our best knowledge, these techniques do not have any correspondences in programming.

A detailed survey of the state of the art in model transformation reuse can be found in [16]. Our specific aim is to explore the different ways of approaching the problem of transformation reuse and to study its differences and similarities from well-understood approaches in program reuse. We assume that the reader is familiar with standard MDE concepts such as models, meta-models and transformations. For a good reference on these, please see [27].

The rest of this paper is organized as follows: In Sect. 2, we describe an example transformation which will be used to illustrate the different reuse strategies. In Sect. 3, we describe approaches that are adapted from program reuse. In Sect. 4, we describe novel reuse approaches that arise from the unique characteristics of MDE. We conclude in Sect. 5 with a discussion of how further progress can be achieved in research on transformation reuse.

2 Example Transformation

We begin with the following example transformation called “Fold Entry Action” [23] referring to it as $\mathtt {FoldEntry}$. Figure 1(a) shows the signature of the transformation. It takes a state machine as input and refactors it by moving common actions on incoming transitions to a state into the entry action for the state to produce the output state machine. Figure 2 shows a graph transformation rule that implements $\mathtt {FoldEntry}$. Specifically, the rule is applied to a state machine by attempting to match it to the location where some state, x, has two incoming transitions with a common action, a, as depicted in the LHS of the rule in the middle of Fig. 2. Then the matched portion is replaced with the RHS of the rule (on the right of the figure) which deletes action a from the transitions and makes it the entry action of state x. The negative application conditions (NACs, on the left of Fig. 2) prevent the rule from being applied when state x already has an entry action (NAC1) or when there are more than two incoming transitions to it (NAC2)¹. The transformation is executed by applying the rule $R_{F}$ to the given state machine G until it can no longer be applied, resulting in a new state machine H; we symbolize this as $G \mathop {\Longrightarrow }\limits ^{R_F~} H$.

$\mathtt {FoldEntry}$ is the simplest type of model transformation – it takes only a single model and produces a single model; however, more complex transformation signatures are possible. For example, Fig. 1(b) shows the signature of $\mathtt {SMmatch}$ (implementation not shown) that takes two state machines as input as produces a model relationship (i.e., a mapping) between them as output. In the rest of this paper, we illustrate transformation reuse scenarios using these example transformations.

Fig. 1.

(a) The signature of transformation $\mathtt {FoldEntry}$; (b) The signature of transformation $\mathtt {SMmatch}$.

Fig. 2.

The rule implementing the $\mathtt {FoldEntry}$ transformation to refactor a state machine.

3 Reuse from Programming Languages

In this section, we describe reuse mechanisms that are well understood for programs and were adapted for model transformations.

3.1 Subtyping

In this section, we discuss model transformation reuse through subtyping.

Subtyping is common a reuse mechanism defined through programming type theory [19]. For example, $\mathtt {Int}$ is a subtype of $\mathtt {Real}$, so any function written to accept $\mathtt {Real}$s should also work for $\mathtt {Int}$s. The simplest form of subtyping semantically defines a subset of values. This is the case with $\mathtt {Int}$ and $\mathtt {Real}$. A more sophisticated form of subtyping is called coercive subtyping. Here, one type can count as a subtype of another if there exists an implicit type conversion function. For example, using an $\mathtt {Int}$ expression directly in a print statement may be possible by coercing the $\mathtt {Int}$ into a $\mathtt {String}$ using a conversion.

The adaption of simple subset-based approaches for model subtyping to support transformation reuse has been studied. Given a transformation $F:T\rightarrow T'$, if we know that another type S is a subtype of T then F should be reusable for inputs of type S. Generally speaking, this works whenever an S model contains all information that F relies on to operate correctly. Interestingly, S need not be a subset of T and we illustrate this below. With model types, we require a relation $\mathbf S <: \mathbf T$ between metamodels (metamodel of a type is indicated by bold font) that ensures that S is a subtype of T.

Kuehne [14, 15] has studied the subtype relation from a theoretical perspective. Several works provide practical definitions for the subtype relation. Steel [31] was the first to propose a set of syntactic matching rules between metamodels. To maximize reuse, Sen et al. [28, 29] recognized the importance of identifying the effective model type of a transformation: the minimal subset of the elements of the input metamodel that is needed for the transformation to function correctly. They present an algorithm for deriving effective model types through static analysis of a model transformation’s code. In later work, Guy et al., [12] improved on Steel’s matching rules as well as defining a number of variants of the subtype matching relationship (which they call isomorphic model subtyping). Non-isomorphic sub-typing allows the definition of an explicit model adaptation function to translate instances of $\mathbf S$ into instances of $\mathbf T$. Of particular interest are bi-directional model adaptations. The paper further distinguishes (on a separate dimension) total and partial sub-typing. Total subtyping corresponds to the usual case. Partial subtyping allows the subtype to reuse only a subset of transformations by satisfying the subtyping relation only for the effective model types of these transformations.

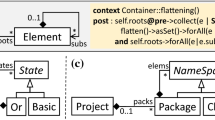
To illustrate transformation reuse through simple subtyping, consider the state machine metamodels shown in Fig. 3. We define subtyping matching rules as follows: $\mathbf S <: \mathbf T$ iff (1) all component (i.e., element, attribute and edge) types in $\mathbf S$ are also found in $\mathbf T$; and (2) the multiplicities on component types in $\mathbf S$ are no less constraining than those in $\mathbf T$.

Rule (1) means that S models have all components of T models but may have more. Rule (2) means that the number of occurrences of components in S models conforms to the constraints on the number of occurrences of these components allowable in T models. The intuition is that if $\mathbf S <: \mathbf T$ and a transformation written for T inputs is given an S model, it will still run since it has access to all component types it expects (Rule 1) and the number of occurrences of these components it expects (Rule 2).

If we check these rules on Fig. 3, we find that $\mathtt {M1}$ is a valid subtype of $\mathtt {M0}$ while neither $\mathtt {M2}$ (violates Rule (2) on number of transition actions) nor $\mathtt {M3}$ (violates Rule (2) on number of start states) are valid subtypes of $\mathtt {M0}$. Indeed, our example transformation $\mathtt {FoldEntry}$ (written for $\mathtt {M0}$) works for $\mathtt {M1}$ models but not for $\mathtt {M2}$ models because the rule (see Fig. 2) assumes at most a single transition action and will behave unpredictably when faced with multiple transition actions. Interestingly, $\mathtt {FoldEntry}$ would work correctly on an $\mathtt {M3}$ model despite that fact that it violates the subtyping rules. This is because it doesn’t “care” about the number of start states. This points to a weakness of the simple subtyping approach – it is overly conservative and may disallow reuse for transformations that can tolerate specific violations.

Fig. 3.

A state machine metamodel $\mathtt {M0}$ and three variants.

Coercive Model Subtyping. The existing work on model subtyping focuses on a simple notion of subtype in which the subtype can be directly substituted for the supertype in a transformation. In our work [10], we have developed the more general notion of coercive model subtyping.

Definition 1

(Coercive Model Typing System). A model typing system is coercive iff it contains a distinguished subset of unary operators called conversion operators satisfying the following properties:

• 1. For every type T, the identity operator $id_T:T\rightarrow T$ defined as $\forall x\in T \cdot id_T(x)=x$ is a conversion operator.

• 2. For every pair $F:T\rightarrow T'$ and $G:T' \rightarrow T''$ of conversion operators, the sequential composition $(F;G):T\rightarrow T''$ is a conversion operator.

In any coercive subtyping scheme, there may be different sequences of conversions that can lead from one type to another. Thus, a set of conversion functions is desired to be coherent, i.e., yielding the same outcome regardless of which conversion sequence is taken. In general, coherence is defined for pairs $F:T \rightarrow T'$, $G:T \rightarrow T'$ of conversion transformations, requiring that F is behaviorally equivalent to G, that is, $\forall x:T \cdot F(x) = G(x)$.

For example, in Fig. 4 we show the three model types from Fig. 3. Type $\mathtt {M1}$ is related to $\mathtt {M0}$ by the subtyping relation discussed above, and $\mathtt {FoldEntry}$ is shown as taking $\mathtt {M0}$ both as input and output. In addition, the transformation $\mathtt {ComposeActions}$ takes $\mathtt {M2}$ models as input and produces $\mathtt {M0}$ models. The transformation composes the set of actions on each transition into a single combined action. The dashed ovals are used to indicate that this is a designated conversion transformation, to be used for type coercions. Specifically, this means that $\mathtt {FoldEntry}$ can be used directly with inputs of type $\mathtt {M2}$ because the coercion system will precompose it with $\mathtt {ComposeActions}$. Coherence is not an issue in this small example since there is only one way coerce $\mathtt {M2}$ into $\mathtt {M0}$. This example illustrates how coercive subtyping can allow for more transformation reuse opportunities than simple subtyping alone. In fact, simple subtyping can be viewed as a special case of coercive subtyping where the conversion transformation is automatically generated from the subtyping relation. In the case of $\mathtt {M1}$, this means that the conversion retypes $\mathtt {FinalState}$ elements as $\mathtt {State}$ elements.

Fig. 4.

A coercive subtyping scenario.

We have implemented a coercive model typing system within our type-driven interactive model management tool called Model Management INTeractive (MMINT) [10]. The tool assists the user in reusing transformations by providing a dynamically generated list of usable transformations for a given input model by computing all possible coercions using conversion transformations. In addition, runtime checking for coherence is performed by ensuring that all possible coercion paths produce the same output for the given input.

3.2 Mapping

In this section, we show how the $\mathtt {map}$ (sometimes called $\mathtt {fold}$) operator provided in many modern programming languages to reuse functions for collections such as lists can also allow the reuse of transformations in MDE [24].

A megamodel [3] is a kind of model that is used to represent collections of models and their relationships at a high level of abstraction. Here the nodes represent models, and edges represent relationships between the models. For example, the bottom left box in Fig. 5 is the megamodel $\mathtt {CarControl}$ of state machine models in a hypothetical automotive system. Megamodels are used in the activity of Model Management [2] – a field that has emerged to help deal with the accidental complexity caused by the proliferation of models during software development.

The usual behaviour of the $\mathtt {map}$ operation is to traverse a collection (e.g., list, tree, etc.) and apply a function to the value at each node in the collection. The result is a collection with the same size and structure as the original with the function output value at each node. For example, given the list of integers $L= [10, 13, 4, 5]$ and the function Double that takes an integer and doubles it, applying map with Double to L yields the list [20, 26, 8, 10]. If the function has more than one argument, the mapped version can take a collection (with the same size and structure) for each argument, and the function is applied at a given node in the collection using the value at that node in each argument in the collection.

We have adapted this operator to allow model transformations to be reused for megamodels [24]. Since a transformation signature is a graph, applying a transformation to each node of a megamodel is not possible. Instead, the $\mathtt {map}$ operator for megamodels applies the transformation for every possible binding of the input part of the signature in the input megamodel(s). The collection of outputs from these applications forms the output megamodel.

When the transformation signature consists of a single input and output type and uses a single input megamodel which happens to be a set (i.e., no relationships) of instances of the input type, then our $\mathtt {map}$ produces the same result as a “programming language” map operator applied to a set.

Fig. 5.

Mapping $\mathtt {FoldEntry}$ and then $\mathtt {SMmatch}$ over the megamodel $\mathtt {CarControl}$ of state machines.

However, in the general case, $\mathtt {map}$ is more complex and differs from the behaviour of the standard map. In particular,

(1) The output megamodel may not have the same structure as the input megamodel since the structure is dependent on the output signature of the transformation.

(2) The size of the output may not be equal to the size of the input. For example, if a transformation takes two models as input and produces one as its output, applying $\mathtt {map}$ to it on a megamodel with n models will produce as many as $n \times (n-1)$ output models since each pair of input models may be matched in a binding. At the other extreme, if no input models form a binding then the output will be the empty megamodel.

(3) When there are multiple input megamodels, each binding of the input signature is split across the input megamodels in a user-definable way.

(4) When the transformation is commutative (i.e., the order of inputs does not affect the result), we want to avoid replication in the output due to isomorphic bindings.

Some of these principles are illustrated in Fig. 5 showing the use of $\mathtt {map}$ to first apply $\mathtt {FoldEntry}$ and then $\mathtt {SMmatch}$ to megamodel $\mathtt {CarControl}$. Mapping $\mathtt {FoldEntry}$ binds to each of the four state machines in $\mathtt {CarControl}$ and produces a new megamodel $\mathtt {CarControl'}$ with corresponding refactored state machines. Then mapping $\mathtt {SMmatch}$ over $\mathtt {CarControl'}$ binds it to every pair of state machines to produce $\mathtt {CarControl''}$. Although there are twelve possible ways to bind the inputs of $\mathtt {SMmatch}$ to the content of $\mathtt {CarControl'}$, the result shows only four relationships. This is because $\mathtt {SMmatch}$ is commutative (eliminating six possible bindings), and only four of the remaining six applications produced a non-empty result.

We have implemented $\mathtt {map}$ for megamodels in our MMINT model management tool [10] along with two other common operators: $\mathtt {filter}$ for extracting subsets of a megamodel satisfying a given property and $\mathtt {reduce}$ for aggregating the models in a megamodel using a given model merge transformation. We have shown that many common model management scenarios can be accomplished using these three operators in different combinations. The details are given in [24].

3.3 Other Approaches

Generic programming [18] is a technique in which parts of a concrete algorithm are abstracted as parameters to an abstract algorithm. This way, the same algorithm can be reused in many contexts with minimal variation. A classical example is an abstract Sort routine that can sort any type of object as long as it implements a $\mathtt {lessThan}$ operator.

De Lara et al. [7] and Rose et al. [21] proposed an idea they call model concepts. The idea of this model transformation reuse approach, inspired by generic programming, is to first define an abstract version of a transformation on a generic metamodel that represents the minimal context in which the transformation could possibly be defined. Then the transformation can be reused for specific concrete metamodels by mapping the concrete metamodel to the generic metamodel and using this mapping to automatically specialize the abstract transformation.

4 Novel Reuse Mechanisms

In this section, we describe reuse mechanisms that were created specifically for model transformations.

4.1 Lifting

In this section, we discuss the approach of reusing transformations for different products within a software product line.

Software Product Line Engineering (SPLE) is an approach to manage large sets of software product variants. This is done by modelling explicitly the variants’ commonalities and variabilities as a single conceptual unit [4]. Most existing transformations (refactoring, code generation, etc.) are developed for individual product models, not taking SPLE variability constructs into account.

Fig. 6.

Example washing machine controller product line W.

Consider the example product line W for washing machine controllers, shown in Fig. 6. W is an annotative product line [5, 13, 22], defined using three parts:

(a) The feature model defines the set of features in W. Specifically, it defines three optional features that can be added to a basic washing machine: Heat adds hot water washing, Dry adds automatic drying, and Delay adds the ability to delay the start time of the wash. In addition, the feature model defines relationships between features, which determine the set of valid configurations $\rho$ of W, denoted by $\mathsf {Conf}(W)$. In W, Heat and Delay are mutually exclusive (shown by the $\mathtt {Excludes}$ constraint), and so $\rho _1=${Wash, Heat, Dry}, $\rho _2=${Wash, Dry} and $\rho _3=${Wash} are some of its valid configurations. Formally, the semantics of the feature model of W is a propositional formula $\varPhi _W$ over the feature variables [6], specifically the formula $\varPhi _W =$ Wash $\wedge$ $\lnot$(Heat $\wedge$ Delay).

(b) The domain model of W is a UML state machine which specifies that after initiating and locking the washer, a basic wash begins or a waiting period is initiated, either for heating the water or for a delayed wash. Then the washing takes place, followed, optionally, by drying. If drying or heating was used, the clothes are cooled and the washer is unlocked, terminating the process.

(c) Depending on which of the features have been selected, only some parts of this process are available. The propositional formulas in boxes throughout the domain model indicate the presence conditions [5] for different model elements, i.e., the configurations of features under which the element is present in a product. For example, the transition from $\mathtt {Locking}$ to $\mathtt {Waiting}$ is only present if Heat or Delay is selected; it is guarded by $\mathtt {heatingEnabled}$ and has action $\mathtt {HeaterOn()}$ only when Heat is selected, while it is guarded by $\mathtt {delayEnabled}$ only if Delay is selected. A particular product can be derived from W by setting the variables in the presence conditions according to some valid configuration and discarding any elements for which the presence condition evaluates to false. For example, the product derived using only the feature Wash will go through the states $\mathtt {{Locking}}$, $\mathtt {{Washing}}$ and $\mathtt {{Unlocking}}$, while the product derived using the features Wash and Dry will go through the states $\mathtt {{Locking}}$, $\mathtt {{Washing}}$, $\mathtt {{Drying}}$ and $\mathtt {{Unlocking}}$.

In [23], we proposed a method of lifting transformations, in order to make them variability-aware. The method applies to arbitrary transformations and model-based product lines. Adapting a transformation R, such as the one in Fig. 2, so that it can be applied to product lines, such as W, results in its lifted version, denoted by $R^\uparrow$. Applying $R^\uparrow$ to a source product line should result in a target product line with the same set of products as it would if R were applied separately to each product in the source product line. Formally:

Definition 2

(Correctness of lifting). Let a rule R and a product line P be given. $R^\uparrow$ is a correct lifting of R iff (1) for all rule applications $P \mathop {\Longrightarrow }\limits ^{R^\uparrow ~} P'$, $\mathsf {Conf}(P') = \mathsf {Conf}(P)$, and (2) for all configurations $\rho$ in $\mathsf {Conf}(P)$, $M \mathop {\Longrightarrow }\limits ^{R~} M'$, where M is derived from P, and $M'$ is derived from $P'$ under $\rho$.

Transformations are lifted automatically, i.e., no manual changes are required to enable them to apply to entire product lines. Instead, we reinterpret the semantics of the transformation engine. Lifting is described in detail in [23]. Here, we illustrate it by applying the lifted version $R_F^\uparrow$ of the rule in Fig. 2 to the example product line W. The result is shown in Fig. 7, with shading indicating changed presence conditions. There are two matching sites for the rule: $K_1$ is the match on the two incoming transitions to state $\mathtt {Washing}$ with common action $\mathtt {wash.Start()}$ and $K_2$ matches on the incoming transitions to state $\mathtt {UnLocking}$ with common action $\mathtt {QuickCool()}$.

Given a matching site, the first step is to check the applicability condition, i.e., to make sure that at least one product can be derived from W such that the non-lifted transformation can be applied at K. For example, there is no valid configuration of W that contains the entire matching site $K_2$ since $\mathtt {QuickCool()}$ cannot appear on both incoming transitions to $\mathtt {Unlocking}$ at once. Therefore, even though there exists a match, the lifted rule is not applied.

For $K_1$, the applicability condition is satisfied only in those products that have Wash, Delay and not Heat. This is because when Heat is selected, the entry action $\mathtt {TempCheck()}$ occurs, and this triggers NAC1, so the rule is not applicable. Since Delay and Heat are mutually exclusive, the configurations of W that satisfy the above condition are uniquely characterized by the formula $\varPhi _{apply}=$ Delay. In other words, the transformation is applicable for those configurations where $\varPhi _{apply}$ is true. Thus, elements added by the transformation, i.e., the new entry action $\mathtt {wash.Start()}$ for state $\mathtt {Washing}$, should have $\varPhi _{apply}$ as their presence condition, i.e., Delay. Conversely, elements deleted by the transformation should only be deleted in configurations where $\varPhi _{apply}$ is true and kept for others. Thus, the presence condition of the action on the transition out of $\mathtt {Locking}$ when Delay is changed to $\lnot \varPhi _{apply}$, i.e., to $\lnot$ Delay. Similarly, the presence condition of the one out of $\mathtt {Waiting}$ becomes Heat $\wedge \lnot \varPhi _{apply}$, i.e., Heat $\wedge \lnot$ Delay. The resulting domain model is shown in Fig. 7.

Fig. 7.

The result of applying the lifted rule $R_F^\uparrow$ from Fig. 2 to the product line W in Fig. 6.

Lifting has been implemented for transformations expressed in the Henshin graph transformation language [1], using the Z3 SMT solver [9] to do the applicability condition checks. Moreover, we have lifted a subset of DSLTrans, a full-fledged model transformation language that combines graph-rewriting with advanced language constructs and is rich enough to implement real-world transformations [17]. Using the lifted version of the DSLTrans engine, we were able to execute an industrial-grade model transformation of product lines from the automotive domain [11].

4.2 Aggregating

In this section, we discuss the approach of reusing transformation fragments to create transformations with variability, and show how variability-based transformation can reuse intermediate execution artifacts [32, 33].

Fig. 8.

Variability-based transformation $\hat{R}_F$, encoding two refactoring variants: $\mathtt {foldEntry}$, shown in Fig. 2, and $\mathtt {foldExit}$, shown in the bottom.

While lifting addresses variability at the transformation’s inputs and outputs, aggregating helps capture and leverage variability in the transformation itself. We distinguish two points in time where variability in transformations is encountered: (a) during transformation creation, and (b) during transformation execution.

When building large transformation systems to perform tasks such as refactoring and code generation, developers often end up creating rules that are similar but different to each other. SPLE techniques offer a typical solution for effectively managing and maintaining such sets of transformation rules, representing them in a single conceptual artifact. Individual variants can then be obtained by configuring this artifact. We illustrate this using the example of a team that wants to create a transformation system for refactoring UML state machines. Among other refactorings, the team wants to create the transformation $\mathtt {foldEntry}$, described in Sect. 2, that moves common actions on incoming transitions to a state into the entry action for the state. The team also wants to create the transformation $\mathtt {foldExit}$, that moves common actions on outgoing transitions from a state into the exit action for the state. The two transformations are similar enough to be considered variants of each other. In order to reuse their common parts, the team can thus employ SPLE techniques to create the transformation $\hat{R}_F$ in Fig. 8, expressed using the annotative approach described in Sect. 4.1. Its feature model defines two mutually exclusive features: foldEntry and foldExit. The two variants are then encoded using presence conditions on the elements of the domain model of $\hat{R}_F$. Configuring $\hat{R}_F$ for $\rho _1=\{\mathbf{foldEntry}\}$ results in the transformation $\mathtt {foldEntry}$, shown in Fig. 2, whereas configuring it for $\rho _2=\{\mathbf{foldExit}\}$ results in the transformation $\mathtt {foldExit}$, shown at the bottom of Fig. 8.

SPLE techniques thus allow developers to reuse model fragments across transformation variants at creation time. For example, the pattern made up of the states $\mathtt {x,x1,x2}$ is reused in both variants encoded by $\hat{R}_F$. Transformations with variability, such as $\hat{R}_F$, are called variability-based transformations.

However, variability can be also leveraged at transformation execution time. To motivate the need for this, consider an aggregate rule such as $\hat{R}_F$ used with an arbitrary input. In order to execute $\hat{R}_F$, each variant must be matched and applied individually, using the classic graph-rewriting approach. Effectively, executing an aggregate transformation requires configuring all variants and applying them individually. “Plain” SPLE of transformations thus addresses the concern of maintainability, without offering any benefits to performance.

In [33], we proposed a technique that lifts the execution of variability-based transformations. The technique applies a variability-based transformation rule $\hat{R}$, such as $\hat{R}_F$, to an input model G without variability. The result should be an output model H, also without variability, that would be the same as if the variants encoded by $\hat{R}$ had been individually applied to G, ordered from largest to smallest. Formally:

Definition 3

(Correctness of Aggregation). Let a variability-based transformation rule $\hat{R}$ and a model G be given. It holds that $G \mathop {\Longrightarrow }\limits ^{\hat{R}~} H$ is isomorphic to Trans(Flat($\hat{R}$),G), where: (a) $G \mathop {\Longrightarrow }\limits ^{\hat{R}~} H$ is the set of direct applications of $\hat{R}$ to G, (b) Flat($\hat{R}$) is a function that produces the set $\mathcal {R}$ of classical rules that is encoded by $\hat{R}$, partially ordered based on the implication of their presence conditions, and (c) Trans($\mathcal {R},G$) is a function that applies a set of partially ordered classical rules $\mathcal {R}$ to G.

The direct application of $\hat{R}_F$ on an input state machine works in three steps. First, application sites for the base rule are determined. The base rule comprises all parts of $\hat{R}_F$ without annotations, that is, nodes $\mathtt {x1}$, $\mathtt {x2}$, and $\mathtt {x}$ without their adjacent edges. Consequently, all combinations of three states in the input state machine are application sites for the base rule. Second, configurations are enumerated systematically, which allows augmenting the original application sites with the variant-specific nodes and edges, yielding full matches. A full match for the foldEntry variant would bind its two edges, in addition to the node bindings of a base application site. Third, these full matches are filtered to yield largest ones. Since both variants of $\hat{R}_F$ are equally large, this set is trivial to obtain. Applying $\hat{R}_F$ at all of these largest matches yields the set of direct applications. Note that the NACs of $\hat{R}_F$ cannot be evaluated incrementally. Since their partial checking would lead to false negatives, they have to be checked on the full matches after the second step (systematic enumeration of configurations).

This application process can offer considerable performance savings since it considers shared patterns just once. In the case of $\hat{R}_F$, first binding the state nodes without considering their interrelating edges may produce a potentially large set of base matches that have to be extended individually. In more sizable examples, the benefit of considering large common patterns becomes more significant. In our experiments on larger rule sets, we were able to show speed ups between a factor of 4 and 158 [32].

Aggregate rules such as $\hat{R}_F$ do not have to be created from scratch. They can also be derived automatically, using a technique called rule merging. Rule merging takes a set of rules, identifies similar variants among these rules and unifies each set of variants into an aggregate rule. In the example, $\hat{R}_F$ is the result of merging the $\mathtt {FoldEntry}$ and $\mathtt {FoldExit}$ rules. To create $\hat{R}_F$, the common state nodes from these rules are unified, whereas variant-specific edges and attributes are annotated with presence conditions using names derived from the input rules. The details for this process are described in [32].

We have implemented variability-based rules and their application as an extension to the Henshin model transformation language [1]. In addition, in our recent work [34], we have devised a tool environment to address the usability of variability-based rules. As known from the SPLE domain, the use of annotative representations poses challenges at design time. Rules with annotations tend to be larger and contain a greater amount of visual information, which may impair their readability. Editing presence conditions manually might also give rise to an increased proneness to errors. Inspired by the paradigm of virtual separation of concerns [13], our tool environment allows users to view and edit the variants expressed in an aggregate rule individually, allowing us to mitigate these issues.

4.3 Other Approaches

Some other novel approaches to model transformation reuse focus on composing transformations either by chaining [36] or by weaving transformation specifications more invasively [37]. More recently, De Lara et al. [8] have defined a way of reusing transformations across families of related domain-specific modeling languages by specifying the transformation at the meta-modeling level used to define these languages. Kusel et al. [16] provide a good overview and empirical evaluation of some of these approaches.

5 Discussion and Future Directions

We have explored two perspectives on model transformation reuse: one the one hand, program reuse techniques can be adapted for model transformations; on the other hand, MDE offers opportunities for novel reuse techniques that leverage the specific affordances of its higher level of abstraction. For each perspective, we have discussed two such approaches: subtyping and mapping, and lifting and aggregating, respectively.

How can these two perspectives guide research in the area of model transformation reuse, as well as program reuse in general? Reflection on the four reuse approaches presented in this paper points us to some directions.

Transformation Intent. Since transformations are specialized programs, any attempt to study transformation reuse must answer the question: how is transformation reuse different from or similar to program reuse? Programs are clearly more general and thus more complex. But transformations, being Unix-like in the sense that they are typically intended for a one-step “task”, typically have clearly identified intents. We observe that the preservation of intent is a common and central concern for all reuse techniques presented here: (1) subtyping aims to preserve intent when applied to subtypes of the original input/output model types of the transformation, (2) mapping aims to have the same intended effect to a collection of models, (3) lifting affects a set of variants in the same way, while (4) the main goal of aggregation is to preserve the intent of individual sub-structures of transformations. In this last case, intent is in fact explicitly captured in the aggregate rule’s feature model. We have investigated the effect of intent for subtyping-based reuse in [26]. We are currently developing a general strategy for analyzing the soundness and completeness of a given transformation reuse mechanism with respect to the preservation of transformation intent [25].

Domain Specificity. Progress in model transformation reuse research can also be achieved by considering the specific requirements for reuse in different software engineering disciplines. The techniques presented earlier follow this pattern. Specifically, subtyping and mapping are reuse techniques inspired by the requirements for reuse in the field of model management [2]; lifting and aggregating specifically tackle issues arising from the need to model variability and make extensive use of software product line theory [20]. New reuse strategies can therefore be identified by combining model transformations with the concerns of other software engineering disciplines. An excellent recent work in this direction is from Juan De Lara et al. [8], where domain-specificity is used to reuse transformations defined at the meta-modeling level.

Adapting MDE Techniques to Programs. Some of the special-purpose techniques developed for model transformation reuse can be ported back to the world of programming languages. For example, Christian Kästner and his colleagues (see, e.g., [35]) extended static and dynamic program analysis techniques to handle programs with variability. Yet correctness of the approach needs to be established for each extension. It would be tremendously exciting to be able to lift a variety of program analyses (with minimal modifications to their implementations!) developed for individual projects to apply to product families.

A Parting Thought. Interdisciplinary research can yield interesting insights and we hope we have demonstrated it somewhat in the exciting field of model transformation reuse.