Hybrid Resource Provisioning for Workflow Scheduling in Cloud Computing

Abstract

In cloud computing, cloud service providers always provide two resource provisioning manners to cloud consumers, reservation and on-demand. Costs can be reduced using these two manners. In this paper, we consider deadline constrained cloud workflow scheduling problem with total resource renting cost minimization by integrating the two manners. An integer programming model of the problem is constructed. A malleable earliest and finish time heuristic is proposed for the problem under study. Experimental results verify the effectiveness of proposed algorithm on instances with different scales and resources with different discounts.

1 Introduction

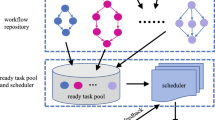
Complex workflow applications are widespread in scientific experiments and business analysis. Cloud computing provides high quality computing and storage resources for workflow applications [3]. Two resources provisioning manners are usually offered by Cloud Service Providers (CSP): the long-term reservation and the short-term on-demand. With the long-term reservation, users can get resources from CSP with a significant discount. However, they possess the resource during the entire renting period, which usually leads to poor resources utilization. The short-term on-demand enables users to rent and release computing capacity according to their demands. The average unit cost of the short-term on-demand is usually higher than that of the long-term reservation. The hybrid resource provisioning method of the two manners reduces the average unit cost and improves the flexibility of resources. Figure 1 shows the workflow scheduling with the hybrid resource provisioning manner. First, users send parameters of workflows (deadlines, tasks, runtimes) to the workflow scheduling module. The module generates scheduling plans according to the parameters. Each plan includes two parts: the workflow scheduling sequence and the cloud resource renting plan. Users rent resources and schedule tasks based on the scheduling plan. Resources are rented from the CSP using the long-term reservation and/or the short-term on-demand.

Fig. 1.

Workflow scheduling with the hybrid resource provisioning manner.

In this paper, we consider the deadline constrained cloud workflow scheduling problem to minimize the total resource renting cost using hybrid resource provisioning manners, which is NP-hard. To the best of our knowledge, no attention has been paid on this problem. The malleable earliest-finish-time heuristic is proposed for the problem under study. First, the task allocation sequence is created based on priorities. In terms of free time periods, reserved and/or on-demand resources are allocated to the tasks in the sequence. New sequences are discovered by a variable neighborhood search.

The rest of the paper is organized as follows. Related works are described in Sect. 2. Section 3 gives the mathematical model for the considered problem. In Sect. 4, we describe the proposed method and illustrate it using an example. Computational results are presented in Sect. 5, followed by conclusions and future works in Sect. 6.

2 Related Works

Workflow scheduling has been studied for many years. Recently, malleable task (tasks can be executed on multiple machines) scheduling in parallel [2] is a hot topic, which first determines the number of machines available for the malleable tasks. Makespans and renting costs minimizing are two common objectives of workflow scheduling problems.

Resources are limited on grids. HEFT [11] and CPA [13] are effective algorithms for workflow scheduling with makespan minimization. Singh et al. [12] used genetic algorithms to map tasks to resources with the objective of minimizing both the renting cost and makespan. Resources are limited and available between different time windows.

In cloud computing, resources are assumed to be unlimited and available all the time. Yu et al. [15] proposed a genetic algorithm to minimize the renting costs, which can minimize the cost with constrained deadline or minimize makespan with limited cost. The time complexity of this algorithm is closely related to the service scale. While a large number of alternative services were provided, the algorithm was not good and with high time complexity. Byun et al. [4] proposed a Balanced Time Scheduling (BTS) algorithm to minimize resource rent costs. The algorithm assumes that the number of hosts are unchanged during the implementation of the entire workflow, and only one type of resource is considered. BTS did not take into account renting on-demand resources either. All the resources are obtained through the long-term reservation. Even if a resource uses only one unit of time, it is paid all the renting time. In their later work [5], a new algorithm Partitioned BTS (PBTS) was proposed, which divides the workflow implementation process into sections according to the total amount of resources. Chaisiri et al. [6] proposed a new algorithm OCRP to optimize the resource provision cost in cloud computing. OCRP considered both reserved and on-demand resources. Tasks are supposed to be independent with known resource requirements. However, for the actual workflow scheduling problem, tasks are precedence constrained. The resource renting method and the resource requirements interact with each other. Abrishami et al. [1] proposed a method to assign workflow tasks to different resources in IaaS clouds. Juan et al. [8] considered to allocate resources to scientific computing workflows with multi-objective in Amazon EC2. Both resource renting cost and makespan were considered. However, they did not consider the problem with different resource provisioning methods.

In summary, there is no work considering both malleable tasks and hybrid resource provisioning though they can reduce the cost for the implementation of the workflow significantly, which is considered in this paper.

3 Mathematical Model

A workflow application can be represented by an activity-on-node Directed Acyclic Graph (DAG) G(V, E), in which $V=\{v_{0},\ldots ,v_{n}\}$ is the set of tasks in G. $E=\{(v_{i},v_{j})|v_{i}\in V, v_{j}\in V, i<j\}$ defines the precedence relationships between tasks, which indicates that $v_{i}$ must be finished before $v_{j}$ starts. Each node $v_{i}$ represents a task. $v_{i}$ is processed on several Virtual Machines (VM). As the computing capacity of a virtual machine is usually in proportion to the price, only homogeneous resources are considered in this paper (i.e., different capacities can be normalized). The processing time of task $v_{i}$ on a single virtual machine is $P_{i}$. All tasks are classified into two types: malleable tasks (the set is denoted as $\mathbb {M}$) and rigid tasks (the set is denoted as $\mathbb {R}$), i.e., $V=\mathbb {M}\cup \mathbb {R}$. A malleable task can be allocated to malleable virtual machines, i.e., it has multiple execution modes. Each malleable task could be executed by different numbers of machines with different processing times. Let $v_{i}\in \mathbb {M}$ be a malleable task. If $m_{i}$ virtual machines are allocated to $v_{i}$, the processing time $p_{i}$ is calculated by $p_{i}=\lceil P_{i}/m_{i}\rceil$, which is varying with the scheduling process. However, the number of virtual machines $m_{i}$ allocated to a rigid task $v_{i}$ ($v_{i}\in \mathbb {R}$) are fixed. The execution mode and the processing time $p_{i}=\lceil P_{i}/m_{i}\rceil$ of a rigid task keep unchanged once they are determined. Tasks $v_{0}$ and $v_{n}$ are dummy nodes, which represent the start and the end of the workflow. Processing times of the two dummy nodes are 0. Let D be the deadline of the workflow application.

Both of the two resource provisioning manners are adopted to rent resources for workflows. Let H be the total amount of rented resources, $H^{r}$ represents the amount of long-term reserved resources and $H_{t}^{0}$ denotes the amount of short-term on-demand resources at time t. $C_{r}$ and $C_{0}$ are the unit costs of a virtual machine with the long-term and the short-term resource provisioning. The ratio of $C_{r}$ to $C_{o}$ means the discount of a resource. i.e., $discount=C_{r}/C_{0}$. The total renting cost of resources includes both the reserved cost and the on-demand cost. The considered problem can be mathematically modeled as follows:

$$\begin{aligned} \min (f_{n}\times H^{r}\times C_{r}+\sum _{t=0}^{f_{n}}{H_{t}^{0}\times C_{0}}) \end{aligned}$$

(1)

s.t.

$$\begin{aligned} x_{iht}= {\left\{ \begin{array}{ll} 1~~v_{i}~\text {is processing on the VM}~h~\text {at time}~t, ~\forall i\in \{0,\ldots ,n\},\\ ~~~~\forall h \in \{1,\ldots ,H\},~\forall t \in \{0,\ldots ,D\} \\ 0~~\text {others}\\ \end{array}\right. } \end{aligned}$$

(2)

$$\begin{aligned} y_{h}= {\left\{ \begin{array}{ll} 1~~h~\text {is an on-demand machine}, ~\forall h \in \{1,\ldots ,H\}\\ 0~~h~\text {is a reserved machine}, ~\forall h \in \{1,\ldots ,H\}\\ \end{array}\right. } \end{aligned}$$

(3)

$$\begin{aligned} m_{i}= \sum _{h=1}^{H}\sum _{t=0}^{D}x_{iht},~\forall v_{i}\in \mathbb {M} \end{aligned}$$

(4)

$$\begin{aligned} p_{i}=\lceil P_{i}/m_{i}\rceil ,~~\forall i\in \{0,\ldots ,n\} \end{aligned}$$

(5)

$$\begin{aligned} s_{i}=\sum _{t=0}^{D}\frac{1}{m_{i}}\sum _{h=1}^{H}t\times x_{iht}, ~\forall i\in \{0,\ldots ,n\} \end{aligned}$$

(6)

$$\begin{aligned} s_{i}+p_{i}\leqslant s_{j}, ~\forall (i,j)\in E \end{aligned}$$

(7)

$$\begin{aligned} f_{n}\leqslant D \end{aligned}$$

(8)

$$\begin{aligned} \sum _{t=s_{j}}^{s_{j}+d_{j}}\sum _{i=0}^{n}x_{iht}=1, ~~\text {if}~x_{jhs_{j}}=1~\forall j\in \{0,\ldots ,n\},~\forall h \in \{1,\ldots ,H\} \end{aligned}$$

(9)

$$\begin{aligned} H_{t_{i}}^{0}=\sum _{h=1}^{H}\sum _{i=0}^{n}\sum _{t=t_{i}-d_{i}+1}^{t_{i}}x_{iht}y_{h},~~\forall t_{i}\in \{0,\ldots ,D\} \end{aligned}$$

(10)

$$\begin{aligned} H^{r}=\sum _{h=1}^{H}(1-y_{h}) \end{aligned}$$

(11)

The binary variables $x_{iht}=1$ in Eq. (2) means the task $v_{i}$ is processed on the VM h at time t. The $y_{h}$ in Eq. (3) takes 1 if the VM h rents resources using the on-demand manner. Equation (4) defines the number of VMs allocated to each mallable task. The processing time and start time of each task are determined by Eqs. (5) and (6). Formulas (7) and (8) specify the precedence and deadline constraints of the workflow. Equation (9) ensures that the execution is consecutive and non-preemptive. The number of reserved and on-demand resources are calculated by Eqs. (10) and (11).

Because of the discounts of the long term reservation, most tasks are allocated to the long-term reserved resources. Some other resources are rented using the short-term on-demand manner to improve the resource utilization.

4 Proposed Heuristic

Rule-based heuristics are common methods for workflow scheduling problems [13]. In this paper, we propose the malleable earliest finish time method (MEFT) for the considered problem which is composed of three components: initial schedule construction (ISC), variable neighborhood search (VNS) and schedule reconstruction (SR).

4.1 Initial Schedule Construction

ISC constructs an initial schedule using three procedures: reservation resources presetting, task sequencing and schedule constructing.

To preset the number of long-term reserved resources, the upper and lower bounds are calculated first. The lower bound is defined as the minimum amount of required resources to accomplish all the tasks with the deadline satisfied assuming all the resources are fully loaded and the precedence constraints between tasks are not involved. If the utilization rate of a resource is less than its discount, the on-demand manner obtains a cheaper cost than the reserved manner according to Formula (1). The upper bound is defined as the maximum amount of required resources with the resource utilization rate equal to the discount. The two bounds are defined as follows:

$$\textstyle H_{\min }^{r}=\lceil \sum _{v_{i}\in V}P_{i}\div D\rceil $$

$$\textstyle H_{\max }^{r}=\lceil \sum _{v_{i}\in V}P_{i}\div D\div discount\rceil $$

The reserved resource presetting process starts from the resources with the lower bound. The reserved resources $H^{r}$ are initialized as $H_{\min }^{r}$. Suppose the reserved resources with the maximum amount are allocated to malleable tasks, i.e., $p_{i}=\lceil P_{i}/H_{i}\rceil$, $\forall v_{i}\in \mathbb {M}$. The earliest start time $est_{i}$ of $v_i$ is calculated according to the critical-path based method given in [7]. If the earliest start time $est_{n}$ of $v_{n}$ is greater than the deadline D, no feasible schedule can be obtained using the current amount of reserved resources $H^{r}$. We increase $H^{r}$ and try again until a feasible schedule is found or the upper bound $H_{\max }^{r}$ is reached.

Based on the obtained long-term reserved resources $H^{r}$, a sequence of tasks is determined by their priorities which are recursively defined as $rank_{u}(v_{i})=P_{i}+\max _{v_{j}\in succ(v_{i})}\{rank_{u}(v_{j})\}$ with $rank_{u}(v_{n})=0$, where $succ(v_{i})$ is the set of all successors of $v_{i}$. If there is more than one task processed in parallel, the task with the biggest processing time is set the highest priority. Therefore tasks on the critical path are allocated as early as possible. An initial sequence is obtained by sorting tasks by the increasing order of their priorities.

Tasks are scheduled according to the task sequence using the free time period-based schedule construction strategy. Resources are denoted by matrix $R=(r_{ij})_{D\times H^{r}}$ in which the column represents the time slots and the row represents the virtual machines, e.g., $r_{ij}=1$ indicates that virtual machine j is occupied at time slot i. The execution of a task is denoted by a sub-matrix with all elements being 1. For example, the sub-matrix $R[i^{'},\ldots , i^{''}; j^{'},\ldots , j^{''}]$ indicates that the activity starts at time slot $i^{'}$ and finishes at time slot $i^{''}$ and virtual machines $j^{'}$ to $j^{''}$ are occupied during this period. The free time period is denoted as a sub-matrix with all elements being 0, which is a continuous period with a number of available resources. For example, the virtual machine is free during the time period between the finish time of the first task and the start time of the second task if a virtual machine is mapped to two tasks. If some other machines are also free during this period, a new free time period is constructed by combining the free time and those on the machines. All possible free time periods are found between the earliest start time of the current task and the latest finish time of the scheduled tasks. The process is given in Algorithm 1. All free time periods are sorted in the increasing order of the start times. The tasks are allocated to the free time periods. For a rigid task $v_i$, it is tried to be allocated from the first free time period. If $v_i$ cannot be allocated to the current time period, there are two cases: no sufficient time or no sufficient resource. The first case implies that the time length of the period is less than that of the task processing time $p_i$. The current time period is unavailable and the next time period is explored. For the second case, the least amount of short-term on-demand resources is calculated. The current free time period would be wasted if it is not allocate to $v_i$. Let the wasted workload be V and the workload of $v_i$ is $w_{i}$. It is economical to rent some on-demand resources if $V\times discount>(w_{i}-V)$. The current task $v_i$ is allocated to the current time period. For a malleable task, the allocation of resources is more complex because of the change of required resources. If resources of the current time period are available for the task, the maximum amount of resources is allocated to the task to make the task finish as early as possible. Otherwise, the maximum economical on-demand resources are rented. After all tasks are allocated, new free time periods followed to them are checked. If there are still some new free time periods, the processing times of the tasks are extended to reduce the amount of rented resources.

4.2 Variable Neighborhood Search

Usually, the cost of the inial schedule obtained by ISC is not the cheapest. It is natural to propose a variable neighborhood search (VNS) to adjust the task sequence, which exerts a great influence on the performance of the MEFT. An insertion operator $I(a,b),~(1<a<n,1<b<n,a\ne b, b-1)$ is adopted to change the order of tasks. The task at the position a is removed and inserted to position b in the sequence without violating the precedence constraints between tasks. Each insertion operator changes a task sequence $\bar{s}$ to a new one $\bar{s^{'}}$. In addition, we define the r-insertion neighborhood $N_{r}(\bar{s})$ is the neighborhood set performing insertion operator r times on $\bar{s}$. Therefore $N_{1}(\bar{s})$ is the set of $\bar{s^{'}}$ with only one insertion operator. Suppose the insertion operator is performed at most K times, i.e., $1\le r\le K$.

The VNS starts from an initial sequence s. $\lambda$ solutions are compared for each scale of neighborhood $N_{r}(\bar{s})$. In every time, a new task sequence is obtained. The above free time period-based schedule construction strategy is adopted to construct a new schedule. If the cost of the new schedule is cheaper than the previous one, the new task allocation sequence is set as the new start point. If no more optimal solution can be found after the K-insertion VNS for a start point, the algorithm stops. The process is described in Algorithm 2.

4.3 Schedule Reconstruction

The obtained schedule is reconstructed by reallocating tasks with on-demand resources after the VNS. These tasks are chosen with certain probability $\omega$ to be reallocated to the reservation resources. If a better new solution is obtained, the current solution is replaced by the new one. If all the tasks with on-demand resources have been reallocated, the schedule reconstruction (SR) procedure terminates. SR aims at destroying structures of solutions by allocating some tasks with cheaper resources to reduce the total renting cost. Surely, the utilization rate of the resources could be decreased during the process. The SR increases the diversification of the search and increases the probability of finding better solutions with multiple iterations.

4.4 An Example

To illustrate the process of the proposed MEFT, an workflow example with 7 tasks is shown in Fig. 2. Let the processing time $P_{i}$ for each task on a single virtual machine be 3, 1, 2, 2, 2, 2, 2 respectively. $v_{3}$ and $v_{4}$ are malleable tasks with malleable resources and variable processing times. The other tasks are rigid tasks requiring rigid resources, in which $v_{5}$ and $v_{6}$ require two virtual machines while the remaining rigid tasks require only one virtual machine. Let the deadline of the workflow be 9 and the discount of the long-term reserved resources be 0.8.

Fig. 2.

An example of workflow instance.

The algorithm starts with the least long term reserved resources ($H^{r}=2$). The priority of each task is calculated first to determine the initial task sequence, which are (1, 3, 2, 4, 5, 6, 7) in this example. $v_{1}$ is allocated first. Since there is only one whole free time period, $v_{1}$ is allocated to the time period 1, 2, 3 of virtual machine 1. $v_{3}$ is allocated next. The time period 1, 2, 3 of virtual machine 2 is the earliest free time period. $v_{3}$ is allocated to the time period 1, 2 of virtual machine 2. The next task $v_{2}$ is allocated to the time period 3 of virtual machine 2. Since $v_{4}$ is a malleable task and can be processed in parallel, it is allocated to the time slot 4 of virtual machine 1 and 2 concurrently. Task $v_{5}$, $v_{6}$, $v_{7}$ are allocated next. Details are shown in Fig. 3. Since no on-demand resources are used in the schedule, the SR procedure is not performed. After several iterations of VNS, a new sequence (1, 3, 2, 4, 5, 7, 6) is found. Tasks are reallocated according to this sequence. While allocating $v_{6}$, the time slots 6 and 7 of virtual machine 2 are free which forms a free time period. The discount 0.8 meets the criteria for on-demand resource renting. A new virtual machine is rented for $v_{6}$ and $v_{6}$ is executed on virtual 2 and 3 concurrently.

Fig. 3.

Task scheduling process and result of MEFT.

5 Experimental Results

The considered workflow scheduling problem with both malleable tasks and hybrid resource provisioning has not been studied yet. The closest problem is that considered in [4] with only reserved resource provisioning and the number of reserved virtual machines minimization. BTS was proposed for the problem. In this paper, we adapted BTS (we call it ABTS in this paper) for the problem under study in two aspects: BTS does not allocate each task to a specific virtual machine. The schedule of BTS considers only the start time and the number of virtual machines for each task. In ABTS, tasks are allocated to a specific virtual machine after BTS gets a schedule. The task with the longest processing time is allocated to the virtual machines with the smallest index in order to minimize the renting cost of on-demand resources. If the utilization rate of a virtual machine is less than discount when calculating the resource renting cost of ABTS, the cost of this virtual machine is computed using the on-demand manner. Otherwise, the cost is computed according to the reserved manner.

The proposed MEFT is compared with ABTS in this paper. All the compared algorithms are coded in Java and executed on the same virtual machine with Intel i5-3470 CPU (4 cores, 3.1GHz) and 1GB memory of RAM. Workflow instances are randomly produced by Rangen [9, 10] (benchmark of project scheduling problem), in which the number of tasks n takes value from $\{10,20,50,100,200\}$, 20 instances are generated for each size of the workflow. The number of resources is 1 and the network complexity is set as 1.8. The processing time of each task is randomly generated from the uniform distribution U(10, 100). The deadline factor of each workflow instance is set as $\theta =1.2$ according to [14], which means $D=Est_{n}\times 1.2$ for each instance.

The relative percentage deviation (RPD) is adopted to evaluate the performance. Let $C_{i}^{F}$ denote the cost of instance i obtained by algorithm F, $F^{*}$ be the best algorithm for instance i. RPD is defined as:

$$\begin{aligned} RPD = \frac{C_{i}^{F}-C_{i}^{F^{*}}}{C_{i}^{F^{*}}}\times 100\,\% \end{aligned}$$

(12)

Three parameters of MEFT are calibrated: the scale of neighborhood $K\in \{3,5,8,10, 12\}$, the number of solutions for each scale $\lambda \in \{6,8,10,12,14\}$ and the reconstruction probability $\omega \in \{0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1\}$. The multi-factor analysis of variance (ANOVA) technique is adopted to analyze the performance of the algorithms with different parameter values. RPD is used as the response variable. First the three main hypotheses (normality, homoscedasticity, and independence of the residuals) are checked. Since all the three hypotheses are close to zero, they are acceptable in this analysis.

Figures 4 and 5 show the means plot with 95 % Tukey HSD confidence intervals for parameters K and $\lambda$ respectively. With the increase of K and $\lambda$, RPD of MEFT decreases because more solutions are searched. However, more CPU time is required. Furthermore, interactions between K and $\lambda$ with 95 % Tukey HSD confidence intervals are shown in Fig. 6. Figure 6 implies that MEFT gets the best performance when K and $\lambda$ take value of 12 and 10 respectively. For the reconstruction probability $\omega$, the means plot with 95 % Tukey HSD confidence intervals is shown in Fig. 7. Figure 7 means that MEFT gets the worst solution when $\omega =0$ (no reconstruction). MEFT gets the best result when $\omega =0.6$.

Fig. 4.

Means plot with 95 % Tukey HSD confidence intervals for parameter K.

Fig. 5.

Means plot with 95 % Tukey HSD confidence intervals for parameter $\lambda$.

Fig. 6.

Interactions with 95 % Tukey HSD confidence intervals between K and $\lambda$.

Fig. 7.

Means plot with 95 % Tukey HSD confidence intervals for parameter $\omega$.

By setting the three parameters as 12, 10 and 0.6, MEFT is compared with ABTS. Instances with different size ($n\in \{10,20,50,100,200\}$) and different discount value ($discount\in \{0.4,0.5,0.6,0.7,0.8\}$) are randomly generated. The means plot with 95 % Tukey HSD confidence intervals of the compared algorithms with different instance sizes is shown in Fig. 8. Figure 8 illustrates that MEFT is better than ABTS on all instances. When $n=10$, the RPD difference between MEFT and ABTS is 15.2 %. However, the difference becomes smaller with the increase of n, e.g., the difference is about 4.5 % when $n=200$. The comparison results of the two algorithms with different discount values are shown in Fig. 9. MEFT outperforms ABTS for all discount values. Smaller discount implies better the performance of MEFT. When the discount becomes bigger, the superiority of MEFT becomes less significant.

Fig. 8.

Comparison result of the two algorithms with different instance size.

Fig. 9.

Comparison result of the two algorithms with different discount values.

6 Conclusion and Future Work

In this paper, the resource renting problem for workflow applications with hybrid resource provisioning was considered, which is closer to real cloud computing scenarios. Based on both long-term reservation and short-term on-demand resource renting manners, a mathematic model was established. A new heuristic MEFT was proposed and compared with the adapted BTS. Experimental results showed that MEFT outperforms ABTS when the scale of instances and the discount are not big. The differences between MEFT and ABTS become smaller with the increase of the scale of instances and discount.

Scheduling problems with multiple types of virtual machines in the cloud will be studied. More real scenarios including data locality and data transfer time between virtual machines are also worth considering.