1 Introduction

In the last decades there has been an explosion of interest in sliding mode observers (SMOs) for fault detection and isolation (FDI), reconstruction and fault tolerant control (FTC). The sliding mode concept based on variable structure control algorithms can be used for controllers and observers. It includes a nonlinear switching term, which establishes and maintains a motion on a so-called sliding surface, where reduced-order dynamics compared to the normal system appears [25, 26].

For observers the sliding motion on the error between the output of the observer and the measured plant output ensures that a SMO produces a set of estimated states, which are precisely corresponding with the current output of the plant. To achieve and maintain the sliding mode an injection signal has to be applied. The average value of this signal, the so-called equivalent injection signal, can be evaluated to yield direct fault estimates, because it contains useful information about the mismatch between the control-oriented model used to define the observer and the actual plant. The fault estimates or rather the reconstruction of the faults can be exploited for fault tolerant control in the sense that sensor and actuator faults are corrected before the measurements are used for the controller or rather the control signal acts on the plant.

Originally, the sliding mode method is based on linear time-invariant (LTI) systems with unknown but bounded terms [4]. An important extension to the sliding mode observer concept is to introduce a convex combination of LTI systems. The combination can be parameter varying and/or state varying. The parameter varying concept was presented in [1] and is based on a class of linear parameter varying (LPV) systems. In contrast, the state varying sliding mode concept was first proposed in [9], where the observer is implemented within a Takagi–Sugeno (TS) model structure to account for system nonlinearities. Both proposed approaches are extensions of the LTI scheme of sliding mode observer design to a convex combination of LTI systems, which is a suitable compromise between a full nonlinear design and the LTI framework.

In this chapter, first, we introduce TS and LPV model structures and describe them by means of an inverted pendulum and a wind turbine benchmark from the literature [14]. Then, the underlying relations between the model classes are exposed and discussed by comparing the necessary conditions and efficiency of the design process. Finally, simulation results of two case studies, the inverted pendulum [3] and a wind turbine benchmark from the literature [17], are presented to illustrate the influence of the underlying design model on the quality of the fault reconstruction and thus the quality of fault compensation.

Notation: Throughout this chapter, the notation \(\Vert \cdot \Vert \) will be used to represent the Euclidean vector norm or its induced matrix norm. The identity and zero matrix of order n are represented by \(\mathbf {I}_n\) and \(\mathbf {0}_n\). \(\mathbf {P}> 0\), (\(\mathbf {P}< 0\)) means that \(\mathbf {P}\) is a positive (negative) definite matrix.

2 Model Structure

2.1 TS Model Structure

Takagi–Sugeno (TS) models provide a uniform framework for controller and observer design of nonlinear systems. Methods based on linear matrix inequalities (LMIs) using a Lyapunov function allow for a unified design for TS models [24, 27]. Introduced 30 years ago in the context of fuzzy systems [21], TS models are weighted combinations of linear submodels. These can either be derived from measured data using offline system identification techniques [20, 21] or from analytical models of nonlinear systems.

A general TS model structure is given by

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) \, \big ( \mathbf {A}_i \, \mathbf {x}+ \mathbf {B}_i \, \mathbf {u}\big ),\\ {\mathbf {y}}&= \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) \, \mathbf {C}_i \, \mathbf {x}, \end{aligned} \end{aligned}$$
(1)

where \(N_r\) denotes the number of linear state-space submodels, which share the common state vector \(\mathbf {x}\in {\mathbb {R}}^n\), the input vector \(\mathbf {u}\in {\mathbb {R}}^m\), and the output vector \(\mathbf {y}\in {\mathbb {R}}^p\) with the constant matrices \(\mathbf {A}_i\in {\mathbb {R}}^{n \times n}\), \(\mathbf {B}_i\in {\mathbb {R}}^{n \times m}\) and \(\mathbf {C}_i\in {\mathbb {R}}^{p \times n}\). The functions \(h_i(\mathbf {z})\), \(i\in \{1,\ldots , N_r\} \) are normalised to fulfil the convex sum condition

$$\begin{aligned} \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) = 1 \, , \quad 0 \le h_i(\mathbf {z}) \le 1 \quad \forall \quad i \in \{ 1, \ldots , N_r \}. \end{aligned}$$
(2)

The vector \(\mathbf {z}\in {\mathbb {R}}^{N_l}\) of premise variables may comprise state variables \(x_k \in {\mathbb {R}}\), inputs \(u_k \in {\mathbb {R}}\), and external variables \(\chi _k~\in ~{\mathbb {R}}\): \(\mathbf {z}= \mathbf {z}(\mathbf {x}, \mathbf {u}, \varvec{\chi })\). To obtain a Takagi–Sugeno form and a Takagi–Sugeno (TS) structure of a nonlinear model respectively, and assuming the mathematical model is given by

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {f}(\mathbf {x}, \mathbf {u}), \quad {\mathbf {y}} = \mathbf {g}(\mathbf {x}), \end{aligned}$$
(3)

there are two different methods to derive (1). The first method is based on an approximation of (3) by local Taylor linearisation of the nonlinear model around \(N_r\) stationary points and following fuzzy blending of the linear submodels \(\{ \mathbf {A}_i, \mathbf {B}_i, \mathbf {C}_i \}\) to a weighted sum according to (1) with the normalisation condition (2). The second method is the so-called sector nonlinearity approach [16, 23], which can be employed to obtain an exact Takagi–Sugeno model representation of a given nonlinear model (3).

In the following, we assume that the sector nonlinearity approach is used to yield a nonlinear system in Takagi–Sugeno’s form. This has the advantage that the switching term in the sliding mode observer (presented in Sect. 4) must only account for the disturbances and faults and not for the approximation error caused by local linearisations and fuzzy blending.

2.2 LPV Model Structure

Linear parameter varying (LPV) descriptions of dynamic systems have been shown to be a powerful modelling approach for data-dependent systems, where the dependence might be governed by a nonlinear term, cf. [13]. The idea emerged from the analysis of gain scheduling techniques and was presented by Shamma in [19]. In [13], Shamma describes the LPV modelling as a framework, which results in linear but non-stationary dynamics shown in (4):

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}} = \mathbf {A}(\mathbf {\varvec{\theta }})\mathbf {x}+\mathbf {B}(\mathbf {\varvec{\theta }})\mathbf {u}, \\ \mathbf {y}=\mathbf {C}(\mathbf {\varvec{\theta }})\mathbf {x}, \end{aligned} \end{aligned}$$
(4)

where \(\mathbf {x}\in \mathbb {R}^{n}\) are the system states, \(\mathbf {u}\in \mathbb {R}^{m}\) the inputs and \(\mathbf {y}\in \mathbb {R}^{p}\) describes the output of the system. \(\varvec{\theta }\) denotes the exogenous (i.e. state independent) varying parameters of the system leading to the non-stationary behaviour. However, this model of the system can be exploited for the description of nonlinear dynamic systems, where the nonlinear behaviour can either be induced by an exogenous or an endogenous (i.e. state-dependent) signal. Stability analysis and observer/controller synthesis have been addressed in literature, for example in [1, 2, 13]. To the authors’ knowledge, however, the obtainment of a LPV model from a nonlinear system description is poorly described in a large quantity of the literature. For this reason, the next section will provide an approach for the construction of an LPV model out of an analytic nonlinear system description.

The basic idea of the LPV approach is to bring a nonlinear function z or an exogenous signal under the exploitation of the knowledge of the range bounds of functions values \(\overline{z}= \text {sup}\{z\}\) and \(\underline{z}= \text {inf}\{z\}\) into a certain structure. Consider the nonlinear function z, which is unknown but bounded, described by

$$\begin{aligned} z=c_1 + \theta \,c_2, \end{aligned}$$
(5)

where \(-1 \le \theta \le 1\) holds and \(c_1\), \(c_2\) are constant values depending on the upper \(\overline{z}\) and lower \(\underline{z}\) bound of z. By the choice of \(c_1 = \underline{z}+ \frac{\varDelta z}{2}\), \(c_2 = \frac{\varDelta z}{2}\) and \(\theta =\frac{z-\underline{z}- \varDelta z/2}{\varDelta z/2}\) with the definition of \(\varDelta z = \overline{z}-\underline{z}\) the aforementioned conditions are fulfilled and it can be easily verified that

$$\begin{aligned} \underbrace{\underline{z}+\frac{\varDelta z}{2}}_{=:c_1} + \underbrace{\frac{z-\underline{z}- \varDelta z/2}{\varDelta z/2}}_{=:\theta } ~ \underbrace{\frac{\varDelta z}{2}}_{=:c_2} = z. \end{aligned}$$
(6)

Since \(-1 \le \theta \le 1\) holds, a convex form is achieved. Consider a nonlinear system of the form

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}=\mathbf {A}(z)\mathbf {x}+\mathbf {B}\mathbf {u}, \\ \mathbf {y}=\mathbf {C}\mathbf {x}, \end{aligned} \end{aligned}$$
(7)

where z can either be an exogenous signal/function or an endogenous nonlinear function depending on a state of the system. Let \(\mathbf {A}\) be defined by

$$\begin{aligned} \mathbf {A}(z) = \begin{bmatrix} a_{11}+z~~~&a_{12} \\ a_{21}&a_{22} \end{bmatrix}. \end{aligned}$$

Then, according to the scheme described before, the system can be described in the LPV structure

$$\begin{aligned} \mathbf {A}(z)&= \begin{bmatrix} a_{11}+\underbrace{c_1+\theta ~c_2}_{z}~~~&a_{12} \\ a_{21}&a_{22} \end{bmatrix} = \begin{bmatrix} a_{11}+c_1~~&a_{12} \\ a_{21}&a_{22} \end{bmatrix}+\theta ~\begin{bmatrix} c_2&0\\ 0&0 \end{bmatrix} \nonumber \\&= \mathbf {A}_0+\theta ~ \mathbf {A}_1 = \mathbf {A}(\theta ). \end{aligned}$$
(8)

If nonlinear functions or exogenous signals appear in \(\mathbf {B}\) or \(\mathbf {C}\), the way for achieving a LPV description can be applied analogously. Since the formulation leads to a convex combination of matrices, this can be exploited in the synthesis of controllers or observers accordingly.

3 Case Studies: Modelling

3.1 Case Study I: Inverted Pendulum

3.1.1 Physical Model

The inverted pendulum benchmark, in particular the cart version illustrated in Fig. 1, has been considered in many references to solve the problem of designing controllers around the unstable operating point or as a nonlinear control problem in the full operating range of \(\varTheta \in [\, 0, \, \pi \,)\) [12]. In this chapter, we use the latter case to be able to use advantageously the LPV and TS sliding mode observer approach.

The cart with inverted pendulum consists of a moveable carriage with one degree of freedom on which a pendulum is mounted and freely rotatable in driving direction (Fig. 1). The carriage is driven by a motor that exerts a force F through a belt-drive transmission. The main control objective is to swing up the pendulum from the stable equilibrium to the unstable equilibrium, and then balance the pendulum at the upright position, and further move the cart to a specified position along the track.

Fig. 1
figure 1

Cart with inverted pendulum

Full size image

The process can be described by the state-space model

$$\begin{aligned} {\dot{\mathbf {x}}} = \begin{pmatrix} {\dot{\varTheta }}\\ \frac{ g \, \sin (\varTheta ) - m \, l \, a \, {\dot{\varTheta }}^2 \cos (\varTheta ) \, \sin (\varTheta ) \,-\, a \, \cos (\varTheta ) \, \big (u - F_f \big ) - \frac{d_{Mf} \, {\dot{\varTheta }}}{m \, l}}{2 \, l \,-\, m \, l \, a \, \cos ^2(\varTheta )} \\ {\dot{x}}\\ \frac{2 a \, \Big (m \, l \, {\dot{\varTheta }}^2 \, \sin (\varTheta ) - \frac{1}{2} \, m \, g \, \cos (\varTheta ) \, \sin (\varTheta ) \,+\, u - F_f + \frac{1}{2 l} \cos (\varTheta ) \, d_{Mf} \, {\dot{\varTheta }}\Big )}{2 \,-\, m \, a \, \cos ^2(\varTheta )} \end{pmatrix} \end{aligned}$$
(9)

with the state vector \(\mathbf {x}= \begin{bmatrix} \; \varTheta \;\; {\dot{\varTheta }} \;\; x \;\; \dot{x} \; \end{bmatrix}^{\text {T}}\), where \(a = 1/(m + M)\), \(F_\text {f}\) denotes the unknown but bounded friction force between the cart and the track and g denotes the gravitational acceleration. The external force F is the input \(u:=F\) and is limited to \(|F| \le F_{\max }\). The angular position of pendulum \(\varTheta \), the linear displacement x, and the speed of the cart \({\dot{x}}\) are the outputs of this system. The parameters and variables of the inverted pendulum on the cart are recorded in Table 1.

Table 1 Variables and parameters of cart with inverted pendulum
Full size table

3.1.2 TS Model

In order to prepare for the observer design, a TS model is derived using the sector nonlinearity approach [22]. First, we rewrite (9) in the form

$$\begin{aligned} \dot{\mathbf {x}} = \underbrace{\begin{bmatrix} 0&1&0&0\\ f_1 \, f_2(\frac{g}{l} - m \, a \, f_3 \, f_4)&-\frac{d_{Mf}}{m l^2} \, f_1&0&0\\ 0&0&0&1\\ m \, a \, f_1 \, f_2 \, (2 \, l \, f_3 - g \, f_4)&\frac{a \, d_{Mf}}{l} \, f_1 \, f_4&0&0\\ \end{bmatrix}}_{\mathbf {A}(\mathbf {x})} \mathbf {x}+ \underbrace{\begin{bmatrix} 0\\ - \frac{a}{l} \, f_1 \, f_4\\ 0\\ {+} 2 \, a \, f_1\\ \end{bmatrix}}_{\mathbf {B}(\mathbf {x})} \big (u - F_f \big ). \end{aligned}$$
(10)

The scalar-valued nonlinear functions \(f_j\), \(j \in \{1, \ldots , N_l\}\) in (10) are given by

$$\begin{aligned} \begin{aligned} f_1 (x_1)&= \frac{1}{2 - m \, a \, \cos ^2(x_1)}, \qquad f_2(x_1) = \frac{\sin (x_1)}{x_1},\\ f_3(x_2)&= x^2_2, \qquad \qquad \qquad \qquad f_4(x_1) = \cos (x_1), \end{aligned} \end{aligned}$$
(11)

where \(N_l=4\) denotes the number of nonlinearities. For the transition to the TS model structure (1), these functions are written in a different form. Let \(\underline{f}_j\) and \(\overline{f}_j\) denote the minimum and maximum values of each function \(f_j\). The following identities hold:

$$\begin{aligned} \begin{aligned}&f_j\left( x_1\right) \, = \, w_{j1}\left( x_1\right) \, \overline{f}_{j} \, + \, w_{j2}\left( x_1\right) \, \underline{f}_{j}, \quad j \in \{ 1,2,4\}\\&f_3\left( x_2\right) \, = \, w_{31}\left( x_2\right) \, \overline{f}_{3} \, + \, w_{32}\left( x_2\right) \, \underline{f}_{3},\quad j=3, \end{aligned} \end{aligned}$$
(12)

where the weighting functions \(w_{jk}\), \(k=1,2\), are given by

$$\begin{aligned} \begin{aligned} w_{j1}\left( x_1\right) \,&:= \,\frac{\displaystyle f_{j}\left( x_1\right) - \underline{f}_{j}}{\displaystyle \overline{f}_{j} - \underline{f}_{j}}, \quad w_{j2}\left( x_1\right) \, := \, \frac{\displaystyle \overline{f}_{j} - f_{j}\left( x_1\right) }{\displaystyle \overline{f}_{j} - \underline{f}_{j}}, \qquad j \in \{1,2,4 \}\\ w_{31}\left( x_2\right) \,&:= \,\frac{\displaystyle f_{3}\left( x_2\right) - \underline{f}_{3}}{\displaystyle \overline{f}_{3} - \underline{f}_{3}}, \quad w_{32}\left( x_2\right) \, := \, \frac{\displaystyle \overline{f}_{3} - f_{3}\left( x_2\right) }{\displaystyle \overline{f}_{3} - \underline{f}_{3}},\qquad j=3, \end{aligned} \end{aligned}$$
(13)

which satisfy the property \(w_{j1} + w_{j2} = 1\). From this property and by defining the sum of the membership functions as the product of the convex sums of weighting functions \(w_{jk}\), we obtain the definition

$$\begin{aligned} \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) := \prod \limits _{j=1}^{N_l = 4} \big ( w_{j1} + w_{j2} \big ), \end{aligned}$$
(14)

where it directly follows that \(\sum _{i=1}^{N_r} \, h_i(\mathbf {z}) = 1\), i.e. the convex sum condition (2) holds. In order to replace the nonlinear functions \(f_j\) in (10) by (12) these are multiplied first by an appropriate choice of the convex sum

$$\begin{aligned} f_j\left( x_2\right) \, = \, \big ( w_{j1} \, \overline{f}_{j} \, + \, w_{j2} \, \underline{f}_{j} \big ) \prod \limits _{i \ne j} \big ( \underbrace{w_{i1} + w_{i2}}_{=1} \big ) \, , \quad i \in \{1,2,3,4 \}. \end{aligned}$$
(15)

Using this formulation of \(f_j\), the nonlinearities have been shifted to the membership functions, which are described in this case study by

$$\begin{aligned} \begin{aligned} h_1(x_1,x_2)&= w_{11}(x_1) \; w_{21}(x_1) \; w_{31}(x_2) \; w_{41}(x_1)\\ h_2(x_1,x_2)&= w_{12}(x_1) \; w_{21}(x_1) \; w_{31}(x_2) \; w_{41}(x_1)\\ h_3(x_1,x_2)&= w_{11}(x_1) \; w_{22}(x_1) \; w_{31}(x_2) \; w_{41}(x_1)\\ h_4(x_1,x_2)&= w_{12}(x_1) \; w_{22}(x_1) \; w_{31}(x_2) \; w_{41}(x_1)\\&\vdots \qquad \qquad \qquad \qquad \vdots \\ h_{16}(x_1,x_2)&= w_{12}(x_1) \; w_{22}(x_1) \; w_{32}(x_2) \; w_{42}(x_1). \end{aligned} \end{aligned}$$
(16)

All other constant matrix entries of (10) are multiplied by \(\sum _{i=1}^{N_r} \, h_i(\mathbf {z}) = 1\), such that \(\mathbf {A}(\mathbf {x})\) and \(\mathbf {B}(\mathbf {x})\) can be written as a weighted sum of \(N_r =\) 16 matrices with constant coefficients according to

$$\begin{aligned} \mathbf {A}(\mathbf {x}) = \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) \, \mathbf {A}_i, \qquad \mathbf {B}(\mathbf {x}) = \sum _{i=1}^{N_r} h_i(\mathbf {z}) \, \mathbf {B}_i, \end{aligned}$$
(17)

where \(\mathbf {z}= \begin{bmatrix} \, x_1, \, x_2 \, \end{bmatrix}^{\text {T}}\). Thus, the matrices of the first submodel \(i=1\) are

$$\begin{aligned} \mathbf {A}_1 = \begin{bmatrix} 0&\quad 1&0&0\\ \overline{f}_1 \, \overline{f}_2(\frac{g}{l} - m \, a \, \overline{f}_3 \, \overline{f}_4)&\quad -\frac{d_{Mf}}{m l^2} \, \overline{f}_1&0&0\\ 0&\quad 0&0&1\\ m \, a \, \overline{f}_1 \, \overline{f}_2 \, (2 \, l \, \overline{f}_3 - g \, \overline{f}_4)&\quad \frac{a \, d_{Mf}}{l} \, \overline{f}_1 \, \overline{f}_4&0&0\\ \end{bmatrix} , \qquad \mathbf {B}_1 = \begin{bmatrix} 0\\ - \frac{a}{l} \, \overline{f}_1 \, \overline{f}_4\\ 0\\ {+}2 \, a \, \overline{f}_1\\ \end{bmatrix} \nonumber . \end{aligned}$$

The state-space model (9) can thus be transformed into the TS form (1)

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \sum _{i=1}^{N_r=16} \, h_i(\mathbf {z}) \, \big ( \mathbf {A}_i \, \mathbf {x}+ \mathbf {B}_i \, ( \, u - F_f \, ) \big ),\\ {\mathbf {y}}&= \mathbf {C}\, \mathbf {x}. \end{aligned} \end{aligned}$$
(18)

Note that the friction force \(F_\text {f}\) is here considered as an additional unknown input.

3.1.3 LPV Model

Consider the nonlinear model of the inverted pendulum presented in Sect. 3.1.1. The nonlinear model can be described by

$$\begin{aligned} \dot{\mathbf {x}}=\begin{bmatrix} 0&1&0&0 \\ \frac{g}{l}\,z_1-m\,a\, z_2&-\frac{d_{Mf}}{ml^2}z_3&0&0 \\ 0&0&0&1\\ 2mla z_5-mag z_6&\frac{ad_{Mf}}{l} z_4&0&0 \end{bmatrix} \mathbf {x}+ \begin{bmatrix} 0 \\ -\frac{a}{l} z_4 \\ 0 \\ 2a z_3 \end{bmatrix}(u-F_f), \end{aligned}$$
(19)

where the nonlinear functions of the model are substitutions using (11) \(z_1=f_1 f_2\), \(z_2=f_1 f_2 f_3 f_4\), \(z_3=f_1\), \(z_4=f_1 f_4\), \(z_5=f_1 f_2 f_3\), and \(z_6=f_1 f_2 f_4\). Based on the knowledge of the individual bounds of the nonlinear functions \(f_i\), the individual bounds of the nonlinear functions \(z_i=c_{1i}+\theta _i c_{2i}\) can be obtained, cf. Table 2. Using the pattern described in Sect. 2.2 and especially the separation of constant matrices and parameter varying components as shown in (8), the LPV model of the inverted pendulum can be described in the form

Table 2 Lower and upper bounds of the inverted pendulum
Full size table
$$\begin{aligned} {\dot{\mathbf {x}}}=\begin{pmatrix} \mathbf {A}_0+\sum \limits _{i=1}^{6}\theta _i\mathbf {A}_i \end{pmatrix}\mathbf {x}+\begin{pmatrix} \mathbf {B}_0+\sum \limits _{i=3}^{4}\theta _i\mathbf {B}_i \end{pmatrix}u, \end{aligned}$$
(20)

with, for example,

$$\begin{aligned} \mathbf {A}_0 = \begin{bmatrix} 0&1&0&0 \\ \frac{g}{l}c_{11}-mac_{12}&-\frac{d_{Mf}}{ml^2}c_{13}&0&0 \\ 0&0&0&1\\ 2mlac_{15}-magc_{16}&\frac{ad_{Mf}}{l}c_{14}&0&0 \end{bmatrix}~\text {and}~ \mathbf {A}_1(\theta _1) = \theta _1\begin{bmatrix} 0&&\\ \frac{g}{l}c_{21}&\mathbf {0}_{\text {4}\times \text {3}}&\\ 0&&\\ 0&&\end{bmatrix}. \end{aligned}$$

The sliding mode observer design for the inverted pendulum based on the LPV problem description—contrary to the TS model—requires a model approximation because of the structure of the fault distribution matrix \(\mathbf {F}(\varvec{\theta })\), which is introduced later in Sect. 4. As proposed by Alwi and Edwards in [1], the distribution matrix can be factorised into

$$\begin{aligned} \mathbf {F}(\varvec{\theta }) = \mathbf {H} \mathbf {E}(\varvec{\theta }), \end{aligned}$$
(21)

where \(\mathbf {H} \in {\mathbb {R}}^{n\times q}\) is fixed and a virtual fault is introduced by \(\mathbf {f}_v = \mathbf {E}(\varvec{\theta })\mathbf {f}\). \(\mathbf {E} \in {\mathbb {R}}^{q \times q }\) varies dependent on the nonlinear terms and is assumed to be invertible. Thus, from the knowledge of \(\mathbf {f}_v\), \(\mathbf {f}\) can be calculated by \(\mathbf {f} = \mathbf {E}(\varvec{\theta })^{-1}\mathbf {f}_v\). Anyhow, in case of the inverted pendulum the distribution matrix \(\mathbf {F}(z_3,\, z_4) = \begin{bmatrix} 0&\frac{a}{l}z_4&0&-2az_3 \end{bmatrix}^{\text {T}}= \mathbf {F}(\varvec{\theta })\) cannot be factorised due to the fact that two nonlinear functions are included in one vector. A possible solution to this problem is the allocation of the distribution vector into a matrix

$$\begin{aligned} \tilde{\mathbf {F}}(z_3,\,z_4) = \begin{bmatrix} 0&0 \\ 0&\frac{a}{l}z_4 \\ 0&0 \\ -2az_3&0 \end{bmatrix}, \end{aligned}$$
(22)

where the presented factorisation can be accomplished by the matrix \(\mathbf {E}(z_3,\,z_4) = \begin{bmatrix} z_3&0 \\ 0&z_4 \end{bmatrix}\), leading to a new distribution matrix \(\tilde{\mathbf {H}}\) for the virtual fault \(\mathbf {f}_v = \mathbf {E}(z_3,\,z_4) \begin{bmatrix} f_F \\ f_F \end{bmatrix}\)

$$\begin{aligned} \tilde{\mathbf {H}}=\begin{bmatrix} 0&0 \\ 0&\frac{a}{l} \\ 0&0 \\ -2a&0 \end{bmatrix}. \end{aligned}$$
(23)

This factorisation violates the necessary assumption from Sect. 4 \(\text {rank}(\tilde{\mathbf {H}})=q=\text {rank}(\mathbf {C}~\tilde{\mathbf {H}})\) in the design process. For this reason, a model approximation has to be deployed to the LPV model of the inverted pendulum. The new distribution matrix is set to \(\mathbf {F}(z_3)_{\text {ap.}}=\begin{bmatrix} 0&0&0&-2az_3 \end{bmatrix}^{\text {T}}=\mathbf {F}(\theta _3)\). Then, the factorisation can be applied using \(\text {E}(\theta _3)=\text {E}(z_3)=z_3\), the virtual fault \(f_v = \text {E}(z_3)f_{F}\) and the distribution matrix for the virtual fault

$$\begin{aligned} \mathbf {H}_{\text {ap.}}=\begin{bmatrix} 0 \\ 0 \\ 0 \\ -2a \end{bmatrix}, \end{aligned}$$
(24)

which is used during the observer design. The observer reconstructs the virtual fault \(\hat{f}_v\). From this reconstruction, the estimated occurring fault \(\hat{f}=\text {E}(z_3)^{-1}\, \hat{f}_v\) can be calculated.

Fig. 2
figure 2

Schematic side-view and submodels of the complete wind turbine benchmark model with the respective inputs and outputs

Full size image

3.2 Case Study II: Wind Turbine

3.2.1 Physical Model

In the second case study, we use a wind turbine benchmark model presented in [14], which describes a generic pitch-controlled three-blade horizontal variable-speed wind turbine with a rated power of \(P = 4.8\) MW. The original purpose of this benchmark was to provide a model on which researchers, who are working in the field of fault diagnosis and fault tolerant control, can compare different FDI/FTC methods to a wind turbine.

The model consists of four submodels: The mechanical submodel, which is reduced to the drive train dynamics, the aerodynamics, the pitch actuators and the generator-converter dynamics. The coupling of these submodels is illustrated in Fig. 2. The mechanical submodel with two degrees of freedom (rotor and generator rotation) is described by the motion equation

$$\begin{aligned} \begin{aligned} J_r \, {\dot{\omega }}_r&= T_r - K_{dt} \, \theta _s - (B_{dt} + B_r ) \omega _r + \frac{B_{dt}}{N_g} \, \omega _g,\\ J_g \, {\dot{\omega }}_g&= \frac{\eta _{dt} \, K_{dt}}{N_g} \, \theta _s + \frac{\eta _{dt} \, B_{dt}}{N_g} \, \omega _r - \Big ( \frac{\eta _{dt} \, B_{dt}}{N_g^2} + B_g \Big ) \omega _g - T_g, \end{aligned} \end{aligned}$$
(25)

where \(\theta _s\) denotes the shaft torsion angle with the angular velocity \({\dot{\varTheta }}_s = \omega _r - \frac{1}{N_g} \omega _g\). For sake of clarity, all parameters and system variables are summarised in Table 3.

Table 3 Variables and parameters of the wind turbine benchmark
Full size table

The aerodynamic submodel comprises the expression for the rotor torque \(T_r\). This torque depends on the aero map \(C_Q\) for the torque coefficient [5]

$$\begin{aligned} T_r&= \frac{1}{2} \rho \; \pi \; R^3 \; v^2 \; \frac{1}{3} \sum _{i=1}^{3} C_Q(\lambda ,\beta _i), \end{aligned}$$
(26)

where \(\rho \) denotes the air density, R is the rotor radius, v is the average wind speed at the rotor, \(\beta _i\) describes the individual pitch angle of blade \(i\in \{1,2,3\}\) and \(\lambda = {\omega _r \; R}/{v}\) characterises the tip speed ratio.

In pitch-controlled wind turbines, the pitch angles of the blades are altered in the full load region to keep the wind turbine at the desired nominal rotor speed by reducing the aerodynamic rotor torque. The blade pitch system with three single pitch drives is modelled by the second-order delay systems [14]

$$\begin{aligned} \ddot{\beta }_i + 2 \, \zeta \, \omega _n \; {\dot{\beta }}_i + \omega _n^2 \; \beta _i = \omega _n^2 \; \beta _{i,d}, \end{aligned}$$
(27)

where \(\beta _i\) and \(\beta _{i,d}\) denote the actual and demanded pitch angles of blade i. To take the generator-converter dynamics into account, and for the purpose of actuator fault detection, a first-order delay model is used in [14]

$$\begin{aligned} \dot{T}_{g} = - \frac{1}{\tau _g} {T}_{g} + \frac{1}{\tau _g} \, {T}_{g,d}, \end{aligned}$$
(28)

where \(T_{g}\) and \(T_{g,d}\) denote the applied and demanded generator torque.

3.2.2 TS Model

As in the first case study (inverted pendulum), a TS model is derived using the sector nonlinearity approach [22]. Equations (25)–(28) are combined to a state-space model with the state and input vector

$$\begin{aligned} \mathbf {x}= \big [ \, \omega _r \;\; \omega _g \;\; \theta _s \;\; T_g \; \; {\dot{\beta }}_1 \;\; \beta _1 \;\; {\dot{\beta }}_2 \;\; \beta _2 \;\; {\dot{\beta }}_3 \;\; \beta _3 \; \, \big ]^{\text {T}}, \qquad \mathbf {u}= \big [ \; T_{g,d} \;\; \beta _{1,d} \;\; \beta _{2,d} \;\; \beta _{3,d} \; \big ]^{\text {T}}\end{aligned}$$

and rewritten in the form

$$\begin{aligned} {\dot{\mathbf {x}}} = \underbrace{ \begin{bmatrix} \tilde{\mathbf {A}}_{11}(x_1,v)&\mathbf {0}_{4 \times 2}&\mathbf {0}_{4 \times 2}&\mathbf {0}_{4 \times 2} \\ \mathbf {0}_{2 \times 4}&\tilde{\mathbf {A}}_{22}&\mathbf {0}_{2 \times 2}&\mathbf {0}_{2 \times 2}\\ \mathbf {0}_{2 \times 4}&\mathbf {0}_{2 \times 2}&\tilde{\mathbf {A}}_{33}&\mathbf {0}_{2 \times 2}\\ \mathbf {0}_{2 \times 4}&\mathbf {0}_{2 \times 2}&\mathbf {0}_{2 \times 2}&\tilde{\mathbf {A}}_{44}\\ \end{bmatrix} }_{\mathbf {A}(x_1,v)} \mathbf {x}+ \underbrace{ \begin{bmatrix}&\quad \mathbf {0}_{3 \times 4}&\\ \frac{1}{\tau _g}&0 \quad&0 \quad&0 \quad \\ 0 \quad&\omega _n^2&0 \quad&0 \quad \\ 0 \quad&0 \quad&0 \quad&0 \quad \\ 0 \quad&0 \quad&\omega _n^2&0 \quad \\ 0 \quad&0 \quad&0 \quad&0 \quad \\ 0 \quad&0 \quad&0 \quad&\omega _n^2\\ 0 \quad&0 \quad&0 \quad&0 \quad \\ \end{bmatrix}}_{\mathbf {B}} \mathbf {u}, \end{aligned}$$
(29)

with

$$\begin{aligned} \tilde{\mathbf {A}}_{11}(x_1,v)= \begin{bmatrix} f_1(x_1,v)&\frac{B_{dt}}{N_g \, J_r}&-\frac{K_{dt}}{J_r}&0 \\ \frac{\eta _{dt} \, B_{dt}}{N_g \, J_g}&- \Big ( \frac{\eta _{dt} \, B_{dt}}{N_g^2 J_g} + \frac{B_g}{J_g} \Big )&\frac{\eta _{dt} \, K_{dt}}{N_g \, J_g}&-\frac{1}{J_g} \\ 1&-\frac{1}{N_g}&0&0\\ 0&0&0&- \frac{1}{\tau _g}\\ \end{bmatrix}, \quad \tilde{\mathbf {A}}_{jj}= \begin{bmatrix} - 2 \; \omega _n \; \zeta&\quad -\omega _n^2 \\ 1&\quad 0 \\ \end{bmatrix} \nonumber \end{aligned}$$

for \(j \in \{2,3,4\}\). The scalar-valued nonlinear function \(f_1\) is given by

$$\begin{aligned} f_1(x_1,v) = - \frac{1}{J_r} \Big ( B_{dt} + B_r \Big ) + \frac{1}{\omega _r} \; \frac{1}{J_r} \; T_r\big (\lambda (x_1,v),v\big ), \quad x_1 \in [\, \underline{x}_1 \; , \; \overline{x}_1 \, ], \end{aligned}$$
(30)

where \(\underline{x}_1 > 0\) and \(\overline{x}_1\) denote the lower and upper bounds of the rotor speed in the wind turbine operating range. For the transition to the TS model structure (1) these functions are written in a different form. Let \(\underline{f}_1\) and \(\overline{f}_1\) denote the minimum and maximum values of the function \(f_1\). The identity

$$\begin{aligned} \begin{aligned} f_1\left( x_1, v\right) \, = \, w_{11}\left( x_1, v\right) \, \overline{f}_{1} \, + \, w_{12}\left( x_1,v\right) \, \underline{f}_{1} \, \end{aligned} \end{aligned}$$
(31)

holds, where the weighting functions \(w_{1k}\), \(k\in \{1,2\}\), are given by

$$\begin{aligned} \begin{aligned} w_{11}\left( x_1,v\right) \, := \,\frac{f_{1}\left( x_1,v\right) - \underline{f}_{1}}{\overline{f}_{1} - \underline{f}_{1}} \, , \quad w_{12}\left( x_1,v\right) \, := \, \frac{\overline{f}_{1} - f_{1}\left( x_1,v\right) }{\overline{f}_{1} - \underline{f}_{1}}.\\ \end{aligned} \end{aligned}$$
(32)

Using this formulation (31), the nonlinearity has been shifted to the membership functions, which in this second case study are described by

$$\begin{aligned} h_1(x_1,v) = w_{11}(x_1,v), \qquad h_2(x_1,v) = w_{12}(x_1,v). \end{aligned}$$
(33)

All other constant matrix entries of (29) are multiplied by \(\sum _{i=1}^{N_r} \, h_i(x_1,v) = 1\), such that \(\mathbf {A}(x_1,v)=\mathbf {A}(z)\) can be written as a weighted sum of \(N_r =\) 2 matrices with constant coefficient:

$$\begin{aligned} \mathbf {A}(z) = \sum _{i=1}^{N_r=2} \, h_i(z) \, \mathbf {A}_i \nonumber , \end{aligned}$$

where \(z = f_1(x_1,v)\). The state-space model (29) can thus be transformed into the TS form (1)

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \sum _{i=1}^{N_r=2} \, h_i(z) \, \big ( \mathbf {A}_i \, \mathbf {x}+ \mathbf {B}\, \mathbf {u}\big ).\\ \end{aligned} \end{aligned}$$
(34)

3.2.3 LPV Model

Consider the nonlinear system of the wind turbine benchmark, where the nonlinear function \(z=T_r/x_1\) is integrated into the system matrix \(\mathbf {A}\) as follows:

$$\begin{aligned} \mathbf {A}(x_1,T_r)= \begin{bmatrix} -\frac{B_{dt}+B_r}{J_r}+\frac{T_r}{x_1 J_r}&a_{12}&a_{13}&\mathbf {0}_{\text {1}\times \text {7}}\\&\mathbf {A}_{\text {(n-1)}\times \text {n}} \\ \end{bmatrix}, \end{aligned}$$
(35)

where \(a_{12}\), \(a_{13}\) and \(\mathbf {A}_{\text {(n-1)}\times \text {n}}\), \(\text {n}=10\) can be found in the descriptions in Sect. 3.2.2. Just as described in Sect. 2.2, the nonlinear function \(\frac{T_r}{x_1}\) can be represented by an affine term \(\theta \) and two constants resulting in a linear function by the use of its bounds. Note that this model is valid for the operation range of the wind turbine, where it is assumed that \(x_1> 0\). The bounds of the nonlinear function \(\frac{T_r}{x_1}\) are \(\overline{z}=\text {sup}\{z\}=1.5458\times 10^{10}\,\frac{\text {Nms}}{\text {rad}}\) and \(\underline{z}=\text {inf}\{z\}=-3.8538\times 10^{11}\,\frac{\text {Nms}}{\text {rad}}\), which are obtained from the information of the operating range of the wind turbine and the knowledge of the specific torque coefficients of the benchmark model presented in [15]. Based on these bounds, the description of the dynamics of the wind turbine can be altered to a LPV model of the form

$$\begin{aligned} \dot{\mathbf {x}}&= \underbrace{\begin{pmatrix}\begin{bmatrix} -\frac{B_{dt}+B_r}{J_r}+\frac{c_1}{J_r} &{} a_{12} &{} a_{13} &{} \mathbf {0}_{\text {1}\times \text {7}}\\ &{} \mathbf {A}_{\text {(n-1)}\times \text {n}} \\ \end{bmatrix}+\theta \begin{bmatrix} \frac{c_2}{J_r} &{} \mathbf {0}_{\text {1}\times \text {9}}\\ &{} \mathbf {0}_{\text {(n-1)}\times \text {n}} \\ \end{bmatrix}\end{pmatrix}}_{\mathbf {A}(\theta )}\mathbf {x} + \mathbf {B}\mathbf {u} \nonumber \\&= \mathbf {A}(\theta )\mathbf {x} + \mathbf {B} \mathbf {u}, ~~~~ \mathbf {y} = \mathbf {C}\mathbf {x}, \end{aligned}$$
(36)

where the coefficients are again defined as \(c_1 = \underline{z}+ \frac{\varDelta z}{2}\), \(c_2 = \frac{\varDelta z}{2}\) and \(\theta =\frac{z-\underline{z}- \varDelta z/2}{\varDelta z/2}\).

4 Fault Reconstruction by Sliding Mode Observation

4.1 System Description and Canonical Form

We consider two different norm-bounded uncertain model structures: The first is based on the previously introduced TS model (1)

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) \, \big ( \mathbf {A}_i \, \mathbf {x}+ \mathbf {B}_i \, \mathbf {u}+ \mathbf {F}_i \, \mathbf {f}_a \big ),\\ {\mathbf {y}}&= \mathbf {C}\, \mathbf {x}, \end{aligned} \end{aligned}$$
(37)

where \(\mathbf {F}_i \in {\mathbb {R}}^{n \times a}\) denotes the fault distribution matrix and the faults are presented by \(\mathbf {f}_a \in {\mathbb {R}}^a\). The common \(\mathbf {C}\) in (37) is only a small restriction, since many applications [7, 12, 18] comprise outputs that are linear in the system states. The second exploits the LPV modelling techniques based on the introduced structure (4)

$$\begin{aligned} \begin{aligned} \dot{\mathbf {x}}&= \mathbf {A}(\varvec{\theta }) \, \mathbf {x}+ \mathbf {B}(\varvec{\theta }) \, \mathbf {u}+ \underbrace{\mathbf {F}(\varvec{\theta }) \mathbf {f}_a }_{\mathbf {H}\; \mathbf {E}(\varvec{\theta }) \mathbf {f}_a },\\ {\mathbf {y}}&= \mathbf {C}\, \mathbf {x}, \end{aligned} \end{aligned}$$
(38)

where \(\mathbf {f}_v = \mathbf {E}(\varvec{\theta }) \mathbf {f}_a\) denotes the virtual fault vector with the special form of the distribution matrix (cf. Sect. 3.1.3). Note that the special form of the distribution matrix and the virtual fault is only needed if the original distribution matrix depends on an affine term \(\theta _i\). This is due to the transformations discussed in the following part of this discourse. Otherwise, this allocation can be ignored.

For the observer design, three existence conditions have to be fulfilled [4, 9, 10]:

  • Condition 1: The faults presented in (37) and (38) are unknown but norm bounded by known positive constants \(\varXi _{f_a} \in {\mathbb {R}}^q\) which satisfy \(\Vert \mathbf {f}_a(t) \Vert \le \varXi _{f_a} \). Moreover, the system states and inputs are assumed to be bounded.

  • Condition 2:

    • TS (37): Let \(q_i = q\) \(\forall i\) be defined as the number of columns of \( \mathbf {F}_i \). Then the condition \(q = \text {rank}(\mathbf {C}\, \mathbf {F}_i ) = \text {rank}( \mathbf {F}_i )\) must be fulfilled and it must hold that \(p > q\), where p is the number of measurable system states.

    • LPV (38): Let q be defined as the number of columns of \( \mathbf {H}\). Then the condition \(q = \text {rank}(\mathbf {C}\, \mathbf {H}) = \text {rank}( \mathbf {H})\) must be fulfilled and it must hold that \(p > q\), where p is the number of measurable system states.

  • Condition 3:

    • TS (37): All invariant zeros of \((\mathbf {A}_i, \mathbf {F}_i, \mathbf {C})\) must lie in \({\mathbb {C}}_{-}\), which denotes the open left half of the complex plane.

    • LPV (38): All invariant zeros of \((\mathbf {A}(\varvec{\theta }), \mathbf {H}, \mathbf {C})\) must lie in \({\mathbb {C}}_{-}\).

The design of a sliding mode observer for fault reconstruction that is applicable for the classes of TS systems (37) or LPV systems (38) is carried out in a special canonical form. With a series of transformations \(\mathbf {T}_i\) for each TS submodel

$$\begin{aligned} \mathbf {T}_i = \mathbf {T}_{L,i} \; \mathbf {T}_{b,i} \; \mathbf {T}_{c}, \end{aligned}$$
(39)

or for the LPV model with the common distribution matrix \(\mathbf {H}\)

$$\begin{aligned} \mathbf {T}= \mathbf {T}_{L} \; \mathbf {T}_{b} \; \mathbf {T}_{c}, \end{aligned}$$
(40)

the TS respectively LPV system is brought into a structure where, first, the last p states of the systems are the outputs \(\mathbf {y}\) and, second, the faults \(\mathbf {f}_a\) only act on the measurable system states (for further details such as the description of the transformation matrices (39) and (40) and proofs see [4, 6, 9]).

The TS model in canonical form is described by

$$\begin{aligned} \begin{aligned} {\dot{\mathbf {x}}}_1&= \sum \limits _{i=1}^{N_r} h_i( \mathbf {z}) \,\big (\pmb {\mathscr {A}}_{11,i} \, \mathbf {x}_1 \, + \, \pmb {\mathscr {A}}_{12,i}\, {\mathbf {y}} \, + \pmb {\mathscr {B}}_{1,i} \,{\mathbf {u}} \big ), \\ {\dot{{\mathbf {y}}}}&= \sum \limits _{i=1}^{N_r} h_i (\mathbf {z}) (\pmb {\mathscr {A}}_{21,i} \mathbf {x}_1 + \pmb {\mathscr {A}}_{22,i} {\mathbf {y}} + \pmb {\mathscr {B}}_{2,i} \, {\mathbf {u}} + \pmb {\mathscr {F}}_{2,i} {\mathbf {f}}_a ), \end{aligned} \end{aligned}$$
(41)

with the non-measurable states \(\mathbf {x}_1 \in {\mathbb {R}}^{(n-p)}\) and the measurable states \(\mathbf {y}\in {\mathbb {R}}^p\). The transformed system matrices in (41) have the following block structures:

$$\begin{aligned} \pmb {\mathscr {A}}_{i}&= {\mathbf {T}}_i \, {\mathbf {A}}_{i} \, {\mathbf {T}}_i^{-1} = \begin{bmatrix} \pmb {\mathscr {A}}_{11,i}&\pmb {\mathscr {A}}_{12,i} \\ \pmb {\mathscr {A}}_{21,i}&\pmb {\mathscr {A}}_{22,i} \end{bmatrix}, \quad \pmb {\mathscr {B}}_{i} = {\mathbf {T}}_i \, {\mathbf {B}}_{i} = \left[ \pmb {\mathscr {B}}_{1,i}^{\text {T}}\, \; \, \pmb {\mathscr {B}}_{2,i}^{\text {T}}\right] ^{\text {T}}, \\ \pmb {\mathscr {F}}_{i}&= {\mathbf {T}}_i \, {\mathbf {F}}_{i} = \left[ \mathbf {0}^{\text {T}}\, \; \, \pmb {\mathscr {F}}_{2,i}^{\text {T}}\right] ^{\text {T}}. \end{aligned}$$

The LPV model in canonical form is described by

$$\begin{aligned} \begin{aligned} {\dot{\mathbf {x}}}_1&= \pmb {\mathscr {A}}_{11}(\varvec{\theta }) \; \mathbf {x}_1 \, + \, \pmb {\mathscr {A}}_{12}(\varvec{\theta }) \; {\mathbf {y}} \, + \pmb {\mathscr {B}}_{1}(\varvec{\theta }) \; {\mathbf {u}}, \\ \dot{{\mathbf {y}}}&= \pmb {\mathscr {A}}_{21}(\varvec{\theta }) \; \mathbf {x}_1 + \pmb {\mathscr {A}}_{22}(\varvec{\theta }) \, {\mathbf {y}} + \pmb {\mathscr {B}}_{2}(\varvec{\theta }) \, {\mathbf {u}} + \pmb {\mathscr {H}}_{2} {\mathbf {f}}_v, \end{aligned} \end{aligned}$$
(42)

with the non-measurable \(\mathbf {x}_1 \in {\mathbb {R}}^{(n-p)}\) and the measurable states \(\mathbf {y}\in {\mathbb {R}}^p\). The transformed system matrices in (41) have the following block structures:

$$\begin{aligned} \pmb {\mathscr {A}}(\varvec{\theta })&= {\mathbf {T}} \, {\mathbf {A}}(\varvec{\theta }) \, {\mathbf {T}}^{-1} = \begin{bmatrix} \pmb {\mathscr {A}}_{11}(\varvec{\theta })&\pmb {\mathscr {A}}_{12}(\varvec{\theta }) \\ \pmb {\mathscr {A}}_{21}(\varvec{\theta })&\pmb {\mathscr {A}}_{22}(\varvec{\theta }) \end{bmatrix} \, , \quad \pmb {\mathscr {B}}(\varvec{\theta }) = {\mathbf {T}} \, {\mathbf {B}}(\varvec{\theta }) = \left[ \pmb {\mathscr {B}}_{1}^{\text {T}}(\varvec{\theta }) \, \; \, \pmb {\mathscr {B}}_{2}^{\text {T}}(\varvec{\theta }) \right] ^{\text {T}}, \\ \pmb {\mathscr {H}}&= {\mathbf {T}} \, {\mathbf {H}}= \left[ \mathbf {0}^{\text {T}}\, \; \, \pmb {\mathscr {H}}_{2}^{\text {T}}\right] ^{\text {T}}. \end{aligned}$$

4.2 Sliding Mode Observation

TS Sliding Mode Observation

The TS sliding mode (TS SM) observer for the system (41) in transformed form is given by

$$\begin{aligned} \begin{aligned} {\dot{\hat{\mathbf {x}}}}_{1}&= \sum \limits _{i=1}^{N_r} h_i\left( {\mathbf {z}}\right) \, \big (\pmb {\mathscr {A}}_{11,i} \,\hat{\mathbf {x}}_{1} + \pmb {\mathscr {A}}_{12,i} \, \hat{\mathbf {y}} + \pmb {\mathscr {B}}_{1,i} \,{\mathbf {u}} - \pmb {\mathscr {A}}_{12,i} {\mathbf {e}}_y \big ), \\ {\dot{\hat{\mathbf {y}}}}&= \sum \limits _{i=1}^{N_r} h_i\left( {\mathbf {z}}\right) \,\big (\pmb {\mathscr {A}}_{21,i} \, \hat{\mathbf {x}}_{1} \, + \pmb {\mathscr {A}}_{22,i}\,\hat{\mathbf {y}} + \pmb {\mathscr {B}}_{2,i} \,\mathbf {u} \, - \, \left( \pmb {\mathscr {A}}_{22,i} \, - \pmb {\mathscr {A}}^s_{22}\right) \mathbf {e}_y \, + \, {\varvec{\nu }} \big ), \end{aligned} \end{aligned}$$
(43)

where \( {\mathbf {e}}_y = \hat{\mathbf {y}} - \mathbf {y}\) denotes the error vector and \(\pmb {\mathscr {A}}_{22}^s\) is a common stable design matrix. An obvious choice for \(\pmb {\mathscr {A}}_{22}^s\) is a diagonal matrix, where the elements are the desired eigenvalues of the output error dynamics. Using the inverse transformation \({\mathbf {T}}_i^{-1}\), the TS sliding mode observer can be obtained in the coordinates \(\mathbf {x}\) of the original model (37)

$$\begin{aligned} \dot{{\hat{\mathbf {x}}}}&= \sum _{i=1}^{N_r} \, h_i(\mathbf {z}) \, \big ( \mathbf {A}_i \, {\hat{\mathbf {x}}} + \mathbf {B}_i \, \mathbf {u}- \mathbf {G}_{l,i} \; \mathbf {e}_y + \mathbf {G}_{n,i} \, \varvec{\nu }\big ) \end{aligned}$$
(44)

with the observer gains

$$\begin{aligned} \mathbf {G}_{l,i} = \mathbf {T}_i^{-1} \, \begin{bmatrix} \pmb {\mathscr {A}}_{12,i} \\ \pmb {\mathscr {A}}_{22,i} - \pmb {\mathscr {A}}_{22}^s \end{bmatrix}, \qquad \mathbf {G}_{n,i} = \mathbf {T}_i^{-1} \, \begin{bmatrix} \mathbf {0}_{(n-p) \times p } \\ \mathbf {I}_p \end{bmatrix}. \end{aligned}$$

LPV Sliding Mode Observation

The LPV sliding mode (LPV SM) observer for the system (42) in transformed form is given by

$$\begin{aligned} \begin{aligned} \dot{{\hat{\mathbf {x}}}}_{1}&= \pmb {\mathscr {A}}_{11}(\varvec{\theta }) \,{\hat{\mathbf {x}}}_{1} + \pmb {\mathscr {A}}_{12}(\varvec{\theta }) \, \hat{\mathbf {y}} + \pmb {\mathscr {B}}_{1}(\varvec{\theta }) \,{\mathbf {u}} - \pmb {\mathscr {A}}_{12}(\varvec{\theta }) {\mathbf {e}}_y, \\ \dot{\hat{\mathbf {y}}}&= \pmb {\mathscr {A}}_{21}(\varvec{\theta }) \, {\hat{\mathbf {x}}}_{1} \, + \pmb {\mathscr {A}}_{22}(\varvec{\theta }) \,\hat{\mathbf {y}} + \pmb {\mathscr {B}}_{2}(\varvec{\theta }) \,\mathbf {u} \, - \, \left( \pmb {\mathscr {A}}_{22}(\varvec{\theta }) \, - \pmb {\mathscr {A}}^s_{22}\right) \mathbf {e}_y \, + \, {\varvec{\nu }}. \end{aligned} \end{aligned}$$
(45)

Using the inverse transformation \({\mathbf {T}^{-1}}\), the LPV sliding mode observer can be obtained in the coordinates \(\mathbf {x}\) of the original model (38)

$$\begin{aligned} \dot{{\hat{\mathbf {x}}}}&= \mathbf {A}(\varvec{\theta }) \, {\hat{\mathbf {x}}} + \mathbf {B}(\varvec{\theta }) \, \mathbf {u}- \mathbf {G}_{l}(\varvec{\theta }) \; \mathbf {e}_y + \mathbf {G}_{n} \, \varvec{\nu }\end{aligned}$$
(46)

with the observer gains

$$\begin{aligned} \mathbf {G}_{l}(\varvec{\theta }) = \mathbf {T}^{-1} \, \begin{bmatrix} \pmb {\mathscr {A}}_{12}(\varvec{\theta }) \\ \pmb {\mathscr {A}}_{22}(\varvec{\theta }) - \pmb {\mathscr {A}}_{22}^s \end{bmatrix}, \qquad \mathbf {G}_{n} = \mathbf {T}^{-1} \, \begin{bmatrix} \mathbf {0}_{(n-p) \times p } \\ \mathbf {I}_p \end{bmatrix}. \end{aligned}$$

The discontinuous term \(\varvec{\nu }\) is necessary for both observer structures in (43), (44) or (45), (46) to establish and maintain a sliding motion. The sliding motion is given by

$$\begin{aligned} {\varvec{\nu }} \,= - \rho \, \frac{\mathbf {P}_2 \; \mathbf {e}_y}{\left\| {\mathbf {P}}_2 \mathbf {e}_y \right\| }, \qquad \text {if} \quad \mathbf {e}_y \ne \mathbf {0}, \end{aligned}$$
(47)

where \(\rho \) is a gain factor and \(\mathbf {P}_2\) is the symmetric, positive definite solution of the Lyapunov equation

$$\begin{aligned} \mathbf {P}_2 \,\pmb {\mathscr {A}}_{22}^s \, + \, {\pmb {\mathscr {A}}_{22}^s}^T \, \mathbf {P}_2 \, = \, - \mathbf {Q}_2, \end{aligned}$$
(48)

where \(\mathbf {Q}_2\) is a symmetric positive definite design matrix. Note that the discontinuous term \(\varvec{\nu }\) in (47) is undefined in the case of \(\mathbf {e}_y = \mathbf {0}\) [6]. Once the sliding surface

$$\begin{aligned} \pmb {\mathscr {S}}=&\{ \mathbf {e}(t) \in {\mathbb {R}}^n : = \pmb {\mathscr {C}}\, \underbrace{[\, \mathbf {e}_1^{\text {T}}\; \mathbf {e}_y^{\text {T}}\, ]^{\text {T}}}_{\mathbf {e}} = \mathbf {0}\; \} \end{aligned}$$
(49)
$$\begin{aligned}&\text {with} \quad \pmb {\mathscr {C}}= \mathbf {C}\; \mathbf {T}_c^{-1} = \big [ \mathbf {0}_{p \times (n-p)} \, \mathbf {I}_p \big ] \end{aligned}$$
(50)

is reached at the time \(t = t_r \), the TS SM observer attempts to maintain the sliding motion on the surface \(\pmb {\mathscr {S}}\).

Actuator Fault Reconstruction by TS SM Observation

For the actuator fault reconstruction we consider first the TS model (41) and the TS SM observer (43) in canonical form. The derivatives of the error of non-measurable and measurable states are \(\dot{\mathbf {e}}_1 = \dot{{\hat{\mathbf {x}}}}_1 - \dot{\mathbf {x}}_1\), \(\dot{\mathbf {e}}_y = \dot{\hat{\mathbf {y}}} - \dot{\mathbf {y}}\) and substituting (41) and (43) it can be verified that

$$\begin{aligned} \dot{\mathbf {e}}_1 = \sum \limits _{i=1}^{N_r} \, h_i(\mathbf {z}) {\pmb {\mathscr {A}}}_{11,i} \, {\mathbf {e}}_1 \end{aligned}$$
(51)

and

$$\begin{aligned} \dot{\mathbf {e}}_y = \sum \limits _{i=1}^{N_r} \, h_i(\mathbf {z}) \big ( \pmb {\mathscr {A}}_{21,i} \, \mathbf {e}_1 + {\pmb {\mathscr {A}}_{22}^s} \, \mathbf {e}_y + {\varvec{\nu }} - \pmb {\mathscr {F}}_{2,i} \; {\mathbf {f}}_a \big ). \end{aligned}$$
(52)

Assume the TS SM observer has been designed and a sliding motion has been established from \(t \ge t_r\). This means that \(\mathbf {e}_y = \mathbf {0}\), \({\dot{\mathbf {e}}}_y = \mathbf {0}\). In this case the error equation (52) is simplified to

$$\begin{aligned} \mathbf {0} = \sum \limits _{i=1}^{N_r} \, h_i(\mathbf {z}) \big ( \pmb {\mathscr {A}}_{21,i} \; \mathbf {e}_1 + {\varvec{\nu }}_{eq} - \pmb {\mathscr {F}}_{2,i} \; {\mathbf {f}}_a \big ) \end{aligned}$$
(53)

and the discontinuous term \({\varvec{\nu }}\) is replaced by the so-called equivalent output injection signal [4]

$$\begin{aligned} {\varvec{\nu }}_{eq} = {\varvec{\nu }}_{\delta }(t \ge t_r), \end{aligned}$$
(54)

where \({\varvec{\nu }}_{\delta }\) denotes an approximation of (47) by introducing a small positive scalar \(\delta \)

$$\begin{aligned} {\varvec{\nu }}_{\delta } \,= - \rho \, \frac{\mathbf {P}_2 \; \mathbf {e}_y}{\left\| {\mathbf {P}}_2 \mathbf {e}_y \right\| + \delta }. \end{aligned}$$
(55)

It should be noted that the value of \(\delta \) should be chosen as small as possible, because it influences the quality of the fault reconstruction [6]. Thus, the equivalent output injection signal is given by rearranging Eq. (53) according to

$$\begin{aligned} {\varvec{\nu }}_{eq} = \sum \limits _{i=1}^{N_r} \, h_i(\mathbf {z}) \big ( \pmb {\mathscr {F}}_{2,i} \; {\mathbf {f}}_a - \pmb {\mathscr {A}}_{21,i} \, \mathbf {e}_1 \big ). \end{aligned}$$
(56)

Substituting the steady-state solution of (51) into (56), we get the relation

$$\begin{aligned} {\mathbf {f}}_a = \left[ \sum \limits _{i=1}^{N_r} h_i(\mathbf {z}) \; \pmb {\mathscr {F}}_{2,i} \right] ^+ \, {\varvec{\nu }}_{eq}, \end{aligned}$$
(57)

where \((\cdot )^+\) denotes the pseudo-inverse of the convex combination of the matrices \(\pmb {\mathscr {F}}_{2,i}\). Note that the pseudo-inverse of the convex combination of matrices exists if the full rank characterization is satisfied by the theorem proposed in [11].

Actuator Fault Reconstruction by LPV SM Observation

Equal to the TS approach, the error equations are defined by \({\dot{\mathbf {e}}}_1 = \pmb {\mathscr {A}}_{11}(\varvec{\theta })\,\mathbf {e}_1\) and \(\dot{\mathbf {e}}_y = \dot{\hat{\mathbf {y}}} - {\dot{\mathbf {y}}}\). On the sliding surface it simplifies to

$$\begin{aligned} \dot{\mathbf {e}}_y = \mathbf {0} = \pmb {\mathscr {A}}_{21}(\varvec{\theta })\, \mathbf {e}_1 + \nu _{eq} - \pmb {\mathscr {H}}_{2}\,\mathbf {f}_v. \end{aligned}$$
(58)

Substituting the steady-state solution of \(\dot{\mathbf {e}}_1\) into (58), which is stable by the design of the transformation matrix \(\mathbf {T}_L\) (cf. Sect. 6), leads to

$$\begin{aligned} \mathbf {f}_v = \begin{bmatrix} \pmb {\mathscr {H}}_2 \end{bmatrix}^+\,\nu _{eq}. \end{aligned}$$
(59)

5 Simulation Results for the Case Studies

After the canonical form of the observer and the existence conditions have been shown, the main focus is directed on the degrees of freedom in the design process having a direct impact on the reachability of the sliding surface. This is a necessary assumption in the reconstruction of the faults. Furthermore, the quality of the fault reconstruction directly depends on the chosen parameters. The design process can be considered as an iterative procedure [8] using the simulation environment including the nonlinear model and the constructed observer. Note that the simulation itself influences the quality of the reconstruction through parameters like the chosen solver, the fundamental sample time and effects like chattering. The following descriptions of the design process are based on the experiences of the authors and sketch a possible way of achieving a well-operating observer. Anyhow, there might be different approaches, which work as well.

The design matrix \(\pmb {\mathscr {A}}_{22}^s\) (cf. (48)) plays an important role in the design process, since it governs the output error dynamics. One way to evaluate the influence of \(\pmb {\mathscr {A}}_{22}^s\) in the simulation is to operate the designed observer in the form similar to the Luenberger observer without the switching term

$$\begin{aligned} \begin{aligned} \hat{\dot{\mathbf {x}}}&= \sum \limits _{i=1}^{N_r}h_i(\mathbf {z})\begin{bmatrix}\mathbf {A}_i\hat{\mathbf {x}}+\mathbf {B}_i \mathbf {u} - \mathbf {G}_{l,i}\mathbf {e}_{\tilde{y}}\end{bmatrix}, ~~ \hat{\mathbf {y}}=\mathbf {C} \hat{\mathbf {x}}, \qquad \text {resp.} \\ \hat{\dot{\mathbf {x}}}&= \mathbf {A}(\varvec{\theta })\hat{\mathbf {x}} + \mathbf {B}(\varvec{\theta })u - \mathbf {G}_l(\varvec{\theta })\mathbf {e}_{\tilde{y}}, ~~ \hat{\mathbf {y}}=\mathbf {C} \hat{\mathbf {x}} \end{aligned} \end{aligned}$$
(60)

until the desired behaviour of the downgraded observer is achieved. Based on the designed Luenberger-like observer and after enabling the switching term again, the parameters \({\varvec{\rho }}\) and \(\delta \) for the equivalent output injection signal can be acquired. As a first step, \(\delta \) can be chosen as a small scalar (cf. Tables 4 and 5) and creates an area around the sliding surface, which reduces effects like chattering. As an indication of the magnitude of the gain matrix \(\mathbf {\rho }\), the proof of the stability of \(\dot{\mathbf {e}}\) through the Lyapunov function, presented for example in [8] for TS and in [1] for the LPV case, can be utilised. Therefore, the maximum values of the errors, matrices, faults and uncertainties have to be estimated. Afterwards, the magnitude of \(\mathbf {\rho }\) can be altered iteratively until the desired results are achieved. In case of the wind turbine observer, a matrix \(\varvec{\rho }\) was used instead of a scalar, which takes account of the different magnitudes of the outputs of the wind turbine. Especially for multiple faults to detect, the use of a matrix can lead to an improvement of the performance. This allows a higher degree of freedom in the design process, but increases the complexity of finding a combination of entries in \(\varvec{\rho }\), which leads to a good reconstruction accuracy. The entries in \(\varvec{\rho }\) have to be well matched for a good reconstruction accuracy. To integrate the extended switching term with \(\varvec{\rho }\) as a matrix, a weighting matrix \(\mathbf {W}\) is introduced into the switching term. The entries of \(\mathbf {W}\) contain the reciprocal values of the maximum estimated faults of the outputs and lead to a normalisation [6]. Note that the iterative alteration of \(\varvec{\rho }\) (or \(\rho \)) does not depend on one specific fault, but rather on the accuracy of the reconstruction over a range of faults is used as a criterion. A well-working combination of parameters for the case studies is shown in Tables 4 and 5. They represent a possible solution for the fault reconstruction; however, other parameter sets might lead to a good reconstruction of faults as well. In case study I the ODE3 Simulink® solver with a fixed sample time of 0.001 s was used. Case study II was calculated by an ODE4 Simulink® solver with a fixed sample time of 0.001 s.

Table 4 Design parameters for case study I
Full size table
Table 5 Design parameters for case study II
Full size table

Note that the observer matrix \(\mathbf {G}_l\) depends on either the membership functions \(h_i\) or the affine term \(\theta _i\). The matrices shown in Tables 4 and 5 are based on the operating point, where \(h_i = 1/N_r~ \forall i\) and \(\theta _i = 0~ \forall i\), and give an idea of the structure of \(\mathbf {G}_l\).

5.1 Simulation Results for Case Study I

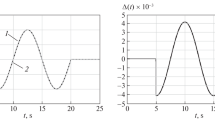
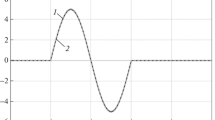
Figure 3 shows the reconstructed fault \(\hat{f}_F\) by the LPV sliding mode observer based on the approximated model compared to the real occurring fault \(f_F\). In Fig. 4 the reconstructed fault \(\hat{f}_F\) of the TS sliding mode observer compared to the real occurring fault \(f_F\) is plotted. Both designed observers show a good accuracy of reconstruction.

Fig. 3
figure 3

Reconstructed fault \(\hat{f}_F\) by the LPV SM observer of the inverted pendulum benchmark

Full size image
Fig. 4
figure 4

Reconstructed fault \(\hat{f}_F\) by the TS SM observer of the inverted pendulum benchmark

Full size image

5.2 Simulation Results for Case Study II

The benchmark model of the wind turbine by Odgaard et al., presented in [15], was created for the evaluation of FDI and FTC methods. For this reason, fault scenarios are implemented in the MATLAB model of the wind turbine. As an example, Fault 8 (cf. [15]), which results in an offset of \(f_a = 100\,\text {Nm}\) on \(T_g\) and is active from \(3800\,\text {s}\le t \le 3900\,\text {s}\), was chosen to give an impression of the performance of the designed sliding mode observer. The observers based on the TS and on the LPV model were simulated in parallel to the nonlinear benchmark model of the wind turbine with the faults included. From \(t=3800\,\text {s}\) to \(t=3900\,\text {s}\) an offset of \(100\,\text {Nm}\) on the generator torque \(T_g\) occurred. The benchmark provides additional noise to the output of the model, which leads to a fluctuation in the fault-free and fault-afflicted reconstruction signal, cf. Figs. 5 and 6. The reconstructed signals of the faults are based on the signals of the noisy benchmark. This is handled by the use of a filter with a transfer function \(H(s)=\frac{10^{-5}s^2+129.33}{s^2+14.91s+130.83}\), which is applied to the noisy reconstructed signals. The plots in Figs. 5 and 6 show the filtered reconstructed signals. Note that, for example in the moment of occurrence of the fault, the fault to the nominal torque magnitude ratio is approx. \(f_a/T_g=0.8\) %. The sensor noise itself can reach magnitudes of \(30\,\text {Nm}\), which makes it harder for the used observers to reconstruct the induced fault. Anyhow, the observers for the LPV and TS model show an identical accuracy of reconstruction of approx. 95 %. This result is not surprising, since the LPV and TS models are an exact representation of the nonlinear model and, as shown in Table 5, the design leads to exactly the same sliding mode observer.

Fig. 5
figure 5

Reconstructed fault \(f_a\) by the TS SMO of the wind turbine benchmark

Full size image
Fig. 6
figure 6

Reconstructed fault \(f_a\) by the LPV SMO of the wind turbine benchmark

Full size image

6 Stability of TS and LPV Systems: A Comparison

Consider the autonomous system in the LPV description as it was introduced in Sect. 2.2

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {A}(\varvec{\theta })\,\mathbf {x}. \end{aligned}$$
(61)

As described by Shamma in [13], the system is quadratically stable if there exists a symmetric, positive definite solution \(\mathbf {P}\) of

$$\begin{aligned} \mathbf {P} \, \mathbf {A}(\varvec{\theta })+\mathbf {A}(\varvec{\theta })^{\text {T}}\, \mathbf {P} <\, 0 \end{aligned}$$
(62)

for all possible trajectories \(\varvec{\theta }\). This condition is based on the exploitation of the characteristics of the Lyapunov function \(V = \mathbf {x}^{\text {T}}\mathbf {P}\, \mathbf {x}\), which ensures quadratic stability. Since the LPV and TS system descriptions lead to a convex formulation, this approach can be handled by the use of linear matrix inequalities (LMI). When comparing LPV and TS models the way they are introduced in this discourse (cf. Sect. 2), it is possible to show that, with the same nonlinear functions, the LMI constraints become the same. Consider the system matrix in (61), where the structure can be arranged to

$$\begin{aligned} \mathbf {A}(\varvec{\theta })=\mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1(\theta _1) + \mathbf {A}_2(\theta _2)+ \cdots + \mathbf {A}_{n_l}(\theta _{n_l}). \end{aligned}$$
(63)

This model has \(n_l\) nonlinearities (\(\varvec{\theta }\in {\mathbb {R}}^{n_l}\)). Note that due to lack of space in the following considerations \(\mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}}\) defines \(\mathbf {A}_0\big |_{\underline{z}_1+\frac{\varDelta z_1}{2},~\underline{z}_2+\frac{\varDelta z_2}{2},\ldots ,~\underline{z}_{n_l}+\frac{\varDelta z_{n_l}}{2}}\). Since the problem was formulated as in Eq. (5), it holds that \(\theta _i\in [-1,1]\,\forall i\). Because this is a convex problem formulation, the LMI constraints are governed by the bounds of each \(\theta _i\). Therefore, there are \(N_r=2^{n_l}\) possible combinations. Setting the matrices according to the possible combinations leads to

$$\begin{aligned} \begin{aligned} \tilde{\mathbf {A}}_1&= \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1(\theta _1 = 1) + \mathbf {A}_2(\theta _2 = 1) + \cdots + \mathbf {A}_{n_l}(\theta _{n_l}=1) \\ \tilde{\mathbf {A}}_2&= \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1(\theta _1 = 1) + \mathbf {A}_2(\theta _2 = 1) + \cdots + \mathbf {A}_{n_l}(\theta _{n_l}=-1) \\ \qquad&\vdots \qquad \qquad \quad \qquad \vdots \qquad \qquad \qquad \qquad \qquad \\ \tilde{\mathbf {A}}_{N_r}&= \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1(\theta _1 = -1) + \mathbf {A}_2(\theta _2 = -1) + \cdots + \mathbf {A}_{n_l}(\theta _{n_l}=-1). \end{aligned} \end{aligned}$$
(64)

From the definition of the LPV model in (6), it is easy to verify that \(\mathbf {A}_i(\theta _i = 1) = \mathbf {A}_i\big |_{\frac{\varDelta z_i}{2}}\) and \(\mathbf {A}_i(\theta _i = -1) = \mathbf {A}_i\big |_{-\frac{\varDelta z_i}{2}}\) holds. Using this knowledge, (64) can be described by

$$\begin{aligned} \begin{array}{l} \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}}+ \mathbf {A}_1\big |_{\frac{\varDelta z_1}{2}} + \mathbf {A}_2\big |_{\frac{\varDelta z_2}{2}} + \cdots + \mathbf {A}_{n_l}\big |_{\frac{\varDelta z_{n_l}}{2}}=\tilde{\mathbf {A}}_1\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\overline{z}_{n_l}} \\ \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1\big |_{\frac{\varDelta z_1}{2}} + \mathbf {A}_2\big |_{\frac{\varDelta z_2}{2}} + \cdots + \mathbf {A}_{n_l}\big |_{-\frac{\varDelta z_{n_l}}{2}}=\tilde{\mathbf {A}}_2\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\underline{z}_{n_l}} \\ \qquad \qquad \vdots \qquad \qquad \qquad \vdots \\ \mathbf {A}_0\big |_{\underline{z}_i+\frac{\varDelta z_i}{2}} + \mathbf {A}_1\big |_{-\frac{\varDelta z_1}{2}} + \mathbf {A}_2\big |_{-\frac{\varDelta z_2}{2}} + \cdots + \mathbf {A}_{n_l}\big |_{-\frac{\varDelta z_{n_l}}{2}}=\tilde{\mathbf {A}}_{N_r}\big |_{\underline{z}_1,~\underline{z}_2,\ldots ,\underline{z}_{n_l}}. \end{array} \end{aligned}$$
(65)

Thus, the LMI constraints to solve equal

$$\begin{aligned} \begin{array}{l} \tilde{\mathbf {A}}_1\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\overline{z}_{n_l}}^{\text {T}}\mathbf {P} + \mathbf {P} \tilde{\mathbf {A}}_1\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\overline{z}_{n_l}}< 0 \\ \tilde{\mathbf {A}}_2\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\underline{z}_{n_l}}^{\text {T}}\mathbf {P} + \mathbf {P} \tilde{\mathbf {A}}_2\big |_{\overline{z}_1,~\overline{z}_2,\ldots ,\underline{z}_{n_l}}< 0 \\ \ \vdots \qquad \qquad \quad \vdots \\ \tilde{\mathbf {A}}_{N_r}\big |_{\underline{z}_1,~\underline{z}_2,\ldots ,\underline{z}_{n_l}}^{\text {T}}\mathbf {P} + \mathbf {P} \tilde{\mathbf {A}}_{N_r}\big |_{\underline{z}_1,~\underline{z}_2,\ldots ,\underline{z}_{n_l}} < 0. \end{array} \end{aligned}$$
(66)

The comparison of the matrices \(\tilde{\mathbf {A}}_i\), \(i \in \{1,2,\ldots ,N_r\}\) to the individual matrices of the submodels in the TS formulation

$$\begin{aligned} \dot{\mathbf {x}}=\sum \limits _{i=1}^{N_r}h_i(\mathbf {z})\,\mathbf {A}_i\,\mathbf {x} \end{aligned}$$
(67)

leads to the realisation that they are the same. When using the Lyapunov function approach for the TS model, it is easy to verify that LMI formulation of the TS and the LPV system result in the same constraints.

As described in [1, 8], the error dynamics for the non-measurable states \(\dot{\mathbf {e}}_1=\pmb {\mathscr {A}}_{11}\,\mathbf {e}_1\) are ensured to be stable by the use of an LMI problem formulation

$$\begin{aligned} \begin{aligned} \mathbf {P}_1> 0, \\ \mathbf {A}_{a,11}(\varvec{\theta })\mathbf {P}_1 + \mathbf {P}_1 \mathbf {A}_{a,11}(\varvec{\theta }) + \mathbf {A}_{a,211}(\varvec{\theta })^{\text {T}}\mathbf {N}^{\text {T}}+ \mathbf {N}\mathbf {A}_{a,211}(\varvec{\theta })< 0, \\ \text {resp.} \\ \mathbf {P}_1 > 0, \\ \mathbf {A}_{a,11,i}\,\mathbf {P}_1 + \mathbf {P}_1 \mathbf {A}_{a,11,i}\, + \mathbf {A}_{a,211,i}\,^{\text {T}}\mathbf {N}_i^{\text {T}}+ \mathbf {N}_i\mathbf {A}_{a,211,i} \, < 0,\, \text {for}~i\in \{1,\ldots ,N_r\}. \end{aligned} \end{aligned}$$
(68)

As outlined, the LMI constraints for the TS and LPV model are equal, when based on the same nonlinear functions. However, there might be a difference in the solution. This is due to the fact that for the TS observer the solver is allowed to find \(N_r\) different solutions for \(\mathbf {N}_i\), since the resulting transformation from the design process can be applied to each individual subsystem \(\{\mathbf {A}_i,\,\mathbf {B}_i,\,\mathbf {C}_i\}\) of the TS system description. In case of the LPV design process one solution for \(\mathbf {N}\) is accepted based on the same constraints. This is due to the fact that no obvious assignment of a solution to individual matrices results from the design process.

7 Conclusions

In this chapter, a LPV and Takagi–Sugeno model-based sliding mode observer design approach was investigated. After a brief introduction of both model structures, the entire modelling process for the observer design was studied in detail by means of two case studies using LPV and TS techniques.

As a result, it can be noted that there exist wide similarities between the LPV and the TS extension of the canonical LTI form of sliding mode observers. Both approaches of the polytopic extension of uncertain LTI systems are suitable for the consideration of nonlinearities of the nominal system dynamics. In particular, there are few differences which can lead to different dynamics of the reconstructed unknown inputs, respectively, occurring faults:

  • In the case of non-factorizable fault distribution matrices \(\mathbf {F}(\varvec{\theta })\) (inverted pendulum), the use of the LPV approach requires a model approximation. In contrast, the TS model approach does not require any approximation and it is therefore straightforward to implement without loss of accuracy.

  • The TS model structure is characterised by weighted convex combinations of linear submodels. This can be exploited in the design process, because the LMI problem formulation allow for different solutions for \(\mathbf {N}_i\) from which \(i\in \{1, \ldots , N_r\}\) observer gains \(\mathbf {G}_{l,i}\) and \(\mathbf {G}_{n,i}\) follow for each individual subsystem. In contrast, the individual matrices in the LPV structure cannot be assigned to related submodels. Based on this fact, the LMI problem formulation caused a common solution \(\mathbf {N}\) whereby the sliding mode observer design is also restricted to a common transformation matrix \(\mathbf {T}\).

However, it must be noted that the performance of the LPV sliding mode observer can be seen as equivalent to the TS sliding mode observer. In both case studies the designed observers achieved a high accuracy of the reconstructed fault signals.