Test Reactive Systems with Büchi-Automaton-Based Temporal Requirements

Abstract

A reactive system is expected to interact with its environment constantly, and its executions may be modeled as infinite words. To capture temporal requirements for a reactive system, Büchi automaton has been used as a formalism to model and specify temporal patterns of infinite executions of the system. A key feature of a Büchi automaton is its ability of accepting infinite words through its acceptance condition. In this paper, we propose a specification-based technique that tests a reactive system with respect to its requirements in Büchi automaton. Our technique selects test suites based on their relevancy to the acceptance condition of a Büchi automaton. By focusing the testing efforts on this key element of a Büchi automaton that is responsible for accepting infinite words, we are able to build a testing process driven by the Büchi automaton specified temporal properties of a reactive system. At the core of our approach are new coverage metrics for measuring how well a test suite covers the acceptance condition of a Büchi automaton. We propose both weak and strong variants of coverage metrics for applications that need tests of different strengths. Each variant incorporates a model-checking-assisted algorithm that automates test case generation. Furthermore our testing technique is capable of revealing not only bugs in a system, but also problems in its requirements. By collecting and analyzing the information produced by a model-checking-assisted test case generation algorithm, our approach may identify inadequate requirements. We also propose an algorithm that refines a requirement in Büchi automaton. Finally, we conduct a thorough computational study to evaluate the performance of our proposed criteria using cross-coverage comparison and fault sensitivity analysis. The results validate the strength of our approach on improving the effectiveness and efficiency of testing, with test cases generated specifically for temporal requirements.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Reactive systems refer to systems that constantly interact with their environments. Many of high dependable systems are reactive systems: they are expected to interact with their environments constantly (e.g. users, physical objects, etc.) even under adversary conditions. Typical safety sensitive systems such as air traffic control systems and nuclear reactor control systems all fall under the definition of reactive systems [26]. As the correct functioning of reactive systems are highly critical, engineers often deploy a mixture of Verification and Validation (V&V) techniques to ensure their correctness. Two of the most frequently used V&V techniques for reactive systems are testing and formal verification.

Testing examines a system by monitoring its behaviors under a fixed set of stimuli, and determines if the system behaves as expected. Based on a “trial and error” ideology, testing has been an essential part of many software V&V processes. In comparison, formal verification refers to a variety of techniques that establish the correctness of a system with respect to a formal requirement, by establishing a mathematically sound proof. Formal verification techniques, particularly model checking, have received much attention from research community, and they are being adopted by the industry as a powerful tool to verify designs of safety-critical systems [15] with an increasing presence.

Testing and formal verification are two complementary V&V techniques, each of which has its own set of pros and cons. Compared with formal verification, testing in general is more feasible in practice, and it may be applied to both specification and implementation. Nevertheless, a major drawback of testing, as notably noted by Dijkstra is that testing can only show the existence of a bug, but not its absence [2]. In contrast, formal verification techniques such as model checking build a mathematically sound proof for the correctness of a design. Nevertheless, formal verification falls short when it is unable to find a conclusive proof. In addition, it does not scale nearly as well as testing, limiting its application to designs or models extracted from implemented systems, such as in the case of software model checking.

A research theme in V&V field is how to harness the synergy of testing and formal verification. Techniques such as model-checking-based test case generation [11] have been proposed to utilize such a synergy. In this paper we are interested in specification-based testing with temporal requirements. In recent years, formal verification techniques, particularly model checking, have become significantly more popular in industrial applications (c.f. [19]). One of the consequences of the proliferation of formal verification techniques is that the formal requirements are also becoming more available. We want to take this opportunity and extend the application of formal requirements into testing. Our objectives are two-fold: (1) improve the effectiveness of testing by centering it around formal requirements; and (2) improve the efficiency of testing by developing a model-checking-assisted test case generator for our proposed test criteria.

In this paper, we extend our original work presented in [30] from both the theoretical and practical aspects. We choose reactive systems as the subject of our study, and focus on specification-based testing for reactive systems whose formal requirements are defined in Büchi automaton. The practical importance of reactive systems in developing safety-critical systems justifies the potential of our work. The essence of a reactive system is its ability of performing infinite executions. A challenge in testing a reactive system is how to specify and test these infinite behaviors. Many of previous works on testing reactive systems (c.f. [18, 21, 24]) have been focusing on testing finite prefixes of infinite executions. We want to develop a testing technique focusing on features of infinite executions themselves, that is, temporal patterns exhibited by an infinite execution of a reactive system. Particularly, we consider requirements encoded in Büchi automaton. Büchi automaton, a type of $\omega$-automata that accept infinite words, has been widely used to specify linear temporal behaviors of a reactive system. It is also instrumental in developing linear temporal model checkers: other formalisms such as Linear Temporal Logic (LTL) are often first translated into Büchi automaton, before being used in model checking.

A first-order question in specification-based testing, or any software testing for that matter, is to measure the adequacy of a test suite. We define two coverage metrics measuring how a test suite covers a requirement in Büchi automaton. The metrics define how thoroughly a test suite covers the acceptance condition of a Büchi automaton. A Büchi automaton differs from a finite automaton in its acceptance condition, which enables the Büchi automaton to accept infinite words. By focusing on the acceptance condition of a Büchi automaton encoding the requirement for a reactive system, our approach centralizes testing efforts on infinite executions of the system. Test criteria derived from these metrics can then be used in producing and executing test suites.

To improve the efficiency of test generation, we also propose model-checking-assisted test case generation algorithms for proposed test criteria. By utilizing the counterexample producing capability of an off-the-shelf model checker, these algorithms automate the test case generation for reactive systems with Büchi automata. We also establish the correctness of said algorithms through mathematical proofs.

By deriving test cases from a reactive system model and its formal requirement, our specification-based testing approach becomes a powerful tool to detect the discrepancy between the model and its requirements. In addition to debugging a reactive system, our approach may also help in detecting the deficiency of a specification. The latter also enables the refinement of a requirement, reducing the gap between the semantics of the requirement and a system implementation. We propose a technique that automates the property-refinement process, by reusing the information from model-checking-assisted test generation algorithms.

We conduct two sets of computational study to compare the effectiveness of the proposed acceptance condition coverage criteria against other existing criteria, including traditional test criteria such as branch coverage, as well as the other LTL or Büchi automaton based test criteria introduced in [21, 23, 31]. The first set of computational study is to measure the cross coverage of different test criteria, that is, how well a test suite generated for one test criterion covers another criterion. The results provide a measurement of the effectiveness of a test criterion in comparison with another criterion. The second set of computational study uses fault-injection technique. Fault-injection technique is a classic method for examining the coverage of a test suite [1]. In this study, we take a test suite generated from a specific test criterion, and use fault-injection technique to measure its ability to spot artificially planted errors. The measurement is an indicator for the effectiveness of the underlying test criterion. Both sets of computational study demonstrate the effectiveness and efficiency of our proposed approach. For these experiments, we select sample applications from a diversified range of fields, including software engineering (GIOP protocol for middleware construction), security (Needham-Schroeder public key protocol), and automobile (a fuel system example).

The rest of the paper is organized as follows: Sect. 2 prepares the notations used in the rest of the paper; Sect. 3 introduces two variants of accepting state combination coverage metrics and criteria for Büchi automata; Sect. 4 describes the model-checking-assisted test case generation algorithms for the proposed criteria; Sect. 5 discusses the requirement refinement using the feedback from the model-checking-assisted test case generation; Sect. 6 discusses the result of our computational study on the performance comparison between the new criteria and other existing test criteria; and finally Sect. 7 concludes the paper.

[Related Works] An important component of our approach is a model-checking-assisted algorithm that utilizes the counterexample mechanism of an off-the-shelf model checker to generate test cases. Model checkers are able to generate counterexamples of a model that violates a temporal formula that describes a desired property. Taking advantage of such ability of model checkers to assist test generation has received a significant amount of attention in recent years. One of the core problems in model-checking-assisted test generation is how to translate test objectives into temporal properties that can be fed to model checkers. Both [5, 9] have discussed the usage of formal specification in software testing. Gaudel further provided an overview for the conjunction area of testing and model checking, encouraging a more clear and uniformed field for the “industrial actors” [6].

Various works have shown that traditional structural test criteria can be used as the core standard for test generation via model checkers. For instance, Fraser et al. show that Modified Condition/Decision Coverage (MC/DC) can be encoded in Computational Tree Logic (CTL) [3], and be used by a model checker such as NuSMV for generating tests. The authors also evaluated different test criteria such as logic expression coverage criteria and dataflow criteria in the context of model-checking-assisted test generation. In [11], Hong et al. expressed the dataflow criteria in CTL. All these works presented their methods of translating one or more existing structure-based test objectives into temporal properties in CTL or LTL.

A key feature of our work is that it is based on Büchi automaton. This enables us to translate and encode linear temporal properties expressed in other formalisms such as LTL. Our work further extends previous research based on LTL [22], in which the authors proposed coverage metrics measuring how well a requirement in LTL was covered by a test suite. In [21, 23, 31] we studied test metrics for covering states and transitions of a Büchi automata. While these works explored specification-based testing with Büchi automata, they were also limited to testing finite prefixes of infinite words. In this paper, we focus on the acceptance condition, which allows us to test temporal properties of infinite words.

Meanwhile, using formal specification to model requirements inspires a variety of automatic test generation and test execution tools. For example, AGEDIS project [8] was created as an effort to automate test generation and execution for distributed systems. Simulink Design Verifier [16] was developed as a verification and test generation tool for Simulink. Reactis [20] is another commercial tool developed by Reactive Systems Inc. that also accepts models in the Simulink and StateFlow modeling language. It uses a guided simulation strategy that is not as exhausting as model checking, hence avoiding the state explosion problem. In this work we developed a model-checking-assisted test generation algorithm that works with requirements encoded in Büchi automaton.

2 Preliminaries

2.1 Kripke Structures, Traces, and Tests

We model systems as Kripke structures. A Kripke structure is a finite transition system in which each state is labeled with a set of atomic propositions. Semantically atomic propositions represent primitive properties held at a state. Definition 1 formally defines Kripke structures.

Definition 1

(Kripke Structures) Given a set of atomic proposition $\mathcal{A}$, a Kripke structure is a tuple $\langle V, v_0, \rightarrow , \mathcal{V} \rangle$, where V is the set of states, $v_0 \in V$ is the start state, $\rightarrow \subseteq V \times V$ is the transition relation, and $\mathcal{V}:V \rightarrow 2^\mathcal{A}$ labels each state with a set of atomic propositions.

We write $v\rightarrow v'$ in lieu of $\langle v, v' \rangle \in \rightarrow$. We let $a, b, \ldots$ range over $\mathcal{A}$. We denote $\mathcal{A}_\lnot$ for the set of negated atomic propositions. Together, $P=\mathcal{A} \cup \mathcal{A}_\lnot$ defines the set of literals. We let $l_1, l_2, \ldots$ and $L_1, L_2, \ldots$ range over P and $2^{P}$, respectively.

We use the following notations for sequences: let $\beta =v_0 v_1 \ldots$ be a sequence, we denote $\beta [i]=v_{i}$ for ith element of $\beta$, $\beta [i, j]$ for the subsequence $v_{i} \ldots v_{j}$, and $\beta ^{(i)}= v_{i} \ldots$ for the ith suffix of $\beta$. A trace $\tau$ of the Kripke structure $\langle V, v_0, \rightarrow , \mathcal V \rangle$ is defined as a maximal sequence of states starting with $v_0$ and respecting the transition relation $\rightarrow$, i.e., $\tau [0]=v_0$ and $\tau [i-1] \rightarrow \tau [i]$ for every $i<|\tau |$. We also extend the labeling function $\mathcal{V}$ to traces: $\mathcal{V}(\tau )=\mathcal{V}(\tau [0])\mathcal{V}(\tau [1])\ldots$.

Definition 2

(Lasso-Shaped Sequences) A sequence $\tau$ is lasso-shaped if it has the form $\alpha (\beta )^\omega$, where $\alpha$ and $\beta$ are finite sequences. $|\beta |$ is the repetition factor of $\tau$. The length of $\tau$ is a tuple $\langle |\alpha |, |\beta | \rangle$.

Definition 3

(Test and Test Suite) A test is a word on $2^\mathcal{A}$, where $\mathcal{A}$ is a set of atomic propositions. A test suite ts is a finite set of test cases. A Kripke structure $K=\langle V, v_0, \rightarrow , \mathcal{V} \rangle$ passes a test case t if K has a trace $\tau$ such that $\mathcal{V}(\tau )=t$. K passes a test suite ts if and only if it passes every test in ts.

2.2 Generalized Büchi Automata

Definition 4

A generalized Büchi automaton is a tuple $\langle S, S_0, \varDelta , \mathcal{F} \rangle$, in which S is a set of states, $S_0 \subseteq S$ is the set of start states, $\varDelta \subseteq S \times S$ is a set of transitions, and the acceptance condition $\mathcal{F}\subseteq 2^S$ is a set of sets of states.

We write $s \rightarrow s'$ in lieu of $\langle s, s' \rangle \in \varDelta$. A generalized Büchi automaton is an $\omega$-automaton, which can accept the infinite version of regular languages. A run of a generalized Büchi automaton $B=\langle S, S_0, \varDelta , \mathcal{F} \rangle$ is an infinite sequence $\rho =s_0s_1 \ldots$ such that $s_0 \in S_0$ and $s_i \rightarrow s_{i+1}$ for every $i \ge 0$. We denote $\inf (\rho )$ for a set of states that appear for infinite times on $\rho$. A successful run of B is a run of B such that for every $F \in \mathcal{F}$, $\inf (\rho )\cap F \ne \emptyset$.

In this work, we extend Definition 4 using state labeling approach in [7] with one modification: we label the state with a set of literals, instead of with a set of sets of atomic propositions in [7]. A set of literals is a succinct representation of a set of sets of atomic propositions: let L be a set of literals labeling state s, then semantically s is labeled with a set of sets of atomic propositions $\varLambda (L)$, where $\varLambda (L)=\{ A\subseteq \mathcal{A} \, | \, (A \supseteq (L \cap \mathcal{A})) \wedge (A \cap (L \cap \mathcal{A}_\lnot )= \emptyset ) \}$, that is, every set of atomic propositions in $\varLambda (L)$ must contain all the atomic propositions in L but none of its negated atomic propositions. In the rest of the paper, we use Definition 5 for (labeled) generalized Büchi automata (GBA).

Definition 5

A labeled generalized Büchi automaton is a tuple $\langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, in which $\langle S, S_0, \varDelta , \mathcal{F} \rangle$ is a generalized Büchi automaton, P is a set of literals, and the label function $\mathcal{L}: S \rightarrow 2^P$ maps each state to a set of literals.

A GBA $B=\langle \mathcal{A}\cup \mathcal{A}_\lnot , S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$ accepts infinite words over the alphabet $2^\mathcal{A}$. Let $\alpha$ be a word on $2^\mathcal{A}$, B has a run $\rho$ induced by $\alpha$, written as $\alpha \vdash \rho$, if and only if for every $i<|\alpha |$, $\alpha [i] \in \varLambda (\mathcal{L}(\rho [i]))$. B accepts $\alpha$, written as $\alpha \models B$ if and only if B has a successful run $\rho$ such that $\alpha \vdash \rho$.

GBAs are of special interests to the model checking community. Because a GBA is an $\omega$-automaton, it can be used to describe temporal properties of a finite-state reactive system, whose executions are infinite words of an $\omega$-language. Formally, a GBA accepts a Kripke structure $K=\langle V, v_0, \rightarrow , \mathcal{V} \rangle$, denoted as $K \models B$, if for every trace $\tau$ of K, $\mathcal{V}(\tau ) \models B$. Efficient Büchi-automaton-based algorithms have been developed for linear temporal model checking. The process of linear temporal model checking generally consists of translating the negation of a linear temporal logic property $\phi$ to a GBA $B_{\lnot \phi }$, and then checking the emptiness of the product of $B_{\lnot \phi }$ and K. If the product automaton is not empty, then a model checker usually produces an accepting trace of the product automaton, which serves as a counterexample to $K \models \phi$.

3 Accepting State Combination Coverage Criteria

A Büchi automaton differs from a finite automaton in its acceptance condition, which enables a Büchi automaton to accept infinite words. Since we are interested in testing a reactive system, and particularly the temporal patterns of its infinite executions, we focus on covering the acceptance condition of a Büchi automaton. In what follows, we denote $\bigcup \mathcal{F}= F_0 \cup \cdots \cup F_{n-1}$, where $\mathcal{F}= \{F_0, \ldots , F_{n-1}\}$.

Definition 6

(Accepting State Combination) Given a Büchi automaton $B = \langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, an accepting state combination (ASC) C is a minimal set of states such that (i) $C \subseteq \bigcup \mathcal{F}$; (ii) $\forall F \in \mathcal{F}$, $F \cap C \ne \emptyset$.

Definition 7

(Covered Accepting State Combinations) Given a GBA $B = \langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, let C be one of B’s ASCs,

• 1. A run $\rho$ of B covers C if $\rho$ visits every state of C infinitely often;

• 2. A test t strongly covers B’s ASC C if t satisfies B and every successful run induced by t on B covers C;

• 3. A test t weakly covers B’s ASC C if at least one run induced by t on B covers C.

Intuitively, an ASC is a basic unit for the sets of acceptance states covered by a successful run. That is, any successful run must visit every state of some ASC infinitely often, as stated in Lemma 1.

Lemma 1

Given a Büchi automaton $B = \langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, $\rho$ is a successful run of B if and only if $\rho$ covers some ASC of B.

Proof

($\Rightarrow$):

Let $inf(\rho )$ be the set of states visited by $\rho$ infinitely often, and $C'=inf(\rho )\cap (\bigcup \mathcal{F})$ be the set of acceptance states visited by $\rho$ infinitely often. Then, $C'$ satisfies the following properties: (i) $C' \subseteq \bigcup \mathcal{F}$; and, (ii) $\forall F \in \mathcal{F}.(F\cap C')\ne \emptyset$. (ii) is due to the assumption that $\rho$ is a successful run of B. Note that by Definition 6 the ASCs are all the minimal sets satisfying (i) and (ii). Therefore, $C'$ has to be a superset of some ASC  say C. It follows that $\rho$ visits every state in C infinitely often, that is, $\rho$ covers C.

($\Leftarrow$):

Let C be an ASC of B covered by $\rho$, that is, $\inf (\rho ) \supseteq C$. By Definition 6 $\forall F \in \mathcal{F}. F \cap C \subseteq F \cap \inf (\rho ) \ne \emptyset$. Therefore, $\rho$ satisifies the acceptance condition of B and hence it is one of B’s successful runs.$\square$

 

Algorithm 1 gives a code example that computes all the ASCs for a given GBA B. We denote $\mathcal{C}(B)$ as the set of the ASCs of B. The coverage metrics are thus about covering these ASCs. Definition 7 presents two different ways to cover an ASC, due to the non-deterministic nature of a GBA. In the strong variant, every successful run induced by a successful test is required to visit the ASC infinitely often; and in the weak variant, only one successful run induced by the test is required to visit the ASC infinitely often. By Lemma 2 the strong coverage criterion subsumes the weak one. Users may pick and choose the type of coverage, depending on the desired strength of testing set forth for an application.

Lemma 2

An ASC C of a Büchi automaton B is weakly covered by a test t if C is strongly covered by t.

Proof

It immediately follows from Definition 7.$\square$

Definition 8

(Strong/Weak ASC Coverage Metric and Criterion)

Given a generalized Büchi automaton $B=\langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, let $\mathcal{C}(B)$ be the set of B’s ASCs, the strong (or weak) ASC coverage metric for a test suite T on B is $\frac{|\delta '|}{|\delta |}$, where $\delta '=\{ C \, | \, t \text { strongly (or weakly) covers } C \}$, and $\delta = \mathcal{C}(B)$. T strongly (or weakly) covers $\delta$ if and only if $\delta '=\delta$.

It shall be noted that the number of all the ASCs is significantly smaller than the number of all the possible combinations of acceptance states. The first is bounded by $O(m ^n )$ and the latter is bounded by $2^{m}$, where $n=|\mathcal{F}|$ is the cardinality of $\mathcal{F}$ and $m=|\bigcup \mathcal{F}|$ is the number of acceptance states. By focusing on covering ASCs instead of every combination of acceptance states, we significantly reduce the complexity of computing our coverage metrics.

4 Model-Checking-Assisted Test Generation for Accepting States Combination Coverage

To improve the efficiency of test case generation, we develop a model-checking-assisted algorithm for generating test cases under proposed criteria. The algorithm uses the counterexample capability of an off-the-shelf linear temporal model checker to generate test cases. One of the fundamental questions in model-checking-assisted test generation is how to specify test objectives in a formalism acceptable by a model checker. The properties specifying test objectives are often referred to as “trap properties” in the context of model-checking-assisted test generation. In our case, “trap properties” are defined in the form of Büchi automaton. We synthesize a set of “trap (Büchi) automata” from the original Büchi automaton, using graphic transformation techniques.

Definition 9

(ASC Excluding Automaton) Given a Büchi automaton $B = \langle P, S, S_0, \varDelta , \mathcal{L}, F\equiv \{ F_0, \ldots , F_{n-1} \}\rangle$ and an ASC C, an ASC excluding (ASC-E) GBA is $B_{\overline{C}}= \langle P, S^e, S^e_0\equiv S_0 \times \{ \bot \}, \varDelta ^e, \mathcal{L}^e, \mathcal{F}^e \equiv \{ F^e_0, \ldots , F^e_{n-1} \} \rangle$, where,

• 1. $S^e=(S\times (C \cup \{ \bot \}))-\bigcup _{s\in C} \{ \langle s,s \rangle \}$

• 2. $F^e_i = \{ \langle s,u \rangle \, | \, s \in F_i\wedge u \ne \bot \}$.

• 3. $\varDelta ^e = \{ (\langle s, u \rangle \rightarrow \langle s', u' \rangle ) \, | \, (s \rightarrow s') \in \varDelta \wedge (u=u' \vee (u=\bot )) \}$

• 4. $\mathcal{L}^e(\langle s,u \rangle ) = \mathcal{L}(s)$

Intuitively speaking, for a Büchi automaton B and an ASC C, its ASC-E-GBA $B_{{\overline{C}}}$ accepts precisely B’s successful runs, except for those visiting C infinitely often. $B_{{\overline{C}}}$ does so by extending B with additional copies. To distinguish these copies, the states of the original copy (denoted as $B_\bot$) is indexed by the symbol $\bot$, whereas the states of each additional copy (denoted as $B_{\lnot s}$) are indexed by a state $s \in C$. $B_{\lnot s}$ inherits all the states from B except for s, the very state indexing B (i.e. $\langle s, s \rangle$ in Definition 9(1)). Intuitively, $B_{\lnot s}$ accepts all the successful runs of B, except for those visiting the indexing state s. Each copy $B_{\lnot s}$ retains the transitions from B (except for, of course, the ones associating with the indexing state s, which is not in $B_{\lnot s}$). In addition, for each transition of the original copy $B_\bot$, say $\langle s, \bot \rangle \rightarrow \langle s', \bot \rangle$, we create |C| copies of that transition, each of which replaces the destination node $\langle s',\bot \rangle$ with its counterpart in a copy $B_{\lnot t}$ indexed by a state $t \in C$ (Definition 9(3)). Formally, for each transition $\langle s,\bot \rangle \rightarrow \langle s',\bot \rangle$, we add more transitions $\delta =\bigcup _{t\in C}\{ \langle s,\bot \rangle \rightarrow \langle s', t \rangle \}$. We refer to these new transitions as “bridging” transitions. Note that these bridging transitions go one-way only, that is, they jump from the original copy $B_\bot$ to a copy $B_{\lnot t}$, where $t \in C$. There are no transitions linking $B_{\lnot t}$ back to $B_\bot$. As a final touch, only the copies indexed by the states of C, not the original one, retain the acceptance condition. Since every additional copy $B_{\lnot s}$ misses its indexing state s, it implies that the indexing state is not part of the acceptance condition of $B_{\lnot s}$.

It follows from the construction of $B_{\overline{C}}$ that a successful run $\rho$ of $B_{\overline{C}}$ must satisfy the following conditions: (1) it starts at $B_\bot$ (i.e. the start states $S^e_0$ in Definition 9) and can spend only a finite number of steps in $B_\bot$, since $B_\bot$ does not have an acceptance state (Definition 9(2)); (2) at some point, $\rho$ will make a non-deterministic choice to take a bridging transition to one of the copies indexed by a state $s \in C$, say $B_{\lnot s}$, and satisfy $B_{\lnot s}$’s acceptance condition. Clearly $\rho$ is also a successful run of the original GBA B, since each state on $\rho$ may be mapped back to a state of B, and the acceptance condition of $B_{\lnot s}$ accepting $\rho$ is a subset of the acceptance condition of B. In addition, because $B_{\lnot s}$ does not have s (Definition 9(1)), $\rho$ cannot visit s infinitely often. Furthermore, no matter which copy the $\rho$ jumps to, there is no way that $\rho$ can visit every state of C infinitely often, since there is one state of C missing in that copy, i.e., its indexing state. It follows that a successful run $\rho '$ of B becomes a successful run of its ASC-E-GBA only if $\rho '$ does not visit every state of C infinitely often.

Theorem 1

Given a GBA $B=\langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F}\rangle$ and an ASC C, $B_{\overline{C}}= \langle P, S^e, S^e_0, \varDelta ^e, \mathcal{L}^e, \mathcal{F}^e\rangle$ be the ASC-E-GBA for B and C, then a test t satisfies $B_{\overline{C}}$ if and only if B has a successful run $\rho$ such that $t \vdash \rho$ and $\inf (\rho ) \not \supseteq C$.

Proof

($\Rightarrow$):

By Definition 9, since t satisfies $B_{\overline{C}}$, $B_{\overline{C}}$ has a successful run $\rho '$ such that $t \vdash \rho '$. We construct a successful run $\rho$ for B from $\rho '$ by projecting states in $B_{\overline{C}}$ to B. Assume that $\rho ' = \langle s_0,u_0 \rangle \langle s_1,u_1 \rangle \ldots$, then $\rho = s_0 s_1 \ldots$. By Definition 9, $\rho$ has to be a successful run of B, since all the transitions in $\rho '$: $\langle s_i,u_i \rangle \rightarrow \langle s_{i+1},u_{i+1} \rangle$ follow the same guards as $s_i \rightarrow s_{i+1}$, and the acceptance conditions in $B_{\overline{C}}$ are the same states in B marking with states in C. We also have $\mathcal{L}^e(\langle s,u \rangle ) = \mathcal{L}(s)$ and $t \vdash \rho '$, therefore $t = \mathcal{L}^e(\rho ') = \mathcal{L}(\rho )$. Hence, $t \vdash \rho$.

Now we will prove $\inf (\rho ) \not \supseteq C$ by showing at least one state in ASC C is not visited by $\rho$ infinitely often. Note that by the construction of $B_{\overline{C}}$ every acceptance state is resided in a copy of B indexed by a state (i.e. not $\bot$). Therefore, since $\rho '$ is a successful run of $B_{\overline{C}}$, $\rho '$ must visit at least one copy of B indexed by a state. Without loss of generality, let s be the indexing state of a B’s copy that $\rho '$ visits. We denote the indexed copy as $B_{\lnot s}$. By Definition 9 there is no outgoing transition from $B_{\lnot s}$ to other copies of B. Therefore once $\rho '$ is in $B_{\lnot s}$, it is “trapped” within $B_{\lnot s}$ and only states $\rho '$ may visit infinitely often are those inside $B_{\lnot s}$. By Definition 9 $B_{\lnot s}$ does not include a copy of state s itself, therefore $\inf (\rho ')$ does not visit s or its indexed copies infinitely often. That is, $s \notin \inf (\rho )$. Note that an indexing state must be a state in ASC C by Definition 9(1). Therefore $\inf (\rho )\not \supseteq C$.

($\Leftarrow$):

Let’s denote $D= C - \inf (\rho )$. Since $\inf (\rho )\not \supseteq C$, $D \ne \emptyset$. Let $\rho = s_0 s_1 \ldots$. Let $s_k$ for the last occurrence of any state in D on $\rho$. If $\rho$ does not visit any state in D, then $k=0$. We randomly pick a state $s \in D$. Now we construct $\rho '=\langle s_0, u_0 \rangle \langle s_1, u_1 \rangle \ldots$ such that $\forall i\le k. u_i=\bot$ and $\forall i > k.u_i = s$. Intuitively speaking, $\rho '$ visits states in the copy indexed by $\bot$ (denoted as $B_\bot$), and then jump to the copy $B_{\lnot s}$. Note that $B_{\lnot s}$ has an (indexed) copy of every state of B, except for s. Since $s_{k+1} s_{k+2} \ldots$ does contain any state of C, it does not visit (an indexed copy of) s either. Clearly $\rho '$ is a run of $B_{\overline{C}}$, since it respects the transition relation in Definition 9.

Next we will show that $\rho '$ also satisfies the acceptance condition of B. As a successful run of B, $\rho$ satisfies B’s acceptance condition, that is, $\forall \mathbf{F}_i \in \mathcal{F}. \inf (\rho )\cap \mathbf{F}_i \ne \emptyset$. Without loss of generality, we pick up $\mathbf{F}_i$ and show that $\rho '$ will visit some state in $\mathbf{F}^e_i$, $B_{\overline{C}}$’s counterpart of $\mathbf{F}_i$, infinitely often. Let $s_f \in \bigcup \mathbf{F}_i$ be a state visited by $\rho$ infinitely often, Because there is an one-to-one mapping between states on $\rho$ and $\rho '$, $\rho '$ also visits $\langle s_f, s \rangle$ infinitely often. By Definition 9, $\langle s_f,s \rangle \in \mathbf{F}^e_i$. Therefore, we have $\forall \mathbf{F}^e_i\in \mathcal{F}^e.\inf (\rho ')\cap \mathbf{F}^e_i \ne \emptyset$.

Finally we show $t \vdash \rho '$ by noting Definition 9(4), that is, $B_{\overline{C}}$ is labelled in the same way as B. Therefore, if t induces $\rho$ on B, it may also induce $\rho '$ on $B'$. Therefore t induces a successful run $\rho '$ of $B_{\overline{C}}$ and hence it satisfies $B_{\overline{C}}$.$\square$

Fig. 1

A general Büchi automaton representing the LTL property $\mathbf{G}(\lnot t \implies ((\lnot p~\mathbf{U}~t) \vee \mathbf{G}\lnot p))$

As an example, consider a GBA in Fig. 1. The GBA represents LTL property $\phi =\mathbf{G}(\lnot t \implies ((\lnot p~\mathbf{U}~t) \vee \mathbf{G}\lnot p))$, a temporal requirement used with the GIOP model [14] in our experimental study. $\phi$’s semantics is explained in Sect. 6. Since its acceptance condition $\{ \{ s_0,s_2 \} \}$ contains only one set of states, its ACSs are the singleton set of each acceptance state, that is, $\{ s_0 \}$ and $\{ s_2 \}$. Figure 2 gives an ASC excluding automaton $B_{\overline{\{ s_0 \}}}$ with respect to the ASC $\{ s_0 \}$. $B_{\overline{\{ s_0 \}}}$ has two copies of B: the original copy $B_\bot$ and the copy indexed by $s_0$, the only state in $C = \{ s_0 \}$. Note that the indexing state itself $s_0$ (i.e. $\langle s_0, s_0 \rangle$) and its transitions are removed from the copy $B_{\overline{\{ s_0 \}}}$. These are represented by the dashed circle and lines in Fig. 2. The highlighted solid links represent bridging transitions linking from the original copy to the copy indexed by $s_0$. Since the only acceptance state, $\langle s_2, s_0 \rangle$ exists in the copy $B_{\lnot {s_0}}$, a successful run of $B_{\overline{\{ s_0 \}}}$ must visit $s_2$ (in the form of $\langle s_2, s_0 \rangle$), not $s_0$ (in the form of $\langle s_0, s_0 \rangle$), infinitely often.

Fig. 2

An ASC excluding general Büchi automaton for the ASC $\{ s_0 \}$ of the GBA in Fig. 1

Algorithm 2 generates a test suite strongly covering all the ASCs of a Büchi automaton B. It makes use of ASC excluding automata. For each of B’s ASCs, Algorithm 2 constructs an ASC excluding GBA $B_{\overline{C}}$ with respect to C. $ASC\_Gen$ is a sub-routine computing all the ASCs for a GBA. The algorithm uses a model checker to search for a successful run $\tau$ on the production of $\lnot {B_{\overline{C}}}$ and $K_m$, and $\tau$ is a successful run of $\lnot {B_{\overline{C}}}$ accepting $K_m$. $MC\_isEmpty$ refers to the emptyness checking algorithm in an off-the-shelf linear temporal model checker. If a run exists, it returns with a test set containing $t = \mathcal{V}(\tau )$, which is a word accepted by $\lnot {B_{\overline{C}}}$. Consequently, t cannot be accepted by $B_{\overline{C}}$. Note that $\tau$ is a successful run of the production of B and $K_m$, therefore based on Theorem 1, for every successful run $\rho$ that $t \vdash \rho$, $\inf (\rho ) \supseteq C$. Based on Definition 7, ts is a test suite that strongly covers C.

Theorem 2

If the test suite ts returned by Algorithm 2 is not empty, then (i) $K_m$ passes ts and (ii) ts strongly covers all the ASCs of B.

Proof

(i) For each test $t \in ts$, there is a related ASC C and $MC\_isEmpty$ $(\lnot {B_{\overline{C}}}, K_m))$ returns a successful run $\tau$ of the product of $\lnot {B_{\overline{C}}}$ and $K_m$ such that $\mathcal{V}(\tau )=t$. It follows that $\tau$ is also a successful run on $K_m$, and $K_m$ shall pass $t=\mathcal{V}(\tau )$. Therefore, $K_m$ passes every test case in ts.

(ii) As shown in (i), for each $t \in ts$, there is a related ASC C and a successful run $\tau$ of the production of $\lnot {B_{\overline{C}}}$ and $K_m$ such that $\mathcal{V}(\tau )=t$. We show that t strongly covers the ASC C.

First, since $\tau$ is also a trace of $K_m$ and $K_m$ satisfies B by the precondition of Algorithm 2, $\tau \models B$.

Second, we will prove by contradiction that every successful run of B that is induced by the test case t shall cover C, i.e., every state in C shall be visited infinitely often. Suppose that it were not the case. Let $\rho$ be a successful run of B that is induced by t, and $\rho$ does not cover C.

We may now construct a run $\rho '$ by “tracing” $\rho$’s states on $B_{\overline{C}}$ as follows: since $\rho$ does not cover C, there must exist at least one state $s \in C$ and $s \not \in \inf (\rho )$. As $\rho$ is a lasso-shaped trace, we label every state in the non-circular prefix of $\rho$ with $\bot$, and every state in the circular subtrace of $\rho$ with s. By this construction and Definition 9, $\rho '$ is a successful run on $B_{\overline{C}}$.

Since t induces $\rho$, and $\rho '$ is obtained by adding labels to the states on $\rho$, t also induces $\rho '$ on $B_{\overline{C}}$. Therefore, t shall be accepted by $B_{\overline{C}}$. However, we have shown that t is accepted by $\lnot (B_{\overline{C}})$ which is a complement of $B_{\overline{C}}$, and thus should have no common words in their languages. If t can be accepted by both automata, then $t \in L(\lnot {B_{\overline{C}}}) \cap L(B_{\overline{C}}) \ne \emptyset$. Therefore, every successful run of B that accepts t shall cover C.$\square$

Compared with constructing an ASC excluding automaton, constructing a Büchi automaton accepting the runs weakly covering an ASC is relatively straightforward: the new automaton may be obtained by removing from the acceptance condition the states not in the ASC, that is, replacing the acceptance condition with C. Definition 10 describes the process.

Definition 10

(ASC Marking Automaton) Given a GBA $B=\langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$ and an ASC C, $B_C=\langle P, S, S_0, \varDelta , \mathcal{L}, \mathcal{F}_C \rangle$ is the ASC-Marking (ASC-M) Büchi automaton for B with respect to C, in which $\mathcal{F}_C = \{ F \cap C | F \in \mathcal{F} \}$.

Clearly $L(B_C) \subseteq L(B)$, since the acceptance condition of $B_C$ is a refinement of that of B, that is, $\forall F \in \mathcal{F}, \exists F' \in \mathcal{F}_C, (F' \subseteq \mathcal{F}')$ and $\forall F' \in \mathcal{F}_C, \exists F \in \mathcal{F}, (F'\subseteq F)$. Note that, $\mathcal{F}_C$ in Definition 10 is a subset of $2^C - \emptyset$. By Definition 6, C has to be a minimal set of states that $\forall F \in \mathcal{F}$, $F \cap C \ne \emptyset$. Combining these two conditions, it is straightforward $\bigcup \mathcal{F}_C = C$. Based on Definition 4, this means that for a run to be successful on $B_C$, all states in C must be visited infinitely often. Therefore we rewrite the acceptance condition for $B_C$ as $\mathcal{F}_C = \{ \{ s \} \, | \, s\in C \}$, i.e., a set of singleton sets of states in C. For the rest of the paper, we consider ASC-M-GBA to be defined with the rewritten acceptance condition.

Lemma 3

Given a GBA $B= \langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F} \rangle$, let C be one of its ASCs and $B_C=\langle P, S, S_0, \varDelta , \mathcal{L}, \mathcal{F}_C \rangle$ be its ASC-marking automaton for C, then $\rho$ covers C if and only if $\rho$ is also a successful run of $B_C$.

Proof

($\Rightarrow$) By the construction of $\mathcal{F}_C$, for every $F' \in \mathcal{F}_C$, there exists a $F \in \mathcal{F}$ such that $F' = F \cap C$. Since $F\cap C \ne \emptyset$ by Definition 6, $F' \cap C \ne \emptyset$. Moreover, since $\rho$ covers C, $\inf (\rho ) \supseteq C$. Therefore, $\inf (\rho )\cap F' \ne \emptyset$. That is, $\rho$ is also a successful run of $B_C$.

($\Leftarrow$) We will use contradition to show that $\rho$ covers C. Suppose not, and let $s \in C$ be an acceptance state not visited by $\rho$ infinitely often. Since $\rho$ is a successful run of $B_C$, by the construction of $\mathcal{F}_C$ we have that for every $F \in \mathcal{F}$, $(F\cap C) \cap \inf (\rho )\ne \emptyset$. Moveover, since $s \notin \inf (\rho )$, $(F\cap (C-\{ s \}) \cap \inf (\rho )\ne \emptyset$. Hence $F\cap (C-\{ s \}) \ne \emptyset$. Moreover, since C is a ASC of B, $C\subseteq \bigcup \mathcal{F}$ and hence $(C-\{ s \})\subset C \subseteq \mathcal{F}$. Therefore, contradicting to the lemma’s condition, C cannot be a ASC of B, which requires C to be a minimal set satisfying (i) $C \subseteq \bigcup \mathcal{F}$; and, (ii) $\forall F\in \mathcal{F}.(F\cap C) \ne \emptyset$. Therefore, the assumption could not be true, and hence $\rho$ covers C. $\square$

Algorithm 3 generates tests that weakly cover the ASC C. We construct an ASC-M-GBA $B_C$ in Algorithm 3, and then search for a successful run on the product of $B_C$ and the system model $K_m$. If such run $\tau$ exists, the test case $t = \mathcal{V}(\tau )$ is then added to ts and return as the singleton test suite. Since $t \in L(B_C)$ and $L(B_C) \subseteq L(B)$, $t \in L(B)$. By Definitions 10 and 7, since $\tau$ is a successful run of $B_C$ that weakly covers C on B, therefore t is a test case that weakly covers C on B.

Theorem 3

If the test suite ts returned by Algorithm 3 is not empty, then (i) $K_m$ passes ts and (ii) ts weakly covers all the ASCs of B.

Proof

(i) For each $t \in ts$, there is a related ASC C and $MC\_{{is}Empty}$ $(B_C, K_m))$ returns a successful run of the production of $B_C$ and $K_m$ such that $\mathcal{V}(\tau )=t$. Since any successful run of the production of $B_C$ and $K_m$ shall also be a trace of $K_m$, $\tau$ is also a trace of $K_m$. Therefore, $K_m$ shall pass t. That is, $K_m$ passes every test case in ts.

(ii) As shown in (i), for each $t \in ts$, there is a related ASC C and a successful run $\tau$ of the production of $B_C$ and $K_m$ such that $\mathcal{V}(\tau )=t$. We show that t weakly covers C, by showing that $\tau$ is also a successful run on B, and visits all states in C infinitely often.

By Definition 10, the only difference bewteen $B_C$ and B is that $B_C$ has the acceptance condition replaced with a set of singleton sets of states in C. By Definition 6, we have two conclusions. First, for each set $F_C \in \mathcal{F}_C$, there exists a set $F \in \mathcal{F}$ that $F_C \subseteq F$. Second, for each set $F \in \mathcal{F}$, there exists at least one state $s \in C$ that $s \in F$. Based on the two conclusions, we have $L(B_C) \subseteq L(B)$. Therefore $\tau$ must be a successful run on B as well, and it covers all states in C infinitely often. $\square$

5 ASC-Induced Property Refinement

ASC coverage metrics measure the conformance of a design against a formal requirement in Büchi automaton. Lacking of ASC coverage may be contributed either by bugs in the design, or by the deficiency of the requirement, or sometimes by both. We develop an algorithm that identifies the deficiency of the requirement and refines the requirement, using the information collected from test case generation (Algorithm 3).

We consider the refinement in terms of language inclusion, that is, if the language of an automaton $B'$ is a subset of that of B, we refer to $B'$ as a refinement of $B'$. Given a Kripke structure K representing a system with its requirement as GBA B, we develop an algorithm to refine B if not every ASC of B can be weakly covered w.r.t. K.

Given a Kripke structure $K_m$ as a system model and a GBA $B=\langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F}\rangle$ as its requirement, the basic steps of refining B w.r.t. B are described below:

• 1. Identify the set of ASCs $\mathcal{C}=\{ C_0, \ldots , C_n \}$ of B that are weakly covered w.r.t. $K_m$. $\mathcal{C}$ may be identified by Algorithm 3 during the test case generation;

• 2. Produce an automaton $B_{\mathcal{C}}= \langle P, S, S_0, \varDelta ,\mathcal{L}, \mathcal{F}_\mathcal{C} \rangle$, where $\mathcal{F}_\mathcal{C}= \{F \cap (\bigcup \mathcal{C})|F\in \mathcal{F}\}$

For example, consider a Büchi automaton B with an acceptance condition $\mathcal{F}= \{ F_0, F_1, F_2 \}$, in which $F_0 = \{ s_1, s_2, s_4 \}$, $F_1 = \{ s_2, s_3, s_4 \}$, $F_2 = \{ s_1, s_3, s_4 \}$. The ASCs for B would be $C_0 = \{ s_1, s_2 \}, C_1 = \{ s_2, s_3 \}, C_2 = \{ s_1, s_3 \}$ and $C_3 = \{ s_4 \}$. Assume that only $C_0$ and $C_2$ can be weakly covered w.r.t. a system K, we can then refine B to $B_\mathcal{C}$, where $B_\mathcal{C}$’s acceptance condition is $\{ \{ s_1, s_2 \}, \{ s_2, s_3 \}, \{ s_1, s_3 \} \}$.

The entire process of property refinement may be automated by extending the test generation algorithm, as described in Algorithm 4 Clearly $L(B_{\mathcal{C}}) \subseteq L(B)$, since the acceptance condition of $B_{\mathcal{C}}$ is a refinement of the acceptance condition of B. Moreover, by the construction of $\mathcal{F}_\mathcal{C}$, $B_\mathcal{C}$ contains all the ASCs of B that can be weakly covered by some tests passed by $K_m$. Theorem 4 states that the refined automaton, $B_\mathcal{C}$, is still satisfied by $K_m$. In other words, by refining B to $B_\mathcal{C}$, we obtain a “restricted” version of the property that more closely specifies a requirement for $K_m$.

Theorem 4

Given a GBA B and a Kripke structure $K_m$ such that $K_m \models B$, let $B_{\mathcal{C}}$ be the GBA returned by $TestGen\_RefineWC(B, K_m)$, then, (i) $L(B_{\mathcal{C}}) \subseteq L(B)$ and (ii) $K_m \models B_{\mathcal{C}}$.

Proof

(i) By the construction of $B_{\mathcal{C}}$, it differs from B only on its acceptance condition. Therefore, each run of $B_\mathcal{C}$ is also a run of B. Moreover, $B_\mathcal{C}$’s acceptance condition $\mathcal{F}_\mathcal{C}$ is also a refinement of B’s acceptance condition $\mathcal{F}$, that is, $\forall F'\in \mathcal{F}_\mathcal{C}.\exists F \in \mathcal{F}. (F' \subseteq F)$ and $\forall F \in \mathcal{F}. \exists F' \in \mathcal{F}_\mathcal{C}. (F' \subseteq F)$. It follows that each successful of $B_\mathcal{C}$ must also be a successful run of B, and hence $L(B_{\mathcal{C}}) \subseteq L(B)$. That is, $B_\mathcal{C}$ is a refinement of B in terms of language inclusion.

(ii) We then prove $K_m$ satisfies $B_{\mathcal{C}}$ by contradiction. Assume it is not the case, then there is a trace t of $K_m$ that does not induce a successful run of $B_{\mathcal{C}}$. Since $K_m \models B$. t induces at least one successful run of B, denoted as $\rho$. By the assumption $\rho$ could not be a successful run of $B_\mathcal{C}$. By Lemma 1, since $\rho \models B$, there has to be at least one ASC, denoted $C_\rho$, that is covered by $\rho$. By Lemma 3, $\rho$ is also a successful run of the ASC-marking automaton $B_{C_\rho }$. Therefore, $MC\_isEmpty(B_{C_\rho }, K_m)$ returns a successful run, and $C_\rho \in \mathcal{C}$.

Now we will show that for every $F' \in \mathcal{F}_\mathcal{C}$, $(C_\rho \cap F')\ne \emptyset$. By the construction of $\mathcal{F}_\mathcal{C}$, there exists at least one $F \in \mathcal{F}$ such that $F'=F\cap (\bigcup \mathcal{C})$. By Definition 6 $F \cap C_\rho \ne \emptyset$. Since $C_\rho \in \mathcal{C}$, $(C_\rho \cap F')\ne \emptyset$.

Finally, since $\rho$ covers $C_\rho$, $\inf (\rho ) superseteq C_\rho$. It follows that for every $F' \in \mathcal{F}_\mathcal{C}$, $(\inf (\rho ) \cap F')\ne \emptyset$. That is, $\rho$ is also a successful run of $B_\mathcal{C}$, which contradicts to our assumption. Therefore, $K_m \models B_{\mathcal{C}}$.$\square$

Note that the refined $B_{\mathcal{C}}$ returned by $TestGen\_RefineWC(B, K_m)$ is not the optimal refinement in terms of semantic equivalency. Consider the same example mentioned above: a Büchi automaton B with an acceptance condition $\mathcal{F}= \{ F_0, F_1, F_2 \}$, and its refinement $B_\mathcal{C}$, where $B_\mathcal{C}$’s acceptance condition is$\{ \{ s_1, s_2 \}, \{ s_2, s_3 \}, \{ s_1, s_3 \} \}$. Based on the given condition, only $C_0 = \{ s_1, s_2 \}$ and $C_2 = \{ s_1, s_3 \}$ can be weakly covered for B. However, a trace that covers $C_1 = \{ s_2, s_3 \}$ can also be accepted by $B_\mathcal{C}$, indicating that there is still space for further refinement.

We propose another alternative for ASC-induced property refinement, based directly upon the ASC-M-GBA. Algorithm 5 describes the refining process. Intuitively, Algorithm 5 collects every ASC-M-GBA generated while generating test cases towards the weak ASC coverage metric. The union of these ASC-M-GBA is a tighter refinement than $B_{\mathcal{C}}$ from Algorithm 4. Theorem 5 proves the legitimacy of this approach.

Theorem 5

Given a GBA B and a Kripke structure $K_m$ such that $K_m \models B$, let $S_{B_{ref}}$ be the set of GBA returned by $TestGen\_RefineWCAlt(B, K_m)$, then, (i) $S_{B_{ref}}$ is a refinement of B and (ii) for any trace t of $K_m$, there exists at least one $B' \in S_{B_{ref}}$ that $t \models B'$.

Proof

First, $S_{B_{ref}}$ includes each ASC-M-GBA that was built w.r.t one of the coverable ASCs. Based on Definition 10, we know that each ASC-M-GBA is a refinement of the original GBA B. Therefore it follows the union of these ASC-M-GBAs, as represented by $S_{B_{ref}}$ are also a refinement of B.

For the second part, we prove by contradiction. By the condition of Algorithm 5, $K_m$ satisfies B, i.e., every trace of $K_m$ can be accepted by B. Suppose there exists a trace t that none of the $B' \in \mathcal{S}_{B_{ref}}$ is able to accept. Since $t \models B$, there must exist at least one run $\rho$ that $t \vdash \rho$ and $\rho$ is a successful run on B. By Lemma 1, $\rho$ must have covered at least one ASC C of B. As a result, $MC\_isEmpty(B_C, K_m))$ in Algorithm 5 would not return empty, and $B_C$ would be included in $S_{B_{ref}}$, and $\rho$ is a successful run on $B_C$. Hence t can be accepted by $B_C \in S_{B_{ref}}$. This contradicts the previous assumption. $\square$

6 Experiments

6.1 Experiment Settings

To obtain a close-to-reality measurement, we select the subjects of our experiments from a diversified range of applications. The first subject is a model of the general Inter-ORB Protocol (GIOP) from the area of software engineering. GIOP is a key component of the Object Management Group (OMG)’s Common Object Request Broker Architecture (CORBA) specification [14]. The second model is a model of the Needham-Schroeder public key protocol from the area of computer security. The Needham-Schroeder public key protocol intends to authenticate two parties involving with a communication channel. Finally, our third subject is a model of a fuel system from the area of control system. The model is translated by Joseph [13] from a classic fuel system example in Stateflow [17].

Each model has a set of linear temporal properties that specify behavior requirement for the underlying syste. We selected the most representative property for each model to use in the experiments. For the GIOP model, the property models the behaviors of a recipient during communication. The LTL property for the Needham-Shroeder public-key protocol is a liveness property requiring that an initiator can only send messages after a responder is up and running. Finally, the properties for the fuel system checks that under abnormal conditions, the system’s fault tolerant mechanism functions properly.

Table 1 provides an overview of the models and properties, showing the size of both the models and properties in terms of the number of branches, ASCs, states/transitions of the LTL property equivalent Büchi automata, and atomic propositions in the properties. All of the information in Table 1 are of relevance to the diversified profiles of test criteria we used in the experiments for the comparison, in terms of the size of test suites generated.

Table 1 Overview of the models and properties used in the experiments

For performance comparison, we select several traditional as well as specification-based testing criteria. Based on the coverage for outcomes of a logic expression (c.f. [12]), branch coverage (BC) is one of the most commonly-used structural test criteria. We include both transition and state variations of strong coverage criteria (SC/strong, TC/strong) and weak coverage criteria (SC/weak, TC/weak) for Büchi automaton [21, 23, 31]. We also include a property-coverage criterion (PC) for Linear Temporal Logic (LTL) [22]. In our experiment, the performances of these criteria, and two ASC coverage criteria (ACC/stong and ACC/weak) are compared with each other.

6.2 Methodologies

To assess the performance of the proposed criteria, we perform an extended computational study using two different methodolgies: one uses the cross-coverage percentage as a measurement indicator, and the other adopts the fault-injection technique to analyse the sensitivity of the test cases towards manually injected errors.

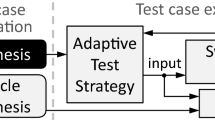
[Cross-coverage analysis] The cross-coverage measures how well a test suite generated for a test criterion covers another test criterion. The cross coverage is used as an indicator for the semantic strength of a test criterion with respect to others. In [28] we developed a tool to compare the effectiveness of test criteria that are used in model-checking-assisted test case generation. This experiment uses an extension of the tool that also supports the proposed ASC criteria. We use GOAL [25] to perform graph transformation required for building ASC-E-GBAs and ASC-M-GBAs. We use SPIN [10] as the underlying model checker to assist test case generation. Figure 3 shows the workflow of model-checking-assisted test case generation under ASC coverage criteria for Büchi automaton. More details of this procedure and an earlier computational study that covers more traditional testing criteria can be found in [29], with a different set of sample models.

Fig. 3

The workflow of model-checking-assisted test case generation under ASC coverage criteria for Büchi automaton

[Fault-injection-based sensitivity analysis] Fault-injection technique (c.f. [27]) is a classic technique used in software engineering for evaluating the sensitivity of a quality assurance tool towards injected faults. For this part, faults are systematically introduced into a system, and the effectiveness of a test suite is measured by its ability of catching these artificially injected errors. More faults being caught indicates that the underlying test criterion is more sensitive in detecting faults. The fault-injection process is achieved by mutating relational operators (e.g. changing $\ge$ to <) within the system model one operator at a time. The faulty model is then used to run a test suite generated for a test criterion. If the execution of the faulty model under a test case exhibit different behaviors from that of the original model, then the injected fault is caught by the test case. In another word, the test criterion is sensitive enough to detect the fault.

6.3 Experiment Results and Analysis

Table 2 shows the measurement of the test cases generated from the aforementioned variety of coverage criteria. We note that for the branch coverage (BC, or BC/All), tests were first specifically generated for every branch of the model. We used the coverage information to further select two more groups of test cases. We applied an Integer Linear Programming solver to obtain an optimal test suite that consists of the least number of test cases and covers the maximum number of branches that can be covered (BC/Opt.). This test suite represents the theoretical lower bound of the number of test cases needed for covering the system model under BC. The other test suite (BC/Grd.) is selected under a greedy algorithm. For example, if the first test case covers branches No. 2 and 3, then test cases for the second and third branches shall no longer be generated, and so on. The greedy algorithm represents the common practice of selecting a near-optimal test suite, to reduce the cost of test execution. “TS Size” in Table 2 indicates the number of test cases each test suite has, and “Max./Min./Avg. Length” specifies the length of the lasso-shaped test cases, i.e., the number of steps in the counterexample trace produced by the model checker. Finally, “Gen. Time” and “Exec. Time” represent the time it took to generate the traces and execute the test cases in milliseconds, respectively.

Table 2 Test suites overview

It shall be noted that for practical purpose, we enforce a time limit for the model checking process. This is due to the fact that SPIN suffers from “state space explosion problem” as an explicit state model checker [7]. SPIN may run out of resources (time and/or space) before reaching a conclusive result. Subsequently, we expect three possible outcomes of the model checking process: (1) returning with a counterexample trace, (2) returning with an answer that there is no counterexample or (3) terminating without returning value. For the third case, we count the time limit towards the generation time, which explains why some entries in Table 2 takes significantly longer time than the other criteria. A specific complication involved with ACC/strong is that, as we can see from Definition 9, the construction of ASC-E-GBA essentially produces several copies of the original automaton, and the number of copies equals the size of the ASC plus one. Hence, when there are more than two states in the ASC, the ASC-E-GBA becomes too large in size, as well as too complicated in its acceptance condition. In this case, the ASC-E-GBA is too complex to be handled by GOAL, which was unable to produce the equivalent never-claims for SPIN. For the purpose of simplicity, we treated this situation the same as when SPIN could not terminate with results in our experiment.

Table 3 Cross-coverage comparison results

Table 3 shows the results from the cross-coverage analysis. The number in each cell indicates the coverage of test cases generated for the criterion on the row w.r.t. the criterion on the column. Numbers on diagonal cells (marked with parentheses) represent the coverage of a test suite generated for the same criterion. A less-than perfect coverage on these diagonal cells indicates any of the following causes: (1) it indicates potential deficiency of a model and/or a requirement or (2) the model checker could not terminate within the time limit. For instance, the test suite of the fuel system model for ACC/weak may only reach 67 % coverage upon all the ASCs because SPIN was unable to return with a conclusive answer. As for ACC/strong for the same model, the same percentage was caused by GOAL unable to produce the equivalent never-claims for SPIN due to the ASC-E-GBA being too complex.

The results show that our proposed ASC coverage criteria, especially the strong variants, have solid and competent performances. They perform on par with the other Büchi automaton based criteria, and fall only barely behind branch coverage criterion. It shall be noted that the test suite generated for the branch coverage criterion is much larger than those generated for the property-based test criteria, including our ASC criteria, indicating that the property-based criteria can potentially make testing more effective by producing smaller and more focused test suites, as shown in Table 2. A smaller test suite, along with a good performance in cross-coverage analysis, makes the new criteria competitive alternatives to a white-box coverage criterion such as the branch coverage criterion.

It shall also be noted that the test suites for ASC coverage criteria, although competent, did not achieve full branch coverage. This is because we only use one temporal property for each model, and the property does not cover all the functional aspects of the models. For instance, the property for the GIOP model specifies the recipient’s behavior at “waiting” or “receiving” modes, it does not concern other modes of operations. Therefore, the generated test suite skips some code segments, which leads to a less-than perfect branch coverage.

This observation leads to an important feature of property-based test criteria, including our ASC coverage criteria. That is, the performance of these criteria are heavily influenced by the quality of underlying requirement. A thorough requirement touching more aspects of a model may result in a test suite with better quality. In Sect. 5 we capitalized this observation via our ASC-induced property refinement. Alternatively, a more complete set of temporal properties that address multiple aspects of a model could also greatly improve the performance on this part.

Last but not least, the results above also establish that ASC coverage criteria correlate nicely with the state and transition coverage criteria. The strong variant performs exactly the same as the state and transition coverage, while the weak variant exhibits the results that are somewhat in between. Superfluously, an ASC being covered indicates that the states and transitions on the path are also covered.

Such correlation proves that we are able to strip the syntax dependency away even more thoroughly, compared with the syntax dependency that still exists for the property coverage criterion in [22]. At the same time, an ASC is also not merely an extension of states and transitions. The traces covering the ASC need to satisfy the “infinite visit” condition upon the acceptance states. Hence, it comes one step closer to the semantic essence of the temporal properties. In some cases, this makes the ASC more challenging to cover. When it does happen, such as in the case of ACC/weak for the fuel system model, it only has 55 % of coverage over the branches, lower than both SC/weak and TC/weak. On the other hand, both ACC/strong and ACC/weak tend to yield smaller size of test suites, while simultaneously have a better grasp on the semantic essence. This also means the refinement process described in Sect. 5 could result in finer tuned refined GBA that other criteria are unable to produce.

Table 4 Injected faults detection results

Table 4 shows the results of fault-injection-based sensitivity analysis. Faults are injected by mutating relational operators in the models. The count of such operators are specified in the parenthesis along side the name of the model at the top row of the table. The rest of the Table 4 lists out the percentage of the faults that were detected by the test suites we generated based on the different test coverage criteria.

We define a Sensitivity Adjusted Cost (SAC) for cost/benefit analysis:

$$SAC = \frac{\text {(Total Length of the Test Suite)}}{\text {(Percentage of Detected Faults)}}$$

Note that the cost of executing a test suite is in general proportional to the size of the test suite. The SAC essentially indicates the adjusted cost of test (execution) w.r.t. the sensitivity of the underlying test criterion, and the lower the cost is the better.

In all three models, the property-based criteria, including our ASC based coverage criteria, are able to detect a good portion of the injected faults. Comparing with branch coverage, it is to be expected that BC would have the best detection rate due to its code-based nature. For the fuel system model, however, some of the test cases are excessively long that they are not executable (the longest one exceeding 50,000, see Table 2). Both the full and greedy test suites consequently can only detect two thirds of the faults, while other test suites catch up or even surpass it with fewer and shorter test cases, as indicated by the SAC values.

While comparing with other property-based criteria (PC, SC and TC), ACC-generated test suites benefit from their smaller sizes, and their SAC values are either the lowest or very close. In particular, ACC out-performs both SC and TC on the GIOP model with both higher detection rate and much lower SAC values. While on the other two models, ACC also at least performs on par with SC and TC with competitive SAC values. It shows that among the GBA based criteria, ACC also demonstrates stronger performances.

In all three models, strong variants of Büchi-automaton-based coverage criteria outperform the related weak variants, and by a large margin in some cases (e.g. Needham Protocol). In theory the strong variants subsume their counterparts in weak variants. In practice, the strong variants of the criteria unveil more subtle features of temporal requirements, often resulting in longer test cases. These longer test cases help find faults deeply buried in models.

7 Conclusions

We proposed a specification-based approach for testing reactive systems with requirement expressed in Büchi automata. At the core of our approach are two variants of property coverage metrics and criteria measuring how well a test suite covers the acceptance condition of a Büchi automaton. By covering the acceptance condition, which is the hallmark of a Büchi automaton defining infinite words, these metrics relate test cases to temporal patterns of infinite executions. This makes testing more effective in debugging infinite executions of the system. To provide a complete tool chain for requirement-based testing with Büchi automaton, we developed a test case generation algorithm for the proposed criteria. The algorithm utilizes the counterexample generation capability of an off-the-shelf model checker to automate the test case generation.

It shall be noted that, although specification-based testing with automata has been studied before (c.f. [4]), the specification concerned in most of these previous works is a system design modeled in a finite automaton. In comparison, we focus on behavioral requirements modeled in Büchi automaton. Moreover, existing approaches for specification-based testing for reactive systems [18, 21, 23, 24, 31] focus on the finite prefixes of its infinite executions. In contrast, our approach works with temporal patterns of its infinite executions. All of these make our approach more advanced and effective in testing the temporal patterns of a reactive system.

Our approach tests the conformance of a reactive system to its requirement in Büchi automaton. It may be used for revealing the deficiency of the system as well as its requirement. We discussed how our approach may be used to debug and even refine the requirement, using the information from the model-checking-assisted test case generation. We proposed a property-refinement algorithm that automated the process of property refinement.

To assess the effectiveness of our approach, we carried out an extended computational study using two methodologies: a cross-coverage measurement among multiple test criteria, and a fault-injection-based sensitivity analysis. Subjects for study are selected from a diversified range of fields. First, we use a cross-coverage metric to measure relative effectiveness of test criteria against each other. Then, we use fault-injection technique to measure how well test suites generated from the proposed criteria can detect faults planted in models. The experimental results indicate that our criteria exhibit competent performance over existing test criteria. These criteria are particularly effective at reducing the size of test suites, making testing more targeted and efficient. For the future work, we want to extend our approach to more complex requirements, such as those in $\mu$-calculus.